Fractional derivative-based normalized viscoelastic model of strain-hardening clays

Introduction: The stress-strain relationship of clays characterized by strain hardening exhibits varying curves under different confining pressures and dry densities.

Methods: Considering the viscoelastic properties of clays, a normalized viscoelastic model of strain-hardening clay was established based on fractional derivatives, and normalization factors were proposed.

Results: The experimental results showed that the stress-strain relationship of the clay was strain hardening. It shows that Chengdu clay has better normalization conditions. Furthermore, the normalized analysis of this clay through the viscoelastic normalization model revealed that the straight line of normalized data displayed a goodness-of-fit of over 0.98. The obtained values were consistent with experimental results, suggesting the reasonability of the normalized strain-hardening parameters and elastic moduli.

Discussion: In addition, the superiority of the developed model was verified by testing the strain-hardening clays in Wuhan, China and Bangkok, Thailand. After analyzing the strain-hardening parameters and normalization factors of our model, it was found that the slope of the normalized line can accurately reflect the strain-hardening ability of the clay. These findings demonstrated that the proposed normalization factor is preferred for a normalized viscoelastic model. It shows that the model proposed in this paper has clearer physical meaning and advancement.

1 Introduction

Clays significantly influence human activities with their wide distribution worldwide (Malehmir et al., 2013; Biswas and Krishna, 2018; Chen et al., 2019; Wang and Chen, 2019; Liu et al., 2020). The physicomechanical properties of clays depend on the interplay of factors such as mineral composition, gradation, structure, density, water content, stress characteristics, and temperature, exhibiting complex mechanical properties (Sun et al., 2015; Liu et al., 2016; Zhang et al., 2017; Shan et al., 2020; Chen et al., 2021; Middelhoff et al., 2021; Bai et al., 2023a; Bai et al., 2023b). Several studies have investigated the stress-strain relationships of clays. For example, Shang et al. (2015) measured the stress-strain characteristics of red clay in China under different consolidation stresses through undrained triaxial compression tests. Under high stress, a significant decrease was observed in the stress-strain curves and shear strength of this clay after reaching peak values. Adachi et al. (1995) probed into the mechanical properties of clay in Osaka, Japan in undrained triaxial tests. According to their findings, the stress-strain relationship of Osaka clay exhibited strain-softening characteristics, and strain rates exerted obvious effects on the stress-strain relationship of lightly consolidated clays. Gens (1982) assessed the mechanical properties of Lower Crorner Till based on triaxial tests and determined the total stress, effective stress strength, and stress-strain characteristics under different triaxial test conditions. The stress-strain and strength properties of two clays, considering different water contents under triaxial tensile and compression loadings, were examined by Ajaz and Parry (1975). Furthermore, Cai et al. (2017) evaluated the mechanical properties of soft clay under traffic loading and reported that traffic loads significantly affected the deformation of soft clay. Graham et al. (1983) considered the influence of time on the stress-strain relationship and strength of clays and summarized that clay plasticity and stress history were not responsible for the impact of strain rates on the stress-strain relationship and undrained shear strength. By investigating the triaxial compression and tensile stress-strain relationship of saturated remolded clay under various stress paths, Mitachi and Kitago (1979) discovered that stress paths and conditions markedly impacted the stress-strain relationship of this clay and proposed a new method for predicting clay stress-strain relationships.

Clay is a typical soil with pronounced viscoelasticity. Hammouda and Mihoubi (2014) compared the elasticity and viscoelastic mechanical properties of clays under dry conditions and observed that the actual mechanical properties of clays highly conformed to viscoelastic mechanical properties. Liu et al. (2015) introduced a generalized Kelvin-Voigt model to analyze the viscoelastic properties of marine clay. They reported that this clay possessed good viscoelasticity, significantly affected by the degree of consolidation. Based on the influence law of three pure clay minerals (kaolinite, montmorillonite, and illite) on viscoelasticity, Ni and Huang (2020) discovered that mineral composition had the maximum influence on the viscoelasticity of clays. Specifically, montmorillonite exerted a greater effect on clay viscoelasticity than the other two minerals. Studies also analyzed the viscoelastic properties of clays, considering their rheological properties (Li and Yang, 2018; Ren et al., 2021).

Strain hardening of clay is an important indicator of stress-strain relationships and viscoelastic properties. Strain-hardening curves are influenced by confining pressure, dry density, etc., typically constituting a family of similar curves. On this basis, a normalized model of strain-hardening clay was proposed to describe the strain-hardening relationship. Vucetic (1990) pointed out that normalized analysis of stress-strain curves could be achieved using effective consolidation stress as a normalization factor in their study on the undrained stress-strain characteristics of marine clay under irregular cyclic simple shear loading. Stróžyk and Tankiewicz (2016) studied the stress-strain relationship and elastic modulus E_u50 of stiff clay and proposed an improved normalized model. Gurtug (2011) established two normalized models to predict the compressive behavior of high plastic clay, considering the void ratio and consolidation pressure. The results showed that both models had a good predictive effect. By investigating the mechanical behavior of normally consolidated and over-consolidated clays under cyclic loading, Vucetic (1988) found that clay shows good normalization behavior under consolidation stress and proposed corresponding normalization methods. Lyu et al. (2020) explored the influencing pattern of structure and depth on the stress-strain relationship of red clay and devised a new normalization method to determine the mechanical law of clays.

Despite diverse perspectives from current studies delving into stress-strain relationships and normalization methods of clays, a research gap on the normalized model characterizing the stress-strain relationship of clays considering viscoelasticity remains. To address this research gap, we developed a normalized viscoelastic model of strain-hardening clay, and the rationality and applicability of this model were analyzed utilizing clays from Chengdu and Wuhan in China and Bangkok in Thailand under varying dry densities and confining pressures. It is found that the normalized linear slope can accurately describe the strain-hardening ability of the clay, conferring a preferred alternative for normalization factors. This paper provides a novel reference for exploring the normalized viscoelastic model of clays, effectively promoting research on the mechanical properties of clays.

2 Stress-strain relationship of the clay

In traditional triaxial compression shear tests, stress-strain relationships of clays under deviatoric shear mainly include strain-hardening, strain-softening, and ideal elastoplastic relationships (1963). The strain-hardening relationship curves exhibit identical trends under different confining pressures, and normalization factors can be employed to unify these curves, allowing for a simplified relationship. Common normalized models for strain hardening of clays are derived from the hyperbolic strain-hardening model by Konder [30], as expressed in Eq. 1.

${\sigma }_1-{\sigma }_3=\frac{{\epsilon }_1}{a+b{\epsilon }_1}(1)$

where a and b represent the hyperbolic parameters, σ₁ and σ₃ are the axial stress and confining pressure of the triaxial test, respectively, and ε₁ stands for the axial shear strain.

According to the property of the hyperbolic strain-hardening relationship, common normalization factors and conditions are listed in Table 1.

TABLE 1

TABLE 1. Normalization factors and conditions for Konder hyperbolic strain-hardening curves.

Although normalization of strain-hardening curves using the Konder hyperbolic model provides a good fitting effect, it has shortcomings such as lacking physical significance, excess restrictions on normalization conditions, and poor performance in reflecting the influence of stress history.

Given the memory effect of fractional calculus on the stress history of materials, it is widely applied to describe the mechanical properties of viscoelastic materials. In this paper, fractional calculus was introduced to reveal the viscoelasticity of clay featuring a strain-hardening relationship.

According to the Riemann-Liouville fractional calculus theory, the integral of the α-order function f(t) is defined as in Eq. 2.

$\frac{{\mathrm{d}}^{-\alpha }f\left(t\right)}{\mathrm{d}{t}^{-\alpha }}=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{{\int }_a^t\left(t-x\right)}^{\alpha -1}f\left(x\right)dx(2)$

Fractional calculus is expressed as in Eq. 5.

${}_{t0}{D}_t^{\alpha }f\left(t\right)=\frac{{\mathrm{d}}^{\alpha }f\left(t\right)}{\mathrm{d}{t}^{\alpha }}=\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}\left[D^{-\left(n-\alpha \right)}f\left(t\right)\right](3)$

where α > 0 indicates a fractional order, $\mathrm{\Gamma }\left(*\right)$ is a Gamma function defined as $\text{Re}\left(z\right)>0$ $\mathrm{\Gamma }\left(\tau \right)={\int }_0^{\infty }{e}^{-x}{t}^{\tau -1}dx$.

The viscoelastic model for strain-hardening of clay is shown in Eq. 4.

${\sigma }_1\left(t\right)=E_0{D}^{\alpha }{\epsilon }_1\left(t\right)(4)$

where E indicates the elastic modulus of clay, α reflects the viscoelasticity and strain-hardening ability of clay, and 0<α < 1.

In triaxial tests, constant strain rate loading is typically used, and the strain-time relationship is described as follows:

$t=\frac{{\epsilon }_1}{v_0}(5)$

where v₀ denotes the applied strain rate in triaxial compression tests.

Substituting Eq. 5 into Eq. 4, a clay viscoelastic model in triaxial tests can be derived in Eq. 6.

${\sigma }_1-{\sigma }_3=E_0{v}_0^{\alpha }\frac{{{\epsilon }_1}^{\left(1-\alpha \right)}}{\mathrm{\Gamma }\left(2-\alpha \right)}(6)$

3 Normalized viscoelastic model

3.1 Normalized model

To establish a normalized model of strain-hardening clay, the logarithms of Eq. 6 are taken from both sides, and the outputs are shown in Eq. 7.

$\ln \left({\sigma }_1-{\sigma }_3\right)=A\times \ln \left({\epsilon }_1\right)+B(7)$

where A and B are model parameters, calculated according to Eq. 8.

$\left\{\begin{array}{l}A=1-\alpha \\ B=\ln \left[\frac{E_0{v_0}^{\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\right]\end{array}\right.(8)$

N is defined as the normalization factor of the model and introduced into Eq. 7 can be obtained as in Eq. 9.

$N\times \ln \left({\sigma }_1-{\sigma }_3\right)=A_N\times \ln \left({\epsilon }_1\right)+B_N(9)$

where A _N and B _N are illustrated in Eq. 10.

$\left\{\begin{array}{l}{A}_N=N\left(1-\alpha \right)\\ B_N=N\times \ln \left[\frac{E_0{v_0}^{\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\right]\end{array}\right.(10)$

A_N and B_N are taken as normalization constants when analyzing the normalized strain-hardening curves.

3.2 Normalization factors

According to Eq. 10, the normalization conditions for the viscoelastic model is that N is inversely proportional to both (1-α) and ln [E₀v₀^α/Г(2-α)]. The normalization factor of clay viscoelasticity can be expressed by Eq. 11.

$N=\frac{1}{\ln \left[{\left({\sigma }_1-{\sigma }_3\right)}_f\right]}(11)$

where (σ₁-σ₃)_f is the deviatoric stress-induced damage in triaxial tests or the deviatoric stress applied to clays under different strain conditions, depending on the needs of the normalized analysis.

Given the plane strain conditions of the triaxial shear test, when (σ₁-σ₃)_f is determined by the deviatoric stress, (σ₁-σ₃)_f can be calculated as Eq. 12.

${\left({\sigma }_1-{\sigma }_3\right)}_f=\left(A_F-1\right){\sigma }_3+B_F(12)$

where A_F and B_F are the criterion parameters of soil failure strength.

After substituting Eq. 11 into Eq. 9, we obtain the clay normalized viscoelastic model, as shown in Eq. 13, where A_N and B_N are illustrated in Eq. 14.

$\frac{\ln \left({\sigma }_1-{\sigma }_3\right)}{\ln \left[{\left({\sigma }_1-{\sigma }_3\right)}_f\right]}=A_N\times \ln \left({\epsilon }_1\right)+B_N(13)$

$\left\{\begin{array}{l}{A}_N=\frac{\left(1-\alpha \right)}{\ln \left[{\left({\sigma }_1-{\sigma }_3\right)}_f\right]}\\ B_N=\ln \left[\frac{E_0{v_0}^{\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\right]/\ln \left[{\left({\sigma }_1-{\sigma }_3\right)}_f\right]\end{array}\right.(14)$

4 Triaxial tests

4.1 Basic properties of the clay

The clay from the construction site in Dayun Village, Chengdu was utilized. Its basic physical properties are shown in Table 2.

TABLE 2

TABLE 2. Basic physical properties of the clay in Dayun Village, Chengdu.

4.2 Test methods

The triaxial shear tests under axisymmetric test conditions are performed: 1) Specimen preparation. The specimens were prepared at 76 mm in height and 38 mm in diameter. Dry densities were determined at 1.60 g cm⁻³, 1.64 g cm⁻³, and 1.68 g cm⁻³, and water content was 23%. Since the samples are fine-grained clays that cannot be easily saturated, specimen 2d (2 days) was saturated by water filling under vacuum conditions, followed by backpressure saturation using GDS. 2) Consolidation. Confining pressure of 100 kPa was applied to the loaded samples at 0.1 kPa/min. After that, the specimens started to consolidate, and this process was completed when the pore water pressures dropped to backpressures, and the corresponding history curve became stable. 3) Consolidated undrained (CU) triaxial shear tests. CU triaxial shear tests were conducted with confining pressures under different dry densities of 100 kPa, 200 kPa, and 300 kPa, a maximum shear strain of 15%, and a shear rate of 0.01%/min.

4.3 Experimental results

Figure 1 shows the deviator stress-strain curves of the clay in Dayun Village. It can be seen that under tested confining pressures, the stress-strain relationship curves of the clay belong to strain hardening, and the deviatoric stress increases with the increasing strain. When the confining pressure elevates, the deviatoric stress upgrades noticeably under the same strain conditions. The cohesive forces and internal friction angles of Chengdu clay under different dry densities are described in Table 3.

FIGURE 1

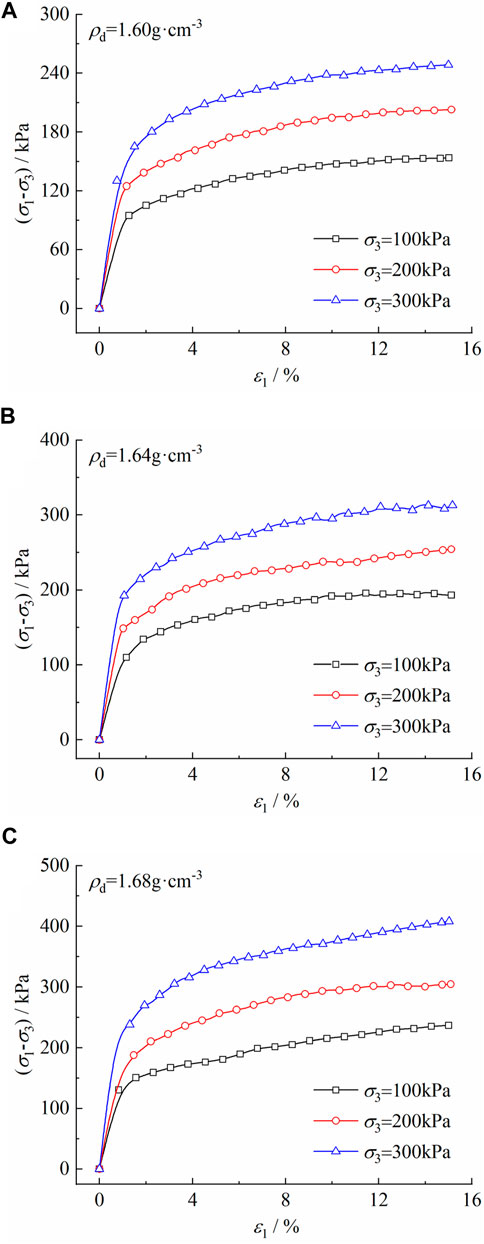
FIGURE 1. Deviator stress-strain curves for the Chengdu clay: (A) ρ_d = 1.60 g cm^-3; (B) ρ_d = 1.64 g cm^-3; (C) ρ_d = 1.68 g cm^-3.

TABLE 3

TABLE 3. Cohesive forces and internal friction angles of Chengdu clay at different dry densities.

5 Analysis of normalized properties of the strain-hardening relationship

5.1 Normalized analysis of Chengdu clay

The soil failure strength was determined following the Mohr-Coulomb failure criterion, and the normalized parameters A_F and B_F are expressed in Eq. 15.

$\left\{\begin{array}{l}{A}_F=\frac{1+\sin \phi }{1-\sin \phi }\\ B_F=\frac{2c\cos \phi }{1-\sin \phi }\end{array}\right.(15)$

From Eqs 12, 15, (σ₁-σ₃)_f can be obtained, as expressed by Eq. 16.

${\left({\sigma }_1-{\sigma }_3\right)}_f=\frac{2c\cos \phi +2{\sigma }_3\sin \phi }{1-\sin \phi }(16)$

The strain-hardening curves of the clay under dry densities and confining pressures in Figure 1 were normalized and analyzed according to Eqs 7–16, and the results are summarized in Figure 2.

FIGURE 2

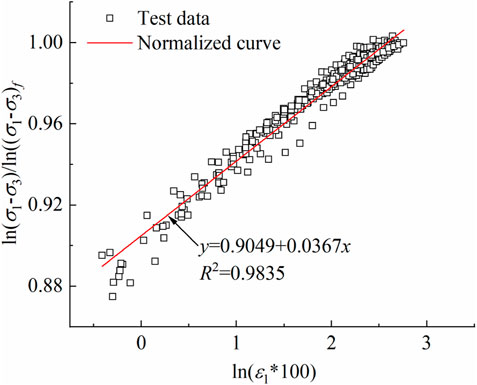
FIGURE 2. Normalized curves of the Chengdu clay under various dry densities and confining pressures.

The viscoelastic parameters E₀ and α of the clay under different dry densities and confining pressures are calculated according to the fitting results in Figure 2 and Eq. 14, and the calculations are given in Table 4.

TABLE 4

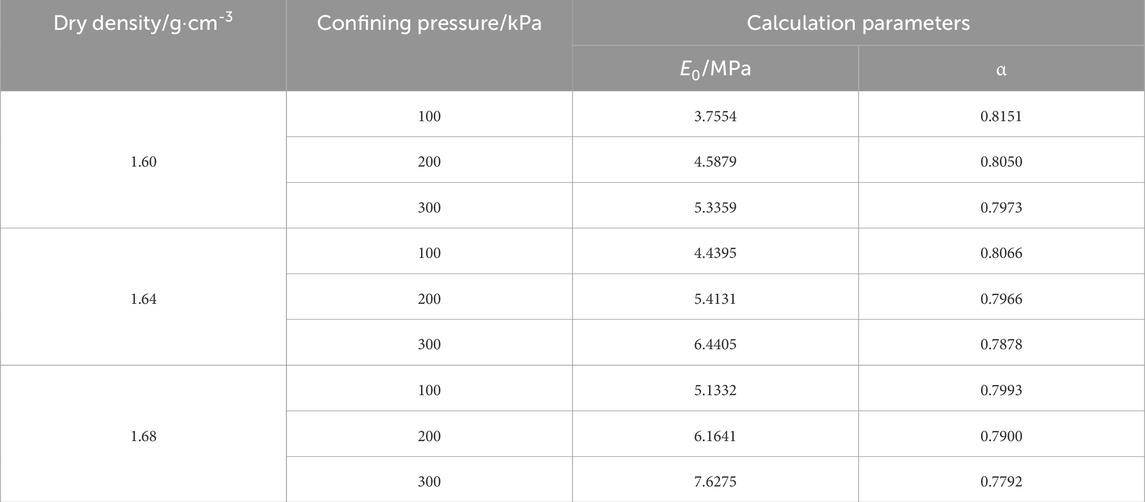
TABLE 4. Calculations of viscoelastic parameters with various dry densities and confining pressures.

Under normalization conditions, the elastic modulus E₀ of Chengdu clay increases with the elevated dry densities and confining pressures. The strain-hardening index α decreases with the increment in dry densities and confining pressures, demonstrating that the soil-hardening ability is enhanced under the influence of dry density and confining pressure. These findings indicate that the viscoelastic mechanical parameters solved under normalization conditions are scientifically reasonable.

The resulting values from tests and the normalized viscoelastic model were compared, and the results are depicted in Figure 3.

FIGURE 3

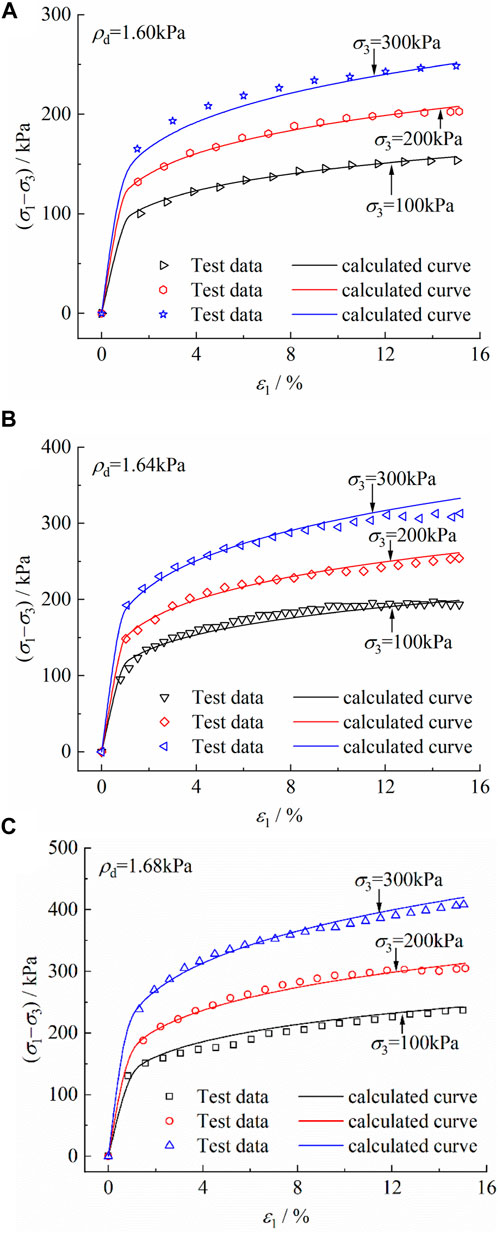
FIGURE 3. Correlation between experimental and calculated values for the Chengdu clay:(A) ρ_d = 1.60 g cm^-3; (B) ρ_d = 1.64 g cm^-3; (C) ρ_d = 1.68 g cm^-3.

The compared values are in good agreement. The computed results can accurately describe the whole process of strain hardening of the clay under different dry density and confinement pressure conditions, indicating the reasonability of the present normalized model.

5.2 Normalized analyses of clays in Wuhan, China and Bangkok, Thailand

To validate the applicability of the proposed model, the strain-hardening curves of clays in Wuhan (Zhang et al., 2006)and Bangkok (Surarak et al., 2012) were normalized, and (σ₁-σ₃)_f represents the deviatoric stress under the maximum strain conditions. The basic physical properties of the two kinds of clay are shown in Table 2 and Table 3. The stress-strain curves for the two clays are plotted in Figure 4. And the relationship curves between the normalized factor and confining pressure of Wuhan clay and Bangkok clay are plotted in Figure 5.

FIGURE 4

FIGURE 4. Deviator stress-strain curves: (A) Wuhan clay; (B) Bangkok clay.

FIGURE 5

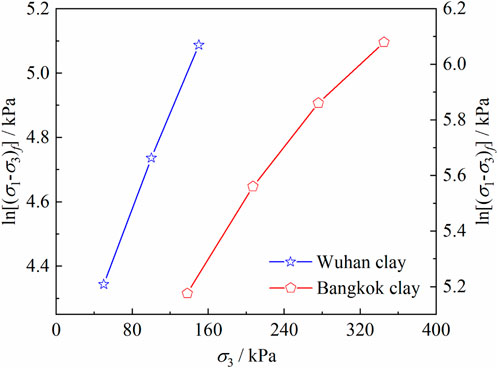
FIGURE 5. The relationship curves between the normalized factor and confining pressure of Wuhan clay and Bangkok clay.

The two clays are characterized by strain hardening. Normalized analyses were conducted on their strain-hardening curves according to Eqs 7–14, and the outcomes are illustrated in Figure 6.

FIGURE 6

FIGURE 6. Normalized curves: (A) Wuhan clay; (B) Bangkok clay.

Referring to the normalized results, the experimental values for strain hardening of the two clays were compared with the calculated values of the normalized viscoelastic model. The comparison results are described in Figure 7.

FIGURE 7

FIGURE 7. Correlation between experimental and calculated values: (A) Wuhan clay; (B) Bangkok clay.

The test values of both strain-hardening clays are highly consistent with the calculated ones of the proposed model, indicating that this model can accurately describe the clay strain-hardening law. In summary, the present normalized viscoelastic model is applicable to strain-hardening clay.

6 Discussion

6.1 Strain-hardening parameter α

From Eq. 6 and Table 3, α decreases with the increasing confining pressure and dry density, indicating that strain hardening is correlated to both factors. In addition, α reflects the strain-hardening ability of the clay, which is also enhanced with the elevation of the two mentioned variables.

The normalized viscoelastic curves under different α values are shown in Figure 8. Curve families under various α rotate in the stress-strain plane with ln (ε₁) = 0 as the center under normalization conditions. When ln (ε₁) < 0, ln (σ₁-σ₃)/ln (σ₁-σ₃)_f increases with the increasing α; otherwise, it decreases with the rising α. Despite the growth at ln (ε₁) < 0 (ε₁ < 1%), the strain-hardening ability of clays is mainly observed after ε₁ > 1%. It can be concluded that α can reflect the strain-hardening ability of clay when the strain is greater than 1%. Within the total strain range, the linear slope of the normalized viscoelastic model decreases with the increasing α, indicating no effects on strain curves. The slope of the straight line can reflect the strain-hardening ability of clay with relatively high accuracy.

FIGURE 8

FIGURE 8. Normalized lines with various strain-hardening parameters.

6.2 Normalization factors

Taking Chengdu clay, Wuhan clay and Bangkok clay as an example, ln (σ₃), ln (σ₁-σ₃)_f, and ln (σ_m) were selected as normalization factors to analyze their influences on the model, and the results are presented in Figure 9. In the case of ln (σ₃), the normalized data for clay of Chengdu and Wuhan are highly discrete. In the case of ln (σ_m), the results of the experimental data of Chengdu clay are poor, but the results of the experimental data of Wuhan clay and Bangkok clay are good. In the case of ln (σ₁-σ₃)_f, the normalization of test data of three kinds of clay is the best. Based on the above analysis, ln (σ₁-σ₃)_f is recommended as the preferred normalization factor for normalized viscoelastic models of clays.

FIGURE 9

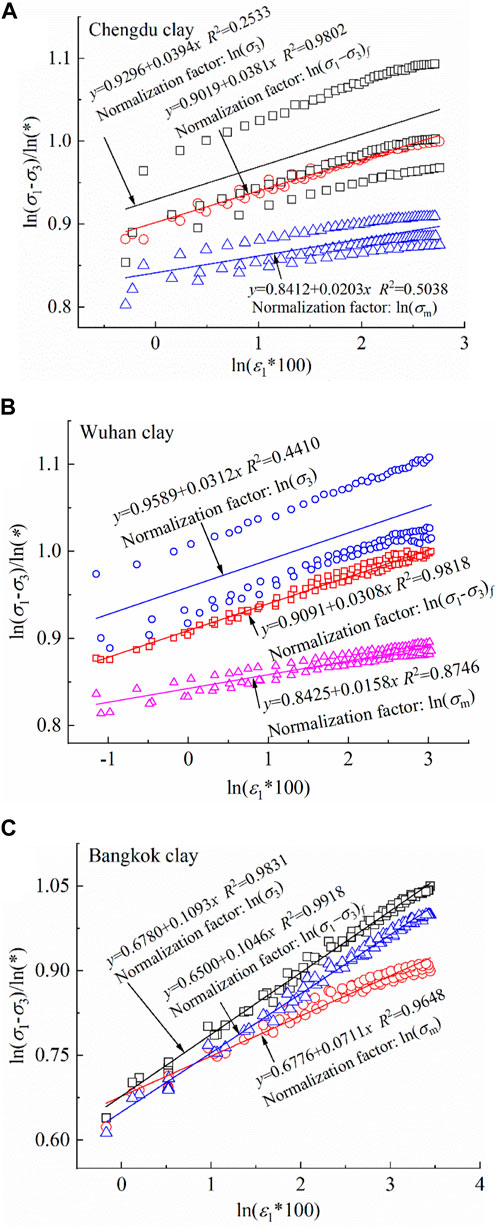
FIGURE 9. Normalized fitting curves with different normalization factors (ln (^*) represents the normalization factor in figures): (A) Chengdu clay; (B)Wuhan clay; (C) Bangkok clay.

7 Conclusion

In this paper, a normalized viscoelastic model for clays under strain-hardening conditions was proposed to investigate the viscoelastic properties and strain-hardening relationships. The main findings are summarized as follows.

(1) A viscoelastic model for strain-hardening clays in triaxial shear tests was established according to fractional calculus theory. Additionally, ln (σ₁-σ₃)_f was selected as the normalization factor to construct a normalized viscoelastic model.

(2) The viscoelastic normalized model is used to normalize the strain hardening test data of clay in different sites. It is found that the fractional derivative viscoelastic normalized model proposed in this paper can accurately describe the strain hardening relationship of clay, indicating that the model proposed in this paper is scientific, applicable and superior.

(3) Through the discussion of strain hardening parameter α and normalization factor of clay, it is found that the normalized linear slope can describe the strain hardening ability of clay more accurately. ln (σ₁-σ₃) f is the preferred normalization factor of clay viscoelastic normalization model. It further shows that the model proposed in this paper has clearer physical meaning and advancement.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YT: Conceptualization, Funding acquisition, Methodology, Writing–original draft. PW: Funding acquisition, Methodology, Resources, Supervision, Writing–original draft. PR: Data curation, Funding acquisition, Resources, Writing–review and editing. HZ: Methodology, Writing–review and editing, Resources.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was financially supported by SichuanHuaxiGroup Co., Ltd. (Nos HXKX 2020/021, HXKX 2019/015, and HXKX 2019/019), and the Open Fund of Sichuan Engineering Research Center for Mechanical Properties and Engineering Technology of Unsaturated Soils (No. SC-FBHT2022-04).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adachi, T., Oka, F., Hirata, T., Hashimoto, T., Nagaya, J., Mimura, M., et al. (1995). Stress-strain behavior and yielding characteristics of Eastern Osaka clay. Soils Found. 35 (3), 1–13. doi:10.3208/sandf.35.1

CrossRef Full Text | Google Scholar

Ajaz, A., and Parry, R.-H.-G. (1975). Stress–strain behaviour of two compacted clays in tension and compression. Geotechnique 25 (3), 495–512. doi:10.1680/geot.1975.25.3.495

CrossRef Full Text | Google Scholar

Bai, B., Bai, F., Nie, Q., and Jia, X. (2023a). A high-strength red mud–fly ash geopolymer and the implications of curing temperature. Powder Technol. 416, 118242. doi:10.1016/j.powtec.2023.118242

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Yang, G., Zou, W., and Yuan, W. (2023b). The constitutive behavior and dissociation effect of hydrate-bearing sediment within a granular thermodynamic framework. Ocean. Eng. 268, 113408. doi:10.1016/j.oceaneng.2022.113408

CrossRef Full Text | Google Scholar

Biswas, A., and Krishna, A.-M. (2018). Behaviour of geocell–geogrid reinforced foundations on clay subgrades of varying strengths. Int. J. Phys. Model. Geotechnics 18 (6), 301–314. doi:10.1680/jphmg.17.00013

CrossRef Full Text | Google Scholar

Cai, Y.-Q., Guo, L., Jardine, R.-J., Yang, Z.-X., and Wang, J. (2017). Stress–strain response of soft clay to traffic loading. Géotechnique 67 (5), 446–451. doi:10.1680/jgeot.15.p.224

CrossRef Full Text | Google Scholar

Chen, Y., Li, B., Xu, Y., and Xu, J. (2019). Field study on the soil water characteristics of shallow layers on red clay slopes and its application in stability analysis. Arabian J. Sci. Eng. 44, 5107–5116. doi:10.1007/s13369-018-03716-3

CrossRef Full Text | Google Scholar

Chen, Z., Zhou, H., Ye, F., Liu, B., and Fu, W. (2021). The characteristics, induced factors, and formation mechanism of the 2018 Baige landslide in Jinsha River, Southwest China. Catena 203, 105337. doi:10.1016/j.catena.2021.105337

CrossRef Full Text | Google Scholar

Gens, A. (1982). Stress-strain and strength characteristics of a low plasticity clay. London: University of London.

Google Scholar

Graham, J., Crooks, J.-H.-A., and Bell, A.-L. (1983). Time effects on the stress-strain behaviour of natural soft clays. Géotechnique 33 (3), 327–340. doi:10.1680/geot.1983.33.3.327

CrossRef Full Text | Google Scholar

Gurtug, Y. (2011). Prediction of the compressibility behavior of highly plastic clays under high stresses. Appl. clay Sci. 51 (3), 295–299. doi:10.1016/j.clay.2010.12.003

CrossRef Full Text | Google Scholar

Hammouda, I., and Mihoubi, D. (2014). Modelling of drying induced stress of clay: elastic and viscoelastic behaviours. Mech. Time-Dependent Mater. 18, 97–111. doi:10.1007/s11043-013-9216-2

CrossRef Full Text | Google Scholar

Kamoun, J., and Bouassida, M. (2018). Creep behavior of unsaturated cohesive soils subjected to various stress levels. Arabian J. Geosciences 11 (4), 77. doi:10.1007/s12517-018-3399-4

CrossRef Full Text | Google Scholar

Kondner, R.-L. (1963). Hyperbolic stress-strain response: cohesive soils. J. Soil Mech. Found. Div. 89 (1), 115–143. doi:10.1061/jsfeaq.0000479

CrossRef Full Text | Google Scholar

Li, J., and Yang, Y. (2018). Matric suction creep characteristics of reticulated red clay. KSCE J. Civ. Eng. 22, 3837–3842. doi:10.1007/s12205-018-0650-1

CrossRef Full Text | Google Scholar

Liu, B., Zhang, D.-W., Yang, C., and Zhang, Q.-B. (2020). Long-term performance of metro tunnels induced by adjacent large deep excavation and protective measures in NanJing silty clay. Tunn. Undergr. space Technol. 95, 103147. doi:10.1016/j.tust.2019.103147

CrossRef Full Text | Google Scholar

Liu, J.-C., Lei, G.-H., and Wang, X.-D. (2015). One-dimensional consolidation of visco-elastic marine clay under depth-varying and time-dependent load. Mar. Georesources Geotechnol. 33 (4), 337–347. doi:10.1080/1064119x.2013.877109

CrossRef Full Text | Google Scholar

Liu, Z., and Shao, J. (2016). Moisture effects on damage and failure of Bure claystone under compression. Geotech. Lett. 6 (3), 182–186. doi:10.1680/jgele.16.00054

CrossRef Full Text | Google Scholar

Lyu, H., Gu, J., Li, W., and Liu, F. (2020). Analysis of compressibility and mechanical behavior of red clay considering structural strength. Arabian J. Geosciences 13, 411–11. doi:10.1007/s12517-020-05352-4

CrossRef Full Text | Google Scholar

Malehmir, A., Bastani, M., Krawczyk, C.-M., Gurk, M., Ismail, N., Polom, U., et al. (2013). Geophysical assessment and geotechnical investigation of quick-clay landslides–a Swedish case study. Near Surf. Geophys. 11 (3), 341–352. doi:10.3997/1873-0604.2013010

CrossRef Full Text | Google Scholar

Middelhoff, M., Cuisinier, O., Masrouri, F., and Talandier, J. (2021). Hydro-mechanical path dependency of claystone/bentonite mixture samples characterized by different initial dry densities. Acta Geotech. 16 (10), 3161–3176. doi:10.1007/s11440-021-01246-1

CrossRef Full Text | Google Scholar

Mitachi, T., and Kitago, S. (1979). The influence of stress history and stress system on the stress-strain-strength properties of saturated clay. Soils Found. 19 (2), 45–61. doi:10.3208/sandf1972.19.2_45

CrossRef Full Text | Google Scholar

Ni, H., and Huang, Y. (2020). Rheological study on influence of mineral composition on viscoelastic properties of clay. Appl. Clay Sci. 187, 105493. doi:10.1016/j.clay.2020.105493

CrossRef Full Text | Google Scholar

Ren, P., Wang, P., Tang, Y., and Zhang, H. (2021). A viscoelastic-plastic constitutive model of creep in clay based on improved nonlinear elements. Soil Mech. Found. Eng. 58 (1), 10–17. doi:10.1007/s11204-021-09701-7

CrossRef Full Text | Google Scholar

Shan, Y., Meng, Q., Yu, S., Mo, h., and Li, Y. (2020). Energy based cyclic strength for the influence of mineral composition on artificial marine clay. Eng. Geol. 274, 105713. doi:10.1016/j.enggeo.2020.105713

CrossRef Full Text | Google Scholar

Shang, X., Zhou, G., and Lu, Y. (2015). Stress-dependent undrained shear behavior of remolded deep clay in East China. J. Zhejiang University-SCIENCE A 3 (16), 171–181. doi:10.1631/jzus.a1400255

CrossRef Full Text | Google Scholar

Stróżyk, J., and Tankiewicz, M. (2016). The elastic undrained modulus Eu50 for stiff consolidated clays related to the concept of stress history and normalized soil properties. Studia Geotechnica Mech. 38 (3), 67–72. doi:10.1515/sgem-2016-0025

CrossRef Full Text | Google Scholar

Sun, L., Cai, Y., Gu, C., Wang, J., and Guo, L. (2015). Cyclic deformation behaviour of natural K 0-consolidated soft clay under different stress paths. J. Central South Univ. 22 (12), 4828–4836. doi:10.1007/s11771-015-3034-4

CrossRef Full Text | Google Scholar

Surarak, C., Likitlersuang, S., Wanatowski, D., Balasubramaniam, A., Oh, E., and Guana, H. (2012). Stiffness and strength parameters for hardening soil model of soft and stiff Bangkok clays. Soils Found. 52 (4), 682–697. doi:10.1016/j.sandf.2012.07.009

CrossRef Full Text | Google Scholar

Vucetic, M. (1988). Normalized behavior of offshore clay under uniform cyclic loading. Can. Geotechnical J. 25 (1), 33–41. doi:10.1139/t88-004

CrossRef Full Text | Google Scholar

Vucetic, M. (1990). Normalized behavior of clay under irregular cyclic loading. Can. Geotechnical J. 27 (1), 29–46. doi:10.1139/t90-004

CrossRef Full Text | Google Scholar

Wang, L., and Chen, K. (2019). Study on failure mechanism of red clay slope under dry and wet cycles. IOP Conf. Ser. Earth Environ. Sci. IOP Publ. 330 (3), 032015. doi:10.1088/1755-1315/330/3/032015

CrossRef Full Text | Google Scholar

Zhang, H., Wan, Z., Ma, D., and Zhou, P. (2017). Coupled effects of moisture content and inherent clay minerals on the cohesive strength of remodelled coal. Energies 10 (8), 1234. doi:10.3390/en10081234

CrossRef Full Text | Google Scholar

Zhang, Y., Kong, L.-W., Meng, Q.-S., and Chen, J.-B. (2006). Normalized stress-strain behavior of Wuhan soft clay. Yantu Lixue Rock Soil Mech. 27 (9), 1509–1513.

Google Scholar