Effect of strain profiling on anisotropic opto-electronic properties of As2X3 (X =S, Te) monolayers from first principles

Strain Engineering is a widely adopted approach to modulate the opto-electronic performance of 2-Dimensional (2D) materials. Recently, anisotropic Van der Waals (vdW) based 2D As₂S₃ monolayer has gained significant attention within the scientific community due to its stability in ambient conditions. Similar compounds like As₂Te₃ have also been theoretically explored. However, its indirect bandgap nature limits its application in optical devices. In this study, a systematic study of compressive and tensile strain on three profiles–Uniaxial along a-axis, Uniaxial along b-axis and biaxial strain from −10% to +10%, is performed for As₂S₃ and As₂Te₃ monolayers. Certain strain profiles like Uniaxial tensile strain of 8% along b-axis results in transition to direct bandgap material. Similarly, for As₂Te₃, shear strain of (−10%, +8%) along (a, b) axis results in direct bandgap material. In addition, the anisotropic optical absorption spectrum is obtained for unstrained and strained monolayers within the random phase approximation (RPA).

1 Introduction

Intrinsic in-plane structural anisotropy in vdW-based 2D materials gives rise to directionally dependent electronic, optical, magnetic, and mechanical properties that can be exploited for device physics. This class of materials known as T and T′ metal dichalcogenides (TMDCs) include ReS₂ (Lin et al., 2015) and ReSe₂ (Wolverson et al., 2014), Phosphorene (Wang et al., 2015), Borophene (Padilha et al., 2016), transition metal monochalcogenides MX (Sarkar and Stratakis, 2020), where M = Ge, Pb, Sn and X = Se, S, P and Te. Other examples of such anisotropic 2D vdW’s materials are Antimonene (Pumera and Sofer, 2017), TiS₃ (Dai and Zeng, 2015), ZrGeTe₄ (Adam et al., 2020), Ta₂NiS₅ (Qiao et al., 2021), and CrOCl (Xu et al., 2021). Such anisotropic 2D materials find wide applications in polarization-sensitive photodetectors, optical components, and linearly polarized light sources (Yuan et al., 2015; Guo et al., 2016; Huang et al., 2019). Amongst these compounds, monolayer black phosphorus exhibits the highest anisotropic ratio of Young’s modulus along the direction of b to a axis of 2 (Tao et al., 2015; Wang et al., 2015). However, phosphorene is unstable in air (Kistanov et al., 2017), which limits its applications in devices like Nano-electro- mechanical systems (NEMS). On the other hand, a recently studied compound, namely, As₂S₃ monolayer with an in-plane anisotropic ratio of 1.7 is found to be stable under ambient conditions (Šiškins et al., 2019).

There were two independent theoretical studies carried out in 2016 (Debbichi et al., 2016; Miao et al., 2017) that predicted the possibility of the formation of few layers to monolayer As₂S₃, As₂Se₃ and As₂Te₃ from its bulk form in naturally occurring orpiment phase. It was predicted that these materials have indirect bandgap semiconductors by using DFT and AIMD calculations (Debbichi et al., 2016; Miao et al., 2017). The anisotropic optical and mechanical properties of As₂S₃ monolayer were verified experimentally (Šiškins et al., 2019). In addition, the anisotropic thermoelectric performance of As₂S₃ and As₂Te₃ monolayers was also studied using DFT calculations (Patel et al., 2020; Gao et al., 2021). However, there is only one report on the effect of uniaxial compressive strain on the electronic properties of As₂S₃ monolayer (Liu et al., 2021a).

Mechanical deformation of two-dimensional materials is one of the most appealing methods to modify their electronic structure. By straining the interatomic distances, the bond-lengths change leading to a change in the overlap of the electronic wavefunctions of the atomic orbitals, which has an impact on the electronic structure of these materials. For instance, the direct bandgap of phosphorene was found to change to indirect by applying biaxial strain (Peng et al., 2014).

The materials in the present work have indirect bandgaps, which limit their applications in optoelectronic devices due to unavoidable thermal dissipation due to phonon scattering. Furthermore, unlike three-dimensional materials, 2D materials can withstand a strain of up to 10% during mechanical exfoliation (Postorino et al., 2020). Hence, it is worthwhile to perform a systematic study of the effect of strain on the opto-electronic response of As₂X₃ monolayers. In this paper, we report the effect of both compressive and tensile, uniaxial, biaxial and a few cases of sheer strain on the electronic and optical properties of 2D monolayer As₂X₃ (X = S,Te) using ab intio calculations. This paper is organized as follows: section- II provides the details of the calculations and computational methodology, section-III is divided in four parts–the structural and electronic properties of unstrained monolayers, the effect of uniaxial and biaxial strain on the electronic properties, a discussion of the effect of shear strain on the electronic properties and finally the effect of mechanical strain on anisotropic optical properties.

2 Computational methodology

Density functional theory calculations are performed using Vienna ab initio simulation package (VASP) code (Kresse and Hafner, 1993; Kresse and Furthmüller, 1996) using Projected Augmented Wave (PAW) type of pseudopotentials (Kresse and Joubert, 1999). The exchange correlation functional was treated using the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) methodology (Perdew et al., 1996) by explicitly introducing the vdW interaction using optB86b functional (Klimeš et al., 2011). The cutoff kinetic energy for plane waves was set to 500 eV. 2D monolayer unit cells for both As₂S₃ and As₂Te₃ compounds were relaxed until the force convergence of 10^–4 was achieved with an energy convergence criterion of 10^–6 eV. The self-consistent field calculations were performed using a 8 × 6×1 Gamma-centered k-mesh. The projected density of states (PDOS) calculations were obtained using a dense k-mesh of 30 × 10×1. The c-axis or vacuum of 23Å was created to simulate the vdW gap to avoid the periodic repetition of the neighboring unit cells.

The linear optical properties are calculated within the random phase approximation using Kubo- Greenwood equations by calculating the microscopic dielectric constant as implemented in VASP code (Gajdoš et al., 2006). The microscopic dielectric function is given by the following Equation 1.

$\left(\mathrm{\omega }\right)={\mathrm{\epsilon }}_1\left(\mathrm{\omega }\right)+\mathrm{i}{\mathrm{\epsilon }}_2\left(\mathrm{\omega }\right)(1)$

The imaginary part of the dielectric function that depends on transition matrix elements and joint density of states is given by Eq 2 as follows:

${\epsilon }_2\left(\omega \right)=\frac{2e^2\pi }{\mathrm{\Omega }{\epsilon }_0}{\sum }_{k,v,c}\underset{}{<{\mathrm{\Psi }}_k^c\left|\widehat{u}.r\right|{\mathrm{\Psi }}_k^v>}\delta \underset{}{\left(E_k^c-E_k^v-E\right)}(2)$

Here, 𝜔 is the frequency of the light, 𝛺 is unit cell volume, 𝜀₀ is the permittivity of free space, 𝛹^𝑐 is the wavefunction of the conduction band (c) at k-point index k and 𝛹^𝑣 denotes the wavefunction of the valence bands, $\widehat{u}$. 𝑟 is the direction of polarization of incident light. The real part 𝜀₁(𝜔) is obtained by Kramer-Kronig transformation. The optical properties are calculated by considering the light parallel to both, a (XX)- and b (YY)-axes. A denser k-mesh of 30 × 10×1 was used for the calculation of linear optical properties.

The strain is calculated by the relation ε = (l-l0/l), where l is the length of the strained unit cell vector and l0 is the unstrained unit cell vector length. Both compressive and tensile uniaxial (along a-axis and b-axis due to anisotropic unit cell) and biaxial strain were applied by varying the strain to the unit cell from −10% to +10%. Moreover, the effect of shear strain for a particular case of applying the compressive strain on a-axis is studied from −2% to −10% and the b-axis was fixed to +8% tensile strain. The postprocessing is performed using VASPKIT (Wang et al., 2021).

3 Results and discussion

3.1 Structural and electronic properties of unstrained monolayers As₂X₃

Figure 1A shows a fully relaxed 3 × 2×1 supercell of As₂S₃ monolayer. The rectangular primitive unit cells of As₂S₃ and As₂Te₃ are shown in Figure 1A. They belong to the orthorhombic lattice with space group Pmn21 (Space group number 31). Each unit cell consists of two formula units of As₂X₃. The As atoms have a coordination number of three and each S/Te atom has a coordination number of two. Figure 1B presents a side view of As₂Te₃ supercell.

FIGURE 1

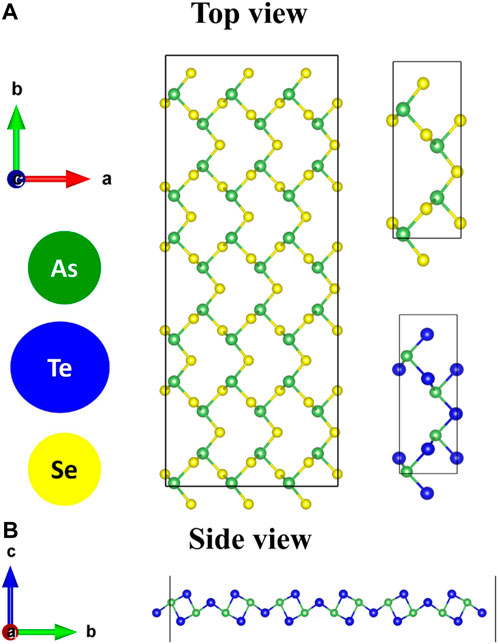
FIGURE 1. (A) Top view of a 3 × 2×1 supercell of As₂S₃ monolayer, Unit cell of As₂S₃ monolayer, Unit cell of As₂Te₃ monolayer and (B) Side view of As₂Te₃ supercell.

The calculated lattice vectors of As₂S₃ are a = 4.54 Å and b = 11.35 Å are comparable with previous theoretical results (a = 4.45 Å and b = 11.35 Å) (Mortazavi et al., 2020). However, they are higher than the experimental findings of 4.22 Å and 11.46 Å (Nobuo, 1954). The optimized lattice parameters of As₂Te₃ are a = 4.56 Å and b = 13.14 Å in this study compare well with previous theoretical results (a = 4.45Å b = 13.11Å) (Mortazavi et al., 2020). In reference (Liu et al., 2021b), the theoretical lattice parameters for monolayer As₂S₃ are a = 4.41 Å and b = 11.41 Å. In these references, the calculations are performed using Grimme’s DFT-D2 input DFT functional for vdW’s interactions, but in the present study, calculations are done differently using optPBE–vdW’s functional as mentioned in the computational methodology. So, the lattice parameters obtained in both the calculations vary slightly. The mechanical anisotropy for As₂S₃ has been studied theoretically (Liu et al., 2021b) and verified experimentally in reference (Šiškins et al., 2019). Similar anisotropic behavior has also been theoretically reported for As₂Te₃ in references (Mortazavi et al., 2020; Gao et al., 2021). The phonon dispersions of both monolayers have already been studied in references (Patel et al., 2020) and (Gao et al., 2021), exhibiting no imaginary frequencies. Hence, both the compounds are dynamically stable.

The electronic band structure and PDOS of As₂S₃ and As₂Te₃ monolayers are shown in Figure 2. Both structures show a semiconducting behavior with indirect bandgap values of 2.12 and 1.01 eV for As₂S₃ and As₂Te₃ as shown in Figures 2A, C, respectively. The CBM is located at the Gamma-point and the VBM is located at line between the Γ and X high symmetry points in the first Brillouin zone. Since the curvature near VBM and CBM is high or the gradient of PDOS near the fermi energy level for VBM and CBM is larger, the charge carriers are highly delocalized. Figures 2B, D show PDOS for As₂S₃ and As₂Te₃, respectively. From 2(b), As-pz orbital has maximum contribution to the conduction band near the Fermi-energy level, whereas S-px and S-py orbitals have most contribution to valence band states near Fermi level. Similarly, for As₂Te₃, Te–px and py orbitals have maximum contribution to the formation of valence bands near EF and the conducting bands are formed mainly from As-pz orbital.

FIGURE 2

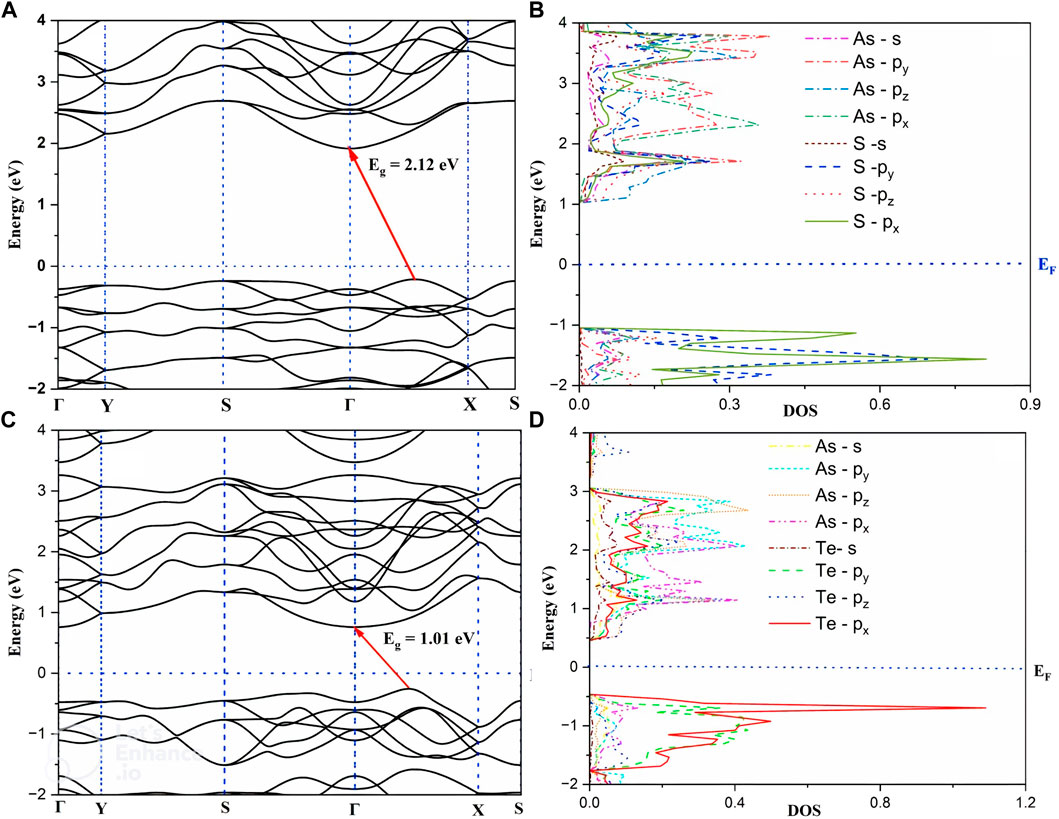
FIGURE 2. Electronic bandstructure and Project Density of States (PDOS) of As₂S₃ (A, B) and As₂Te₃ (C, D).

3.2 The effect of uniaxial and biaxial compressive and tensile strains on the electronic properties of As₂X₃ monolayers

In this subsection, the effect of strain on electronic properties of these monolayers is investigated in a comprehensive manner. Here, we consider compressive and tensile strain profiles of three different types: 1) Uniaxial strain along a_axis (Uni_a), 2) Uniaxial strain along b_axis (Uni_b), 3)Biaxial strain varying from −10% to +10% (compressive to tensile - biaxial). Figure 3 shows the graph of DFT energies versus strain for Uni_a, Uni_b and biaxial strains for (a) As₂S₃ and (b) As₂Te₃. It is clear from Figure 3 that the unstrained structure has a minimum or ground state, which indicates the most stable structure for both monolayers. In addition, the energy of the biaxial strain profile is always higher compared to uniaxial strain profiles. Also, the strain energies for Uni_a are consistently lower than that of Uni_b, implying that the structure undergoes maximum deformation along the a_axis. It is also important to note that the strain energies are always lower for As₂Te₃ as compared to As₂S₃, implying that As₂Te₃ can be deformed more easily.

FIGURE 3

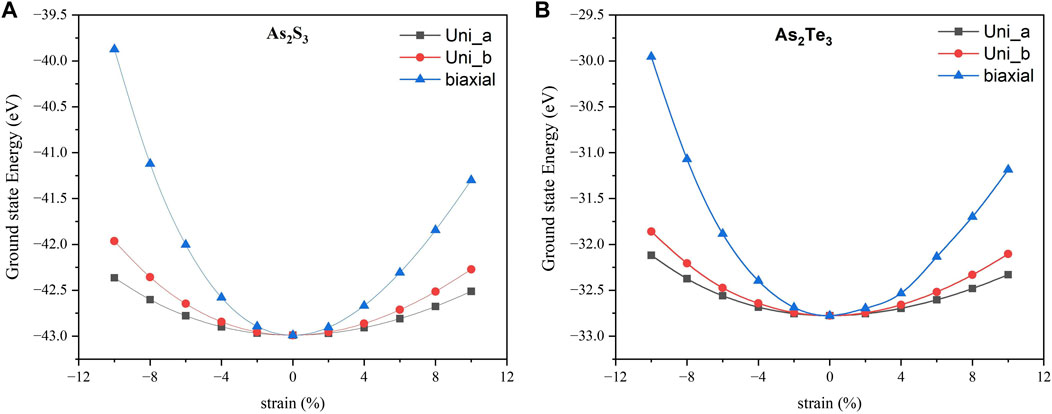
FIGURE 3. Strain energies Vs. strain percentage for (A) As₂S₃ and (B) As₂Te₃. Here, black squares represent Uni_a, red circles are for Uni_b and blue triangles are for biaxial strain profiles.

The most important property for optoelectronic applications is the bandgap, E.g., Figure 4 shows the effect of strain on the bandgap of As₂S₃ and As₂Te₃ monolayers. In this work, the effect of strain is studied in the range from −10% to +10% (with increasing bond length from −10% to +10% strain) as shown in Figure 4A, where the bandgap is maximized at Uni_a tensile strain of +8% for both As₂S₃ and As₂Te₃ monolayers. However, the bandgap maxima of As₂S₃ and As₂Te₃ monolayers are located at +4% and +2% for Uni_b tensile strain and biaxial tensile strain, respectively, see Figures 4B, C. A single example for Uni_b As₂S₃ case is considered in this study to understand this trend of the band structure changes (see Figure 5). As evident from Figure 5, the CBM shifts from Γ–point towards X-point, with increasing strain from −10% to +10%. This trend can be explained using the projected density of states for all strain profiles varying from −10% to +10%, see Supplementary Figures S1A–J. As evident from the Supplementary Figures S1A–C, for strain profiles −10%, −8% and −6%, the major contribution to CBM comes from As- py, As-pz and S-pz orbitals. On further reducing the compressive strain percentage for −4% and −2%, S- py orbital also contributes to CBM. Further going from the unstrained profile of 0% to +10%, As-px orbital also makes a significant contribution to CBM states near the Fermi energy level and it increases with increasing tensile strain. However, as we go from +2% to +10%, the contributions from As-py and S-pz orbitals cease to exist, see Supplementary Figures S1E–J, This results in the shift of CBM from Γ–point towards X-point.

FIGURE 4

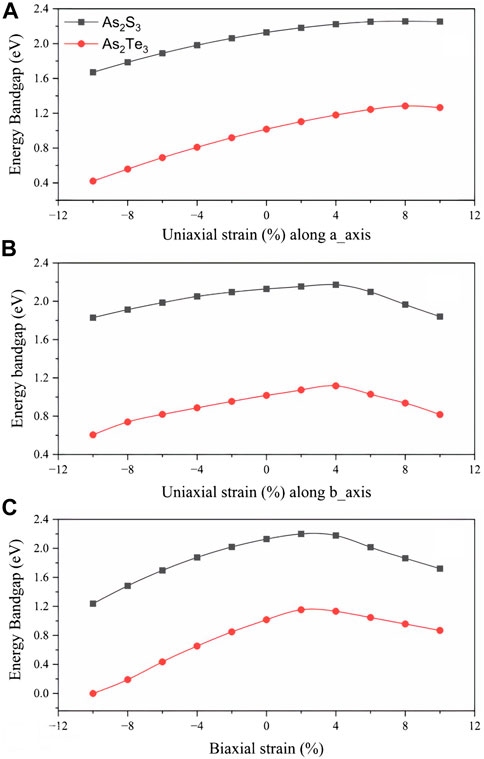
FIGURE 4. Effect of strain on electronic bandgap, E.g., (A) Uniaxial strain along a-axis, (B) Uniaxial strain along b-axis and (C) Biaxial strain. Squared symbol for As₂S₃ and circle for As₂Te₃.

FIGURE 5

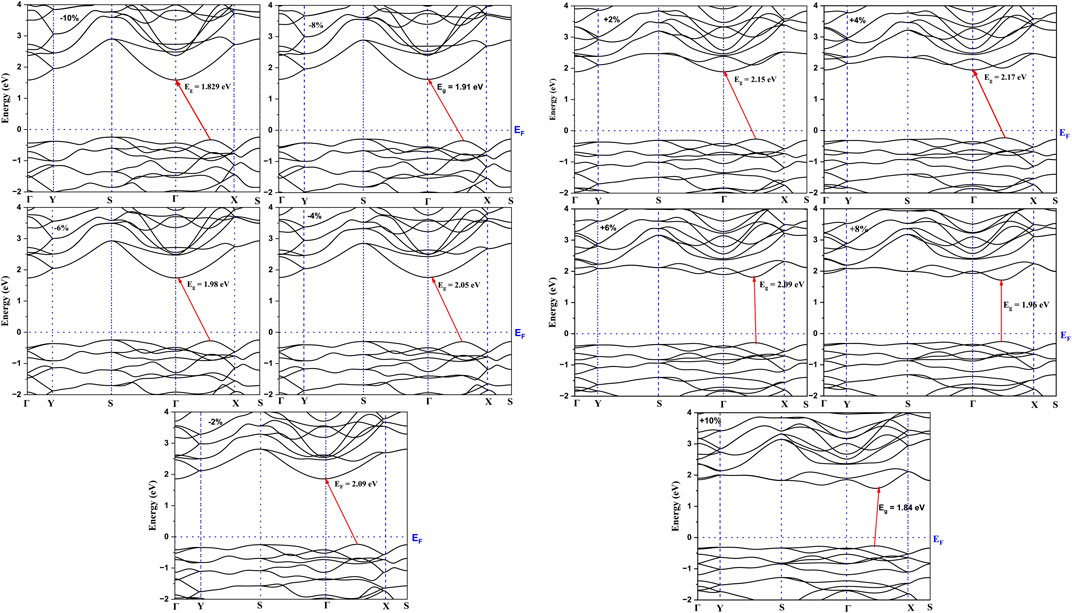
FIGURE 5. Demonstration of variation in electronic band-structure with strain for As₂S₃ Uni_b strain profile.

There is a transition from indirect to direct bandgap in As₂S₃ for uniaxial strain of 8% along b-axis (See the electronic band structure in Figure 5, whereas it retains its indirect nature for all the other strain profiles. Although, it seems that for +6% and +10%, the CBM and VBM are located closely along the Γ-X line, they are still indirect. Moreover, the system becomes metallic for the case of As₂Te₃ at biaxial compressive strain of −10% (Supplementary Figure S2) but is indirect semiconducting in all other strain profiles.

3.3 The effect of shear strain on the electronic properties of As₂X₃ monolayers

The employed strategy for selecting a limited number of shear strain profiles was as follows: Since the uniaxial strain along b-axis (Uni_b) resulted in a transition to direct bandgap semiconductor in As₂S₃ at +8%, it is kept fixed at this b-axis tensile strain, whereas that along the a_axis was varied from −2% to −10% for both compounds. As a result, As₂Te₃ transformed to a direct band gap material, whereas, As₂S₃ lost its direct bandgap nature. As indicated in Figures 6, 7 the comparative effect of shear strain in As₂Te₃ and As₂S₃ is shown for two cases: (0%, +8%) and (−10%, 8%), respectively.

FIGURE 6

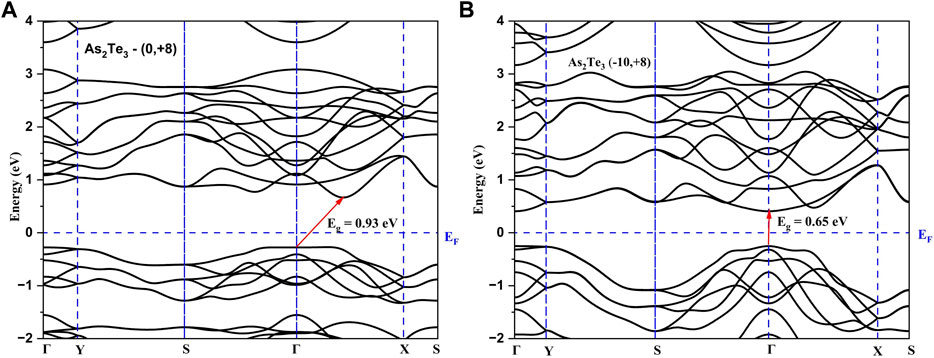
FIGURE 6. Demonstrating a transition to direct bandgap semiconductor in As₂Te₃ for a shear strain of (A, B) = (−10%, 8%) as shown in (B) as compared to Uni_b strain of +8% as shown in (A).

FIGURE 7

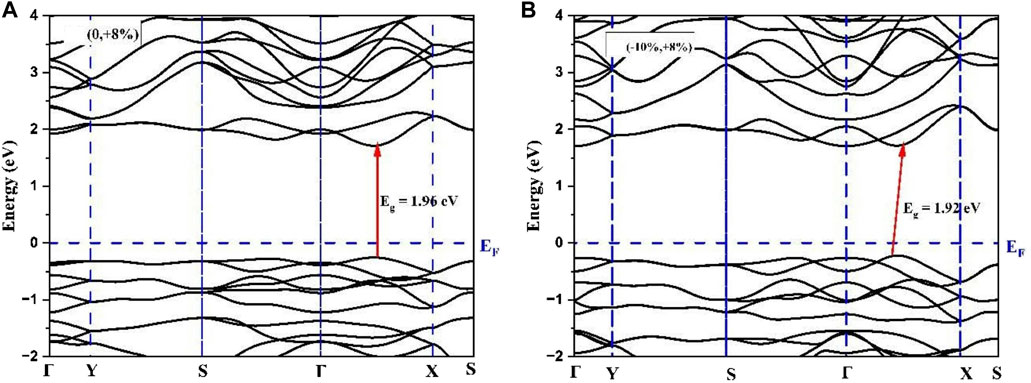
FIGURE 7. Demonstrating the loss of direct band gap nature from (A) (0, +8%) to (B) (−10%, +8%) in As₂S₃ monolayer.

3.4 Optical properties

In this section, the anisotropy in the optical absorption spectrum is discussed in the case of unstrained As₂S₃ and As₂Te₃ monolayers. As shown in Figures 8A, B, there is a strong anisotropic behavior as demonstrated in the absorption along XX and YY-direction. For the case of As₂S₃, there is a strong absorption in the UV range in the XX direction, which spans to some part of VIS spectrum as well. However, for the YY direction, the absorption peak is in the mid to near UV range and green, blue, violet and cyan parts of VIS spectrum. Similarly, for As₂Te₃ the absorption along both directions is in the near-IR, VIS and near-UV range. The optical bandgap can be calculated by drawing a tangential line to the absorption edge along XX direction, because the band gap is along the Γ- X line in the first Brillouin zone. Figures 8A, B show that the optical, E.g., for As₂S₃ and As₂Te₃ are 1.98 and 0.88 eV, respectively.

FIGURE 8

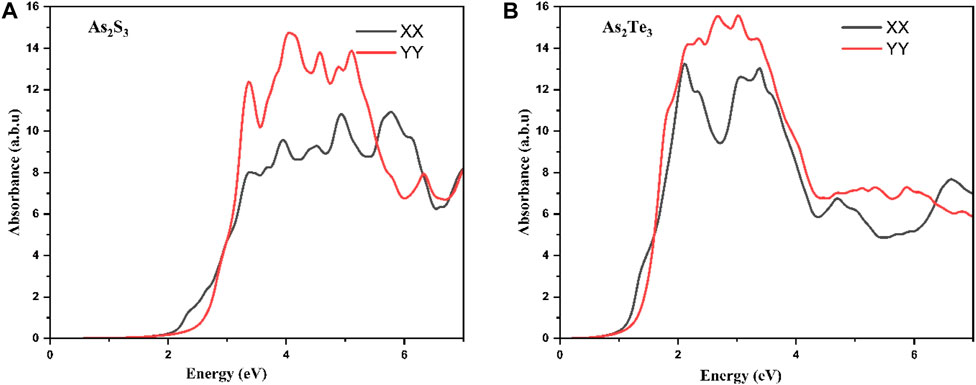
FIGURE 8. Optical absorption spectra for unstrained (A) As₂S₃ and (B) As₂Te₃ monolayers exhibiting anisotropic dependence along XX and YY direction.

The next step was devoted to study the effect of strain on the band gap. Here only the case of strained As₂S₃ monolayer along Uni_b (Uniaxial b-axis) is considered, since there was a transition to a direct bandgap behavior at +8% tensile strain as depicted in Figures 9A, B. It is also important to note that only the XX-direction is considered since the bandgap is located along the Γ-X line. The absorption band-edge is red shifted along with increasing compressive strain from 0% to −10% and is again red shifted for increasing tensile strain from 0 to +10%.

FIGURE 9

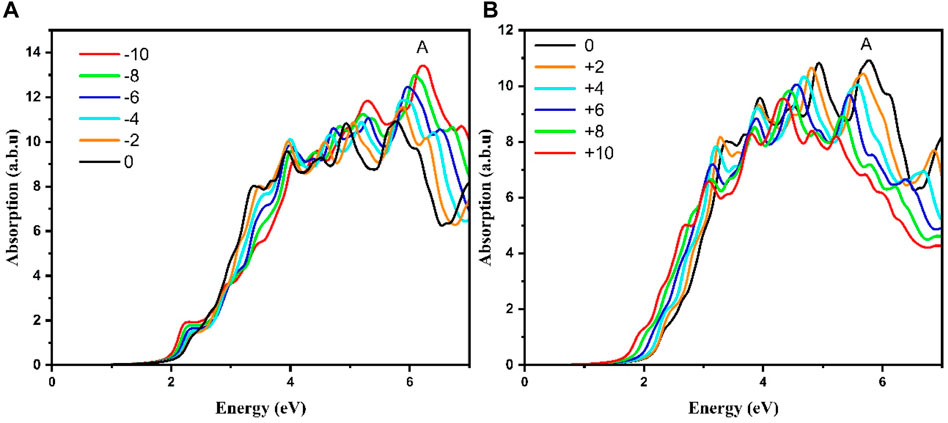
FIGURE 9. Effect of strain on optical absorption spectrum of (A) compressive strain and (B) tensile strain for Uni_b As₂S₃ monolayer.

The other important quantity is the static dielectric constant ε1 (0) and the effect of strain on it as shown in Figure 10A for As₂S₃ and Figure 10B for As₂Te₃. This is because it has the following relation with the bandgap:

${\mathrm{\epsilon }}_1\left(0\right)=1+{\left(\frac{{\mathrm{h}\omega }_{\mathrm{p}}}{2\mathrm{\pi }*E_{\text{g}}}\right)}^2(3)$

FIGURE 10

FIGURE 10. Static dielectric constant Vs. strain for monolayer As₂S₃ (A) and As₂Te₃ (B).

Hence, it can be said that opposite trends of decreasing bandgaps with increasing ε1 (0) should be observed. For all the three types of strain - Uni_a, Uni_b and biaxial strain, the minima occur at +8% tensile strain whereas, for As₂Te₃ minima occurs at 0% strain for Uni_b, however, it does not reach a minimum value for Uni_a and Biaxial strain. This shows that the plasma frequency plays an important role in all the above cases.

4 Conclusion

The effect of strain profiling on the optoelectronic performance of As₂X₃ monolayers is studied. One can expect a quantifiable increase in the, E.g., values on considering the above computationally extensive calculations like the use of hybrid functionals or GW-method implementation. The strain effect on the electronic and optical properties of As₂X₃ (X = S, Te) monolayers is investigated and presented. It was observed that for both monolayers, E.g., has maxima for at 8%, 4%, and 2% for uniaxial a-axis, uniaxial b-axis and biaxial strain profiles, respectively. There is a direct effect of strain on red shifting or blue shifting of the absorption spectrum depending on the material and strain profiling.

5 Scope statement

I am submitting the attached paper entitled “Effect of Strain Profiling on Anisotropic Opto-Electronic Properties of As₂X₃ (X = S, Te) Monolayers from First Principles,” by Andharia, et al. for your consideration of publishing it in Frontiers in Materials, section semiconductor materials and device. In this paper, we report on the effect of strain profiling on the optoelectronic performance of As₂X₃ monolayers. The band gap (E.g.,) values of these 2D materials were obtained by computationally extensive calculations. The strain effect on the electronic and optical properties of As₂X₃ (X = S, Te) monolayers is investigated and presented in this paper. It was observed that for both monolayers, E.g., has maxima for at 8%, 4%, and 2% for uniaxial a-axis, uniaxial b-axis and biaxial strain profiles, respectively. There is a direct effect of strain on red shifting or blue shifting of the absorption spectrum depending on the material and strain profiling. We believe this paper is very useful for the research community and we would like for you to give it a full consideration in publishing it in your journal.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

EA: Investigation, Methodology, Writing–original draft. HA: Investigation, Methodology, Software, Writing–review and editing. IE: Investigation, Methodology, Software, Writing–review and editing. BH: Investigation, Software, Supervision, Writing–review and editing. OM: Investigation, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. BH is supported by the MonArk Quantum Foundry that is funded by the National Science Foundation Q-AMASE-i program under NSF Award No. DMR-1906383.

Acknowledgments

The authors would like to thank Arkansas High Performance Computing Center (AHPCC), University of Arkansas, for the computing resources.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2023.1325194/full#supplementary-material

References

Adam, M. L., Moses, O. A., Rehman, Z. u., Liu, Z., Song, L., and Wu, X. (2020). Band gap engineering of monolayer zrgete4 via strain: a first-principles study. Mater. Chem. Phys. 253, 123308. doi:10.1016/j.matchemphys.2020.123308

CrossRef Full Text | Google Scholar

Dai, J., and Zeng, X. C. (2015). Titanium trisulfide monolayer: theoretical prediction of a new direct-gap semiconductor with high and anisotropic carrier mobility. Angew. Chem. Int. Ed. 54, 7572–7576. doi:10.1002/anie.201502107

PubMed Abstract | CrossRef Full Text | Google Scholar

Debbichi, L., Kim, H., Björkman, T., Eriksson, O., and Lebègue, S. (2016). First-principles investigation of two-dimensional trichalcogenide and sesquichalcogenide monolayers. Phys. Rev. B 93, 245307. doi:10.1103/PhysRevB.93.245307

CrossRef Full Text | Google Scholar

Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J., and Bechstedt, F. (2006). Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 73, 045112. doi:10.1103/physrevb.73.045112

CrossRef Full Text | Google Scholar

Gao, Z., Zhu, T., Sun, K., and Wang, J.-S. (2021). Highly anisotropic thermoelectric properties of two-dimensional As₂Te₃. ACS Appl. Electron. Mater. 3, 1610–1620. doi:10.1021/acsaelm.0c01100

CrossRef Full Text | Google Scholar

Guo, Q., Pospischil, A., Bhuiyan, M., Jiang, H., Tian, H., Farmer, D., et al. (2016). Black phosphorus mid-infrared photodetectors with high gain. Nano Lett. 16, 4648–4655. doi:10.1021/acs.nanolett.6b01977

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y., Ning, J., Chen, H., Xu, Y., Wang, X., Ge, X., et al. (2019). Mid-infrared black phosphorus surface-emitting laser with an open microcavity. ACS Photonics 6, 1581–1586. doi:10.1021/acsphotonics.9b00096

CrossRef Full Text | Google Scholar

Kistanov, A. A., Cai, Y., Zhou, K., Dmitriev, S. V., and Zhang, Y.-W. (2017). The role of h2o and o2 molecules and phosphorus vacancies in the structure instability of phosphorene. 2D Materials 4, 015010. doi:10.1088/2053-1583/4/1/015010

CrossRef Full Text | Google Scholar

Klimeš, J., Bowler, D. R., and Michaelides, A. (2011). Van der waals density functionals applied to solids. Phys. Rev. B 83, 195131. doi:10.1103/physrevb.83.195131

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561. doi:10.1103/PhysRevB.47.558

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Lin, Y.-C., Komsa, H.-P., Yeh, C.-H., Björkman, T., Liang, Z.-Y., Ho, C.-H., et al. (2015). Single-layer res2: two-dimensional semiconductor with tunable in-plane anisotropy. ACS Nano 9, 11249–11257. doi:10.1021/acsnano.5b04851

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Lv, B., Ding, Z., and Luo, Z. (2021a). External uniaxial compressive strain induced built-in electric field in bilayer two-dimensional As₂S₃ for photocatalytic water splitting: a first-principles study. Appl. Surf. Sci. 535, 147701. doi:10.1016/j.apsusc.2020.147701

CrossRef Full Text | Google Scholar

Liu, X., Zhang, Z., Ding, Z., Lv, B., Luo, Z., Wang, J.-S., et al. (2021b). Highly anisotropic electronic and mechanical properties of monolayer and bilayer As₂S₃. Appl. Surf. Sci. 542, 148665. doi:10.1016/j.apsusc.2020.148665

CrossRef Full Text | Google Scholar

Miao, N., Zhou, J., Sa, B., Xu, B., and Sun, Z. (2017). Few-layer arsenic trichalcogenides: emerging two-dimensional semiconductors with tunable indirect-direct band-gaps. J. Alloys Compd. 699, 554–560. doi:10.1016/j.jallcom.2016.12.351

CrossRef Full Text | Google Scholar

Mortazavi, B., Shojaei, F., Azizi, M., Rabczuk, T., and Zhuang, X. (2020). As₂S₃, As₂Se₃ and As₂Te₃ nanosheets: superstretchable semiconductors with anisotropic carrier mobilities and optical properties. J. Mater. Chem. C 8, 2400–2410. doi:10.1039/C9TC05904K

CrossRef Full Text | Google Scholar

Nobuo, M. (1954). The crystal structure of orpiment (As₂S₃) refined. Mineralogical J. 1, 160–169. doi:10.2465/minerj1953.1.160

CrossRef Full Text | Google Scholar

Padilha, J. E., Miwa, R. H., and Fazzio, A. (2016). Directional dependence of the electronic and transport properties of 2d borophene and borophane. Phys. Chem. Chem. Phys. 18, 25491–25496. doi:10.1039/C6CP05092A

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel, A., Singh, D., Sonvane, Y., Thakor, P. B., and Ahuja, R. (2020). Bulk and monolayer As₂S₃ as promising thermoelectric material with high conversion performance. Comput. Mater. Sci. 183, 109913. doi:10.1016/j.commatsci.2020.109913

CrossRef Full Text | Google Scholar

Peng, X., Wei, Q., and Copple, A. (2014). Strain-engineered direct-indirect band gap transition and its mechanism in two-dimensional phosphorene. Phys. Rev. B 90, 085402. doi:10.1103/physrevb.90.085402

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Postorino, S., Grassano, D., D’Alessandro, M., Pianetti, A., Pulci, O., and Palummo, M. (2020). Strain-induced effects on the electronic properties of 2d materials. Nanomater. Nanotechnol. 10, 184798042090256. doi:10.1177/1847980420902569

CrossRef Full Text | Google Scholar

Pumera, M., and Sofer, Z. (2017). 2d monoelemental arsenene, antimonene, and bismuthene: beyond black phosphorus. Adv. Mater. 29, 1605299. doi:10.1002/adma.201605299

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiao, J., Feng, F., Wang, Z., Shen, M., Zhang, G., Yuan, X., et al. (2021). Highly in-plane anisotropic two-dimensional ternary ta2nise5 for polarization-sensitive photodetectors. ACS Appl. Mater. Interfaces 13, 17948–17956. doi:10.1021/acsami.1c00268

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, A. S., and Stratakis, E. (2020). Recent advances in 2d metal monochalcogenides. Adv. Sci. 7, 2001655. doi:10.1002/advs.202001655

PubMed Abstract | CrossRef Full Text | Google Scholar

Šiškins, M., Lee, M., Alijani, F., van Blankenstein, M. R., Davidovikj, D., van der Zant, H. S. J., et al. (2019). Highly anisotropic mechanical and optical properties of 2d layered As₂S₃ membranes. ACS Nano 13, 10845–10851. doi:10.1021/acsnano.9b06161

PubMed Abstract | CrossRef Full Text | Google Scholar

Tao, J., Shen, W., Wu, S., Liu, L., Feng, Z., Wang, C., et al. (2015). Mechanical and electrical anisotropy of few-layer black phosphorus. ACS Nano 9, 11362–11370. doi:10.1021/acsnano.5b05151

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Kutana, A., Zou, X., and Yakobson, B. I. (2015). Electro-mechanical anisotropy of phosphorene. Nanoscale 7, 9746–9751. doi:10.1039/C5NR00355E

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, V., Xu, N., Liu, J.-C., Tang, G., and Geng, W.-T. (2021). Vaspkit: a user-friendly interface facilitating high-throughput computing and analysis using vasp code. Comput. Phys. Commun. 267, 108033. doi:10.1016/j.cpc.2021.108033

CrossRef Full Text | Google Scholar

Wolverson, D., Crampin, S., Kazemi, A. S., Ilie, A., and Bending, S. J. (2014). Raman spectra of monolayer, few-layer, and bulk rese2: an anisotropic layered semiconductor. ACS Nano 8, 11154–11164. doi:10.1021/nn5053926

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, C., Zhang, J., Guo, Z., Zhang, S., Yuan, X., and Wang, L. (2021). A first-principles study on the electronic property and magnetic anisotropy of ferromagnetic crof and crocl monolayers. J. Phys. Condens. Matter 33, 195804. doi:10.1088/1361-648X/abe477

CrossRef Full Text | Google Scholar

Yuan, H., Liu, X., Afshinmanesh, F., Li, W., Xu, G., Sun, J., et al. (2015). Polarization-sensitive broadband photodetector using a black phosphorus vertical p–n junction. Nat. Nanotechnol. 10, 707–713. doi:10.1038/nnano.2015.112

PubMed Abstract | CrossRef Full Text | Google Scholar