An elastic-viscoplastic creep model for describing creep behavior of layered rock

To describe the full-stage creep behavior of layered rock accurately, a new elastic-viscoplastic creep model is proposed based on fractional order theory in this manuscript, which consists of a Hooke elastomer, a fractional Abel dashpot, a Kelvin body, and a new non-linear visco-plastic component. The non-linear creep model can not only describe the changes in three creep stages (primary creep, steady-state creep and accelerating creep) but also reflect the influence of different bedding angles of rock. The constitutive equations of the non-linear creep model are deduced by the empirical model method and plastic theory method, respectively. The parameters of the non-linear creep model are identified using the Levenberg-Marquardt algorithm from Origin. It shows that the creep model in this paper are highly consistent with the experimental data under different load levels, creep stages and bedding angles, and the accuracy and rationality of the model are verified. Moreover, the creep constitutive equations for layered rock derived by the two methods have the same fitting effect on the same set of experimental data.

1 Introduction

Rock rheology refers to the continuous adjustment and recombination of rock and mineral fabric (skeleton) with the growth of time, resulting in the continuous increase and change of its stress and strain state with time (Sun, 2007a). The rheology of rock includes creep, stress relaxation and elastic aftereffects. Especially, the creep characteristics of rock are of great significance to the stability of rock engineering, and the research on this aspect is also of great significance and engineering application value. The study of creep characteristics of rock began in the 1930s, Griggs (Griggs, 1939) carried out a series of creep tests on rocks such as limestone, shale and sandstone in 1939, and concluded that rock creep occurs when the load reaches 12.5%–80.0% of its compressive strength. Several elasto-viscoplastic creep models have been proposed that can well describe the time-dependent behavior of rock under certain conditions (Wu et al., 2018; Brantut et al., 2013; Sone et al., 2014; Xia et al., 2009). In general, the classical rock rheological model theory is mainly limited to linear rheological problems, and there are two main methods to describe non-linear rheological problems of rock. The first method is to replace the linear model theory with a new non-linear rheological theory completely, such as internal time theory, fracture and damage mechanics theory, etc. The other method is to improve the classical model theory by using non-linear components (non-linear spring or non-linear dashpot) instead of linear elements.

The component model is widely used because of its intuitive concept and clear meaning. Classical component combination models include the Maxwell model, Kelvin model, Poyting-Thomson model, Burgers model and Nishihara model. However, the basic element of the classical model is linear, it is still linear whether connection in series or parallel, and can not describe the non-linear creep characteristics of the rock in the accelerating stage. Therefore, establishing a creep model which can describe the non-linear characteristics of the rock creep process has always been a hot and difficult point in the theoretical research of rock mechanics. In the present research, scholars (Cheng et al., 2020; Shan et al., 2020; Wang and Wan, 2016; Yang and Jiang, 2022) having been established different non-linear creep models by introducing creep damage theory (Shen et al., 2023a; Zhang et al., 2022a) and fractional calculus theory. The constitutive model based on fractional calculus theory with fewer parameters and better fitting effect has been widely applied in rock rheological mechanics. A classical example is Koeller (Koeller, 1984) used Riemann–Liouville (R-L) fractional dashpot to replace the traditional Newtonian dashpot in the component model in 1978. The R-L type (Zhou et al., 2018) or Caputo type (Liu et al., 2020) fractional order calculus theory is used to construct fractional dashpot to replace the traditional Newtonian dashpot in the element model, and to establish a creep model that can describe the three stages (primary creep, steady-state creep and accelerating creep) of rock creep. However, it lacks physical significance in the accelerating creep, and it can not well characterize the internal mechanism of accelerating creep of rock. Therefore, damage factors were introduced to describe the accelerating creep of rock, and establish an elasto-viscoplastic creep model reflecting the complete creep process of rock by combining fractional calculus theory and damage theory (Deng et al., 2022; Shen et al., 2022; Wu et al., 2018) becoming a relatively popular study method. In addition, scholars have study the mechanical characteristics about the concrete-rock combination (Shen et al., 2022; Zhang et al., 2019) and other interface (Shen et al., 2023b; Zhang et al., 2023). By comparing the creep model established by fractional calculus theory, it is based on the assumption that there are two stages (hardening and damage) in the creep of rock, and with clear physical significance for describing the accelerating creep stage. However, due to various ways of defining damage factors and increasing model parameters, the calculation is inconvenient.

There are abundant of achievements on creep characteristics for common rock, but few studies on creep characteristics for layered rock. In the basic mechanics study area, Ramamurthy (Ramamurthy, 1993) carried out a study on the physical and mechanical properties of rock with different bedding angles, explored the anisotropy law of strength and deformation. Yong (Yong Tsao, 2000; Yong, 2001) studied the effect of the bedding angle on the strength and elastic modulus for layered rock, proposed corresponding damage guidelines. Fortsakis (Fortsakis et al., 2012) modeled the bedding as separate units and the rock masses as anisotropic materials to investigate the differences in the analysis of isotropic, anisotropic and transverse isotropic analysis methods. Studies has also shown the influence of bedding angles in the basic mechanical properties for layered rock (Celleri et al., 2018; Chang et al., 2020; Hb et al., 2003; Saeidi et al., 2014; Wu et al., 2015; Yang et al., 2021). In the experimental creep study, Dubey (Dubey and Gairola, 2008) investigated the creep properties of salt rocks containing horizontal, vertical and diagonal laminations at different stress levels by uniaxial compression creep tests, and noted that the higher the stress level, the less the laminations affected the anisotropy of the creep properties of salt rocks. In recent years, some scholars (Hu et al., 2019; Liu et al., 2015; Xu et al., 2019; Zhang et al., 2021) have also studied the anisotropic creep law of layered rock by uniaxial compression creep tests and triaxial compression creep tests. In addition, the creep properties of layered rock under the coupling of multiple factors have been studied (Tang et al., 2018). In the study of creep constitutive model for layered rock, an approach is to inductively derive an empirical model from experimental phenomena (Park et al., 2016; Zhang et al., 2022b). It is based on the assumption of constant volume modulus, then to establish a creep constitutive model by identifying the creep parameters in different directions as different mutually independent values. Another approach is the plasticity theory model by assumption of Poisson’s ratio constant (Aravas et al., 1995; Kou et al., 2023; Wang et al., 2018), which to establish the three-dimensional creep constitutive model for transverse isotropic rock by using the transverse isotropic flexibility matrix replace the isotropic flexibility matrix.

Based on the above analysis, the creep mechanics properties of rock has been widely studied, but less for layered rock. Therefore, a non-linear fractional creep model for layered rock was established in this manuscript by introducing a non-linear Abel dashpot. The model connected the Hooke body, non-linear Abel dashpot body, linear Kelvin body and non-linear viscoplastic body in series. Further more, the non-linear elastic-viscoplastic creep constitutive equations for layered rock were derived. A practical method for model parameters identification is proposed, and finally the accuracy and applicability of the model is verified by using different rock compression creep test data from relevant literature.

2 Rock creep processes and basic mechanical models

The typical creep curve of rock is shown in Figure 1. The $ABCD$ is strain curve, and the $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ is strain rate curve, stage I, II, III is the primary creep, steady-state creep and accelerating creep, respectively.

FIGURE 1

FIGURE 1. Three stages of the typical creep curve.

When a load is applied, the rock then undergoes a transient elastic creep in section $OA$. Continuing to loading, the rock enters primary creep in the $AB$ section, which exhibits a non-linear viscoelastic character. With increasing loading stress, the rock then undergoes steady-state creep in the $BC$ section, which exhibits an approximately linear viscoelastic-viscoplastic character. When the loading stress level exceeds the long-term strength of the rock, the rock undergoes primary creep, steady-state creep and then enters the accelerating creep phase in the $CD$ section until creep damage. Thus, the basic equation for the variation of rock creep strain with time can be expressed as

$\epsilon \left(t\right)={\epsilon }_e\left(t\right)+{\epsilon }_{ve}\left(t\right)+{\epsilon }_{vp}\left(t\right)(1)$

Where ${\epsilon }_e\left(t\right),{\epsilon }_{ve}\left(t\right),{\epsilon }_{vp}\left(t\right)$ are elastic strain, viscoelastic strain and viscoplastic strain, respectively.

In rheological theory, a rock creep model should be able to characterise the processes of decay creep, steady-state creep and accelerating creep, and reflect the creep characteristics of the rock at different stress levels. The basic units of the rheological model are generally divided into elastic, plastic and viscous elements, and the mechanical model of the three basic units is shown in Table 1.

TABLE 1

TABLE 1. The basic mechanical components.

As the intrinsic relationships of the basic components are linear, the various classical rheological models, such as the Maxwell, Kelvin, Burgers and Nishihara models (Behbahani et al., 2016; Feng, 2021), which consist of basic components connected in series or parallel, are also linear in nature.

3 Establishment of elastic-viscoplastic creep model

3.1 Plastic body elements based on fractional order derivatives

3.1.1 Definition of fractional calculus

Fractional order calculus is an extension of integer order calculus. Since the 1990s, the theory and methods of fractional order calculus have been widely applied to various fields of the natural and social sciences. In the area of viscous fluid mechanics, the introduction of fractional order calculus theory allows for more realistic theoretical models to be developed in the study of mechanical physical problems associated with real fluids, leading to accurate conclusions. The Riemann–Liouville (R-L) type fractional order calculus is commonly used in the theory of rock rheology studies (Zhou et al., 2018), but its fractional order derivatives are hyper-singular and limited in applications in engineering and technology and in physical modeling. In this paper, we use a theory of fractional order derivatives with weak singular properties proposed by the Italian geophysicist Caputo. The Caputo fractional order derivative solves the fractional order initial value problem in the definition of R-L type fractional order calculus and has been widely used in the modeling process of many practical application problems (Liu et al., 2021). The definition of Caputo fractional order derivative is

${}_0{}^C{D}_t^{\beta }f\left(t\right)=0^{D_t^{\beta -n}}{D}^{n}f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(n-\beta \right)}{\int }_0^t{\left(t-\xi \right)}^{n-\beta -1}{f}^{\left(n\right)}\left(\xi \right)d\xi ,\left(\beta >0\right)(2)$

where $n$ is the smallest integer greater than or equal to $\beta$; $\xi$ is an integral variable of $\left[0,t\right]$; $f^{\left(n\right)}\left(\xi \right)$ is the $n$ th order derivative of function $f\left(\xi \right)$; $\mathrm{\Gamma }$ is Gamma function, defined as

$\mathrm{\Gamma }\left(z\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt=2{\int }_0^{\infty }{t}^{2z-1}{e}^{-t^2}dt(3)$

$\mathrm{\Gamma }\left(1+z\right)=z\mathrm{\Gamma }\left(z\right)\left(z\in N^{*}\right),\text{Re}\left(z\right)>0.(4)$

The Caputo fractional operator is shown in Eq. 5:

${}_0{}^C{D}_t^{-\beta }f\left(t\right)=0^{D_t^{-\beta }}f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^t{\left(t-\xi \right)}^{\beta -1}f\left(\xi \right)d\xi ,\left(\beta >0\right)(5)$

The Laplace transform formula for the Caputo fractional order derivative is

$L\left({}_0{}^C{D}_t^{\beta }f\left(t\right)\right)=s^{\beta }U\left(s\right)-{\displaystyle \sum _{j=0}^{n-1}}{u}^{\left(j\right)}\left(0\right)s^{\beta -j-1},\left(n-1<u\le n\right)(6)$

where $U\left(s\right)$ is the Laplace transform operator of the function $f\left(t\right)$.

3.1.2 Establishment of fractional order viscoelastic and viscoplastic bodies

The theory of fractional order calculus is applied to the traditional Newtonian dashpot to construct a fractional dashpot, called the Abel dashpot. As shown in Figure 4:

Define the stress-strain equation for the Abel dashpot as

$\sigma \left(t\right)={\eta }_0\frac{d^{\beta }\epsilon \left(t\right)}{d{t}^{\beta }}(7)$

Where η is the viscosity coefficient; $\sigma \left(t\right)$ is the axial stress and $\epsilon \left(t\right)$ is the axial strain.

When $\beta =0,{\eta }_0=E,\sigma =E\epsilon ,$ representing linear elastomer, namely, Hooke elastomer; When $\beta =1,\sigma ={\eta }_{0}d\epsilon /dt,$ corresponding to Newtonian dashpot and satisfying the ideal fluid. So, the physical meaning of Abel dashpot can be defined as a fluid element between Hooke elastomer and Newtonian body.

In the study of rock creep mechanics, $\sigma \left(t\right)=\sigma =const$, Eq. 7 is integrated with Caputo fractional operator, and the creep equation of fractional Abel dashpot can be expressed as

$\epsilon \left(t\right)=\frac{\sigma }{{\eta }_0}\cdot \frac{t^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)},m\le \beta \le m+1(8)$

For Eq. 8, if $\sigma /{\eta }_0$ is a constant, select $0<\beta \le 1$ and $\beta >1$ to draw the figure of strain time as follows:

As shown in Figures 2, 3, the growth rate of $\epsilon$ is variate non-linear follow $\beta$. Combining with Figure 1, the constitutive relationship curves of Abel dashpot can be used to describe the typical creep properties of the rock. When the stress level is below the long-term strength of the rock, the decay creep stage can be characterized by Abel daspot with $0<\beta <1$. When the stress level exceed the long-term strength of the rock, the accelerating creep stage can be characterized by Abel despot with $\beta >1$. Therefore, the Abel dashpot body is introduced by paralleling with the friction plate to construct a fractional order viscoplastic body, as shown in Figure 4. The stress relationship of fractional order plastic body as:

$\sigma ={\sigma }_s+{\sigma }_{Abel}(9)$

FIGURE 2

FIGURE 2. $0<\beta \le 1$.

FIGURE 3

FIGURE 3. $\beta >1$.

FIGURE 4

FIGURE 4. The six-element non-linear elastic-viscoplastic creep model.

Substituting Eq. 7 into Eq. 9, the fractional order viscoplastic body creep constitutive relationship as:

${\epsilon }_{vp}\left(t\right)=\frac{\sigma -{\sigma }_s}{{\eta }_2}\cdot \frac{t^k}{\mathrm{\Gamma }\left(1+k\right)},\left(k>1\right)(10)$

where ${\eta }_2$ is the viscosity coefficient of the viscoplastic body, and ${\sigma }_s$ is the long-term strength of the rock.

3.2 Elastic-viscoplastic creep model

3.2.1 The elastic-viscoplastic creep model and one-dimensional creep equation

Based on fractional order calculus theory and Boltzmann superposition principle, a six-element non-linear elastic-viscoplastic creep model is proposed as shown in Figure 4 in this paper. The model consists of a Hooke elastomer, an Abel dashpot body, a Kelvin body, and a fractional order viscoplastic body in series. In this case, the instantaneous creep of the rock is characterized by Hooke elastomer. The non-linear decay creep is characterized by the Abel dashpot body. The steady-state creep is approximated by a constant strain with time, as $t\to \infty$, the slope of the strain-time curve $k=\raisebox{1ex}{$d\epsilon \left(t\right)$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.=const$, and the constitutive relationship for this stage is described by the conventional linear Kelvin body. Finally, the accelerating creep stage is described by the fractional order viscoplastic body.

According to the series-parallel law for the combined element model, when the stress is a constant, the stress-strain relationship for the six-element non-linear elastic-viscoplastic creep model as the following equation shows:

$\left.\begin{array}{l}\sigma ={\sigma }_e={\sigma }_{ve0}={\sigma }_{vel}={\sigma }_{vp}\\ \epsilon \left(t\right)={\epsilon }_e\left(t\right)+{\epsilon }_{ve0}\left(t\right)+{\epsilon }_{vel}\left(t\right)+{\epsilon }_{vp}\left(t\right)\end{array}\right\}(11)$

where ${\sigma }_e,{\sigma }_{ve0},{\sigma }_{vel},{\sigma }_{vp}$ is the stress of Hooke elastomer, Abel dashpot body, Kelvin body and fractional order viscoplastic body, respectively. $\epsilon {\left(t\right)}_e,\epsilon {\left(t\right)}_{ve0},\epsilon {\left(t\right)}_{vel},\epsilon {\left(t\right)}_{vp}$ is the strain of Hooke elastomer, Abel dashpot body, Kelvin body and fractional order viscoplastic body, respectively.

(i) When $\sigma <{\sigma }_s$, there is only transient elastic creep, decay creep and steady-state creep in the rock, no accelerating creep has occurred, and only Hooke elastomer, Abel dashpot, kelvin body at work, the stress-strain relationship of the model equation is

$\left.\begin{array}{l}\sigma ={\sigma }_e={\sigma }_{ve0}={\sigma }_{vel}\\ \epsilon \left(t\right)={\epsilon }_e\left(t\right)+{\epsilon }_{ve0}\left(t\right)+{\epsilon }_{vel}\left(t\right)\end{array}\right\}(12)$

The creep equation of the Hooke elastomer and Abel dashpot body is

$\left.\begin{array}{l}{\epsilon }_e\left(t\right)=\frac{\sigma }{E_0}\\ {\epsilon }_{ve0}\left(t\right)=\frac{\sigma }{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}\end{array}\right\}(13)$

For kelvin body, according to the parallel law, there is

$\left.\begin{array}{l}\sigma ={\sigma }_{E_1}+{\sigma }_{{\eta }_1}\\ \epsilon ={\epsilon }_{E_1}+{\epsilon }_{{\eta }_1}\\ {\sigma }_{E_1}=E_1\epsilon \\ {\sigma }_{{\eta }_1}={\eta }_1\dot{\epsilon }\end{array}\right\}(14)$

So, the creep constitutive equation of kelvin body is

$\sigma =E_1\epsilon +{\eta }_1\frac{d\epsilon }{dt}(15)$

Solve Eq. 15, obtain the creep equation of the linear kelvin body is

${\epsilon }_{vel}\left(t\right)=\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right](16)$

where $\sigma$ is strain, $E_1,{\eta }_1$ is elastic modulus and viscosity coefficient, respectively.

Substituting Eqs 13, 16 into Eq. 12, access the equation of $\epsilon \left(t\right)$ as

$\epsilon \left(t\right)=\frac{\sigma }{E_0}+\frac{\sigma }{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right],\left(\sigma <{\sigma }_s,0<p<1\right)(17)$

(ii) When $\sigma \ge {\sigma }_s$, the rock undergoes accelerating creep and the fractional order viscoplastic body is added to the work, the stress-strain relationship of the model is given by

$\left.\begin{array}{l}\sigma ={\sigma }_e={\sigma }_{ve0}={\sigma }_{vel}={\sigma }_{vp}\\ \epsilon \left(t\right)={\epsilon }_e\left(t\right)+{\epsilon }_{ve0}\left(t\right)+{\epsilon }_{vel}\left(t\right)+{\epsilon }_{vp}\left(t\right)\end{array}\right\}(18)$

Combining Eq. 10, Eq. 13 and Eq.16 and substituting them into Eq. 18, access the equation of $\epsilon \left(t\right)$ as

$\epsilon \left(t\right)=\frac{\sigma }{E_0}+\frac{\sigma }{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]+\frac{\sigma -{\sigma }_s}{{\eta }_2}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)},\left(\sigma \ge {\sigma }_s,k>1\right)(19)$

In summary, the non-linear creep equation for rock in a one-dimensional stress state is as follows:

$\epsilon \left(t\right)=\left\{\begin{array}{l}\frac{\sigma }{E_0}+\frac{\sigma }{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right],\left(\sigma <{\sigma }_s,0<p<1\right)\\ \frac{\sigma }{E_0}+\frac{\sigma }{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]+\frac{\sigma -{\sigma }_s}{{\eta }_2}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)},\left(\sigma \ge {\sigma }_s,k>1\right)\end{array}\right.(20)$

3.2.2 Three-dimensional creep equation

In geotechnical engineering, rocks are often in a complex three-dimensional stress state. Therefore, in order to reflect the creep properties of rocks in geotechnical engineering more accurately, the three-dimensional creep constitutive equation should be adopted. According to the theory of elasticity, the internal stress tensor ${\sigma }_{ij}$ of rock can be decomposed into a spherical stress tensor ${\sigma }_m$ and deviatoric stress tensor $s_{ij}$ under the condition of the three-dimensional stress. Similarly, the total strain tensor ${\epsilon }_{ij}$ of rock can be decomposed into a spherical strain tensor ${\epsilon }_m$ and a deviatoric strain tensor $e_{ij}$, and their constitutive relationship can be expressed, respectively, as follow:

$\left\{\begin{array}{l}{\sigma }_{ij}=s_{ij}+{\sigma }_{ij}{\delta }_{ij}\\ {\epsilon }_{ij}=e_{ij}+{\epsilon }_m{\delta }_{ij}\end{array}\right.(21)$

where ${\sigma }_{ij}$ is the Kronecker delta. The relationship between different stress tensors and strain tensors is as follows:

$\left.\begin{array}{l}{\sigma }_m=\frac{1}{3}\left({\sigma }_1+{\sigma }_2+{\sigma }_3\right)=\frac{1}{3}{\sigma }_{kk}\\ {\epsilon }_m=\frac{1}{3}\left({\epsilon }_1+{\epsilon }_2+{\epsilon }_3\right)=\frac{1}{3}{\epsilon }_{kk}\end{array}\right\}(22)$

Under the condition of the three dimensional stress, assuming the total strain of the non-linear creep model is ${\epsilon }_{ij}\left(t\right)$. ${\epsilon }_{ij}^0\left(t\right)$, ${\epsilon }_{ij}^{ve0}\left(t\right)$, ${\epsilon }_{ij}^{vel}\left(t\right)$, ${\epsilon }_{ij}^{vp}\left(t\right)$ is the strain of Hooke elastomer, Abel dashpot body, Kelvin body and fractional order viscoplastic body, respectively. Based on the theoretical superposition principle of the component combination model, the relationship of strain is

${\epsilon }_{ij}\left(t\right)={\epsilon }_{ij}^e\left(t\right)+{\epsilon }_{ij}^{ve0}\left(t\right)+{\epsilon }_{ij}^{vel}\left(t\right)+{\epsilon }_{ij}^{vp}\left(t\right)(23)$

In rock creep tests, when the first order stress level applied is less than the long-term strength of the rock, the rock develops transient strain rapidly, and the constitutive relationship at this stage can be described by a Hooke elastomer.

For the Hooke elastomer, the elastic constitutive relation can be expressed by Hooke’s Law as

$\left.\begin{array}{l}{s}_{ij}=2G{e}_{ij}\\ {\sigma }_{ij}=3K{\epsilon }_{ij}\end{array}\right\}(24)$

where $G$, $K$ is the shear modulus and bulk modulus, respectively. The relationship between the shear modulus $G$, bulk modulus $K$, elastic modulus $E$, and Poisson`s ratio $\mu$ of soil is

$\left.\begin{array}{l}G=\frac{E}{2\left(1+\mu \right)}\\ K=\frac{E}{3\left(1-2\mu \right)}\end{array}\right\}(25)$

Hence, the strain of the Hooke elastomer can be written as

${\epsilon }_{ij}^e\left(t\right)=\frac{1}{2G_0}{S}_{ij}+\frac{1}{3K_0}{\sigma }_m{\delta }_{ij}(26)$

When the stress keep loading, the rock enters a non-linear decay creep phase, which is described by the Abel dashpot in this paper, and the three-dimensional creep constitutive equation as:

${\epsilon }_{ij}^{ve0}=\frac{1}{2{\eta }_0}{S}_{ij}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}(27)$

Then, the rock will undergo steady-state creep, use the conventional linear Kelvin body to describe this phase of the rock creep process in this paper. Assuming that the volume change is elastic and the rheological properties are mainly in terms of shear deformation (Sun, 2007b), the three-dimensional creep constitutive equation is

${\epsilon }_{ij}^{ve1}=\frac{1}{2G_1}{S}_{ij}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right](28)$

where $G_1$ and ${\eta }_1$ are the shear modulus and viscosity coefficient of the Kelvin body, respectively.

When the stress deviator tensor $s\ge {\sigma }_s$, significant plastic deformation occurs, and the rock enters a phase of accelerating creep until it breaks down.

In a three-dimensional stress state, when stress exceeds the viscoplastic yield surface, a viscoplastic strain will be generated. Based on Perzyna’s limit stress flow law (Perzyna, 1966; Aydan, 2016), the three-dimensional creep equation for fractional order viscoplastic body in the accelerating creep phase can be obtained as

${\epsilon }_{ij}^{vp}\left(t\right)=\frac{1}{{\eta }_2}〈\mathrm{\Phi }\left(\frac{F}{F_0}\right)〉\frac{\partial Q}{\partial {\sigma }_{ij}}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)},\left(k>1\right)(29)$

where $\mathrm{\Phi }\left(\frac{F}{F_0}\right)$ is the power function, $\mathrm{\Phi }\left(\frac{F}{F_0}\right)={\left(\frac{F}{F_0}\right)}^m$. $Q$ is the plastic potential function. $〈•〉$ is switch function, expressed as:

$\langle \mathrm{\Phi }\left(\frac{F}{F_0}\right)\rangle =\left\{\begin{array}{l}0,F<0\\ \left(\frac{F}{F_0}\right),F\ge 0\end{array}\right.(30)$

$F$ is the rock yield function. $F_0$ is the initial value of the rock yield function, generally taken as $F_0=1$ (Al-Rub et al., 2013). The exponent $m$ is a constant and generally taken as $m=1.$

Combining Eqs 26–30 into Eq. 23, obtain the three-dimensional creep equation as follow

${\epsilon }_{ij}\left(t\right)=\left\{\begin{array}{l}\frac{1}{2G_0}{S}_{ij}+\frac{1}{3K_0}{\sigma }_m{\delta }_{ij}+\frac{1}{2{\eta }_0}{S}_{ij}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{1}{2G_1}{S}_{ij}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]\\ \left(F<0\right)\\ \frac{1}{2G_0}{S}_{ij}+\frac{1}{3K_0}{\sigma }_m{\delta }_{ij}+\frac{1}{2{\eta }_0}{S}_{ij}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{1}{2G_1}{S}_{ij}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]\\ +\frac{1}{{\eta }_2}{\left(\frac{F}{F_0}\right)}^m\frac{\partial Q}{\partial {\sigma }_{ij}}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)}\\ \left(F\ge 0\right)\end{array}\right.(31)$

The classical rock strength criterion includes Mohr-coulomb criterion, Tresca criterion, Von-Mises criterion and Drucker-Prager criterion, et al. However, the Mohr-coulomb and Tresca criterion considers only the maximum and minimum principal stress of the three principal stresses and does not consider the effect of intermediate principal stresses in the material. The Von-Mises criterion does not consider the effect of hydrostatic pressure on yielding and damage. The Drucker-Prager yield criterion improves the corner singularity problem of the Mohr-Coulomb criterion, and is also suitable for describing the yield behavior of rock materials. Therefore, the Drucker-Prager criterion is chosen as the yield criterion for rock creep analysis in this paper. In creep deformation, the creep yield deformation of rock materials mainly results from the deviator stress tensor, and the spherical stress tensor has little effect on yield deformation (Zheng and Kong, 2006), which is defined by

$F=\sqrt{J_2}-{\sigma }_s/\sqrt{3}(32)$

where $J_2$ is the second deviatoric stress tensor invariant. The tested material is suitable for the associated flow rule when $F=Q$ (Moghadam et al., 2013).

In the true triaxial stress environment, the rock is stressed from three directions, and there is

$\left.\begin{array}{l}{\sigma }_1>{\sigma }_2>{\sigma }_3\\ {\sigma }_m=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}\\ S_{11}={\sigma }_1-{\sigma }_m=\frac{2{\sigma }_1-{\sigma }_2-{\sigma }_3}{3}\end{array}\right\}(33)$

Considering the triaxial creep experiment in the normal triaxial stress status, i.e., σ1 >σ2 = σ3, we can obtain

$\left.\begin{array}{l}{\sigma }_m=\frac{{\sigma }_1+2{\sigma }_3}{3}\\ S_{11}=\frac{2\left({\sigma }_1-{\sigma }_3\right)}{3}\\ \sqrt{J_2}=\frac{1}{\sqrt{3}}\left({\sigma }_1-{\sigma }_3\right)\\ F\frac{\partial F}{\partial {\sigma }_{11}}=\frac{{\sigma }_1-{\sigma }_3-{\sigma }_s}{3}\end{array}\right\}(34)$

Substituting Eqs 32–34 into Eq. 31, the full-stage creep strain under the three-dimensional stress state is obtained as follows:

${\epsilon }_{11}\left(t\right)=\left\{\begin{array}{l}\frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1+2{\sigma }_3}{9K_0}+\frac{1}{{\eta }_0}\frac{\left({\sigma }_1-{\sigma }_3\right)}{3}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]\\ \left({\sigma }_1-{\sigma }_3<{\sigma }_s\right)\\ \frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1+2{\sigma }_3}{9K_0}+\frac{1}{{\eta }_0}\frac{\left({\sigma }_1-{\sigma }_3\right)}{3}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}\\ +\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]+\frac{1}{{\eta }_2}\frac{{\sigma }_1-{\sigma }_3-{\sigma }_s}{3}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)}\\ \left({\sigma }_1-{\sigma }_3\ge {\sigma }_s\right)\end{array}\right.(35)$

Where ${\epsilon }_{11}\left(t\right)$ represents the vertical strain of the sample under constant stress.

3.3 Non-linear creep model for layered rock

Due to the existence of weak bedding planes, layered rock often shows obvious anisotropy characteristic, specifically transverse isotropic characteristics. According to the results of tests in the available literature (Hu et al., 2019; Liu et al., 2015; Xu et al., 2019; Zhang et al., 2021), the angle of the laminae has a large influence on the creep properties of the rock. For transverse isotropic material creep models, the research literature (Wang et al., 2018) is divided into two main types, namely, empirical models generalized by experiment and theoretical models resolved by plasticity theory. Based on the viscoelastic-plastic creep model established in this paper, the empirical model method and the plasticity theory analytical method are used to derive the intrinsic constitutive equations of the creep model for layered rock, and the relevant experimental data are used for comparative analysis and verification.

3.3.1 Creep equation of empirical model

The establishment method of the empirical model for layered rock creep is based on the model of isotropic materials. The creep equation of layered rock is derived by introducing the influence of laminae on the mechanical properties of rock creep. For example, Tang (Tang et al., 2018) gave the relationship between the elastic modulus, creep rate and bedding angle at the same moisture content by uniaxial compression creep test as

$\left.\begin{array}{l}E=A\underset{B\beta }{e}\\ \frac{1}{\eta }=D\underset{m\beta }{e}\end{array}\right\}(36)$

where $A,B,C,D,m$ is a fitting coefficient, $\beta$ is the bedding angle.

The paper introduces functional expressions of elastic modulus and creep rate, and proposes a one-dimensional creep constitutive equation for layered shale based on the Burgers model. However, the creep model for the accelerating creep stage was not given in that paper. Wang (Wang, 2020) obtained the anisotropic characteristics of long-term strength, peak strength and elastic modulus of sandstones with different bedding angles by triaxial creep tests.

In this paper, based on the research, the non-linear elastic-viscoplastic whole process creep equation for layered rock is derived analogously from the isotropic rock material creep model constitutive equation. The one-dimensional creep equation of the elastic-viscoplastic creep of layered rock is

$\epsilon \left(t\right)=\left\{\begin{array}{l}\frac{\sigma }{E_0\left(\beta \right)}+\frac{\sigma }{{\eta }_0\left(\beta \right)}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right],\left(\sigma <{\sigma }_s,0<p<1\right)\\ \frac{\sigma }{E_0\left(\beta \right)}+\frac{\sigma }{{\eta }_0\left(\beta \right)}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]+\frac{\sigma -{\sigma }_s\left(\beta \right)}{{\eta }_2}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)},\left(\sigma \ge {\sigma }_s,k>1\right)\end{array}\right.(37)$

where $\beta$ is bedding angle, and the diagram of bedding angle is shown in Figure 5. $E_0\left(\beta \right),{\eta }_0\left(\beta \right),{\sigma }_s\left(\beta \right)$ is the functions of the effect of changes in bedding angle on the elastic modulus, viscosity coefficient and long-term strength of rock, respectively.

FIGURE 5

FIGURE 5. Diagram of bedding angle.

Accordingly, with reference to the derivation of the three-dimensional creep equation for isotropic rock materials, the three-dimensional creep equation of the elastic-viscoplastic creep of layered rock is

${\epsilon }_{11}\left(t\right)=\left\{\begin{array}{l}\frac{{\sigma }_1-{\sigma }_3}{3G_0\left(\beta \right)}+\frac{{\sigma }_1+2{\sigma }_3}{9K_0\left(\beta \right)}+\frac{1}{{\eta }_0\left(\beta \right)}\frac{\left({\sigma }_1-{\sigma }_3\right)}{3}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]\\ \left({\sigma }_1-{\sigma }_3<{\sigma }_s\left(\beta \right)\right)\\ \frac{{\sigma }_1-{\sigma }_3}{3G_0\left(\beta \right)}+\frac{{\sigma }_1+2{\sigma }_3}{9K_0\left(\beta \right)}+\frac{1}{{\eta }_0\left(\beta \right)}\frac{\left({\sigma }_1-{\sigma }_3\right)}{3}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}\\ +\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]+\frac{1}{{\eta }_2}\frac{{\sigma }_1-{\sigma }_3-{\sigma }_s\left(\beta \right)}{3}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)}\\ \left({\sigma }_1-{\sigma }_3\ge {\sigma }_s\left(\beta \right)\right)\end{array}\right.(38)$

3.3.2 Creep equation based on plastic theory

The plasticity theory analytical method based on the assumption of constant Poisson’s ratio (Dathe et al., 2001). It is assumed that Poisson’s ratio does not change with time and stress, and is equivalent to the value of elastic stage, $\mu \left(\sigma ,t\right)=\mu$. Based on the creep constitutive equation established under one-dimensional condition, the equation can be extended from one-dimensional stress state to three-dimensional. Let the creep compliance $J\left(t\right)$ in Eq. 20 is given as:

$J\left(t\right)=\left\{\begin{array}{l}\frac{1}{E_0}+\frac{1}{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{1}{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right],\left(\sigma <{\sigma }_s\right)\\ \frac{1}{E_0}+\frac{1}{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{1}{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]+\frac{1-{\sigma }_s/\sigma }{{\eta }_2}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)},\left(\sigma \ge {\sigma }_s\right)\end{array}\right.(39)$

Then, Eq. 20 can be described as

$\epsilon =J\left(t\right)\sigma (40)$

For isotropic rock, the creep compliance substitution method can be used to obtain the basic form of the three-dimensional creep equation of rock as follows (Li et al., 2021):

$\left\{\epsilon \right\}=J\left(t\right)\left[A\right]\left\{\sigma \right\}(41)$

where $\left[A\right]$ is Poisson’s ratio matrix for isotropic material; $\left\{\epsilon \right\}$ and $\left\{\sigma \right\}$ are strain tensor and stress tensor, respectively.

For Eq. 41, scholars (Aravas et al., 1995; Kou et al., 2023) have carried out a detailed solution, which is not repeated in this paper. Based on the creep constitutive model established in this paper, the three-dimensional creep constitutive equation for layered rock is derived as

$\begin{array}{l}{\epsilon }_{11}\left(t\right)=\left\{\frac{1}{E_0}+\frac{1}{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{1}{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]+\frac{1-\raisebox{1ex}{${\sigma }_s$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.}{{\eta }_2}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)}\right\}\\ \times \left\{-\frac{{\mu }^{\prime }}{n}\left({\sin }^4\theta +{\cos }^4\theta +\frac{{\sin }^{2}2\theta }{2}\right){\sigma }_x+\left[{\sin }^4\theta +\frac{{\cos }^4\theta }{n}+\frac{{\sin }^{2}2\theta }{4}\left(1+\frac{1}{n}\right)\right.]{\sigma }_y-\left(\mu {\sin }^2\theta \frac{{\mu }^{\prime }}{n}{\cos }^2\theta \right){\sigma }_z\right.\}\end{array}(42)$

where $\mu ,{\mu }^{\prime }$ is Poisson’s ratio parallel to and perpendicular to foliation plane, respectively. $\theta$ is the bedding angle, defined as the angle with the horizontal plane. Defining $n=\stackrel{\theta =90°}{E}/\stackrel{\theta =0°}{E}$, $E_{\theta =90°}、E_{\theta =0°}$ is elastic modulus perpendicular to and parallel to foliation plane, individually. ${\sigma }_x,{\sigma }_y,{\sigma }_z$ are the three axes of positive pressure in the direction of the overall orthogonal coordinate axes, respectively.

4 Parameter identification and model validation

4.1 Parameter identification of non-layered rock creep model

4.1.1 The one-dimensional non-linear creep model

The uniaxial compression non-linear creep model is shown in Eq. 20, and parameters of the model to be determined are $E_0,{\eta }_0,p,E_1,{\sigma }_s,{\eta }_2,k.$

(i) The parameters of $E_0,{\sigma }_s$

In the transient elastic creep stage, $E_0$ could be calculated from $E=\sigma /\epsilon$. ${\sigma }_s$ could be obtained from experimental data.

(ii) The parameters of ${\eta }_0,p,E_1,{\eta }_1$

$\sigma ,E_0$ already known. Selecting the corresponding creep test data of $\sigma \left(\sigma <{\sigma }_s\right)$ to establish the non-linear function of Eq. 17, fitted by Origin using the Levenberg-Marquardt iterative method, then ${\eta }_0,p,E,{\eta }_1$ were obtained.

(iii) The parameters of ${\eta }_2,k$

Selecting the corresponding creep test data of $\sigma \left(\sigma \ge {\sigma }_s\right)$ to perform step-by-step fitting, the operation process as follows: the first step is to take the test data from the decay creep and steady creep stages and follow the operation of (i) and (ii) in turn to obtain $E_0,{\eta }_0,p,E_1,{\eta }_1,{\sigma }_s$, the second step is to take the test data of $\sigma \left(\sigma \ge {\sigma }_s\right)$ to perform the non-linear fitting, then ${\eta }_2,k$ obtained.

4.1.2 Three-dimensional non-linear creep model

The triaxial compression non-linear creep model is shown in Eq. 35, and the model parameters to be determined are $G_0,K_0,{\eta }_0,G_1,{\eta }_1,p,{\sigma }_s,{\eta }_2,k$. Let the constant as

$\left.\begin{array}{l}M=\frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1+2{\sigma }_3}{9K_0}\\ N=\frac{{\sigma }_1-{\sigma }_3}{3}\\ R=\frac{{\sigma }_1-{\sigma }_3-{\sigma }_s}{3}\end{array}\right\}(43)$

then Eq. 35 can be described as

${\epsilon }_{11}\left(t\right)=\left\{\begin{array}{l}M+\frac{1}{{\eta }_0}N\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{N}{G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]\\ \left({\sigma }_1-{\sigma }_3<{\sigma }_s\right)\\ M+\frac{1}{{\eta }_0}N\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{N}{G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]+\frac{1}{{\eta }_2}R\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)}\\ \left({\sigma }_1-{\sigma }_3\ge {\sigma }_s\right)\end{array}\right.(44)$

The process of parameter identification is:

(i) The parameters of $G_0,K_0,{\eta }_0,G_1,{\eta }_1,p$

Based on the elastic modulus $E$ and Poisson’s ratio μ from conventional triaxial compression tests on rocks under the same circumferential pressure, $G_0$ and $K_0$ are obtained through Eq. 25. Then, combining $G_0,K_0$ into Eq. 35 to perform the non-linear fitting with the creep experimental data from the stress of $\sigma \left(\sigma <{\sigma }_s\right)$.

(ii) The parameters of ${\sigma }_s,{\eta }_2,k$

The parameter of ${\sigma }_s$ could be calculated from triaxial creep experimental data. Selecting the full process of high-stress creep experimental data and fitting it to obtain $G_0,K_0,{\eta }_0,G_1,{\eta }_1,p$ firstly, then referring to the step-wise fitting method in Section 4.1.1, we could obtain ${\eta }_2,k$.

4.2 Parameter identification of layered rock creep model

The non-linear creep model for layered rock is shown in Eqs 37, 38 and Eq. 42, and the parameters identification method is similar to the non-layered rock creep model. In view of space, do not repeat.

4.3 Parameter identification and model validation

4.3.1 One-dimensional non-linear creep model

The experimental data used for parameter identification in the one-dimensional creep equation is chosen from Wang (Wang et al., 2020). The test was carried out using the MTS815.02 Multifunctional Servo Test System for uniaxial compression creep testing of sandstone with graded loading, and the long-term strength given in the paper is 70 MPa. In this paper, data from the water content test set $\omega =0\%$ is taken for parameter identification of the creep model. The graded loading scheme of the uniaxial compression creep test is $60MPa,70MPa,80MPa,90MPa,100MPa,$ respectively. The contrastive analysis of the creep calculation curve and experimental data are illustrated in Figure 6.

FIGURE 6

FIGURE 6. Creep equation fitting curves ($\omega =0\%$).

Showing in Figure 7, the proposed creep model can accurately describe the characteristics of three phases of rock creep, the rationality is verified. The parameters of the creep model listed in Table 2.

FIGURE 7

FIGURE 7. Creep equation fitting curves ($\omega =4.56\%$).

TABLE 2

TABLE 2. Parameters of the one-dimensional creep model.

4.3.2 The three-dimensional non-linear creep model

The experimental data used for parameter identification in the three-dimensional creep equation is chosen from Ye (Ye et al., 2022). This test was carried out for triaxial compression creep tests at different water contents $\omega$ at an confining pressure of 1 MPa. The graded loading scheme of the triaxial compression creep test is shown in Table 3 and the long-term strength of rock is $2.48MPa,1.28MPa,0.88MPa,$ respectively.

TABLE 3

TABLE 3. Graded loading scheme.

Using the method of the previous Section 4.1.2 for model parameters identification. When the loading stress level is less than the yield strength, the first equation of Eq. 35 is used for nonlinear fitting. The fit of the experimental data to the creep equation was obtained as shown in Figures 8–10.

FIGURE 8

FIGURE 8. Creep equation fitting curves ($\omega =8.47\%,\omega =12.38\%$).

FIGURE 9

FIGURE 9. Creep equation fitting curve ($\omega =8.47\%$).

FIGURE 10

FIGURE 10. Creep equation fitting curve ($\omega =12.38\%$).

When the loading stress level is greater than the yield strength, a step-wise non-linear fitting is made by the second equation of Eq. 35. The fitting curve of the moisture content under low-stress level is shown in Figure 8, and the fitting curve of the moisture content of $\omega =8.47\%,\omega =12.38\%$ under high-stress level is shown in Figures 11, 12. The parameters of the creep model listed in Table 4.

FIGURE 11

FIGURE 11. Creep equation fitting curves ($\omega =0\%$).

FIGURE 12

FIGURE 12. Creep equation fitting curves of different bedding angles $\left(\beta =0°,30°,45°\right)$.

TABLE 4

TABLE 4. Parameters of the three-dimensional creep model.

Analyzing Figures 7, 10, the creep model not only describes the viscoelastic behavior in the decay creep and steady-state creep phases of the rock in uniaxial creep experiment and triaxial creep experiment well under low stress, but also has a good representation of the non-linear mechanical behavior in the accelerating creep phase of the rock under high-stress conditions. Furthermore, as seen in Tables 2, 4, the correlation between experimental data and fitting curves is high. The reasonableness and applicability of the fractional order creep model proposed in this paper are verified.

4.3.3 Creep model for layered rock

(i) Creep Equation of Empirical Model

The experimental data used for parameter identification in the one-dimensional creep equation is chosen from Tang (Tang et al., 2018). Selecting the data of ${60}^0$ ($\omega =0\%$), and fitting by Eq. 37. The fitting curves are shown in Figure 11.

The parameters of the creep model listed in Table 5.

TABLE 5

TABLE 5. Parameters of the creep model.

The experimental data used for parameter identification in the three-dimensional creep equation is chosen from Wang (J. Wang et al., 2020). The author took the triaxial compression creep tests on five sets of specimens with bedding angles of $0^0,{30}^0,{45}^0,{60}^0$ and ${90}^0$ under the confining pressure condition of 5 MPa. In this paper, selecting five sets of experimental data from the accelerating creep phase with different bedding angles to be fitted to identify the model parameters. The fitting curve is shown in Figures 12, 13.

FIGURE 13

FIGURE 13. Creep equation fitting curves of different bedding angles $\left(\beta =60°,90°\right)$.

The parameters of the creep model are listed in Table 6.

TABLE 6

TABLE 6. Parameters of creep model.

Based on the parameters from Table 6, giving the plotting of $G_0$ and $1/{\eta }_0$ with different bedding angles separately, and comparing with the experimental data in the original paper. We find that the parameters have a similar trend to the parameters from the experiment, verifying the influence of the bedding angle on the creep properties of the rock. As shown in Figures 14, 15.

(ii) Creep Equation of Plasticity Theory

FIGURE 14

FIGURE 14. Shear modulus vs. elastic modulus.

FIGURE 15

FIGURE 15. Steady-state creep rate.

Experimental data were used from the literature (Kou et al., 2023). In the literature, step-wise loading triaxial creep tests of phyllite specimens with three kinds of bedding angles (0°, 45° and 90°) are carried out with the confining pressure of 10 MPa. In this paper, the last stage accelerating creep test data of 0° and 90° layered rock is taken to validate the plasticity theory creep equation and compared with the empirical model creep equation simultaneously. The elastic mechanical parameters of the rock are shown in Table 7. For the bedding angle of 0°, the elastic modulus, poission ratio and long-term strength of rock is $26.25GPa,\mathrm{0.29,91}MPa,$ respectively. For the bedding angle of 90°, the elastic modulus, poission ratio and long-term strength of rock is $29.31GPa,\mathrm{0.36,91}MPa,$ respectively.

TABLE 7

TABLE 7. Creep parameters of plasticity theory model and empirical model.

For Eq. 42, let

$\begin{array}{l}F\left(\theta \right)=-\frac{{\mu }^{\prime }}{n}\left({\sin }^4\theta +{\cos }^4\theta +\frac{{\sin }^{2}2\theta }{2}\right){\sigma }_x+\left[{\sin }^4\theta +\frac{{\cos }^4\theta }{n}+\frac{{\sin }^{2}2\theta }{4}\left(1+\frac{1}{n}\right)\right]{\sigma }_y\\ -\left(\mu {\sin }^2\theta \frac{{\mu }^{\prime }}{n}{\cos }^2\theta \right){\sigma }_z\end{array}(45)$

Then Eq. 42 is expressed as

${\epsilon }_{11}\left(t\right)=F\left(\theta \right)\left\{\frac{1}{E_0}+\frac{1}{{\eta }_0}\frac{t^p}{\mathrm{\Gamma }\left(1+p\right)}+\frac{1}{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]+\frac{1-\raisebox{1ex}{${\sigma }_s$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.}{{\eta }_2}\frac{t^k}{\mathrm{\Gamma }\left(1+k\right)}\right.\}(46)$

Substituting the elastic parameters from Table 9 into Eq. 45, then

$F\left(\theta \right)=\left\{\begin{array}{l}76.6305,\theta =0°\\ 85.6391,\theta =90°\end{array}\right.(47)$

Substituting Eq. 47 into Eq. 46, fitting the experimental data as shown in Figure 16. For the creep equation of the empirical model, the same set of experimental data was fitted by Eq. 38 using the method described in Section 4.1.2.

FIGURE 16

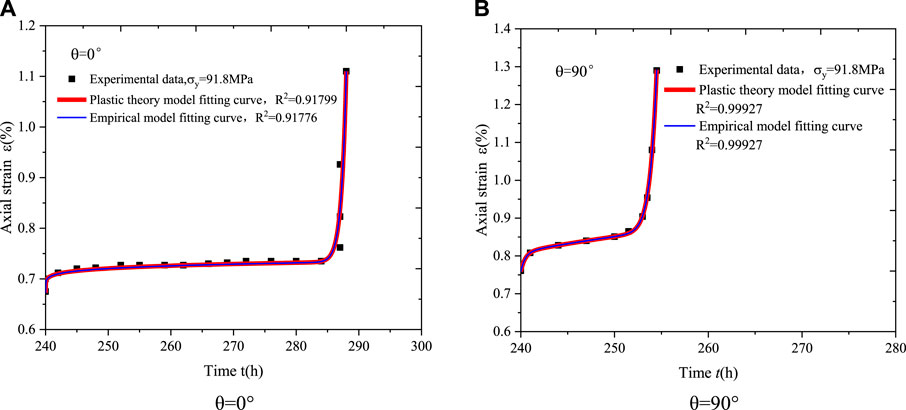
FIGURE 16. Fitting curves of creep equation by empirical model and plastic theory model [(A,B) is the bedding angle of 0°,90° respectively].

The creep constitutive equations for layered rock derived by the above two methods were fitting by the same set of experimental data, and a curve fit of the experimental data to the creep equation was obtained as shown in Figure 16.

The parameters of the two models are shown in Table 7.

As seen in Figure 16 and Table 7, the fitting curves of the creep constitutive equation for layered rock derived by the two methods are almost identical and have the same fitting correlation coefficients.

In summary, the non-linear creep model derived in this paper can not only better characterize the creep properties of layered rock under low and high-stress conditions, but also better reflect the influence of different bedding angles on the creep mechanical properties of rocks. In addition, the empirical creep constitutive equation derived in this paper and the plastic theory creep constitutive equation has almost the same fitting results for the same set of experimental data, which further verifies the accuracy and applicability of the creep constitutive model for layered rock established in this paper.

5 Conclusion

Based on fractional-order calculus theory and rheological element combination model theory, a six-element nonlinear elastic-viscoplastic creep model is given. The model is used as the basis for deriving the non-linear elastic-viscoplastic creep constitutive equation for layered rock, and the accuracy and applicability of the creep constitutive equation are verified by selecting creep experimental data for rocks of different lithologies. The main conclusions are as follows:

(1) Based on fractional calculus theory to introduce the Abel dashpot body, combined with the classical creep strain-time curve of rock for analysis, the Hooke elastomer, Abel dashpot body, Kelvin body and non-linear viscoplastic body are connected in series, and a six-element non-linear elastic-viscoplastic creep model is established. Then, the creep constitutive equation for one-dimensional and three-dimensional are derived respectively.

(2) Analysing the creep experimental data of layered rock, and concluding that the effects of different bedding angles on the creep properties of the rock are mainly the elastic modulus, creep rate and long-term strength, and deriving the full process creep constitutive equation for layered rock by empirical model method and the plastic theory method, respectively.

(3) Based on the Levenberg-Marquardt iterative method of Origin software, a practical identification method of creep model parameters is proposed, and parameters are identified by using rocks of different lithologies under different stress conditions from experimental data.

(4) By fitting the creep experimental data of layered rock with different lithologies to the theoretical curves of the model, it is shown that the model proposed in this paper can not only accurately describe the full-stage creep (primary creep, steady-state creep and accelerating creep) of layered rock, but also better reflect the influence of different bedding angles on the creep properties of rocks. As shown in the tables, the average value of $R^2$ is beyond 0.97, with the meaning of highly accuracy and applicability for the creep constitutive equation proposed in this paper. In addition, the empirical model creep constitutive equation and plastic theory constitutive equation have almost the same fitting results for the same set of experimental data.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Data curation, Investigation, Writing–original draft, Writing–review and editing. MS: Investigation, Methodology, Writing–review and editing, Writing–original draft. BD: Funding acquisition, Investigation, Methodology, Resources, Supervision, Writing–review and editing. SY: Investigation, Writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the National Natural Science Foundation of China (No. 52268022). The author BD is the leader of this project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer JJ declared a shared affiliation with the authors to the handling editor at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Rub, R., Darabi, M. K., Kim, S. M., Little, D. N., and Glover, C. J. (2013). Mechanistic-based constitutive modeling of oxidative aging in aging-susceptible materials and its effect on the damage potential of asphalt concrete. Constr. Build. Mater. 41 (apr), 439–454. doi:10.1016/j.conbuildmat.2012.12.044

CrossRef Full Text | Google Scholar

Aravas, N., Cheng, C., and Casta Eda, P. P. (1995). Steady-state creep of fiber-reinforced composites: constitutive equations and computational issues. Int. J. Solids Struct. 32 (15), 2219–2244. doi:10.1016/0020-7683(94)00251-Q

CrossRef Full Text | Google Scholar

Aydan, Ö. (2016). Time-dependency in rock mechanics and rock engineering.

Google Scholar

Behbahani, H., Ziari, H., and Kamboozia, N. (2016). Evaluation of the visco-elasto-plastic behavior of glasphalt mixtures through generalized and classic burger's models modification. Constr. Build. Mater. 118, 36–42. doi:10.1016/j.conbuildmat.2016.04.157

CrossRef Full Text | Google Scholar

Celleri, H. M., Martín, S., and Otegui, J. L. (2018). Fracture behavior of transversely isotropic rocks with discrete weak interfaces: fracture behavior of ti rocks with discrete weak interfaces. Int. J. Numer. Anal. Methods Geomech. 42, 2161–2176. doi:10.1002/nag.2849

CrossRef Full Text | Google Scholar

Chang, X., Zhao, H., and Cheng, L. (2020). Fracture propagation and coalescence at bedding plane in layered rocks. J. Struct. Geol. 141 (2), 104213. doi:10.1016/j.jsg.2020.104213

CrossRef Full Text | Google Scholar

Cheng, H., Zhou, X., Pan, X., and Berto, F. (2020). Damage analysis of sandstone during the creep stage under the different levels of uniaxial stress using nmr measurements. Fatigue Fract. Eng. Mater. Struct. 44, 719–732. doi:10.1111/ffe.13389

CrossRef Full Text | Google Scholar

Dathe, A., Eins, S., Niemeyer, J., and Gerold, G. (2001). The surface fractal dimension of the soil-pore interface as measured by image analysis. Geoderma Int. J. Soil Sci. 103 (1/2), 203–229. doi:10.1016/S0016-7061(01)00077-5

CrossRef Full Text | Google Scholar

Deng, H., Zhou, H., Jia, W., Li, L., and Su, T. (2022). A nonlinear triaxial damage creep model for granite based on atangana–baleanu fractional derivative. Int. J. Appl. Mech. 14. doi:10.1142/S1758825122500685

CrossRef Full Text | Google Scholar

Dubey, R. K., and Gairola, V. K. (2008). Influence of structural anisotropy on creep of rocksalt from simla himalaya, India: an experimental approach. J. Struct. Geol. 30 (6), 710–718. doi:10.1016/j.jsg.2008.01.007

CrossRef Full Text | Google Scholar

Feng, Z. Q., Yang, X. J., Liu, J. G., and Chen, Z. Q. (2021). A new fractional nishihara-type model with creep damage considering thermal effect. Eng. Fract. Mech. 242 (1), 107451. doi:10.1016/j.engfracmech.2020.107451

CrossRef Full Text | Google Scholar

Fortsakis, P., Nikas, K., Marinos, V., and Marinos, P. (2012). Anisotropic behaviour of stratified rock masses in tunnelling. Eng. Geol. 141-142 (none), 74–83. doi:10.1016/j.enggeo.2012.05.001

CrossRef Full Text | Google Scholar

Griggs, D. (1939). Creep of rocks. J. Geol. 47 (3), 225–251. doi:10.1086/624775

CrossRef Full Text | Google Scholar

Hb, M., Nasseri, H., S, K., Rao, , et al. (2003). Anisotropic strength and deformational behavior of himalayan schists. Int. J. Rock Mech. Min. Sci. 40, 3, 23. doi:10.1016/S1365-1609(02)00103-X

CrossRef Full Text | Google Scholar

Hu, B., Yang, S. Q., Xu, P., and Cheng, J. L. (2019). Cyclic loading–unloading creep behavior of composite layered specimens. Acta geophys. 67, 449–464. doi:10.1007/s11600-019-00261-x

CrossRef Full Text | Google Scholar

Koeller, R. C. (1984). Applications of fractional calculus to the theory of viscoelasticity. Trans. Asme J. Appl. Mech. 51 (2), 299–307. doi:10.1115/1.3167616

CrossRef Full Text | Google Scholar

Kou, H., He, C., Yang, W., Wu, F., Zhou, Z., Fu, J., et al. (2023). A fractional nonlinear creep damage model for transversely isotropic rock. Rock Mech. Rock Eng. 56 (56), 831–846. doi:10.1007/s00603-022-03108-y

CrossRef Full Text | Google Scholar

Li, L., Guan, J., Xiao, M., and Zhuo, L. (2021). Three-dimensional creep constitutive model of transversely isotropic rock. Int. J. Geomech. 21 (8), 21. doi:10.1061/(asce)gm.1943-5622.0002111

CrossRef Full Text | Google Scholar

Liu, X., Li, D., and Han, C. (2020). A nonlinear damage creep model for sandstone based on fractional theory. Arab. J. Geosci. 13 (6), 246. doi:10.1007/s12517-020-5215-1

CrossRef Full Text | Google Scholar

Liu, X., Li, D., and Han, C. (2021). A caputo fractional damage creep modeland its experimental validation. Mech. Time-Depend. Mater. 26 (26), 909–922. doi:10.1007/s11043-021-09519-8

CrossRef Full Text | Google Scholar

Liu, Z. B., Xie, S. Y., Shao, J. F., and Conil, N. (2015). Effects of deviatoric stress and structural anisotropy on compressivecreep behavior of a clayey rock. Appl. Clay Sci. 114, 491–496. doi:10.1016/j.clay.2015.06.039

CrossRef Full Text | Google Scholar

Moghadam, S. N., Mirzabozorg, H., and Noorzad, A. (2013). Modeling time-dependent behavior of gas caverns in rock salt considering creep, dilatancy and failure. Tunn. Undergr. Space Technol. 33 (Jan.), 171–185. doi:10.1016/j.tust.2012.10.001

CrossRef Full Text | Google Scholar

Park, K. H., Jung, Y. H., and Chung, C. K. (2016). Evolution of stiffness anisotropy during creep of engineered silty sand in South Korea. KSCE J. Civ. Eng. 21, 2168–2176. doi:10.1007/s12205-016-1105-1

CrossRef Full Text | Google Scholar

Perzyna, P. (1966). Fundamental problems in viscoplasticity. Adv. Appl. Mech. 9 (2), 243–377. doi:10.1016/S0065-2156(08)70009-7

CrossRef Full Text | Google Scholar

Ramamurthy, T. (1993). Strength and modulus responses of anisotropic rocks.

Google Scholar

Saeidi, O., Rasouli, V., Vaneghi, R. G., Gholami, R., and Torabi, S. R. (2014). A modified failure criterion for transversely isotropic rocks. Geosci. Front. 5 (2), 215–225. doi:10.1016/j.gsf.2013.05.005

CrossRef Full Text | Google Scholar

Shan, R. L., Bai, Y., Ju, Y., Han, T. Y., and Li, Z. L. (2020). Study on the triaxial unloading creep mechanical properties and damage constitutive model of red sandstone containing a single ice-filled flaw. Rock Mech. Rock Eng. 54 (6), 833–855. doi:10.1007/s00603-020-02274-1

CrossRef Full Text | Google Scholar

Shen, M., Bi, J., Zhao, Y., Wang, C., Wei, T., and Du, B. (2022). Study on the mechanical characteristics and damage evaluation of concrete-rock combination after high temperatures exposure. Constr. Build. Mater. 330, 127278. doi:10.1016/j.conbuildmat.2022.127278

CrossRef Full Text | Google Scholar

Shen, M., Zhao, Y., Bi, J., Wang, C., Du, B., and Zhang, K. (2023b). In situ experimental study on mechanical properties of interlayer in roller compacted concrete (rcc) dam. Constr. Build. Mater. 379, 131268. doi:10.1016/j.conbuildmat.2023.131268

CrossRef Full Text | Google Scholar

Shen, M., Zhao, Y., Bi, J., Wang, C., Ning, L., Deng, X., et al. (2023a). Micro-damage evolution and macro-mechanical property of preloaded sandstone subjected to high-temperature treatment based on nmr technique. Constr. Build. Mater. 369, 130638. doi:10.1016/j.conbuildmat.2023.130638

CrossRef Full Text | Google Scholar

Sun, J. (2007a). Rock rhelogical mechanicals and its advance in engineering applications. Chin. J. Rock Mech. Eng. 26 (6), 1081–1106. doi:10.1097/00000542-199411000-00017

CrossRef Full Text | Google Scholar

Sun, J. (2007b). Rock rhelogical mechanicals and its advance in engineering applications. Chin. J. Rock Mech. Eng. 26 (6), 1081–1106.

Google Scholar

Tang, J., Teng, J., and Zhang, C. (2018). Experimental study of creep characteristics of layered water bearing shale. Rock Soil Mech. 39 (S1), 33–41. doi:10.16285/j.rsm.2017.1709

CrossRef Full Text | Google Scholar

Wang, J., Meng, L., Liu, T., and Chen, H. (2020). Analysis of the influence of sandstone bedding structure on its mechanical properties. Railw. Stand. Des. 64 (04), 130–135. doi:10.13238/j.issn.1004-2954.201904040003

CrossRef Full Text | Google Scholar

Wang, X., and Wan, L. (2016). Nonlinear creep model of rock in consideration of damage. Sci. Technol. Eng.

Google Scholar

Wang, Y. (2020). Study on uniaxial compression creep test of sandstone and improvement of nishihara model. J. Lanzhou Inst. Technol. 27 (05), 10–14.

Google Scholar

Wang, Z., Zong, Z., Qiao, L., and Li, W. (2018). Elastoplastic model for transversely isotropic rocks. Int. J. Geomech. 18 (2), 4017141–4017149. doi:10.1061/(ASCE)GM.1943-5622.0001070

CrossRef Full Text | Google Scholar

Wu, B., Jia, S. P., and Luo, J. Z. (2015). Anisotropic composite model for layered rock mass based on characteristics of soft interfaces. Material Res. Innovations 19 (1)–S1-245. doi:10.1179/1432891715Z.0000000001478

CrossRef Full Text | Google Scholar

Wu, F., Jie, C., and Zou, Q. (2018). A nonlinear creep damage model for salt rock. Int. J. Damage Mech. 28, 1281561184. doi:10.1177/1056789518792649

CrossRef Full Text | Google Scholar

Xu, G., He, C., Yan, J., and Ma, G. (2019). A new transversely isotropic nonlinear creep model for layered phyllite and its application. Bull. Eng. Geol. Environ. 78, 5387–5408. doi:10.1007/s10064-019-01462-w

CrossRef Full Text | Google Scholar

Yang, X., and Jiang, A. (2022). An improved nonlinear creep damage model of slates considering freeze–thaw damage and bedding damage. Bull. Eng. Geol. Environ. 81, 240–246. doi:10.1007/s10064-022-02740-w

CrossRef Full Text | Google Scholar

Yang, X. W., Zhang, X. P., Zhang, Q., Li, C. D., and Wang, D. J. (2021). Study on the mechanisms of crack turning in bedded rock. Eng. Fract. Mech. 247, 107630. doi:10.1016/j.engfracmech.2021.107630

CrossRef Full Text | Google Scholar

Ye, W., Qili, W., Wenjing, L., Xiongyao, X., and Biao, Z. (2022). Compressive creep property and model for unsaturated argillaceous siltstone. J. TONGJI Univ. Sci. 50 (08), 1154–1162. doi:10.11908/j.issn.0253-374x.21326

CrossRef Full Text | Google Scholar

Yong, M. T., and Tsao, P. F. (2000). Preparation and mechanical properties of artificial transversely isotropic rock. Int. J. Rock Mech. Min. Sci. 37 (6), 1001–1012. doi:10.1016/S1365-1609(00)00024-1

CrossRef Full Text | Google Scholar

Yong, T., and Kuo, M. C. (2001). A failure criterion for transversely isotropic rocks. Int. J. Rock Mech. Min. Sci. 38, 399–412. doi:10.1016/S1365-1609(01)00007-7

CrossRef Full Text | Google Scholar

Zhang, J., Zhang, X., Huang, Z., and Fu, H. (2022a). Transversely isotropic creep characteristics and damage mechanism of layered phyllite under uniaxial compression creep test and its application. Environ. Earth Sci. 81 (20), 499–518. doi:10.1007/s12665-022-10585-5

CrossRef Full Text | Google Scholar

Zhang, J., Zhang, X., Huang, Z., Yi, Y., and Zhao, X. (2021). Energy evolution mechanism of the mechanical and creep properties of layered phyllite under uniaxial compression and creep tests. Arab. J. Geosci. 14 (22), 2437–2513. doi:10.1007/s12517-021-08757-x

CrossRef Full Text | Google Scholar

Zhang, Z., Jin, X., and Luo, W. (2019). Long-term behaviors of concrete under low-concentration sulfate attack subjected to natural variation of environmental climate conditions. Cem. Concr. Res. 116, 217–230. doi:10.1016/j.cemconres.2018.11.017

CrossRef Full Text | Google Scholar

Zhang, Z., Pang, K., Xu, L., Zou, Y., Yang, J., and Wang, C. (2023). The bond properties between uhpc and stone under different interface treatment methods. Constr. Build. Mater. 365, 130092. doi:10.1016/j.conbuildmat.2022.130092

CrossRef Full Text | Google Scholar

Zhang, Z., Zou, Y., Yang, J., and Zhou, J. (2022b). Capillary rise height of sulfate in portland-limestone cement concrete under physical attack: experimental and modelling investigation. Cem. Concr. Compos. 125 (125-), 104299. doi:10.1016/j.cemconcomp.2021.104299

CrossRef Full Text | Google Scholar

Zheng, Y., and Kong, L. (2006). Generalized plastic mechanics and its application. Eng. Sci. 4 (1), 21–36. doi:10.1007/s11769-005-0030-x

CrossRef Full Text | Google Scholar

Zhou, H., Di, L., Lei, G., Xue, D., and Yang, Z. (2018). The creep-damage model of salt rock based on fractional derivative. Energies 11 (9), 2349. doi:10.20944/preprints201807.0584.v1

CrossRef Full Text | Google Scholar