An evolutionary variational autoencoder for perovskite discovery

Machine learning (ML) techniques emerged as viable means for novel materials discovery and target property determination. At the vanguard of discoverable energy materials are perovskite crystalline materials, which are known for their robust design space and multifunctionality. Previous efforts for simulating the discovery of novel perovskites via ML have often been limited to straightforward tabular-dataset models and compositional phase-field representations. Therefore, the present study makes a contribution in expanding ML capability by demonstrating the efficacy of a new deep evolutionary learning framework for discovering stable and functional inorganic materials that adopts the complex $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$ double perovskite stoichiometries. The model design is called the Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD), which is comprised of a semi-supervised variational autoencoder (SS-VAE), an evolutionary-based genetic algorithm, and a one-to-one similarity analytical model. The genetic algorithm performs adaptive metaheuristic search operations for finding the most theoretically stable candidates emerging from a target-learnable latent space of the generative SS-VAE model. The integrated similarity analytical model assesses the deviation in three-dimensional atomic coordination between newly generated perovskites and proven standards, and as such, recommends the most promising and experimentally feasible candidates. Using Density Functional Theory (DFT), the novel perovskites are subjected to thorough variable-cell optimization and property determination. The current study presents 137 new perovskite materials generated by the proposed EVAPD model and identifies potential candidates for photovoltaic and optoelectronic applications. The new materials data are archived at NOMAD repository (doi.org/10.17172/NOMAD/2023.05.31-1) and are made openly available to interested users.

1 Introduction

The discovery of new materials is fundamental to addressing numerous technological challenges. Traditionally, the process consists of experimental synthesization and/or quantum mechanics first-principles calculations. Despite the significant contributions of both approaches, they remain inadequate for substantially large search spaces as they tend to be considerably difficult, unpractical, uneconomical and computationally expensive. In Edisonian experiments, for example, new materials have to be synthesized by reacting chemical participants to produce new chemical compounds. Such experimental effort will strongly depend on experiential knowledge, and in some cases, trial-and-error, thereby limiting their usability over a wider spectrum of design requirements and/or material class. Similarly, first-principles (ab initio) methods are generally known to be computationally expensive due to the heavy price of solving the costly Schrödinger equation on a many-body Hamiltonian system. In this context, data-driven Artificial Intelligence (AI) technologies, that are based on Deep Generative Modeling (DGM), have emerged as potentially more reliable, inexpensive, and more rapid alternatives for the systematic identification of novel (unknown) and complex materials. By solving an inverse design scheme (Fuhr and Sumpter, 2022), DGM processes can efficiently accelerate the search for new materials within a robust chemical combinatorial or design space. In several contemporary studies, DGMs are trained on target-specific material properties by learning from a materials dataset in a semi-supervisory manner. The semi-supervisory approach comprises an unsupervisory algorithm used to regenerate new materials and a supervisory algorithm for conditioning a target-property of interest. A proven semi-supervisory DGM used in solving the inverse design challenge is the Semi-Supervisory Variational AutoEncoder (SS-VAE) (Kingma et al., 2014), which is a variant of the traditional Variational Autoencoder (VAE) (Kingma and Welling, 2013). The SS-VAE is a directed graphical model and operates by projecting a probabilistic distribution of the original data onto a compact latent space. At the same time, the SS-VAE learns a representative labeled data associated with the training dataset during the unsupervised learning process. The latent space itself can be visualized as a hyperdimensional reduced representative form of the original data, whereby explorative and forensic investigations can be conducted (Kamnitsas et al., 2018). Moreover, the efficiency of a SS-VAE model can be influenced by several factors that evolve around the application field of interest and/or hyper-parameter tunings. Within the context of materials discovery, two aspects are of high importance for influencing the performance and design architecture of SS-VAE models. First are material inductive biases, which leverage on the current physicochemical state of the material class. Such biases are known to influence the choice of descriptor design, such as choosing between implementing graph-based modeling (Xie and Grossman, 2018; Mansimov et al., 2019), image-based modeling (Ren et al., 2022; Chenebuah et al., 2023) or phase-field modeling (Jena et al., 2019). Second are target-specific search optimizations. Optimizing for specific target properties is normally conducted in the latent space and, thus, influences the overall modeling architecture and sampling strategy. Customarily, SS-VAE models are instinctive latent space optimizers, which is due to the effect of the incorporated supervisory learning algorithm. The supervisory target-learning network predicts a labeled material’s property of interest in hyperdimension and, as such, organizes the latent space based on inferred knowledge from the prediction process.

In prior studies moreover, the practicality of SS-VAE models has been demonstrated for systematic materials discovery. For instance, as applied in a vanadium oxide (V-O) SS-VAE generator, new polymorphic compounds were successfully identified by target-learning the latent space using features that quantitatively assess stability from a strict formation energy perspective (Noh et al., 2019). In another research, a novel target-property predicting SS-VAE model was combined with a diffusive decoding model for generating thermodynamically stable 2D materials (Lyngby and Thygesen, 2022). Likewise, a Fourier Transformed Crystal Property (FTCP) representation was used to describe a wide stoichiometry of inorganic crystals for simulating the prediction of new stable compounds in a target-learnable SS-VAE latent space (Ren et al., 2022). In as much as SS-VAE models have achieved considerable successes, some technical challenges persist with their target-learning capabilities. Specifically, a common limitation is a phenomenon referred to as posterior collapse (Lucas et al., 2019), whereby the model fails to properly utilize the latent space, and therefore, generates unknown materials that are substantially different from the predefined target objective. Another major challenge is that a significant proportion of generated materials from an explorative sampling strategy are decoded to be chemically infeasible or inaccurate due to overlapping geometrical coordination of constitutive atoms (Ren et al., 2022).

To address the aforementioned challenges, the current study develops an evolutionary-based deep learning materials generator that enhances target-specific search optimization in the latent space while applying a geometrical similarity analysis on atomic coordination for recommending novel materials that are theoretically more likely to be chemically stable. The proposed Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD) model progressively combines a SS-VAE deconstructive algorithm, an evolutionary-based genetic algorithm (Michalewicz and Schoenauer, 1996), and a one-to-one similarity analysis based on geometrical coordination. Moreover, the study focusses on the discovery of host materials that adopts the perovskite stoichiometry. Perovskites in general are well known for their appealing functionalization, in-demand applications, and robust design space afforded by their chemical flexibility (Johnsson and Lemmens, 2005; Zhang et al., 2022). Common bulk perovskite stoichiometries include the simple ternary structures (${ABX}_3$) and the quaternary double B-site ($A_{2}B{B}^{\prime }{X}_6$), as well as the more complex quinary structures with combined double A- and double B-sites ($A{A}^{\prime }B{B}^{\prime }{X}_6$). Previous efforts for developing machine learning frameworks for novel perovskite discovery have been limited to straightforward tabular-dataset models with phase-field compositional representation and ternary organic/inorganic ${ABX}_3$ structures (Pilania et al., 2016; Chenebuah et al., 2021; Tao et al., 2021). In contrast, the current study demonstrates the efficacy of a deep evolutionary learning architecture for discovering stable and synthesizable double inorganic perovskites (i.e., $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$). A significant proportion of the newly identified perovskite candidates are confirmed to be unique (i.e., not found in the training dataset), and with functional properties that can be serviceable in photovoltaic and optoelectronic applications. Using the Quantum Espresso software package (Giannozzi et al., 2009), the identified candidates are subjected to first-principles Density Functional Theory (DFT) validation. Novel perovskites that successfully undergo full variable-cell DFT relaxation are then recommended for further investigation and/or potential synthesization.

The present study is organized as follows. First, the study highlights the unlimited design space afforded by the perovskite material class and describes the proposed modeling approach used in representing multi-stoichiometrical compounds that adopts the perovskite chemical formula. Second, the performance of the EVAPD model is assessed and the results of the forward and inverse design modeling experiments are presented based on standardized evaluation metrics. Third, the generative modeling approach is demonstrated for some newly predicted host materials and their properties are determined using machine learning and DFT. Finally, the developed EVAPD model is compared to other contemporary design architectures to demonstrate the scientific contribution of the current study.

2 Materials and methods

2.1 Perovskite chemical combinatorial design space

The bulk ternary ${ABX}_3$ compound is the most fundamental and prevalent stoichiometry for perovskite crystal structures. Consisting of three distinctive chemical sites, the A- and B-sites are occupied by cationic elements, whereas the X-site is anionic. The coordination environment for both A- and B-sites corresponds to twelve and six X-site anions, respectively, to form the $Pm\overline{3}m$ cubic closed packed (CCP) crystal structure (Johnsson and Lemmens, 2005). Moreover, considerable non-idealized and ionic-swapping (i.e., inverse- or anti-perovskites) can form (Wang et al., 2020), which creates other complex variants with multifunctional properties. Examples of two complex variants are the double B-site ($\left.A_{2}B{B}^{\prime }{X}_6\right)$ and double A- and B-sites ($A{A}^{\prime }B{B}^{\prime }{X}_6$) perovskites (Mitchell et al., 2017). Both double stoichiometrical forms are higher derivatives of the primitive ${ABX}_3$ and are generally formed through several phenomena that encompass cationic displacements/defects, local ionic-site sharing, and deliberate extrinsic doping, among others (Woodward, 1997; Lufaso and Woodward, 2004). Figure 1 illustrates the arrangement of constitutive chemical ions with respect to single ${ABX}_3$ and double B-site $A_{2}B{B}^{\prime }{X}_6$ perovskites. Considering the $A_{2}B{B}^{\prime }{X}_6$ formula, for example, the B-site ionic location is consecutively shared by two different chemical elements to form a rock-salt coordinated structure. Although less common in natural forms, the double A-site ($A{A}^{\prime }B{B}^{\prime }{X}_6$) perovskite can be regarded as a more advanced extension to their double B-site counterpart. Equally characterized by their ionic sharing behavior, both predominant A- and B-sites are conjointly occupied by two different chemical elements to produce a more complex stoichiometry. As such, the emerging materials from both $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$ perovskite crystals are suggested to be of even higher importance to materials scientists and engineers due to their unique properties that stem from the contributing effect of more chemical elements at distinctive ionic site locations. Furthermore, the chemical flexibility afforded by these respective stoichiometries to accommodate numerous elements from the periodic table, is also what makes double perovskites very diverse. For instance, exclusively permuting the 94 naturally occurring chemical elements, while mindful of anti-perovskite stoichiometrical possibilities and charge imbalances from Jahn-Teller electronic instabilities (Knapp and Woodward, 2006), the potential number of $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$ structures are estimated at ${\mathbb{C}}_4^{94}=\mathrm{3,049,501}$ and ${\mathbb{C}}_5^{94}=\mathrm{54,891,018}$, respectively. This rough estimate does not take into account the possibility of polymorphic variants, which are of a different physical phase and, thus, exhibit special behaviors that are unrelated to their duplicate peers (Zhao et al., 2020). As a result, an unlimited number of novel perovskite materials are potentially yet to be discovered, which only data-driven technologies can facilitate at a considerably rapid rate. In this context, the evolutionary deep learning model developed in the current study provides an accelerated discovery approach towards the design of serviceable perovskite materials.

FIGURE 1

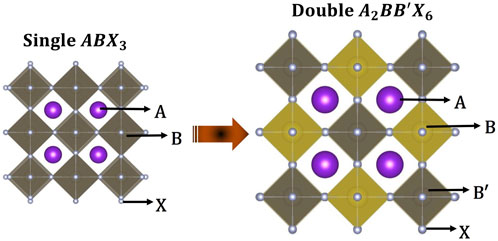
FIGURE 1. The double B-site perovskite crystal structure relative to the single ${ABX}_3$ (ternary) perovskite structure. For the double B-site, the single B-site ionic location is consecutively shared by two cations ($B$ and $B^{\prime }$) to form a complex $A_{2}B{B}^{\prime }{X}_6$ quaternary structure (Mitchell et al., 2017).

2.2 Image-based descriptor design

Molecular and organic materials have standard representative forms for feature engineering their chemical structures, such as Simplified Molecular Linear Input Specification (SMILES) representations (Weininger, 1988) and graph-based methods (Mansimov et al., 2019). For crystalline materials however, there currently exists no absolute descriptor design, which is a consequence of material-inductive biases. Modeling descriptor design for crystalline materials will have to take into consideration the crystal material class, the physicochemical state of the material, the stoichiometry, and the periodic effect of the reciprocal lattice. Previous efforts for broadly representing general inorganic crystals have been proposed using the Fourier Transformed Crystal Property (FTCP) (Ren et al., 2022). However, such a broad descriptor design is constrained by local exploitative search mechanisms (e.g., perturbative search operations), in order to randomly capture theoretically feasible materials within a diverse pool of material classes. To address this limitation, the present study constructs a user-interpretable image-based descriptor design for optimizing the explorative search of multi-stoichiometrical perovskite materials. The design consists of two sections that play crucial roles in the modeling objectives of the current study. The first section contains six crystallographic features that include: discretized atomic number (i.e., elemental label), stoichiometrical type, ionic occupancy, lattice parameters, number of atoms in the unit cell, and fractional atomic coordinates. The aforementioned features are essential for generative modeling, as they define the arrangement and bonding of atoms for all newly discovered perovskites. The second section provides thirteen discretized (one-hot encoded) features that comprehensively describe the thermochemistry behavior of all constitutive chemical elements that build the crystal structure. They include group number, row number, electronegativity, covalent radius, valence, ionization, electron affinity, spdf block, molar volume, average ionic radius, polarizability, specific heat, and thermal conductivity. The discretized features are crucial for mapping perovskites to their corresponding target properties (Xie and Grossman, 2018). As such, the thermochemistry properties assist in the organization of the latent space via the target-learning model, in addition to the supportive feedback models that are integrated into the evolutionary learning branch. Figure 2 illustrates the stacking arrangement and matrix array size of all contributing feature embedding. Both distinctive sections are horizontally concatenated, three-dimensionally reshaped, and zero-padded to produce an RGB (image-based) perovskite descriptor with an overall input matrix array of size $\left(94\times 8\times 3\right)$.

FIGURE 2

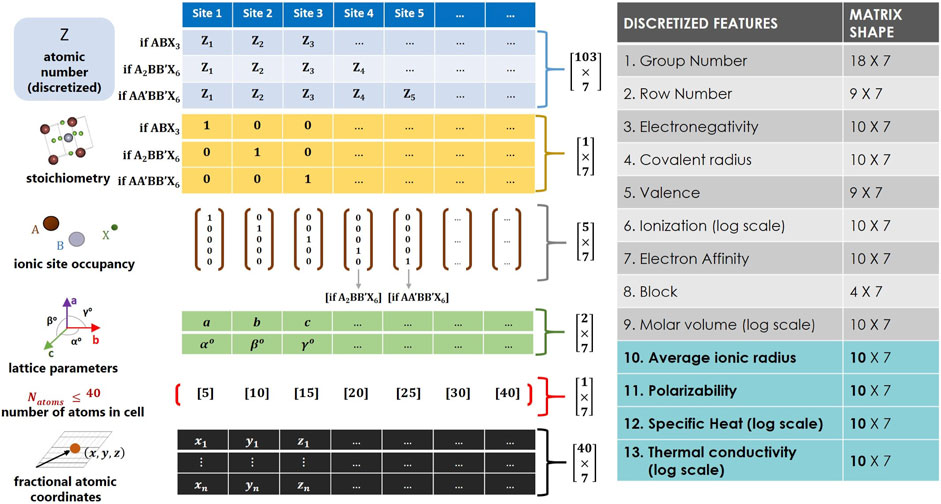
FIGURE 2. Image-based descriptor design for representing ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$ perovskite stoichiometries, which serve as input in the generative modeling exercise.

2.3 Semi-supervised variational autoencoder (SS-VAE) model

For generative modeling, a regularized latent space is crucial for smoothly transitioning between data points in hyperdimension. Emerging from Bayes theorem, Variational Autoencoders (VAE) enable such regularization by encoding feed inputs using predefined probability distributions (Kingma and Welling, 2013). For a known set of original perovskite samples (i.e., $\left\{{\mathit{x}}_{\mathit{i}}\right\}\subseteq \mathit{X}\in {\mathbb{R}}^{\mathit{R}}$), the encoded VAE latent vectors (i.e., $\left\{{\mathit{z}}_{\mathit{i}}\right\}\subseteq \mathit{Z}\in {\mathbb{R}}^{\mathit{Q}}$) are obtained using a probabilistic recognition (i.e., encoding) network, whereby $\mathit{Q}\ll \mathit{R}$ denotes dimensionality reduction or feature extraction. The goal of VAE is therefore to approximate the true posterior ${\mathit{p}}_{\mathit{\theta }}\left(\mathit{z}|\mathit{x}\right)$ in the decoding phase by learning the distribution ${\mathit{q}}_{\mathit{\varphi }}\left(\mathit{z}|\mathit{x}\right)$ at the encoding phase. Due to the competing nature of the encoding and decoding functions, training losses occur, and can be optimized by minimizing the measurable distance between both probabilistic functions. The divergence between both functions is estimated using the Kullback-Leibler (KL) loss metric (Kullback and Leibler, 1951), in addition to other loss functions that measure reconstruction. Through a sequence of back-propagation and stochastic gradient descent, the general VAE loss function ${\mathcal{L}}_{\mathit{v}\mathit{a}\mathit{e}}$ can be expressed using Equation-1:

${\mathcal{L}}_{\mathit{v}\mathit{a}\mathit{e}}\left(\mathit{\varphi },\mathit{\theta }\right)=\mathit{K}\mathit{L}\left[{\mathit{q}}_{\mathit{\varphi }}\left(\mathit{z}|\mathit{x}\right)\Vert {\mathit{p}}_{\mathit{\theta }}\left(\mathit{z}\right)\right]-\frac{\mathbf{1}}{\mathit{n}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{n}}}\left[\mathbf{log}{\mathit{P}}_{\mathit{\theta }}\left(\mathit{x}|\mathit{z}\right)\right](1)$

$\mathit{\varphi }$ and $\mathit{\theta }$ are parameters corresponding to recognition and generative models, respectively. On averaging the distribution $\mathbf{log}{\mathit{P}}_{\mathit{\theta }}\left(\mathit{x}|\mathit{z}\right)$ over $i=\mathrm{1,2},\dots ,n$ entries, the reconstruction error of all perovskite feature embedding can be calculated, which is practically equivalent to the Mean Squared Error (MSE). Based on a reparameterization technique, the sampling efficiency and overall optimization of the VAE model can thus be further improved using Equation-2:

$\mathit{z}=\mathit{\mu }+\mathit{\sigma }\odot \mathit{ϵ},\mathbf{w}\mathbf{h}\mathbf{e}\mathbf{r}\mathbf{e}\mathbf{ϵ}\sim \mathcal{N}\left(\mathbf{0},\mathbf{I}\right)(2)$

$\mathit{z}$ is the perovskite latent vector that is drawn from the distribution ${\mathit{q}}_{\mathit{\varphi }}\left(\mathit{z}|\mathit{x}\right)$; $\mathit{\mu }$ and $\mathit{\sigma }$ are deterministic vectors denoting mean and standard deviation, respectively; and $\mathit{ϵ}$ is a random variable from the standard Gaussian (normal) distribution $\mathcal{N}$. Moreover, the latent space of the general VAE model can be further organized on specific targets to produce the Semi-Supervised Variational Autoencoder (SS-VAE) (Kingma et al., 2014). A common SS-VAE technique is by using a target-learning (prediction) arm for optimization, which assists in organizing target properties in hyperdimension. The current study implements such technique by incorporating a feed-forward neural network (i.e., Multi-Layer Perceptron (MLP)) for capturing thermodynamically stable perovskites. The target to be regressively learnt in hyperdimension is the formation energy (${\mathit{E}}_{\mathit{f}}$). Moreover, the study prefers regressive-based supervisory modeling for classification (Noh et al., 2019) as it allows the cardinal reflection of intrinsic data distribution in continuous values within the latent space. As a result, the overall objective function, comprising of training losses from the unsupervisory VAE model and the supervisory MLP model, can be expressed using Equation-3:

${\mathcal{L}}_{\mathit{s}\mathit{v}\mathit{a}\mathit{e}}={\mathcal{L}}_{\mathit{v}\mathit{a}\mathit{e}}\left(\mathit{\varphi },\mathit{\theta }\right)+\underset{\text{regression}}{\underbrace{\left[\frac{\mathbf{1}}{\mathit{n}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\left({\mathit{E}}_{{\mathit{f}}_{\mathit{i}}}-\widehat{{\mathit{E}}_{{\mathit{f}}_{\mathit{i}}}}\right)}^{\mathbf{2}}\right]}}(3)$

${\mathcal{L}}_{\mathit{v}\mathit{a}\mathit{e}}\left(\mathit{\varphi },\mathit{\theta }\right)$ are VAE losses previously defined in Eq. 2. The regression part of Eq. 3 is the MSE (or L2-loss) from the MLP model, which minimizes the differential error between the targeted ${\mathit{E}}_{\mathit{f}}$ and predicted ${\widehat{\mathit{E}}}_{\mathit{f}}$ values.

2.4 Developed deep evolutionary learning framework

As illustrated in Figure 3, the deep evolutionary framework implemented in the current study begins by transforming perovskite samples (i.e., ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$ stoichiometries) into image-based representative forms $\left\{{\mathit{x}}_{\mathit{i}}\right\}\subseteq \mathit{X}\in {\mathbb{R}}^{\mathit{R}}$ (Figure 2). For training, the probabilistic SS-VAE encoder $\mathit{e}\left(.\right)$ dimensionally reduces all image-based input perovskites to produce hyperdimensional vectors (i.e., $\mathit{e}\left(\mathit{X}\right)\mapsto \mathit{Z}$) that are contained within a smooth and continuous latent space. The encoded latent space is pre-optimized on thermodynamic stability by conditioning a target-learning MLP model to regressively predict the formation energy (i.e., $f\left(\mathit{Z}\right)\mapsto {\mathit{E}}_{\mathit{f}}$). The target-learning operation assists in organizing the latent space by distinguishing stable versus unstable regions. For sampling the interested stable region, the current study applies the Spherical Linear Interpolation (SLERP) technique (Shoemake, 1985). In principle, SLERP is based on the theory of spherical quaternions and achieves explorative search by carrying out semantic vector interpolations in conformity to the volumetric shape of the hyperdimensional space. Given the interested latent space vectors (i.e., $\left\{\mathit{z}\right\}\subseteq \mathit{Z}\in {\mathbb{R}}^{\mathit{Q}}$), SLERP can be formulated as in Equation-4:

${\overrightarrow{\mathit{Z}}}_{\mathit{i}\mathit{j}}\left({\mathit{z}}_{\mathit{i}},{\mathit{z}}_{\mathit{j}};\mathit{t}\right)={\mathit{z}}_{\mathit{i}}\frac{\mathbf{sin}\left(\mathbf{1}-\mathit{t}\right)\mathit{\theta }}{\mathbf{sin}\mathit{\theta }}+{\mathit{z}}_{\mathit{j}}\frac{\mathbf{sin}\mathit{t}\mathit{\theta }}{\mathbf{sin}\mathit{\theta }}(4)$

FIGURE 3

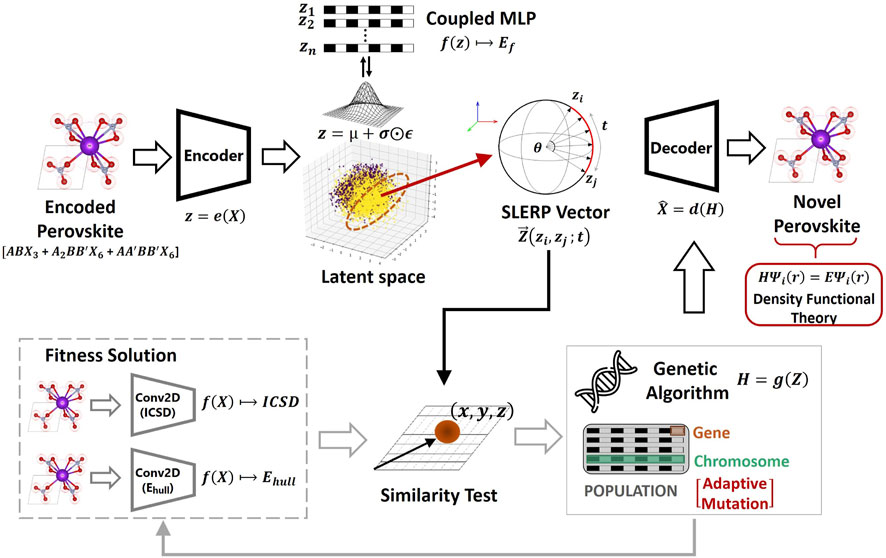
FIGURE 3. Proposed Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD). The modeling approach progressively combines a Semi-Supervised Variational Autoencoder (SS-VAE), a Genetic Algorithm (GA), two fitness-scoring convolutional neural networks (Conv2D), and a geometrical similarity-screening test to form the deep evolutionary learning framework.

${\overrightarrow{\mathit{Z}}}_{\mathit{i}\mathit{j}}\Rightarrow \left({\mathbb{R}}^{\mathit{Q}}:\mathbf{1}\times \mathit{Q}\right)$ is the interpolated vector in hyperdimensional $\mathit{Q}$ space along spherical finite length $\mathit{t}\in \left[\mathbf{0,1}\right]$ (i.e., line-space). In the current study, $\mathit{t}$ is evenly distributed within a spacing interval of 0.2, with $\mathit{Q}$ equals 256. The interpolation process therefore produces new data points at an angle $\mathit{\theta }$ between two interpolated points. As a result, iteratively exploring all regional sampling points produces $\left(\frac{{\mathit{t}}_{\mathit{max}}}{\mathbf{0.2}}-\mathbf{1}\right)\times {\mathbb{C}}_{\mathbf{2}}^{\mathit{Z}}$ unique data points that possess hereditary properties of both ${\mathit{z}}_{\mathit{i}}$ and ${\mathit{z}}_{\mathit{j}}$ reduced perovskite forms.

Moreover, the SLERP technique is characterized by its tendency to lean more towards the variety extreme in the variety-validity tradeoff (Ren et al., 2022). Here, validity refers to the price in generating structurally feasible candidates (i.e., exploitation), but at the expense of diversity. Variety on the other hand pertains to diversification in generated candidates (i.e., exploration), but at the expense of feasibility. The present study attempts to manage the higher variety extreme from SLERP by implementing an exploitative similarity test analysis that improves validity. In addition, the present study integrates an evolutionary algorithm for further optimizing the sampled solutions generated from the SLERP process. The evolutionary search algorithm performs metaheuristic search operations and ranks the generated solutions based on a fitness-scoring process. For this purpose, the Genetic Algorithm (GA) is preferred over other similar evolutionary models due to its computational flexibility in allowing user-defined fitness functions and non-derivative problem-solving capability (Michalewicz and Schoenauer, 1996). The GA model searches for the most promising perovskite candidates by conducting dynamic iterative operations over a batch population via a process that is inspired by biologically motivated crossover and mutation of genes (scalars) and chromosomes (vectors). Moreover, the current study modifies the mutation process of the GA model to be quality-adaptive, by flipping the genes of low-quality solutions twice as much as high-quality solutions. To comprehensively search for high-quality candidates, the fitness function of the GA model ($g\left(\mathit{Z}\right)$) outputs and ranks the quality of the derived solutions based on three important factors. The first consideration takes into account the energy above convex hull (${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$) parameter, which represents the thermodynamic decomposition state of a compound and has been recommended in previous studies for indexing synthesizability. As demonstrated on 80% of sulfides and oxides, compounds with ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}\le 0.08$ eV/atom are highly stable upon synthesization (Singh et al., 2019). As such, the fitness function of the GA model is configured to search and rank solutions based on an ideal ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ value that equals zero. For this purpose, a two-dimensional convolution neural network (Conv2D) is pre-trained to predict the labeled ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ target of training perovskite samples (i.e., $f\left(\mathit{X}\right)\mapsto {\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$). The ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ Conv2D model interacts with the GA model by providing feedback analysis for updating the fitness function. The second consideration complements the first by using information from the Inorganic Crystal Structure Database (ICSD) (Belsky et al., 2002) labeling to predict the most synthesizable perovskite solutions. In general, ICSD materials are chemical compounds that have been certified mostly from physical experiments. The current study justifies the usage of ICSD labels by using explainable interpretability technique to connect them to the ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ parameter. Thus, in addition to the ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ Conv2D model, the GA also progressively updates the fitness function by using feedback information from a pre-trained secondary Conv2D model that is conditional on ICSD classification (i.e., $f\left(\mathit{X}\right)\mapsto \mathit{I}\mathit{C}\mathit{S}\mathit{D}$). As such, the GA model highly ranks perovskite solutions that are predicted to be ICSD compounds (1) and lowly ranks perovskites that are not predicted as ICSD compounds (0). It should be noted moreover that highly ranked $\mathit{H}=\mathit{g}\left(\mathit{Z}\right)$ GA solutions do not necessarily mean that they all would be chemically feasible upon post-processing. Therefore, a third consideration is applied for post-analytical screening of all high-quality solutions. By simulating a similarity analysis, the study seeks to minimize the concern of overlapping atomic coordinates in a unit cell, which leads to the detrimental reconstruction of invalid or unfeasible materials. Using a one-to-one differential comparison approach, the similarity test empirically evaluates the geometrical deviation in coordinated environment of all constitutive atoms in the unit cell, relative to some perovskite standards. Given a latent vector ${\overrightarrow{\mathit{Z}}}_{\mathit{i}\mathit{j}}\in {\mathbb{R}}^{\mathit{Q}}$ from the SLERP-GA process, the similarity analytical test calibrates structural feasibility for reconstructed perovskite outputs (i.e., $\left\{{\widehat{\mathit{x}}}_{\mathit{i}\mathit{j}}\right\}\subseteq \widehat{\mathit{X}}\in {\mathbb{R}}^{\mathit{R}}$) using the mathematical expression in Equation-5:

$\frac{\sum \left|\mathrm{\Omega }\left({\widehat{\mathit{x}}}_{\mathit{i}\mathit{j}}\right)-\mathit{\Omega }\left(\acute{\mathit{x}}\right)\right|}{{\mathit{N}}_{\mathit{a}\mathit{t}\mathit{o}\mathit{m}\mathit{s}}}\le \mathcal{F}(5)$

$\acute{\mathit{x}}$ is the perovskite standard used for comparison, which conforms to the specific type of perovskite stoichiometry in addition to the number of atoms ${\mathit{N}}_{\mathit{a}\mathit{t}\mathit{o}\mathit{m}\mathit{s}}$ in the unit cell; $\mathrm{\Omega }\left(.\right)$ evaluates the absolute one-to-one differences in three-dimensional atomic coordination between decoded latent vectors and corresponding standards. As such, Eq. 5 measures the average dissimilarity value ($\mathcal{F}$) in fractional atomic coordinate with respect to standards.

2.5 Variable-cell DFT relaxation using Quantum Espresso

Using the first-principles Density Functional Theory (DFT) simulation technique, the novel candidates emerging from the EVAPD pipeline are chemically and geometrically validated to ascertain their synthesizability potential. For this purpose, the Quantum Espresso (QE) DFT software package (Giannozzi et al., 2009) is used to perform plane-wave Generalized Gradient Approximation (GGA) calculations, as parametrized on a Perdew-Burke-Ernzerhof (PBE) (Perdew et al., 1996) - Projector Augmented Wave (PAW) pseudopotential class (Blöchl, 1994; Kresse and Joubert, 1999). For validating the novel candidates, the current study applies two successive DFT approaches. First, non-spin polarized DFT relaxation is performed on stationary unit cells of the crystal lattice in order to find the most stable three-dimensional configuration of constitutive atoms or ionic positions. The preliminary relaxation exercise saves computational resource by ensuring that only chemically-balanced and atomically-optimized candidates (i.e., novel perovskites with converged total electronic energy) are selected for further investigation. For the second relaxation phase, the overall crystal structure is thoroughly examined by performing variable-cell relaxation (vc-relax) on all axes and angles of previously converged unit cell candidates. Moreover, the second optimization phase includes spin polarized (magnetic) calculation by inducing collinear starting magnetization values on the initially relaxed geometry. Such spin polarization is beneficial for understanding the magnetic behavior of the material, i.e., di-, para-, ferro-magnetism, etc. For both relaxation phases, appropriate K-points grid meshes are used to sample the three-dimensional Brillouin zone of the reciprocal crystal lattice, as recommended by Materials Cloud (Talirz et al., 2020). The Broyden-Fletcher-Goldfarb-Shanno (BFGS) iterative algorithm is applied for ionic and cell optimizations. Self-consistent field (SCF) electronic convergence is achieved by setting energy accuracy, force and pressure at 1.0e-7 Rydberg, 1.0e-3 Rydberg/Bohr, and 0.5 kbar, respectively. The energy cutoff threshold for charge density is set at ten times the corresponding value for wave function from the chemical element pseudopotential’s condition (Prandini et al., 2018). To ensure that a smooth integration of electron occupation occurs across the fermi energy level, Gaussian-smearing technique with low broadening (0.01 Rydberg) is used.

3 Experiment and simulation results

3.1 Perovskite dataset

For training the Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD) model, the current study uses scientific data from the Materials Project (Jain et al., 2013). Using pymatgen MPRester, the training samples are extracted from the platform by searching for only generic entries that adopt the three interested perovskite stoichiometries, i.e., ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$. The extracted perovskite data are screened to ensure that compounds with no more than forty atoms in a conventional unit cell are selected for investigation (i.e., $N_{atoms}\le 40$). Limiting to forty atoms is necessary because of inadequate data beyond this threshold. The screening process resulted into 8,228 inorganic perovskite compounds for experimentation. As illustrated in Figure 4A, the data prevalence with respect to the three investigated stoichiometries is about 51%, 46%, and 3% for ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$, respectively. Likewise, Figure 4B illustrates the stacked percentage of atomic unit cells for each stoichiometry. It can be seen that $N_{atoms}=5$, $N_{atoms}=10$, and $N_{atoms}=20$ dominates ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$, respectively. For all cases however, $N_{atoms}=10$ constitutes a significant amount of data representation corresponding to about 21%, 65.2%, and 21.2% for ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$, respectively. On assessing targets based on stability, 23% of all experimented data are considered to be perfectly stable (i.e., ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}=\mathbf{0}$), and 97.9% have negative formation energies (i.e., ${\mathit{E}}_{\mathit{f}}<\mathbf{0}$). The dataset also contains about 32.1% of experimentally certified ICSD perovskites. Using Figures 4C, D, the correlation in distributed data between ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ and labeled ICSD perovskites are graphically displayed. It can be observed that for perovskites with decorated ICSD labels, the data frequency is highly distributed towards the zero mark of idealized stability.

FIGURE 4

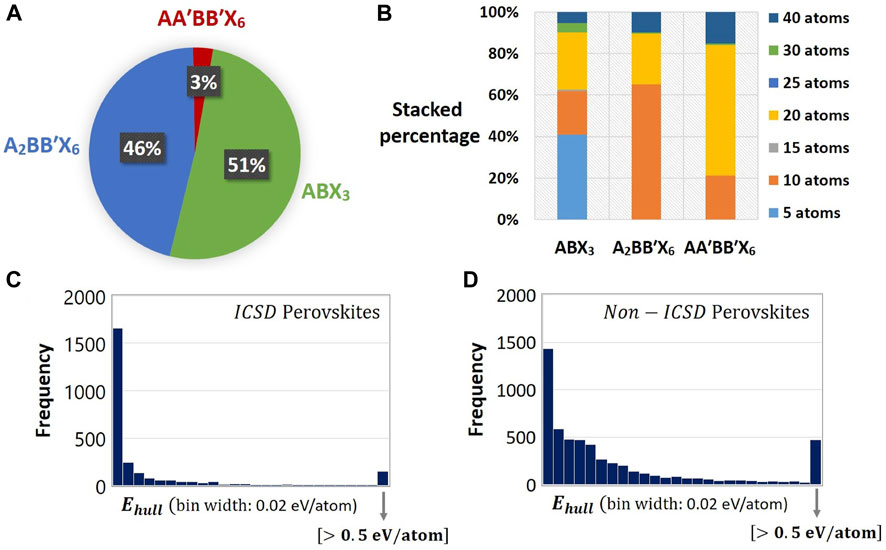
FIGURE 4. Data statistics of ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$ perovskite stoichiometries used in the training experiment: (A) pie chart of sample occurrences; (B) relative percentage in the number of constitutive atoms in the unit cell of a stoichiometry; (C) and (D) reveal the frequency in data distribution with respect to the energy above convex hull (${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$) target for ICSD and Non-ICSD compounds, respectively.

3.2 Preliminary forward design evaluation on target-property prediction

The forward design can be formulated as: given the perovskite crystal structure, find the corresponding target (i.e., $f\left(\mathit{X}\right)\mapsto \mathit{y}$), whereby $\mathit{X}$ is the image-based perovskite material as described in Figure 2, and $\mathit{y}$ are the interested targets. By solving the forward design, the study investigates the target-property prediction quality of the developed image-based descriptor used to represent a perovskite material in the training dataset. The targets considered for simulation include the formation energy (${\mathit{E}}_{\mathit{f}}$), the energy above convex hull (${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$), and ICSD labeling. For predicting ${\mathit{E}}_{\mathit{f}}$, a different approach is used however, since the prediction variable itself is conditional on the general performance of the inverse design SS-VAE model, and not on the feedback loops that are used to update the fitness function of the genetic algorithm. For predicting ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ and classifying ICSD labels, independent two-dimensional convolutional neural networks (Conv2D) are pre-trained for modeling their respective forward design functions $f\left(.\right)$. The forward design experiment is conducted on the preprocessed dataset (Section 3.1) and is evaluated using five-fold cross-validation. The Conv2D architectures for modeling both ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ and ICSD targets are identical and comply with the type of supervisory analysis, i.e., linear and sigmoidal functions for regression (${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$) and binary classification (ICSD), respectively. Details on the design architecture are provided in Supplementary Material. In the case of regressive analysis, the study uses standardized metrics in the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE) and coefficient of determination (R²%) to assess the accuracy. As a result, Figure 5A reveals cross-validated results on the prediction of ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ based on the three distinctive stoichiometries. The average MAE (± standard deviated) scores are estimated at 0.109 ± 0.006 eV/atom, 0.047 ± 0.004 eV/atom, and 0.059 ± 0.005 eV/atom for ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$, respectively. Likewise, RMSE scores are estimated at 0.262 ± 0.038 eV/atom, 0.143 ± 0.046 eV/atom, and 0.085 ± 0.023 eV/atom, respectively. For classifying ICSD versus Non-ICSD labeled perovskites, standardized metrics in the average Receiver Operating Characteristic (ROC) on all five-fold cross-validated sets was applied, with average Area Under the Curve (AUC) determined at 84.35% ± 1.08%. To further highlight the importance of the ICSD label, the current study introduces a model interpretability technique in the Shapley additive explanations (SHAP) (Shapley, 1953; Lundberg and Lee, 2017). SHAP analyzes the average marginal contribution of an input feature across all possible feature coalitions towards the prediction of a target. For this purpose, eight DFT-predicted variables are used as inputs to ascertain their relationship with the ICSD target. The inputs include ${\mathit{E}}_{\mathit{f}}$, ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$, energy band gap (${\mathit{E}}_{\mathit{g}}$), structural density, unit cell volume, and three-dimensional inter-axial cell angles (i.e., alpha, beta, and gamma). From the SHAP summary plots in Figure 5B, the ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ parameter is strongly recognized as the best correlative feature with the ICSD target. The horizontal axis indicates the impact of a feature value for positively or negatively influencing the classification process. As such, the plot confirms the positive influence of lower ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ values (i.e., blue in the plot) and the negative influence of higher ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ values (i.e., red) for classifying ICSD labelled perovskites. The results demonstrated by the Shapley process are consistent with the data distributive analysis, as illustrated in Figures 4C, D. More information on the forward design modeling results are provided in Supplementary Material.

FIGURE 5

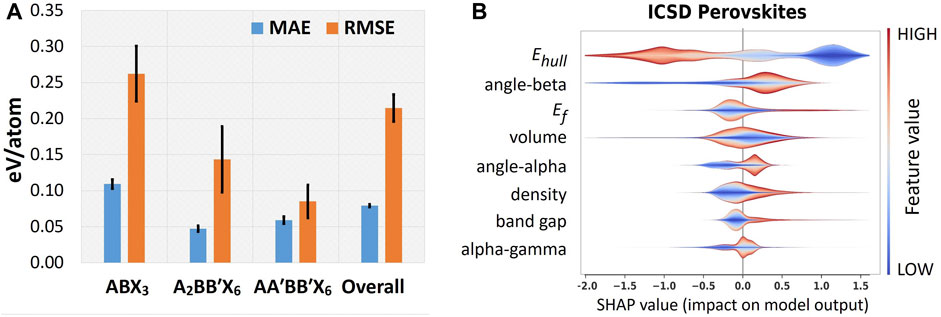
FIGURE 5. Results on forward design modeling. (A) Stoichiometric-specific MAE and RMSE evaluations on the prediction of ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ with average overall MAE at 0.079 ± 0.002 eV/atom, as experimented using five-fold cross-validation; (B) SHAP summary plot with correlative features arranged according to average marginal importance towards the classification of ICSD labeled perovskites.

3.3 Performance of the SS-VAE inverse design model

The proposed SS-VAE model is used to inversely generate unknown perovskites while using target-learning information from a supervisory Multi-Layer Perceptron (MLP) model. For evaluating the model’s performance, the reconstructive errors from the encoding-decoding phases of important feature embedding is investigated. In addition, the efficacy of the target-learning MLP for organizing the latent space based on predicted formation energy is evaluated. For predicting the formation energy, the latent space vectors (i.e., $\left\{{\mathit{z}}_{\mathit{i}}\right\}\subseteq \mathit{Z}\in {\mathbb{R}}^{\mathit{Q}}$) from the encoding SS-VAE model are mapped to ${\mathit{E}}_{\mathit{f}}$ via the branched MLP network (i.e., $f\left(\mathit{z}\right)\mapsto {\mathit{E}}_{\mathit{f}}$). The branched MLP architecture is progressively downsized using dense layers, and is linearly activated at the final output layer to comply with the prediction of continuous values (i.e., regression). Figure 6A displays the regressive fitting analysis of the MLP model with overall average R² at 92.31% ± 1.23%, while Figure 6B displays a comparative chart on the relative performance of each stoichiometry from the prediction process. The realized MAE values for predicting ${ABX}_3$, $A_{2}B{B}^{\prime }{X}_6$, and $A{A}^{\prime }B{B}^{\prime }{X}_6$ formation energies are estimated at 0.191 ± 0.010 eV/atom, 0.104 ± 0.006 eV/atom, and 0.181 ± 0.022 eV/atom, respectively. For evaluating the generative modeling behavior, the current study applies standardized loss metrics for measuring the deviation in reconstruction between originally encoded perovskites (i.e., $z=e\left(X\right)$) with their corresponding decoded forms (i.e., $\widehat{X}=d\left(z\right)$). The functions $e\left(.\right)$ and $d\left(.\right)$ denote encoding and decoding, respectively. Table 1 reports average stoichiometry-specific results of important feature embedding, as carried on a five-fold cross-validation experiment. From the reported results, it can be observed that for one-hot encoded features, the reconstructive performance is fairly similar, and practically negligible among all stoichiometries. For feature embedding that is not one-hot encoded, the average overall MAE values are reported at 0.739 ± 0.033 Å, 5.196° ± 0.220° and 0.022 ± 0.001 Å/Å for lattice edge vectors, inter-axial angles and fractional atomic coordinates, respectively. More information on the modeling architecture, including hyperparameter specifications for guiding the SS-VAE learning process, is provided in Supplementary Material.

FIGURE 6

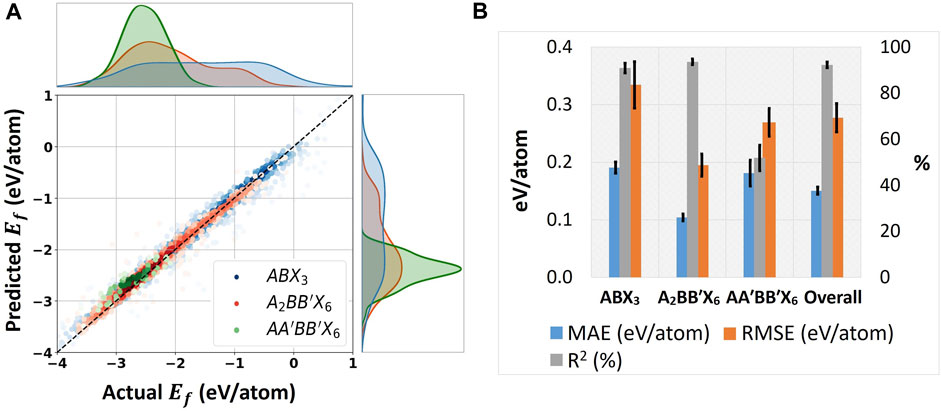
FIGURE 6. Modeling performance of the SS-VAE model for inversely designing perovskites. (A) MLP’s regression fitting on ${\mathit{E}}_{\mathit{f}}$ for target-learning the latent space with average overall R² at 92.31% ± 1.23%; (B) Comparative chart of different stoichiometries on the average prediction performance of ${\mathit{E}}_{\mathit{f}}$, as evaluated on all five-folds cross-validation experimented sets.

TABLE 1

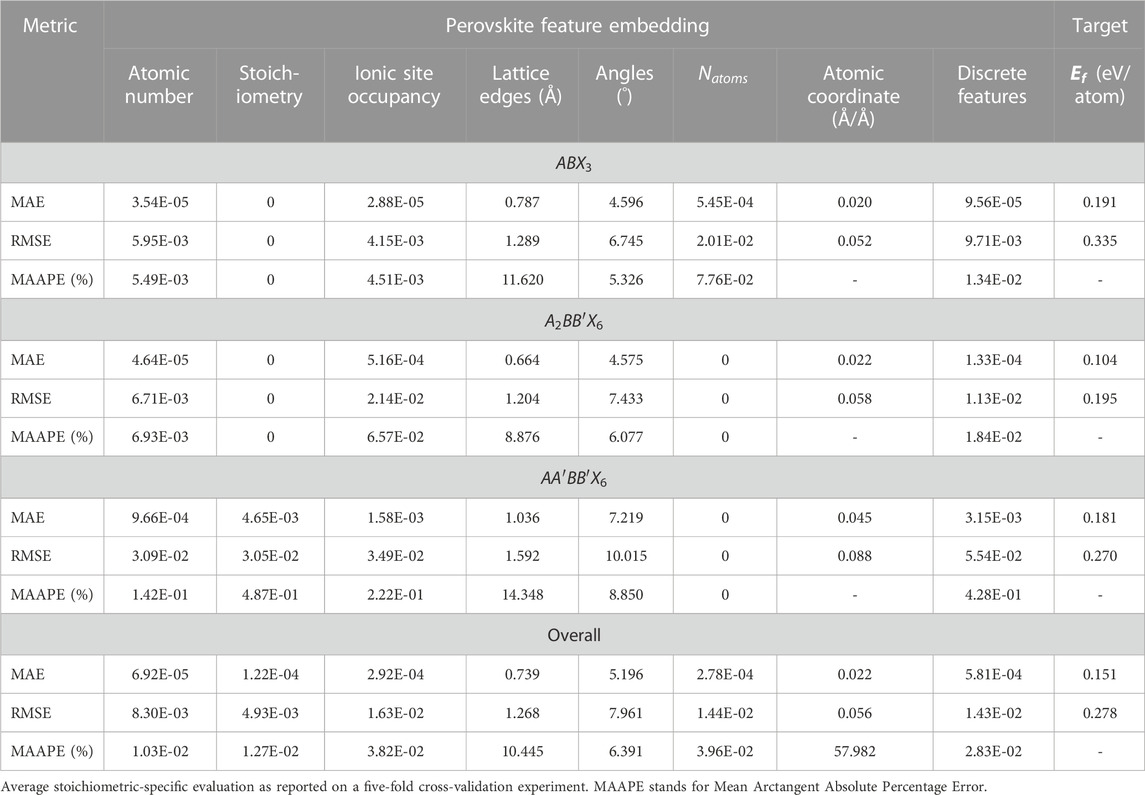
TABLE 1. Reconstruction of important input feature embedding from the image-based descriptor, in addition to formation energy determination from the target-learning arm of the SS-VAE model.

3.4 Generating novel and stable perovskites of the double stoichiometry

The architectural design of the SS-VAE model dimensionally reduces each image-based perovskite into encoded data points of vector length ${\mathbb{R}}^{\mathbf{256}}:1\times 256$ in the latent space. Figure 7 illustrates the smooth transitional behavior of the latent space and displays the distinctive regions that qualify stable and unstable data points. To gain more insight into the pattern of the encoded latent space, Figures 7A, B use principal component analysis (PCA) to plot the top two orthogonal axes that produce the largest variance from the data transformation process. The PCA algorithm used is the t-Distributed Stochastic Neighbor Embedding (t-SNE), and is chosen due to its better functionalization for capturing complex or nonlinear data structures (van der Maaten and Hinton, 2008). The t-SNE illustrations are shown for real/continuous (Figure 7A) and discrete/binary formation energy points (Figure 7B). Categorizing the formation energy into discrete values simply enables a quicker identification of highly stable points. Highly stable perovskites are predefined by their formation energy values within the range ${\mathit{E}}_{\mathit{f}}\le -1.5$ eV/atom. Such a stable threshold constitute good proxies for designing formable photovoltaic materials (Ren et al., 2022). In the corresponding figures, they are colored yellow and constitute about 69.3% of the overall perovskite dataset used in the deep evolutionary learning experiment. Emerging from the t-SNE plot, the effect of the target-learning arm can be visualized with respect to the distinctive separation of highly stable data points (yellow) from their unstable counterparts (blue). However, for sampling stable data points, the current study refers to the direct latent space and not to the t-SNE transformative space. This is based on the rationale that PCA techniques are irreversible due to the loss of information that comes with the data transformation process. Hence, the two-dimensional plane that best captures the displacement of stable versus unstable data points from the ${\mathbb{R}}^{\mathbf{256}}$ real latent space is carefully examined for explorative sampling operation. Figures 7C, D exemplary demonstrate visualizations from the displacement of stable versus unstable points in the real latent space (i.e., 2D plane). By plotting the 164th against the 179th axis from a stochastic training process, the region of interest in space can be viewed as the most captivating locality where the probability of generating new stable data points is highest. Using Figure 8, all data points within the region of interest are shown to be isolated and aggregate to about 1,584 interested perovskite points. Statistically, 88% are stable perovskites, i.e., ${\mathit{E}}_{\mathit{f}}\le -1.5$ eV/atom (Figure 8A), 30% are experimentally certified with ICSD labeling (Figure 8B), and 70% are perovskites that demonstrate good synthesizability potential, i.e., ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}\le 0.08$ eV/atom (Figure 8C). In addition, the relative occurrences of interested data points with respect to different stoichiometries are displayed using Figure 8D. A majority of the isolated perovskites are $A_{2}B{B}^{\prime }{X}_6$, constituting about 63% of all data points. ${ABX}_3$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$ stoichiometries occur less at 30% and 8%, respectively. A majority (i.e., 60%) of $A_{2}B{B}^{\prime }{X}_6$ points within the region of interest are primitive or singular formula units (i.e., ten atoms in their unit cell). This suggests that primitive crystal cell types are more likely to produce stable perovskites, and therefore, they are used for generating new data points in the sequel SLERP sampling operation. For 589 distinctive $A_{2}B{B}^{\prime }{X}_6$ interested points with singular formula units, interpolating against one another using the Eq. 4, produces about six hundred and ninety thousand (∼690,000) new $A_{2}B{B}^{\prime }{X}_6$ points. Likewise, generating new $A{A}^{\prime }B{B}^{\prime }{X}_6$ data points is schemed to follow the sampling strategy previously used for their $A_{2}B{B}^{\prime }{X}_6$ counterparts. However, unlike $A_{2}B{B}^{\prime }{X}_6$ that strictly interpolates between the same stoichiometry, $A{A}^{\prime }B{B}^{\prime }{X}_6$ data points are additionally allowed to cross-interpolate $A_{2}B{B}^{\prime }{X}_6$ stoichiometries. Cross-interpolating is a consequence of $A{A}^{\prime }B{B}^{\prime }{X}_6$ smaller data prevalence relative to other stoichiometries. Moreover, the benefit with cross-interpolation is in the generation of a chemically more diverse collection of unique data points, given that $A{A}^{\prime }B{B}^{\prime }{X}_6$ perovskites are simply Jahn-Teller distortional derivatives of the $A_{2}B{B}^{\prime }{X}_6$ stoichiometry (Knapp and Woodward, 2006). For ranking the most promising double perovskites emerging from the SLERP process, the new data points are further analyzed using geometrical similarity assessment and evolutionary-based search optimization.

FIGURE 7

FIGURE 7. Visualization of the stability-structured latent space. (A) Transformed t-SNE PCA latent space with respect to real $E_f$ values; (B) Transformed t-SNE PCA latent space with respect to discrete $E_f$ values; (C) Direct plane in latent space capturing the displacement of perovskite data points with respect to real $E_f$ values; (D) Direct plane in latent space capturing the displacement of perovskite data points with respect to discrete $E_f$ values. The direct plane is plotted for the 164th against the 179th axis from a stochastic training process. For discrete plots, yellow denotes stable perovskites based on ${\mathit{E}}_{\mathit{f}}\le -1.5$ eV/atom, whereas blue denotes unstable points. The region of interest in space for SLERP sampling operation is circled in (C) and (D).

FIGURE 8

FIGURE 8. Displacement of data points within the interested latent space region corresponding to the 164th versus 179th axis. (A) Stable versus unstable points based on ${\mathit{E}}_{\mathit{f}}$; (B) ICSD versus Non-ICSD labeled points; (C) Stable versus unstable points based on ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$; (D) Relative occurrence of different stoichiometries.

3.5 Ranking high-quality candidates and geometrical similarity analysis

For ranking high-quality candidates, the SLERP latent vectors are evolutionary learnt using the Genetic Algorithm (GA). The GA model iteratively searches for the most stable and promising perovskite candidates using feedback loops from two pre-trained convolutional neural networks (Conv2D) for updating the fitness function. The first Conv2D model transmits information based on predicted stability for an expected/idealized value of ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}=0$ eV/atom. Simultaneously, a second Conv2D model imposes the fitness function to only recognize optimized solutions that are predicted to have ICSD labels. Through a sequence of single-point crossover and mutation, the GA search operations are performed on batch populations for a specific number of iterations or generations. Moreover, the mutation process is adaptively designed to flip genes (i.e., scalars) of low-ranked candidates twice as much as high-ranked candidates, which helps to solve the problem of constant mutation and premature convergence (Libelli and Alba, 2000; Gad, 2021). Figure 9A illustrates a sensitivity investigation on the effect of mutation rate for outputting the best solutions from the GA generative process. It can be observed that for a higher gene mutation rate of 15% used to flip low-ranked candidates, the model steeply descends to a local optimum (premature convergence), thereby generating solutions that are potentially suboptimal (i.e., indistinguishable from individuals in the iterated batch population). As the mutation rate decreases, the search operation gradually descends to better optimized solutions, which are considerably improved candidates from their mating individuals currently populated in a batch population. Considering an optimized mutation rate of 5%, Figure 9B reveals the evolution in predicted formation energy (${\mathit{E}}_{\mathit{f}}$) and energy above convex hull (${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$) for the best-ranked perovskite solutions across 100 generations. It can be observed that for the best solutions per generation, the predicted ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ value gradually descends and converges to the idealized ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ value after 40 generations, whereas ${\mathit{E}}_{\mathit{f}}$ unsteadily descends, but maintains predicted stability at ${\mathit{E}}_{\mathit{f}}\le -2.75$ eV/atom after 30 generations. Due to the conditional imposition of the secondary feedback Conv2D loop, all high-quality solutions outputted by the GA model are predicted to be ICSD compounds. The current study prioritizes best-ranked solutions from a batch iteration for novel candidates that are within an overstated synthesizability criterion of ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}\le 0.08$ eV/atom, as demonstrated for experimental sulfides and oxides (Singh et al., 2019). It should be noted moreover, that the developed GA model conditions the metaheuristic search process to perform crossover and gene mutation of the SLERP latent space vectors within the boundaries of the minimum and maximum gene values (i.e., scalar) in a batch population assembly. This ensures that all generated and optimized GA solutions remain confined within the stability region of interest in the latent space.

FIGURE 9

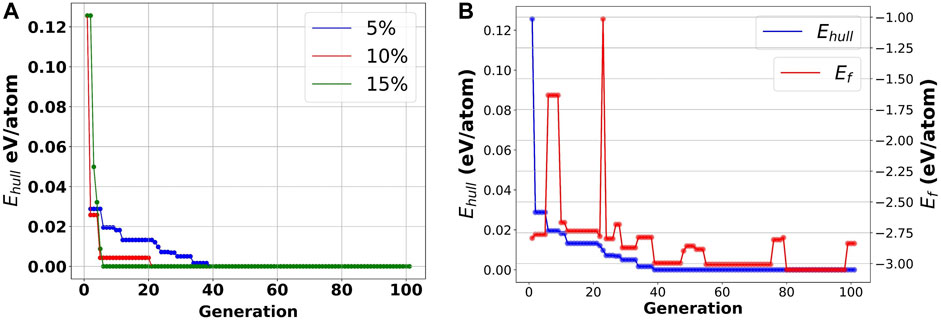
FIGURE 9. Evolutionary learning process for searching for the most optimized solution using the genetic algorithm. (A) Sensitivity analysis on the mutation rate across 100 generations; (B) Predicted ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ and ${\mathit{E}}_{\mathit{f}}$ for the best-ranked solutions per generation.

Furthermore, the high-quality solutions emerging from the joint SLERP-GA processes are further screened to ensure their geometrically coordinated environment is consistent with proven standard perovskite forms. As described in Eq. 5, the similarity analytical model measures the deviation in one-to-one atomic coordination between standards and newly generated perovskites. A dissimilarity value of $\mathcal{F}=0$ indicate that the geometrical coordination between standard reference forms and newly generated perovskites are indistinguishable. As such, the current study uses a threshold of $\mathcal{F}\le 0.2\mathit{\AA }/\mathit{\AA }$ for selecting a good portion of promising candidates while ensuring that the computed deviation is within tolerable limits. Figure 10 illustrates the proportion of dissimilar compounds with respect to each considered standard perovskite form from the Materials Project (MP) database (Jain et al., 2013). The standards are chosen to represent a mixed setting in perovskite geometry, as it relates to crystal system and space group symmetry. The current study equally selects six highly stable perovskites for evaluating newly generated $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$ perovskites. For $A_{2}B{B}^{\prime }{X}_6$ specifically, the standard perovskites are proven ICSD experimentally certified materials with ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}=0$. For $A{A}^{\prime }B{B}^{\prime }{X}_6$, the chosen standards are MP materials that are highly suggested for synthesization due to their very low ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$ values (i.e., ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}\le 15$ meV/atom). For over 100,000 newly generated perovskites, it can be observed that some standards appear to be geometrically more similar to generated candidates when compared to others (see Figure 10). The superiority in geometrical similarity with respect to a specific standard is suggested to be partly due to the chemical prevalence of the respective crystal structure in the training dataset. For example, $A_{2}B{B}^{\prime }{X}_6$ standard evaluators in mp-1079615 Ba₂UCdO₆ $\left(Fm\overline{3}m\right)$ and mp-13356 Ba₂SrTeO₆ $\left(R\overline{3}\right)$ highly conform geometrically with newly generated $A_{2}B{B}^{\prime }{X}_6$ compounds. Likewise, the mp-1227325 BaSrMgTeO₆ $\left(F4\overline{3}m\right)$ standard is noticeably more similar with newly generated $A{A}^{\prime }B{B}^{\prime }{X}_6$ compounds. On assessing the overall impact of the similarity analytical model for screening potentially valid candidates, the present study confirms a success rate of ∼80%. The success rate scores the proportion of valid candidates (i.e., non-overlapping geometrical coordination of constitutive atoms) to the total number of screened novel candidates that are post-processed using the Density Functional Theory (DFT).

FIGURE 10

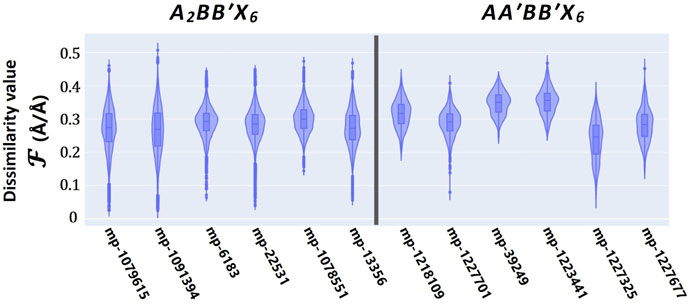
FIGURE 10. Similarity analysis as it relates to the three-dimensional geometrical (atomic) coordination between proven perovskite standards from the Materials Project (MP) database and newly generated perovskite compounds from the SLERP-GA process.

4 Discovered perovskites, analysis and Discussion

4.1 Newly discovered double perovskites and property determination

The present study reports the successful discovery of 114 $A_{2}B{B}^{\prime }{X}_6$ and 23 $A{A}^{\prime }B{B}^{\prime }{X}_6$ novel perovskite materials from the EVAPD model. All presented materials fully underwent variable-cell DFT relaxation, and are therefore optimized on atomic coordination and unit cell lattice geometry. From the presented $A_{2}B{B}^{\prime }{X}_6$ discovered materials, 87 are confirmed not to be contained in either the experimented dataset or Materials Project used for the simulation, among which 59 have not yet been reported in any known database, including the Open Quantum Materials Database (OQMD) (Saal et al., 2013) and the Novel Materials Discovery (NOMAD) (Draxl and Scheffler, 2018). The other 27 are polymorphic duplicate chemical compounds, which are characterized by their different unit cell geometry and evaluated target properties. With respect to the discovered $A{A}^{\prime }B{B}^{\prime }{X}_6$ perovskites, all 23 materials are unique, novel and not yet reported in any known database. Using ML modeling and DFT simulation, the newly discovered perovskite candidates are further investigated in order to ascertain their target properties. For ML determination, the pre-trained Conv2D networks for predicting stability properties in the energy above convex hull (${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}$) and formation energy (${\mathit{E}}_{\mathit{f}}$) of the relaxed candidates are used. For evaluating the energy band gap (${\mathit{E}}_{\mathit{g}}$) and total magnetization however, DFT simulation is rather used, given that ${\mathit{E}}_{\mathit{g}}$ and magnetization are universal and not extensive on total energy. Upon investigation, 73% of all DFT relaxed perovskites are predicted to meet initially prescribed stability and synthesizability requirements (i.e., ${\mathit{E}}_{\mathit{h}\mathit{u}\mathit{l}\mathit{l}}\le 0.08$ eV/atom and ${\mathit{E}}_{\mathit{f}}\le -1.5$ eV/atom). Moreover, taking into account a safer metastable threshold of ${\mathit{E}}_{\mathit{f}}\le 0.5$ eV/atom as suggested for screening promising vanadium oxide materials in past study (Noh et al., 2019), all newly discovered perovskites are confirmed to be at least metastable with negative formation energies. A comprehensive list of the newly discovered materials is provided in Table 2, in addition to their determined target properties. The Crystallographic Information Files (CIF) and electronic structure code simulations for all materials are made openly available (see Data availability statement). With reference to their DFT determined band gaps, the current study identifies some promising candidates, which can potentially serve as host materials for serviceable photovoltaic and/or optoelectronic applications. The Shockley-Queisser limits are used as basis, postulating that materials with band gaps within $1-1.7$ eV are highly theoretically efficient single junction solar cell materials due to their power conversion efficiencies (PCEs) in excess of 30% (Shockley and Queisser, 1961; Rühle, 2016). For high potential material candidates with band gaps close to the ideal 1.3 eV, the study further investigates the DFT-determined relative energies $\left({\mathit{E}}_{\mathit{r}\mathit{e}\mathit{l}}\right)$, in addition to their electronic and magnetic behaviors using band structure and Projected Density of States (PDOS) plots. The materials include ${\text{In}}_2\text{YSb}{\mathrm{O}}_6$ (CIF ID: 3), ${\text{Sr}}_2\text{LiAl}{\mathrm{H}}_6$ (CIF ID: 64) and $\text{SrLiWTe}{\mathrm{O}}_6$ (CIF ID: 132), and their properties are provided in Figure 11. For these compounds, the band structure in momentum-space are found to possess indirect bandgaps. For assessing relative energies of these materials, a similar approach is applied as previously demonstrated for hybrid organic-inorganic perovskites (Emery and Wolverton, 2017; Kim et al., 2017), which is originally inspired by actual formation energy calculations. In essence, the relative energy accounts for the simple difference in total DFT-computed energies between the relaxed crystalline material and the sum of the isolated constitutive elements at the same level of theory as the crystalline material calculation. Further details on computational methodology and equations are provided in Supplementary Material. Band structures are computed along high-symmetry line segments in the irreducible Brillouin zone of their primitive crystal structures (Setyawan and Curtarolo, 2010). For evaluating the PDOS, denser K-point grid meshes are used in the Quantum Espresso code.

TABLE 2

TABLE 2. Newly discovered double perovskites emerging from the EVAPD model that successfully underwent thorough DFT-relaxation.

FIGURE 11

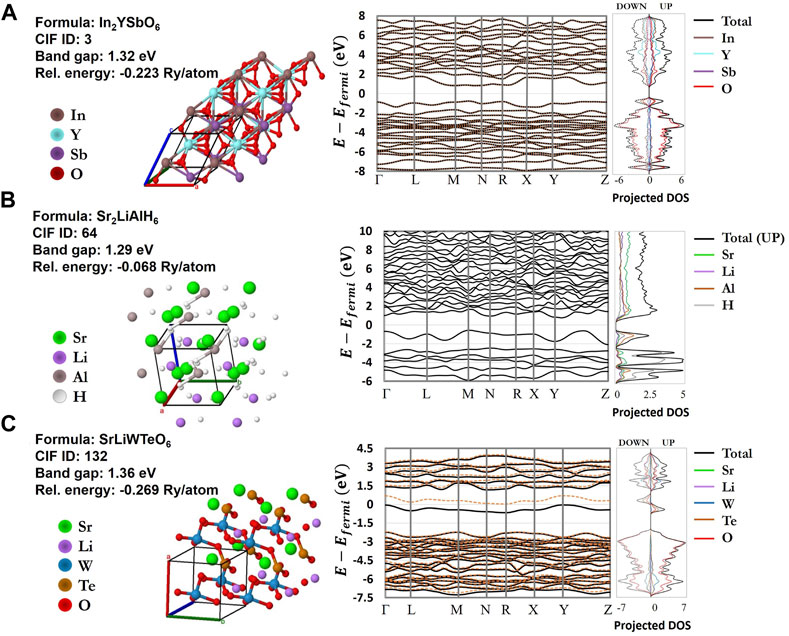
FIGURE 11. Electronic band structure and projected density of states (PDOS) properties for three promising photovoltaic host perovskite materials from the EVAPD model, with idealized band gaps close to 1.3 eV (A) ${\text{In}}_2\text{YSb}{\mathrm{O}}_6$- CIF ID: 3; (B) ${\text{Sr}}_2\text{LiAl}{\mathrm{H}}_6$- CIF ID: 64; and (C) $\text{SrLiWTe}{\mathrm{O}}_6$- CIF ID: 132. The new materials each contain ten atoms in their relaxed unit cells. Relative (Rel.) energy in units of Rydberg (Ry) per atom.

4.2 Experimental impact of the EVAPD model and future improvements

The unlimited design space afforded by perovskite stoichiometries suggests that data-mining Deep Generative Modeling (DGM) can be a more efficient alternative over first-principles techniques and/or Edisonian experiments for making accelerated discovery. The current study points to this potential advantage by cost-effectively demonstrating the efficacy of a deep evolutionary learning framework for discovering stable and functional perovskites that adopt the $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$ higher stoichiometries. The model extends beyond ideal perovskite symmetrisation by searching for non-idealized and/or non-electroneutral compounds, as well as similar chemical compounds that share the same formulation with perovskites (e.g., ilmenite). In general, the main reason for non-idealized perovskites is the Jahn-Teller distortional effect from the electronic instabilities of constitutive atoms, which translates into the form of ${BX}_6$ octahedral tilting/rotation (Knapp and Woodward, 2006). As such, in addition to finding novel candidates that are chemically and structurally idealized, the current study contributes by also discovering new inorganic perovskite candidates that are influenced by the Jahn-Teller non-idealized effect. It shall be noted moreover, that the screening of some non-electroneutral compounds by the EVAPD model is equally a reflection of the training dataset from the Materials Project database (Jain et al., 2013), as most proven perovskite compounds do not strictly obey charge neutrality laws. The successful convergence/relaxation of these compounds via density functional theory (DFT) validates their potential formability upon synthesization. The developed EVAPD model is architectured to highly rank novel candidates based on target properties that are predefined on stability and synthesizability. Moreover, the EVAPD model could be re-engineered for application on other material classes and/or multi-objective target optimizations. Such re-engineering would necessitate modifications to the current descriptor concept and mechanism for performing target-objective search optimization. To shed more insight on the contribution of the present study in the field, Table 3 compares the developed EVAPD model to some prior designs for accelerated materials discovery using the DGM approach. In general, deep evolutionary learning has achieved substantial successes in molecular design and de novo drug discovery (Kwon et al., 2021; Mukaidaisi et al., 2022) in previous years. However, they have not been broadly expanded to energy materials discovery. Specifically, the Fourier Transformed Crystal Property (FTCP) representation (Ren et al., 2022) and the Image-based Materials Generator (iMatGen) (Noh et al., 2019) utilize semi-supervised variational autoencoders (SSVAE) for generating novel materials. Both approaches rely singularly and strictly on a target-learnable latent space, which may be insufficient for target-property optimization due to the distribution of the dataset and in situations where the DGM model fails to properly assimilate the latent space [e.g., posterior and mode collapse (Lucas et al., 2019)]. To overcome this challenge, the proposed EVAPD model integrates a genetic algorithm for target-property optimization. This is achieved by performing in-depth search operations about a global optimizable minimum for generating high quality solutions. In addition, the inclusion of a geometrical similarity analysis enables streamlining the search for novel candidates to the most promising and theoretically feasible ones. As a result, a considerably advanced model performance is achieved with increased capacity for the discovery of novel crystalline materials, as demonstrated on the perovskite material class for application in the field of regenerative energy.

TABLE 3

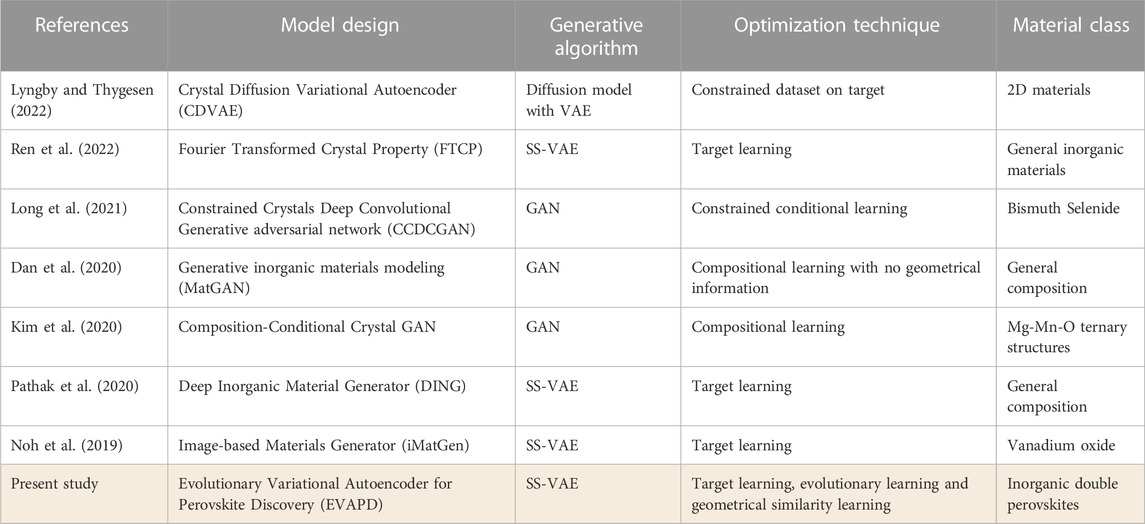
TABLE 3. Proposed model as compared to the prior arts on invertible deep generative modeling (DGM) approaches for accelerated materials discovery.

On the downside, VAE models, including the proposed model, are also prone to several challenges that affect their general performance for generating quality samples in the latent space. In addition to the aforementioned posterior and mode collapse phenomena, other concerns are related to their computational efficiency on high-dimensional data structures. The current study observes such lapses in the higher errors that were realized in reconstructing the lattice edge vectors and inter-axial angles associated with the input image-based descriptor (Table 1). Possible solutions to mitigate such limitations are by replacing the conventional autoencoder with a more efficient Wasserstein autoencoder (Tolstikhin et al., 2017), or by entirely remodeling using a different DGM, e.g., generative adversarial networks (GAN) (Goodfellow et al., 2014) and denoising diffusion models (Sohl-Dickstein, et al., 2015). This is the focus of future studies aiming at improving the EVAPD model by comparing and contrasting the results generated in the current study with other advanced DGM techniques. Another potential improvement is to better integrate DFT in the EVAPD model. In the current design architecture, post-optimizing novel perovskites using DFT validation is performed after generative and sampling processes have taken place. A better design alternative might be by directly integrating on-the-fly first-principles DFT validation and/or laboratory synthesization into the evolutionary learning space to produce an adaptive EVAPD model. This could ensure that novel materials with definitive targets are generated on a more successful rate. This is also an area of future studies.

5 Conclusion

In the present study, an Evolutionary Variational Autoencoder for Perovskite Discovery (EVAPD) model is proposed for accelerating the search for stable and functional perovskite candidates. The perovskite stoichiometries of interest are the complex $A_{2}B{B}^{\prime }{X}_6$ and $A{A}^{\prime }B{B}^{\prime }{X}_6$ double chemical compounds. The developed EVAPD model comprises a Semi-Supervised Variational Autoencoder (SS-VAE), an evolutionary-based Genetic Algorithm (GA), and a similarity analytical model to form a deep evolutionary learning framework. The SS-VAE model generates new perovskites from a target-learnable space, which is pre-optimized on the formation energy target. To find the most stable and synthesizable candidates, the GA model performs metaheuristic search operations on the newly generated perovskites, based on a predefined fitness function that adapts to the supervisory learning of the energy above hull parameter and inorganic crystal structure database (ICSD) label. Moreover, the similarity analytical model assesses the novel candidates to ensure that their three-dimensional geometric coordination is in close approximation with proven standards. As proof of concept, the EVAPD model is experimented on about 8,000 training samples from the Materials Project (MP) and has successfully predicted 137 materials so far, of which 59 $A_{2}B{B}^{\prime }{X}_6$ and 23 $A{A}^{\prime }B{B}^{\prime }{X}_6$ are unique and novel (i.e., not included in the experimented dataset, MP in general, or any other known materials database). Among them, seventeen are identified as candidates with promising potential as host materials for photovoltaic and/or optoelectronic applications. Overall, the current study illustrates the potential of the EVAPD deep evolutionary learning framework for novel materials discovery and opens up a new avenue for further advancements in the field.

Data availability statement

The new materials dataset generated for this study can be found in the NOMAD repository (doi.org/10.17172/NOMAD/2023.05.31-1). The preprocessed dataset used for machine learning, relevant source codes for developing the EVAPD model, and Crystallographic Information Files (CIF) of newly generated materials are made available on GitHub (github.com/chenebuah/EVAPD).

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was supported by the National Research Council of Canada (NRC) through its Artificial Intelligence for Design Program led by the Digital Technologies Research Centre.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2023.1233961/full#supplementary-material

References

Belsky, A., Hellenbrandt, M., Karen, V. L., and Luksch, P. (2002). New developments in the inorganic crystal structure database (ICSD): accessibility in support of materials research and design. Acta Cryst. B58, 364–369. doi:10.1107/S0108768102006948

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, R. F., and Neaton, J. B. (2012). Computational design of low-band-gap double perovskites. Phys. Rev. B 86 (16), 165211. doi:10.1103/PhysRevB.86.165211

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50 (24), 17953–17979. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Chenebuah, E. T., Nganbe, M., and Tchagang, A. B. (2023). A Fourier-transformed feature engineering design for predicting ternary perovskite properties by coupling a two-dimensional convolutional neural network with a support vector machine (Conv2D-SVM). Mater. Res. Express. 10, 026301. doi:10.1088/2053-1591/acb683

CrossRef Full Text | Google Scholar

Chenebuah, E. T., Nganbe, M., and Tchagang, A. B. (2021). Comparative analysis of machine learning approaches on the prediction of the electronic properties of perovskites: A case study of ABX₃ and A₂BB′X₆. Mater. Today Commun. 27, 102462. doi:10.1016/j.mtcomm.2021.102462

CrossRef Full Text | Google Scholar

Dan, Y., Zhao, Y., Li, X., Li, S., Hu, M., and Hu, J. (2020). Generative adversarial networks (GAN) based efficient sampling of chemical composition space for inverse design of inorganic materials. npj Comput. Mater 6, 84. doi:10.1038/s41524-020-00352-0

CrossRef Full Text | Google Scholar

Draxl, C., and Scheffler, M. (2018). Nomad: the fair concept for big data-driven materials science. MRS Bull. 43, 676–682. doi:10.1557/mrs.2018.208

CrossRef Full Text | Google Scholar

Emery, A., and Wolverton, C. (2017). High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO₃ perovskites. Sci. Data 4, 170153. doi:10.1038/sdata.2017.153

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuhr, A. S., and Sumpter, B. G. (2022). Deep generative models for materials discovery and machine learning-accelerated innovation. Front. Mater. 9, 865270. doi:10.3389/fmats.2022.865270

CrossRef Full Text | Google Scholar

Gad, A. F. (2021). PyGAD: an intuitive genetic algorithm Python library. arXiv:2106.06158v1 [cs.NE]. doi:10.48550/arXiv.2106.06158

CrossRef Full Text | Google Scholar

Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). Quantum espresso: A modular and open-source software project for quantum simulations of materials. J. Phys.:Condens. Matter. 21 (39), 395502. doi:10.1088/0953-8984/21/39/395502

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative adversarial networks. arXiv:1406.2661v1 [stat.ML]. doi:10.48550/arXiv.1406.2661

CrossRef Full Text | Google Scholar

Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the materials project: A materials genome approach to accelerating materials innovation. Apl. Mater. 1 (1), 011002. doi:10.1063/1.4812323

CrossRef Full Text | Google Scholar

Jena, A. K., Kulkarni, A., and Miyasaka, T. (2019). Halide perovskite photovoltaics: background, status, and future prospects. Chem. Rev. 119 (5), 3036–3103. doi:10.1021/acs.chemrev.8b00539

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnsson, M., and Lemmens, P. (2005). Crystallography and chemistry of perovskites. arXiv:cond-mat/0506606v1 [cond-mat.str-el]. doi:10.48550/arXiv.cond-mat/0506606

CrossRef Full Text | Google Scholar

Kamnitsas, K., Castro, D. C., Le Folgoc, L., Walker, I., Tanno, R., Rueckert, D., et al. (2018). Semisupervised learning via compact latent space clustering. arXiv:1806.02679v2 [cs.LG]. doi:10.48550/arXiv.1806.02679

CrossRef Full Text | Google Scholar

Kim, C., Huan, T. D., Krishnan, S., and Ramprasad, R. (2017). A hybrid organic-inorganic perovskite dataset. Sci. Data 4, 170057. doi:10.1038/sdata.2017.57

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Noh, J., Gu, G. H., Aspuru-Guzik, A., and Jung, Y. (2020). Generative adversarial networks for crystal structure prediction. ACS Cent. Sci. 6 (8), 1412–1420. doi:10.1021/acscentsci.0c00426

PubMed Abstract | CrossRef Full Text | Google Scholar

Kingma, D. P., Rezende, D. J., Mohamed, S., and Welling, M. (2014). Semi-supervised learning with deep generative models. arXiv:1406.5298v2 [cs.LG]. doi:10.48550/arXiv.1406.5298

CrossRef Full Text | Google Scholar

Kingma, D. P., and Welling, N. (2013). Auto-encoding variational Bayes. arXiv:1312.6114v11 [stat.ML]. doi:10.48550/arXiv.1312.6114

CrossRef Full Text | Google Scholar

Kiselyovaa, N. N., Dudareva, V. A., Stolyarenkoa, A. V., Dokukina, A. A., Sen’koc, O. V., Ryazanovc, V. V., et al. (2022). Prediction of space groups for perovskite-like A₂^IIB^IIIB′^VO₆ compounds. Inorg. Mater Appl. Res. 13 (2), 277–293. doi:10.1134/S2075113322020228

CrossRef Full Text | Google Scholar

Knapp, M. C., and Woodward, P. M. (2006). A-site cation ordering in AA′BB′O₆ perovskites. J. Solid State Chem. 179 (4), 1076–1085. doi:10.1016/j.jssc.2006.01.005

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Kullback, S., and Leibler, R. A. (1951). On information and sufficiency. JSTOR. 22 (1), 79–86. doi:10.1214/aoms/1177729694

CrossRef Full Text | Google Scholar

Kwon, Y., Kang, S., Choi, Y. S., and Kim, I. (2021). Evolutionary design of molecules based on deep learning and a genetic algorithm. Sci. Rep. 11, 17304. doi:10.1038/s41598-021-96812-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Libelli, S. M., and Alba, P. (2000). Adaptive mutation in genetic algorithms. Soft Comput. 4, 76–80. doi:10.1007/s005000000042

CrossRef Full Text | Google Scholar

Long, T., Fortunato, N. M., Opahle, I., Zhang, Y., Samathrakis, I., Shen, C., et al. (2021). Constrained crystals deep convolutional generative adversarial network for the inverse design of crystal structures. npj Comput. Mater. 7, 66. doi:10.1038/s41524-021-00526-4

CrossRef Full Text | Google Scholar

Lucas, J., Tucker, G., Grosse, R. B., and Norouzi, M. (2019). Understanding posterior collapse in generative latent variable models. DGS@ICLR.

Google Scholar

Lufaso, M. W., and Woodward, P. M. (2004). Jahn–Teller distortions, cation ordering and octahedral tilting in perovskites. Acta Cryst. B 60, 10–20. doi:10.1107/S0108768103026661

PubMed Abstract | CrossRef Full Text | Google Scholar

Lundberg, S. M., and Lee, S. I. (2017). A unified approach to interpreting model predictions advances in neural information processing systems. arXiv:1705.07874v2 [cs.AI]. doi:10.48550/arXiv.1705.07874

CrossRef Full Text | Google Scholar

Lyngby, P., and Thygesen, K. S. (2022). Data-driven discovery of 2D materials by deep generative models. npj Comput. Mater 8, 232. doi:10.1038/s41524-022-00923-3

CrossRef Full Text | Google Scholar

Mansimov, E., Mahmood, O., Kang, S., and Cho, K. (2019). Molecular geometry prediction using a deep generative graph neural network. Sci. Rep. 9, 20381. doi:10.1038/s41598-019-56773-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Michalewicz, Z., and Schoenauer, M. (1996). Evolutionary algorithms for constrained parameter optimization problems. Evol. Comput. 4 (1), 1–32. doi:10.1162/evco.1996.4.1.1

CrossRef Full Text | Google Scholar

Mitchell, R., Welch, M., and Chakhmouradian, A. (2017). Nomenclature of the perovskite supergroup: A hierarchical system of classification based on crystal structure and composition. Mineral. Mag. 81 (3), 411–461. doi:10.1180/minmag.2016.080.156

CrossRef Full Text | Google Scholar

Mukaidaisi, M., Vu, A., Grantham, K., Tchagang, A., and Li, Y. (2022). Multi-objective drug design based on graph-fragment molecular representation and deep evolutionary learning. Front. Pharmacol. 13, 920747. doi:10.3389/fphar.2022.920747

PubMed Abstract | CrossRef Full Text | Google Scholar

Noh, J., Kim, J., Stein, H. S., Sanchez-Lengeling, B., Gregoire, J. M., Aspuru-Guzik, A., et al. (2019). Inverse design of solid-state materials via a continuous representation. Matter 1 (5), 1370–1384. doi:10.1016/j.matt.2019.08.017

CrossRef Full Text | Google Scholar

Pathak, Y., Juneja, K. S., Varma, G., Ehara, M., and Priyakumar, U. D. (2020). Deep learning enabled inorganic material generator. Phys. Chem. Chem. Phys. 22, 26935–26943. doi:10.1039/D0CP03508D

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilania, G., Balachandran, P. V., Kim, C., and Lookman, T. (2016). Finding new perovskite halides via machine learning. Front. Mater 3 (19), 19. doi:10.3389/fmats.2016.00019

CrossRef Full Text | Google Scholar

Prandini, G., Marrazzo, A., Castelli, I. E., Mounet, N., and Marzari, N. (2018). Precision and efficiency in solid-state pseudopotential calculations. npj Comput. Mater 4, 72. doi:10.1038/s41524-018-0127-2

CrossRef Full Text | Google Scholar

Ren, Z., Tian, S. I. P., Noh, J., Oviedo, F., Xing, G., Li, J., et al. (2022). An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties. Matter 5 (1), 314–335. doi:10.1016/j.matt.2021.11.032

CrossRef Full Text | Google Scholar

Rühle, S. (2016). Tabulated values of the Shockley–Queisser limit for single junction solar cells. Sol. Energy 130, 139–147. doi:10.1016/j.solener.2016.02.015

CrossRef Full Text | Google Scholar

Saal, J. E., Kirklin, S., Aykol, M., Meredig, B., and Wolverton, C. (2013). Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). JOM 65, 1501–1509. doi:10.1007/s11837-013-0755-4

CrossRef Full Text | Google Scholar

Setyawan, W., and Curtarolo, S. (2010). High-throughput electronic band structure calculations: challenges and tools. Comput. Mater. Sci. 49 (2), 299–312. doi:10.1016/j.commatsci.2010.05.010

CrossRef Full Text | Google Scholar

Shapley, L. S. (1953). “A value for n-person games,” in Contributions to the theory of games, annals of mathematical studies. Editors H. W. Kuhn, and A. W. Tucker (Princeton University Press), 307–317. doi:10.1515/9781400881970-018

CrossRef Full Text | Google Scholar

Shockley, W., and Queisser, H. J. (1961). Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32 (3), 510–519. doi:10.1063/1.1736034

CrossRef Full Text | Google Scholar

Shoemake, K. (1985). Animating rotation with quaternion curves. SIGGRAPH Comput. Graph. 19 (3), 245–254. doi:10.1145/325165.325242

CrossRef Full Text | Google Scholar

Singh, A. K., Montoya, J. H., Gregoire, J. M., and Persson, K. A. (2019). Robust and synthesizable photocatalysts for CO₂ reduction: A data-driven materials discovery. Nat. Commun. 10, 443. doi:10.1038/s41467-019-08356-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sohl-Dickstein, J., Weiss, E. A., Maheswaranathan, N., and Ganguli, S. (2015). Deep unsupervised learning using nonequilibrium thermodynamics. arXiv:1503.03585v8 [cs.LG]. doi:10.48550/arXiv.1503.03585

CrossRef Full Text | Google Scholar

Talirz, L., Kumbhar, S., Passaro, E., Yakutovich, A. V., Granata, V., Gargiulo, F., et al. (2020). Materials Cloud, a platform for open computational science. Sci. Data. 7, 299. doi:10.1038/s41597-020-00637-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Tao, Q., Xu, P., Li, M., and Lu, W. (2021). Machine learning for perovskite materials design and discovery. npj Comput. Mater 7, 23. doi:10.1038/s41524-021-00495-8

CrossRef Full Text | Google Scholar

Tolstikhin, I., Bousquet, O., Gelly, S., and Schoelkopf, B. (2017). Wasserstein auto-encoders. arXiv:1711.01558v4 [stat.ML]. doi:10.48550/arXiv.1711.01558

CrossRef Full Text | Google Scholar

van der Maaten, L., and Hinton, G. (2008). Visualizing Data using t-SNE. JMLR 9 (86), 2579–2605.

Google Scholar

Wang, Y., Zhang, H., Zhu, J., Lü, X., Li, S., Zou, R., et al. (2020). Antiperovskites with exceptional functionalities. Adv. Mater. 32, 1905007. doi:10.1002/adma.201905007

PubMed Abstract | CrossRef Full Text | Google Scholar

Weininger, D. (1988). SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 28 (1), 31–36. doi:10.1021/ci00057a005

CrossRef Full Text | Google Scholar

Woodward, P. M. (1997). Octahedral tilting in perovskites. I. Geometrical considerations. Acta Cryst. B 53, 32–43. doi:10.1107/S0108768196010713

CrossRef Full Text | Google Scholar

Xie, T., and Grossman, J. C. (2018). Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120 (14), 145301. doi:10.1103/physrevlett.120.145301

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, P., Li, M., and Chen, W. C. (2022). A perspective on perovskite solar cells: emergence, progress, and commercialization. Front. Chem. 10, 802890. doi:10.3389/fchem.2022.802890

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, X-G., Dalpian, G. M., Wang, A., and Zunger, A. (2020). Polymorphous nature of cubic halide perovskites. Phys. Rev. B 101, 155137. doi:10.1103/PhysRevB.101.155137

CrossRef Full Text | Google Scholar