Simultaneously focusing electromagnetic and acoustic waves by double-physical-fields null medium

A novel double-physical-fields lens that can simultaneously focus acoustic and electromagnetic waves into a given region is designed based on double-physical-fields null medium, which can be realized by metal plates with subwavelength separations/thicknesses and precisely designed lengths. Numerical simulations show the proposed double-physical-fields lens can create exactly the same focusing effect for both electromagnetic and acoustic waves, i.e., the same focal spot size and efficiency at the same focal length. Four typical lens with different output surfaces are studied, which shows different focusing characteristics, e.g., noodle-shaped focal spot, tiny focal spot, and capsule-shaped focal spot. With the help of the designed double-physical-fields lens, an additional degree of freedom for control can be provided by simultaneously focusing acoustic and electromagnetic waves, which may lead to wider range of applications than single-field focusing.

1 Introduction

The focusing of acoustic wave or electromagnetic wave alone has already been applied in various important application. For example, it is an effective non-invasive way of treating tumors by focusing ultrasound/microwave onto the tumor area, where focused high ultrasound/electromagnetic energy can raise the temperature of the tumor cells to produce thermal coagulation or ablation (Sato et al., 1996; Fan et al., 2013; Shi et al., 2015; Xia and Sun, 2015). Usually, tumour treatment by focused ultrasound is more accurate than the treatment by focused microwave. However, some tissues (e.g., esophagus and rectum) cannot be penetrated by ultrasound and can only be treated by focused microwave. Acoustic/electromagnetic tweezers, which can capture the target particles noninvasively by forces and torques generated from the focused acoustic/electromagnetic fields, have been widely used to manipulate the movement of micro-nano particles (e.g., biological molecules and living cells) (Janssen et al., 2012; Ozcelik et al., 2018; Vidiasheva et al., 2018; Marzo and Drinkwater, 2019). Currently, the focused acoustic beam can be achieved by acoustic metasurfaces/metamaterials (Zhang et al., 2009; Qi et al., 2017; Xia et al., 2018), negative or zero refractive index lenses (Fang et al., 2006; Gao et al., 2016), acoustic crystal lens (Yang et al., 2004), graded index lens (Li et al., 2012), anisotropic material lens (Li et al., 2017), and etc. Common methods of focusing electromagnetic waves include various electromagnetic lenses (Kwon and Werner, 2009; Kundtz and Smith, 2010; Roy et al., 2013; Khorasaninejad et al., 2016; Chen et al., 2018), time reversal mirrors (Lerosey et al., 2004; de Rosny et al., 2010), structures designed by deep learning methods (Rivenson et al., 2017; Ma et al., 2021), and etc.

Compared with single-physical-field focusing, focusing acoustic and electromagnetic waves simultaneously has better application value. If the simultaneous focus of acoustic and electromagnetic waves can be achieved, the advantages of the two focused physical fields can complement each other. In tumor therapy, simultaneous focused ultrasound and microwave will provide both the high precision of focused acoustic waves for tumour treatment (Kohrmann et al., 2002) and the high penetration of focused microwaves for tumour treatment (Leggio et al., 2015; Lim and Yoon, 2021). Double-physical-fields tweezers by simultaneous focused ultrasound and microwave can provide additional degrees of freedom in the manipulation of captured targets, e.g., the focused acoustic beam can capture targets in the given region while the focused electromagnetic beam can rotate them at the same time. In industrial inspection, the focused acoustic wave can be used to locate cracks in pipes and castings, while the focused electromagnetic beam can help to repair these cracks (e.g., the thermal effect of focused infrared waves can help repair cracks by dissolving the material at the crack). In double-field focusing, the focused acoustic waves may image/capture/locate the target, and the focused electromagnetic waves may simultaneously perform an additional manipulation (e.g., destruction/rotation/repairment) on the same target. In recent years, various structures have been designed to simultaneously manipulate electromagnetic and acoustic waves, such as electromagnetic-acoustic cloaking (Sun et al., 2020), electromagnetic shielding and sound absorption (Gao et al., 2022), and electromagnetic-acoustic splitter (Chen et al., 2023). However, there is little research on how to achieve simultaneous focusing of electromagnetic and acoustic waves with the same structure.

In order to focus acoustic and electromagnetic waves simultaneously, a novel double-physical-fields lens (DPFL) is proposed in Figure 1. The designed DPFL can be realized by metal plates with subwavelength separations/thicknesses and precisely designed lengths, which performs as a reduced double-physical-fields null medium that can convert the incident electromagnetic/acoustic wavefront on the input surface of the lens into the desired electromagnetic/acoustic wavefront on the output surface of the lens (Sun et al., 2020). Note that the ‘subwavelength’ means the size of the separation and thickness of the metal plates are smaller than the wavelength of the electromagnetic/acoustic wave, e.g., one-third of the working wavelength.

FIGURE 1

FIGURE 1. Schematic diagram of the DPFL by sub-wavelength air channels enclosed by metal plates.

2 Design method

Double-physical-fields null medium, which performs as a perfect endoscope for electromagnetic waves and acoustic waves simultaneously, has been theoretically studied (Sun et al., 2020). Based on the perfect directional projection properties of the double-physical-fields null medium, double-physical-fields surface transformation has been proposed in our previous study (Sun et al., 2020), which is a graphical method to design double-physical-fields devices. In this study, we use double-physical-fields surface transformation to design DPFL that can focus both electromagnetic waves and acoustic waves into the same focal point. The parameters of the ideal double-physical-fields null medium can be obtained from the extreme space compression transform by transformation optics and transformation acoustics, which can be summarized as (Sun et al., 2020):

$\left\{\begin{array}{l}\epsilon =\mu =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\frac{1}{\Delta },\Delta ,\Delta \right)\\ \rho =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\Delta ,\frac{1}{\Delta },\frac{1}{\Delta }\right)\\ \kappa =\frac{1}{\Delta }\end{array}\right.,\Delta \to 0.(1)$

From Eq. 1, the permittivity, permeability and modulus of the ideal double-physical-fields null medium are extremely anisotropic, whose values approach infinity along their main axis and are close to zero in other orthogonal directions. After some theoretical calculations (Sun et al., 2020), it shows that the metallic plates with subwavelength separations and thicknesses, whose lengths satisfy the Fabry-Perot resonance condition, can perform as a reduced double-physical-fields null medium. The reduced double-physical-fields null medium can still project TM-polarized electromagnetic waves and acoustic waves simultaneously along the orientations of metallic plates.

As shown in Figure 1, the input and output surfaces of the DPFL are designed as a plane and a curved surface (described by the equation y = f (x)), respectively. The DPFL is composed by an array structure of 2N + 1 parallel metal plates with equally subwavelength separation d and thickness t. 2N air channels are formed between two adjacent metal plates, which are labeled from the centre of the lens outwards as channel 1, channel 2, … and channel N. The size of the input surface of the DPFL is h = 2Nd + t, which can be adjusted by increasing or decreasing the number of metal plates for matching the width of the incident wave. The length of the k-th air channel approximately satisfying the Fabry-Perot resonance condition (i.e., L_k = mλ₀, m = 1, 2, 3…, where λ₀ is the working wavelength) to obtain the best transmittance, which is defined as the efficiency of the DPFL for electromagnetic waves (Xia et al., 2018):

$\eta =\frac{{\displaystyle \underset{l}{\int }}\overline{S}\cdot d\overline{A}}{{\displaystyle \underset{h}{\int }}\overline{S}\cdot d\overline{A}},(2)$

where S is the Poynting vector (i.e., the energy flow density vector), l and h are the transverse sizes of the focusing spot and input surface along the y-axis, respectively (see Figure 1). Although there is no concept of Poynting’s vector for acoustic waves, the z component of magnetic field H_z field for TM polarized electromagnetic waves and the acoustic pressure for acoustic waves satisfy the same Heimholtz equation, and the subsequent simulation results show that the designed structure has exactly the same focusing effect on both magnetic field and acoustic pressure, therefore the efficiency defined by Eq. 2 is also suitable for the focusing efficiency of acoustic wave.

In this study, the efficiency of the lens is calculated as follows: we first remove the DPFL and calculate the integration of the incident energy flow over the air surface with the same size of the DPFL’s input surface, which gives the denominator of Eq. 2, i.e., the total incident energy. Then, we add the DPFL and calculate the integration of energy flow density over the width of the focused spot, which gives the numerator of Eq. 2, i.e., the energy at the focused spot. Since all simulations show that the lens produces exactly the same field distribution for both electromagnetic wave and acoustic wave, the simulated results for electromagnetic waves are used to calculate the lens efficiency in the subsequent optimization calculations.

The designed DPFL by metal plates in Figure 1 performs as reduced double-physical-fields null medium for TM-polarized electromagnetic and acoustic waves, whose function is to simultaneously project the electromagnetic/acoustic field distributions from the input surface along the direction of the air channel onto the output surface (Sun et al., 2020). When the wavefront of the incident EM wave/acoustic wave coincides with the shape of the DPFL’s input surface (e.g., plane wave), the wavefront of the outgoing wave can be converted to coincide with the shape of the DPFL’s output surface after passing through the DPFL. Therefore, a double-physical-field focusing effect can be obtained by designing various geometrical shapes of output surfaces.

3 Simulation results for various DPFLs

The double-physical-fields focusing effect of various DPFLs with different output surfaces are studied numerically. All numerical simulations in this study are carried out by COMSOL Multiphysics 5.6 (license number 9406999). All numerical simulations are 2D simulations in this study, which means that the metal plates are infinite along the z direction. The radio frequency module and the acoustic module are utilized to calculate electromagnetic field distribution and acoustic pressure distribution, respectively. The working wavelength is designed as λ₀ = 30 mm, which corresponds to the working frequencies 10 GHz for electromagnetic wave and 11.4 kHz for acoustic wave, respectively. The metal is modeled as perfect electric conductor and hard wall boundary condition for electromagnetic simulation and acoustic simulation, respectively. Note that metallic plates can perform as reduced null medium for only TM-polarized electromagnetic waves, we only simulate the DPFLs for TM-polarized electromagnetic waves in this study. The double-physical-fields focusing effect of DPFLs with four different shapes of the output surface are studied, which include the parabolic surface in Figure 2, the hyperbolic surface in Figure 3, the elliptical surface in Figure 4, and the circular surface in Figure 5.

FIGURE 2

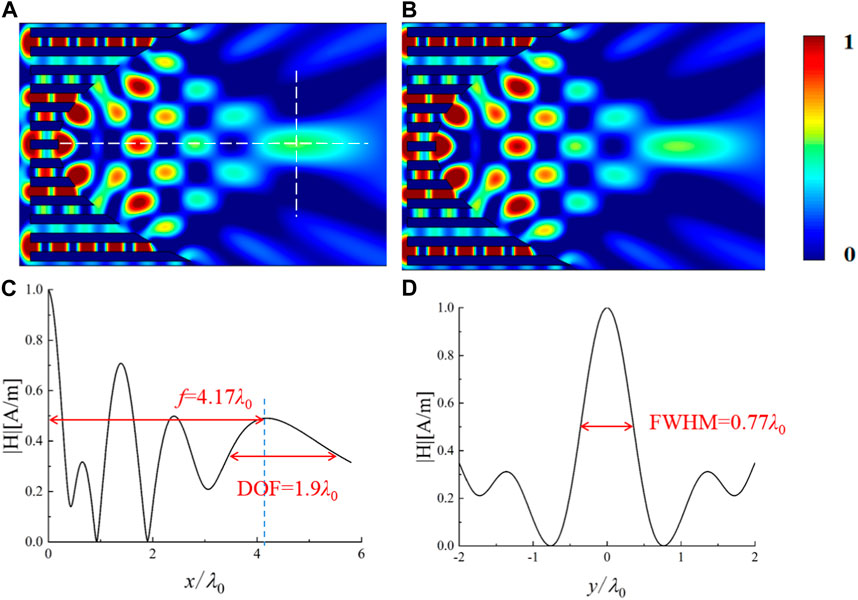
FIGURE 2. Simulated normalized magnetic field distribution (A) and normalized acoustic pressure distribution (B), respectively, when a TM-polarized plane electromagnetic wave and a plane acoustic wave are incident onto the designed DPFL with a parabolic output surface f(x) = $\sqrt{55x}$. In this design, N = 6, d = λ₀/3, t =λ₀/6, L₁ = 0.5λ₀, L₂ = 0.58λ₀, L₃ = 0.78λ₀, L₄ = 1.14λ₀, L₅ = 1.6λ₀, L₆ = 2.17λ₀, and λ₀ = 30 mm. (C, D) show the normalized magnetic field (the same as acoustic pressure) distribution along the x and y directions [marked by white dashed lines in (A)], respectively.

FIGURE 3

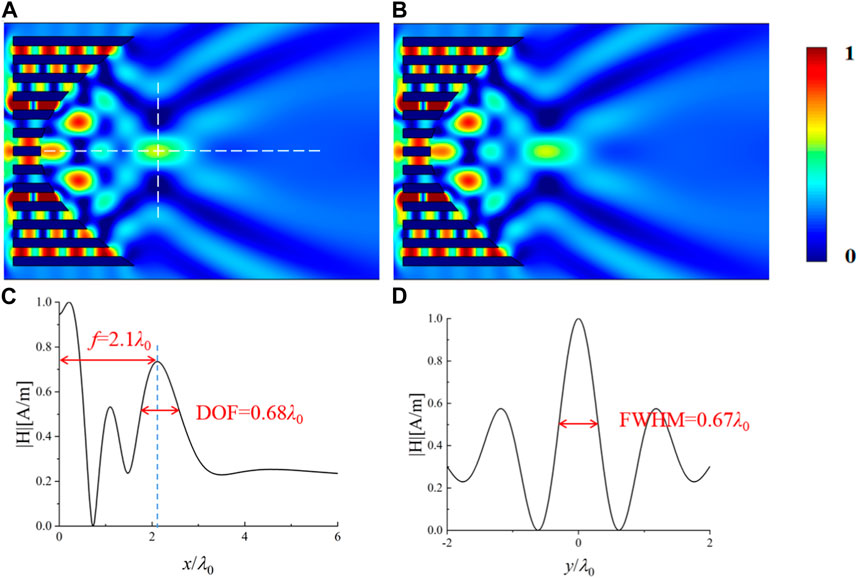
FIGURE 3. Simulated normalized magnetic field distribution (A) and normalized acoustic pressure distribution (B), respectively, when a TM-polarized plane electromagnetic wave and a plane acoustic wave are incident onto the designed DPFL with a hyperbolic output surface equation f(x) = 70 $\sqrt{-1+x^2/22500}$. In this design, N = 6, d = λ₀/3, t = λ₀/6, L₁ = 0.5λ₀, L₂ = 0.58λ₀, L₃ = 0.75λ₀, L₄ = 1.01λ₀, L₅ = 1.35λ₀, L₆ = 1.75λ₀, and λ₀ = 30 mm. (C, D) show the normalized magnetic field (the same as acoustic pressure) distribution along the x and y directions [marked by white dashed lines in (A)], respectively.

FIGURE 4

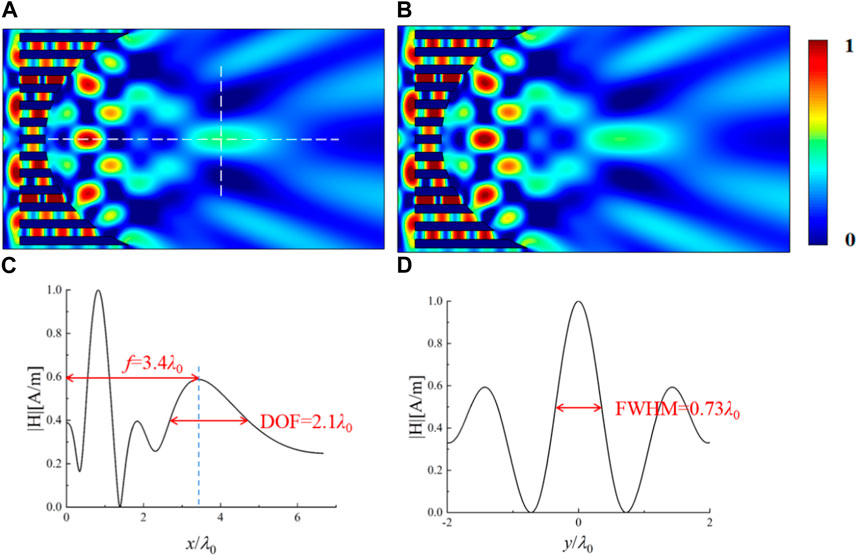
FIGURE 4. Simulated normalized magnetic field distribution (A) and normalized acoustic pressure distribution (B), respectively, when a TM-polarized plane electromagnetic wave and a plane acoustic wave are incident onto the designed DPFL with an elliptical output surface equation f(x) = 70 $\sqrt{1-x^2/8100}$. In this design, N = 6, d = λ₀/3, t = λ₀/6, L₁ = 0.5λ₀, L₂ = 0.55λ₀, L₃ = 0.66λ₀, L₄ = 0.84λ₀, L₅ = 1.12λ₀, L₆ = 1.52λ₀, and λ₀ = 30 mm. (C, D) show the normalized magnetic field (the same as acoustic pressure) distribution along the x and y directions [marked by white dashed lines in (A)], respectively.

FIGURE 5

FIGURE 5. Simulated normalized magnetic field distribution (A) and normalized acoustic pressure distribution (B), respectively, when a TM-polarized plane electromagnetic wave and a plane acoustic wave are incident onto the designed DPFL with a circular output surface equation f(x) = $\sqrt{8464-x^2}$. In this design, N = 8, d = 11λ₀/30, t = 11λ₀/60, L₁ = 0.93λ₀, L₂ = 0.97λ₀, L₃ = 1.05λ₀, L₄ = 1.17λ₀, L₅ = 1.36λ₀, L₆ = 1.61λ₀, L₇ = 1.96λ₀, L₈ = 2.47λ₀, and λ₀ = 30 mm. (C, D) show the normalized magnetic field (the same as acoustic pressure) distribution along the x and y directions [marked by white dashed lines in (A)], respectively.

The designed working wavelength (λ₀ = 30 mm) and corresponding frequencies (11.4 kHz and 10 GHz for acoustic and electromagnetic waves, respectively) is used as one example in this study, which can be changed to other values according to different applications. For example, we can first determine the required acoustic frequency for a specific application (e.g., ultrasonic detection), and then the new working wavelength can be calculated accordingly, thereafter the parameters of the DPELs can be redesigned by using Fabry-Perot resonance condition L_n = mλ₀, m = 1, 2, 3…, where λ₀ is the new working wavelength.

The lens designed in this study involves metal and air. For air, it can be considered a loss-free material for both electromagnetic and acoustic waves. Considering the conductivities of metals are extremely high (e.g., the conductivity of the copper is 6*10⁷ [S/m]) in the microwave band (the designed working frequency 10 GHz), whose skin depth can be treated as zero (modeled as perfect electric conductor), the material loss of the metal has essentially no effect on the focusing effect of the electromagnetic waves in the designed working frequency. Similarly, metals can usually be treated as a hard wall boundary condition for acoustic waves (Yang et al., 2016), i.e., acoustic waves cannot enter. Therefore, the material loss of the metal has no effect on the focusing effect of the acoustic waves.

The simulated results verify the designed DPFL with a parabolic output surface (i.e., the equation of the output surface is chosen as a parabolic equation f(x) = $\sqrt{55x}$) can focus both TM-polarized electromagnetic plane wave in Figure 2A and acoustic plane wave in Figure 2B, respectively. When a planar electromagnetic wave and a planar acoustic wave are incident onto the designed DPFL, the normalized magnetic/acoustic field distributions are identical in Figures 2A, B, which show exactly the same focusing spots for both fields can be created at the same distance f (i.e., the focal length) from the output surface of the DPFL. The depth of focus (DOF) is the distance range measured normal to the lens over which the spot remains tightly focused (Banerji et al., 2020). In this study, DOF is used to describe longitudinal scale of focal spot. The simulated results show that the parabolic DPFL simultaneously focus electromagnetic waves and acoustic waves into a capsule-shaped spot with a relatively moderate size, which is often described by full width at half maxima (FWHM = 0.77λ₀) and depth of focus DOF = 1.9λ₀, at relatively long focal length f = 4.17λ₀ with efficiency η = 31.42% (see Figures 2C, D).

Please note that the amplitudes of magnetic field and acoustic pressure are normalized, which leads to a range of values between 0 (minimum) and 1 (maximum), and the color bars in all figures are in the range 0–1. In this case, the blue regions in the color bar indicate that the amplitude of magnetic field or acoustic pressure at these positions are zero ‘0’, the red regions in the color bar indicate that the amplitude of magnetic field or acoustic pressure at these positions are the maximum ‘1’, and the other colors mean that the amplitude of magnetic field or acoustic pressure are between the zero ‘0’ and the maximum “1”.

The hyperbolic DPFL, whose output surface satisfy a hyperbolic equation f(x) = 70 $\sqrt{-1+x^2/22500}$, can also focus both TM-polarized electromagnetic plane wave in Figure 3A and acoustic plane wave in Figure 3B, respectively. The simulated results in Figure 3 show that the hyperbolic DPFL can produce a tiny focal spot with smaller size FWHM = 0.67λ₀ and depth of focus DOF = 0.68λ₀ for both fields at short focal length f = 2.1λ₀ with efficiency η = 26.86% (see Figures 3C, D), which is more suitable for the double-fields manipulation of small particles.

The elliptical DPFL, whose output surface satisfy a elliptical equation f(x) = 70 $\sqrt{1-x^2/8100}$, can simultaneously focus TM-polarized electromagnetic plane wave in Figure 4A and acoustic plane wave in Figure 4B, respectively. The simulated results in Figure 4 show that the parameters of the focal spot created by the elliptical DPFL are FWHM = 0.73λ₀, DOF = 2.1λ₀, and f = 3.4λ₀, which are close to the parameters of the focal spot created by the parabolic DPFL in Figure 2. Compared the parabolic DPFL in Figure 2, the elliptical DPFL has significant side spots around the focal spot, which leads to a small efficiency η = 22.37%.

The circular DPFL, whose output surface satisfy a circular equation f(x) = $\sqrt{8464-x^2}$, can simultaneously focus TM-polarized electromagnetic plane wave in Figure 5A and acoustic plane wave in Figure 5B, respectively. The simulated results in Figure 5 show that the circular DPFL can produce a noodle-shaped focal spot with the size FWHM = 0.95λ₀ and depth of focus DOF = 4.13λ₀ for both fields at long focal length f = 6.7λ₀ with efficiency η = 37.71% (see Figures 5C, D), which is more suitable for the double-physical-fields noninvasive processing/treatment.

Theoretically, according to the double-physical-fields surface transformation theory, when the output surface of the lens is chosen to be of different geometrical shapes, the wave front of the output wave will be modulated to that shape accordingly. In this design, the output surfaces are designed as parabola, hyperbola, ellipse and circle, respectively, and according to the nature of perfect projection of null medium, the wave fronts of the output waves are modulated into these four surfaces accordingly. In these four cases, the output wave is focused at the focal point of the parabola/hyperbola/ellipse and at the centre of the circle, and the position of the focal point can be adjusted by changing the geometrical parameters of the corresponding output surface.

The key parameters of the DFPL with four different output surfaces are given in Tab. 1, which can be a guidance for different applications. For the parabolic DPFL, the energy of the sidelobe is concentrated before the focal point, and the energy distribution of the sidelobe is weaker after the focal point and the focal plane, which leads to a relatively high efficiency (∼31.42%). The focal spot of the parabolic DPFL is capsule-like spot with a relatively moderate size (FWHM∼0.77λ₀ and DOF∼1.9λ₀), and the long focal length is relatively long (f ∼ 4.17λ₀). For the hyperbolic DPFL, the energy of the sidelobe is distributed before and after focusing plane, which in turn leads to lower efficiency (∼26.86%). The hyperbolic DPFL can produce the smallest focal spot with very compact sizes in both horizontal direction (DOF = 0.68λ₀) and vertical direction (FWHM = 0.67λ₀) at the shortest focal length f = 2.1λ₀, which is very suitable for precisely confining tiny objects to small area. For the elliptical DPFL, the energy of the sidelobe is distributed before and after focusing plane, which has the lowest efficiency (∼22.37%). The elliptical DPFL can create a capsule-shaped spot with a relatively moderate size (FWHM∼0.73λ₀ and DOF∼2.1λ₀) and moderate focal length (f ∼ 3.4λ₀). For the circular DPFL, the energy of the sidelobe is concentrated before the focal point, and the energy distribution of the sidelobe is weaker after the focal point and the focal plane, which has the highest efficiency (∼37.71%). The circular DPFL can produce a noodle-shaped focal spot at the longest focal length (f ∼ 6.7λ₀), which can be used for noninvasive processing/treatment that requires penetration of surfaces (e.g., inside pipes and human bones). In summary, elliptical/parabolic DPFLs are moderate-focal-length lenses with moderate focal spot sizes, hyperbolic DPFL is short-focal-length lens with smallest focal spot size, and circular DPFL is long-focal-length lens with noodle-shaped focal spot.

TABLE 1

TABLE 1. Key parameters of the DPFLs with different output surfaces.

4 Parameters scanning

From the above analysis, the parabolic DPFL has relatively moderate parameters, which is chosen as an example to study how to further improve the efficiency of the DPFL by choosing suitable structural parameters. Simulation results show separation distance d in Figure 1 and surface parameter A (f(x) = $\sqrt{Ax}$) both affect the focusing efficiency of the parabolic DPFL. As show in Figure 6, both d and A has a significant impact on the efficiency of the parabolic DPFL.

FIGURE 6

FIGURE 6. Efficiency of the parabolic DPFL when parameters d and A are scanned.

If d is too large, then the metal plates in Figure 1 will no longer behave as an effective medium for double fields; while if d is too small, it is difficult to ensure that each channel approximately meets the Fabry-Perot resonance condition, thus the scan range of d is limited to d = 3λ₀ ∼ 4.3λ₀ in Figure 6. If A is too small, the shape of the output surface will be reduced to a plane, and the focusing effect will disappear; while if A is too large, more number of metal plates are required to mimic the sharp curvature variation at the output surface, which is difficult to ensure that each channel approximately meets the Fabry-Perot resonance condition, thus the scanning range of A is limited to A = 1.4λ₀ ∼ 3λ₀ in Figure 6.

During the scanning, the number of air channels 2N = 12, the thickness of the metal plate t = d/2, and the working wavelength λ₀ = 30 mm are kept unchanged. As shown in Figure 6, the best efficiency η = 37.59% can be obtained when d = 3.27λ₀ and A = 1.5λ₀ for the optimized parabolic DPFL. The optimized parabolic DPFL with a higher energy utilization can still focus both electromagnetic and acoustic waves simultaneously with a relatively moderate size (FWHM = 0.59λ₀ and DOF = 1.93λ₀) and focal length (f = 4.3λ₀), which is verified by numerical simulations in Figure 7.

FIGURE 7

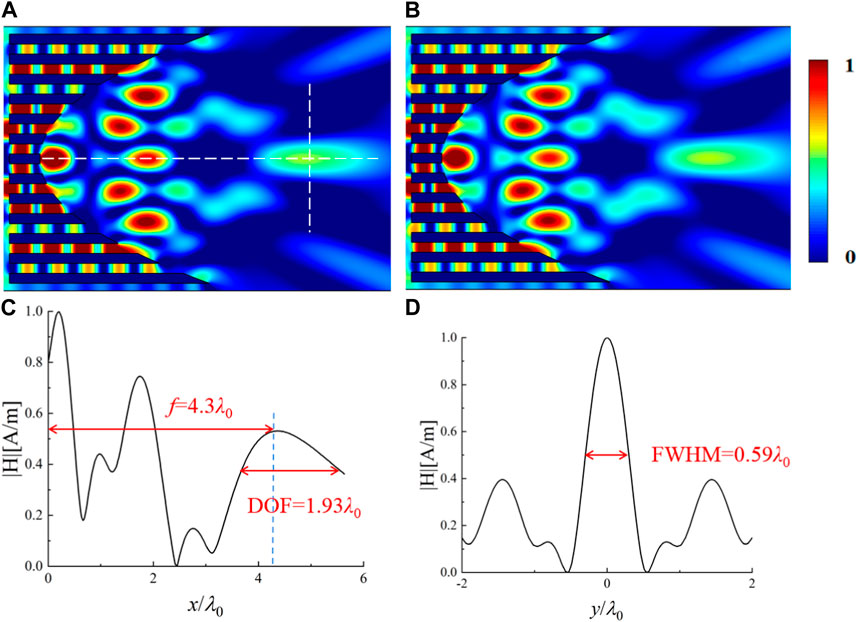
FIGURE 7. Simulated normalized magnetic field distribution (A) and normalized acoustic pressure distribution (B), respectively, when a TM-polarized plane electromagnetic wave and a plane acoustic wave are incident onto the optimized parabolic DPFL with a output surface $f\left(x\right)=\sqrt{45x}$. In this design, N = 6, d = 3.27λ₀, t = d/2, L₁ = 0.5λ₀, L₂ = 0.61λ₀, L₃ = 0.86λ₀, L₄ = 1.25λ₀, L₅ = 1.78λ₀, L₆ = 2.46λ₀, and λ₀ = 30 mm. (C, D) show the normalized magnetic field (the same as acoustic pressure) distribution along the x and y directions [indicated by white dashed lines in (A)], respectively.

For a perfect DPFL realized by ideal double-physical-fields null medium, the shape of the outgoing wave should be exactly the same as the shape of the output surface. However, for the reduced null medium by metallic array, the length of each air channel must be an integer multiple of the wavelength to obtain the best transmittance, which leads to the shape of the outgoing wave is not exactly the same as the output surface. In this case, the focal point is the result of the interference of the outgoing waves from multiple air channels, which results in a non-peak energy at the focal point along the x axis. To solve this problem, the waveguide metamaterials (Zheng et al., 2019), instead of an array of metal plates, can be used to realize the reduced null medium, where the FP condition does not need to be satisfied for each channel. In this case, the energy at the focal point can be a peak along the x axis. However, such a lens based on waveguide metamaterials would only be effective for electromagnetic waves and cannot be able to focus both electromagnetic and acoustic waves.

Our design principle is different from the current method on designing metasurfaces, which often needs to numerically calculate the phase shift and transmittance of each metasurface, and then adjust the geometric parameters of each unit to make its transmittance phase satisfy a specific distribution (on the premise of ensuring that the transmittance of each unit is close to 1) to achieve the focusing or other desired effect (Liu et al., 2020; Cai et al., 2021). In our design method, metal channels are used to mimic null medium for both electromagnetic wave and acoustic wave, which perform as the reduced null medium (Sun et al., 2020; Chen et al., 2023). For the ideal null medium, the transmittance should be 100% and the transmission phase should be zero. In this case, the wavefront of the output wave can be directly modulated by changing the geometry of the output surface. To achieve the ideal null medium, the length of each metallic channel needs to be close to an integer multiple of the operating wavelength (i.e., the FP condition) to ensure that the transmittance is close to 1 while the transmission phase is almost 0. Therefore, we do not plot the phase shift and transmittance of each metallic channel. From the simulation results in Figures 2–5, it can be seen that a stable integer number of half standing waves are generated in each metal channel, i.e., the desired FP resonance conditions are met.

In this study, the sound and electromagnetic waves are focused at the same wavelength by the designed DPFL. If we want to simultaneously focus acoustic and electromagnetic waves at individually different wavelengths rather than the same one, some gas [e.g., hydrogen (Li et al., 2017)] may be filled in each metallic channel instead of air. In this case, the effective optical path and acoustic path are different in each metallic channel, which will lead to different wavelengths that satisfy the FP resonance condition for electromagnetic wave and acoustic wave. As the FP resonance condition should be satisfied for each metal channel to mimic null medium for both electromagnetic wave and acoustic wave, the focusing performance of the designed lens is not broadband. The focusing efficiency of the designed lens may be improved by adding some internal structures inside of each metallic channel (see arXiv:2305.00910). The proposed lens is a bulk lens, which has the curved output surface. To achieve a flat lens, metasurface may be a good choice (Liu et al., 2020; Cai et al., 2021). However, the current metasurface can only work for single-physical-field (i.e., electromagnetic wave or acoustic wave). Many prior groundwork are still needed to achieve metasurface-based flat lens for double-physical-field focusing.

5 Conclusion

By designing sub-wavelength air channels surrounded by metal plates, which performs as reduced double-physical-fields null medium, a DPFL lens that can simultaneously focus both electromagnetic and acoustic waves is designed. By adjusting the geometrical shape of the output surface, the focal spot size and focal length for both fields can be modified. Four typical DPFL lenses with different output surfaces are numerically studied, which shows different focusing characteristics and key parameters, e.g., long focal length and noodle-shaped spot for circular DPFL, short focal length and tiny spot for hyperbolic DPFL, and capsule-shaped spot with a moderate size for parabolic/elliptical DPFLs. As an example, the relationship between the key parameters of the parabolic DPFL and its efficiency is studied. This study provides a new way to focus electromagnetic and acoustic waves simultaneously, which may provide an additional degree of freedom for modulation than single-field focusing and have potential applications in medical therapy, sensors/detectors and tweezers.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

BW and FS contributed equally to this work. BW and FS wrote and edited the manuscript together. BW performed theoretical analysis and numerical simulations. FS conceived this work, made conceptualization and supervised the work. YL, XL, and XZ helped on simulations. YY, ZC, SL, ZW, and BW helped on revising of the manuscript. FS and BW provide funding support. All authors contributed to the article and approved the submitted version.

Funding

This study is supported by the National Natural Science Foundation of China (Grant Nos. 61971300 and 12274317), Open Foundation of China-Belarus Belt and Road Joint Laboratory on Electromagnetic Environment Effect (No. ZBKF2022031202), 2022 University Outstanding Youth Foundation of Taiyuan University of Technology, and Scientific and Technological Innovation Programs (STIP) of Higher Education Institutions in Shanxi (Nos. 2019L0159 and 2019L0146).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Banerji, S., Meem, M., Majumder, A., Sensale-Rodriguez, B., and Menon, R. (2020). Extreme-depth-of-focus imaging with a flat lens. Optica 7, 214–217. doi:10.1364/optica.384164

CrossRef Full Text | Google Scholar

Cai, T., Tang, S., Zheng, B., Wang, G., Ji, W., Qian, C., et al. (2021). Ultrawideband chromatic aberration-free meta-mirrors. Adv. Photonics 3, 016001. doi:10.1117/1.ap.3.1.016001

CrossRef Full Text | Google Scholar

Chen, W. T., Zhu, A. Y., Sanjeev, V., Khorasaninejad, M., Shi, Z., Lee, E., et al. (2018). A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 13, 220–226. doi:10.1038/s41565-017-0034-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Sun, F., Ma, X., Chen, H., Chao, K., Liu, Y., et al. (2023). Electromagnetic-acoustic splitter with a tunable splitting ratio based on copper plates. Opt. Lett. 48, 3407–3410. doi:10.1364/ol.492941

PubMed Abstract | CrossRef Full Text | Google Scholar

de Rosny, J., Lerosey, G., and Fink, M. (2010). Theory of electromagnetic time-reversal mirrors. Ieee. Trans. Biomed. Eng. 58, 3139–3149. doi:10.1109/tap.2010.2052567

CrossRef Full Text | Google Scholar

Fan, T., Liu, Z., Zhang, D., and Tang, M. (2013). Comparative study of lesions created by high-intensity focused ultrasound using sequential discrete and continuous scanning strategies. Ieee. Trans. Biomed. Eng. 60, 763–769. doi:10.1109/tbme.2011.2167719

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, N., Xi, D., Xu, J., Ambati, M., Srituravanich, W., Sun, C., et al. (2006). Ultrasonic metamaterials with negative modulus. Nat. Mat. 5, 452–456. doi:10.1038/nmat1644

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, H., Gu, Z., Liang, B., Zou, X., Yang, J., Yang, J., et al. (2016). Acoustic focusing by symmetrical self-bending beams with phase modulations. Appl. Phys. Lett. 108, 073501. doi:10.1063/1.4941992

CrossRef Full Text | Google Scholar

Gao, N., Guo, X., Deng, J., and Cheng, B. (2022). Design and study of a hybrid composite structure that improves electromagnetic shielding and sound absorption simultaneously. Compos. Struct. 280, 114924. doi:10.1016/j.compstruct.2021.114924

CrossRef Full Text | Google Scholar

Janssen, X. J. A., Lipfert, J., Jager, T., Daudey, R., Beekman, J., and Dekker, N. H. (2012). Electromagnetic torque tweezers: A versatile approach for measurement of single-molecule twist and torque. Nano Lett. 12, 3634–3639. doi:10.1021/nl301330h

PubMed Abstract | CrossRef Full Text | Google Scholar

Khorasaninejad, M., Chen, W. T., Devlin, R. C., Oh, J., Zhu, A. Y., and Capasso, F. (2016). Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194. doi:10.1126/science.aaf6644

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohrmann, K. U., Michel, M. S., Gaa, J., Marlinghaus, E., and Alken, P. (2002). High intensity focused ultrasound as noninvasive therapy for multilocal renal cell carcinoma: Case study and review of the literature. J. Urol. 167, 2397–2403. doi:10.1016/s0022-5347(05)64992-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kundtz, N., and Smith, D. R. (2010). Extreme-angle broadband metamaterial lens. Nat. Mat. 9, 129–132. doi:10.1038/nmat2610

PubMed Abstract | CrossRef Full Text | Google Scholar

Kwon, D., and Werner, D. (2009). Beam scanning using flat transformation electromagnetic focusing lenses. IEEE Antennas Wirel. Propag. Lett. 8, 1115–1118. doi:10.1109/lawp.2009.2033619

CrossRef Full Text | Google Scholar

Leggio, L., de Varona, O., and Dadrasnia, E. (2015). A comparison between different schemes of microwave cancer hyperthermia treatment by means of left-handed metamaterial lenses. Prog. Electromagn. Res. 150, 73–87. doi:10.2528/pier14101408

CrossRef Full Text | Google Scholar

Lerosey, G., de Rosny, J., Tourin, A., Derode, A., Montaldo, G., and Fink, M. (2004). Time reversal of electromagnetic waves. Phys. Rev. Lett. 92, 193904. doi:10.1103/physrevlett.92.193904

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B., Sun, F., and He, S. (2017). Acoustic surface transformation realized by acoustic-null materials using bilayer natural materials. Appl. Phys. Express 10, 114001. doi:10.7567/apex.10.114001

CrossRef Full Text | Google Scholar

Li, Y., Liang, B., Tao, X., Zhu, X., Zou, X., and Cheng, J. (2012). Acoustic focusing by coiling up space. Appl. Phys. Lett. 101, 233508. doi:10.1063/1.4769984

CrossRef Full Text | Google Scholar

Lim, S., and Yoon, Y. J. (2021). Phase compensation technique for effective heat focusing in microwave hyperthermia systems. Appl. Sci. Basel 11, 5972. doi:10.3390/app11135972

CrossRef Full Text | Google Scholar

Liu, Y., Fu, J., Dong, H., Gong, C., Sun, F., and He, S. (2020). Extending the scanning angle of a phased-array antenna using a thin radome of curved metasurface. Phys. Status Solidi-R 14, 1900624. doi:10.1002/pssr.201900624

CrossRef Full Text | Google Scholar

Ma, W., Liu, Z., Kudyshev, Z. A., Boltasseva, A., Cai, W., and Liu, Y. (2021). Deep learning for the design of photonic structures. Nat. Photonics 15, 77–90. doi:10.1038/s41566-020-0685-y

CrossRef Full Text | Google Scholar

Marzo, A., and Drinkwater, B. W. (2019). Holographic acoustic tweezers. Pnas 116, 84–89. doi:10.1073/pnas.1813047115

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozcelik, A., Rufo, J., Guo, F., Gu, Y., Li, P., Lata, J., et al. (2018). Acoustic tweezers for the life sciences. Nat. Methods 15, 1021–1028. doi:10.1038/s41592-018-0222-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, S., Li, Y., and Assouar, B. (2017). Acoustic focusing and energy confinement based on multilateral metasurfaces. Phys. Rev. Appl. 7, 054006. doi:10.1103/physrevapplied.7.054006

CrossRef Full Text | Google Scholar

Rivenson, Y., Gorocs, Z., Gunaydin, H., Zhang, Y., Wang, H., and Ozcan, A. (2017). Deep learning microscopy. Optica 4, 1437–1443. doi:10.1364/optica.4.001437

CrossRef Full Text | Google Scholar

Roy, T., Rogers, E. T. F., and Zheludev, N. I. (2013). Sub-wavelength focusing meta-lens. Opt. Express 21, 7577–7582. doi:10.1364/oe.21.007577

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, M., Watanabe, Y., Ueda, S., Iseki, S., Abe, Y., Sato, N., et al. (1996). Microwave coagulation therapy for hepatocellular carcinoma. Gastroenterology 110, 1507–1514. doi:10.1053/gast.1996.v110.pm8613057

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, H., Liu, T., Fu, C., Li, L., Tan, L., Wang, J., et al. (2015). Insights into a microwave susceptible agent for minimally invasive microwave tumor thermal therapy. Biomaterials 44, 91–102. doi:10.1016/j.biomaterials.2014.12.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, F., Liu, Y., and He, S. (2020). Surface transformation multi-physics for controlling electromagnetic and acoustic waves simultaneously. Opt. Express 28, 94–106. doi:10.1364/oe.379817

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidiasheva, I. V., Abalymov, A. A., Kurochkin, M. A., Mayorova, O. A., Lomova, M. V., German, S. V., et al. (2018). Transfer of cells with uptaken nanocomposite, magnetite-nanoparticle functionalized capsules with electromagnetic tweezers. Biomater. Sci. 6, 2219–2229. doi:10.1039/c8bm00479j

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, J. P., and Sun, H. X. (2015). Acoustic focusing by metal circular ring structure. Appl. Phys. Lett. 106, 392–396. doi:10.1063/1.4908117

CrossRef Full Text | Google Scholar

Xia, J., Zhang, X., Sun, H., Yuan, S., Qian, J., and Ge, Y. (2018). Broadband tunable acoustic asymmetric focusing lens from dual-layer metasurfaces. Phys. Rev. Appl. 10, 014016. doi:10.1103/physrevapplied.10.014016

CrossRef Full Text | Google Scholar

Yang, S., Page, J. H., Liu, Z., Cowan, M. L., Chan, C. T., and Sheng, P. (2004). Focusing of sound in a 3d phononic crystal. Phys. Rev. Lett. 93, 024301. doi:10.1103/physrevlett.93.024301

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Wang, H., Yu, F., Xu, Z., and Chen, H. (2016). A metasurface carpet cloak for electromagnetic, acoustic and water waves. Sci. Rep. 6, 20219. doi:10.1038/srep20219

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Yin, L., and Fang, N. (2009). Focusing ultrasound with an acoustic metamaterial network. Phys. Rev.Lett. 102 (19), 194301. doi:10.1103/physrevlett.102.194301

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, B., Yang, Y., Shao, Z., Yan, Q., Shen, N., Shen, L., et al. (2019). Experimental realization of an extreme-parameter omnidirectional cloak. Research 2019, 8282641. doi:10.34133/2019/8282641

PubMed Abstract | CrossRef Full Text | Google Scholar