Effect of shear ratio on rheological properties of suspension in two-step flocculation process for fine iron tailings

In the two-step flocculation process, shear has a significant impact on the rheological properties of the flocculating slurry. In this study, the orthogonal experiments of two-step flocculation process for fine iron tailings were designed. Based on the change of shear ratio, different shear rates and shear time were designed, the yield stress, plastic viscosity and maximum packing fraction of the flocculated suspension in each group were measured and calculated with a rheometer. The result of range and variance analysis shows the shear rate in the primary broken phase was the biggest factor affecting the yield stress and plastic viscosity of the flocculated slurry in two-step flocculation process. When the shear rate increased from 100 s^-1 to 400 s^-1, the yield stress and the plastic viscosity of the flocculated slurry increased by 7.14% and 21.30%, respectively. When the shear rate changed from 400 s^-1 to 800 s^-1, they decreased by 23.27% and 33.17%, respectively. Since the shear ratio in a two-step flocculation process is also related to both shear action and floc structure parameter, the shear ratio was introduced into the first-order reversible kinetic rate equation. Through establishing the relationship between the shear ratio and the floc structural parameter of flocculating suspension, a theoretical model of the shear-dependent maximum packing fraction was established. The measured values and theoretical calculated values of the maximum packing fraction in two-step flocculation experiments were in good agreement and the error was within 5%. Last but not least, the internal mechanism of the theoretical model was discussed from the microscopic point of view.

1 Introduction

In the field of mineral processing, pipeline transportation and water treatment, solid-liquid suspensions are frequently encountered. In order to properly handle the suspensions, it is important to understand the diverse suspension behavior and then obtain the required rheological properties. Rheological properties, especially maximum packing fraction, depend on the nature of the suspension constituents, the interactions among these suspension constituents and the external forces in the processing (Jiao et al., 2022). Therefore, it is necessary to understand how the factors affect rheological properties during processing, predict the key rheological parameters of suspensions, such as maximum packing fraction, and even put forward reasonable suggestions for processing. Great progress both in theoretical analysis and experimental measurements has been made (Xue et al., 2016), but it still needs a complete explanation for the suspension rheological properties.

For flocculating suspensions, shear is a key factor affecting rheological properties mainly through changing the floc network structure and the particle size distribution. On one hand, shear can induce the formation or re-aggregation of floc network structure and then the particle sizes increase, which leads to the increase of rheological properties of suspensions (Fan et al., 2020; Wu et al., 2022). On the other hand, shear can also disrupt the floc network structure when it exceeds the shear resistance of the structure and then the rheological properties will decrease (Farrokhpay, 2012; Ishigami et al., 2022). In order to study the effect of shear on flocculating suspensions, it is important to select reasonable shear parameters (Clark, 2016; Zhang et al., 2022). Studies on the shear rate and the shear time have always been concerned. For example, Webster et al. (Webster et al., 2019) ‘s research on the dehydration of oil sand tailings shows that shear rate adversely affected the water release and compressibility of tailings. Pang, Zheng and Jiang (He et al., 2018) thought that the first-stage shear rate, second-stage shear rate, shear time, and the interactive action all have a significant effect on sludge dewatering. In short, shear rate and shear time both play essential roles in the process of coagulation-flocculation.

Based on the effect of shear on flocculating suspensions, researchers have established many theoretical models to calculate the suspension rheology, but the models of highly-concentrated suspensions had been inaccurate until the focus was put on the maximum packing fraction. The maximum packing fraction is closely related to the floc network structure (Kumar, 2017; Kusuma, 2017; Sudduth, 2018) and the particle size distribution (Mwasame et al., 2016; Wang et al., 2022) which are both easily changed by shear. Therefore, it is feasible to calculate the maximum packing fraction by establishing the relationship between the floc network structure and shear (O'Neill et al., 2017). However, some of the existing models are empirical equations, while other theoretical ones are not easy to be used in practice. It may have drawbacks on a deeper understanding on the rheological properties of flocculating suspensions, especially the suspensions with a complex processing, such as the two-step flocculating suspensions. In the study of the two-step flocculation process, it is urgent to analyze the influence of shear action at different phases on the rheological parameters of the flocculating slurry, and it is also necessary to establish corresponding theoretical models.

Therefore, a series of two-step flocculation experiments of fine iron tailings will be designed in the study. Based on the change of shear ratio, referring to the ratio of the shear disruption and the shear re-aggregation, shear disruption in the broken phase and shear re-aggregation in the secondary flocculation phase will be designed with different shear rates and shear time. The yield stress, plastic viscosity and maximum packing fraction of the flocculated suspension in each group were measured and calculated with a rheometer. According to the orthogonal experiments scheme of two-step flocculation process for fine iron tailings, the range and variance analysis of the experimental results were carried out to explore the influence of different factors on the rheological parameters of flocculated slurry. Through introducing the shear ratio into the first-order reversible kinetic rate equation and establishing the relationship between the shear ratio and the floc structural parameter of flocculating suspension, a theoretical model of the shear-dependent maximum packing fraction will be established. The measured values and theoretical calculated values of the maximum packing fraction in two-step flocculation experiments will be compared to verify the theoretical model. Last but not least, the internal mechanism of the theoretical model will be discussed from the microscopic point of view to explain the effect of shear on the maximum packing fraction and rheological properties of flocculation suspension.

2 Materials and methods

2.1 Materials

In this study, the tailings were a type of iron tailings supplied by ArcelorMittal USA, a steel and mining company operating in the United States. The particle size distribution result was measured by the Malvern Mastersizer 2000 Laser Dffraction Particle Size Analyser (Figure 1). The volume fraction of tailings with particle size less than 20μm, 37μm and 74 μm was 55.66%, 76.43% and 94.58%, respectively.

FIGURE 1

FIGURE 1. Particle size distribution of tailings.

Two kinds of commercial flocculants were supplied by SNF. The anionic polyacrylamide, 923VHM, and the cationic polyacrylamide, 4800SSH. Both of them have high molecular weight and good water solubility. All materials are commercially available. Their basic physical and chemical properties are reported in Table 1.

TABLE 1

TABLE 1. Basic physical and chemical properties of flocculants.

2.2 Suspension preparation and experimental apparatus

Through previous experiments, the optimal flocculant combination was selected (923VHM and 4800SSH). The anionic polyacrylamide, 923VHM, was used as the primary flocculant and the cationic polyacrylamide, 4800SSH, was used as the second flocculant. Stock solutions for the two kinds of flocculants were prepared at a concentration of 0.1% solids (w/v %), to be used within 7 days from mixing. To prevent mineral impurities from affecting test results, deionized water was used in all water-based tests.

In this study, a rheometer (Thermo Haake VT 550, Germany) was used. The cup and bob fixture of the rheometer was a concentric cylinder geometry of which the radius of the fixed outer cylinder and the rotatable inner cylinder was 21.00 mm and 20.04 mm, respectively, so there was a gap between the cup and bob fixture to minimize non-Newtonian shear rate effects, particle bridging across the shear surfaces, and the magnitude of wall slip errors. The rheometer was used to provide both shear disruption and shear re-aggregation in the two-step flocculation tests. It was also used to measure rheological property of the suspension.

2.3 Methods and procedures

In this study, a two-step flocculation experiment included four phases, primary flocculation phase, primary broken phase, secondary flocculation phase, and rheology test phase, as shown in Figure 2.

FIGURE 2

FIGURE 2. A scheme of the two-step flocculation process.

Firstly, in the primary flocculation phase, the slurry of 15% solids (w/v %) was prepared in a 1 L beaker using 150 g tailings and 850 mL deionized water. The slurry was homogenized by agitating at a rotational speed of 600 rpm for 30 s, and at 280 rpm for 10 min. Subsequently, 3 mL of the primary flocculant stock solution (corresponding to the polymer optimum dosage of 20 g/t, determined from previous experiments) was added to the slurry and then agitation was ceased immediately to avoid breaking flocs. Allow the slurry to stand for 5 min and remove the supernatant.

Secondly, in the primary broken phase, 34 mL of the primary flocculated underflow was stirred in the rheometer measuring cup, at a constant shear rate (shear rate G₁) for a desired period (shear time T₁), as shown in Table 2, during which the rheometer was only used as a shear disruption device. The rheometer temperature was fixed at 23 °C by the Poly science 9,100 constant temperature circulator.

TABLE 2

TABLE 2. Orthogonal design of shear parameters in two-step flocculation process.

Then, in the secondary flocculation phase, 1 mL of the secondary flocculant stock solution with the concentration of 0.1% was added to the suspension in the cup and the slurry was stirred at a constant shear rate (shear rate G₂) for a desired period (shear time T₂), as shown in Table 2, during which the rheometer was only used as a shear mixing device.

Finally, in the rheology test phase, the rheological properties of flocculating sus-pension in each test were measured by the rheometer with the increase of shear rate from 0 to 300 s⁻¹ and the decrease from 300 s⁻¹ to 0 within 120 s. Based on the Bingham model, the viscosity of suspension was obtained, and the maximum packing fraction was calculated according to the relationship between viscosity and the maximum packing fraction.

In order to study the rheological properties of slurry for fine iron tailings in the two-step flocculation process, four factors were selected to carry out the orthogonal experiments to test the yield stress and plastic viscosity of the tailings, using L16 (4⁴) orthogonal experimental table. The four factors were the shear rate in the primary broken phase (G₁), the shear time in the primary broken phase (T₁), the shear rate in the secondary flocculation phase (G₂) and the shear time in the secondary flocculation phase (T₂). The information of four factors and four levels and the design scheme of orthogonal experiment are shown in Table 2.

In the process of determining the levels for each factor, based on practical engineering cases of tailings flocculation dewatering and discharge sedimentation, the reasonable levels of each factor was selected, which maybe can provide reference for practical engineering applications. In addition, in order to distinguish shear failure and shear coagulation, the shear rate in the primary broken phase (G₁) was significantly higher than that in the secondary flocculation phase (G₂), and the shear time of the two phases was basically the same. In order to protect the floc structure formed in the two-step flocculation process, the design of shear ratio should not be too large. In this study, only the shear ratio in the range of 0–100 was considered.

3 Results

3.1 Analysis of experimental results

According to the above experimental design method, the yield stress and the plastic viscosity of experimental tailing slurry were measured by rheometer. The curves of the yield stress and the plastic viscosity of the experimental tailing slurry with four factors and four levels are drawn in Figure 3. The influence of different factors on the rheological parameters of the flocculated slurry in the two-step flocculation process was analyzed.

FIGURE 3

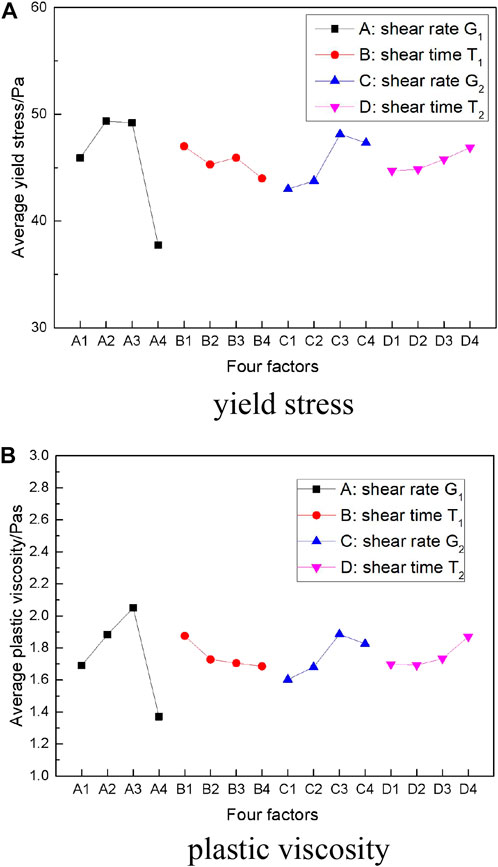
FIGURE 3. The change of rheological properties at different levels of the four factors. (A) the change of yield stress. (B) the change of plastic viscosity

The shear rate in the primary broken phase had a significant effect on the yield stress and plastic viscosity of flocculated slurry in the two-step flocculation process. With the increase of shear rate (G₁), the rheological parameters first increased and then decreased. From the range analysis, it can be seen that when the shear rate changed from A1 (100 s^-1) to A3 (400 s^-1), the yield stress and the plastic viscosity of the flocculated slurry increased by 7.14% and 21.30%, respectively. When the shear rate changed from A3 (400 s^-1) to A4 (800 s^-1), the yield stress and the plastic viscosity of the flocculated slurry decreased by 23.27% and 33.17%, respectively.

With the increase of shear time (T₁), the rheological parameters gradually decreased. When the shear time changed from B1 (30s) to B4 (300s), the yield stress and the plastic viscosity of the flocculated slurry decreased by 6.40% and 10.13%, respectively.

With the increase of shear rate (G₂), the rheological parameters first increased and then decreased. From the range analysis, it can be seen that when the shear rate changed from C1 (10 s^-1) to C3 (40 s^-1), the yield stress and the plastic viscosity of the flocculated slurry increased by 11.96% and 17.63%, respectively. When the shear rate changed from C3 (40 s^-1) to C4 (80 s^-1), the yield stress and the plastic viscosity of the flocculated slurry decreased by 1.66% and 3.18%, respectively.

With the increase of shear time (T₂), the rheological parameters gradually increased. When the shear time changed from D1 (30s) to D4 (300s), the yield stress and the plastic viscosity of the flocculated slurry increased by 4.87% and 10.16%, respectively.

According to the orthogonal experimental design table, the range and variance analysis of the rheological properties of the flocculated slurry in the two-step flocculation process were carried out, and the results are shown in Table 3. From the range results of yield stress of flocculated slurry, it can be seen that the ranking of influence degree on yield stress was the shear rate in the primary broken phase (G₁), the shear rate in the secondary flocculation phase (G₂), the shear time in the primary broken phase (T₁) and the shear time in the secondary flocculation phase (T₂). Similarly, the ranking of influence degree on plastic viscosity was the shear rate in the primary broken phase (G₁), the shear rate in the secondary flocculation phase (G₂), the shear time in the primary broken phase (T₁), and the shear time in the secondary flocculation phase (T₂).

TABLE 3

TABLE 3. Analysis of range and variance of experimental results.

Obviously, the shear rate in the primary broken phase (G₁) was the biggest factor affecting the yield stress and plastic viscosity of the flocculated slurry in two-step flocculation process. The influence degree of each factor can be clearly obtained through range analysis, but the error size generated in the experiment cannot be estimated. Therefore, the variance analysis was also carried out. From the results of variance analysis, it can be concluded that the influence ranking of different factors on the rheological parameters of flocculated slurry in two-step flocculation process was consistent with the results of range analysis.

3.2 Development of a theoretical model of maximum packing fraction

The maximum packing fraction of flocculating suspension is an important rheological parameter. The determination of maximum packing fraction dependents on shear action and floc structure parameter, which can describe the non-Newtonian effects over the entire concentration range for flocculating suspension. In this study, the two-step flocculation process was analyzed from the perspective of flocculation kinetics. Through establishing the relationship between shear and floc structural parameter, a theoretical model of the shear-dependent maximum packing fraction was established.

The basic assumptions in the process of establishing the theoretical model were.

(1) Shear breakage and shear flocculation occurred at different phases;

(2) The shear action during the primary broken phase was only used for shear breakage;

(3) The shear action during the secondary flocculation phase was only used for shear flocculation.

3.2.1. Establishment of a theoretical model

According to the principle of flocculation kinetics, the relationship between the maximum packing fraction and floc structure parameters under any condition was in accordance with the following Formula 1.

$\frac{d{\varphi }_m}{{\varphi }_m^2}=\left(\frac{1}{{\varphi }_{m,0}}-\frac{1}{{\varphi }_{m,\infty }}\right)d\lambda (1)$

By integrating Formula 1, the mathematical relationship of the maximum packing fraction and floc structural parameter in the two-step flocculation process was obtained.

$\frac{1}{{\varphi }_m}=\frac{1}{{\varphi }_{m,\infty }}+\left(\frac{1}{{\varphi }_{m,0}}-\frac{1}{{\varphi }_{m,\infty }}\right)\lambda (2)$

Here is the shear-dependent maximum packing fraction and λ is a structural parameter that represents the state of suspension aggregation when suspension architecture reaches the dynamic equilibrium. λ = 0 means the suspension architecture is in a solid-like state, while λ = 1 means the suspension architecture is in a liquid -like state. ϕ_m,0 and ϕ_m,ꝏ are limiting maximum packing fraction that respectively correspond to λ = 0 and λ = 1.

In the two-step flocculation process, shear can change the maximum packing fraction by changing the floc network structure of suspension. Therefore, in order to establish the relationship between the floc structure parameter, λ, and the shear force, the reversible kinetic rate equation (Formula 3) was used to describe the relationship between the aggregation state of the flocculated slurry and the relevant force balance.

$\frac{d\lambda }{dt}=\frac{{\left(1-\lambda \right)}^{\alpha }}{k_A}-\frac{{\lambda }^{\beta }}{k_S}(3)$

Here l/k_A and 1/k_S are the rate coefficients for aggregation and disaggregation of suspension structure, respectively. α and β are the aggregation kinetic order and the disaggregation kinetic order in the rate equation, respectively.

It is noted that the change of the aggregation kinetic order and the disaggregation kinetic order in the rate equation “does not significantly affect the resultant relation in the equilibrium state” (Flatt and Bowen, 2010). Therefore, it was assumed that both the aggregation kinetic order and the disaggregation kinetic order are equal to 1 (α = β = 1).

In the process of the two-step flocculation, the dynamic equilibrium depends on the balance between the floc structure disruption and the broken flocs re-aggregation. It is worth noting that both of these two effects need to be completed over a period of time. In many studies of flocculation (Choi and Schowalter, 2015; Yang et al., 2020), the product of shear rate and shear time is usually used as a key parameter affecting the flocculation effect. Therefore, in this study, the product of shear rate G₁ and shear time T₁ in the primary broken phase was used as an index of the shear disruption degree of the primary floc network structure, while the product of shear rate G₂ and shear time T₂ in the secondary flocculation phase was used as an index of the shear re-aggregation degree of the broken flocs.

Through establishing the relationship between l/k_A and 1/k_S for a two-step flocculation process, Formula 4 was obtained. p was a model fitting parameter that reflected the respond of the aggregation state of the suspension to the two shear effects.

$\frac{1/k_S}{1/k_A}={\left(\frac{G_1{T}_1}{G_2{T}_2}\right)}^p(4)$

On the basis of the definition of shear ratio, referred to the ratio of the product of shear rate and shear time in the primary broken phase and that in the secondary flocculation phase, indicating the difference between shear disruption and the shear re-aggregation.

$\frac{G_1{T}_1}{G_2{T}_2}=n(5)$

Combining Formula 2, 3, 4 and 5, the relationship between shear and floc structural parameter was established and Formula 6 was obtained, that is, a theoretical model of the shear-dependent maximum packing fraction was established.

$\frac{1/{\varphi }_m-1/{\varphi }_{m,\infty }}{1/{\varphi }_{m,0}-1/{\varphi }_{m,\infty }}=\frac{1}{1+n^p}(6)$

3.2.2 Verification of the theoretical model

According to the orthogonal experiment results of rheological parameters in two-step flocculation process, the shear ratio was calculated according to Formula 5. The curves of yield stress and plastic viscosity with shear ratio are shown in Figure 4.

FIGURE 4

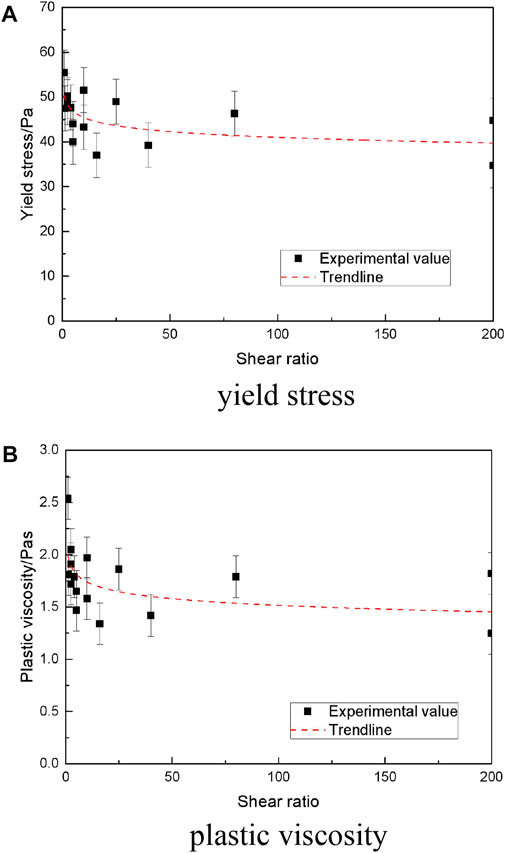
FIGURE 4. Variation of rheological parameters of flocculated slurry with shear ratio in the two-step flocculation process. (A) the change of yield stress. (B) the change of plastic viscosity.

As shown in Figure 4, with the increase of shear ratio, the yield stress of flocculated slurry in the two-step flocculation process decreased slightly and basically remained within the range of 40–50Pa. The plastic viscosity of flocculated slurry decreased slightly and basically remained within the range of 1.5–2.0 Pas.

Through comprehensive analysis of the change of rheological parameters of flocculated slurry, the yield stress and plastic viscosity of flocculated slurry both showed a downward trend with the increase of shear ratio.

This may be because when the shear ratio was small, with the appropriate increase of the shear ratio, the size distribution of the floc fragments generated in the primary broken phase was more uniform. The broken flocs were more inclined to form a more compact structure in the secondary flocculation phase. However, under the condition of a certain solids content of tailings, it resulted in poor structural integrity. Therefore, the rheological parameters slightly decreased. Due to the limit of this change, the rheological parameters remained basically unchanged when the shear action was large.

In order to further explain this phenomenon, the maximum packing fraction of the flocculated slurry in the two-step flocculation process was further calculated, and the change rule of the maximum packing fraction with the shear ratio was analyzed in combination with the theoretical model of the shear-dependent maximum packing fraction was established.

As shown in Figure 5, the measured values of maximum packing fraction were consistent with the theoretical curve. It proved the rationality of Formula 6 and three parameters in Formula(6 were also calculated, ${\mathrm{\varphi }}_{\mathrm{m},0}=61.75\%$, ${\mathrm{\varphi }}_{\mathrm{m},\infty }=70.79\%$ and p = 0.57. The coincidence degree was high (R² = 0.895). Therefore, the relationship between the maximum packing fraction and the shear ratio is shown in Formula 7.

${\varphi }_m=\frac{1+n^{0.57}}{1.62\left(1.13+n^{0.57}\right)}(7)$

FIGURE 5

FIGURE 5. Comparison between measured values and theoretical curve of maximum packing fraction.

From the curve of the maximum packing fraction, it can be seen that when shear ratio was small, with the increase of shear action, more uniform broken flocs tended to form a denser structure, resulting in an increase of the maximum packing fraction. under the condition of a certain solids content of tailings, the integrity of the slurry was worse, leading to a decrease in rheological parameters.

4 Discussion

Based on the principle of flocculation, the effect of shear ratio on the maximum packing fraction and rheological properties of suspensions in the two-step flocculation process was further explained.

When the shear ratio was small, the floc network showed large fragment breakage in the primary broken phase (Yang et al., 2019). In the secondary flocculation phase, large broken flocs tended to form a loose structure. Therefore, the maximum packing fraction was still small, but the integrity of secondary floc structure forms certain rheological characteristics of flocculated tailings suspension.

With the appropriate increase of the shear ratio, the size distribution of the floc fragments generated during the primary broken phase was more uniform. In the secondary flocculation phase, the broken flocs were more inclined to form a more compact structure. However, under the condition of a certain solids content of tailings, more binding sites remained in the compact structure, resulting in poor structural integrity. Therefore, the maximum packing fraction of the flocculated slurry increased but the rheological parameters decreased in the two-step flocculation process.

When the shear ratio was large, the improvement of broken flocs size distribution had basically reached the limit by increasing the shear action in the primary broken phase. Therefore, the maximum packing fraction and rheological parameters of the flocculated slurry in the two-step flocculation process had little change.

In addition, the limitation of the research results lies in the fact that this study only used one type of tailings sample and optimized the selection and dosage of flocculants. Quantitative results may not be applicable to other tailings, but the idea of establishing a theoretical model may be applicable to other situations; In this study, the range of shear ratio (0–100) cannot cover all situations, and the shear ratio in actual engineering may be larger. Therefore, it is necessary to study the possible changes in existing results under different types of tailings and larger shear ratios in the future.

5 Conclusion

In this study, the orthogonal experiments of two-step flocculation process for fine iron tailings were designed. Based on the change of shear ratio, different shear rates and shear time were designed to analyze the change rule of the rheological parameters and the maximum packing fraction.

The result of range and variance analysis shows the shear rate in the primary broken phase was the biggest factor affecting the yield stress and plastic viscosity of the flocculated slurry in two-step flocculation process. When the shear rate increased from 100 s^-1 to 400 s^-1, the yield stress and the plastic viscosity of the flocculated slurry increased by 7.14% and 21.30%, respectively. When the shear rate changed from 400 s^-1 to 800 s^-1, they decreased by 23.27% and 33.17%, respectively.

The shear ratio was introduced into the first-order reversible kinetic rate equation. Through establishing the relationship between the shear ratio and the floc structural parameter of flocculating suspension, a theoretical model of the shear-dependent maximum packing fraction was established.

The measured values and theoretical calculated values of the maximum packing fraction in two-step flocculation experiments were in good agreement and the error was within 5%. Last but not least, the internal mechanism of the theoretical model was discussed from the microscopic point of view.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding author.

Author contributions

YY contributions mainly include conceptualization, experimental research, data curation and manuscript writing. AW contributions mainly include funding acquisition and supervision. XW contributions mainly include funding acquisition and project administration. GW contributions mainly include project administration and supervision. All authors contributed to the article and approved the submitted version.

Funding

The China Postdoctoral Science Foundation (2021M701516).

Acknowledgments

The authors would like to thank the China Postdoctoral Science Foundation (2021M701516), the JCHX Mining Management Co., Ltd and the University of Science and Technology Beijing.

Conflict of interest

YY, XW and GW are all employed by the JCHX Mining Management Co., Ltd.

The authors declare that this study received contribution from JCHX Mining Management Co., Ltd.. The company had the following involvement in the study: experimental research, data curation, manuscript writing, funding acquisition and project administration.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Choi, S. J., and Schowalter, W. R. (2015). Rheological properties of nondilute suspensions of deformable particles. Phys. Fluids 18 (7), 420–427. doi:10.1063/1.861167

CrossRef Full Text | Google Scholar

Clark, M. M. (2016). Critique of camp and stein's RMS velocity gradient. J. Environ. Eng. 111 (6), 741–754. doi:10.1061/(asce)0733-9372(1985)111:6(741)

CrossRef Full Text | Google Scholar

Fan, Y., Ma, X., Dong, X., Song, S., Chen, R., and Dong, Y. (2020). Effect of shear-induced breakage and reflocculation on the floc structure, settling, and dewatering of coal tailings. Physicochem. Problems Mineral Process., 56, (2). doi:10.37190/ppmp/118148

CrossRef Full Text | Google Scholar

Farrokhpay, Saeed. (2012). The importance of rheology in mineral flotation: A review. Miner. Eng. 36, 272–278. doi:10.1016/j.mineng.2012.05.009

CrossRef Full Text | Google Scholar

Flatt, R. J., and Bowen, P. (2010). Yield stress of multimodal powder suspensions: An extension of the YODEL (yield stress mODEL). J. Am. Ceram. Soc. 90 (4), 1038–1044. doi:10.1111/j.1551-2916.2007.01595.x

CrossRef Full Text | Google Scholar

He, J., Heliang, P., Zheng, Y., Jiang, T., Xin, Z., Zhang, P., et al. (2018). Breakage–reflocculation implemented by two-stage shear for enhancing waste-activated sludge dewaterability: Effects of shear condition and extracellular polymeric substances. An Int. J. 36 (1a4), 418–434. doi:10.1080/07373937.2017.1336174

CrossRef Full Text | Google Scholar

Ishigami, T., Karasudani, T., Onitake, S., Shirzadi, M., Fukasawa, T., Fukui, K., et al. (2022). Effect of liquid volume fraction and shear rate on rheological properties and microstructure formation in ternary particle/oil/water dispersion systems under shear flow: two-dimensional direct numerical simulation. Soft Matter 18. doi:10.1039/D2SM00373B

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, H., Chen, W., Wu, A., Yu, Y., Ruan, Z., Honaker, R., et al. (2022). Flocculated unclassified tailings settling efficiency improvement by particle collision optimization in the feedwell. Int. J. Minerals, Metallurgy Mater. 29 (12), 2126–2135. doi:10.1007/s12613-021-2402-3

CrossRef Full Text | Google Scholar

Kumar, A. (2017). The influence of shear on the dewaterability of flocculated particulate systems. PhD thesis. Parkville (VIC): University of Melbourne

Google Scholar

Kusuma, T. E. (2017). Microscopic inter-particle friction and shear rheology of particulate suspensions.

Google Scholar

Mwasame, P. M., Wagner, N. J., and Beris, A. N. (2016). Modeling the viscosity of polydisperse suspensions: Improvements in prediction of limiting behavior. Phys. Fluids 28 (6), 061701–061798. doi:10.1063/1.4953407

CrossRef Full Text | Google Scholar

O'Neill, R., Mccarthy, H. O., Montufar, E. B., Ginebra, M. P., Wilson, D., Lennon, A., et al. (2017). Critical review: Injectability of calcium phosphate pastes and cements. Acta Biomater. 50, 1–19. doi:10.1016/j.actbio.2016.11.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Sudduth, R. D. (2018). Optimum formulation derivation for the ultimate packing fraction using monodispersed particle sizes when optimizing suspension viscosities. Pigment Resin Technol. 48 (1), 45–56. doi:10.1108/prt-01-2018-0006

CrossRef Full Text | Google Scholar

Wang, Z., Wang, Y., Wu, L., Wu, A., Ruan, Z., Zhang, M., et al. (2022). Effective reuse of red mud as supplementary material in cemented paste backfill: Durability and environmental impact. Constr. Build. Mater. 328, 127002. doi:10.1016/j.conbuildmat.2022.127002

CrossRef Full Text | Google Scholar

Webster, S., Aydin, T., Gomez, C., Sorta, A., Sukuhuni, G., et al. (2019). Effects of shear on dewatering and compressibility of treated oil sands tailings. Tailings Mine Waste Conf. 15.

Google Scholar

Wu, A., Ruan, Z., and Wang, J. (2022). Rheological behavior of paste in metal mines. Int. J. Minerals, Metallurgy Mater. 29 (4), 717–726. doi:10.1007/s12613-022-2423-6

CrossRef Full Text | Google Scholar

Xue, S., Zhu, F., Kong, X., Wu, C., Huang, L., Huang, N., et al. (2016). A review of the characterization and revegetation of bauxite residues (Red mud). Environ. Sci. Pollut. Res. Int. 23 (2), 1120–1132. doi:10.1007/s11356-015-4558-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Wang, H. J., Klein, B., and Wu, A. (2020). Shear-dependent yield stress of iron ore fine tailings in two-step flocculation process. Adv. Mater. Sci. Eng. 2, 1–12. doi:10.1155/2020/6611392

CrossRef Full Text | Google Scholar

Yang, Y., Wu, A., Klein, B., and Wang, H. (2019). Effect of primary flocculant type on a two-step flocculation process on iron ore fine tailings under alkaline environment. Miner. Eng. 132, 14–21. doi:10.1016/j.mineng.2018.11.053

CrossRef Full Text | Google Scholar

Zhang, C., Liu, R., Chen, M., Li, J., Wang, X., Liu, Y., et al. (2022). Influence of the flocculation effect on the rheological properties of cement slurry. Powder Technol. An Int. J. Sci. Technol. Wet Dry Part. Syst. 398 (398-), 117118. doi:10.1016/j.powtec.2022.117118

CrossRef Full Text | Google Scholar