Research on mechanical properties and impact resistance of origami-based metamaterial for GIL

Gas insulated metal enclosed transmission line (GIL) is a high voltage, high current power transmission equipment, widely used in large hydropower stations, large-scale energy hubs and other occasions. Aiming at the shock environment that GIL may face, such as earthquake shock and water flow shock, a mirror folded mechanical metamaterial based on the Miura-ori patterned is proposed in this paper, and its mechanical responses and shock resistance performance were studied through the numerical simulation and experiment. The results showed that compared with the single-layer folded structure, the mirror connection mode increased the plastic hinge in the deformation process of the structure, causing the better energy absorption. Moreover, the parameters research indicated that reducing the plane angle and increasing the dihedral angle can improve the energy absorption. Most importantly, the structure can achieve more than 60% energy absorption under the impact load, showing a good buffer energy absorption effect. This paper can provide some significant reference and guidance for the impact resistance of the GIL in the practical engineering.

1 Introduction

GIL is a kind of high voltage and high current power transmission equipment insulated by SF6 gas or SF6/N2 mixed gas (Ruan et al., 2003). The common GILs and laying ways were shown in Figure 1 (Qi et al., 2015). Due to the use of compressed gas as the insulating medium, the size and layout spacing of the equipment are greatly reduced, which can minimize the footprint of the equipment and reduce the amount of civil engineering. With the construction of ultra-high voltage and ultra-high voltage power grids and the advancement of urbanization, the contradiction between ultra-high voltage power grids and urbanization development in urban areas has become increasingly prominent (Shang et al., 2011; Zhang et al., 2023). By applying GIL technology, overhead EHV (Extra High Voltage) and UHV (Ultra High Voltage) power grids can be relocated from above ground to underground through pipe gallery tunnels, thus solving the spatial contradiction between power grids and urban development (Xiang et al., 2022). However, changes in the laying methods of GIL make the service conditions more complex, and may encounter conditions such as water flow impact, seismic wave impact, and other impact loading conditions, which put forward higher requirements for the impact resistance of its structure. Generally speaking, when laying GILs, steel supporting structures will be added to fix them. When encountering impact loading conditions, these steel supports and the external cylinder of the GIL are vulnerable to impact damage. Therefore, it is necessary to consider adding other components to improve the impact resistance of these key components.

FIGURE 1

FIGURE 1. The common GILs and laying places. (A) lay on the underground (B) lay under the underground (C) lay in the tunnel.

In the existing research, the honeycomb porous structure is a common energy-absorbing structure (Zhao et al., 2021). With the rapid development of material science, various new materials and structures are constantly being created. Inspired by the art of origami, origami-based mechanical metamaterials has been proposed, which possess the negative Poisson’s ratio, programmability, and excellent energy absorption capability. The structure can be designed as a plane or curved surface, with a high designability and space compatibility. Origami-based mechanical metamaterial is a kind of porous structural metamaterial based on origami thinking design, which includes not only origami structures formed by folding a single layer, but also three-dimensional structures assembled by multiple origami structures (Turner et al., 2015; Lee et al., 2021; Wu et al., 2022). The metamaterial has a wide range of design, and different types of basic folding mode and assembly mode can be selected. With reasonable structural design, special mechanism and mechanical properties such as negative Poisson’s ratio and double (multiple) steady state can be realized (You et al., 2014; Zhang et al., 2018; Jeong et al., 2019; Yang et al., 2023). Combined with the geometric characteristics of origami patterns, the mechanical characteristics of origami patterns have been widely studied. Because of its specific topology, metamaterials based on Origami Design have anisotropy, and show different mechanical properties according to different loading directions. These properties can be adjusted by using different topologies. Filipov (Filipov et al., 2015) introduced a unique direction of coupling rigid folding origami tube by “zipper”, which greatly increases the stiffness of the system. The energy absorbed by metamaterials in quasi-static or dynamic compression process also changes with its mechanical properties.

For the energy absorption device, high specific energy absorption, stable deformation mode and lower initial peak load are required (Ma et al., 2014; Xiang, et al., 2020). As one of the most common origami patterns, the energy absorption and dissipation ability of Miura-ori have been studied and explored by many scholars (Rodrigues et al., 2017; Chen et al., 2018). Miura-ori can be applied to folded core materials to obtain new structures with excellent mechanical properties (such as specific rigidity, strength) and multi-functions (such as heat insulation and sound insulation). The mechanical properties of sandwich plate with folded metamaterial as the core body have also attracted extensive attention. Miura (1975) proposed that Miura-origami could be used to make sandwich core, and studied the shear modulus and strength of this core using theoretical and experimental methods. Pydah et al. (2017) found that under low to medium load strength, the sandwich plate with Miura-ori core is always superior to the corresponding honeycomb core in terms of plastic energy dissipation. Basily et al. (2004); Elsayed et al. (2004) prepared multi-layer sandwich plates and studied their impact resistance in three orthogonal directions. Schenk et al. (2014) believe that the equivalent blasting mitigation effect can be achieved by changing the folding form and sheet thickness of the core without changing the core density or the mass distribution of the sandwich beam. At the same time, these origami structures have better energy absorption capacity (Zhang et al., 2019). Ma et al. (2017) designed a hierarchical structure based on Miura-ori mode. The gradient structure can be adjusted by its Angle and side length parameters to achieve multi-level stiffness. The absorption efficiency of SEA is three times higher than that of uniform structure. Gattas et al. (2014) study the failure mode and response of the indented folding core under the quasi-static impact load were studied. The literature points out that only five models are established for each geometric parameter, so the parameter study has limitations. Karagiozova et al. (2019) proposed the analytical models of dynamic strength enhancement, impact velocity attenuation and energy absorption for materials with uniform initial density and positive density gradient. However, the models have not been verified by experiments.

So far, the research on porous folded metamaterials has made a lot of achievements, but there are still some problems to be solved. For example, the energy absorption mechanism of the structure under compression was not further explored. The research on the compression performance of the metamaterial mainly focuses on the quasi-static compression. The energy absorption characteristics of the complex combination folding structure under dynamic conditions have not been fully studied. Therefore, in order to further improve the energy absorption capacity of folded metamaterials, to be applied to solve the related problems in the impact protection of the GIL, the compression performance and energy absorption of the mirror-based folding mechanical metamaterial were studied on the basis of Miura folding mode.

Firstly, the deformation modes of Miura-ori and mirror folded metamaterials under quasi-static loading are studied by FE (Finite element) method, and the reason for the enhanced energy absorption of mirror folded metamaterials are discussed. Then, the deformation and mechanical responses of the structure under different loading velocities were also analyzed, and the effects of impact forces and velocities on the dynamic responses of the structure are studied. Finally, the validity of the FE model is verified by experiments. This paper proposed a novel mirror-based folding mechanical metamaterial and proved the excellent mechanical performance and impact resistance, which can provide a reference of protecting the critical components in the GIL from the impact loading, and guide the optimal design of related structures of the GIL, like sliding support in Figure 2.

FIGURE 2

FIGURE 2. The installation schematic diagram of the structure in the critical components of GIL.

2 Geometrical design

Porous materials are usually characterized by their relative density, stress-strain (force-displacement) relationship and densification strain. When analyzing porous materials with regular structure, a unit is usually selected to obtain these characteristics. The basic folding mode of folded metamaterials constructed in this chapter is Miura-origami, which was proposed by Japanese astronomer Miura in 1975 (Miura, 1975). Due to the characteristics of cell periodicity, easy to control and unfold, Miura-origami is one of the most concerned folding modes.

The plane crease of Miura-origami is shown in Figure 3. As shown in Figure 3A, its geometry is a herringbone pattern formed by a series of protruding mountain lines and concave valley lines. The mountain line and valley line in the figure are represented by solid lines and dashed lines. The pattern shown in Figure 3A can be folded along a given crease to form the three-dimensional folding state in Figure 3B. The basic Miura-ori unit is shown in Figures 3C, D. Figure 3C is the plane state of the basic element. It is composed of four identical parallelograms, where a, b and $\phi$ respectively represent the side length and angel of the parallelogram.

FIGURE 3

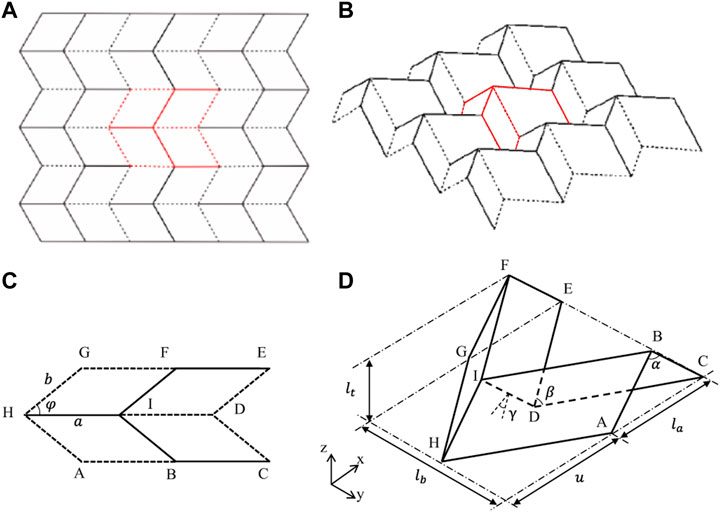
FIGURE 3. Miura-ori folding patterns: (A,B) the planar unfolding and folding state of Miura-ori folding patterns; (C,D) plane expansion and folding state of Miura-ori unit.

Figure 3D is the three-dimensional geometry and size representation of Miura folding basic unit, in which the angle between face $DEFI$ and face $BCDI$ is defined as dihedral angle $\gamma$, the angle between side $AB$ and side $BC$ is defined as side angle $\alpha$, and the angle between side $CD$ and side $DE$ is defined as side angle $\beta$. The geometric relationship among the parameters of Miura-ori cell presented in Figure 3D are:

$l_a=\frac{2a\cos \phi }{\sqrt{\frac{\cos \gamma {\sin }^2\phi {+\cos }^2\phi +1}{2}}}(1)$

$u=b\sqrt{\frac{\cos \gamma {\sin }^2\phi {+\cos }^2\phi +1}{2}}(2)$

$l_b=2b\sqrt{1-\frac{\cos \gamma {\sin }^2\phi {+\cos }^2\phi +1}{2}}(3)$

$l_t=a\sqrt{1-\frac{2{\cos }^2\phi }{\cos \gamma {\sin }^2\phi +{\cos }^2\phi +1}}(4)$

Space angles $\alpha$ and $\beta$, dihedral angle $\gamma$ and plane angle $\phi$ satisfy the following relations:

$\cos \phi =\sin \frac{\alpha }{2}\cos \frac{\beta }{2}(5)$

$\cos \beta =\cos \gamma {\sin }^2\phi {+\cos }^2\phi (6)$

The unit schematic diagram of the mirror folded metamaterial is shown in Figure 4A, and it is constructed by symmetrically connected along the surface ACE. Figure 4B shows the spatial structure of the mirror folded metamaterial.

FIGURE 4

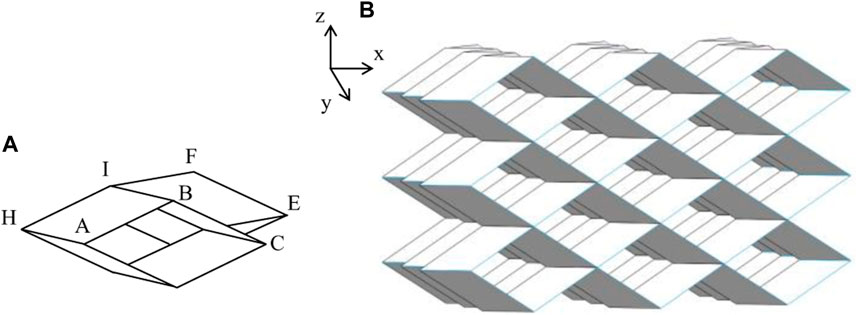
FIGURE 4. Schematic diagram of the mirror folded metamaterial: (A) folding unit; (B) spatial structure.

The overall length $L_a$, width $L_b$, height $L_t$ of the Miura-ori folding structure can also be obtained:

$L_a=m{l}_a+u(7)$

$L_b=m{l}_b(8)$

$L_t=2m{l}_t(9)$

where, m represents the number of units in either x, y or z directions. It can be seen from the above formulas that the length parameters $L_a,L_b,L_t$ of folding structure can be determined by the dihedral angle $\gamma$ or $\phi$ after determining the shape of the basic parallelogram unit. In addition, the relative density of the structure has an important influence on its energy absorption capacity. It can be defined as:

${\rho }_0={\rho }_b\overline{\rho }(10)$

$\overline{\rho }=\frac{4hab\sin \phi }{l_a{l}_b{l}_t}(11)$

where, ${\rho }_b$ and $\overline{\rho }$ are respectively the density of the matrix material and the relative density of the metamaterial.

3 Simulation results and discussion

The FE software ABAQUS/Explicit is used to simulate the mechanical properties and energy absorption characteristics of the folded structure. As shown in Figure 5, the structure is located between two rigid plates and the boundary condition is that the lower rigid plate is fixed and the top rigid plate is loaded along the y direction. The mechanical properties and energy absorption characteristics of the structure under uniform and quasi-static impact loads are simulated by imposing constraints on the top rigid plate.

FIGURE 5

FIGURE 5. FE model of the folded structure.

The aluminum alloy material is selected for the folded structure with isotropic elastic-plastic material properties of density ${\rho }_0$ = 2710 kg/m³, Young’s modulus E = 69 GPa, Poisson’s ratio $\nu$ = 0.33, yield strength ${\sigma }_Y$ = 36.8 MPa. The strain hardening data of aluminum alloy are given by Table 1(Gattas et al., 2014).

TABLE 1

TABLE 1. Aluminum alloy material’s true plastic stress-strain data.

The general contact is used for the upper panel contact, the lower panel contact and the contact of the cell-thickness, in which the friction coefficient is 0.25. Reduced integration points shell elements SR4 are used for the cellular material, and the mesh element size is approximately 1 mm. Through the study of grid convergence, the crushing stress of the structure is convergent under the grid density.

First, the quasi-static compression simulation analysis is carried out for the monolayer Miura-ori unit in Figure 3D and the mirror metamaterial unit in Figure 4A. The geometric parameters of the structure are as follows: $a=20\mathrm{m}\mathrm{m}$, $b=20\mathrm{m}\mathrm{m}$, $h=1\mathrm{m}\mathrm{m}$, $\phi =45°$, $\gamma =100°$. The top rigid plate compresses the structure downward at the speed of 1 m/s. In this case, the kinetic energy and internal energy ratio of the model are less than 0.5%, which can be seen as quasi-static compression. Other settings of the simulation model, such as material parameters, are described in the above.

The quasi-static compression force of the top rigid plate on the single-layer folded structure and the mirror folded structure is extracted respectively, and the equivalent stress is obtained by dividing it by the equivalent compression area of the structure. The equivalent strain is obtained by dividing the compression deformation distance of the structure by the length in the compression direction. The equivalent stress-strain curves are shown in Figure 6. In this case, strain is a dimensionless physical quantity. The quasi-static compression process can be divided into three stages according to the stress-strain variation law. In the first elastic stage, the stress increases rapidly to a peak with the increase of strain. In the second plastic stage, the stress platform appears and all the elements of the mirror folded metamaterial are compressed. Until all elements of the structure cannot be compressed again, the densification stage is entered, and the stress of the structure increases rapidly. The plastic yield stage of the structure corresponds to a large range of strain, high and stable stress, which is the main stage of energy absorption. The peak stress and platform stress of the mirror folded metamaterial are higher than that of single layer Miura-ori, which helps to improve the energy absorption ability.

FIGURE 6

FIGURE 6. The equivalent stress-strain curves under in-plane quasi-static compression.

The specific energy absorption (SEA) is the energy absorbed per unit mass of the structure and it is an important index to measure the energy absorption capacity of the structure. According to the calculation of stress-strain curve, the SEA of the mirror folded metamaterial and Miura-ori is shown in Table 2. It can be seen that through the combination of mirror symmetry, the platform stress of the structure increased by 73% and the specific energy absorption value increased by 60%.

TABLE 2

TABLE 2. Energy absorption values of the mirror folded metamaterial and Miura-ori cells.

The corresponding deformation modes of mirror folded metamaterial and Miura-ori in the stress platform stage are shown in Figure 7. It can be seen from (a) and (b) that the stress is concentrated at the creases of mirror folded metamaterial and Miura-ori, and the rhomboid plane rotates around the creases, forming plastic hinges at the creases. As can be seen from Figure 7B, two new plastic hinges (dashed blue lines) appear in mirror folded metamaterial during the compression deformation compared with Miura-ori in Figure 7A. The plastic hinge bears a large stress in the compression process, which is the main way of structural deformation and energy absorption. Therefore, the corresponding platform stress of the structure increases, so does the energy absorption. Compared with Miura, the energy absorption capacity of the mirror folded metamaterial is significantly improved. Through mirror symmetry connection, plastic hinge in the deformation process is increased, which is beneficial to improve the energy absorption capacity of the structure.

FIGURE 7

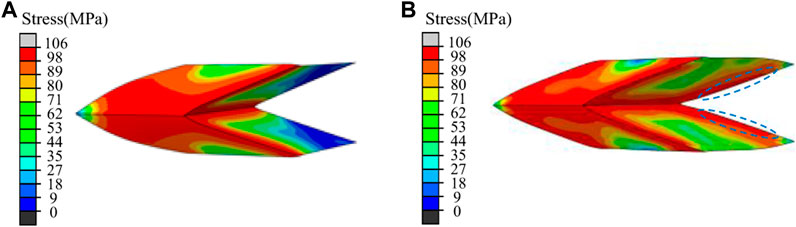
FIGURE 7. Deformation patterns in stress platform stage: (A) Miura-ori; (B) mirror folded metamaterial.

In order to ensure the periodicity of the structure and simplify the calculation, a 3 × 3 × 3 cell number model is adopted in the FE simulation. The overall dimensions in x, y and z directions are as follows: $L_a=117.76mm$, $L_b=65.00mm$, $L_t=64.89mm$. Figures 8, 9 respectively show the deformation cloud images when the strain reaches 18% and 76%. In the two figures, (a) and (b) represent views of structure in the x-y and y-z plane respectively. It can be seen from Figure 8 that in the initial stage of deformation, plastic hinge is formed at the junction of rhombic plane, i.e., the red area in the figure. The stress on each rhombic plane is very small, and it remains approximately undeformed. The whole structure folds along the crease, and the structure dissipates energy mainly through the formation and folding of plastic hinge.

FIGURE 8

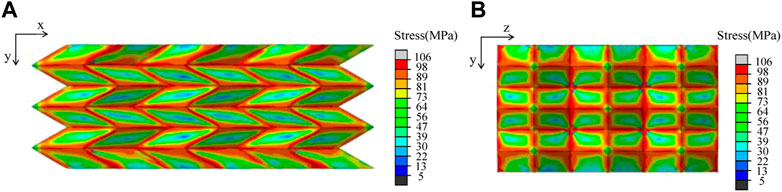
FIGURE 8. Deformation cloud images of the mirror folded metamaterial compressed in y direction, $\epsilon =18\%$: (A) x-y plane; (B) y-z plane.

FIGURE 9

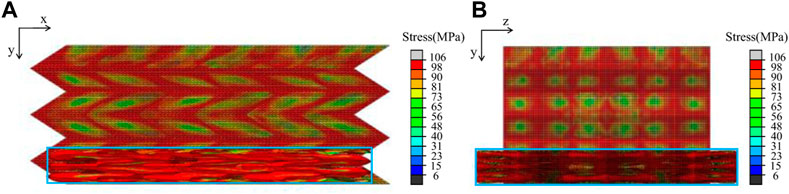
FIGURE 9. Deformation cloud images of the mirror folded metamaterial compressed in y direction, $\epsilon =76\%$: (A) x-y plane; (B) y-z plane.

As shown in Figure 9, when the strain reaches 76%, the whole structure is completely folded along the crease. The stress in the crease and diamond surface increases sharply, and the mirror folded metamaterial is finally compressed into a flat plate. The blue solid line in Figure 9 shows the state of the structure after compression. Comparing the state of the structure before and after compression, it can be seen that when the structure is compressed along the y direction, the x direction shrinks inward, showing a negative Poisson’s ratio effect, while the z direction expands outward, and the Poisson’s ratio is positive. The basic folding unit of the mirror folded metamaterial is Miura-ori element. The mirror connected mode makes it maintain the deformation mode of single-layer Miura-ori structure when compressed in the y direction. Therefore, the mirror folded metamaterial presents negative Poisson’s ratio effect in one direction.

Next, the influence of geometric parameters on structural mechanics and energy absorption characteristics is further studied. With other parameters unchanged and plane angle $\phi$ changed, the stress-strain curves of the structure under quasi-static loading is shown in Figure 10. With the increase of $\phi$, the corresponding peak stress in the elastic stage and mean stress in the plastic stage decrease. However, the decrease trend of the peak stress and mean stress decreases with the equidistance increase of $\phi$. When $\phi$ increases to $55°$, the peak stress and the mean stress no longer change significantly with the increase of $\phi$. The stress-strain curves of $\phi =55°$ and $\phi =65°$ are almost overlapping. As we can see from Figure 11, the SEA and the mean stress have the same trend with the change of $\phi$. The maximum value of SEA is 4000 J/kg when $\phi =25°$.

FIGURE 10

FIGURE 10. Influence of $\phi$ on mirror folded metamaterial’s stress-strain curve.

FIGURE 11

FIGURE 11. Influence of $\phi$ on average stress and specific energy absorption.

The influence of changing the dihedral angle $\gamma$ on the stress response and energy absorption of the structure is shown in Figures 12, 13. With the increase of $\gamma$, the corresponding peak stress in the elastic stage and the mean stress in the plastic stage increase. In addition, the increased amplitude of stress increases. When $\gamma$ increases to $140°$, the peak stress in the elastic stage is much larger than the platform stress, which leads to the decrease of stress uniformity, so it is not conducive to the stable energy absorption of the structure. As seen from Figure 13, the SEA can reach 6400 J/kg when $\gamma =140°$.

FIGURE 12

FIGURE 12. Influence of $\gamma$ on mirror folded metamaterial’s stress-strain curve.

FIGURE 13

FIGURE 13. Influence of $\gamma$ on average stress and specific energy absorption.

On the basis of the research on the quasi-static compression performance, the buffering energy absorption effect and impact resistance under the dynamic impact loading were studied. The deformation and stress clouds of the mirror folded metamaterial under impact load ($I=2.5Ns$) is shown in Figure 14. The mass of the impact plate is 0.033 kg and the impact velocity is 75 m/s. As shown in Figure 14 respectively represent the stress and deformation nephogram when the impact time are 0.02, 0.1, 0.2, and 0.5 ms. When subjected to impact load, the maximum stress occurs at the junction of the structure that has been compacted and the part that has not been deformed. With the beginning of the impact, the maximum stress first appears at the top of the structure, and the stress propagates downward along the deformation of the structure. Before the structure is compacted, the stress at the impact end is always greater than the stress at the bottom. The structure is completely compressed in a short period of time under the impact load. Observing its deformation mode, it can be found that the structure does not deform in the rhombic plane, and the rhombic surface of each layer folds in turn along the crease. Therefore, the structure mainly absorbs and dissipates energy through the generation and movement of plastic hinge. When the structure is subjected to the impact load in the y direction, the structure shrinks in the x direction and retains the same negative Poisson’s ratio property as in the quasi-static compression.

FIGURE 14

FIGURE 14. Deformation and stress nephogram of the mirror folded metamaterial during impact.

The buffering and energy absorption characteristics of the structure under low-speed impact v = 50 m/s and high-speed impact v = 150 m/s are studied respectively. Figure 15 shows the force-displacement curves of the proximal (blue solid line) and distal (red dotted line) end of the structure under two kinds of impact loading. In Figure 15A, when v = 75 m/s, the impact force at the proximal end of the structure reaches its peak soon at a displacement equal to 5 mm. With the increase of structural deformation, the velocity is weakened, and the impact force at the proximal end drops rapidly between 5 and 20 mm displacement, and then steadily decreases. Finally, the impact force at the proximal end and the distal end tends to be the same when the structural deformation is 62%. Due to the buffering effect of the structure, the impact force at the far end is much smaller than that at the near end. When the displacement is between 0 and 2 mm, the impact force at the far end is equal to 0, indicating that the impact load has not been propagated from the impact end to the bottom. In Figure 15B, when v = 150 m/s, due to the large impact velocity, the peak value of impact force increases significantly, and it decreases rapidly after appearing at 5 mm displacement, indicating that a higher impact velocity will accelerate the deformation of the structure, thus rapidly weakening the impact velocity.

FIGURE 15

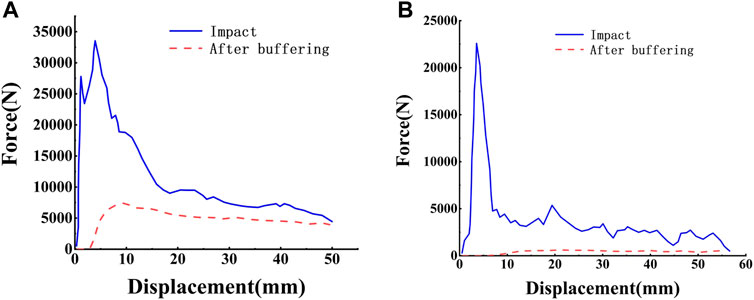
FIGURE 15. Force-displacement curves at both ends of the structure under different impact velocities: (A) v = 75 m/s; (B) v = 150 m/s.

The numerical values of velocity buffer and energy absorption in the impact process of the mirror folded metamaterial are shown in Table 3. The energy absorption rate can be calculated by $e=\frac{E_1-E_2}{E_1}=1-{\left(\frac{v_2}{v_1}\right)}^2$, where v₁ and v₂ represent the initial impact velocity and the remaining velocity after buffering. The peak force at the impact end corresponding to the higher speed impact is much larger than that of the lower speed impact, but the peak force at the buffer end is similar. This is because the greater the impact velocity is, the greater the structure deformation is, and the greater the corresponding platform stress is, which weakens the more impact force. However, the energy absorption rate of the structure is basically the same under the two speeds, indicating that different impact velocities have little influence on the energy absorption effect of the structure.

TABLE 3

TABLE 3. Structure buffer energy absorption value.

The energy absorption rate of the structure can reach more than 60% as shown in Table 3. Usually the propagation rate of the shock wave on the formation surface is between 120–260 m/s. The structure designed in this paper can effectively absorb the external shock wave. So, it will have great application value in the improvement of the anti-vibration and shock performance of GIL.

4 Experiment

In order to validate the accuracy of the above analysis based on the FE simulation, the quasi-static compression experiment of mirror folded metamaterial is carried out. The traditional manufacturing method of folding structure is progressive stamping. The cost of folding structure made by stamping method is low, but the manufacturing process is complex and the production cycle is long. The model made by this method is easy to separate in the compression process, which affects the continuity of the experiment and the accuracy of the results. Therefore, the aluminum alloy 3D printing method is selected to make the model. The model produced by 3D printing has high precision and does not need to be glued. The model produced is shown in Figure 16, where $a=10mm$, $b=10mm$, $h=1mm$, $\phi =45°$, $\gamma =100°$.

FIGURE 16

FIGURE 16. Mirror symmetric folding model.

In order to obtain the properties of structural matrix materials, standard tensile specimens are prepared and tested by INSTRON Universal Testing machine. The elastic modulus E = 70.41GPa, and the average true stress-strain data are calculated as shown in the Table 4.

TABLE 4

TABLE 4. True stress strain of aluminum alloy material.

The same as the tensile test, the quasi-static compression experiment of the model was carried out on Instron universal test machine, and the experimental device is shown in Figure 17. In order to ensure static loading, the loading rate of compression load was set as 1 mm/min, and the end time of loading was set as the collapse of the model. The direction of compression was vertically downward along the arrow in Figure 17A. The results of the quasi-static compression experiment of the mirror-folded structure are shown in Figure 17B. When subjected to quasi-static load in y direction, the structure as a whole is compressed and deformed. Each layer element folds along the crease at the rhomboid plane connection, and basically no deformation occurs in the plane. The stress concentrates at the crease, and is finally pressed into the flat plane. The structure fracture occurred at the crease, and cracks appeared in part of the rhombus plane.

FIGURE 17

FIGURE 17. Experimental results: (A) Before compression; (B) After compression.

During quasi-static compression, the simulation results of the deformation mode are shown in Figure 18. Figures 18A, B are the views in the x-y and x-z planes respectively. Figure 18A is the front view before compression. As can be seen from Figure 18A, in the process of in-plane compression, the mirror folding structure in the panel basically does not deform, each layer of rhombus plane folds around the crease, and the stress is concentrated at the crease. As can be seen from Figure 18B, the structure is fully compacted, the red area represents the stress concentration part, and the blue area represents the position that bears less stress. The stress is concentrated at the herringbone crease. Therefore, after the compression experiment, the structure is subjected to greater stress at the crease and breaks. The simulation results of the deformation mode of the mirror folding structure in the quasi-compression process are basically consistent with the experimental results.

FIGURE 18

FIGURE 18. Simulation results: (A) Before compression; (B) After compression.

Considering that the 3D-printed aluminum alloy model broke at the crease when compressed, the finite element model is modified to simulate the crack of thin-walled element. Set the triaxial stress of aluminum alloy as 0.33 and the input fracture strain as 0.045. In order to simulate the damage evolution process, the linear softening displacement is selected, and the failure displacement is set at 0.001. The stress and strain of the aluminum alloy material in the plastic stage are obtained by the matrix material parameters obtained from the tensile test. Boundary conditions of the structure are as follows: the upper panel moves downward for compression, the lower panel is fixed, the contact type is a universal tangential friction model with friction coefficient of 0.25.

The stress changes of the structure during compression obtained from the experiment and simulation are shown in Figure 19. It can be seen that the stress-strain curve has a peak value at the original platform stage since the model is fractured at the crease, and the peak value of the stress fluctuates up and down near the stress platform.

FIGURE 19

FIGURE 19. The stress-strain curve of the structure under compression.

5 Conclusion

In this paper, based on Miura’s folding mode, a mirror symmetric folded metamaterial is designed by combining single-layer folded metamaterials with mirror symmetry. The compression performance and energy absorption effect of the material under static and dynamic loading conditions are studied theoretically and numerically. The results show that: 1) The number of plastic hinges in compression is increased by mirror symmetry connection, and the appearance of plastic hinge is beneficial to improve the platform stress of structure. Compared with Miura-ori, the platform stress and energy absorption of mirror folded metamaterial are increased by 73% and 60% respectively. 2) The geometric angle parameters of mirror folded metamaterial have influence on the energy absorption effect. The specific performance is as follows: reducing the plane angle or increasing the dihedral angle can improve the specific energy absorption of the structure. 3) Under the impact load, the larger the impact velocity, the greater the deformation of the structure, so the more impact force is weakened. The energy absorption rate of the structure is basically the same under different impact speeds, which indicates that the impact speed has little impact on the energy absorption effect of the structure. 4) The structure designed in this article can provide some significant reference and guidance for the impact resistance of the GIL in the practical engineering.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Lead author: WX Co-writing: YH and HL participating in the experiment: WX, YH, HL, YL, and YW. All authors contributed to the article and approved the submitted version.

Funding

The Research on key design technologies of 500 kV underground transmission line (EV06201W).

Acknowledgments

The research is supported by the Research on key design technologies of 500 kV underground transmission line (EV06201W). The authors are grateful for the support.

Conflict of interest

Authors WX, YH, HL, YL, and YW were employed by the company China Energy Engineering Group Guangdong Electric Power Design Institute Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Basily, B. B., and Elsayed, E. A. (2004). Dynamic axial crushing of multilayer core structures of folded Chevron patterns. Int. J. Mater. Prod. Technol. 21 (1-3), 169–185. doi:10.1504/IJMPT.2004.004750

CrossRef Full Text | Google Scholar

Chen, Z., Wu, T., Nian, G., Shan, Y., Liang, X., Jiang, H., et al. (2018). Ron resch origami pattern inspired energy absorption structures. J. Appl. Mech. 86 (1), 011005. doi:10.1115/1.4041415

CrossRef Full Text | Google Scholar

Elsayed, E. A., and Basily, B. B. (2004). A continuous folding process for sheet materials. Int. J. Mater. Prod. Technol. 21 (1-3), 217–238. doi:10.1504/IJMPT.2004.004753

CrossRef Full Text | Google Scholar

Filipov, E. T., Tachi, T., and Paulino, G. H. (2015). Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl. Acad. Sci. U. S. A. 112 (40), 12321–12326. doi:10.1073/pnas.1509465112

PubMed Abstract | CrossRef Full Text | Google Scholar

Gattas, J. M., and You, Z. (2014). Quasi-static impact of indented foldcores. Int. J. Impact. Eng. 73, 15–29. doi:10.1016/j.ijimpeng.2014.06.001

CrossRef Full Text | Google Scholar

Jeong, H. Y., An, S. C., Seo, I. C., Lee, E., Ha, S., Kim, N., et al. (2019). 3D printing of twisting and rotational bistable structures with tuning elements. Sci. Rep. 9 (1), 324. doi:10.1038/s41598-018-36936-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Karagiozova, D., Zhang, J., Lu, G., and You, Z. (2019). Dynamic in-plane compression of Miura-ori patterned metamaterials. Int. J. Impact. Eng. 129, 80–100. doi:10.1016/j.ijimpeng.2019.02.012

CrossRef Full Text | Google Scholar

Lee, T.-U., Chen, Y., Heitzmann, M. T., and Gattas, J. M. (2021). Compliant curved-crease origami-inspired metamaterials with a programmable force-displacement response. Mater. Des. 207, 109859. doi:10.1016/j.matdes.2021.109859

CrossRef Full Text | Google Scholar

Ma, J., Song, J., and Chen, Y. (2017). An origami-inspired structure with graded stiffness. Int. J. Mech. Sci. 136, 134–142. doi:10.1016/j.ijmecsci.2017.12.026

CrossRef Full Text | Google Scholar

Ma, J., and You, Z. (2014). Energy absorption of thin-walled square tubes with a pre-folded origami pattern-part I: Geometry and numerical simulation. J. Appl. Mech. 81 (1), 011003. doi:10.1115/1.4024405

CrossRef Full Text | Google Scholar

Miura, K. (1975). New structural form of sandwich core. J. Aircr. 12 (5), 437–441. doi:10.2514/3.44468

CrossRef Full Text | Google Scholar

Pydah, A., and Batra, R. C. (2017). Crush dynamics and transient deformations of elastic-plastic Miura-ori core sandwich plates. Thin-Walled Struc. 115, 311–322. doi:10.1016/j.tws.2017.02.021

CrossRef Full Text | Google Scholar

Qi, B., Zhang, G., Li, C., Gao, C., Zhang, B., and Chen, Z. (2015). Research status and application prospect of gas-insulated metal-enclosed transmission lines. High. Volt. Technol. 41 (5), 1466–1473. doi:10.13336/j.1003-6520.hve.2015.05.007

CrossRef Full Text | Google Scholar

Rodrigues, G. V., Fonseca, L. M., Savi, M. A., and Paiva, A. (2017). Nonlinear dynamics of an adaptive origami-stent system. Int. J. Mech. Sci. 133, 303–318. doi:10.1016/j.ijmecsci.2017.08.050

CrossRef Full Text | Google Scholar

Ruan, Q., Shi, W., and Sang, Z. (2003). Questions to be considered for using 750 kV GIL at Laxiwa hydroelectric power station. High. Volt. Appar. 39 (4), 66–69. doi:10.3969/j.issn.1001-1609.2003.04.023

CrossRef Full Text | Google Scholar

Schenk, M., Guest, S. D., and Mcshane, G. J. (2014). Novel stacked folded cores for blast-resistant sandwich beams. Int. J. Solids Struct. 51 (25-26), 4196–4214. doi:10.1016/j.ijsolstr.2014.07.027

CrossRef Full Text | Google Scholar

Shang, T., and Li, G. (2011). Discussion on the characteristics of GIL and its application in power systems. South. Power Syst. Technol. 5 (1), 81–84. doi:10.13648/j.cnki.issn1674-0629.2011.01.021

CrossRef Full Text | Google Scholar

Turner, N., Goodwine, B., and Sen, M. (2015). A review of origami applications in mechanical engineering. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 230 (14), 2345–2362. doi:10.1177/0954406215597713

CrossRef Full Text | Google Scholar

Wu, J., Zhang, Y., Li, K., and Su, L. (2022). Origami-inspired metamaterials hierarchical structure with tailorable crushing behavior. Constr. Build. Mater. 345, 128328. doi:10.1016/j.conbuildmat.2022.128328

CrossRef Full Text | Google Scholar

Xiang, X. M., Lu, G., and You, Z. (2020). Energy absorption of origami inspired structures and materials. Thin-Walled Struct. 157, 107130. doi:10.1016/j.tws.2020.107130

CrossRef Full Text | Google Scholar

Xiang, Z., Niu, B., Ma, F., Ni, H., Sun, J., and An, Z. (2022). Direct fluorination and DC flashover performance of GIS spacers. High. Volt. Eng. 48 (11), 4306–4315. doi:10.13336/j.1003-6520.hve.20220352

CrossRef Full Text | Google Scholar

Yang, Q., Li, Z., Hao, H., and Chen, W. (2023). Compressive mechanical properties and dynamic behaviour of origami-inspired tri-directional auxetic metastructure. Eng. Struct. 281, 115751. doi:10.1016/j.engstruct.2023.115751

CrossRef Full Text | Google Scholar

You, Z. (2014). Folding structures out of flat materials. Science 345 (6197), 623–624. doi:10.1126/science.1257841

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Zhang, B., Li, M., Li, Y., Li, X., Lv, J., et al. (2023). Review of key insulation technologies of HVDC GIL. High. Volt. Technol. 49 (3), 920–936. doi:10.13336/j.1003-6520.hve.20222016

CrossRef Full Text | Google Scholar

Zhang, J., Karagiozova, D., You, Z., Chen, Y., and Lu, X. (2019). Quasi-static large deformation compressive behaviour of origami-based metamaterials. Int. J. Mech. Sci. 153, 194–207. doi:10.1016/j.ijmecsci.2019.01.044

CrossRef Full Text | Google Scholar

Zhang, J., Lu, G., Ruan, D., and Wang, Z. (2018). Tensile behavior of an auxetic structure: Analytical modeling and finite element analysis. Int. J. Mech. Sci. 136, 143–154. doi:10.1016/j.ijmecsci.2017.12.029

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, Q., Li, Y., Wang, B., and Ma, F. (2021). Theoretical, emulation and experimental analysis on auxetic re-entrant octagonal honeycombs and its applications on pedestrian protection of engine hood. Compos. Struct. 260, 113534. doi:10.1016/j.compstruct.2020.113534

CrossRef Full Text | Google Scholar