Influence of the fracture on the seepage stability of loess slopes

The development of fractures in loess slopes often has a great influence on the stability of slopes. In this paper, taking the homogeneous slope model as an example, fractures with different distances and depths from the slope top angle are provided at the top of the slope. Firstly, the influence of single fracture location and depth on slope stability is analyzed, and after the most unfavorable location and depth of the fractures are determined, the influence of the slope top fractures on the slope seepage field and slope stability under the conditions with and without rainfall is studied secondly. The results show that with the increase of the distance from the fracture to the top angle of the slope, the safety coefficient of the slope shows the change law of decreasing first and then increasing. The critical fracture depth corresponding to the fractures at different locations is different, and when the critical fracture depth is exceeded, the slope safety factor tends to be stable. At the end of the rainfall moment through 1-1 section to analyze, it is found that at this time the pore water pressure and volume water content of the soil at the bottom of the fracture at different depths are greater than those of the upper soil, and the shallow fracture has less influence on the seepage field of the slope, and through 2-2 section it is found that the pore water pressure and volume water content in the soil far from the fracture are greater than those of the soil near the location of the fracture. When 288 h after the end of rainfall, the pore water pressure and volumetric water content of the soil around the fracture in section 2-2 were greater than those far from the fracture location. With the passage of time, the pore water pressure at the location of the fracture gradually dissipated and the corresponding volumetric water content gradually decreased, indicating that the fracture had an obvious influence on the characteristics of the seepage field in the soil at different times of rainfall. Under the condition of no rainfall, there exists a critical depth of fractures affecting slope safety stability, while under the condition of rainfall, the slope safety coefficient continuously decreases with the increase of fracture depth, and there is no critical fracture depth. The research results promote the understanding of the safety and stability of loess fracture slopes and provide a reference for slope management.

1 Introduction

Landslides are one of the most common geological hazards in loess areas. The occurrence of landslides often causes significant property losses (Wang et al., 1996; Zhang et al., 2011). The main reason is that the tensile stress of the slope exceeds its tensile strength, resulting in tension cracks at the trailing edge of the slope. The cracks intersect and cut structural plane of the loess, which weakens the overall stability of the slope. The loess soil of the slope will further deteriorate and accelerate the formation of landslides under precipitation infiltration, wind erosion, earthquake and human factors (Wang et al., 2018; Sun et al., 2019; Wu et al., 2019; Yan et al., 2019; Zhang et al., 2019).

Slope stability analysis methods are usually divided into three types categories: limit analysis method, limit equilibrium method and numerical analysis method (Chen et al., 2002). Spencer (1967) introduced tension fractures and derived the formulae of fracture depth to analyze the effect of unit weight, cohesion and internal friction angle on the fracture depth. Michalowski (2012) and Utili (2013) proposed a stability analysis method for slopes with fractures based on limit analysis theory to analyze the effect of fracture depth as well as fracture location on slope stability. Zhu et al. (2022) analyzed the influence of constraint width, slope grade, internal friction angle and fracture depth on the critical height of three-dimensional vertical fracture loess slope. He et al. (2021) studied the effect of slope top dip angle on the stability of fractured slopes, and analyzed it using a logarithmic spiral rotating mechanism of plane strain of plane strain. Yan et al. (2022) studied the variation of slope stability under three working conditions, such as seepage of fracture water from the trailing edge to the foot of the slope, drainage at the foot of slope and elevation of the watered point on the slope. Zhou et al. (2021) established the sliding model of single fracture and multi-fracture and the ultimate limit state of slope, deduced the formula for calculating the limit depth of vertical fracture at the top of loess inclined slope, and explored the variation of fracture depth with different influencing factors. The formula was verified according to the limit analysis upper bound method and practical engineering examples.

The seepage and stability of fractured soil slope under rainfall are also the research hotspots of scholars. The research methods are mainly numerical simulation and laboratory test. Scholars (Zeng et al., 2020; Zhang et al., 2020; Zhou et al., 2020) divided slopes containing fractures into soil zone and fracture zone and assigned different material properties to them respectively. They analyzed the rainfall infiltration characteristics of fracture slopes in conditions of accumulated water and influence of the depth of fracture depth, inclination angle and location on the seepage characteristics of slope. Gao et al. (2021) established the relationship between slope material parameters as a function of fracture rate, and studied the influence of rainfall conditions, the development degree of fractures and the types of the vegetation root system on the stability of red clay slope by finite element method. It showed that fracture development can easily lead to shallow damage of red clay slope and significantly reduce slope stability. Yao et al. (2001) analyzed the stability of expansive soil slope considering fractures and rainfall infiltration, and compared the stability of expansive soil slope between considering fractures and without considering fractures through engineering examples. Cao et al. (2022) carried out model experiment on the fracture evolution, rainfall infiltration and scour of red clay slopes to reveal the fracture evolution law of red clay slopes and analyze the influence of the fracture development and rainfall intensity on the seepage characteristics and scour pattern of red clay slopes. Chen et al. (2019) discussed the seepage mechanism of fissured soil, established a two-dimensional saturated-unsaturated seepage analytical model of fissured soil based on the one-dimensional analytical solution, and derived the explicit analytical solution of the two-dimensional seepage control equation by Fourier integral variation. Zeng et al. (2022) carried out indoor model tests of red clay slopes with different parameters in the overbreak zone under rainfall by fluorescence tracer method and digital image processing techniques to analyze the variation of moist sharp, transient saturated zone and volumetric water content of red clay slope. Liu et al. (2017) studied the infiltration law of slope under the combined action of fracture anisotropy and different rainfall intensities. He (2018) studied the effect of fracture content variation on the seepage field of slopes with the increase of rainfall holding time, and also considered the variation of fracture network volume to explore its effect on the safety factor. Wang et al. (2020) and Qian et al. (2020) investigated the influence of different shapes of fractures on the seepage field of the slope by physical simulation experiment. Therefore, little literature is available on the seepage stability of slopes with fractures.

Taking the homogeneous slope model as an example, this paper calculates the influence of a single fracture on the slope stability at different locations and depths from the slope top. After determining the most unfavorable location and depth of fractures, the influence of fractures at the top of the slope on the seepage field and stability of the slope is further analyzed with and without rainfall.

2 Influence of fracture location and depth on slope stability

The influence of a single fracture on the stability of the slope at different positions and depths of the slope top is calculated. The ideal homogeneous slope calculation model with slope angle of 45° is adopted. Fracture are located at the top of the slope, which with a distance from the top of the slope top angle are 2 m, 3 m, 4 m, 5 m, 6 m, 7 m, 8 m, 9 m, 10 m respectively, and the depth of the fracture continues to expand from 0 m to 10 m. The groundwater level is located at a depth of 35 m below the slope top. The natural density of the soil is 16.5 kN/m³, the cohesion is 30 kPa, and the internal friction angle is 25°. The computational model of the slope is shown in Figure 1.

FIGURE 1

FIGURE 1. The schematic diagram of slope calculation model.

The effect of fracture extension depth on slope stability is shown in Figure 2, where L is the distance from the fracture locations to the slope top angle. Figure 2 shows that the safety factor of the slope decreases obviously with the increase of the spacing within the range of 7 m from the fracture locations to the slope top angle, the reduction magnitude of safety factor increases gradually with the expansion of the fracture depth. When the fracture is 7 m away from the slope top angle and the fracture depth expands to about 4 m, the safety factor of the slope tends to a minimum value, and the curve change tends to be flat. The crack depth at this time is called the critical crack depth. The fracture depth in this case is defined as the critical fracture depth. When the fracture depth is greater than 8 m, the fracture at different locations has little influence on the slope safety factor. The closer the distance between the fracture and the slope top angle, the deeper the fracture depth when the slope safety factor reaches a stable value. The reason for these phenomena is that when the shallow fracture is close to the top of the loess slope, the failure mode of the slope is in the form of sliding damage through the arc at the top of the slope. When the sliding surface is far away from the bottom of fracture, fracture has little effect on slope stability. When the fracture depth at the top of the slope extends deeper, the sliding surface of the slope develops from the initial arc-shaped sliding surface to the combined sliding surface through crack. In this case, the position of the sliding surface intersects with the fracture, which changes the stress of the slope and seriously affects the stability of the whole slope. As the crack depth continues to expand, the intersection of the circular slip surface and the fracture continues to move downward, and the safety factor of slope also shows a decreasing trend. When the fracture at the top of the slope continues to expand to a certain depth and the intersection of the circular slip surface and the bottom of the crack reaches the critical value, the safety factor of the slope reaches the minimum value, after which the safety coefficient tends to stabilize. The slope safety factor remains unchanged at first with the deepening of the fracture depth, then decreases rapidly and finally tends to be gentle.

FIGURE 2

FIGURE 2. The effect of crack propagation depth on slope stability.

Figure 3 shows that with the increase of the distance from the fracture to the slope top angle, the influence of the fracture on the slope stability gradually increases and the reduction rate of safety factor gradually increases. When it reaches 7 m, the fracture has the greatest influence on the slope stability and the safety factor is the smallest. When it is greater than 7 m and less than 9 m, the influence of the fracture on the slope stability decreases rapidly. When it is greater than 9 m, fracture have little effect on slope stability. Therefore, the critical fracture depth has a critical location at the top of the slope. Attention should be paid to the treatment of fractures in this area in the process of slope management.

FIGURE 3

FIGURE 3. Effect of fracture location on slope stability.

3 Influence of slope top fractures on seepage field and slope stability under rainfall

3.1 Numerical calculation model

A slope model with a fissure at the top of the slope is established. It is assumed that there is a fissure at 7 m from the slope top angle, the length of the model bottom is 80 m, the slope toe is 45°, the height is 50 m, and the distance from the bottom of the model is 15 m. In order to analyze the influence of pore water pressure and volume water content of soil on slope stability in the process of rainwater seepage, two observation sections are set in the model. Section 1-1 passes through the fracture, which is consistent with the extension direction of the fracture. Section 2-2 is located at the bottom of the fracture at 1 m, which is perpendicular to the extension direction of the fracture. Volumetric water content and pore water pressure of each section obtained by numerical calculation of this model. The finite element mesh is divided into 12,953 nodes and 12,826 elements. The specific model and mesh division are shown in Figure 4.

FIGURE 4

FIGURE 4. Computational model and grid division.

3.2 Calculation parameters and their boundary condition settings

In this paper, the mechanical parameters of loess are obtained by consulting a large number of literatures. According to the characteristics of loess material, the soil-water characteristic curve of slope is obtained by V-G model. The permeability coefficient function of unsaturated loess is obtained by soil-water characteristic curve and saturated permeability coefficient.

Because there are fractures, there is no strength parameter. Therefore, when calculating the transient seepage field, the equivalent permeability coefficient method is used for the fractures. The permeability coefficient of the fracture is large relative to the surrounding soil, and adopts the saturated permeability coefficient. The natural gravity of soil is 16.5 kN/m³, the effective cohesion is 30 kPa, the effective internal friction angle is 25°, the saturated permeability coefficient is 2 × 10^-6 m/s. The natural gravity, the effective cohesion and the effective internal friction angle of fracture are all 0, and the saturated permeability coefficient is 0.78 m/s. The soil-water characteristic curve of unsaturated soil is shown in Figure 5.

FIGURE 5

FIGURE 5. Soil water characteristic curve and osmotic coefficient function of slope soil.

The strength parameters of soil materials, soil-water characteristic curves and permeability coefficient functions provided above should also be used for calculations under other working conditions.

Boundary conditions: for the following part of the water table on both sides of the model set the head boundary, the position of the fixed head is at the water table line, and the part above the water table line is set as the zero-flow boundary. The surface of the slope is set as the free infiltration boundary, and the flow boundary is taken, and the bottom of the model is set as the impermeable boundary. The rainfall intensity is 2 mm/h. It is considered that the rainfall is all infiltrated into the slope, and no surface runoff is formed on the slope surface. The rainfall time is 72 h, and the duration after rain is 288 h.

Initial conditions: when calculating the transient seepage field of the slope, the water content of the slope soil in its natural state and the distribution of pore water pressure within the slope soil should be obtained first and used as the initial conditions to calculate the subsequent conditions of the seepage field at different moments.

The boundary conditions of the model set the rainfall infiltration boundary as AB, BC, CD. In the process of rainfall, there will be a catchment inflow at the fracture location, so the infiltration flow relative to other infiltration boundaries should be added at the fracture width position. The impervious boundary is DE, FG, AH, and the constant head boundary is EF and GH. The groundwater level and the constant head height are the same. The initial conditions and boundary conditions of the model are shown in Figure 6.

FIGURE 6

FIGURE 6. The boundary condition of the model and the initial pore water pressure.

3.3 Influence of the depth of slope top fracture on the seepage field of slopes under rainfall

Before the instability failure of soil slope, there will be some tension cracks at the top of the slope. These cracks make the isolated soil column formed inside the slope, which is equivalent to the unconfined condition (Li et al., 2006). The fracture will provide a potential sliding surface for the slope failure to increase the sliding surface of the slope.

Fracture provide infiltration channels for rainwater and enhance the infiltration capacity of water under rainfall. On the one hand, the infiltration rainwater into the soil increases the weight of the soil itself. On the other hand, the fracture is filled with water, and the downward infiltration of water under gravity will soften the potential sliding surface of the slope. In addition, it will produce hydrostatic pressure on the structural plane, which will lead to the decrease of stability of slope, short the creep time of slope body and increase the possibility of slope failure.

Therefore, it is necessary to study the influence of fractures on slope seepage field under rainfall when analyzing the influence of fractures on slope stability. In this paper, the equivalent model with rainfall intensity of 3 mm/h is used. The rainfall time is 72 h and the post-rain time is 288 h. The fracture depth at the position of 7 m from the slope top angle is 0 m, 2 m, 4 m, 6 m, 8 m, and 10 m respectively. The seepage field of the slope is calculated by SEEP/W software, and then the calculated results are imported into SLOPE/W software for slope stability analysis.

Figures 7, 8 show that when the rainfall ends, as the crack depth continues to expand, the water stored in the fracture gradually increases, and the corresponding pore water pressure and volumetric water content gradually increase. The pore water pressure and volumetric water content at the bottom of the fracture reach the maximum under gravity, which is much larger than the pore water pressure and volumetric water content of the upper soil. When the fracture depth is shallow and the depth is 2 m, the pore water pressure on the 1-1 section is almost the same as that without fracture, indicating that the shallow fracture has little effect on the seepage field of the slope. When the rainfall ended 288 h, the water molecules had enough time to move from the fracture with high saturation to the surrounding with low saturation. The pore water pressure in the fracture gradually dissipates, and the water content at the bottom of the fracture also decreases.

FIGURE 7

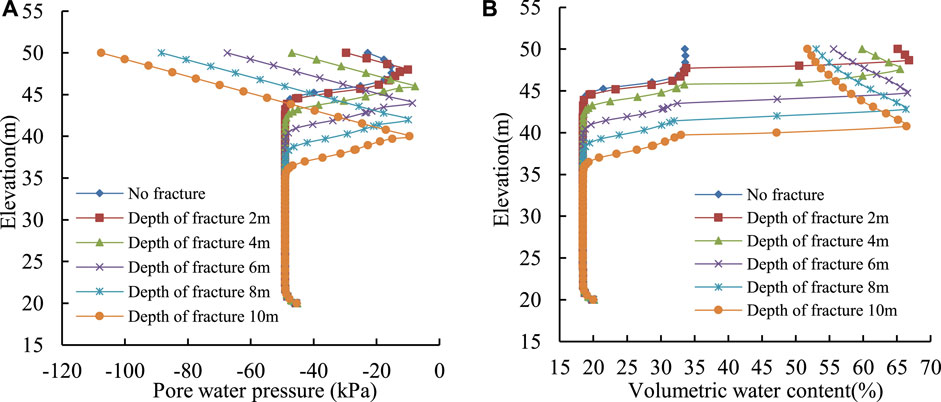
FIGURE 7. (A) The variation curve of pore water pressure. (B) The variation curve of and volume water content.

FIGURE 8

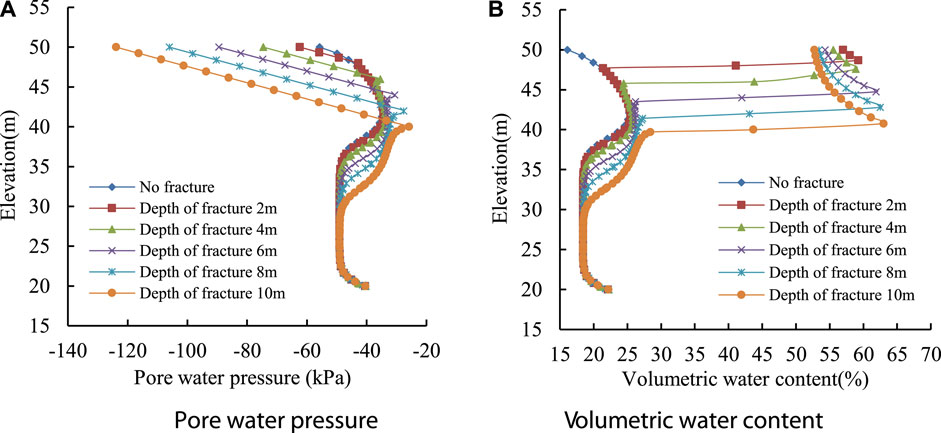
FIGURE 8. The variation curve of pore water pressure and volume water content at 288 h 1-1 section after the end of rainfall at different depths (A) Pore water pressure (B) Volumetric water content.

Figures 9, 10 show that the fracture in the soil provide a channel for the diffusion of rainwater, and the water inside the fracture diffuses from high saturation to low saturation through the bottom and side of the fissures during rainfall. In the process of water diffusion, the pore water pressure and volumetric water content of the soil around the fracture are larger than those of the soil away from the fracture due to the loss of hydraulic gradient. When the rainfall ends, the wetting front depth of rainwater infiltration is greater than the depth of the fracture, resulting in the pore water pressure and volumetric water content in the soil far from the fracture is greater than the soil near the fracture. When the rainfall ends 288 h, the pore water pressure and volumetric water content of the soil around the fracture are greater than those far away from the fracture. Because the soil lacks the supply of rainwater, and the water diffuses around under the action of gravity, the pore water pressure in a certain depth of the slope surface continues to dissipate, and the corresponding volumetric water content also continues to decline. Because the lack of rainwater supply in the soil and the continuous diffusion of water under gravity, the pore water pressure in a certain depth of the slope is continuously dissipated, and the corresponding volumetric water content is also decreasing.

FIGURE 9

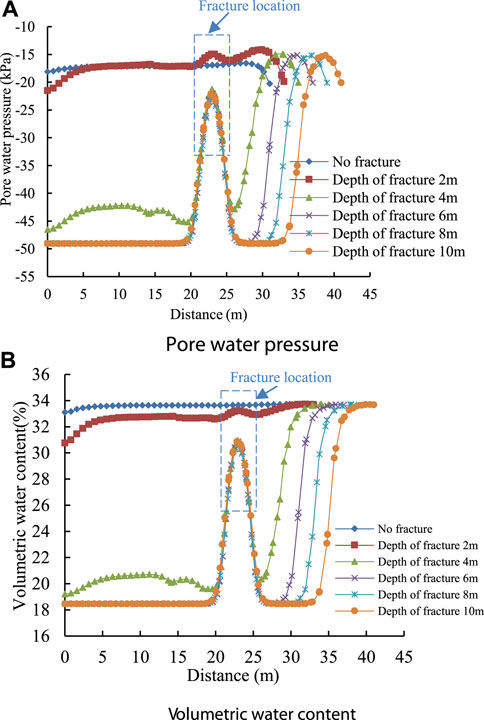
FIGURE 9. The variation curve of pore water pressure and volume moisture content of 2-2 sections at the end of rainfall were observed in different depths (A) Pore water pressure (B) Volumetric water content.

FIGURE 10

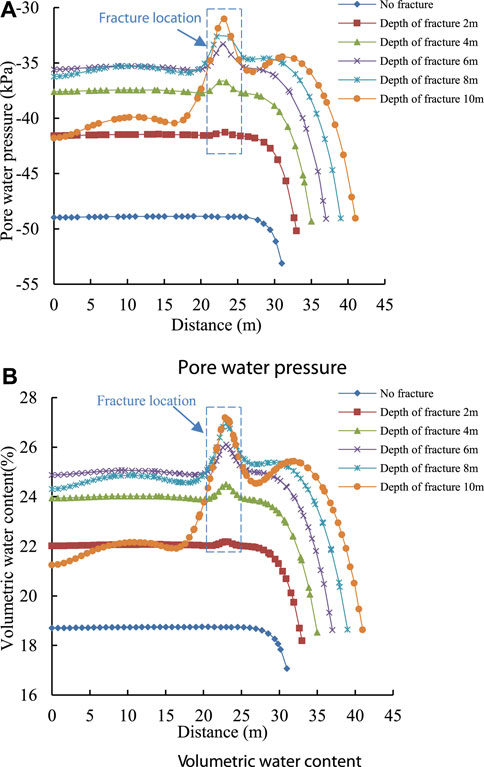
FIGURE 10. Variation curves of pore water pressure and volumetric water content of 2-2 fracture surface at different depths at 288 h after rainfall (A) Pore water pressure (B)Volumetric water content.

3.4 Influence of the depth of slope top fractures on slope stability under rainfall

By analyzing the seepage field of the slope with fracture, the safety factor of the slope is further analyzed in the case of fracture affecting the seepage field. In this paper, the seepage results calculated by SEEP/W are imported into SLOPE/W software. The influence of fracture depth change on slope stability under rainfall is analyzed by M-P method.

Figure 11 shows that in the absence of rainfall, the decrease of safety factor is small and tends to be a stable value when the fracture depth exceeds 4 m. Under rainfall, the safety factor of slope is decreases obviously and the magnitude of decline varies greatly. As the time of rain increases, the safety factor decreases more, the critical depth disappears, and the deeper the crack depth, the smaller the slope safety factor.

FIGURE 11

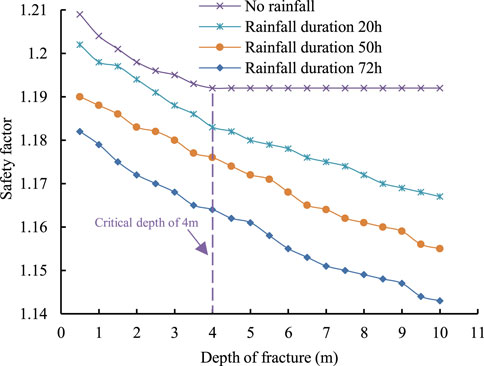
FIGURE 11. The influence of fracture depth on slope safety coefficient under different rainfall duration.

4 Conclusion

By establishing a two-dimensional calculation model, the influence of different locations and depths of fracture at the top of the slope on slope stability was studied. The distribution of pore water pressure and volumetric water content of the slope under rainfall is obtained. The influence of fracture depth on slope stability under rainfall is explored. The conclusions are as follows.

(1) With the increase of the distance from the fracture to the slope top angle, the safety factor of the slope decreases first and then increases. The critical fracture depth has a critical position at the slope top. When the fracture is 7 m away from the slope top angle and the fracture propagation depth exceeds 4 m, the slope safety factor is the smallest.

(2) With the increase of fracture depth, the safety factor of slope decreases rapidly at first and then tends to be stable. There is a critical crack depth, and the critical crack depth corresponding to different positions is different. Beyond the critical crack depth, the safety factor of slope tends to be stable.

(3) At the end of rainfall, with the increase of fracture depth, the pore water pressure and volumetric water content of the soil at the bottom of the fracture of 1-1 section are greater than those of the upper soil, and the shallow fracture has little effect on the seepage field of the slope. Since the damp-surface depth of rainwater infiltration is greater than the depth of the fissure, the pore water pressure and volumetric water content in the soil far from the fracture in 2-2 section are greater than those in the soil near the fracture.

(4) At 288 h after the end of rainfall, the pore water pressure and volumetric water content of the soil around the fracture of 2-2 section are greater than those of the soil far away from the fracture. Due to the lack of water supply in the fracture, the water is continuously diffused around under gravity. Finally, the pore water pressure of the soil at the location of the fracture gradually dissipates, and the corresponding volumetric water content gradually decreases. Due to the lack of water recharge in the fracture, the water spreads around under gravity, and finally the pore water pressure of the soil at the location of the fracture gradually dissipates, and the corresponding volumetric water content gradually decreases.

(5) When there is no rainfall, with the increase of fracture depth, the safety factor of slope decreases slightly, and the existence of critical fracture depth makes the safety factor of slope tend to a stable value. Under rainfall, the safety factor of slope decreases continuously with the increase of fracture depth, and the critical fracture depth disappears, which is less than the safety factor of slope stability under the condition of no rainfall (Wang, et al., 2021).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

HL provided overall guidance on the article and wrote this paper. MY and TD modified the article language. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Loess Soil Mechanics and Engineering Key Laboratory of Shaanxi Province Foundation (13JS073) and Natural Science Foundation of Shaanxi Province (2017JM5059).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, S., Fu, H., Gao, Q., Guangtao, Z., and Zeng, L. (2022). Seepage characteristics and erosion patterns of fractured red clay slope under rainfall. China J. Highw. Transp. 35 (05), 33–43.

Google Scholar

Chen, Z., Ren, H., and Ring, Y. (2019). Two-dimensional analytical analysis of coupling deformation and seepage coupling of fractured unsaturated soil. Geol. Hazards Environ. Preserv. 30 (04), 29–35.

Google Scholar

Chen, Z. (2002). Limit analysis for the classic problems of soil mechanics. Chin. J. Geotechnical Eng. 24 (1), 1–11.

Google Scholar

Gao, Q. F., Zeng, L., and Shi, Z. N. (2021). Effects of desiccation cracks and vegetation on the shallow stability of a red clay cut slope under rainfall infiltration. Comput. Geotechnics 140, 104436. doi:10.1016/j.compgeo.2021.104436

CrossRef Full Text | Google Scholar

He, Y., Yu, J., Yuan, R., and Fang, Y. (2021). Stability analysis of soil fracture slope considering slope top inclination. China J. Highw. Transp. 34 (05), 45–54.

Google Scholar

Li, R., Yu, Y., and Guangxin, L. I. (2006). Application of strength reduction finite element method in slope stability analysis of unsaturated soil. Water Resour. Hydropower Eng. 36 (3), 42–45.

Google Scholar

Liu, D., He, Z., Zhou, K., Li, T., and Zeng, L. (2017). Influence of fracture anisotropy on slope seepage under rainfall conditions. Min. Metallurgical Eng. 37 (04), 14–18.

Google Scholar

Lu, H. E. (2018). Analysis of seepage field and stability of fractured soil slope under rainfall conditions. Zhejiang, China: Zhejiang University.

Google Scholar

Michalowski, R. L. (2012). “Cracks in slopes: Limit analysis approach to stability assessment,” in Proceedings of the GeoCongress 2012: State of the Art and Practice in Geotechnical Engineering, Oakland, California, March, 2012, 442–450.

CrossRef Full Text | Google Scholar

Qian, Z., Tu, G., Zhao, S., and Li, M. (2020). Differential effects of X and Y shaped fractures on rainfall infiltration of accumulation. Hydroelectr. Power 46 (08), 92–98.

Google Scholar

Spencer, E. (1967). A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique 17 (1), 11–26. doi:10.1680/geot.1967.17.1.11

CrossRef Full Text | Google Scholar

Sun, P., Wang, G., Li, R., Zhang, Z., Huo, X., Li, Z., et al. (2019). Field test of loess slope under rainfall condition. J. Eng. Geol. 27 (2), 466–476.

Google Scholar

Utili, S. (2013). Investigation by limit analysis on the stability of slopes with cracks. Geotechnique 63 (2), 140–154. doi:10.1680/geot.11.p.068

CrossRef Full Text | Google Scholar

Wang, Q., Tu, G., Zhao, S., and Qiu, X. (2020). Effects of Y-shaped and primary and secondary plume fractures on rainfall infiltration of accumulations. Yangtze River 51 (11), 179–184.

Google Scholar

Wang, G., and Liao, X. (1996). Study on land-slide disaster and its prevention and control of China railway. Chin. J. Geol. Hazard Control 1, 6–9.

Google Scholar

Wang, L., Pu, X., Wu, Z., Xu, S., and Liu, K. (2018). Shaking table test study on dynamic response of loess slope under the coupling effect of earthquake and rainfall. J. Geotechnical Eng. 40 (7), 1287–1293.

Google Scholar

Wang, L., Liu, F., and Zhang, Z. (2021). Research on characteristics of unsaturated soil water characteristic curve. Adhesion 46 (05), 147–150.

Google Scholar

Wu, Z., Chen, Y., Wang, Q., Zhao, D., and Zhang, D. (2019). Mechanism analysis of yongguangcun landslide caused by the 6.6 earthquake in zhangxian county, minxian county. J. Geotechnical Eng. 41 (2), 165–168.

Google Scholar

Yan, G., Yin, Y., Huang, B., Zhang, Z., and Dai, Z. (2019). Genesis mechanism and deformation characteristics of jinjiling landslide in the three gorges. Reservoir area. Rock Soil Mech. 40 (S1), 329–340.

Google Scholar

Yan, J., Huo, Z., Li, H., Zhou, Y., and Liu, Y. (2022). Study on seepage sliding analysis and stability of near-horizontal slope under fracture water. J. Min. Saf. Eng. 39 (03), 607–614.

Google Scholar

Yao, H., Zheng, S., and Chen, S. (2001). Analysis on the slope stability of expansive soils considering cracks and infiltration of rain. Chin. J. Geotechnical Eng. 23 (5), 606–609.

Google Scholar

Zeng, L., Xiao, L., Zhang, J., and Gao, Q. (2020). Effect of the characteristics of surface cracks on the transient saturated zones in colluvial soil slopes during rainfall. Bull. Eng. Geol. Environ. 79 (2), 699–709. doi:10.1007/s10064-019-01584-1

CrossRef Full Text | Google Scholar

Zeng, L., Chen, J., Liu, J., Gao, Q., Yuan, Y., and Kuang, B. (2022). Study on seepage characteristics of fracture-bearing red clay slope based on fluorescence tracer method. China J. Highw. Transp. 36, 1–13. doi:10.19721/j.cnki.1001-7372.2023.03.010

CrossRef Full Text | Google Scholar

Zhang, J., Zhu, D., and Zhang, S. H. (2020). Shallow slope stability evolution during rainwater infiltration considering soil cracking state. Comput. Geotechnics 117, 103285. doi:10.1016/j.compgeo.2019.103285

CrossRef Full Text | Google Scholar

Zhang, M., and Li, T. (2011). Study on the inducing factors and forming mechanism of loess land-slides. J. Eng. Geol. 19 (4), 530–540.

Google Scholar

Zhang, S., Pei, X., Huang, R., Zhang, X., Chang, Z., and Zhang, Z. (2019). Model test on rainfall infiltration characteristics and deformation failure mode of loess fill slope. China J. Highw. Transp. 32 (9), 32–41.

Google Scholar

Zhou, Z., Zhang, J., Ning, F., Luo, Y., and Wang, J. (2020). Temporal and spatial characteristics of moisture migration and instability mechanism of cracked soil slope under rainfall infiltration. J. Traffic Transp. Eng. 20 (4), 107–119. doi:10.19818/j.cnki.1671-1637.2020.04.008

CrossRef Full Text | Google Scholar

Zhou, Z., Zhu, L., and Chen, L. (2021). Calculation method of vertical fracture depth of loess slope at inclined slope. China J. Highw. Transp. 34 (05), 37–44.

Google Scholar

Zhu, X., Shao, S., Shen, X., Shao, S., and Liu, X. (2022). Three-dimensional stability limit analysis of fractured loess slope. Rock Soil Mech. 43 (10), 2735–2743+2756.

Google Scholar