Observation of linear magnetoelectric effect in a Dirac magnon antiferromagnet Cu3TeO6

Cu₃TeO₆, a three-dimensional antiferromagnet forming a unique spin-web lattice of spin-1/2 Cu²⁺ ions below the Néel temperature T_N ≈ 62 K, has recently been found to exhibit topological Dirac or nodal magnon dispersion. In this study, we report the discovery of the linear magnetoelectric (ME) effects in Cu₃TeO₆ below T_N. Our pyroelectric current measurements at a constant magnetic field (H) reveal a linear increase of electric polarization (P) with H for both P//H and P⊥ H configurations; a maximum P//[110] = 20 µC/m² is obtained at µ₀H//$\left[1\overline{1}0\right]$ = 14 T, corresponding to a linear ME coefficient 1.8 ps/m. Magnetic point group analysis and Monte-Carlo simulations confirm that finite linear ME coefficients are allowed in the off-diagonal and diagonal ME tensor components, consistent with the magnetic point group of ${\overline{3}}^{\prime }$. As the parity-time symmetry can be broken in the presence of H or electric field E in the linear ME materials, we envisage that Cu₃TeO₆ should exhibit a H- or E-induced transformation in the topological magnon dispersion from a Dirac point/nodal line type into two Weyl point types.

Introduction

In the linear magnetoelectric (ME) materials, electric polarization (P) can be linearly induced by magnetic field (H) or magnetization (M) can be linearly induced by electric field (E). The linear ME effect was first discovered experimentally in an antiferromagnet Cr₂O₃ by Astrov (Astrov, 1960), after the theoretical predictions first by Landau and Lifshitz (Landau and Lifshitz, 1984) and later by Dzyaloshinskii (Dzyaloshinskii, 1959). The linear ME effect occurs when a material breaks space inversion (I) and time-reversal (t) symmetry separately but conserves the simultaneous operation of I ⊗ t.

Since the first discovery, numerous linear ME materials have been discovered and studied, particularly in the 1960–1970s (O’Dell, 1970; Smolenskiĭ and Chupis, 1982). Furthermore, in the early 2000s, research interests on the ME effects were reignited by the discoveries of large non-linear ME effects in several multiferroic materials (Kimura et al, 2003; Wang et al, 2003; Hur et al, 2004). Over the last 2 decades, research on the multiferroics has been very active, leading to the discovery of numerous emergent multiferroics and new mechanisms for generating ME coupling (Cheong and Mostovoy, 2007; Spaldin and Ramesh, 2019). Very recently, even 2D van der Waals materials have been found to exhibit multiferroic behavior (Park et al, 2022). Moreover, a topologically protected switching mechanism has been recently identified in a multiferroic GdMn₂O₅ (Ponet et al, 2022). Additionally, while BiFeO₃ films have been studied for a long time, Shin et al, 2022 successfully grew high-quality thin films of Co₂Z hexaferrites exhibiting ME behavior at room temperature. Thus, scientific research on multiferroic and magnetoelectric materials seems to be still actively performed.

The ME materials possess unique properties that enable cross-coupling between magnetic and electrical properties, making them increasingly valuable for various next-generation electronic devices. Examples include highly sensitive H sensors with pico-tesla sensitivity (Zhai et al, 2006) and low-power non-volatile memories (Bibes and Barthélémy, 2008). Moreover, ME and/or multiferroic materials can be utilized as tunable filters, antennas, and resonators in millimetre-wave devices for wireless communication and radar (Li and Luk, 2016), ME logic circuits, which operate at a low voltage of ∼ 100 mV, provide an energy-efficient alternative to traditional CMOS technology (Manipatruni et al, 2019), and flexible ME nanogenerators for energy harvesting (Ghosh et al, 2020). Thus, recent research has demonstrated the potential of ME materials to offer promising alternatives to the conventional technologies, making them highly attractive for applications.

In addition to research efforts aimed at finding practical applications for ME materials, studying the ME effects in magnetic insulators can be useful for understanding their basic properties. For example, the ME tensor characteristics of a magnetic insulator can serve as an effective means of determining its magnetic point group when neutron scattering fails to determine magnetic symmetry unambiguously. Moreover, as found in this work, the ME effect can also be utilized to manipulate the topological magnon properties of a magnetic insulator.

Cu₃TeO₆ belongs to corundum related compounds of A₃TeO₆ (A = Mn, Co, Ni, and Cu) family, which has recently attracted scientific attention due to its each members unique properties. Although they nominally have the same chemical formula, each member of A₃TeO₆ family exhibits different structural and physical properties based on the type of ions at the A-site. Mn₃TeO₆, for instance, adopts a trigonal structure ($R\overline{3}$ space group) and exhibits a complex incommensurate magnetic structure with multiferroic properties (Zhao et al, 2015; Ivanov et al, 2017), while Co₃TeO₆ crystallizes in a monoclinic structure (C2/c space group) and exhibits H-induced electric polarization (P) (Hudl et al, 2011; Leo et al, 2018). Moreover, Ni₃TeO₆ has a trigonal structure (R3 polar space group) and exhibits P in the spin-flop phase induced by H above 8 T (T) (Oh et al, 2014; Kim et al, 2015). On the other hand, Cu₃TeO₆ is known to crystalize in a cubic lattice structure of high symmetry (Ia $\overline{3}$ centrosymmetric space group) without any report on its electrical properties. It forms a unique bixbyite-type structure, in which 24 Cu²⁺, 8 Te⁶⁺, and 48 O²⁻ ions are contained in a unit cell, forming a network of 8 hexagons composed of 6 Cu²⁺ ions and a central Te⁶⁺ ion (See, Figure 1A). (Falck et al, 1978; Herak et al, 2005)

FIGURE 1

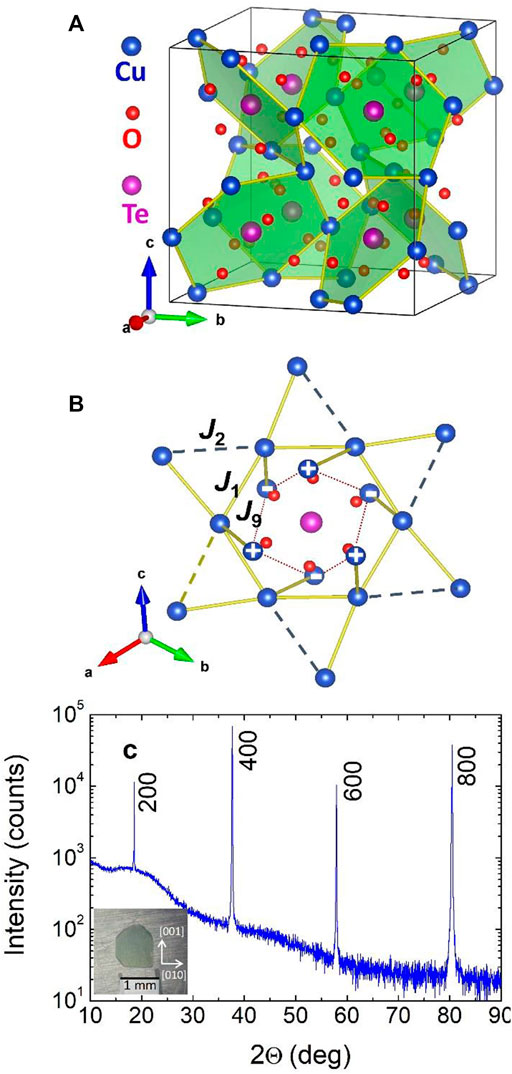
FIGURE 1. (A) The crystal structure of Cu₃TeO₆ including the eight Cu hexagons surrounding TeO₆ octahedra. (B) First (solid line), second (bold dash line), and nineth (weak dash line) nearest neighbor (NN) exchange interactions are drawn as J₁, J₂, and J₉, respectively. The plus (+) and minus (−) signs indicate Cu ions of neighbouring Cu hexagon at equal distance above and below the shown Cu hexagon of solid line and J₉ is exchange interactions between these two Cu ions. The 1^st NN forms a hexagon and the 1^st with the 2^nd NN forms a hyper kagome structure. (C) XRD data taken along the [100] crystallographic direction with the inset picture of the Cu₃TeO₆ single crystal.

Upon the temperature being lowered, Cu₃TeO₆ undergoes a paramagnetic to an antiferromagnetic (AFM) spin ordering at the Néel temperature (T_N) of 62 K. This leads to the stabilization of a unique three-dimensional spin-web lattice of Cu²⁺ ions with S = ½ spins (Herak et al, 2005; Herak, 2011; Månsson et al, 2012; He and Itoh, 2014). An earlier report based on neutron powder diffraction and torque magnetometry measurements suggest the appearance of either a collinear AFM order or a slightly canted AFM order with the dominant spin moment along one of [±1 ± 1±1] directions (Herak et al, 2005), forming a trigonal symmetry in the spin system (Herak et al, 2005). Recent theoretical predictions by Li et al (Li et al, 2017) suggest the existence of Dirac and the nodal line magnons for the collinear and spin canted state of Cu₃TeO₆, respectively. This was subsequently confirmed by Bao et al. (2018) and Yao et al. (2018), who reported the spin excitation spectra of Cu₃TeO₆ from the inelastic neutron scattering (INS) measurements. These experiments provided experimental evidence for the novel topological Dirac/nodal line magnons. However, the resolution of the magnon spectra from those two experiments was not sufficient to distinguish possible nodal lines from the Dirac point.

According to the theoretical prediction using the first-principles calculations and a linear-response theory by Wang et al, 2019, the Dirac point (or the Nodal line) in the magnon dispersion is coined to the absence (or presence) of a spin canting in the AFM state. The spin canting in Cu₃TeO₆ is most likely induced by the Dzyaloshinskii-Moriya interactions (DMI). These topological Dirac point and nodal line in the magnon dispersion suggest that I ⊗ t symmetry is preserved without any biased E and H, thus allowing the linear ME effect consistent with a magnetic point group. However, applied H and E for the ME poling may lead to the eventual stabilization of one type of ME domain and emergence of the transversal electric polarization. This would imply that the I ⊗ t symmetry is broken by the application of H or E. In this case, the magnon bands are expected to carry non-zero Berry curvature/Chern numbers, which may transfrom each Dirac point/nodal line into two Weyl points with opposite charges (Owerre, 2018). Therefore, investigating the ME effects in Cu₃TeO₆ can further our understanding of characteristic magnon dispersion at zero and finite H or E.

In this letter, we report the discovery of both off-diagonal and diagonal linear ME coupling in Cu₃TeO₆ below T_N = 62 K. Our findings indicates that the electric polarization (P//[110]) exhibits a linear increase under a magnetic field (H//$\left[1\overline{1}0\right]$) up to 14 T with the configuration of $P\perp H$ . We conducted a combined symmetry analysis and Monte-Carlo calculations to confirm that the observed linear ME effect with both off-diagonal and diagonal components can be attributed to the magnetic point group $\overline{3}$′.

Results and discussions

Magnetic and electrical properties

The lattice structure of Cu₃TeO₆ and the arrangement of its magnetic ions (Cu²⁺) are shown in Figures 1A,B, respectively. Cu₃TeO₆ crystalizes in a bixbyite-type high-symmetric cubic structure (Ia$\overline{3}$ space group) with 12 Cu²⁺ (S = ½) ions per primitive cell and with a lattice parameter of a = 9.537 Å at room temperature (Falck et al, 1978). Despite its simple structure, Cu₃TeO₆ exhibits a spin-web type antiferromagnetic ordering with topological magnon dispersion. The spin-lattice is composed of nearly coplanar hexagons formed by six Cu²⁺ (S = ½) ions with normal along the [±1 ± 1±1] directions. There are four different orientations of hexagons with normal along [111], [11–1], [1–11], or [−111], and each Cu²⁺ ion is shared by two hexagons, forming an unusual hyper kagome network (see, Figure 1B). A nearly straight Cu-O-O-Cu path can be observed between the 9^th nearest neighbors. Recent INS (Yao et al, 2018) measurements and first-principles calculations (Wang et al, 2019) have shown that the strength of the 9^th nearest-neighbour exchange interaction, which is antiferromagnetic, is comparable to the first nearest neighbor interaction, while the second and other nearest-neighbour exchange interactions are rather weak.

X-ray diffraction (XRD) data measured in the Cu₃TeO₆ single crystal with {100} plane are shown in Figure 1A. The data confirm that the Cu₃TeO₆ single crystal was grown without chemical impurities. Since the Cu₃TeO₆ has a cubic structure, the crystals have a clear rectangular shape with a size of ∼1 mm³, as seen in the inset of Figure 1C; Figure 2A displays the magnetic susceptibility (χ) data measured at H = 1 kOe along the cubic directions [100], [110], and [111] after zero-field cooling. The χ curves exhibit a downturn at T_N = 62 K along all directions, indicating the onset of a long-range AFM ordering below T_N. The χ curves are similar for each direction but show a minimum value along the [111] direction. (Herak et al, 2005; He and Itoh, 2014), suggesting that the [111] direction is the easy axis, although the magnetic anisotropy is quite weak. These results are consistent with earlier neutron scattering data (Herak et al, 2005), that suggest the spins are oriented parallel to the [111] axis in the AFM phase and the magnetic anisotropy is quite weak. This behavior is also qualitatively consistent with magnetic data reported by other groups (Caimi et al, 2006; Choi et al, 2008; Månsson et al, 2012; He and Itoh, 2014).

FIGURE 2

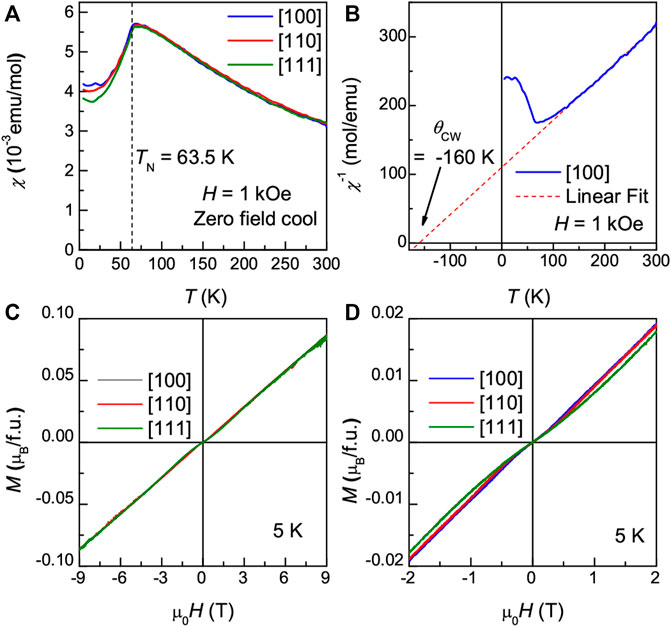
FIGURE 2. Temperature and magnetic dependence of magnetic properties of Cu₃TeO₆. (A) Magnetic susceptibility and (B) inverse susceptibility as a function of temperature and (C, D) magnetic field dependence of magnetization with two field ranges along each direction in the Cu₃TeO₆ single crystals.

The Curie-Weiss fit of the inverse χ (Figure 2B) shows the Curie-Weiss temperature θ_CW = −160 K, whose absolute value is much higher than T_N. This θ_CW = −160 K is consistent with previously reported values ranging from −134 K to −213 K (Herak et al, 2005; Månsson et al, 2012; Bao et al, 2018; Yao et al, 2018) and indicates that the magnetic interactions are predominantly AFM. The value of the frustration index (f = |θ_CW|/T_N) of 2.58 in our case and 2.23–3.55 in other previous reports suggests that the Cu₃TeO₆ is moderately frustrated (Herak et al, 2005; Månsson et al, 2012; Bao et al, 2018; Yao et al, 2018). It has been reported that except for the strong first “J₁,” & ninth “J₉” and the moderate second “J₂,” fourth “J₄,” & 10th “J₁₀” exchange interactions, all other exchange interactions up to J₂₀ are rather weak. The strong J₁ and J₉ are compatible with the collinear AFM ground state, while the modest frustration possibly comes from the incompatibility of the sizeable J₂, J₄, and J₁₀ exchange interactions with the collinear AFM state (Wang et al, 2019). Besides, it is further found that χ starts to deviate from the Curie-Weiss law below −126 K possibly indicates the onset of short-range spin order (Yao et al, 2018).

We also measured the H-dependent magnetization (M) along three crystallographic directions ([100], [110] & [111]) at 5 K (Figures 2C,D). The M-H curve along the [111] direction shows a slight curve between −1.5 T and 1.5 T, whereas it is almost linear for the [100] and [110] directions (Herak et al, 2005). This change in the slope of the M-H curve along the [111] direction is due to the presence of four types of domains, each with the spins oriented along one of the body diagonal [111], [11–1], [1–11], or [−111] directions of the cubic unit cell, which then yield their H -induced rotation and alignment (Herak et al, 2005). The magnetization M increases almost linearly up to −0.086 µ_B/f.u at 9 T, which is still much lower than the expected saturation value of M_s = 3 µ_B/f.u. This confirms that the AFM spin configuration is maintained at least up to 9 T.

To investigate ME coupling in Cu₃TeO₆, we measured the pyroelectric currents (I_p) and dielectric constant ε at selected H in a transverse configuration, i.e., I_p and ε//[110] and H//[1–10], as summarized in Figures 3A–D. Without the application of H, no observable I_p is measured, as shown in Figure 3A. However, upon application of H = 3 T, I_p at low temperature starts to decrease linearly above 20 K and shows a sharp dip near T_N = 62 K. As H increases beyond 3 T, the linear decrease and dip feature in I_p are progressively enhanced up to a maximum applicable field of H = 14 T, implying that P is continually enhanced with increasing H. The sign of I_p was reversed by a negative electric poling (-E_P) (data not shown here), which indicates that P is intrinsically induced by the broken inversion symmetry under H.

FIGURE 3

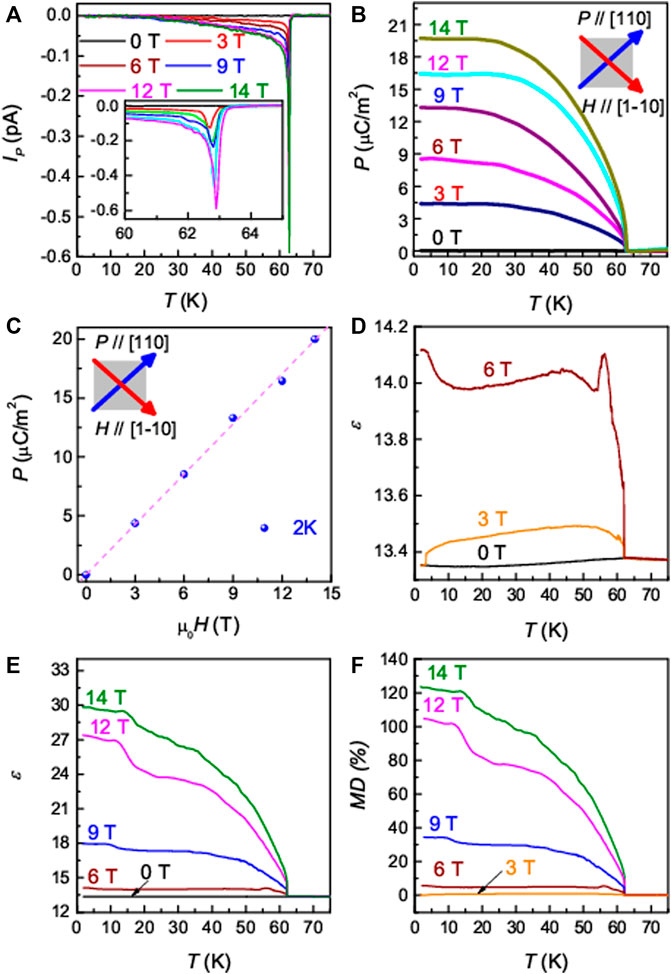
FIGURE 3. Temperature dependence of electric properties of Cu₃TeO₆. The (A) pyroelectric current along [110] for E//[110] at various H//[1–10], (B) the electric polarization P//[110] at various H//[1–10], (C) summarizes the electric polarization P//[110] at various H//[1–10] at 2 K (D, E) the dielectric constant for P,E//[110] and H//[1–10] and (F) the corresponding magnetodielectric (MD) effect in Cu₃TeO₆ single crystals.

Figure 3B summarizes the temperature-dependence of the P obtained by integrating the I_p with time. For all applied H, P is nearly constant below 20 K, decreases above 20 K approximately as $\sqrt{T_N-T}$, and finally drops to zero at T_N. The reported temperature dependence of the staggered moment obtained from the neutron diffraction measurement (Herak et al, 2005) is similar to that of the P(T) curves. This implies that the evolution of the magnetic order parameter in Cu₃TeO₆ below T_N is directly coupled to the evolution of P under H. These results provide further evidence of the strong ME coupling in Cu₃TeO₆.

In Figure 3C, we summarize the resultant P value at 2 K at each constant H. The figure shows that the p-value increases nearly linear with H until it reaches the maximum value of 20 µC/m² at µ₀H = 14 T, which supports the linear ME coupling. We obtained linear ME coefficient α of 1.8 ps/m, which is lower than those observed in other important linear ME compounds such as TbPO₄ (730 ps/m, 1.5 K) (Rivera, 2009), and LiCoPO₄ (30.6 ps/m, 4.2 K) (Rivera and Schmid, 1994). However, the α value of ∼1.8 ps/m is higher than those of BiFeO₃ (0.3 ps/m, 300 K), GaFeO₃ (0.06 ps/m, 300 K) (Niu et al, 2017), (NH₄)₂ [FeCl₅·(H₂O)] (1.2 ps/m, 1.5 K) (Hughey et al, 2022), and LiNiPO₄ (1.7 ps/m, 20 K) (Vaknin et al, 2004) although it is comparable to those of Cr₂O₃ (2.8 ps/m, 300 K) (Iyama and Kimura, 2013), NdCrTiO₅ (−1.84 ps/m, 10 K) (Li et al, 2018) and Sm₂BaCuO₅ (4.4 ps/m, 2 K) (Yanda et al, 2019). The relatively small ME effect of Cu₃TeO₆ might be due to the isotropic nature of S = ½ spins and the small spin-orbit coupling. It’s worth noting that this linear ME effect is quite unique in the Cu²⁺ (S = 1/2) systems since most of the linear ME effect have been discovered in large spin (S > 1/2) systems with magnetic ions such as Cr, Fe, Mn, and Ni. Recently, in the family of Cu²⁺ (S = ½) system, we observed H-induced ferroelectricity in a kagome staircase compound PbCu₃TeO₇, whose origin is related to the type II multiferroicity coming from a spiral spin structure (Yoo et al, 2018).

Figures 3D,E summarizes the temperature dependence of the dielectric permittivity ε for E//[110] at several magnetic fields (i.e. 0, 3, 6, 9, 12 & 14 T) applied along the H//[1–10] direction. At zero H, ε exhibits a weak drop at T_N = 62 K. When H = 3 T is applied, there is a sharp jump of ε at T_N and the magnitude of this jump increases greatly with increasing H. It is worth noting that ε at 2 K increases tremendously from 13.4 at 0 T to 29.8 at 14 T. Moreover, the dielectric loss also shows a large change under H (not shown here). The magneto-dielectric (MD) effect, calculated using the formula, $\mathrm{M}\mathrm{D}\left(H\right)=\frac{{\epsilon }^{\prime }\left(H\right)-{\epsilon }^{\prime }\left(0\right)}{{\epsilon }^{\prime }\left(0\right)}\times 100\%$, is summarized in Figure 3F as a function of T at different H. This shows that Cu₃TeO₆ exhibits a positive, giant MD response below T_N with maximum MD of 123% at 2 K at H = 14 T. The observation of the giant MD effect in Cu₃TeO₆ directly reflects the presence of large modulations in the lattice degrees of freedom under an applied H, thereby supporting the intrinsic nature of the magnetoelectric effect.

To investigate the possibility of a ME response induced by H in other crystallographic directions and configurations, we conducted measurements of the I_p curves in different H and P directions. The P curves obtained by integrating the I_p data over time are presented in Figure 4. These P curves show that the polarization for all configurations emerges at T_N, at which ε exhibits an anomaly for all the investigated configurations. Further, the P(T) curves show the same line shapes but different values for different directions. At 2 K and 9 T, P values for the (P//[110], H//[1–10]), (P//[110], H//[110]), (P//[100], H//[010]), and (P//[100], H//[100]) configurations are 13.3 μC/m², 1.4 μC/m², 7.4 μC/m², and 0.8 μC/m², respectively. These observations indicate that the emergence of P with H in this linear ME system is not restricted to only one highly symmetric lattice direction. Among them, the maximum ME coefficient of 1.8 ps/m is realized in the direction of P//[110] with H//[1–10]. It is worth noting that P is an order of magnitude larger in the H⊥P configurations than in the H//P configurations, indicating that the off-diagonal components of the linear ME tensor are dominant. These experimental results thus reveal that a particular form of the linear ME tensor associated with a specific magnetic point group should be responsible for the induced P at a finite H below T_N.

FIGURE 4

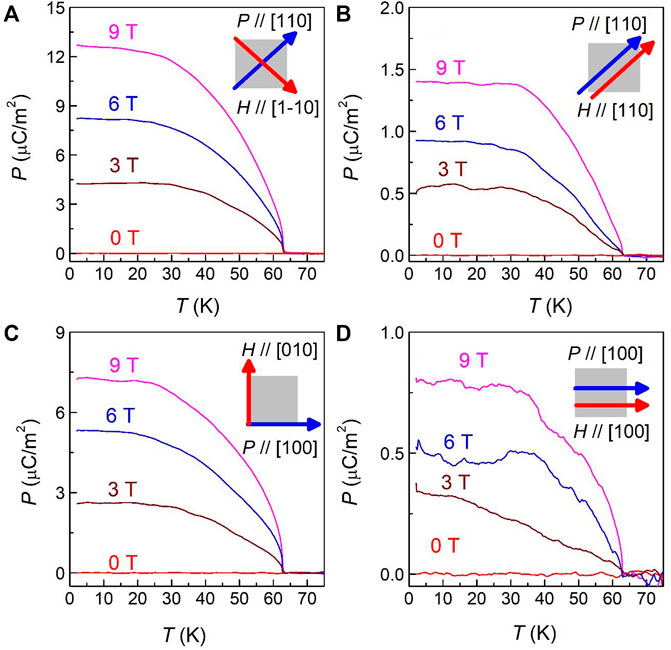
FIGURE 4. Temperature dependence of electric polarization of Cu₃TeO₆ single crystals measured for various directions of P and H directions, as represented by schematic inset figures for each dataset. The data were collected at various H and presented for (A) P//[110] with H//[1-10], (B) P//[110] with H//[110], (C) P//[100] with H//[010] and (D) P//[100] with H//[100]. The transverse configurations exhibit a significantly large P, providing evidence for the presence of dominant off-diagonal ME tensors in Cu₃TeO₆.

The symmetry analysis and the classical Monte-Carlo simulations

Next, we would like to discuss the possible mechanism of ME coupling in Cu₃TeO₆. For that, we performed symmetry analysis and conducted classical Monte-Carlo simulations using the exchange constants available from the literature data (Yao et al, 2018; Wang et al, 2019). According to the neutron diffraction data (Herak et al, 2005), the magnetic structure appearing below T_N is described by the wavevector $\overrightarrow{k}=0$. The magnetic representation ${\mathrm{\Gamma }}_m$ for the 12 magnetic Cu²⁺ ions in the primitive cell is split into

${\mathrm{\Gamma }}_m={\mathrm{\Gamma }}^{1+}\oplus {\mathrm{\Gamma }}^{1-}\oplus {\mathrm{\Gamma }}^{2+3+}\oplus {\mathrm{\Gamma }}^{2-3-}\oplus 5{\mathrm{\Gamma }}^{4+}\oplus 5{\mathrm{\Gamma }}^{4-},$

where ${\mathrm{\Gamma }}^{2+3+}$ and ${\mathrm{\Gamma }}^{2-3-}$ are physically irreducible representations (IR). The AFM ordering observed by the neutron diffraction experiment is described by IR ${\mathrm{\Gamma }}^{4-}$, which enters five times into ${\mathrm{\Gamma }}_m$ and according to which five order parameters are transformed. Three of these order parameters $\left(a_1,a_2,a_3\right)$, $\left(b_1,b_2,b_3\right)$, and $\left(c_1,c_2,c_3\right)$ describe the collinear magnetic structure. The phase state of the form $\left(a,a,a\right)$ with all three order parameters being equal gives the direction of spins along the [111] direction. The proposed noncollinearity is described either by the remaining two order parameters transforming according to IR ${\mathrm{\Gamma }}^{4-}$, which are necessarily condensed at the ${\mathrm{\Gamma }}^{4-}$ instability at T_N, or by the order parameter $q$ described by IR ${\mathrm{\Gamma }}^{1-}$, which is induced by ${\mathrm{\Gamma }}^{4-}$ in an improper way due to the interaction

$a_1{a}_2{a}_{3}q.$

The magnetoelectric interactions that result in H-induced electric polarization below T_N are

$I_1=a_1{M}_y{P}_z+a_2{M}_z{P}_x+a_3{M}_x{P}_y,(1)$

$I_2=a_1{M}_z{P}_y+a_2{M}_x{P}_z+a_3{M}_y{P}_x,(2)$

where any of the five order parameters transformed according to ${\mathrm{\Gamma }}^{4-}$ can replace $\left(a_1,a_2,a_3\right)$. As mentioned above, the magnetic structure belongs to the phase state $\left(a,a,a\right)$, which has eight domains (the spins can be oriented predominantly along one of the four spatial diagonals of the cubic cell). Magnetoelectric poling prior to the measurements partially lifts this degeneracy.

For the analysis of the ME behavior one can write the expansion of the thermodynamic potential as a function of the order parameters in the form

$\begin{array}{l}\mathrm{\Phi }={\mathrm{\Phi }}_0+{\kappa }_1\left(I_1-I_2\right)+{\kappa }_2\left(I_1+I_2\right)-\overrightarrow{M}\overrightarrow{H}-\overrightarrow{P}\overrightarrow{E}\\ ={\mathrm{\Phi }}_0+{\kappa }_1\left[a_1\left(M_y{P}_z-M_z{P}_y\right)+a_2\left(M_z{P}_x-M_x{P}_z\right)+a_3\left(M_x{P}_y-M_y{P}_x\right)\right]\\ +{\kappa }_2\left[a_1\left(M_y{P}_z+M_z{P}_y\right)+a_2\left(M_z{P}_x+M_x{P}_z\right)+a_3\left(M_x{P}_y+M_y{P}_x\right)\right]-\overrightarrow{M}\overrightarrow{H}-\overrightarrow{P}\overrightarrow{E},\end{array}(3)$

with

${\mathrm{\Phi }}_0=\frac{A}{2}\left(a_1^2+a_2^2+a_3^2\right)+\frac{B_1}{4}\left(a_1^4+a_2^4+a_3^4\right)+\frac{B_2}{4}{\left(a_1^2+a_2^2+a_3^2\right)}^2+\frac{1}{2\epsilon }\left(P_x^2+P_y^2+P_z^2\right)+\frac{1}{2\chi }\left(M_x^2+M_y^2+M_z^2\right),$

where A, B₁, and B₂ are phenomenological coefficients, and ε and χ are dielectric and magnetic susceptibilities, respectively.

According to our results, the H-induced polarization for the P//[110] and H//[1–10] geometry is much larger than for P//[110] and H//[110]. In the former case, the ME coefficient is ${\kappa }_1$, while in the latter, it is ${\kappa }_2$. This indicates that ${\kappa }_1$ is much larger than ${\kappa }_2$. In the case of P//[100] and H//[010], the ME coefficient is ${\kappa }_1-{\kappa }_2$ and, therefore, should be close to the case of P//[110] and H//[1–10]. However, for the former case (i.e., the case of P//[100] and H//[010] in Figure 4C, the H-induced polarization is about as twice lower than for the latter case (i.e., the case of P//[110] and H//[1–10] in Figure 4A. In our view, this larger than-expected difference is the result of higher order ME interactions with respect to the AFM order parameter. Indeed, there are many additional third-order ME interactions in the AF order parameter, which are linear with respect to magnetization and electric polarization, e.g.,

$a_1{a}_2{a}_3\left(M_x{P}_x+M_y{P}_y+M_z{P}_z\right).$

From our point of view, such interactions are responsible for the electric polarization induced by H in the P//[100] and H//[100] geometry, for which interactions (1) and (2) give 0 ME effect.

To gain further insights into the microscopic interactions, we rewrote the magnetoelectric interactions (1) and (2) in terms of the spins of the ions in the primitive cell, and we analyzed and discussed the resulting numerous microscopic interactions in the Supporting Material.

Implications of the ME effects on the topological magnon dispersion

Although Cu₃TeO₆ with a centrosymmetric Ia$\overline{3}$ space group possesses a global center of inversion, Cu-O-Cu bond angles smaller than 180° lead to the breaking of the local inversion symmetry around the region where a ligand ion lies between two magnetic ions. The absence of this local inversion symmetry allows in principle the DMI leading to spin canting. According to the neutron diffraction study of Herak et al (Herak et al, 2005), the AFM ordering of Cu₃TeO₆ below T_N = 62 K leads to either collinear or slightly tilted non-collinear spin configuration with a dominant magnetic moment along one of the [±1 ± 1±1] directions. This concomitantly results in a decrease in crystal symmetry from cubic to trigonal.

According to theoretical calculations by Li et al (Li et al, 2017), who refer to the experimental spin canting angles of 6° within the spin pair connected by the strongest interaction J₁, the value of $\left.{\left|D\right.}_1\right|/\left|J_1\right|$ in Cu₃TeO₆ was estimated as ∼ 0.2. However, Wang et al (Wang et al, 2019) has considered all the J_i (i = 1–20) superexchange interactions, in which J₉ is the second strongest one, and estimated $\left.{\left|D\right.}_1\right|/\left|J_1\right|$ ∼0.06 in Cu₃TeO₆, resulting in only the spin canting angle of only ∼1.3° between the J₁ pair. Moreover, in this case, the value of |D₉| corresponding to the second strongest J₉ was found to be negligible, because the bond angle corresponding to this exchange coupling (i.e., J₉) is very close to 180°. As a result, Wang et al (Wang et al, 2019) have predicted that the length of the nodal line should be proportional to ${\left.\left.{\left[|D\right.}_i\right|/\left|J_i\right|\right]}^2$. However, the expected length of the nodal line is indeed very short so that it is difficult to differentiate the nodal line from the Dirac point according to the available INS data (Bao et al, 2018; Yao et al, 2018).

According to the theoretical calculations of Li et al. (2017) and Wang et al. (2019) the Dirac point and the Nodal line in the magnon dispersion are coined to the absence and the presence of a spin canting in the AFM state of Cu₃TeO₆, respectively. However, from our point of view, the prediction of nodal lines in Cu₃TeO₆ is the consequence of the simplicity of the model with only two exchange interactions (Li et al, 2017). Indeed, experimental INS results suggest the absence of nodal lines, and an involvement of many exchange paths, which is also supported by theoretical calculations (Bao et al, 2018; Yao et al, 2018). The INS experiment, however, indicates possible presence of Dirac points in the Γ and Ρ points of the Brillouin zone, which should be allowed if the conservation of I ⊗ t -symmetry is valid.

Below T_N, the linear ME effect causes the electric and magnetic fields to have the same symmetry in Cu₃TeO₆. As a result, applying either field in Cu₃TeO₆ will break the remaining I ⊗ t symmetry, leading to either the transformation of Dirac points into the Weyl points or the appearance of energy gaps. The extent of the splitting or gap formation will be proportional to the applied field strength. Since magnons are neutral without any orbital effect and do not change quasi-momentum under external fields, the Weyl points will persist even under strong fields. Therefore, the magnon spectra in Cu₃TeO₆ can be manipulated by both H and electric field via a Zeeman coupling and the ME coupling, respectively. We expect both magnetic and electric fields to be equally effective in manipulating the topological magnon structure, but experimental verification is required to confirm their effectiveness.

Conclusion

In conclusion, we observed a linear ME effect in Cu₃TeO₆ with a maximum value of P = 20 µC/m² at µ₀H = 14 T and a corresponding linear ME coefficient α = 1.8 ps/m for the P//[110] and H//[1–10] configuration. Moreover, the ME coefficient is one order of magnitude higher for transversal configurations compared to parallel configurations. Detailed symmetry analysis indicates that the linear ME effect originates from the ME tensor components allowed by the magnetic point group ${\overline{3}}^{\prime }$ symmetry. Thus, Cu₃TeO₆ is a rare material that exhibits both topological quantum spin excitations and linear magnetoelectricity, demonstrating the richness of its physics. We suggest that the manipulation of topological properties can be achieved by both applied electric and magnetic fields, leading to the transformation of Dirac points into Weyl points or the appearance of energy gaps. This work will pave the way for electric field control of topological magnon dispersion in Cu₃TeO₆. Further research on neutron scattering under magnetic or electric fields, as well as theoretical simulation, will be useful in shedding more light on the intriguing possibility of manipulating topological magnon dispersion.

Experimental methods

Single crystals of Cu₃TeO₆ were grown by the flux method. First, a polycrystalline Cu₃TeO₆ powder was prepared using high purity CuO (>99.99%) and TeO₂ in molar ratio of 3:1 via the solid-state reaction method. The powder was calcined at 600°C for 12 h twice and sintered at 850°C for 24 h. Then single crystals were grown using a mixture of polycrystalline Cu₃TeO₆ and PbO/TeO₂ flux (a molar ratio 1:1) at a mass ratio of 1:2. The mixture was heated at 950°C for 12 h and then cooled to 700°C at a rate of 1.25°C/h. Single crystals, ∼1 mm³ size and cubic in shape, were mechanically separated from the flux. The lattice structure of the grown Cu₃TeO₆ single crystals was characterized using an X-ray diffractometer (Empyrian™, Malverin Pananalytycal).

To conduct electrical measurements, the single crystals were shaped into a thin plate form along the [100] and [110] directions, and electrodes were made with silver epoxy on both sides of the plate. Magnetic properties were investigated using a vibrating sample magnetometer (VSM). Pyroelectric current (I_p) and dielectric constant (ε) were measured using an electrometer (Keithley, KE617) and a capacitance bridge (Andeen-Hagerling, AH2550A), respectively. These measurements were performed in a temperature (T) range from 2 to 75 K using a PPMS™ (Quantum Design, 9 T) or a Janis cryostat equipped with a 14 T superconducting magnet (Cryogenic^LTD). Prior to I_p measurements, the sample was first cooled down from 70 to 2 K under applications of an electric field of 1.2 MV/m and magnetic fields of 0, 3, 9, 12, and 14 T. After cooling, the electric field was removed and both sides of the electrode were short-circuited until stray charges were fully nullified. The I_p at zero electric field was recorded during temperature-warming mode under applications of constant magnetic fields. Electric polarization (P) was obtained by integrating I_p over time. Furthermore, for all the configurations, it has been confirmed that the sign of the P is reversed by reversing the direction of a poling electric field.

Note added in submission

During the preparation of the manuscript, we became aware that the linear magnetoelectric effect in Cu₃TeO₆ has been similarly reported in a recent preprint by Kisiček et al, arXiv:2211.08902. However, in the preprint paper, only P along [100] direction was measured, while we carried out investigations along different crystallographic directions. Thus, the authors of arXiv:2211.08902 have only found the off-diagonal components of ME tensor, in contrast to the results in this manuscript.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

BK prepared the single-crystal samples. KY measured the magnetization and susceptibility in PPMS. KY performed the dielectric constant, pyrocurrent, and ME current measurements in a 14 T magnet. NT-O did the MC calculation. AS, KY, NT-O, and KK. analyzed the data and wrote the manuscript. KK. devised the project and advised the research. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Ministry of Science and ICT through NRF of the National Research Foundation of South Korea funded by Ministry of Science and ICT (2019R1A2C2090648, 2022H1D3A3A01077468) and core facility program funded by the Ministry of Education (2021R1A6C101B418).

Acknowledgments

We acknowledge financial support from the Ministry of Science and ICT through NRF of the National Research Foundation of South Korea funded by Ministry of Science and ICT (2019R1A2C2090648, 2022H1D3A3A01077468) and core facility program funded by the Ministry of Education (2021R1A6C101B418) for supporting this work. NT-O acknowledges financial support by the Ministry of Science and Higher Education of the Russian Federation (State assignment in the field of scientific activity, Southern Federal University, 2023, Project No. FENW-2023-0015) and AS acknowledges financial support from the Department of Science and Technology in India through the Ramanujan Faculty Award (RJF/2021/000122/SSC). BK acknowledges the funding from Department of Science and Technology, India.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2023.1179651/full#supplementary-material

References

Astrov, D. N. (1960). The magnetoelectric effect in antiferromagnetics. J. Exp. Theor. Phys. 38, 984–985. doi:10.1021/jp000114x

CrossRef Full Text | Google Scholar

Bao, S., Wang, J., Wang, W., Cai, Z., Li, S., Ma, Z., et al. (2018). Discovery of coexisting Dirac and triply degenerate magnons in a three-dimensional antiferromagnet. Nat. Commun. 9, 2591. doi:10.1038/s41467-018-05054-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Bibes, M., and Barthélémy, A. (2008). Towards a magnetoelectric memory. Nat. Mater. 7, 425–426. doi:10.1038/nmat2189

PubMed Abstract | CrossRef Full Text | Google Scholar

Caimi, G., Degiorgi, L., Berger, H., and Forró, L. (2006). Optical evidence for a magnetically driven structural transition in the spin web Cu3TeO6. Europhys. Lett. 75, 496–502. doi:10.1209/epl/i2005-10603-3

CrossRef Full Text | Google Scholar

Cheong, S.-W., and Mostovoy, M. (2007). Multiferroics: A magnetic twist for ferroelectricity. Nat. Mater 6, 13–20. doi:10.1038/nmat1804

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, K. Y., Lemmens, P., Choi, E. S., and Berger, H. (2008). Lattice anomalies and magnetic excitations of the spin web compound Cu³TeO⁶. J. Phys. Condens. Matter 20, 505214. doi:10.1088/0953-8984/20/50/505214

CrossRef Full Text | Google Scholar

Dzyaloshinskii, I. E. (1959). On the magnetoelectrical effect in antiferromagnetics. J. Exp. Theor. Phys. 37, 881–882.

Google Scholar

Falck, L., Lindqvist, O., and Moret, J. (1978). Tricopper(II) tellurate(VI). Acta Crystallogr. B 34, 896–897. doi:10.1107/S0567740878004276

CrossRef Full Text | Google Scholar

Ghosh, S. K., Roy, K., Mishra, H. K., Sahoo, M. R., Mahanty, B., Vishwakarma, P. N., et al. (2020). Rollable magnetoelectric energy harvester as a wireless IoT sensor. ACS Sustain Chem. Eng. 8, 864–873. doi:10.1021/acssuschemeng.9b05058

CrossRef Full Text | Google Scholar

He, Z., and Itoh, M. (2014). Magnetic behaviors of Cu3TeO6 with multiple spin lattices. J. Magn. Magn. Mater 354, 146–150. doi:10.1016/j.jmmm.2013.11.009

CrossRef Full Text | Google Scholar

Herak, M., Berger, H., Prester, M., Miljak, M., Živković, I., Milat, O., et al. (2005). Novel spin lattice in Cu3TeO6: An antiferromagnetic order and domain dynamics. J. Phys. Condens. Matter 17, 7667–7679. doi:10.1088/0953-8984/17/48/017

CrossRef Full Text | Google Scholar

Herak, M. (2011). Cubic magnetic anisotropy of the antiferromagnetically ordered Cu3TeO6. Solid State Commun. 151, 1588–1592. doi:10.1016/j.ssc.2011.07.024

CrossRef Full Text | Google Scholar

Hudl, M., Mathieu, R., Ivanov, S. A., Weil, M., Carolus, V., Lottermoser, Th., et al. (2011). Complex magnetism and magnetic-field-driven electrical polarization of Co3TeO6. Phys. Rev. B 84, 180404. doi:10.1103/PhysRevB.84.180404

CrossRef Full Text | Google Scholar

Hughey, K. D., Lee, M., Nam, J., Clune, A. J., O’Neal, K. R., Tian, W., et al. (2022). High-field magnetoelectric and spin-phonon coupling in multiferroic (NH4)2[FeCl5·(H 2O)]. Inorg. Chem. 61, 3434–3442. doi:10.1021/acs.inorgchem.1c03311

PubMed Abstract | CrossRef Full Text | Google Scholar

Hur, N., Park, S., Sharma, P. A., Ahn, J. S., Guha, S., and Cheong, S. W. (2004). Electric polarization reversal and memory in a multiferroic material induced by magnetic fields. Nature 429, 392–395. 2004. (6990 429), doi:10.1038/nature02572

PubMed Abstract | CrossRef Full Text | Google Scholar

Ivanov, S. A., Ritter, C., Nordblad, P., Tellgren, R., Weil, M., Carolus, V., et al. (2017). New insights into the multiferroic properties of Mn3TeO6. J. Phys. D. Appl. Phys. 50, 085001. doi:10.1088/1361-6463/aa5621

CrossRef Full Text | Google Scholar

Iyama, A., and Kimura, T. (2013). Magnetoelectric hysteresis loops in Cr2O3 at room temperature. Phys. Rev. B 87, 180408. doi:10.1103/PhysRevB.87.180408

CrossRef Full Text | Google Scholar

Kim, J. W., Artyukhin, S., Mun, E. D., Jaime, M., Harrison, N., Hansen, A., et al. (2015). Successive magnetic-field-induced transitions and colossal magnetoelectric effect in Ni3TeO6. Phys. Rev. Lett. 115, 137201. doi:10.1103/PhysRevLett.115.137201

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimura, T., Goto, T., Shintani, H., Ishizaka, K., Arima, T., and Tokura, Y. (2003). Magnetic control of ferroelectric polarization. Nature 426, 55–58. 55 426. doi:10.1038/nature02018

PubMed Abstract | CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshitz, E. M. (1984). “Ferromagnetism and antiferromagnetism,” in Electrodynamics of continuous media (Amsterdam, Netherlands; Elsevier, 130–179.

CrossRef Full Text | Google Scholar

Leo, N., Carolus, V., White, J. S., Kenzelmann, M., Hudl, M., Tolédano, P., et al. (2018). Magnetoelectric inversion of domain patterns. Nature 560, 466–470. doi:10.1038/s41586-018-0432-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, K., Li, C., Hu, J., Li, Y., and Fang, C. (2017). Dirac and nodal line magnons in three-dimensional antiferromagnets. Phys. Rev. Lett. 119, 247202. doi:10.1103/PhysRevLett.119.247202

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Liu, M., Wang, Y., Tian, L., Shi, R., Yang, L., et al. (2018). Magnetoelectric mutual-control in collinear antiferromagnetic NdCrTiO5. Appl. Phys. Lett. 113, 122903. doi:10.1063/1.5047077

CrossRef Full Text | Google Scholar

Li, Y., and Luk, K.-M. (2016). A multibeam end-fire magnetoelectric dipole antenna array for millimeter-wave applications. IEEE Trans. Antennas Propag. 64, 2894–2904. doi:10.1109/TAP.2016.2554601

CrossRef Full Text | Google Scholar

Manipatruni, S., Nikonov, D. E., Lin, C., Gosavi, tanay A., Liu, H., Prasad, B., et al. (2019). Scalable energy-efficient magnetoelectric spin–orbit logic. Nature 565, 35–42. doi:10.1038/s41586-018-0770-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Månsson, M., Prša, K., Sugiyama, J., Andreica, D., Luetkens, H., and Berger, H. (2012). Magnetic order and transitions in the spin-web compound Cu3TeO6. Phys. Procedia 30, 142–145. doi:10.1016/j.phpro.2012.04.059

CrossRef Full Text | Google Scholar

Niu, H., Pitcher, M. J., Corkett, A. J., Ling, S., Mandal, P., Zanella, M., et al. (2017). Room temperature magnetically ordered polar corundum GaFeO3 displaying magnetoelectric coupling. J. Am. Chem. Soc. 139, 1520–1531. doi:10.1021/jacs.6b11128

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Dell, T. H. T. (1970). The electrodynamics of magneto-electric media. North-Holland, Amsterdam: North-Holland.

Google Scholar

Oh, Y. S., Artyukhin, S., Yang, J. J., Zapf, V., Kim, J. W., Vanderbilt, D., et al. (2014). Non-hysteretic colossal magnetoelectricity in a collinear antiferromagnet. Nat. Commun. 5, 3201. doi:10.1038/ncomms4201

PubMed Abstract | CrossRef Full Text | Google Scholar

Owerre, S. A. (2018). Floquet Weyl magnons in three-dimensional quantum magnets. Sci. Rep. 8, 10098. doi:10.1038/s41598-018-28508-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, C. B., Shahee, A., Kim, K., Patil, D. R., Guda, S. A., Ter-Oganessian, N., et al. (2022). Observation of spin-induced ferroelectricity in a layered van der Waals antiferromagnet CuCrP2S6. Adv. Electron Mater 8, 2101072. doi:10.1002/aelm.202101072

CrossRef Full Text | Google Scholar

Ponet, L., Artyukhin, S., Kain, T., Wettstein, J., Pimenov, A., Shuvaev, A., et al. (2022). Topologically protected magnetoelectric switching in a multiferroic. Nature 607, 81–85. 81 607. doi:10.1038/s41586-022-04851-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Rivera, J.-P., and Schmid, H. (1994). Search for the piezomagnetoelectric effect in LiCoPO4. Ferroelectrics 161, 91–97. doi:10.1080/00150199408213357

CrossRef Full Text | Google Scholar

Rivera, J. P. (2009). A short review of the magnetoelectric effect and related experimental techniques on single phase (multi-) ferroics. Eur. Phys. J. B 71, 299–313. 3 71. doi:10.1140/EPJB/E2009-00336-7

CrossRef Full Text | Google Scholar

Shin, K. W., Soroka, M., Shahee, A., Kim, K. H., Buršík, J., Kužel, R., et al. (2022). Observation of anomalously large magnetoelectric coupling in the hexagonal Z-type ferrite films. Adv. Electron Mater 8, 2101294. doi:10.1002/aelm.202101294

CrossRef Full Text | Google Scholar

Smolenskiĭ, G. A., and Chupis, I. E. (1982). Ferroelectromagnets. Sov. Phys. Uspekhi 25, 475–493. doi:10.1070/PU1982v025n07ABEH004570

CrossRef Full Text

Spaldin, N. A., and Ramesh, R. (2019). Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212. 3 18. doi:10.1038/s41563-018-0275-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaknin, D., Zarestky, J. L., Rivera, J.-P., and Schmid, H. (2004). Commensurate-incommensurate magnetic phase transition in magnetoelectric single crystal LiNiPO4. Phys. Rev. Lett. 92, 207201. doi:10.1103/PhysRevLett.92.207201

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D., Bo, X., Tang, F., and Wan, X. (2019). Calculated magnetic exchange interactions in the Dirac magnon material Cu3TeO6. Phys. Rev. B 99, 035160. doi:10.1103/PhysRevB.99.035160

CrossRef Full Text | Google Scholar

Wang, J., Neaton, J. B., Zheng, H., Nagarajan, V., Ogale, S. B., Liu, B., et al. (2003). Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 299, 1719–1722. 1979. doi:10.1126/science.1080615

PubMed Abstract | CrossRef Full Text | Google Scholar

Yanda, P., Ter-Oganessian, N. V., and Sundaresan, A. (2019). Linear magnetoelectric effect in antiferromagnetic Sm2BaCuO5. Phys. Rev. B 100, 104417. doi:10.1103/PhysRevB.100.104417

CrossRef Full Text | Google Scholar

Yao, W., Li, C., Wang, L., Xue, S., Dan, Y., Iida, K., et al. (2018). Topological spin excitations in a three-dimensional antiferromagnet. Nat. Phys. 14, 1011–1015. doi:10.1038/s41567-018-0213-x

CrossRef Full Text | Google Scholar

Yoo, K., Koteswararao, B., Kang, J., Shahee, A., Nam, W., Balakirev, F. F., et al. (2018). Magnetic field-induced ferroelectricity in S = 1/2 kagome staircase compound PbCu3TeO7. NPJ Quantum Mater 3, 45. doi:10.1038/s41535-018-0117-0

CrossRef Full Text | Google Scholar

Zhai, J., Xing, Z., Dong, S., Li, J., and Viehland, D. (2006). Detection of pico-Tesla magnetic fields using magneto-electric sensors at room temperature. Appl. Phys. Lett. 88, 062510. doi:10.1063/1.2172706

CrossRef Full Text | Google Scholar

Zhao, L., Hu, Z., Kuo, C. Y., Pi, T. W., Wu, M. K., Tjeng, L. H., et al. (2015). Mn3TeO6 - a new multiferroic material with two magnetic substructures. Phys. Status Solidi - Rapid Res. Lett. 9, 730–734. doi:10.1002/pssr.201510347

CrossRef Full Text | Google Scholar