Bioinspired acoustic metamaterials: From natural designs to optimized structures

Dal Poggetto, Vinícius F.

doi:10.3389/fmats.2023.1176457

REVIEW article

Front. Mater., 05 April 2023

Sec. Metamaterials

Volume 10 - 2023 | https://doi.org/10.3389/fmats.2023.1176457

This article is part of the Research Topic Acoustic and Mechanical Metamaterials for Various Applications - Volume II View all 8 articles

Bioinspired acoustic metamaterials: From natural designs to optimized structures

Vinícius F. Dal Poggetto*

Department of Civil, Environmental and Mechanical Engineering, University of Trento, Trento, Italy

Artificial structures known as phononic crystals and acoustic metamaterials can be designed by spatially arranging one or more materials to obtain desired wave manipulation characteristics. The combination of various materials in complex composites is also a common feature of biological systems, which have been shaped in the course of evolution to achieve excellent properties in various requisites, both static and dynamic, thus suggesting that bioinspired concepts may present useful opportunities to design artificial systems with superior dynamic properties. In this work, a set of biological systems (nacre composites, spider webs, fractals, cochlear structures, and moth wings) and corresponding bioinspired metamaterials are presented, highlighting their main features and applications. Although the literature on some systems is vast (e.g., fractals), spanning multiple length scales for both structural and acoustic applications, much work remains to be explored concerning other biological structures (e.g., moth wings). Especially, bioinspired systems achieved by considering diverse objectives seem to be a promising yet relatively unexplored field of research.

1 Introduction

Phononic crystals (PCs) and acoustic metamaterials (MMs) are artificially architected structures obtained by spatially arranging one or more different materials to design systems with specific frequency-dependent characteristics (Lu et al., 2009; Deymier, 2013; Hussein et al., 2014; Khelif and Adibi, 2016). The resulting superior control over mechanical waves allows a wide range of applications over several length scales such as wave filtering (Vadalà et al., 2018), waveguiding and splitting (Wang Y-F et al., 2018), non-destructive evaluation (Gliozzi et al., 2019), seismic vibration shielding (Miniaci et al., 2016a), and subwavelength imaging (Sukhovich et al., 2009).

The combination of different materials to design composites, however, is not only observable in synthetic structures, but also commonly occurring in biological systems. Although the single components that form such structures usually present extremely concurrent performance in antagonistic aspects (e.g., stiffness vs. damping), the interplay between distinct components can result in an excellent compromise between these characteristics (Wegst and Ashby, 2004; Chen et al., 2009). Some examples of biological systems where this concept can be observed include spider silk (Cranford et al., 2012), nacre shells (Huang et al., 2014), bone and teeth (Davies et al., 2014), and fish scales (Ikoma et al., 2003). Biological systems often also display hierarchical structuring, in which elements with different characteristic lengths are combined, thus contributing to the enhancement of their mechanical properties (Lakes, 1993). Furthermore, biological systems often display excellent wave attenuation properties, thus indicating that the evolutionary processes found in nature can suggest prompt candidates for the investigation and design of bioinspired systems (Bosia et al., 2022).

Although commonly considered for the design of novel structures in the static and quasi-static regime (Wegst et al., 2015), the concepts observed in biological systems may present inspiration opportunities that can also be used in the design of artificial systems with superior dynamic properties, such as PCs and acoustic MMs. Recent examples include nacre-like composites (Chen and Wang, 2015), spider web-inspired MMs (Miniaci et al., 2016b), diatom- and hub-spoke-inspired hierarchical materials (Miniaci et al., 2018), and cochlea-inspired graded structures (Zhao and Zhou, 2019). Some other noticeable examples include MMs able to manipulate acoustic waves based on bioinspired concepts drawn from aquatic animals, such as sharkskin-inspired MMs that use magnetic stimuli to enable the active switching of acoustic transmission and waveguiding (Lee et al., 2020) and hybrid MMs inspired on the porpoise’s biosonar system designed using composite structures able to achieve underwater broadband transmission directivity (Dong et al., 2019).

Due to the extreme versatility shown by biological systems, the number of design possibilities stemming from different material combinations and spatial distributions becomes endless. Also, additional complications are expected, such as the consideration of simultaneous concurrent properties in the static and dynamic domains (e.g., stiffness and wave attenuation), structures which span multiple length scales due to their hierarchical configuration, and damping owed to the presence of viscosity in many biological components. Such virtually infinite design freedom makes the creation of bioinspired solutions not always obvious since the favorable organization of biological structures is achieved over millions of years through the evolution process. Thus, the design of bioinspired systems envisaging practical applications may require the use of optimization techniques to properly select configurations and parameters that yield the best possible designs, balancing the trade-off between conflicting objectives and incorporating diverse factors.

This literature review provides an overview of the recent advances in the field of bioinspired PCs and acoustic MMs. A brief introduction on the basic concepts regarding wave propagation in periodic lattices is given in Section 2. Specific bioinspired structures are then presented in Section 3, including example systems such as nacre, spider webs, fractals, cochlea, and moth wings. Conclusions and further comments are presented in Section 4.

2 Phononic crystals and acoustic metamaterials

2.1 Bragg scattering and one-dimensional PCs

Mechanical waves (i.e., elastic and acoustic) can propagate while exhibiting typical behaviors of motion (e.g., longitudinal, shear, and flexural), which also depend on the characteristics of the medium in which the wave propagates. The interaction between a wave that is incident upon a boundary or a region of non-uniformity enables diverse phenomena, including scattering, which can be defined as the redirection of energy flux, usually in various directions, due to the presence of non-uniformities (Fahy and Gardonio, 2007). The result of including scatterers is the modification of the dispersion relations between the frequencies (ω) and wave vectors (k) which characterize the mechanical waves propagating in the system.

The analysis of the dispersion relations of mechanical waves propagating in periodic structures dates back to the work of Sigalas and Economou (1992). Later on, the term “phononic band gap” was used by Kushwaha et al. (1993) to refer to frequency regions where no elastic waves are allowed to propagate freely in PCs (i.e., all waves become evanescent), using a terminology derived from analogies with photonic crystals (Yablonovitch, 1994). This seminal work led to the exploitation of the subject of PCs in diverse configurations, such as two-dimensional periodic arrangements of metallic rods (Kushwaha et al., 1994; Kushwaha and Halevi, 1994) and three-dimensional arrays of spherical inclusions (Kushwaha and Djafari-Rouhani, 1996; Kushwaha and Halevi, 1997). Importantly, many complete band gaps (i.e., independent of both the wave polarization and its propagation direction) could be achieved by employing these systems. Complete band gaps may be of particular importance for the manipulation of waves in mechanical systems, where non-trivial polarization characteristics combining distinct behaviors of motion are commonly observed.

The most significant mechanism responsible for the formation of band gaps in PCs is Bragg scattering, which is generated by the destructive interference of waves due to periodically arranged scatterers (Deymier, 2013). Although other mechanisms may also be observed, such as 1) the hybridization between the resonant modes of individual scatterers and the propagating modes of the hosting material and 2) the weak coupling between the resonant states of neighboring scatterers, Bragg scattering remains the fundamental mechanism responsible for the formation of band gaps (Sigalas et al., 2005; Croënne et al., 2011).

An example of a one-dimensional PC with distributed scatterers whose periodicity is given by the unit cell length a is shown in Figure 1A. Consider, for the sake of simplicity, that a one-dimensional propagating wave described as e^i(kx−ωt), where k = 2π/λ is the wavenumber for a given wavelength λ, x is the spatial coordinate, ω is the circular frequency of the wave, and t is the time, impinges on a scatterer. The rate at which this wave propagates is given by the phase velocity, c = ω/k. After being excited by the impinging wave, the scatterer radiates waves in both directions (+x and −x) with a phase difference φ (Figure 1B). If this process is repeated for contiguous scatterers with a distance a from each other, the sum of the waves excited by these scatterers can be written as

e^{i (k x - ω t + φ)} + e^{i (k x - ω t + φ + k a)} = e^{i (k x - ω t + φ)} (1 + e^{i k a}), (1)

which presents its maxima (minima) corresponding to the (constructive) destructive interference conditions for e^ika = +1 (e^ika = −1). These relations lead to the Bragg condition nλ = 2a, $n \in N$ , yielding a = λ/2 as the first minimal spacing capable of resulting in destructive interference.

FIGURE 1

FIGURE 1. One-dimensional PC and Bragg scattering phenomenon. (A) Example of one-dimensional PC composed of scatterers (grey circles) with a unit cell with length a in a matrix material (blue area). (B) Incident wave (black line) on scatterer and subsequent radiated wave (blue line), which is combined with the wave radiated by the contiguous scatterer (red line). (C) Dispersion relation (curves) and Bragg band gap (highlighted region), with distinct branches marked as P₁, E, and P₂. (D) Example of the effect of increasing values of damping (η) on the dispersion curves. (E) Examples of (P₁) positive phase and group velocities (E) spatial decay of waves excited inside the band gap, and (P₂) positive phase velocity and negative group velocity. The colorbar indicates normalized displacements.

The dynamic behavior of periodic systems can be described using partial differential equations with periodic coefficients, whose solutions date back to (Floquet, 1883). The analysis of wave propagation in such media can be performed by employing the Bloch-Floquet theory (Bloch, 1929) to consider periodicity conditions on a representative unit cell, restricting the analyzed wave vectors to the first Brillouin zone (Brillouin, 1953) and analyzing a single unit cell. An example of a dispersion relation (k × ω) is illustrated by the band diagram shown in Figure 1C, with high-symmetry points labeled as Γ (k = 0) and X (k = π/a). The band diagram is divided into the real and imaginary parts of the wavenumber, respectively Re(k) and Im(k), describing the propagating and evanescent behaviors of the wave. The band gap opened due to the Bragg scattering mechanism is also indicated, where only purely evanescent waves exist.

An important characteristic that can also be observed in band diagrams is material damping, which is typically present at the interfaces of the constituents forming biological systems (Barthelat et al., 2016), such as soft proteins in bones (Rho et al., 1998) and the organic phase of nacre (Levi-Kalisman et al., 2001). Figure 1D illustrates the typical effect of increasing the viscosity of one component of the system (η), showing that the previous band gap is no longer distinguishable since there is no region of purely evanescent waves, but rather, all waves present some spatial attenuation, as described by Im(k).

The band diagram shown in Figure 1C can also be used to characterize the propagation velocity of an envelope of combined waves, named group velocity, given by the derivative of each branch with respect to the wavenumber, $c_{g} = \frac{\partial ω}{\partial k}$ (Brillouin, 2013). For the first branch represented in the band diagram (P₁ in Figure 1C), one obtains $\frac{\partial ω}{\partial k} > 0$ , thus indicating a positive group velocity. This result is illustrated in Figure 1E, where the white region presents a forward-moving (+x direction) propagation, as highlighted by the dashed line. Inside the band gap (E in Figure 1C), all waves present a spatial decay, thus not being able to propagate, as shown in Figure 1E. Finally, in the second branch (P₂ in Figure 1C), the obtained group velocity is characterized by $\frac{\partial ω}{\partial k} < 0$ , thus representing backward-moving waves (−x direction), as indicated by the white region and highlighted by the dashed line in Figure 1E.

An immediate application of PCs is the use of the evanescent behavior of waves in the frequency ranges identified as band gaps to achieve a significant spatial attenuation (Laude et al., 2009). Less obvious applications include, for instance, 1) wave guiding obtained using PCs by confining waves in a core or by coupling defects along a given direction (Laude, 2021) and 2) demultiplexing of acoustic waves achieved by combining scatterers with different properties to selectively transport waves at various frequencies (Pennec et al., 2004).

2.2 Local resonance and two-dimensional MMs

Acoustic MMs, on the other hand, are typically characterized by locally resonant phenomena, as proposed in the seminal work of Liu et al. (2000), with many examples found in the literature, including one-dimensional systems based on rods (Xiao et al., 2012c; Nobrega et al., 2016), beams (Xiao et al., 2012a; 2013; Beli et al., 2018), two-dimensional plates with spring-mass resonators (Xiao et al., 2012b; Miranda Jr et al., 2019) or coated inclusions (Xiao et al., 2008; Dal Poggetto and Serpa, 2021), and three-dimensional structures (Mitchell et al., 2014; Dal Poggetto and Serpa, 2020). The use of unit cells with locally resonant structures also justifies the alternative denomination of locally resonant PCs. In this type of structure, Fano-like interference is employed to open band gaps in the sub-wavelength regime (Goffaux et al., 2002), thus yielding band gaps at much lower frequencies (even orders of magnitude) than those compared to the expected when using Bragg scattering band gaps, which are associated with the lattice constant. The resulting local resonance-based band gaps also present as a noticeable characteristic a low group velocity (i.e., $\frac{\partial ω}{\partial k} \approx 0$ ), thus leading to a practically wavelength-independent behavior.

The possible effects stemming from the use of locally resonant PCs are not restricted to energy trapping in the sub-wavelength elements (Colombi et al., 2014), and can be used to yield unusual effects such as negative refraction (Pendry, 2000) and double-negative effective properties (Li and Chan, 2004). When strategically placed on plates or surfaces, the locally resonant elements can be used to design metasurfaces (Colombi et al., 2017b) and metalenses (Colombi, 2016). The use of locally resonant structures is also characterized by a superior degree of tunability, thus leading to excellent wave control capabilities (Aguzzi et al., 2022) and a wide range of applications, ranging from the ultrasonic range (Colombi et al., 2017a) to large-scale seismic applications (Krödel et al., 2015; Miniaci et al., 2016a).

In the case of waves propagating in two-dimensional media, dispersion relations become more intricate when compared to the one-dimensional case, since the wave vector presents a second order dimension, thus resulting in relations that represent dispersion surfaces. Consider, for instance, a two-dimensional medium with distributed scatterers whose periodicity is described by the lattice vectors a₁ and a₂, shown in Figure 2A as a square lattice for illustration purposes (i.e., $a_{1} = a \hat{i}$ and $a_{2} = a \hat{j}$ , where $\hat{i}$ and $\hat{j}$ denote the x- and y-direction unit vectors). An example of a dispersion surface is shown in Figure 2B, represented by contour lines restricted to {k_x, k_y} ∈ [−π/a, π/a], where k_x and k_y represent the Cartesian components of k. In this case, the group velocity is defined as $c_{g} = \frac{\partial ω}{\partial k_{x}} \hat{i} + \frac{\partial ω}{\partial k_{y}} \hat{j}$ , which represents the gradient of the dispersion surface.

FIGURE 2

FIGURE 2. Two-dimensional periodic media and typical dispersion relations. (A) Example of a PC with direct lattice vectors a₁ and a₂, with (B) its first dispersion surface spanning the first Brillouin zone for a square lattice, {k_x, k_y}∈[−π/a, π/a], showing the high-symmetry points given by Γ (0,0), X (π/a,0), and M (π/a, π/a), and (C) the corresponding band diagram obtained using the contour of the irreducible Brillouin zone (ΓXMΓ path). (D) Locally resonant structures (pillars) embedded in a square lattice with the (E) corresponding band diagram showing propagating waves (blue lines), evanescent waves in specific direction (red lines), and a highlighted local resonance band gap.

Notice also that, due to the symmetry of the dispersion surface, it is a common practice to characterize the dispersion relations by considering the lines connecting the high-symmetry points which form the contour of the irreducible Brillouin zone (Γ (0,0), X (π/a, 0), and M (π/a, π/a), in the case of a square lattice), thus considerably reducing the computational effort required to calculate the dispersion relation of the periodic medium for various types of lattices (Maurin et al., 2018). This procedure leads to band diagrams as shown in Figure 2C. Alternatively, an example of a two-dimensional square lattice with embedded locally resonant structures is illustrated in Figure 2D. In this case, a typical band diagram is shown in Figure 2E, for both real and imaginary parts (for the specific directions ΓX and ΓM) of the wave vector, with a highlighted local resonance band gap indicating a low group velocity (flat band) for a large portion of the wave vector.

Although the literature on the mechanisms for wave manipulation using PCs and acoustic MMs is vast, including examples of wave conversion (Chaplain et al., 2020; De Ponti et al., 2021), scattering (Yang et al., 2016; Cao et al., 2021), cloaking (Farhat et al., 2008; 2009), and topological effects (Mousavi et al., 2015; Foehr et al., 2018), the literature on bioinspired structures concerning their dynamic properties, and in special, wave manipulation and the effects of viscoelasticity, which are certainly relevant for biological structures, is considerably more restrict. Thus, in the next section, a literature review is presented on different bioinspired PCs and acoustic MMs.

3 Bioinspired structures

3.1 Nacre

Nacre (or mother-of-pearl) is an organic-inorganic platelet-reinforced composite material whose mechanical properties are fundamental for the toughness of mollusk shells (Jackson et al., 1988). The nacre structure is composed of a ceramic mineral (calcium carbonate) in the form of aragonite platelets separated by elastic biopolymer interfaces, forming a brittle structure connected by thin organic layers (Gim et al., 2019) (see Figure 3A). The resulting brick-and-mortar structure (see Figure 3B) can be arranged in a variety of microstructures (Barthelat, 2010), with an interplay between components resulting in superior energy dissipation when subjected to dynamic loadings (Huang et al., 2014).

FIGURE 3

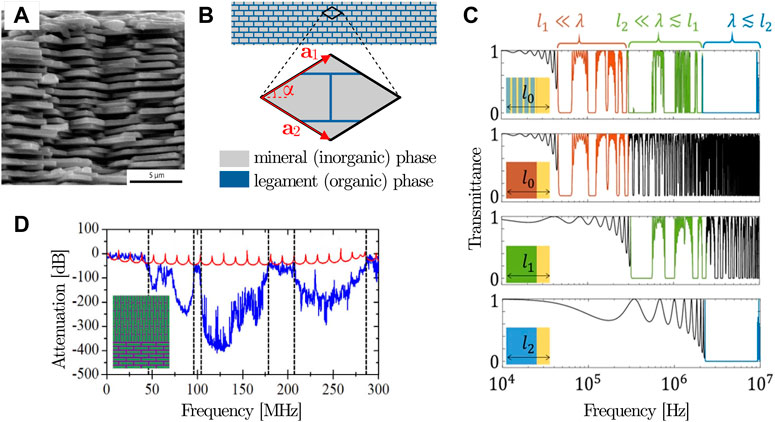
FIGURE 3. Nacre structure and associated bioinspired PC applications. (A) Cross-section of nacre showing the brick-and-mortar microstructure [adapted from (Ferrand, 2022)]. (B) Example of a brick-and-mortar periodic structure with an inset representing the hexagonal lattice unit cell (angle α between the basis vectors) with both inorganic (hard, in grey) and organic (soft, in blue) phases. (C) Transmittance profile for a hierarchical PC (first row) and corresponding homogenized structures (second to fourth rows), with l₀≫ l₁≫ l₂ [adapted from (Lee and Jeon, 2020)]. (D) Attenuation relative to a finite structure obtained by combining lattices with different orientations [adapted from (Chen and Wang, 2015)].

Yin et al. (2014) have demonstrated the existence of wide low-frequency band gaps in nacreous composites using a one-dimensional tension-shear chain model for the brick and mortar structure, considering aluminum (brick) and silicone rubber (mortar) material properties, computing the band diagrams with the transfer matrix method. The nth band gap relative width was used to quantify a normalized metric, defined as

Δ {\bar{ω}}_{n} = \frac{w_{n, u} - w_{n, l}}{(w_{n, u} + w_{n, l}) / 2}, (2)

where w_n,l and w_n,u denote, respectively, the lower and upper frequencies of the nth complete band gap. Using this metric, the authors have calculated a relative band gap width of 0.486 for the first band gap (301.95–495.79 Hz), thus indicating a significantly wide frequency region. These results were later used in (Yin et al., 2015) to design two- and three-dimensional nacreous PCs which can be tuned to manipulate the opening of band gaps, demonstrating a relative band gap width of 1.388 (84.42–467.57 Hz) for the 3D case, with a strong reduction in the transmission coefficient for both longitudinal and transverse excitation directions. The robustness of the obtained band gaps in these systems was also assessed in (Yin et al., 2016) against various types of defects. Point and line defects were modeled by considering smaller specific mass density and elastic constants in selected “brick” (hard phase) elements, showing that the first computed band gap is relatively insensitive to both types of defects. On the other hand, a considerable narrowing of the existing band gaps was observed when cracks are introduced by removing “mortar” (soft phase) elements, thus highlighting the fundamental role of the soft matrix connecting the hard phase elements.

Zhang and To (2013) have demonstrated that a multilayered hierarchical bioinspired PC obtained by alternating a hard material with soft layers in one dimension (considered, respectively, as hydroxyapatite and protein) is able to achieve a broadband wave filtering effect. The reflectance spectra of incident P-waves (longitudinal) was evaluated for increasing levels of hierarchy (n), using the nth level unit cell as a building block for the (n + 1)-th level. Reflectance levels close to 1 (and thus, corresponding to band gap regions) were computed for n = 1 in the 4 × 10¹⁰–2 × 10¹¹ rad/s frequency region, while for n = 2 the lower edge is set at 5 × 10⁹ rad/s, and for n = 3, at 6 × 10⁸ rad/s. The resulting superposition of adjacent band gaps is able to attenuate incident waves over two decades, ranging from $\sim 1 0^{9}$ rad/s to $\sim 1 0^{12}$ rad/s, thus demonstrating the broadband effect achieved using hierarchical structuring. Later, Lee and Jeon (2020) investigated these findings with the support of a homogenization theory to consider wavelengths at diverse hierarchical levels in a one-dimensional PC composed of aluminum (hard phase) and polydimethylsiloxane (soft phase). The authors confirmed that the band gaps emerging from the non-homogenized structure can be regarded as the union of band gaps stemming from each hierarchical level, corresponding to different wavelengths. The superposition of band gaps, however, cannot be observed if the homogenization of structures with smaller features are considered (see Figure 3C, where l₀ ≫ l₁ ≫ l₂ represent the unit cell lengths at each hierarchical level), thus representing a significant computation limitation for the investigation of hierarchical structures.

Chen and Wang (2014) have proposed a periodic composite considering a two-dimensional rhombic lattice formed by staggered mineral platelets embedded in an organic matrix. Complete band gaps due to both Bragg scattering and local resonances are observed, leading to multiple band gaps, which can be tuned by engineering the length scale and arrangement of the mineral platelets. For a fixed 90% volume fraction of the platelets, multiple band gaps exist for unit cells with small lattice angles (i.e., the angle between the lattice vectors, α in Figure 3B), while wide single band gaps exist for large lattice angles. A remarkable band gap with a normalized width of 1.11 is obtained for α = 30^o. The combination of platelet layers in an organic matrix following distinct orientations relative to each other (see Figure 3D) was also shown to yield broadband effects (Chen and Wang, 2015) due to the superposition of wide attenuation zones in three regions (46–96 MHz, 104–179 MHz, and 207–285 MHz) obtained from the combination of attenuation regions associated with layers having distinct orientations (46–179 MHz and 104–285 MHz). In this case, local resonance band gaps dominate the band diagrams, with a high degree of localization in the organic phase.

The effect of matrix viscosity on the wave attenuation of nacre-like composites was investigated by Liu et al. (2020) using a dynamic shear-lag model. By defining a dimensionless frequency $\bar{ω} = ω / λ c$ , where $λ = \sqrt{2 G / E h b}$ relates the shear modulus G, Young’s modulus E, and geometric parameters bh, and $c = \sqrt{E / ρ}$ is the longitudinal wave velocity for a specific mass density ρ, the authors indicate that the viscosity present in the elastic matrix materials may be used to enhance the wave attenuation in the low-frequency regime, $\bar{ω} < 1$ , but hinders wave attenuation for excessively large viscosity values. A viscoelastic model was used in (Lu et al., 2022) to consider the sacrificial bond behavior for the organic matrix phase and investigate longitudinal elastic waves propagating in nacre-like materials. The shear-lag model was used to simulate the deformation of the brick-and-mortar structure, revealing that the attenuation in the low-frequency range is given by the combined effects of both shear stiffness and viscosity, while in the high-frequency range it is dominated by viscosity, with a transition between these regimes occurring around a cut-off frequency.

3.2 Spider webs

Spider webs are natural structures able to transmit vibrations efficiently (Masters and Markl, 1981) and have long been the subject of investigation in many fields of knowledge (Greco et al., 2021). Orb webs, in particular, help the spider to discriminate vibration sources and localize prey impacts (Dal Poggetto et al., 2022a; Lott et al., 2022), acting as an outsourced hearing structure in orb-weaving spiders (Zhou et al., 2022). The prey localization objective is concurrent with other requisites, such as the absorption of kinetic energy (Sensenig et al., 2012), thus suggesting that spider webs are natural multifunctional structures. The diversity in the composition of the different types of silk used by the spiders to build webs also allows a wide range of mechanical properties (Arakawa et al., 2022). Their resulting versatility has led to the emergence of many spider web-based applications in the past years, such as stress-sensitive silk for soft robotics (Spizzo et al., 2022) and hybrid biomaterials for bone tissue engineering applications (Dellaquila et al., 2020). Spider dragline silk has also been shown to possess an indirect hypersonic phononic band gap and a negative group velocity region (Schneider et al., 2016), thus suggesting that this type of material can also be used as a means to control the flow of phonons, serving as tunable heat management devices (Su and Buehler, 2016).

Spider orb webs have shown to be a fruitful source of inspiration to design structures able to achieve wave controlling characteristics. Miniaci et al. (2016b) have numerically designed a spider web-inspired structure using a beam square lattice based on the Nephila orb web architecture (Klärner and Barth, 1982). The proposed structure (see Figure 4A) considers a square lattice with length a, size of square joints b, thickness of ligaments c, and radius of the Nth ring resonator given by R_N, made of a supporting frame (primary, radial elements) and concentric secondary circular elements. For a 10/1 ratio between the Young’s modulus values of the primary (radial) and secondary (circular) frame elements and a unit cell length of 1 m, locally resonant band gaps are opened below 400 Hz for the in-plane (longitudinal and shear behaviors), regardless of the material properties (larger or smaller Young’s modulus) assigned for the circular elements, suggesting a high degree of tunability to achieve localized modes. Preferred directions of propagation (θ = 0 and θ = 90^o, i.e., +x and +y directions of the square lattice) are also revealed, thus indicating a strong anisotropic behavior.

FIGURE 4

FIGURE 4. Spider web-inspired PCs and MMs. (A) MM with an external frame supporting radial and circumferential ligaments [reprinted from (Miniaci et al., 2016b), with the permission of AIP Publishing]. (B) Spider web-inspired hexagonal lattice obtained from the repetition from the unit cell, highlighted by dashed red lines, with radial (red continuous lines) and spiral-like elements (blue lines); the inset represents the possibilities of tuning in the unit cell, i.e., the cross-section of elements and included point masses [adapted from (Dal Poggetto et al., 2021) with permission from Elsevier]. (C) Labyrinthine acoustic MM composed of solid aluminum walls and air, respectively shown in blue and purple [adapted from (Krushynska et al., 2017)]. (D) Membrane-type acoustic MMs with a thin film fixed to a circumferential substrate and additional fixed elements [adapted from Huang et al. (2021)].

Sepehri et al. (2020) have expanded this concept by introducing spider web-inspired hierarchical structures in hexagonal lattices, thus facilitating the opening of locally resonant band gaps in close frequency ranges, with a second band gap opened in the frequency range equal to 1.39–1.51 times the fundamental resonant frequency of the considered beams. Also based on the exploitation of locally resonant band gaps, Zhao et al. (2022) have proposed tunable spider web-inspired resonators, showing that multiple locally resonant band gaps can be achieved by increasing the fractal order of the structure. In this case, however, an increase in the fractal order simply corresponds to an increase in the number of elements attached to the radial structures (similar to the circumferential elements in Figure 4A), in which case, locally resonant features are introduced. Ruan and Li (2022) have also considered the role of hierarchy for octagonal, hexagonal, and quadrilateral unit cells, investigating the influence of temperature in a unit cell containing two materials with contrasting thermal expansion coefficients. In this case, the band gaps relative to the first and second modes, which lie respectively in the ranges 322.79–1,026.90 Hz and 321.91–1,025.97 Hz for an ambient temperature of 20°C, shift to 302.78–913.84 Hz and 304.29–934.20 Hz, respectively, for 200°C. Examples of applications of spider web-inspired PCs can also be found in reduced length scales. Bao et al. (2019) presented a spider web-inspired single-phase system with a complete band gap having a normalized band gap width of 20.9% able to reduce the energy dissipation in micro-electro-mechanical resonator systems, increasing its Q-factor by a 12.2-fold with the application of the bioinspired solution.

A systematic approach for the design of spider web-inspired PCs was also proposed by Dal Poggetto et al. (2021). In this case, hexagonal periodic lattices were developed considering a single material in two distinct dispositions, namely, radial and viscid threads (represented as the red and blue lines, respectively, in Figure 4B). The unit cell was tuned by considering the variation of the circular cross section of the threads and the inclusion of point masses in the crossings between radial and viscid threads (red inset, Figure 4B), obtaining a system with a rich dynamic behavior which presents both Bragg scattering and local resonance band gaps. Optimization processes were employed to obtain various resulting structures considering distinct optimization objectives such as 1) maximizing the normalized band gap width, 2) attenuating a fundamental frequency and/or its harmonics, 3) maximizing the decoupling between in- and out-of-plane modes, and 4) creating isolated Dirac cones (Miniaci and Pal, 2021). The objective 1) was used to validate the approach, obtaining a normalized band gap width of 38.5%; objective 2) was used to either achieve a band gap at the fundamental frequency of 2000 Hz or at the fundamental frequency and its harmonics, {2000, 4,000, 6,000} Hz, respectively, thus demonstrating that multiple band gaps can be opened at will; objective 3) was used to fully decouple distinct polarization modes in the 350–1750 Hz, 2,100–4,550 Hz, and 6,300 Hz–7000 Hz frequency ranges; finally, isolated Dirac cones were created considering two distinct bands, at approximately 3,000 and 4,500 Hz, to verify the validity of objective iv). Importantly, the proposed objective functions are general and in theory can be applied to any periodic system with a sufficient degree of tunability.

Finally, spider web-inspired MMs have also been explored for sound control applications. In (Krushynska et al., 2017), labyrinthine acoustic MMs (Zhang and Hu, 2016) were proposed to achieve efficient subwavelength sound control stemming from multiple resonant modes associated with the characteristic architecture of a spider web-inspired configuration. A typical unit cell is proposed (see Figure 4C, where solid aluminum walls and air are represented in blue and purple, respectively), with parameters given by the unit cell length a, wall thickness d, wall spacing h, internal radius r, external wall length l, and radius of the nth wall given by r_n. The obtained dispersion diagrams present subwavelength band gaps with flat bands (near-zero group velocity) associated with pressure distributions typical of Mie monopole and multipole resonances. The normalized frequency (Ω = ωa/2πc, where a is the lattice length and c is the speed of sound in air) is used to indicate typical resonances of the monopole and dipole pressure distributions, found in the 0.168–0.186 and 0.331–0.379 normalized frequency ranges, with a normalized absolute pressure reduction of up to 10^–5 for a configuration of 5 contiguous unit cells.

Membrane-type acoustic MMs were also proposed by Huang et al. (2021) as an alternative to achieve low-frequency sound attenuation in wide frequency ranges. Two models for the bioinspired resonators were proposed using polyimide thin films as a substrate fixed to a circumferential boundary, with additional elements attached to the membrane to represent the crossings of radial and circumferential elements typical of spider orb webs (see Figure 4D). The proposed models, namely, I and II, present a different number of inclusions in the membrane, with model II showing a larger number of elements when compared to I. Experimental tests for the sound isolation performance are conducted up to 3,000 Hz using an acoustic impedance tube to confirm the numerical predictions, showing that the computed anti-resonance modes can localize the vibration energy and thus yield significant sound transmission loss levels over a relatively broad bandwidth. Although model I presents a slight decrease in the peak sound transmission loss (45.4 dB) when compared to the reference solution (46.5 dB), a significant weight reduction (47%) is also reported when compared to the reference model weight. In the case of model II, a slight increase in the sound transmission loss peak is reported (49.2 dB), showing also a 305 Hz increase in the low-frequency bandwidth (within 1,600 HZ) where an attenuation of at least 10 dB is achieved, and a slight weight reduction (19%) when compared to the reference model. The applications the concerning use of spider web-inspired membranes are not only restricted to sound attenuation, as Rostam-Alilou et al. (2021) have demonstrated using a structure which consists of a composite hydrogel substrate with embedded filaments with silk properties. The resulting microscale structure, whose pressure-induced motion are compared against those of a humane tympanic membrane, show a generally good correlation below 1,000 Hz, suggesting its potential applications as tympanic membrane grafts.

3.3 Fractals

Fractal structures are a recurrent feature found in nature (Mandelbrot, 1982), which typically exhibits self-similar topology at various length scales (Meakin, 1990), thus characterizing themselves as hierarchical structures. Fractals have long been under investigation in diverse fields of knowledge, such as non-linear dynamics (Aguirre et al., 2009), granular materials (McDowell et al., 1996), and telecommunications (Gianvittorio and Rahmat-Samii, 2002). Also, fractals have been widely explored for the development of photonic crystal subwavelength phenomena (Wen et al., 2002), waveguides (Monsoriu et al., 2005), and topological insulators (Yang et al., 2020), thus motivating its exploitation in PC structures.

Kuo and Piazza (2011) presented the design and numerical testing of a microscale fractal structure in aluminum nitride. The proposed design (Figure 5A, where the unit cell has a length a, thickness d, the central square has a side length c, and the additional squares have a side length s) extends the frequency of operation of the phononic band gaps for a fixed unit cell length and minimum feature size (a = 5 μm, d = 1 μm, c = 2 μm, and s = 1.5 μm). Two band gaps were obtained for the ΓX direction in the high-frequency range, centered at 900 MHz and 1.10 GHz, with normalized band gap widths of 11.1% and 9.1% and a maximum attenuation of 40 dB. Norris et al. (2008) considered the effect of periodic fractal-shaped inclusions in two-dimensional PCs composed of a solid matrix with either solid or fluid inclusions, comparing distinct fractal structures with increasing fractal dimensionalities. In the case of solid-fluid systems (aluminum matrix and mercury inclusions), the frequency response presented an increase in the number of attenuation bands upon an increasing fractal dimensionality. In the case of solid-solid systems (silicon matrix, tungsten or nickel inclusions), changes in the fractal dimensionality did not result in significant changes in lower frequencies, with subtle variations in higher frequencies.

FIGURE 5

FIGURE 5. Fractal-like PCs and MMs. (A) Fractal-like square unit cell with a length of a, thickness d, and square features of dimensions c and s [reprinted from (Kuo and Piazza, 2011), with the permission of AIP Publishing]. (B) Sierpinski equilateral triangles with increasing fractal orders n. (C) Sierpinski carpet with increasing fractal orders n and unit cell length a, where the squares included in each new hierarchical order have a side length of a/3ⁿ⁺¹. (D) Labyrinthine acoustic MM unit cell (one-quarter represented, F indicates the rotational symmetry of the unit cell), with light blue parts representing solid plates with a unit cell length b and thickness t, while white regions represent air; for the regular structure (n =0) the characteristic lengths are given by d₁ and l₁; for the first (second) hierarchical order n =1 (n =2), structures with a length l₂ (l₃) are included, as shown in red (yellow) [adapted from Liu et al. (2018)].

Sierpinski fractals (Sierpinski, 1916) have also been explored as possible self-similar fractal solutions for the design of PCs. In (Wang et al., 2016; Wang K et al., 2018), Sierpinski equilateral and isosceles triangles (see Figure 5B, where n is the fractal order) were used to investigate the effects of fractal hierarchy and porosity in the band structures of the resulting porous PCs. Using an aluminum solid phase and considering in-plane behavior, the authors showed that when compared to the ordinary case, fractal structuring increases the critical porosity (area ratio of vacuum/solid phase) necessary for the opening of complete band gaps, also decreasing their central frequencies; on the other hand, an increase in the order of hierarchy for the same porosity increases the band gap central frequency.

In (Huang et al., 2017a), periodic structure waveguides were designed using Sierpinski carpet unit cells (see Figure 5C, where a is the unit cell length, and elements included in the nth hierarchical order have a side length of a/3ⁿ⁺¹) considering the in-plane behavior in periodic media composed by square lead cylinders in a rubber matrix. Using the normalized frequency Ω = ωa/2πc_t, where c_t is the speed of transverse waves in the matrix material, the authors have demonstrated band gaps in the normalized frequency ranges of 0.753–0.825 for the first hierarchical level (single inclusion per unit cell), 2.300–2.653 and 3.706–3.882 for the second hierarchical level, and 2.288–2.350 and 2.434–2.508 for the third hierarchical level, thus revealing that the interplay between the increasing number of scatterers and the matrix leads to a complex band gap formation pattern, which is counter-intuitive with the notion of larger band gaps for larger filling fractions. Also, the directional propagation characteristics in this type of structure were analyzed through the computation of group velocities. The authors have shown, for instance, that in the frequency Ω = 0.580, the wave propagation is confined to the x- and y-directions for the first and third hierarchical orders, thus indicating the use of these structures as waveguides, while a strong reflection was observed for the second hierarchical order, due to a negative group velocity. The tunability of this type of structure was later on investigated in (Huang et al., 2017b), with the relaxation of the initial Sierpinski carpets to quasi-Sierpinski carpets by varying the filling fraction of the scatterers. The authors have demonstrated that quasi-Sierpinski structures present a higher degree of tunability, being able to open band gaps in the low-frequency range for the first hierarchical order, and multiple wide band gaps in higher frequency ranges for the second and third hierarchical orders. Interestingly, for some specific configurations, only low group velocity bands appear for Ω > 3 in second- and third-order fractals.

In (Dal Poggetto et al., 2022b), the authors have used Sierpinski carpets to compute the out-of-plane wave propagation in plate structures considering the Mindlin-Reissner theory (Bathe and Dvorkin, 1985) and the presence of viscoelastic components using a Kelvin-Voigt model (Ferry, 1980; Lakes, 2009; Krushynska et al., 2021). Increasing levels of hierarchy were evaluated, combining a pixel-based approach to describe the plate geometry and the extended plane wave expansion method (Miranda Jr et al., 2022) to consider a frequency-dependent viscoelastic behavior. The evanescent behavior of waves was investigated for media composed of hard elastic (lead) and soft viscoelastic (rubber) phases, with constituents arranged as either 1) a hard elastic matrix with soft viscoelastic inclusions or 2) a soft viscoelastic matrix with hard elastic inclusions. Locally resonant modes are typically noticed in 1), whose associated flat bands remain practically unchanged upon an increase in the hierarchical order, which can then be regarded as a weight reduction approach (since dense matrix material is substituted by light inclusions). Also, in this case, an increase in the considered viscosity of the soft inclusions indicate a reduction in the attenuation peaks associated with the locally resonant modes. On the other hand, Bragg scattering band gaps are noticed in 2), which are drastically changed upon an increase in the considered hierarchical order, although not in a monotonic trend (i.e., previously opened band gaps may disappear). For this configuration, an increase in the viscosity of the components indicates a general increase in wave attenuation.

Fractal structures have also been successfully used in acoustic applications. Liu et al. (2018) have proposed labyrinthine acoustic MMs using planar structures containing self-similar zigzag channels (see Figure 5D for a representation of a quarter of each unit cell), considering a hierarchical structuring scheme where the zero-th order structure (n = 0) shows a unit cell with a side length of b = 90 mm, thickness t = 2 mm, and dimensions l₁ = 32 mm and d₁ = 14 mm, with the solid parts made of lead. In the first (n = 1) and second (n = 2) hierarchical orders, structures with dimensions of l₂ = 12.8 mm and l₃ = 4.8 mm are introduced, respectively (indicated in red and yellow in the schematic), thus introducing a coiled path in which sound waves must propagate. Several types of lattices are considered, namely, 1) square, 2) centered square, 3) triangular, 4) hexagonal, and 5) Kagomé lattices. Considering frequencies in the 0–2000 Hz range, the total proportion of the band gaps can be summarized, for the hierarchical orders n = 0, n = 1, and n = 2, respectively as 1) 15.8%, 31.3%, and 17.6%, 2) 18.7%, 29.9%, and 34.6%, 3) 29.2%, 40.9%, and 41.1%, 4) 17.6%, 43.6%, and 42.1%, 5) 21.4%, 51.7%, and 62.3%, indicating that, in general, an increase in the fractal hierarchical order widens the band gaps in the considered frequency range. The first band gap, in each case, is opened, for increasing hierarchical orders n = 0, n = 1, and n = 2, respectively at 1) 658.8 Hz, 305.2 Hz, and 146.3 Hz, 2) 653.1 Hz, 307.9 Hz, and 133.8 Hz, 3) 637.9 Hz, 309.6 Hz, and 150.6 Hz, 4) 799.6 Hz, 305.6 Hz, and 150.7 Hz, 5) 472.4 Hz, 293.1 Hz, and 149.7 Hz, thus indicating that an increase in the hierarchical order leads to the opening of band gaps in decreasing frequencies.

Another type of fractal structure successfully applied to acoustic MMs is the Hilbert curve (Hilbert, 1891). Song et al. (2016) have demonstrated, both numerically and experimentally, that Hilbert fractal acoustic MM absorbers with hierarchical orders ranging from 1 to 4 are able to attenuate low-frequency sounds. The largest characteristic dimension of each hierarchical level is given, respectively, by 4.4 mm, 12.4 mm, 28.4 mm, and 60.4 mm, presenting sound transmission loss levels above 10 dB for the 225 Hz–1,175 Hz frequency range in a planar waveguide experiment. In (Zhao et al., 2018), the authors showed that transmission coefficient at the resonant frequencies in this type of structure is greatly weakened due to viscothermal losses, thus indicating Hilbert-based fractal acoustic MMs as broadband sound insulation devices.

3.4 Cochlea

The cochlea is a coiled structure present in the auditory system of mammalians that acts as a sensing organ capable of distinguishing wide frequency (nearly ten octaves) and amplitude ranges (up to 120 dB) (Robles and Ruggero, 2001; Dallos and Fay, 2012). One of the most fascinating features of the cochlea is its tonotopic organization, which enables the detection of sound waves based on their frequency content due to its mechanotransduction characteristic responsible for converting sound energy into neural impulses depending on the different locations of excitation (Lighthill, 1991; LeMasurier and Gillespie, 2005). As a consequence, the spatial discrimination of waves based on their spectral content may present an opportunity as a paradigm for sensing applications (Pennec et al., 2019).

The cochlea can be regarded as a coiled long tube filled with fluid and divided into two cavities by the cochlear partition, which supports the basilar and tectorial membranes. Impinging sound waves elicit acoustic waves in the fluid, which in turn excites the basilar membrane, stimulating motion receptor cells (Reichenbach and Hudspeth, 2014). Ma et al. (2014) have designed a spiral structure with 2.7 turns (similar to the human cochlea) to mimic the behavior of the complex cochlea structure, which acts as a spiral locally resonant structure. The proposed structure (see Figure 6A) presents a radius of 2 mm at the apex (top) and 4 mm at the base (bottom), a width of 1.8 mm at the apex and 3 mm at the base, with an internal membrane having a thickness of 10 μm at the apex and 30 μm at the base, and an overall length of 32 mm, presenting resonant frequencies ranging from approximately 20 Hz, close to the base, to approximately 20 kHz at the apex. The resulting structure also presents a negative dynamic effective mass characteristic. In another study, Ma et al. (2016) proposed a bioinspired MM based on the outer hair cells of the mammalian cochlea. Unlike the usual approach of developing materials with a tonotopic configuration, the objective of the proposed structure is to act as an acoustic MM with negative effective dynamic properties (Fang et al., 2006; Yang et al., 2008), presenting low-frequency bending wave band gaps in the 21–76 Hz and 57–173 Hz ranges.

FIGURE 6

FIGURE 6. Systems mimicking cochleas and tonotopic properties. (A) Spiral locally resonant structure mimicking the cochlea (left), with a highlighted region corresponding to the maximum vibration in the membrane for a given frequency excitation (right) [reprinted from (Ma et al., 2014), with the permission of AIP publishing]. (B) Cochlea-inspired resonator with controlled curvature, width, and thickness variations (left). The out-of-plane vibration modes of this structure present a shift in their maxima from the outer to the inner region of the spiral along the centerline for increasing excitation signal frequencies (right) (Dal Poggetto et al., 2023). (C) Spiral array of graded Helmholtz resonators [adapted from (Zhao and Zhou, 2019)]. (D) Line array of graded quarter-wavelength resonators [adapted from (Rupin et al., 2019)]. (E) Array of graded resonators along the x direction with varying properties contrasting with the background (medium) properties.

In (Dal Poggetto et al., 2023), the authors have proposed the systematic design of a cochlea-inspired structure that acts as a tonotopic resonator (see Figure 6B). A logarithmic spiral model is employed to yield a curved structure that presents prescribed values of coiling, width, and thickness variations. Through an optimization procedure that maximizes the spatial separation of the maxima of out-of-plane vibration modes along the spiral centerline, the authors have demonstrated the tonotopic features of the structure using both numerical simulations and experiments. By attaching the proposed structure to a small platform to which out-of-plane excitations were applied through a piezoelectric actuator, the tonotopy of the structure was verified by scanning the vibrations at the centerline of the structure with a laser vibrometer, showing that for a range of nearly 2 decades (from $\sim 100$ Hz to $\sim 10$ kHz), the maxima of out-of-plane vibration modes increasingly move from the outer position to the center of the cochlea as the excitation frequency increases. Examples of sensing applications were also discussed, demonstrating the detection of single- and multiple-frequency excitation signals through the monitoring of distinct points in the structure.

The use of graded arrays of subwavelength resonators is common in the context of MMs to produce the rainbow trapping effect (Zhu et al., 2013), which is able to spatially separate impinging waves based on their frequency content (Bennetts et al., 2018). In (Zhao and Zhou, 2019), the authors have proposed a cochlea-inspired spiral tube with a series of Helmholtz resonators arranged at subwavelength intervals (see Figure 6C). The spiral curve is described mathematically using the polar coordinates (r, θ) as x = rθ cos(θ) and y = rθ sin(θ), with r = 20 mm, and θ in the 0–2.1π range, yielding a total length of 0.3 m, coiled within an area of 0.1 × 0.1 m². The resonators are periodically placed every 7 cm, with a neck of 0.7 mm radius and 4 mm length, and a cavity of 2.5 mm radius and an increasing length, starting from 1 mm (first cylinder) to 15 mm (40-th cylinder). Locally resonant band gaps are opened between the first and second branches of each respective resonator, which produce a gradient in the group velocity due to the increasing height of the resonators. Numerical analyses were performed to show that the number of elements with significant acoustic pressure decrease with an increase in the frequency of the excited pressure wave in the 1–10 kHz range. The proposed MM was experimentally tested to confirm the numerical calculations, demonstrating the expected behavior for the frequencies of 1, 2, 3, and 4 kHz.

Later on, Karlos and Elliott (2020) proposed a bio-inspired design using Helmholtz resonators following a design strategy with the objective of achieving a smoothly varying response, yielding an exponential frequency distribution along the resonators. A sufficient number of elements per wavelength must be considered in the direction of propagation for the discrete system to accurately approximate the desired continuous waveguide. In this case, 6 elements were considered for the smallest wavelength. A tonotopic mapping of the form f_n(x) = f_B e^−x/l, where f_B is the natural frequency of the base, x is the waveguide longitudinal coordinate, and l is the lengthscale of the exponential decrease in frequency, which can be approximated as $f_{1} (n) = f_{B} e^{- (n - 1) l_{D} / l}$ , where f₁(n) is the first natural frequency of the nth element and l_D is the element length, which estimates the distribution of elements per octave. An example system is designed in the 300–3,400 Hz frequency range (width of 3.5 octaves), using a total of 50 elements, with a variation in the quality factor from 5.2 to 17.5. Numerical computations were used to predict the variation of the acoustic pressure along the waveguide for three different frequencies (0.5, 1, and 2 kHz), with the pressure increasing along the waveguide until a peak is reached for a specific resonator, rapidly decaying after this maximum. The design of rainbow sensors consisting of an array of Helmholtz resonators with distinct resonant frequencies was later shown to be, in the limit case of small elements, equivalent in form to the cochlear wave equation, for which analytical solutions have been derived (Marrocchio et al., 2021).

Rupin et al. (2019) have proposed an active one-dimensional acoustic MM to mimic the behavior of a cochlea. An initial passive structure is designed considering a 33 mm long one-dimensional waveguide with evenly spaced graded subwavelength resonators every 8 μm, which can reproduce the behavior of a cochlea by modeling the individual transmission and reflection of each resonator inside the waveguide, showing a correlation between the location of the pressure maximum and its corresponding excitation frequency. The resulting structure is scaled for an experimental realization (see Figure 6D) using a 10 cm diameter pipe with embedded quarter-wavelength resonators made of 2.8 cm pipes, evenly spaced every 4.3 cm, limiting the resonant frequencies to the 300–800 Hz interval. Small microphones were placed inside each resonator, and the response envelope was measured for several distinct monochromatic excitations with different phases, showing the enhancement of the amplitude of the envelope at a frequency-dependent position, thus confirming numerical simulations. Finally, the cochlear amplification at low-level sounds is reproduced by incorporating active acoustic resonators, which provide an analogous function to that of the hair cells of the cochlea. These elements can obtain an amplified response over small variations in the input signal (amplitude and frequency), which is partially owed to their non-linear behavior, operating at a regime named Hopf bifurcation (Eguíluz et al., 2000). The operation at this regime was demonstrated for very small amplitudes, ensuring a zero gain for large amplitudes. Due to experimental limitations, only a reduced number of resonators were considered active. Nevertheless, high-amplitude incoming waves were demonstrated to reproduce the behavior observed for the passive configuration, while for low-amplitude sounds, the tonotopic effect becomes enhanced, focusing the envelope of the incoming traveling waves and thus revealing an increased sensitivity to low-level waves.

In (Ammari and Davies, 2020), the authors presented the design of an acoustic MM to mimic the active behavior of the cochlea. The proposed design is endowed with an array of size-graded cylindrical subwavelength resonators (see Figure 6E) to represent the variation of parameters such as stiffness and width, which present a grading along the cochlea structure, thus leading to a tonotopic configuration. The proposed set of resonators is obtained by considering a line array of elements with material properties (e.g., bulk modulus and specific mass density) contrasting with the background (matrix) in which they are embedded and producing resonant frequencies corresponding to wavelengths much larger than the dimensions of the resonator (Ammari and Davies, 2019). The response of each resonator is modeled as a differential equation with a cubic non-linearity presenting an enhanced response for frequencies close to the resonant frequency. Using a set of 22 resonators forming a 32 mm long structure with the largest width of 0.28 mm, the authors showed that each elicited mode presents a position of maximum amplitude varying with the resonant frequency, in the 1,290–13900 Hz range, thus representing a range of audible frequencies (20 Hz–20 kHz). After introducing non-linearity to account for the cubic amplification mechanism of the model, the response amplitude was shown to be consistently excited in the vicinity of each associated resonant frequency, with a considerable decay away from these frequencies. Later on, this device was demonstrated to be robust against small imperfections in the positions and sizes of the resonators (Davies and Herren, 2022), revealing mechanisms that may enable sufficiently large structures to be robust against large perturbations.

3.5 Moth wings

Among the countless number of structural and behavioral adaptations shaped by nature along the course of evolution, anti-predator defense mechanisms are certainly among the most intriguing. Through these features, prey organisms are endowed with structures that enable avoiding detection, fighting, or escaping predators, thus maximizing their survival rate. One typical example is the interaction between nocturnal bats and their prey. Bats use a biosonar that acts as an echolocating device, a known and well-studied mechanism (Simmons, 1979; Simmons and Stein, 1980). As an evolutionary response, some moth species have developed various strategies to avoid being found by bats, such as detecting the ultrasound frequency emitted by bats and then performing evasive maneuvers (Miller and Surlykke, 2001) or producing ultrasonic sounds which effectively confuse the predatory biosonar (Corcoran et al., 2009). An alternative mechanism has been proposed by Shen et al. (2018), who demonstrated that the wings of moths act as ultrasound absorbers, thus not reflecting the sounds emitted by the predators and troubling their efforts to localize prey. This functionality is achieved by a series of overlapping scales which are fixed to the wings and made of a thin chitinous membrane. Apart from possessing a highly porous and hierarchical structure, each scale displays a leaf-like shape that starts as a narrow region, which is connected to the wing surface, ending in several elongated extensions (see Figure 7A). Using laser Doppler vibrometry measurements, the authors have shown that the resonant frequencies of the scales, measured as 27.6, 90.8, and 152.3 kHz, and corresponding to flexural and twisting modes, fall within the same frequency range as the echolocation system frequencies of bats (20–150 kHz range). An ultrasonic absorption model showed also that an absorption coefficient of 0.50 is achieved for a rectangular grid covered by a single type of scale, thus indicating a mechanism that enables moths to be undetected by bats.

FIGURE 7

FIGURE 7. Moth wing scales and related bioinspired systems. (A) Individual scale observed using scanning electron microscopy [adapted from (Zeng et al., 2011)]. (B) Numerical testing using an arrangement of scales with varying resonant frequencies in a unit cell (Neil et al., 2020). (C) Cross section of wing membrane (red, middle) with scales (blue, top and bottom regions) and configurations for testing of reflectance using a circular metal disc (grey), wing membrane (red), and scales at specific regions (blue) [adapted from (Neil et al., 2022)]. (D) Model of a wing membrane covered by scales, represented by a plate with locally resonant elements with masses m_t (m_b) connected to the top (bottom) surface by a stiffness S_t (S_b) (Wang et al., 2022). (E) Representations of proposed panel solutions, considering either a space-dependent thickness panel (PC solution) or a unit cell with a set of distributed spring-mass resonators presenting four-fold symmetry (MM solution) (Dal Poggetto et al., 2022c).

Later, Neil et al. (2020) noted that moth wings can be regarded as acoustic MMs, highlighting the correlation between moth wing scales and the role they play as locally resonant structures. The layer formed by the scales, with a 0.3 mm thickness, is 111 (5) times thinner than the longest (shortest) absorbed wavelength, at 160 (20) kHz, thus indicating these elements act in the deep-subwavelength regime. After quantifying the wave reflection for normal sound incidence with and without the presence of scales in two different areas of the wings (leading and trailing edges), the authors found that the wings of two different moth species reduced the reflected waves in the 20–60 kHz range by −3.51 ± 1.02 dB and −4.80 ± 0.61 dB, for the first species, and −3.03 ± 0.69 dB and −5.02 ± 1.09 dB, for the second species, respectively. As each scale acts as a locally resonant element, their absorption is restricted to a narrow frequency range. This drawback can be overcome by associating resonators with different resonant frequencies (Yang et al., 2017). The authors also used a numerical model of a 4 × 4 array of scales fixed to a single membrane (see the simplified schematic in Figure 7B) to reveal that the interaction between scales with contrasting tuned resonant frequencies gives rise to a broadband acoustic absorption property. The scales were selected to show resonant frequencies in the 30–45 kHz frequency range (1 kHz interval) with a constant damping loss factor of 0.045, which also serves to diminish the gaps between individual resonant peaks. The resulting structure was numerically tested considering an infinite number of unit cells, showing an asymmetric broadband absorption coefficient with a peak of 0.47 at approximately 40 kHz and rapidly decaying after this frequency, demonstrating also that the vibroacoustic response of the resulting structure is affected by the disposition of individual scales.

The reduced thickness-to-wavelength ratio in the considered frequency range of absorbed acoustic waves suggests that moth wings can act as efficient sound-absorbing metasurfaces. In (Neil et al., 2022), the authors have tested this hypothesis utilizing sound reflection tests, assessing the reflection coefficient (ratio between the returned sound intensity at a 0.1 m distance and the incident sound intensity) by performing measurements in the 20–160 kHz frequency range. The samples were laid on an 8 mm diameter aluminum disc in different configurations, initially considering the wing membrane covered with scales, the wing covered with membranes only at one side (both facing the microphone and in contact with the substrate), and without scales, sonifying either the dorsal or ventral faces (see Figure 7C). For the case where the dorsal surface (bare wing side) is facing the incident sound (bottom scales), the reflection coefficient is slightly larger than in the case with scales on both sides and considerably smaller when compared to the case with no scales. In the case where the ventral surface (with wings) is facing the incident sound (top scales), the reflection coefficient is similar to the case with no scales, and considerably larger when compared to the case with scales on both sides. The authors have explained the differences in the observed configuration stating that the coupling between the resonating scales and the wing membrane leads to the correct energy dissipation mechanism, which could not be achieved if the membrane was regarded as a fixed substrate.

Wang et al. (2022) have proposed an analytical model to describe the interaction between the wing membrane, attached scales, and the surrounding fluid. Each scale is considered a flat rigid rectangle with a mass m_t or m_b, connected to the wing membrane by a spring with stiffness S_t or S_b, where the subscripts t and b refer to the top and bottom surfaces of the wing membrane, respectively (see Figure 7D). Each scale is assumed to be sufficiently close to the wing so that the gap between these elements is negligible. The wing is idealized as a thin elastic plate that interacts with the surrounding fluid. The proposed theory is investigated considering an isotropic plate (specific mass density 1,300 kg/m³, Young’s modulus 65 GPa, Poisson’s ratio 0.35, and thickness 3 μm) immersed in air (specific mass density 1.21 kg/m³ and sound speed 343 m/s); the mass of the scales are taken as m_t = m_b = 2.56 × 10⁻¹¹, with the stiffness of springs equal to 1.2 N/m (estimated size of 44 × 44 μm²), and an additional dynamical loss impedance correction. The corresponding idealized model, considered as a periodic lattice with a square unit cell with dimensions 185 × 185 μm², was shown to correctly represent the reflection, transmission, and absorption coefficients previously simulated for the biological system for a 20–50 kHz frequency range. Also, the model is used to evaluate the broadband behavior considering a unit cell with a 4 × 4 array of spring-mass resonators obtained by introducing a randomness factor to each element mass, with each resonator corresponding to a unit cell area of 50 × 50 μm². The broadening of the absorption bandwidth was shown to increase with a larger mass randomness factor, accompanied by a flattening in the absorption peak.

Although the use of absorptive materials to dissipate acoustic energy is a common sound insulation engineering solution (Doutres et al., 2007), another possible approach consists in the use of systems able to reflect sound energy through the use of barriers with a sufficient impedance mismatch, such as single- and double-leaf panels (Tadeu et al., 2004). The design of optimized bioinspired systems was then proposed in (Dal Poggetto et al., 2022c), where the performance in terms of sound transmission loss of panels consisting of either 1) a constant-thickness plate with resonant elements (MM solution), 2) a thickness-varying plate (PC solution, see (Dal Poggetto and Arruda, 2021)), or a combination of both 1) and 2), are evaluated for both the single- and double-leaf configurations (see Figure 7E). By using spring-mass resonators attached to a thin plate substrate, analogous to scales fixed in the wing membrane, the authors have proposed an optimization approach that maximizes the sound transmission loss over a given frequency range while keeping a constant unit cell mass. The characterization of the resonators is given by a fixed mass, equally distributed to all resonators, and a theoretical surface with four-fold symmetry from which specific points are sampled to acquire a stiffness value, and consequently the resonant frequency of each resonator, thus yielding a process that can be used for a large number of resonant elements. Although the PC solution is shown to possess partial band gaps which impede the acoustic waves from being fully transmitted (zero sound transmission loss condition), these do not guarantee a good diffuse field performance. On the other hand, the wavelength-independent behavior observed in the dispersion relation, owed to the presence of locally resonant elements (see Figure 2), ensures the existence of a non-zero sound transmission loss regardless of the orientation of impinging acoustic waves. Also, the performance of several distributed resonators with smaller masses and contrasting resonant frequencies is shown to be preferable to obtain a broadband sound transmission loss increase, thus confirming that concepts present in moth wings are not only worth investigating for acoustic absorbers, but also for panels and possibly other bioinspired solutions.

4 Conclusion

In this work, biological systems and corresponding bioinspired structures were presented, highlighting their typical features in varying length scales and distinct domains, such as structural and acoustic. After briefly introducing the main concepts related to wave propagation in periodic materials, a set of systems of interest is presented.

Nacre-based PCs can yield wide band gaps, which may be opened due to either Bragg scattering or local resonances (concentrated in the soft phase), with relative robustness against defects in the hard phase, but sensitive to crack defects in the soft phase. When hierarchical structuring is considered, this type of system is able to achieve broadband filtering effects, which can be demonstrated if no homogenization procedures are employed. Viscosity also plays an important role in this type of structure, with the most noticeable effects in higher frequencies.

Spider orb webs can be a source of inspiration for both structural and acoustic applications. In the context of two-dimensional elastic wave manipulation, the creation of periodic media with a unit cell consisting in the basic spider web geometry (i.e., the combination of radial and circumferential elements with contrasting properties) leads to a strong anisotropic behavior and a multitude of band gaps which can be tuned through the variation of geometric features to achieve diverse objectives. The use of spider web-inspired acoustic devices for sound control can also be performed using either labyrinthine or membrane MMs, which offer significant control over vibration modes and resonant frequencies.

Fractal systems have been widely explored in the field of PCs and MMs. Examples can be found in diverse length scales, ranging from micro to centimeter scales. In the structural domain, self-similar architectures (e.g., Sierpinski triangles and carpets) can be used to manipulate dispersion relations, although not in an obvious manner, since an increase in the hierarchical order can open new band gaps, but may also close previously existing ones. Although broadband effects can be achieved, the change in hierarchical orders is likely more associated with the variation of other characteristics, such as weight reduction of the unit cell. Viscosity can also be an important factor to achieve broadband attenuation, especially when considering the effect of multiple local resonances. In the acoustic domain, labyrinthine MMs (e.g., using Hilbert fractals) are a common choice, leading to low-frequency band gaps, although not necessarily broadband.

Cochlea-inspired structures can be used to harness the feature of tonotopy, thus presenting a correlation between the spatial localization of waves and their frequency content, revealing unique sensing properties. The rainbow trapping effect is typically used to achieve such spatial separation for acoustic waveguides with an array of graded resonators (e.g., quarter-wavelength or Helmholtz) or a series of resonators in a background fluid. Other examples include bi-partitioned cavities with a separating membrane featuring a tonotopic organization or curved plate structures with variations of width and thickness along the spiral centerline, thus leading to a tailored spatial separation of the maxima of out-of-plane vibration modes according to their resonant frequencies. Although the spiral architecture seems beneficial in terms of compactness, it is not necessary in cases where locally resonant elements are employed. Also, the Hopf bifurcation regime is an important feature to be included in the locally resonant elements, which must present a considerable gain for low-amplitude excitations.

Moth wings are natural structures that evolved to act as broadband sound absorbers, constituted by flexible wing membranes with a multitude of attached scales. Although each scale acts as a locally resonant structure, thus operating, for each resonant frequency, within a narrow frequency range, the ensemble of scales with various resonant frequencies leads to a broadband characteristic with significant absorption of impinging acoustic waves. The resonant behavior of separate scales, however, is not sufficient to provide a significant sound absorption efficiency, which is achieved by the interaction between different scales and the substrate itself. The resulting system provides a fruitful source of inspiration for acoustic application devices. Systems consisting of spring-mass resonators attached to both faces of host plates can be used to faithfully model the desired behavior, and bioinspired panels can be designed following the concept of multiple resonators to achieve optimal sound transmission loss levels within target frequency ranges.

Although many examples of bioinspired systems can be found concerning diverse biological systems, current studies are typically limited to designs that consider single objectives and specific applications. On the other hand, nature seems to produce systems that present a compromise between simultaneous objectives, such as stiffness, fatigue resistance, and wave attenuation. The immense design freedom associated with these systems suggests that a multi-disciplinary approach, concatenating various objectives, might be a fruitful opportunity offered by bioinspired artificial systems. When combined with the ever-present challenge of achieving lightweight solutions to reduce the environmental impact of manufactured solutions, the investigation of bioinspired optimized systems still presents many open questions which may be explored in the future.

Author contributions

VFDP contributed to the conception of the manuscript, wrote the first draft and performed the revision of the manuscript and submitted version.

Funding

VFDP is supported by the EU H2020 FET Open “Boheme” grant No. 863179.

Acknowledgments

VFDP thanks Federico Bosia for the meaningful discussions and Nicola M. Pugno for the overall supervision on the topics regarding bioinspired hierarchical metamaterials and for supporting the publication of this manuscript.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aguirre, J., Viana, R. L., and Sanjuán, M. A. (2009). Fractal structures in nonlinear dynamics. Rev. Mod. Phys. 81, 333–386. doi:10.1103/revmodphys.81.333