Analysis of an improved Nishihara creep model considering plastic strain accumulation

Rock-engineering structures, particularly subway excavation rock-engineering structures, are subjected to the long-term effects of external loading that may gradually damage and cause creep and severe plastic deformations or even progressive failure. The traditional Nishihara creep model cannot accurately describe the accelerated creep stage of rock with particularly obvious nonlinear characteristics. Based on this model, a damage variable that can consider the plastic strain accumulation is introduced in this study to replace the viscoplastic body in the traditional model with a damaged viscoplastic body and establish an improved Nishihara creep model. Using the superposition principle, the creep equations of the improved model in the one- and three-dimensional stress states are derived. The accuracy and rationality of the improved model are verified using uniaxial and conventional triaxial creep tests of mudstone and sandstone under different confining pressures. The improved model can not only accurately reflect the nonlinear characteristics of the creep curve in the decay and constant velocity stages but also describe the accelerated creep characteristics of mudstone and sandstone in a high-stress state. Its applicability and accuracy are superior to those of the traditional model. This study can provide a theoretical reference for subway tunnel excavation and stability analysis of deep roadway surrounding rocks.

1 Introduction

In the excavation process of underground engineering structures, such as tunnels and subways, the original stress and energy balance states of the surrounding rock are disturbed, and they undergo creep deformation. Creep deformation gradually accumulates over time, and it affects the stability of the surrounding rock and threatens the safety of construction personnel (Zhang and Wang, 2019). Therefore, the study of the creep characteristics of rock is of great significance for analyzing the surrounding rock deformation and selecting the support time and method.

Rock creep has always been a contentious and challenging topic in rock mechanics. Because the parameters of classical element creep models such as Burgers, Bingham, and Kelvin are constant, regardless of the complexity of the combination form of element models, they cannot accurately describe the nonlinear creep characteristics of rocks, specifically the nonlinear accelerated creep when the stress level exceeds the long-term strength of the rock (NazaryMoghadam et al., 2013; Liu H. Z. et al., 2017). In recent years, scholars at home and abroad have conducted numerous creep tests and theoretical studies on different rock types under stress path conditions. Zhang et al. (2021) conducted an indoor creep model test on a deep-buried soft rock roadway and used field measurements and a discrete element simulation method to analyze the influence of surrounding rock creep deformation on the stress deformation of the lining. Zhao et al. (2019) established a simple and practical mathematical model for rheological fracture of rock cracks under the combined effect of hydraulic pressure and far-field stresses. Chao et al. (2021) conducted conventional triaxial compression creep tests on salt rocks under high temperature and pressure, studied the influence of temperature and pressure on constant velocity creep rates, and established a fractional-order creep model. The results showed that this model can accurately describe the creep behavior of salt rocks and fully reflect the rheological properties of salt rocks under high-temperature and -pressure conditions. Wang et al. (2020) studied the creep characteristics of mudstone under disturbance loads, and the results showed that the instantaneous deformation, decay creep time, and constant velocity creep rate of mudstone have an exponential function growth relationship with stress level, and they linearly increase with the increase in disturbance amplitude and frequency. Wu et al. (2021) conducted true triaxial loading tests under high-stress conditions on a deep-mine horizontal roadway in inclined strata and studied the failure patterns of surrounding rock in the roadway over time. Mingyuan et al. (2020) proposed a new model to describe accelerated creep based on the Nishihara model, deduced the creep constitutive relationship of the model, and verified the rationality and accuracy of the model using the total creep test curves of sandy mudstone and sandstone. Cao et al. (2016) established a new nonlinear damage creep constitutive model for high-stress soft rocks based on nonlinear damage creep characteristics and damage variables of rocks combined with the improved Burgers, Hooke, and St. Venant models. Their model could accurately describe the deformation process of a typical soft rock in the Jinchuan No. 2 mine under different initial creep, steady creep, and accelerated creep stages. Zhang and Wang (2021) studied the nonlinear creep characteristics of rocks subjected to cyclic loads and proposed a damage viscoelastic creep model. The loading and unloading creep curves of lherzolite and limestone described by the model were consistent with the experimental curves, verifying the rationality and feasibility of the model. Zhao et al. (2017a) and Zhao et al. (2017b) conducted multi-level triaxial cyclic loading unloading creep tests on intact and cracked limestone and lherzolite, studied the creep characteristics of two types of rocks, and established corresponding creep models.

Rock creep leads to instantaneous elastic deformation, time-dependent viscoelastic deformation, and viscoplastic deformation. Because the elastic deformation is reversible, the instantaneous elastic deformation recovers instantly during the unloading process, and the viscoelastic deformation can also recover after a period. However, the viscoplastic deformation cannot be recovered, and it gradually increases with time and accumulates in the rock. When plastic deformation accumulates to a certain extent, it causes creep failure in the rock. Therefore, rock creep failure is caused by the accumulation of viscoplastic strain during creep. In this study, a new creep damage variable is established to describe the viscoplastic strain accumulation process during the loading process. The damage variable was introduced into the classical Nishihara creep model to establish an improved Nishihara creep model. The creep equation of this model was derived under one- and three-dimensional stress states. Finally, uniaxial and conventional triaxial compression creep tests were conducted to verify the accuracy and applicability of the improved Nishihara creep model.

2 Improved Nishihara creep model

2.1 Classical Nishihara model

The classical Nishihara model comprises a Hooke body, Kelvin body, and viscoplastic body connected in series. It can simultaneously describe the instantaneous elastic, viscoelastic, and viscoplastic deformations. When the applied stress is less than the long-term strength of the rock, the Nishihara creep model degenerates into a generalized Kelvin creep model, which can better describe the steady creep of the rock under a low-stress state. When the applied stress exceeds the long-term strength of the rock, it can describe the unsteady creep of the rock (Qi et al., 2012). Therefore, the Nishihara model is widely used in theoretical research and practical engineering applications, and a schematic of its mechanical model is shown in Figure 1.

FIGURE 1

FIGURE 1. Nishihara creep model.

Under a one-dimensional stress state, the constitutive equation of the Nishihara creep model is as follows:

$\left\{\begin{array}{l}\frac{{\eta }_1}{E_0}\dot{\sigma }+\left(1+\frac{E_1}{E_0}\right)\sigma ={\eta }_1\dot{\epsilon }+E_1\epsilon \left(\sigma <{\sigma }_s\right)\\ \ddot{\sigma }+\left(\frac{E_1}{{\eta }_1}+\frac{E_1}{{\eta }_2}+\frac{E_0}{{\eta }_1}\right)\dot{\sigma }+\frac{E_0{E}_1}{{\eta }_1{\eta }_2}\left(\sigma -{\sigma }_s\right)=E_1\ddot{\epsilon }+\frac{E_0{E}_1}{{\eta }_1}\dot{\epsilon }\left(\sigma \ge {\sigma }_s\right).\end{array}\right.(1)$

where σ and ε are the stress and strain, respectively; ${\epsilon }_{\mathrm{e}}、{\epsilon }_{\mathrm{v}\mathrm{e}}、{\epsilon }_{\mathrm{v}\mathrm{p}}$ are the elastic, viscoelastic, and viscoplastic strains, respectively; E₀ is the elastic modulus of the Hooke body; $E_1、{\eta }_1$are the elastic modulus and viscosity coefficient of the Kelvin body, respectively; ${\eta }_2$ is the viscosity coefficient of the viscoplastic body; and ${\sigma }_s$ is the long-term strength of the rock.

According to the superposition principle, the creep equation of Nishihara’s model can be obtained as follows:

$\epsilon \left(t\right)=\left\{\begin{array}{l}\frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]\left(\sigma <{\sigma }_s\right)\\ \frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]+\frac{\sigma -{\sigma }_s}{{\eta }_2}t\left(\sigma \ge {\sigma }_s\right).\end{array}\right.(2)$

The Nishihara model can evaluate the unsteady creep process of rocks under a high-stress state. When the rocks undergo creep failure, they experience the decay creep, constant velocity creep, and accelerated creep stages and exhibit nonlinear characteristics. However, the classical Nishihara creep model cannot describe the accelerated creep process of rocks because its model parameters are linear. The model is limited to describing the creep failure process of rocks.

2.2 Improved Nishihara creep model

2.2.1 Damage variable

Under the long-term effect of an external load, a rock produces irrecoverable internal plastic strain. With an increase in the duration of the load, the internal microcracks in the rock develop rapidly and penetrate further, forming macrocracks. As plastic strain gradually develops and accumulates in the rock, the degree of damage to the rock becomes increasingly severe, thereby decreasing its ability to resist load until the final creep failure. The damage process of the rock owing to the accumulation of plastic strain can be represented by the following damage variables (Wen et al., 2016; Zhao et al., 2021):

$D={\int }_0^t\frac{\dot{\epsilon }}{{\epsilon }^{*}}\mathrm{d}t,(3)$

where D is the damage variable, which is zero when loading and one when creep occurs, $t$ is time, and $\dot{\epsilon }$ is the steady-state creep strain rate, which can be calculated using the Norton power law (Norton, 1929) as

$\dot{\epsilon }=A\times {\left(\overline{\sigma }\right)}^n,(4)$

where A is a material constant and n denotes the creep exponent. The values of the two parameters can be obtained from uniaxial creep tests under different applied stresses. Here, $\overline{\sigma }$ is the deviatoric stress, and it can be calculated as follows:

$\overline{\sigma }={\sigma }_1-{\sigma }_3,(5)$

where ${\sigma }_1$ and ${\sigma }_3$ are the maximum and minimum principal stresses, respectively.

Here, ${\epsilon }^{*}$ is the multi-axial creep strain, which was defined based on the uniaxial creep fracture strain according to the Cocks and Ashby model (Oh et al., 2011). The creep exponent n is used to determine the multi-axial creep strain as follows:

${\epsilon }^{*}=\frac{{\epsilon }_c}{\sinh \left[2\left(n-0.5\right)/3\left(n+0.5\right)\right]/\sinh \left[2{\sigma }_m\left(n-0.5\right)/{\sigma }_{eq}\left(n+0.5\right)\right]},(6)$

where ${\epsilon }_c$ is the creep fracture strain; ${\sigma }_m$ is the mean stress; ${\sigma }_{eq}$ represents the equivalent stress; and h is the stress triaxiality, which was defined by the ratio of ${\sigma }_m$ and ${\sigma }_{eq}$. The abovementioned parameters can be calculated according to the following formula:

$\left\{\begin{array}{l}{\sigma }_m=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}\\ {\sigma }_{eq}=\sqrt{\frac{1}{2}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2\right]}\\ h=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3\sqrt{\frac{1}{2}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2\right]}},\end{array}\right.(7)$

where ${\sigma }_2$ is the intermediate principal stress.

We substitute Eqs 4–6 in Eq. 3 to obtain the damage variable expression as follows:

$D={\int }_0^t\frac{A\times {\left({\sigma }_1-{\sigma }_3\right)}^n}{\frac{{\epsilon }_c}{\sinh \left[2\left(n-0.5\right)/3\left(n+0.5\right)\right]/\sinh \left[2{\sigma }_m\left(n-0.5\right)/{\sigma }_{eq}\left(n+0.5\right)\right]}}\mathrm{d}t.(8)$

For conventional triaxial testing, substituting Eq. 7 in Eq. 8, we can obtain

$D={\int }_0^t\frac{A\times {\left({\sigma }_1-{\sigma }_3\right)}^n\sin \left[\frac{2\left({\sigma }_1+2{\sigma }_3\right)\left(n-0.5\right)}{9\left({\sigma }_1-{\sigma }_3\right)\left(n+0.5\right)}\right]}{{\epsilon }_c\sin \left[\frac{2\left({\sigma }_1+2{\sigma }_3\right)\left(n-0.5\right)}{9{\left({\sigma }_1-{\sigma }_3\right)}^2\left(n+0.5\right)}\right]}\mathrm{d}t.(9)$

By integrating Eq. 9, the following equation is obtained:

$D=\frac{A\times {\left({\sigma }_1-{\sigma }_3\right)}^n\sin \left[\frac{2\left({\sigma }_1+2{\sigma }_3\right)\left(n-0.5\right)}{9\left({\sigma }_1-{\sigma }_3\right)\left(n+0.5\right)}\right]}{{\epsilon }_c\sin \left[\frac{2\left({\sigma }_1+2{\sigma }_3\right)\left(n-0.5\right)}{9{\left({\sigma }_1-{\sigma }_3\right)}^2\left(n+0.5\right)}\right]}t.(10)$

As can be seen from Eq. 10, the damage variable is related to not only the stress level, material parameters, and time but also the plastic strain, which can reflect the cumulative time effect of plastic strain. Therefore, it can be used to describe the damage process during rock creep.

2.2.2 One-dimensional creep equation

To describe the characteristics of the nonlinear accelerated creep of rocks under high stress, damage variables were introduced into the viscous body, which was connected in parallel with the plastic body to form a damaged viscoplastic body. Subsequently, the viscoplastic body in the Nishihara creep model was replaced with the damaged viscoplastic body, and an improved Nishihara creep model was established. A schematic of the mechanical model is shown in Figure 2.

FIGURE 2

FIGURE 2. Improved Nishihara creep model.

As observed from Figure 2, the Hooke and Kelvin bodies can accurately describe the instantaneous elastic and viscoelastic strains during rock loading. For damaged viscous bodies, according to Lemaitre’s strain equivalence principle (Xu et al., 2006), the constitutive equation of damaged viscous bodies can be expressed as follows:

${\dot{\epsilon }}_{\mathrm{v}\mathrm{p}}=\frac{\stackrel{\sim }{\sigma }}{{\eta }_2}=\frac{\sigma }{{\eta }_2\left(1-D\right)},(11)$

where $\stackrel{\sim }{\sigma }$ is the effective stress

By substituting Eq. 10 in Eq. 11, the constitutive equation for the damaged viscous body can be obtained as follows:

${\dot{\epsilon }}_{\mathrm{v}\mathrm{p}}=\frac{\sigma }{{\eta }_2\left(1-mt\right)},(12)$

where m can be expressed as $m=\frac{A\times {\left({\sigma }_1-{\sigma }_3\right)}^n\sin \left[\frac{2\left({\sigma }_1+2{\sigma }_3\right)\left(n-0.5\right)}{9\left({\sigma }_1-{\sigma }_3\right)\left(n+0.5\right)}\right]}{{\epsilon }_c\sin \left[\frac{2\left({\sigma }_1+2{\sigma }_3\right)\left(n-0.5\right)}{9{\left({\sigma }_1-{\sigma }_3\right)}^2\left(n+0.5\right)}\right]}$.

By integrating Eq. 12, the creep equation of the damaged viscous body can be obtained as follows:

${\epsilon }_{\mathrm{v}\mathrm{p}}=-\frac{\sigma }{m{\eta }_2}\ln \left(1-mt\right)+C,(13)$

where $C$ is the integral constant.

When $t=0$ and $\epsilon =0$, the integral constant becomes zero.

$C=0.(14)$

Substituting Eq. 14 in Eq. 13 yields the following:

${\epsilon }_{\mathrm{v}\mathrm{p}}=-\frac{\sigma }{m{\eta }_2}\ln \left(1-mt\right).(15)$

For a damaged viscoplastic body in a one-dimensional stress state, the creep equation can be obtained by replacing $\sigma$ with $\sigma -{\sigma }_s$ in Eq. 15. Therefore,

${\epsilon }_{\mathrm{v}\mathrm{p}}=-\frac{\sigma -{\sigma }_{\mathrm{s}}}{m{\eta }_2}\ln \left(1-mt\right).(16)$

According to the superposition principle, the creep equation of the improved Nishihara creep model can be expressed as follows:

(1) When $\sigma <{\sigma }_s$,

$\epsilon \left(t\right)=\frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right].(17)$

(2) When $\sigma \ge {\sigma }_s$,

$\epsilon \left(t\right)=\frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left[1-\exp \left(-\frac{E_1}{{\eta }_1}t\right)\right]-\frac{\sigma -{\sigma }_{\mathrm{s}}}{m{\eta }_2}\ln \left(1-mt\right).(18)$

In conclusion, an improved Nishihara creep model was established, and the creep equation under a one-dimensional stress state was derived. By comparing Eq. 18 with Eq. 2, it can be found that the improved Nishihara creep model adds only one model parameter compared with the classical Nishihara creep model, and the form of the creep equation is simple, which is conducive to practical engineering applications.

3 Three-dimensional creep equation

In practical rock mass engineering, rock is often in a complex three-dimensional stress state, and the conventional triaxial graded loading method is generally used in laboratory creep tests. Therefore, to facilitate comparison and analysis with the test results, it is necessary to establish the creep constitutive relationship of the rock in a three-dimensional stress state.

When the rock is in a three-dimensional stress state, it is assumed that the total strain of the improved Nishihara creep model is ${\epsilon }_{ij}^{\mathrm{t}}$, the strain of the Hooke body is ${\epsilon }_{ij}^{\mathrm{e}}$, the strain of the Kelvin body is ${\epsilon }_{ij}^{\mathrm{v}\mathrm{e}}$, and the strain of the damaged viscoplastic body is ${\epsilon }_{ij}^{\mathrm{v}\mathrm{p}}$. According to the superposition principle,

${\epsilon }_{ij}^{\mathrm{t}}={\epsilon }_{ij}^{\mathrm{e}}+{\epsilon }_{ij}^{\mathrm{v}\mathrm{e}}+{\epsilon }_{ij}^{\mathrm{v}\mathrm{p}}.(19)$

For the Hooke body, the stress tensor ${\sigma }_{ij}$ at any point on the rock in a three-dimensional stress state can be divided into a spherical stress tensor ${\sigma }_m{\delta }_{ij}$ and deviatoric stress tensor $S_{ij}$. Similarly, the strain tensor ${\epsilon }_{ij}$ at any internal point can also be divided into a spherical strain tensor ${\epsilon }_m{\delta }_{ij}$ and deviatoric strain tensor $e_{ij}$ (Bao et al., 2015). Therefore,

$\left\{\begin{array}{l}{\sigma }_m=S_{\mathit{ij}}+{\delta }_{ij}{\sigma }_m\\ {\varepsilon }_{ij}=e_{\mathit{ij}}+{\delta }_{ij}{\epsilon }_m,\end{array}\right.(20)$

where ${\delta }_{ij}$ is the Kronecker tensor.

According to generalized Hooke’s law,

$\left\{\begin{array}{l}{\sigma }_m=3K_0{\epsilon }_m\\ S_{ij}=2G_0{e}_{ij},\end{array}\right.(21)$

where $K_0$ is the bulk modulus and $G_0$ is the shear modulus.

By substituting Eq. 21 in Eq. 20, the three-dimensional creep equation of the Hooke body can be obtained as follows:

${\epsilon }_{ij}^{\mathrm{e}}=\frac{1}{2G_0}{S}_{ij}+\frac{1}{3K_0}{\delta }_{ij}{\sigma }_m.(22)$

The three-dimensional creep equation of the Kelvin body (Yan et al., 2010; Zhao et al., 2018) can be expressed as follows:

${\epsilon }_{ij}^{\mathrm{v}\mathrm{e}}=\frac{S_{ij}}{2G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right],(23)$

where $G_1$ is the shear modulus of the Kelvin body.

The three-dimensional creep equation of the damaged viscoplastic body can be expressed as follows:

${\epsilon }_{ij}^{\mathrm{v}\mathrm{p}}=\frac{\ln \left(1-mt\right)}{m{\eta }_2}〈\mathrm{\Phi }\left(\frac{F}{F_0}\right)〉\frac{\partial Q}{\partial {\sigma }_{ij}},(24)$

where $〈\mathrm{\Phi }\left(\frac{F}{F_0}\right)〉=\left\{\begin{array}{l}\mathrm{\Phi }\left(\frac{F}{F_0}\right)\left(F\ge 0\right)\\ 0\left(F<0\right)\end{array}\right.,〈•〉$ denotes the switch function, $F$ is the rock yield function, and $F_0$ is the initial value of the rock yield function, which is typically 1 for simplicity (Hu, 2018). Furthermore, $\mathrm{\Phi }\left(\frac{F}{F_0}\right)$ is generally an exponential or power function, and $\mathrm{\Phi }\left(\frac{F}{F_0}\right)={\left(\frac{F}{F_0}\right)}^k$. Here, k is a constant, generally 1 (Tang et al., 2022), and $Q$ is the plastic potential function. Moreover, for the convenience of calculation, the associated flow rule is used; therefore, $F=Q$ (Ren et al., 2022).

For a viscoplastic body, certain yield conditions must be met before it works; therefore, an appropriate yield function and yield criterion must be selected (Shi et al., 2022). Currently, the Tresca or von Mises yield criterion is mostly used as the criterion for the effectiveness of plastic elements. In the conventional triaxial compression creep test, ${\sigma }_2={\sigma }_3$; therefore, the expressions of the Mises and Tresca yield functions are only different in terms of the constant coefficient terms. For the convenience of expression, the Tresca yield criterion was selected, and the yield function was defined (Wu et al., 2022).

$F=\frac{1}{2}\left({\sigma }_1-{\sigma }_3\right)-\frac{{\sigma }_s}{2}.(25)$

Substituting Eq. 25 in Eq. 24 yields the following:

${\left.\left(\frac{F}{F_0}\right)\frac{\partial F}{\partial {\sigma }_{ij}}\right|}_{\begin{array}{l}{F}_0=1\\ i=j=1\end{array}}=\frac{1}{4}\left({\sigma }_1-{\sigma }_3-{\sigma }_s\right).(26)$

By substituting Eq. 26 in Eq. 24, the three-dimensional creep equation of the damaged viscoplastic body can be obtained as follows:

${\epsilon }_{11}^{\mathrm{v}\mathrm{p}}=\frac{\ln \left(1-mt\right)}{4m{\eta }_2}\left({\sigma }_1-{\sigma }_3-{\sigma }_s\right).(27)$

For conventional triaxial axial creep of rock,

$\left\{\begin{array}{l}i=j=1\\ {\delta }_{ij}={\delta }_{11}=1\\ {\sigma }_m=\frac{{\sigma }_1+2{\sigma }_3}{3}\\ S_{11}={\sigma }_1-{\sigma }_m=\frac{2\left({\sigma }_1-{\sigma }_3\right)}{3}.\end{array}\right.(28)$

By substituting Eq. 28 in Eqs 22, 23, the three-dimensional creep equations of the Hooke and Kelvin bodies can be obtained as follows:

$\left\{\begin{array}{l}{\epsilon }_{11}^{\mathrm{e}}=\frac{{\sigma }_1+2{\sigma }_3}{9K_0}+\frac{{\sigma }_1-{\sigma }_3}{3G_0}\\ {\epsilon }_{11}^{\mathrm{v}\mathrm{e}}=\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right].\end{array}\right.(29)$

Simultaneous Eqs 27, 29 were solved according to the superposition principle, and the axial creep equation of the improved Nishihara creep model of rock under the three-dimensional stress state was obtained as follows:

${\epsilon }_{11}\left(t\right)=\left\{\begin{array}{l}\frac{{\sigma }_1+2{\sigma }_3}{9K_0}+\frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]\left({\sigma }_1-{\sigma }_3<{\sigma }_s\right)\\ \frac{{\sigma }_1+2{\sigma }_3}{9K_0}+\frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-\exp \left(-\frac{G_1}{{\eta }_1}t\right)\right]\\ +\frac{\ln \left(1-mt\right)}{4m{\eta }_2}\left({\sigma }_1-{\sigma }_3-{\sigma }_s\right)\left({\sigma }_s\le {\sigma }_1-{\sigma }_3\right).\end{array}\right.(30)$

4 Model validation

In this study, the applicability of the improved Nishihara creep model was verified using conventional triaxial compression creep test data of mudstone. First, a TAW-2000 rock material testing machine (Figure 3) was used to conduct conventional uniaxial and triaxial compression tests on mudstone. The basic mechanical parameters of mudstone are listed in Table 1.

FIGURE 3

FIGURE 3. TAW-2000 rock material testing machine.

TABLE 1

TABLE 1. Mechanical parameters of mudstone.

Then, uniaxial compression creep tests and conventional triaxial compression creep tests with confining pressures of 5 MPa and 10 MPa were performed to obtain the creep curves of mudstone under different stress conditions. There are five test loading levels, the first level of stress is 40% of ${\sigma }_c$, the second level of stress is 50% of ${\sigma }_c$, the third level of stress is 60% of ${\sigma }_c$, the fourth level of stress is 70% of ${\sigma }_c$, and the fifth level of stress is 80% of ${\sigma }_c$. The stress of each level is listed in Table 2. At each stress level, the loading time is 36 h.

TABLE 2

TABLE 2. Stress levels of the compression creep step loading test.

After processing the uniaxial and triaxial creep test data of mudstone, the creep curves of mudstone under 0 MPa, 5 MPa, and 10 MPa confining pressure are obtained, and the results are shown in Figure 4. It can be seen from the figure that under different confining pressures, the mudstone is damaged at the fifth stress level. The creep deformation of mudstone under the first to fourth stress level is relatively small, while the creep deformation of mudstone under the fifth stress level increases sharply with time. At this stress level, plastic deformation of mudstone accumulates rapidly and creep failure occurs in a short time. At the same time, it can also be seen from the figure that under any level of stress, the greater the confining pressure, the greater the creep deformation of mudstone.

FIGURE 4

FIGURE 4. Creep curves of mudstone under different confining pressures.

The creep failure mode of mudstone under different confining pressures is shown in Figure 5. It can be seen from the figure that during uniaxial compression creep, the damage degree of mudstone is relatively serious, there are more vertical cracks, and the crack width is relatively large. During triaxial compression creep, the mudstone is mainly subject to oblique shear failure, with only one crack, a small width, and a certain angle with the axial direction of the mudstone sample.

FIGURE 5

FIGURE 5. Failure modes of mudstone under different confining pressures.

According to the creep test data of mudstone under different confining pressures, the rationality and accuracy of the improved Nishihara model established in this paper are verified. The parameters $K_0=\frac{E}{3\left(1-2\mu \right)}$ and $G_0=\frac{E}{2\left(1+\mu \right)}$ of the improved Nishihara creep model are the bulk and shear moduli, respectively, and they can be determined using the elastic modulus E and Poisson’s ratio $\mu$. The model parameters $G_1、{\eta }_1、{\eta }_2、m$ can be obtained by inversion using MATLAB, according to the test results.

In the uniaxial compression creep test, stress in the first four levels was less than the long-term strength of 24.9 MPa; therefore, Eq. 17 was used to perform curve fitting, and the accuracy of the fit was evaluated using the correlation coefficient square (R²). As stress in the fifth level exceeded the long-term strength, Eq. 18 was used to perform curve fitting and obtain the model parameters listed in Table 3. A comparison of the fitting and test curves is shown in Figure 6.

TABLE 3

TABLE 3. Uniaxial compression creep model parameters.

FIGURE 6

FIGURE 6. Comparisons between creep test curves and theoretical curves when ${\sigma }_3=0$ MPa.

As shown in Figure 6, during the uniaxial compression creep, when the stress level is lower than the long-term strength of mudstone, the improved Nishihara creep model transforms into the generalized Kelvin creep model. The theoretical curve of this model coexists with the test curve, which can describe the attenuated creep and constant velocity creep of mudstone under low-stress conditions. When the stress level exceeded the long-term strength of mudstone, an obvious accelerated creep stage is developed. The improved Nishihara creep model results were consistent with the experimental results, and R2 was 0.996. This indicates that the improved Nishihara creep model can not only accurately describe the steady creep of mudstone under a low-stress state but also describe unsteady creep, which is nonlinear when the rock is in a high-stress state.

During the triaxial compression creep, the first four stress levels were below 5 MPa and 10 MPa, and the confining pressures were less than their long-term strengths of 31.8 and 42.3 MPa. Therefore, the first formula in Eq. 30 was used to perform curve fitting. As the fifth stress level exceeded the long-term strength of mudstone, the second formula in Eq. 30 was used to perform curve fitting. The model parameters obtained through curve fitting are listed in Tables 4, 5, and comparisons of the results obtained through curve fitting and tests are shown in Figures 7, 8.

TABLE 4

TABLE 4. Compression creep model parameters when ${\sigma }_3=5$ MPa.

TABLE 5

TABLE 5. Compression creep model parameters when ${\sigma }_3=10$ MPa.

FIGURE 7

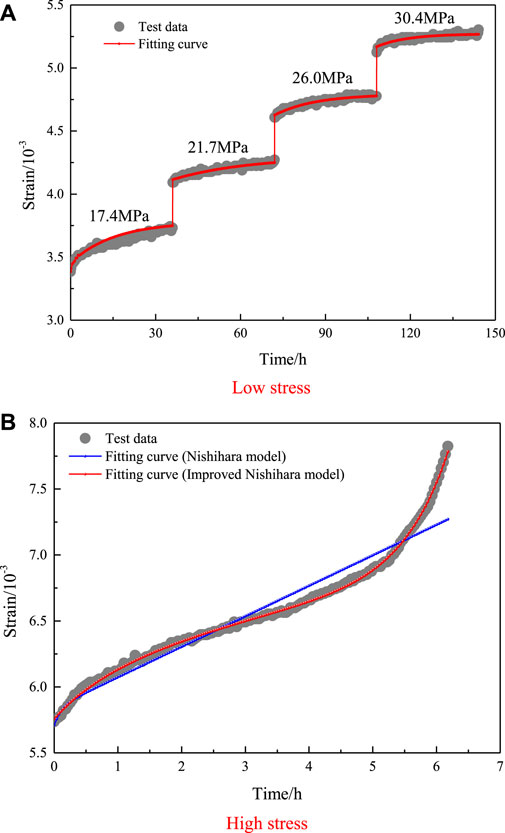
FIGURE 7. Comparisons between creep test curves and model curves when ${\sigma }_3=5$ MPa. (A) Low stress. (B) High stress.

FIGURE 8

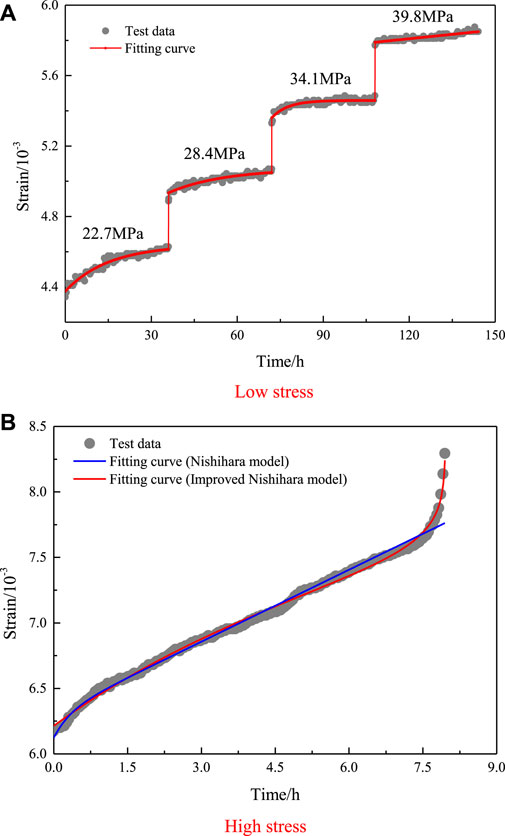
FIGURE 8. Comparisons between creep test curves and model curves when ${\sigma }_3=10$ MPa. (A) Low stress. (B) High stress.

As observed from Figures 7, 8, when the confining pressures were 5 MPa and 10 MPa, the theoretical curves of the improved Nishihara creep model were consistent with the test curves, and R² was above 0.985. This indicates that the improved Nishihara creep model can describe not only the uniaxial creep characteristics of mudstone but also the creep characteristics of mudstone under different confining pressures. Simultaneously, to compare the applicability and accuracy of the traditional and improved Nishihara models, the results obtained using the two models were fitted to the mudstone creep test results for the fifth level of stress. The comparison results show that the fitting curve of the traditional Nishihara model was significantly different from the test results for the decay creep and accelerated creep stages, and the model results were only consistent with the test results for the constant velocity creep stage. Therefore, the traditional Nishihara creep model has difficulty reflecting the nonlinear creep characteristics of mudstone; however, the improved Nishihara model can accurately describe the nonlinear characteristics of mudstone in the stages of attenuation, constant velocity, and accelerated creep under the condition of high-stress level, and the fitting curve is consistent with the test results. Therefore, the applicability and accuracy of the improved Nishihara creep model are higher than those of the traditional Nishihara model, and the improved model describes the mudstone nonlinear creep process with higher accuracy.

In order to further verify the applicability of the improved Nishihara creep model to other types of rocks, the model was validated using sandstone creep test data from the work of Liu D. Y. et al. (2017). There are six test loading stages, and the stress levels of each stage are listed in Table 6. The comparison results between the test data and the theoretical curve of the model are shown in Figures 9–11.

TABLE 6

TABLE 6. Stress levels of the compression creep test.

FIGURE 9

FIGURE 9. Comparisons between creep test curves and theoretical curves when ${\sigma }_3=0$ MPa.

FIGURE 10

FIGURE 10. Comparisons between creep test curves and model curves when ${\sigma }_3=5$ MPa.

FIGURE 11

FIGURE 11. Comparisons between creep test curves and model curves when ${\sigma }_3=10$ MPa.

From Figures 9–11, it can be seen that under three different confining pressures, the experimental data at any stress level are basically consistent with the theoretical curve. Especially after the stress level exceeds the long-term strength of the sandstone, the sandstone undergoes attenuation creep, constant velocity creep, and accelerated creep processes, with particularly obvious nonlinear characteristics. The improved Nishihara creep model can accurately describe the three creep stages of the sandstone, and its applicability and accuracy are further verified.

The accuracy (R²) of the creep fitting curve for sandstone at each stress level is shown in Table 7.

TABLE 7

TABLE 7. Stress levels of the compression creep step loading test.

According to Table 7, the fitting accuracy of the experimental data and theoretical model is relatively high under different confining pressures. Especially under high-stress conditions, the fitting accuracy of the improved Nishihara creep model is 0.996, 0.994, and 0.998, respectively, which is basically close to 1, indicating that the improved model can describe the sandstone non-linear creep process with higher accuracy.

5 Conclusion

1. A creep damage variable considering the accumulation of plastic deformation was introduced into a viscoplastic body that was connected in parallel to a plastic body to establish a damaged viscoplastic body. This was used to replace the viscoplastic body of the traditional Nishihara creep model, thereby establishing an improved Nishihara creep model. When the applied stress level is less than the long-term strength of the rock, the improved Nishihara model reduces to the generalized Kelvin creep model.

2. According to the series–parallel stress–strain relationship and superposition principle, the one- and three-dimensional creep equations of the improved Nishihara creep model under low- and high-stress conditions were derived, respectively. Compared with the creep equation of the traditional Nishihara model, the creep equation of the improved Nishihara model has only one additional model parameter, and therefore, the equation is simple.

3. The applicability and accuracy of the improved Nishihara creep model were verified using uniaxial and conventional triaxial compression creep test results for mudstone and sandstone under different confining pressures. The results show that the creep model can not only accurately reflect the nonlinear characteristics of the creep curve in the attenuation and constant velocity stages but also describe the accelerated creep characteristics of mudstone and sandstone under high-stress conditions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors contributed to the study conception and design. Material preparation and data collection and analysis were performed by YC and LZ. The first draft of the manuscript was written by YC. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Natural Science Research Project in the Universities of Anhui Province (KJ2021A1056) and the National Natural Science Foundation of China (51874005).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, W. J., Rong, X. L., Ping, S. Z., and Shan, S. Z. (2015). An improved Maxwell creep model for salt rock. Geo Mech. Eng. 9, 499–511. doi:10.12989/gae.2015.9.4.499

CrossRef Full Text | Google Scholar

Cao, P., Wen, Y. D., Wang, Y. X., Yuan, H. P., and Yuan, B. X. (2016). Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ. Earth Sci. 75, 900–908. doi:10.1007/s12665-016-5699-x

CrossRef Full Text | Google Scholar

Chao, L., Feng, L. J., Wei, C. Z., Da, L. G., Cheng, L., and Yi, R. (2021). Study on salt rock creep characteristics of wellbore under high temperature and high pressure. J. Porous Media 25, 51–69. doi:10.1615/JPORMEDIA.2021040126

CrossRef Full Text | Google Scholar

Hu, Y. Y. (2018). Shear hyperbolic-type equivalent-time rheological model. Chin. J. Geotech. Eng. 40, 1549–1555. doi:10.11779/CJGE201808023

CrossRef Full Text | Google Scholar

Liu, D. Y., Xie, L. J., Tuo, X. F., and Long, L. J. (2017b). Creep properties of sandstone under different confining pressures and research on a nonlinear viscoelasto-plastic creep model. Chin. J. Rock Mech. Eng. 36 (S2), 3705–3712. doi:10.13722/j.cnki.jrme.2017.0023

CrossRef Full Text | Google Scholar

Liu, H. Z., Xie, H. Q., He, J. D., Xiao, M. L., and Zhuo, L. (2017a). Nonlinear creep damage constitutive model for soft rocks. Mech. Time Depend. Mater 21, 73–96. doi:10.1007/s11043-016-9319-7

CrossRef Full Text | Google Scholar

Mingyuan, Y., Liu, B., Sun, Jinglai, Feng, W., and Wang, Q. (2020). Study on improved nonlinear viscoelastic-plastic creep model based on the Nishihara Model. Geotechnical Geol. Eng. 38, 1–12. doi:10.1007/s10706-020-01217-5

CrossRef Full Text | Google Scholar

Nazary Moghadam, S., Mirzabozorg, H., and Noorzad, A. (2013). Modeling time-dependent behavior of gas caverns in rock salt considering creep, dilatancy and failure. Tunn. Undergr. Space Technol. 33, 171–185. doi:10.1016/j.tust.2012.10.001

CrossRef Full Text | Google Scholar

Norton, F. H. (1929). The creep of steel at high temperatures. New York: McGraw-Hill Book Company Incorporated.

Google Scholar

Oh, C. S., Kim, N. H., Kim, Y. J., Davies, C., Nikbin, K., and Dean, D. (2011). Creep failure simulations of 316H at 550°C: Part I. A method and validation. Eng. Fract. Mech. 78, 2966–2977. doi:10.1016/j.engfracmech.2011.08.015

CrossRef Full Text | Google Scholar

Qi, Y. J., Wang, Z. J., and Zhou, C. B. (2012). 3D creep constitutive equation of modified Nishihara model and its parameters identification. Chin. J. Rock Mech. Eng. 31, 347–355. doi:10.3969/j.issn.1000-6915.2012.02.014

CrossRef Full Text | Google Scholar

Ren, X., Xin, Y., Jia, B., Gao, K., Li, X., and Wang, Y. (2022). Large stress-gradient creep tests and model establishment for red sandstone treated at high temperatures. Energies 15, 7786. doi:10.3390/en15207786

CrossRef Full Text | Google Scholar

Shi, H., Song, L., Zhang, H., Chen, W., Lin, H., Li, D., et al. (2022). Experimental and numerical studies on progressive debonding of grouted rock bolts. Int. J. Min. Sci. Technol. 32, 63–74. doi:10.1016/j.ijmst.2021.10.002

CrossRef Full Text | Google Scholar

Tang, S., Li, J., Ding, S., and Zhang, L. (2022). The influence of water-stress loading sequences on the creep behavior of granite. Bull. Eng. Geol. Environ. 81, 482. doi:10.1007/s10064-022-02987-3

CrossRef Full Text | Google Scholar

Wang, J. G., Sun, Q. L., Liang, B., Yang, P. J., and Yu, Q. R. (2020). Mudstone creep experiment and nonlinear damage model study under cyclic disturbance load. Sci. Rep. 10, 9305. doi:10.1038/s41598-020-66245-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, J., Tu, S., Xuan, F., Zhang, X., and Gao, X. (2016). Effects of stress level and stress state on creep ductility: Evaluation of different models. J. Mater Sci. Technol. 32, 695–704. doi:10.1016/j.jmst.2016.02.014

CrossRef Full Text | Google Scholar

Wu, H., Jia, Q., Wang, W. J., Zhang, N., and Zhao, Y. M. (2021). Experimental test on nonuniform deformation in the tilted strata of a deep coal mine. Sustainability 13, 13280. doi:10.3390/su132313280

CrossRef Full Text | Google Scholar

Wu, Y., Hu, J., and Wen, G. (2022). Study on creep characteristics of water saturated phyllite. Sustainability 14, 12508. doi:10.3390/su141912508

CrossRef Full Text | Google Scholar

Xu, W. Y., Yang, S. Q., and Chu, W. J. (2006). Nonlinear viscoelasto-plastic rheological model (Hohai model) of rock and its engineering applications. Chin. J. Rock Mech. Eng. 25, 433–437. doi:10.3321/j.issn:1000-6915.2006.03.001

CrossRef Full Text | Google Scholar

Yan, Y., Si-jing, W., and En-zhi, W. (2010). Creep equation of variable parameters based on Nishihara model. Rock Soil Mech. 31, 3025–3035. doi:10.16285/j.rsm.2010.10.019

CrossRef Full Text | Google Scholar

Zhang, L. L., and Wang, X. J. (2019). Rock damage creep model based on generalized Burgers model. China Saf. Sci. J. 29, 125–131. doi:10.16265/j.cnki.issn1003-3033.2019.01.021

CrossRef Full Text | Google Scholar

Zhang, L. L., and Wang, X. J. (2021). Study on nonlinear damage creep model for rocks under cyclic loading and unloading. Adv. Mater Sci. Eng. 2021, 1–10. doi:10.1155/2021/5512972

CrossRef Full Text | Google Scholar

Zhang, X., Wei, C., and Zhang, H. (2021). Analysis of surrounding rock creep effect on the long-term stability of tunnel secondary lining. Shock Vib. 2021, 1–8. doi:10.1155/2021/4614265

CrossRef Full Text | Google Scholar

Zhao, K., Ma, H. L., Yang, C. H., Chen, X. C., Liu, Y. B., Liang, X. P., et al. (2021). Damage evolution and deformation of rock salt under creep-fatigue loading. Rock Mech. Rock Eng. 54, 1985–1997. doi:10.1007/s00603-020-02342-6

CrossRef Full Text | Google Scholar

Zhao, Y. L., Wang, Y. X., Wang, W. J., Tang, L. M., Liu, Q., and Cheng, G. M. (2019). Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 101, 59–66. doi:10.1016/j.tafmec.2019.01.026

CrossRef Full Text | Google Scholar

Zhao, Y. L., Wang, Y. X., Wang, W. J., Wan, W., and Tang, J. Z. (2017a). Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. Sci. 93, 66–75. doi:10.1016/j.ijrmms.2017.01.004

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. Y., Asce, M., Wang, W. J., Wan, W., and Ma, W. H. (2018). Separation of elastoviscoplastic strains of rock and a nonlinear creep model. Int. J. Geomech. 18 (1), 04017129. doi:10.1061/(asce)gm.1943-5622.0001033

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. Y., Wang, W. J., Wan, W., Li, S. Q., Ma, W. H., et al. (2017b). Creep behavior of intact and cracked limestone under multi-level loading and unloading cycles. Rock Mech. Rock Eng. 50, 1409–1424. doi:10.1007/s00603-017-1187-1

CrossRef Full Text | Google Scholar