Coaxially swirled porous disks flow simultaneously induced by mixed convection with morphological effect of metallic/metallic oxide nanoparticles

This study focuses on the numerical modeling of coaxially swirling porous disk flow subject to the combined effects of mixed convection and chemical reactions. We conducted numerical investigations to analyze the morphologies of aluminum oxide (Al₂O₃) and copper (Cu) nanoparticles under the influence of magnetohydrodynamics. For the flow of hybrid nanofluids, we developed a model that considers the aggregate nanoparticle volume fraction based on single-phase simulation, along with the energy and mass transfer equations. The high-order, nonlinear, ordinary differential equations are obtained from the governing system of nonlinear partial differential equations via similarity transformation. The resulting system of ordinary differential equations is solved numerically by the Runge–Kutta technique and the shooting method. This is one of the most widely used numerical algorithms for solving differential equations in various fields, including physics, engineering, and computer science. This study investigated the impact of various nanoparticle shape factors (spherical, platelet and laminar) subject to relevant physical quantities and their corresponding distributions. Our findings indicate that aluminum oxide and copper (Al₂O₃-Cu/H₂O) hybrid nanofluids exhibit significant improvements in heat transfer compared to other shape factors, particularly in laminar flow. Additionally, the injection/suction factor influences the contraction/expansion phenomenon, leading to noteworthy results concerning skin friction and the Nusselt number in the field of engineering. Moreover, the chemical reaction parameter demonstrates a remarkable influence on Sherwood’s number. The insights gained from this work hold potential benefits for the field of lubricant technology, as they contribute valuable knowledge regarding the behavior of hybrid nanofluids and their associated characteristics.

1 Introduction

Multiple inorganic materials combined in hybrid magnetic nanoparticles provide versatile platforms for achieving efficient heat transport in response to various external stimuli. The amalgamation of copper (Cu) and aluminum oxide (Al₂O₃) makes available a stable hybrid nanofluid system with superior thermal properties. Cu–Al₂O₃ hybrid nanoparticles can be made stable in this way. Yi et al. (1999) presented a thermodynamic examination of aluminate balance withinside the eutectic bonding of Cu with Al₂O₃. In their study on MHD hybrid alumina-copper/water nanofluid flow through a porous medium, Yashkun et al. (2021) discovered that the hybrid nanofluid exhibits faster heat transmission compared to pure nanofluids on a porous stretching/shrinking surface. Ahmad et al. (2021) analyzed the hybrid nanofluid flow of mass and thermal transfer parameters with nanoparticles Al₂O₃-Cu flowing over permeable media. In the nonlinear flow of mixed Marangoni convection with entropy generation, Li et al. (2021) examined the dynamics of aluminum oxide and copper hybrid nanofluids. An experimental and theoretical evaluation of thermal transfer increases utilizing a hybrid nanofluid of CuO/Al₂O₃ nanoparticles in water was carried out by Plant et al. (2020). The flowing of radiated magnetohydrodynamic hybrid nanofluids along a permeability porous plate with a temperature source to support incorporated in the porous medium was explored by Agrawal et al. (2021). Ramzan et al. (2022) investigated the hybrid MHD nanofluid CuO-Al₂O₃/C₂H₆O₂ entropy development of a flow amidst two rotating discs. The alliance of thermal radiation and nonlinear mixed convection is especially important in human physiological organs, skin vasodilation, and changing environments. Adeniyan et al. (2021) numerically examined the effect of thermal radiation and generating second-grade mixed convection flow with varying physical characteristics. Jasim et al. (2021) used a vented encloser with an inner spinning cylinder to investigate the hybrid nanofluids (HNF) mixed convection flow. Jawad et al. (2021) analytically investigated the MHD mixed convection flow for a Maxwell nanofluid with the influence of Dufour and Soret. Othman et al. (2017) investigated the stagnation point flowing of the MC fluid thicknesses on a steeply growing medium. Hayat et al. (2016) investigated the impact of heat conduction and simultaneous energy absorption/generation using MHD nanofluids in the region of a porous plate. GoharSaeed Khan et al. (2022) studied mixed convection and the flow of thermally radiative hybrid nanofluids on a curved surface.

Fluids containing coaxially swirled disks have also been employed as enhanced lubricants in modern lubrication technology and have many significant implications in the areas of crystal formation, biomechanical, viscometer, rotating machinery, and storage devices for computers (Ali et al., 2014). Usha and Ravindran (2001) studied the numerical analysis of film cooling on a revolving disk. The thermal resistance in nanofluids flowing across a revolving porous disk was studied by Bachok et al. (2011). Anuar et al. (2020) conducted a study to investigate the influence of magnetohydrodynamics (MHD) on the characteristics of a steady two-dimensional (2D) mixed convection flow that is induced by a nonlinear surface within carbon nanotubes. Turkyilmazoglu (2022) undertook a study in which they utilized a horizontally uniform magnetic field to regulate the flow dynamics induced by a rotating disk. The research also focused on scrutinizing the energy equation when subjected to such a horizontal magnetic field. The numerical study discussed the radial viscous fluid flow, whereas the steady viscous flow between two permeable disks was addressed in other studies (Rasmussen, 1970; Elcrat, 1976; Raza et al., 2022; Raza et al., 2023).

The morphology of nanomaterials has been found to have a significant impact on their interactions with optical photons and waves, as well as with nanoparticle (NP) mobility inside the circulatory system, behavior within internalized cells, and immunological responses. The nonspherical NPs persist longer in the blood than spherical ones due to their higher blood circulation time. Similarly, rod-shaped NPs perform better than cubical, cylindrical, and spherical NPs in terms of uptake. The use of long carbon nanotubes (CNTs) to connect an electrical circuit is an example of how nanoparticle morphologies tend to fulfill their various roles (Abdelmalek et al., 2021). A computational experiment was conducted by Vanaki et al. (2014) to examine how different nanofluids affected heat or fluid processes across cylinder-shaped, wavy surface lakes. Their main objective was to explore the thermal profile of different nonmetallic nanoparticle fluid flow properties, as well as their distribution and forms (platelets, blades, bricks, spheres, and cylinders). The impact of NPs on nanofluid dynamics viscosity was investigated by Ghozatloo et al. (2015). Zhang et al. (2016) examined the thermal characteristics, photothermal process potency, and heat transfer-physical parameters of ionic liquid (IL)-based nanofluids with various CNT morphologies. The impact of temperature, volume fraction, size, variety of substance, and form on morphology to depth for nanofluid sweetening was investigated by Soroush et al. (Sadripour and Chamkha (2019). The melted temperature distribution, changelessness investigation, and stochastic heat flux of a hybrid Cu-Al₂O₃/H₂O nanofluids flow were investigated by Mabood et al. (2021). Khashi’ie et al. (2021) investigated the unstable compressing movement of Cu-Al₂O₃/water hybrid nanofluids in a magnetically fluxed horizontal tube. Biswas et al. (2021) studied the MHD heat dispersion of Cu-Al₂O₃/water hybrid nanofluids filled with porous materials subjected to half-sinusoid nonuniform heating. Hussain S. M. et al. (2022) used computational and statistical techniques to study the dynamic behavior of Cu-Al₂O₃/water hybrid nanofluids moving across an enormously flexible layer with Navier’s partial slip and heat leap situations. Turkyilmazoglu (2023a) investigated the fluid flow and heat transfer phenomena between a rotating cone and a stretching disk. Armaghani et al. (2021) investigated MHD mixed convection of a localized heat source/sink in an Al₂O₃-Cu/water hybrid nanofluid in an L-shaped cavity. Kumar (2022) examined the movement of Cu-Al₂O₃/engine oil Williamson hybrid nanofluids with viscous dissipation and radiation across a stretching/shrinking Riga plate. Asghar et al. (2022) delved into the intricacies of the 2-D flow behavior of an extraordinary hybrid nanofluid, encompassing the synergistic interplay of mixed convection and radiative phenomena. The study focused on a vertically exponentially declining sheet with partial slip conditions and revealed novel insights into this complex system.

Examples of flow between two discs include biomechanics, oceanography rotating machinery, heat and mass exchangers, crystal formation processes, lubricants, computer storage systems, and viscometry. Proper lubrication of thrust bearings helps keep the discs apart. As lubricating oils have improved, modern lubrication technology has used fluids with polymer additives (Iqbal et al., 2015). The main goal of an article by Zubair et al. (Qureshi et al., 2021a) is to explain how to optimize entropy creation by inducing hybrid magnetized nanoparticles between two coaxially rotating porous discs. To generate 3-D hybrid nanofluid flow and thermal diffusion, a flexible (stretching/shrinking) surface with power-law velocity and orthogonal surface shear was studied by Khashi’ie et al. (2020). Bilal et al. (2022) observed that as single-phase nano-liquids flow between permeable discs, the shape of induced hybridized metallic and nonmetallic nanoparticles changed. Umair et al. (Khan et al., 2021) examined the hybrid nanofluid flow computational modeling of a porous radially heated shrinking/stretching disc. Turkyilmazoglu (2023b) carried out an extensive investigation to analyze the intricate dynamics of 3-dimensional viscous flow induced by the expansion or contraction of a porous slider. Rahman et al. (2022) investigated the repercussions of uniform suction and MHD on diverse nanofluids as they traverse a decelerating rotating disk. Hussain T. et al. (2022) found spinning discs suspended in a porous medium with microorganisms and nanoparticles create unstable three-dimensional MHD flow.

A new and novel study related to the coaxial swirled porous disks is deliberated here for hybrid nanofluid flow. Two types of nanoparticles with different morphologies are considered for heat and mass transfer purposes along with a mixed convection and chemical reaction. Improving the thermal performance inside the base fluid is challenging, and nanoparticles have a significant role in overcoming this challenge. In the aforementioned literature, there are no studies about the present elaborated fluid model according to the best of our knowledge. Because of dimensionless ordinary differential equations (ODEs), achieved expressions are transmuted using the similarity variable transformation approach. The Runge–Kutta method is used to achieve the solution of ODEs and compare two numerical methods, the Bvp4c and the shooting method. The literature review has been addressed in the first part. The problem formulation and solution approach are covered in Section 2. The results and discussion are provided in Section 3. Section 4 is devoted to the conclusion.

2 Mathematical modeling

The study investigates the time-dependent heat and mass transfer phenomena in a 2-D laminar flow. It incorporates factors such as viscous dissipation, thermal radiation, MHD, chemical reactions, Soret and Dufour effects, and mixed convection. The flow involves hybrid nanofluid combinations of metallic and nonmetallic nanoparticles suspended in water as the base fluid (specifically, Al₂O₃-Cu/H₂O). The hybrid nanofluid flows between two permeable porous disks. The separation between the disks is given by $2k\left(t\right)$, where both disks possess distinct permeability and undergo uniform expansion or contraction at a time-varying pace represented by $k^{\prime }\left(t\right)$. A magnetic field of consistent intensity ${\beta }_0$ is imposed in a direction perpendicular to the disks. In the context of a cylindrical coordinate system (r, 0, z), the velocity component u varies along the r-axis, while the component w is aligned with the z-axis. In the physical model depicted in Figure 1, ${\widehat{T}}_1$ and ${\widehat{\mathrm{C}}}_1$ refer to the temperature and concentration of the lower disk, whereas ${\widehat{T}}_u$ and ${\widehat{\mathrm{C}}}_u$ correspond to the temperature and concentration of the upper disk. The governing equations, presented in Ramesh et al. (2019) and Ullah et al. (2019), are as follows:

$\frac{\partial \widehat{u}}{\partial r}+\frac{\partial \widehat{w}}{\partial z}+\frac{\widehat{u}}{r}=0,(1)$

${\rho }_{hnf}\left(\frac{\partial \widehat{u}}{\partial t}+\widehat{u}\frac{\partial \widehat{u}}{\partial r}+\widehat{w}\frac{\partial \widehat{u}}{\partial z}\right)=-\frac{\partial P}{\partial r}+{\mu }_{hnf}\left(\frac{{\partial }^2\widehat{u}}{\partial r^2}-\frac{\widehat{u}}{r^2}+\frac{1}{r}\frac{\partial \widehat{u}}{\partial r}+\frac{{\partial }^2\widehat{u}}{\partial z^2}\right)-{\sigma }_{el}{\beta }_0^2\widehat{u}$

$+g{\left(\rho {\beta }_T\right)}_{hnf}\left(\widehat{T}-T_u\right)+g{\left(\rho {\beta }_C\right)}_{hnf}\left(\widehat{\mathrm{C}}-{\widehat{\mathrm{C}}}_u\right),(2)$

${\rho }_{hnf}\left(\frac{\partial \widehat{w}}{\partial t}+\widehat{u}\frac{\partial \widehat{w}}{\partial r}+\widehat{w}\frac{\partial \widehat{w}}{\partial z}\right)=-\frac{\partial P}{\partial z}+{\mu }_{hnf}\left(\frac{{\partial }^2\widehat{w}}{\partial r^2}+\frac{1}{r}\frac{\partial \widehat{w}}{\partial r}-\frac{\widehat{w}}{r^2}+\frac{{\partial }^2\widehat{w}}{\partial z^2}\right),(3)$

${\left(\rho C_p\right)}_{hnf}\left(\frac{\partial \widehat{T}}{\partial t}+\widehat{u}\frac{\partial \widehat{T}}{\partial r}+\widehat{w}\frac{\partial T}{\partial z}\right)=K_{hnfl}\left(\frac{{\partial }^2\widehat{T}}{\partial r^2}++\frac{1}{r}\frac{\partial \widehat{T}}{\partial r}+\frac{{\partial }^2\widehat{T}}{\partial z^2}\right)-{\mu }_{hnf}{\left(\frac{\partial \widehat{u}}{\partial \mathrm{z}}\right)}^2-\left(\frac{\partial q_r}{\partial z}\right),(4)$

$\left(\frac{\partial \widehat{C}}{\partial t}+\widehat{u}\frac{\partial \widehat{C}}{\partial r}+\widehat{w}\frac{\partial \widehat{C}}{\partial z}\right)=D\left(\frac{{\partial }^2\widehat{C}}{\partial r^2}+\frac{1}{r}\frac{\partial \widehat{C}}{\partial r}+\frac{{\partial }^2\widehat{C}}{\partial z^2}\right)-k_r\left(\widehat{\mathrm{C}}-{\widehat{\mathrm{C}}}_u\right)+\frac{{DK}_T}{T_m}\left(\frac{{\partial }^2\widehat{\mathrm{T}}}{\partial z^2}\right),(5)$

where ${\rho }_{hnf},{\mu }_{hnf}$, and ${\left(\rho C_p\right)}_{hnf}$ stand for the density, viscosity, and specific heat capacity of hybrid nanofluid, respectively, $g$ shows the gravitational acceleration, ${\sigma }_{el}$ represents the electrical conductivity, ${\beta }_0$ demonstrates the strength of the magnetic field, P shows the pressure, $k_r$ demonstrates the reaction rate, $D$ shows the coefficient of mass diffusivity, ${\beta }_C$ and ${\beta }_T$ explain the concentration and temperature coefficient of volumetric expansion, $q_r$ denotes the thermal radiation, $K_{hnfl}$ presents the nanolayer thermal conductivity of the hybrid nanofluid, ${DK}_T$ denotes the thermal diffusion ratio, $T_m$ represents the mean fluid temperature, and $\widehat{T}$ and $\widehat{C}$ represent the temperature and concentration.

FIGURE 1

FIGURE 1. Physical model.

The prescribed procedure for implementing the suitable boundary conditions is as follows:

Lower disk: At $z$ = $-$ k(t), the lower boundary and variable are shown by

$\widehat{u}=0,\widehat{w}=-A_{\ast }{k}^{\prime }\left(t\right),\widehat{\mathrm{T}}=T_l,\widehat{C}=C_l.$

Upper disk: At $z$ = k(t), the upper boundary and variable are shown by

$\widehat{u}=0,\widehat{w}=A_{\ast }{k}^{\prime }\left(t\right),\widehat{\mathrm{T}}=T_u,\widehat{C}=C_u.(6)$

The dash signifies the derivative concerning time t, and $A_{\ast }$ is the measure of partition penetrability. The appropriate similarity variables are

$\eta =\frac{z}{k},\widehat{u}=-\frac{r{\upsilon }_f}{k^2}{F}_{\eta }\left(\eta ,t\right),\widehat{w}=\frac{2{\upsilon }_f}{k}F\left(\eta ,t\right),\theta =\frac{\widehat{T}-T_u}{T_l-T_u},\chi =\frac{\widehat{C}-C_u}{C_l-C_u}.(7)$

Apply Eq. 7 in Eqs 2–5, then

$\frac{{\upsilon }_{hnf}}{{\upsilon }_f}{F}_{\eta \eta \eta \eta }+{\alpha }_{\ast }\left(3F_{\eta \eta }+\eta F_{\eta \eta \eta }\right)-2F{F}_{\eta \eta \eta }-\frac{K^2}{{\upsilon }_f}{F}_{\eta \eta t}-\frac{{\rho }_f}{{\rho }_{hnf}}{M}_{\ast }{F}_{\eta \eta }+{\lambda }_a\left(\frac{e_2}{e_1}\right){\theta }_{\eta }+{\lambda }_b\left(\frac{e_3}{e_1}\right){\chi }_{\eta }=0,(8)$

${\left(1+\frac{4}{3}{R}_d{e}_4{e}_5\right)\theta }_{\eta \eta }+\frac{{\upsilon }_f}{{\alpha }_{hnf}}\left({\alpha }_{\ast }\eta -2F\right){\theta }_{\eta }-{\mu }_{hnf}{e}_5{E}_c{F}_{\eta }^2-\frac{k^2}{{\alpha }_{hnf}}{\theta }_t=0,(9)$

${\chi }_{\eta \eta }-k^2{\chi }_t-S_c\left(2F-\eta {\alpha }_{\ast }\right){\chi }_{\eta }-S_c{K}_l\chi +S_r{\theta }_{\eta \eta }=0,(10)$

where thermal diffusivity is demonstrated by ${\alpha }_{hnf}=\frac{K_{hnfl}}{{\left(\rho C_p\right)}_{hnf}}$ of the hybrid nanofluid. Furthermore, kinematics viscosity shows ${\upsilon }_{hnf}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}$ of the HNF, where $K_{hnfl}$ is the nanolayer thermal conductivity, ${\left(\rho C_p\right)}_{hnf}$ is the specific heat capacitance of HNF, the concentration buoyancy parameter is ${\lambda }_b=\frac{bg{k^4\left({\beta }_C\right)}_f}{{\upsilon }_f}$, ${\lambda }_a=\frac{bg{k^4\left({\beta }_T\right)}_f}{{\upsilon }_f}$ shows the thermal buoyancy parameter, $S_r=\frac{D{k}_T}{T_m{v}_f}$ represents the Soret number, $K_l=\frac{k_r}{k^2}$ is the chemical reaction parameter, $E_c=\frac{u^2}{\left(T_1-T_2\right){\left(\rho C_p\right)}_f}$ is the Eckert number, ${\mu }_{hnf}$ is the viscosity of the HNF, ${\rho }_{hnf}$ is the density of HNF, and $S_c=\frac{{\upsilon }_f}{D}$ is the Schmidt number, and

$e_1=\frac{{\rho }_{hnf}}{{\rho }_f},e_2=\frac{{\left(\rho {\beta }_T\right)}_{hnf}}{{\left(\rho {\beta }_T\right)}_f},e_3=\frac{{\left(\rho {\beta }_C\right)}_{hnf}}{{\left(\rho {\beta }_T\right)}_f},e_4=\frac{k_f}{k_{hnfl}},e_5=\frac{{\left(\rho C_p\right)}_f}{{\left(\rho C_p\right)}_{hnf}}.$

The associated boundary conditions are:

Lower disk boundary condition:

$\eta =-1,F=-R_e,,{,F}_{\eta }=0,\theta =1,\mathrm{o}\mathrm{r}\chi =1.$

Upper disk boundary condition:

$at\eta =1,F=R_e,,{,F}_{\eta }=0,\theta =0,\mathrm{o}\mathrm{r}\chi =0.(11)$

Here, the Reynold’s number is denoted by $R_e=\frac{A_{\ast }k{k}^{\prime }\left(t\right)}{2{\upsilon }_f}$, the permeability parameter is shown by $A_{\ast }$, and $A_{\ast }=A_{\ast }\left({\alpha }_{\ast },R_e\right)=$ $\frac{R_e}{2{\alpha }_{\ast }}$ , where ${\alpha }_{\ast }=\frac{k{k}^{\prime }\left(t\right)}{{\upsilon }_f}$ is the ratio of wall expansion.

We use the approximation of Rosseland to simplify $q_r$ as

$q_r=\left(\frac{4{\sigma }^{*}}{3k^{*}}\right)\frac{\partial {\widehat{T}}^4}{\mathit{\partial }z}=\left(\frac{16{\sigma }^{*}{\widehat{T}}_u^3}{3k^{*}}\right)\frac{\partial \widehat{T}}{\partial z},$

where ${\sigma }^{*}$ stands for Stefan Boltzmann’s fixed values ${\sigma }^{*}=5.66970\times {10}^{-8}W{m}^{-2}{K}^{-4}$ and the $k^{*}$ parameter shows the mean absorption coefficient.

Here, the $\alpha$ is constant, and then $f=f\left(\eta \right)$, $\theta =\theta \left(\eta \right)$, and $\chi =\chi \left(\eta \right)$. Therefore, ${\theta }_t=0$ and $f_{\eta \eta t}=0$. Following Kashif et al. (Ali et al., 2014), we set $F=f{R}_e$ for the analysis. Thus, we have

$\frac{{\upsilon }_{hnf}}{{\upsilon }_f}{f}_{\eta \eta \eta \eta }+{\alpha }_{\ast }\left(3f_{\eta \eta }+\eta f_{\eta \eta \eta }\right)-2R_{e}f{f}_{\eta \eta \eta }-\frac{1}{e_1}{M}_{\ast }{f}_{\eta \eta }+{\lambda }_a\left(\frac{e_2}{e_1}\right){\theta }_{\eta }+{\lambda }_b\left(\frac{e_3}{e_1}\right){\chi }_{\eta }=0,(12)$

${\left(1+\frac{4}{3}{R}_d{e}_4{e}_5\right)\theta }_{\eta \eta }+\frac{e_4}{e_5}{P}_r\left({\alpha }_{\ast }\eta -2R_{e}f\right){\theta }_{\eta }-{\mu }_{hnf}{e}_5{E}_c{R}_e^2{f}_{\eta }^2=0,(13)$

${\chi }_{\eta \eta }-S_c\left(2R_{e}f-\eta {\alpha }_{\ast }\right){\chi }_{\eta }-S_c{K}_l\chi +\frac{S_{r}a}{b}{\theta }_{\eta \eta }=0.(14)$

The associated boundary conditions are:

Upper disk final boundary condition:

$f=-1,f_{\eta }=0,\theta =1,and\chi =1\eta =-1,$

at Lower disk boundary condition:

$f=1,f_{\eta }=0,\theta =0,and\chi =0,\mathrm{a}\mathrm{t}\eta =1.(15)$

Table 1 shows the thermophysical properties of the hybrid nanofluid, and Table 2 denotes the base fluid and different nanoparticle properties. Where the first and second nanoparticle volume fractions are indicated by ${\varphi }_{s1}$ and ${\varphi }_{s2}$, the density of solid or base fluid nanoparticles is demonstrated by ${\rho }_{s1}$, ${\rho }_{s2}$, and ${\rho }_f$. The specific heat capacities of the first or second solid and base fluid nanoparticles are represented by ${\left(\rho C_p\right)}_{s2},{\left(\rho C_p\right)}_{s2}$, and ${\left(\rho C_p\right)}_f$, the thermal and concentration expansions of the hybrid nanofluid or the first and second nanoparticles are denoted by ${\left(\rho {\beta }_T\right)}_{hnf},{{\left(\rho {\beta }_C\right)}_{hnf},{\left(\rho {\beta }_C\right)}_{s1},\left(\rho {\beta }_T\right)}_{s1}$, ${\left(\rho {\beta }_T\right)}_{s2}$, and ${\left(\rho {\beta }_C\right)}_{s2}$, the nanolayer thermal conductivity of the HNF is shown by $k_{hnfl}$, $k_{nf}$, and $k_{bf}$ representing the nanolayer thermal conductivity of the hybrid nanofluid, nanofluid, and base fluid, ${\mathrm{k}}_{\mathrm{n}\mathrm{f}\mathrm{l}}$ is the TC of the nanofluid, S indicates the shape of the nanoparticles, and the first and second solid nanoparticles and base fluid thermal conductivities are denoted by ${\mathrm{k}}_{\mathrm{s}1}$ and ${\mathrm{k}}_{\mathrm{s}2}$, ${\mathrm{k}}_{\mathrm{b}\mathrm{f}}.$

TABLE 1

TABLE 1. Thermophysical properties of the HNF (Islam et al., 2020).

TABLE 2

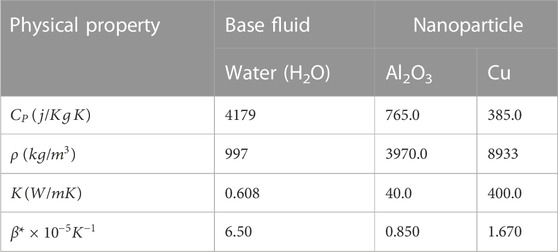
TABLE 2. Physical properties of the base fluid and the nanoparticles (Qureshi et al., 2021b and Xu, 2019).

2.1 Quantities of engineering interest

The engineering-related coefficients, including the Nusselt number, the Sherwood variable, and the skin friction coefficients at both permeable disks, are estimated in the following paragraph.

Skin friction coefficients (SFC): $C_{f1}$ and $C_{f-1}$ are the SFCs of the upper and lower porous disks and are expressed as

$C_{f-1}=\frac{r{\varsigma }_{zr}{\mathrm{ǀ}}_{\eta =-1}}{k{\rho }_f{\left(K^{\prime }{A}_1\right)}^2}=\frac{\left({\left(1-{\varphi }_{\mathrm{s}1}-{\varphi }_{\mathrm{s}2}\right)}^{-2.5}\right)}{R_e}{f}^{″}\left(-1\right)and{C}_{f1}=\frac{r{\varsigma }_{zr}{ǀ}_{\eta =1}}{k{\rho }_f{\left(K^{\prime }{A}_1\right)}^2}=\frac{\left({\left(1-{\varphi }_{\mathrm{s}1}-{\varphi }_{\mathrm{s}2}\right)}^{-2.5}\right)}{R_e}{f}^{″}\left(1\right),(16)$

where the radial direction of the shear stress above and below the porous disk is denoted by ${\varsigma }_{zr}$.

${\varsigma }_{zr}{ǀ}_{\eta =-1}={\mu }_{hnf}\left(\frac{\partial \widehat{u}}{\partial z}\right){ǀ}_{\eta =-1}\mathrm{a}\mathrm{n}\mathrm{d}{\varsigma }_{zr}{ǀ}_{\eta =1}={\mu }_{hnf}\left(\frac{\partial \widehat{u}}{\partial z}\right){ǀ}_{\eta =1}.(17)$

Nusselt number: $N_u{ǀ}_{\eta =-1}$ and $N_u{ǀ}_{\eta =1}$ denote the upper and lower flow of calculated heat transfer, respectively.

$N_u{ǀ}_{\eta =-1}=\frac{k{s}_z}{k_f\left(T_1-T_2\right)}{ǀ}_{\eta =-1}=\frac{k_{hnf}}{k_f}{\theta }^{\prime }\left(-1\right),\mathrm{a}\mathrm{n}\mathrm{d}{N}_u{ǀ}_{\eta =1}=\frac{k{s}_z}{k_f\left(T_1-T_2\right)}{ǀ}_{\eta =1}=\frac{k_{hnf}}{k_f}{\theta }^{\prime }\left(1\right),(18)$

where $s_z$ denotes the flow of heat flux, which is followed as

$s_z{ǀ}_{\eta =-1}=-k_{hnf}\left(\frac{\partial T}{\partial z}\right){ǀ}_{\eta =-1}and{s}_z{ǀ}_{\eta =1}=-k_{hnf}\left(\frac{\partial T}{\partial z}\right){ǀ}_{\eta =1}.$

Sherwood number: The Sherwood numbers (mass transfer rate) ${Sh⃓}_{\eta =1}$ and ${Sh⃓}_{\eta =-1}$ at the upper and lower disks have the following equations:

${Sh⃓}_{\eta =1}=\frac{{kq}_z}{D\left(C_l-C_u\right)}{⃓}_{\eta =1}=-{\chi }^{\prime }\left(1\right)\mathrm{a}\mathrm{n}\mathrm{d}{Sh⃓}_{\eta =-1}=\frac{{kq}_z}{D\left(C_l-C_u\right)}{⃓}_{\eta =-1}=-{\chi }^{\prime }\left(-1\right),(19)$

where

$q_z{⃓}_{\eta =1}=-D\left(\frac{\partial C}{\partial z}\right){ǀ}_{\eta =1}\mathrm{a}\mathrm{n}\mathrm{d}{q}_z{⃓}_{\eta =-1}=-D\left(\frac{\partial C}{\partial z}\right){ǀ}_{\eta =-1}.$

2.2 Numerical procedure

The complexity and boundary value constraints of the ODEs presented in Eqs 12–15 make it impractical to obtain analytical solutions. Therefore, we used the shooting technique to convert the complex boundary problems into initial problems and then used the Runge–Kutta method to obtain an accurate solution. The Runge–Kutta approach offers advantages in terms of computational speed and its ability to handle initial value problems. Various numerical techniques are used to solve the boundary values problem numerically using different numerical methods (Hidayat, 2021; Hidayat, 2023). It efficiently addresses the issue of finding the missing initial value through a shooting strategy, which is particularly important in real-world applications. Overall, the Runge–Kutta method is important because it provides accurate, versatile, stable, efficient, and robust approximations to solutions of ordinary differential equations. It allows researchers and practitioners to solve complex problems in various fields, leading to advancements and practical solutions in science and engineering. The shooting approach allows the differential equation to be integrated as an initial value issue, successfully accounting for the absence of initial values at the start of the interval. If there is an error, a new value for the missing starting condition is added. This iterative approach is repeated until the computed results match the criteria. The final forms of the system of ordinary differential equations are:

$\frac{{\left(1-{\varphi }_{s1}-{\varphi }_{s2}\right)}^{-2.5}}{e_1}{f}_{\eta \eta \eta \eta }+{\alpha }_{\ast }\left(3f_{\eta \eta }+\eta f_{\eta \eta \eta }\right)-2R_{e}f{f}_{\eta \eta \eta }-\frac{1}{e_1}{M}_{\ast }{f}_{\eta \eta }+{\lambda }_a\left(\frac{e_2}{e_1}\right){\theta }_{\eta }+{\lambda }_b\left(\frac{e_3}{e_1}\right){\chi }_{\eta }=0.(20)$

${\theta }_{\eta \eta }+\frac{1}{\left(1+\frac{4}{3}{R}_d{e}_4{e}_5\right)}\left(\frac{e_4}{e_5}{P}_r\left({\alpha }_{\ast }\eta -2R_{e}f\right){\theta }_{\eta }-{\mu }_{hnf}{e}_5{E}_c{R}_e^2{f}_{\eta }^2\right)=0.(21)$

${\chi }_{\eta \eta }-S_c\left(2R_{e}f-\eta {\alpha }_{\ast }\right){\chi }_{\eta }-S_c{K}_l\chi +\frac{S_{r}a}{b}{\theta }_{\eta \eta }=0.(22)$

By putting the value from Table 3 into Eqs 24–26, the final results are

$G_1{f}_{\eta \eta \eta \eta }+{\alpha }_{\ast }\left(3f_{\eta \eta }+\eta f_{\eta \eta \eta }\right)-2R_{e}f{f}_{\eta \eta \eta }-\frac{1}{e_1}{M}_{\ast }{f}_{\eta \eta }+{\lambda }_a\left(\frac{e_2}{e_1}\right){\theta }_{\eta }+{\lambda }_b\left(\frac{e_3}{e_1}\right){\chi }_{\eta }=0,(23)$

${\theta }_{\eta \eta }+G_2\left(\frac{e_4}{e_5}{P}_r\left({\alpha }_{\ast }\eta -2R_{e}f\right){\theta }_{\eta }-G_3{f}_{\eta }^2\right)=0,(24)$

${\chi }_{\eta \eta }-S_c\left(2R_{e}f-\eta {\alpha }_{\ast }\right){\chi }_{\eta }-S_c{K}_l\chi +G_4{\theta }_{\eta \eta }=0.(25)$

TABLE 3

TABLE 3. Coefficients of the equations.

2.3 Solution of the problem

We employed the RK technique to ascertain the solution for the prevailing current flow model. The modification must be as follows to begin the process:

$j_1^{*.}=f\left[\eta \right],j_2^{*.}=f^{\prime }\left[\eta \right],j_3^{*.}=f^{″}\left[\eta \right],j_4^{*.}=f^{‴}\left[\eta \right],j_5^{*.}=\theta \left[\eta \right],j_6^{*.}={\theta }^{\prime }\left[\eta \right],j_7^{*.}=\chi \left[\eta \right],j_8^{*.}={\chi }^{\prime }\left[\eta \right].(26)$

Using Eq. 26 and Eqs 23–25, we obtain:

$j_1^{*{.}^{\prime }}=j_2^{*.},(27)$

$j_2^{*{.}^{\prime }}=j_3^{*.},(28)$

$j_3^{*{.}^{\prime }}=j_4^{*.},(29)$

$j_4^{\ast {.}^{\prime }}=\frac{1}{G_1}\left(-{\alpha }_{\ast }\left(3j_3^{\ast .}+\eta j_4^{\ast .}\right)+2R_e{j}_1^{\ast .}{j}_4^{\ast .}+\frac{1}{e_1}{M}_{\ast }{j}_3^{\ast .}-{\lambda }_a\left(\frac{e_2}{e_1}\right)j_6^{\ast .}-{\lambda }_b\left(\frac{e_3}{e_1}\right)j_8^{\ast .}\right),(30)$

$j_5^{*{.}^{\prime }}=j_6^{*.},(31)$

$j_6^{*{.}^{\prime }}={-G}_2\left(\frac{e_4}{e_5}{P}_r\left({\alpha }_{\ast }\eta -2R_{e}f\right)j_6^{*.}-G_3{j}_2^{{*.}^2}\right),(32)$

$j_7^{*{.}^{\prime }}=j_8^{*.},(33)$

$j_8^{*{.}^{\prime }}=S_c\left(2R_{e}f-\eta {\alpha }_{\ast }\right)j_8^{*.}+S_c{K}_l{j}_7^{*.}+G_4{G}_2\left(\frac{e_4}{e_5}{P}_r\left({\alpha }_{\ast }\eta -2R_{e}f\right)j_6^{*.}-G_3{j}_2^{{*.}^2}\right).(34)$

As a result, the initial circumstance is:

$j_{1\left(\mathrm{\eta }=-1\right)}^{\ast .}=-1,j_{2\left(\mathrm{\eta }=-1\right)}^{\ast .}=0,j_{3\left(\mathrm{\eta }=-1\right)}^{\ast .}=a,j_{4\left(\mathrm{\eta }=-1\right)}^{\ast .}=b,j_{5\left(\mathrm{\eta }=-1\right)}^{\ast .}=1,j_{6\left(\mathrm{\eta }=-1\right)}^{\ast .}=0,j_{7\left(\mathrm{\eta }=-1\right)}^{\ast .}=1,j_{8\left(\mathrm{\eta }=-1\right)}^{\ast .}=0,$

where initial conditions ‘a' and ‘b' are unavailable, the aforementioned system is now solved, beginning with suitable initial conditions using Mathematica until the required accuracy is achieved.

3 Results and discussion

The numerical effects of flow as determined by Eqs 12–14 on velocity, temperature, and concentration profile are explained through Figures 2–7 in this section. The suction/injection permeable Reynolds number is $R_e$, S shows the shape size factor, the expansion ratio constraint is shown by α, ${\varphi }_{s1}$, and ${\varphi }_{s2}$ represent the first and second nanoparticles of volume friction parameters, the magnetic parameter is indicated by $M_{\ast }$, the concentration buoyancy parameter is shown by ${\lambda }_b$, the thermal radiation parameter is shown by $R_d$, $P_r$ is the Prandtl number, $K_l$ indicates the chemical reaction, $S_c$ is the Schmidt number, and the thermal buoyancy parameter is ${\lambda }_a$. Furthermore, numerical computations are conducted for the pertinent engineering parameters, such as the upward and downward skin friction coefficient (SHF) of the disk, the Nusselt number, and the Sherwood number, as presented in Tables 4, 5.

FIGURE 2

FIGURE 2. Radial velocity profile effect on
the thermal buoyancy parameter for
$$\begin{gathered} {\alpha }_{*}=-1,R_e=-1,P_r=6.2,{\varphi }_1={\varphi }_2=0.02, \\ h=0.4,r=0.8,{\lambda }_b=0.3,R_d=2,K_l=0.2, \\ {M}_{*}=1 \end{gathered}$$.

FIGURE 3

FIGURE 3. Influence of the radial velocity profile
on the magnetic parameter for $$\begin{gathered} {\alpha }_{*}=-1, \\ {R}_e=-1,P_r=6.2,{\varphi }_1={\varphi }_2=0.02,h=0.4, \\ r=0.8,{\lambda }_a=0.3,{\lambda }_b=0.3,R_d=2,K_l=0.2 \end{gathered}$$.

FIGURE 4

FIGURE 4. Chemical reaction parameter effect
on the mass concentration profile for
$$\begin{gathered} {\alpha }_{*}=-1,R_e=-1,P_r=6.2,{\varphi }_1={\varphi }_2=0.02, \\ r=1.6,{\lambda }_a=0.3,{\lambda }_b=0.3,R_d=2 \end{gathered}$$.

FIGURE 5

FIGURE 5. Influence of ${\mathit{R}}_{\mathit{d}}$ on the temperature
profile for $$\begin{gathered} {\alpha }_{*}=-1, \\ {R}_e=-1,P_r=6.2,{\varphi }_1={\varphi }_2=0.02,h=0.4, \\ r=0.8,{\lambda }_a=0.3,{\lambda }_b=0.3,K_l=0.2,M_{*}=1 \end{gathered}$$.

FIGURE 6

FIGURE 6. Impact on the radial velocity profile
on the contour for $$\begin{gathered} R_e=-1,r=0.8, \\ {\varphi }_{s1}={\varphi }_{s2}=0.02,M_{*}=1,P_r=6.2,{\alpha }_{*}=1. \end{gathered}$$

FIGURE 7

FIGURE 7. Contour of the temperature profile for $$\begin{gathered} R_e=-1,r=0.8,{\varphi }_{s1}={\varphi }_{s2}=0.02,M_{*}=1, \\ {P}_r=6.2,{\alpha }_{*}=1. \end{gathered}$$

TABLE 4

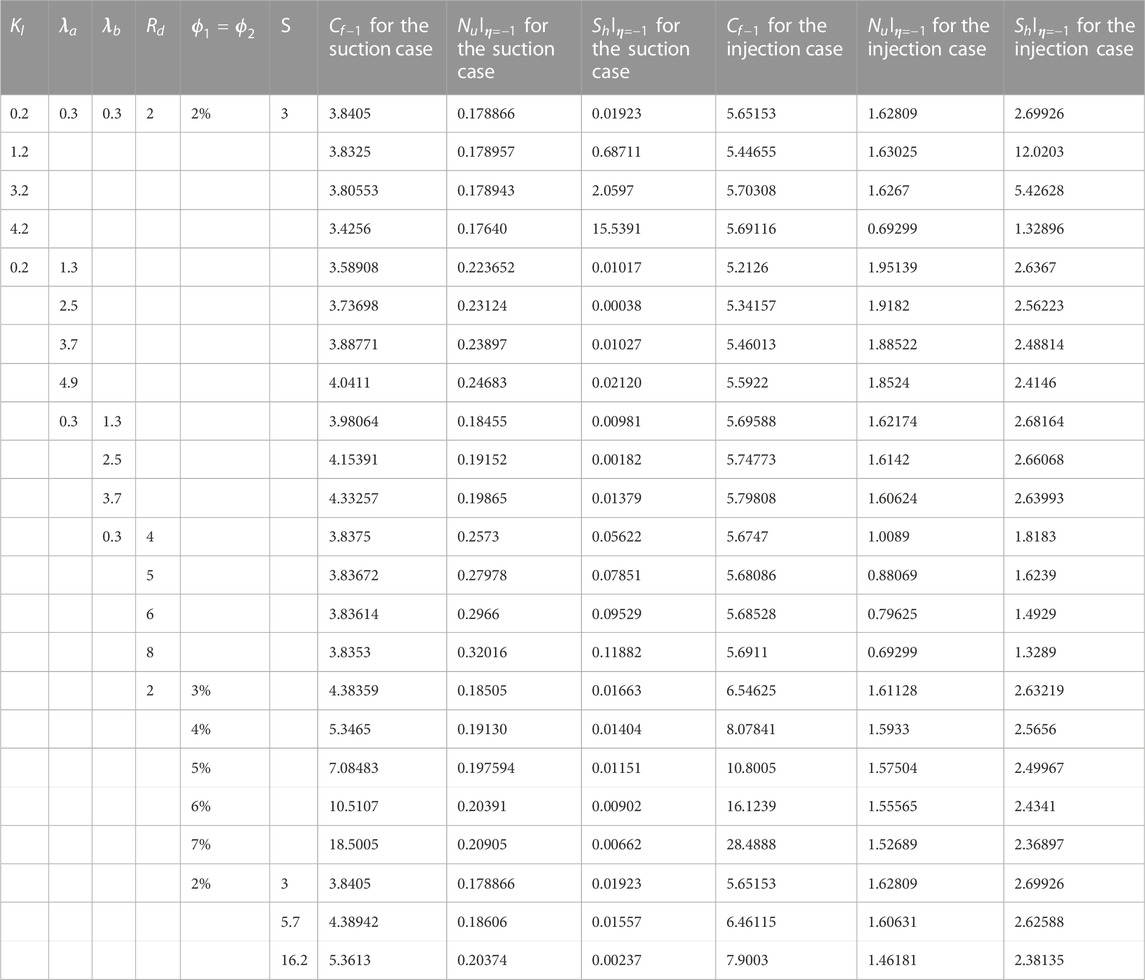
TABLE 4. Results of calculating the impact of the SFC, the Nusselt number, and the Sherwood number in cases ${\alpha }_{*}<0$ and ${\alpha }_{*}>0$ at the lower disk.

TABLE 5

TABLE 5. Comparison of the Bvp4c and shooting methods on the SFC at the lower wall.

The study analyzed the impact of the thermal buoyancy parameter on the radial velocity profile, and the results are illustrated in Figure 2. In Figure 2, the radial velocity demonstrates a dual behavior depending on the value of the thermal buoyancy parameter. Specifically, within the interval of −1 < η < 0, the radial velocity increases. However, within the interval of 0 < η < 1, the trend is inverted, as the radial velocity decreases with higher values of the thermal buoyancy parameter. This physical observation reveals that the radial velocity exhibits a growth trend for negative values of the thermal buoyancy parameter, while it experiences a decline for positive values, indicating the significant influence of thermal buoyancy on the flow dynamics.

The behavior of $M_{\ast }$ on the radial velocity profile is illustrated in Figure 3. The observed trend reveals that as the magnetic parameter increases, the radial velocity component decreases. This physical phenomenon can be attributed to the magnetic field’s influence on the flow dynamics. The magnetic field exerts a restraining effect on the motion of charged particles or conducting fluid, leading to a reduction in radial velocity. Essentially, the magnetic field acts as a controlling factor, impeding the flow and causing a decrease in the radial velocity magnitude. Figure 4 illustrates the influence of a chemical reaction parameter on the mass concentration profile. The findings indicate that as the value of the chemical reaction parameter increases, there is an augmentation in the flow of mass transfer within the concentration profile for both porous disks. This physical observation highlights the significant role played by chemical reactions in enhancing mass transfer. As the chemical reaction becomes more prominent, it facilitates the transport of species, resulting in an intensified flow of mass transfer within the system. Figure 5 illustrates the influence of thermal radiation parameters on the temperature profile. Thermal radiation in the fluid flow of porous disks refers to the transfer of heat energy through electromagnetic waves. It influences the temperature distribution by increasing heat transfer at the lower disk and decreasing it at the upper disk as the thermal radiation parameters increase. Figure 6 exhibits contour lines depicting the influence of the magnetic field strength (M) on the variation of radial velocity. The contour lines reveal that the most significant changes in velocity occur toward the boundaries, while the center remains unaffected. This physical observation demonstrates that the magnetic field exerts its effect predominantly at the periphery, leading to a pronounced alteration in the radial velocity profile.

In Figure 7, contour lines are employed to visualize the temperature variations associated with the magnetic field strength (M). The contour lines depict a consistent pattern of temperature reduction across the problem’s parameters, indicating a diminishing trend. Moreover, the contour lines appear relatively closer together around the midpoint of the problem. This suggests that the temperature changes are more significant in this region, highlighting the sensitivity of the system to magnetic field strength. Physically, the magnetic field interacts with the fluid flow, influencing the velocity and temperature profiles. In this context, the magnetic field primarily impacts the radial velocity near the boundaries, causing significant variations. Similarly, it induces temperature changes, leading to a diminishing pattern throughout the problem and a more pronounced effect in the vicinity of the system’s midpoint.

Table 4 provides valuable insights into the system’s behavior. It shows that when suction occurs ($R_e<0$) due to lower inertia than viscosity, an increase in the Nusselt number and Sherwood number is observed with higher values of the chemical reaction and thermal radiation parameters. This implies that heat transfer and mass transfer rates are enhanced in such conditions. On the other hand, when the thermal buoyancy parameter increases, the SFC and Nusselt numbers increase while the Sherwood number decreases. This indicates that the convective heat transfer is enhanced, while the rate of mass diffusion diminishes. Furthermore, the concentration buoyancy parameter and volume fraction play a significant role in heat flux, SFC, and Sherwood number. Their increase leads to significant improvements in heat transfer, fuel consumption, and mass transfer. As the values of different shapes and size factors (such as spheres, platelets, and lamina) increase, the heat transfer in the suction cases, measured by the Nusselt number, is enhanced. The shape and size factors play a role in influencing the laminar flow, with an increase in heat transfer observed as the value of the shape size factor increases. In the case of injection ($R_e>0$), where inertia exceeds viscosity, the influence of parameters like ${\lambda }_a$, ${\lambda }_b$, $R_d$, S, and ${\varphi }_1$ and ${\varphi }_2$ volume fraction on the Nusselt number varies. However, the effect of $K_l$, and ${\lambda }_a$ on the Sherwood number remains consistent. Additionally, the behavior of parameters such as ${\lambda }_a$, ${\lambda }_b$, $R_d$, S, and ${\varphi }_1$ and ${\varphi }_2$ volume fraction differs between the upper and lower porous surfaces.

Table 5 highlights the comparison between the Bvp4c method and the shooting method for the SFC at the lower wall. It is revealed that an augmentation in the magnetic parameter amplifies the SFC in both methodologies. The similarity between the results obtained from the bvp4c and the shooting method suggests the reliability and consistency of the approaches in predicting the SFC. Table 6 presents a numerical comparison between the results obtained in the previous study and the current investigation regarding the flow of Sherwood numbers on porous disks.

TABLE 6

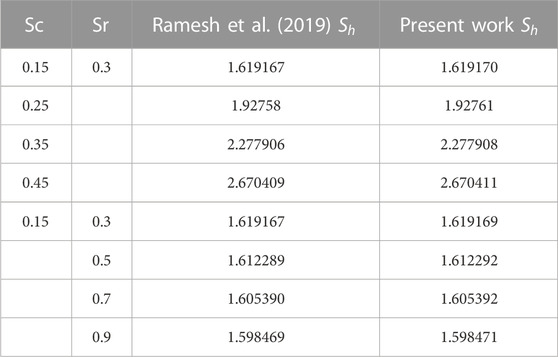
TABLE 6. Present results for the Sherwood number compared to the previous findings by Ramesh et al. (2019).

4 Conclusion

This study explores the impact of the shape and size of two porous disks on the nanolayer thermal conductivity of an HNF. Additionally, the numerical analysis conducted in this research investigates the effects of the thermal radiation parameter and buoyancy on the MHD flow of the HNF through the orthogonal porous disks. The obtained results encompass numerical and graphical representations of the SFC, the Nusselt number, the Sherwood number, and the velocity, temperature, and concentration profiles.

• The presence of the chemical reaction parameter $K_l$ exerts a substantial influence on both the mass concentration and the Sherwood number of the HNF.

• Increasing the values of different shape factors (spheres, platelets, and lamina) enhances the heat transfer in terms of the Nusselt number. However, the laminar shape factor exhibits significantly improved heat transfer characteristics compared to the other shape factors.

• Increasing the magnetic parameter values reduces the flow of momentum boundary layer thickness in a modified radial velocity profile for both porous disks.

• Raising the ${\mathit{R}}_{\mathit{d}}$ values results in an augmentation of the thermal boundary layer thickness on the upper permeable porous disk.

• In the presence of nonzero chemical reaction values, there is an augmentation in the mass transfer flow within the concentration profiles of the mutually permeable disks.

• For the suction situation, the Nusselt number grows as S, ${\lambda }_b$, ${\varphi }_{s1},{\varphi }_{s2}$, and ${\lambda }_a$ all have higher values.

• SFC rises with the augmented values of ${\lambda }_b$, ${\varphi }_{s1},{\varphi }_{s2}$, and the ${\lambda }_a$ or reduced opposite behavior flow fluid shown in $R_d$ for the suction case.

• The Sherwood number appears to increase with larger values of the chemical reaction parameter, volume fraction parameters, concentration buoyancy parameter, and thermal radiation parameter. Conversely, a decrease in the Sherwood number is observed with increased values of the thermal buoyancy parameter for the suction case.

• The thermal radiation parameter values rise more than the Nusselt numbers increase in the suction case (Pushpalatha et al., 2017).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

Software, QR; validation, XW; formal analysis, AH; investigation, QR; writing—original draft, IS and IA; writing—review and editing, BA; project administration. All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially funded by the research center of the Future University in Egypt, 2022.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelmalek, Z., Qureshi, M. Z. A., Bilal, S., Raza, Q., and Sherif, E. S. M. (2021). A case study on morphological aspects of distinct magnetized 3D hybrid nanoparticles on fluid flow between two orthogonal rotating disks: An application of thermal energy systems. Case Stud. Therm. Eng. 23, 100744. doi:10.1016/j.csite.2020.100744

CrossRef Full Text | Google Scholar

Adeniyan, A., Mabood, F., and Okoya, S. S. (2021). Effect of heat radiating and generating second-grade mixed convection flow over a vertical slender cylinder with variable physical properties. Int. Commun. Heat Mass Transf. 121, 105110. doi:10.1016/j.icheatmasstransfer.2021.105110

CrossRef Full Text | Google Scholar

Agrawal, P., Dadheech, P. K., Jat, R. N., Baleanu, D., and Purohit, S. D. (2021). Radiative MHD hybrid-nanofluids flow over a permeable stretching surface with heat source/sink embedded in porous medium. Int. J. Numer. Methods Heat Fluid Flow 31 (8), 2818–2840. doi:10.1108/hff-11-2020-0694

CrossRef Full Text | Google Scholar

Ahmad, S., Ali, K., Rizwan, M., and Ashraf, M. (2021). Heat and mass transfer attributes of copper–aluminum oxide hybrid nanoparticles flow through a porous medium. Case Stud. Therm. Eng. 25, 100932. doi:10.1016/j.csite.2021.100932

CrossRef Full Text | Google Scholar

Ali, K., Iqbal, M. F., Akbar, Z., and Ashraf, M. (2014). Numerical simulation of unsteady water-based nanofluid flow and heat transfer between two orthogonally moving porous coaxial disks. J. Theor. Appl. Mech. 52 (4), 1033–1046. doi:10.15632/jtam-pl.52.4.1033

CrossRef Full Text | Google Scholar

Anuar, N. S., Bachok, N., Turkyilmazoglu, M., Arifin, N. M., and Rosali, H. (2020). Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alexandria Eng. J. 59 (1), 497–507. doi:10.1016/j.aej.2020.01.024

CrossRef Full Text | Google Scholar

Armaghani, T., Sadeghi, M. S., Rashad, A. M., Mansour, M. A., Chamkha, A. J., Dogonchi, A. S., et al. (2021). MHD mixed convection of localized heat source/sink in an Al2O3-Cu/water hybrid nanofluid in L-shaped cavity. Alexandria Eng. J. 60 (3), 2947–2962. doi:10.1016/j.aej.2021.01.031

CrossRef Full Text | Google Scholar

Asghar, A., Ying, T. Y., and Zaimi, W. M. K. A. W. (2022). Two-dimensional mixed convection and radiative Al2O3-Cu/H2O hybrid nanofluid flow over a vertical exponentially shrinking sheet with partial slip conditions. CFD Lett. 14 (3), 22–38. doi:10.37934/cfdl.14.3.2238

CrossRef Full Text | Google Scholar

Bachok, N., Ishak, A., and Pop, I. (2011). Flow and heat transfer over a rotating porous disk in a nanofluid. Phys. B Condens. Matter 406 (9), 1767–1772. doi:10.1016/j.physb.2011.02.024

CrossRef Full Text | Google Scholar

Bilal, S., Shah, I. A., Ramzan, M., Nisar, K. S., Elfasakhany, A., Eed, E. M., et al. (2022). Significance of induced hybridized metallic and non-metallic nanoparticles in single-phase nano liquid flow between permeable disks by analyzing shape factor. Sci. Rep. 12 (1), 3342–3416. doi:10.1038/s41598-022-07251-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Biswas, N., Sarkar, U. K., Chamkha, A. J., and Manna, N. K. (2021). Magneto-hydrodynamic thermal convection of Cu–Al2O3/water hybrid nanofluid saturated with porous media subjected to half-sinusoidal nonuniform heating. J. Therm. Analysis Calorim. 143 (2), 1727–1753. doi:10.1007/s10973-020-10123-0

CrossRef Full Text | Google Scholar

Elcrat, A. R. (1976). On the radial flow of a viscous flu id between porous disks. Archive Rotaioal Mechenics Analysis 61, 91–96. doi:10.1007/bf00251865

CrossRef Full Text | Google Scholar

Ghozatloo, A., Azimi, M. S., Shariaty, N. M., and Morad, R. A. (2015). Investigation of nanoparticles morphology on viscosity of nanofluids and new correlation for prediction. J. Nanostructures 5, 161–168.

Google Scholar

GoharSaeed Khan, T., Khan, I., Gul, T., and Bilal, M. (2022). Mixed convection and thermally radiative hybrid nanofluid flow over a curved surface. Adv. Mech. Eng. 14 (3), 16878132221082848.

CrossRef Full Text | Google Scholar

Hayat, T., Ullah, I., Muhammad, T., and Alsaedi, A. (2016). Magnetohydrodynamic (MHD) three-dimensional flow of second grade nanofluid by a convectively heated exponentially stretching surface. J. Mol. Liq. 220, 1004–1012. doi:10.1016/j.molliq.2016.05.024

CrossRef Full Text | Google Scholar

Hidayat, M. I. P. (2023). A meshfree approach based on moving kriging interpolation for numerical solution of coupled reaction-diffusion problems. Int. J. Comput. Methods 20 (05), 2350002. doi:10.1142/s0219876223500020

CrossRef Full Text | Google Scholar

Hidayat, M. I. P. (2021). Meshless finite difference method with B-splines for numerical solution of coupled advection-diffusion-reaction problems. Int. J. Therm. Sci. 165, 106933. doi:10.1016/j.ijthermalsci.2021.106933

CrossRef Full Text | Google Scholar

Hussain, S. M., Sharma, R., and Chamkha, A. J. (2022a). Numerical and statistical explorations on the dynamics of water conveying Cu-Al2O3 hybrid nanofluid flow over an exponentially stretchable sheet with Navier's partial slip and thermal jump conditions. Chin. J. Phys. 75, 120–138. doi:10.1016/j.cjph.2021.11.007

CrossRef Full Text | Google Scholar

Hussain, T., Xu, H., Raees, A., and Zhao, Q. K. (2022b). Unsteady three-dimensional MHD flow and heat transfer in porous medium suspended with both microorganisms and nanoparticles due to rotating disks. J. Therm. Analysis Calorim. 147 (2), 1607–1619. doi:10.1007/s10973-020-10528-x

CrossRef Full Text | Google Scholar

Iqbal, M. F., Ali, K., and Ashraf, M. (2015). Heat and mass transfer analysis in unsteady titanium dioxide nanofluid between two orthogonally moving porous coaxial disks: A numerical study. Can. J. Phys. 93 (3), 290–299. doi:10.1139/cjp-2014-0243

CrossRef Full Text | Google Scholar

Islam, S., Khan, A., Deebani, W., Bonyah, E., Alreshidi, N. A., and Shah, Z. (2020). Influences of Hall current and radiation on MHD micropolar non-Newtonian hybrid nanofluid flow between two surfaces. AIP Adv. 10 (5), 055015. doi:10.1063/1.5145298

CrossRef Full Text | Google Scholar

Jasim, L. M., Hamzah, H., Canpolat, C., and Sahin, B. (2021). Mixed convection flow of hybrid nanofluid through a vented enclosure with an inner rotating cylinder. Int. Commun. Heat Mass Transf. 121, 105086. doi:10.1016/j.icheatmasstransfer.2020.105086

CrossRef Full Text | Google Scholar

Jawad, M., Saeed, A., Khan, A., Ali, I., Alrabaiah, H., Gul, T., et al. (2021). Analytical study of MHD mixed convection flow for Maxwell nanofluid with variable thermal conductivity and Soret and Dufour effects. AIP Adv. 11 (3), 035215. doi:10.1063/5.0029105

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Al-Mubaddel, F. S., Bakar, S. A., Alotaibi, H., et al. (2021). Computational modeling of hybrid SiskoNanofluid flow over a porous radially heated shrinking/stretching disc. Coatings 11 (10), 1242. doi:10.3390/coatings11101242

CrossRef Full Text | Google Scholar

Khashi'ie, N. S., Arifin, N. M., Pop, I., Nazar, R., Hafidzuddin, E. H., and &Wahi, N. (2020). Flow and heat transfer past a permeable power-law deformable plate with orthogonal shear in a hybrid nanofluid. Alexandria Eng. J. 59 (3), 1869–1879. doi:10.1016/j.aej.2020.05.029

CrossRef Full Text | Google Scholar

Khashi’ie, N. S., Waini, I., Arifin, N. M., and Pop, I. (2021). Unsteady squeezing flow of Cu-Al2O3/water hybrid nanofluid in a horizontal channel with magnetic field. Sci. Rep. 11 (1), 14128–14211. doi:10.1038/s41598-021-93644-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, L. (2022). Cu–Al₂O₃/engine oil Williamson hybrid nanofluid flow over a stretching/shrinking Riga plate with viscous dissipation and radiation effect. Heat. Transf. 51 (2), 2279–2305. doi:10.1002/htj.22400

CrossRef Full Text | Google Scholar

Li, Y. X., Khan, M. I., Gowda, R. P., Ali, A., Farooq, S., Chu, Y. M., et al. (2021). Dynamics of aluminum oxide and copper hybrid nanofluid in nonlinear mixed Marangoni convective flow with entropy generation: Applications to renewable energy. Chin. J. Phys. 73, 275–287. doi:10.1016/j.cjph.2021.06.004

CrossRef Full Text | Google Scholar

Mabood, F., Yusuf, T. A., and Khan, W. A. (2021). Cu–Al2O3–H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J. Therm. Analysis Calorim. 143 (2), 973–984. doi:10.1007/s10973-020-09720-w

CrossRef Full Text | Google Scholar

Othman, N. A., Yacob, N. A., Bachok, N., Ishak, A., and Pop, I. (2017). Mixed convection boundary-layer stagnation point flow past a vertical stretching/shrinking surface in a nanofluid. Appl. Therm. Eng. 115, 1412–1417. doi:10.1016/j.applthermaleng.2016.10.159

CrossRef Full Text | Google Scholar

Plant, R. D., Hodgson, G. K., Impellizzeri, S., and Saghir, M. Z. (2020). Experimental and numerical investigation of heat enhancement using a hybrid nanofluid of copper oxide/alumina nanoparticles in water. J. Therm. Analysis Calorim. 141 (5), 1951–1968. doi:10.1007/s10973-020-09639-2

CrossRef Full Text | Google Scholar

Pushpalatha, K., Reddy, J. R., Sugunamma, V., and Sandeep, N. (2017). Numerical study of chemically reacting unsteady Casson fluid flow past a stretching surface with cross diffusion and thermal radiation. Open Eng. 7 (1), 69–76. doi:10.1515/eng-2017-0013

CrossRef Full Text | Google Scholar

Qureshi, M. Z. A., Bilal, S., Ameen, M. B., Mushtaq, T., and Malik, M. Y. (2021a). Numerical examination about entropy generation in magnetically effected hybridized nanofluid flow between orthogonal coaxial porous disks with radiation aspects. Surfaces Interfaces 26, 101340. doi:10.1016/j.surfin.2021.101340

CrossRef Full Text | Google Scholar

Qureshi, M. Z. A., Bilal, S., Malik, M. Y., Raza, Q., Sherif, E. S. M., and Li, Y. M. (2021b). Dispersion of metallic/ceramic matrix nanocomposite material through porous surfaces in magnetized hybrid nanofluids flow with shape and size effects. Sci. Rep. 11 (1), 12271–12319. doi:10.1038/s41598-021-91152-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahman, M., Sharif, F., Turkyilmazoglu, M., and Siddiqui, M. S. (2022). Unsteady three-dimensional magnetohydrodynamics flow of nanofluids over a decelerated rotating disk with uniform suction. Pramana 96 (4), 170. doi:10.1007/s12043-022-02404-0

CrossRef Full Text | Google Scholar

Ramesh, K., Ojjela, O., and Nareshkumar, N. (2019). Second law analysis in radiative mixed convective squeezing flow of Casson fluid between parallel disks with Soret and Dufour effects. Heat Transfer—Asian Res. 48 (4), 1483–1500. doi:10.1002/htj.21442

CrossRef Full Text | Google Scholar

Ramzan, M., Riasat, S., and Alotaibi, H. (2022). EMHD hybrid squeezing nanofluid flow with variable features and irreversibility analysis. Phys. Scr. 97 (2), 025705. doi:10.1088/1402-4896/ac49b1

CrossRef Full Text | Google Scholar

Rasmussen, H. (1970). Steady viscous flow between two porous disks. Z. für Angew. Math. Phys. ZAMP 21 (2), 187–195. doi:10.1007/bf01590643

CrossRef Full Text | Google Scholar

Raza, Q., Qureshi, M. Z., Khan, B. A., Kadhim Hussein, A., Ali, B., Shah, N. A., et al. (2022). Insight into dynamic of mono and hybrid nanofluids subject to binary chemical reaction, activation energy, and magnetic field through the porous surfaces. Mathematics 10 (16), 3013. doi:10.3390/math10163013

CrossRef Full Text | Google Scholar

Raza, Q., Wang, X., Qureshi, M. Z., Eldin, S. M., Abd Allah, A. M., Ali, B., et al. (2023). Mathematical modeling of nanolayer on biological fluids flow through porous surfaces in the presence of CNT. Case Stud. Therm. Eng. 45, 102958. doi:10.1016/j.csite.2023.102958

CrossRef Full Text | Google Scholar

Sadripour, S., and Chamkha, A. J. (2019). The effect of nanoparticle morphology on heat transfer and entropy generation of supported nanofluids in a heat sink solar collector. Therm. Sci. Eng. Prog. 9, 266–280. doi:10.1016/j.tsep.2018.12.002

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2022). Flow and heat over a rotating disk subject to a uniform horizontal magnetic field. Z. für Naturforsch. A 77 (4), 329–337. doi:10.1515/zna-2021-0350

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2023a). The flow and heat in the conical region of a rotating cone and an expanding disk. Int. J. Numer. Methods Heat Fluid Flow 33, 2181–2197. doi:10.1108/hff-11-2022-0655

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2023b). Three dimensional viscous flow due to a squeezing porous slider. Eur. J. Mechanics-B/Fluids 98, 253–259. doi:10.1016/j.euromechflu.2022.12.015

CrossRef Full Text | Google Scholar

Ullah, I., Waqas, M., Hayat, T., Alsaedi, A., and Ijaz Khan, M. (2019). Thermally radiated squeezed flow of magneto-nanofluid between two parallel disks with chemical reaction. J. Therm. Analysis Calorim. 135, 1021–1030. doi:10.1007/s10973-018-7482-6

CrossRef Full Text | Google Scholar

Usha, R., and Ravindran, R. (2001). Numerical study of film cooling on a rotating disk. Int. J. non-linear Mech. 36 (1), 147–154. doi:10.1016/s0020-7462(99)00095-5

CrossRef Full Text | Google Scholar

Vanaki, S. M., Mohammed, H. A., Abdollahi, A., and Wahid, M. A. (2014). Effect of nanoparticle shapes on the heat transfer enhancement in a wavy channel with different phase shifts. J. Mol. Liq. 196, 32–42. doi:10.1016/j.molliq.2014.03.001

CrossRef Full Text | Google Scholar

Xu, H. (2019). Modelling unsteady mixed convection of a nanofluid suspended with multiple kinds of nanoparticles between two rotating disks by generalized hybrid model. Int. Commun. Heat Mass Transf. 108, 104275. doi:10.1016/j.icheatmasstransfer.2019.104275

CrossRef Full Text | Google Scholar

Yashkun, U., Zaimi, K., Abu Bakar, N. A., Ishak, A., and Pop, I. (2021). MHD hybrid nanofluid flow over a permeable stretching/shrinking sheet with thermal radiation effect. Int. J. Numer. Methods Heat Fluid Flow 31 (3), 1014–1031. doi:10.1108/hff-02-2020-0083

CrossRef Full Text | Google Scholar

Yi, S., Trumble, K. P., and Gaskell, D. R. (1999). Thermodynamic analysis of aluminate stability in the eutectic bonding of copper with alumina. Acta mater. 47 (11), 3221–3226. doi:10.1016/s1359-6454(99)00187-1

CrossRef Full Text | Google Scholar

Zhang, L., Chen, L., Liu, J., Fang, X., and Zhang, Z. (2016). Effect of morphology of carbon nanomaterials on thermo-physical characteristics, optical properties and photo-thermal conversion performance of nanofluids. Renew. Energy 99, 888–897. doi:10.1016/j.renene.2016.07.073

CrossRef Full Text | Google Scholar