Stability, phonon calculations, electronic structure, and optical properties of a VO2(M) nanostructure: A comprehensive density functional theory study

This work aimed to precisely evaluate the physical properties of vanadium dioxide (M), particularly the optical characteristics. We employed different exchange-correlation functionals to determine the phase stability, band gap properties, and optical characteristics of an experimentally recognized monoclinic VO₂(M) polymorph. The calculations not only correctly interpreted the VO₂(M) origin but also predicted other optical properties including the extinction coefficient ($\mathit{k}$) and refractive index ($\mathit{n}$), which have not been reported in experimental measurements. Phonon dispersion calculations confirmed the presence of negative frequencies for acoustic modes in the phononic curves. When the HSE functional correctly reproduced the experimental band gap, here for the first time, our calculations based on PBE and PBEsol yielded non-zero electronic bandgaps of 0.23 and 0.15 eV for bulk VO₂(M). Our predictions showed that semi-local functionals can adequately predict the semiconductor properties of VO₂(M) and performed better than all previously reported theoretical works on nulled band gaps. In addition to the better prediction of the peak position in the absorption spectra with HSE hybrid functional, this method also reasonably well described the static dielectric constant of 7.54, showing an excellent match to the experimental values. In general, the results of this study reveal that hybrid functionals yield superior outcomes compared to semi-local functionals for optical properties of a VO₂(M) polymorph. Our results suggest that the PBEsol + HSE approach allows the efficient characterization of smart materials for electronic and optoelectronic applications.

1 Introduction

Strongly correlated vanadium dioxide (VO₂) materials exhibit a diversity of polymorphs, leading to outstanding electric, electronic, magnetic, and optical properties (Ruzmetov et al., 2008; Popuri et al., 2015; Huang et al., 2016; Hattori et al., 2020). This type of material has attracted interest due to its reversible metal–insulator transition (MIT) at a phase transition temperature of ∼340 K. Through this phase transition, the VO₂ structure can transit between an insulating (low temperature) state by a monoclinic M-phase with alternative V−V distances and a metallic (high temperature) state with a tetragonal rutile phase (R) with uniform V−V distances (Goodenough, 1971; Bai et al., 2015; Zylbersztejn and Mott, 1975). The MIT near room temperature has attracted interest related to controversy regarding the transitional mechanism and the potential technological applications such as electronic and photonic operations (He et al., 2020; Pendse et al., 2020), sensors (Huang et al., 2021; Xu et al., 2021) smart windows (Kang et al., 2011; Gao et al., 2012), and Mott field effect transistors (FETs) (Sasaki et al., 2015).

The monoclinic M phase (P2₁/c ($D_{2h}^5$)) is one of the most debated smart materials. Recent studies suggest that this phase should be considered a Peierls–Mott insulator (Babulanam et al., 1987) since both electron–electron correlations and V-V ions dimerization contributed to the opening of an insulating gap. The literature has reported semiconducting experimental bandgaps of 0.6–0.7 eV (Verleur et al., 1968; Tanaka, 2003; Haverkort et al., 2005; Pandurang et al., 2017) and optical absorption in the infrared-visible region (Eaton et al., 2018) for this polymorph.

Traditional density functional theory (DFT) calculations have predicted different outcomes of the physical features of VO₂(M) using different codes. For instance, whereas several exchange-correlation (XC) functionals have wrongly proposed a ferromagnetic property for this phase, these functionals also failed to reproduce the semiconducting bandgap of 0.6–0.7 eV or the optical absorption features of monoclinic VO₂(M) in the infrared region (Grau-Crespo et al., 2012; Yuan et al., 2012; Ganesh et al., 2020). In particular, the LDA, GGA, and sometimes the meta-GGA functionals using PBE or PBEsol XC functionals have incorrectly described the non-metallic behavior of VO₂(M) by predicting a conduction band below the Fermi level (Grau-Crespo et al., 2012; Yuan et al., 2012; Ganesh et al., 2020; Kylänpää et al., 2017). The failure to open the bandgap of this structure by GGA and LDA does not mean that it is a strongly correlated system; rather, this occurs because conventional theoretical approaches cannot correctly predict the experimentally observed properties of this system. The hybrid Heyd–Scuseria–Ernzerhof (HSE) and PBE0 functionals used in other studies (Grau-Crespo et al., 2012; Tran and Blaha., 2017; Xu et al., 2017) also indicated a strong discrepancy with the experimental characteristics of this polymorph. However, several studies have aimed to overcome these issues. For instance, Sakuma et al. (2008) predicted the electronic property of the monoclinic VO₂(M) structure based on G₀W₀ calculations. They reported that this approach did not display the experimental satellite features of conduction and valence bands above and below the Fermi level; however, in their computational study, Gatti et al., 2015 reported a better approach of self-consistent GW (COHSEX calculations), which successfully opened the band gap of 0.78 eV, quite close to the experimental value (0.6–0.7 eV) in the electronic properties of the monoclinic phase of VO₂. Another approach is the dynamical mean field theory (DMFT), which provides a view of the role of electron correlation in the physical properties of the VO₂(M) phase. Brito et al. (2016) suggested a distinct mechanism for the gap opening in the monoclinic phase utilizing different computational approaches. However, the results have led to some controversy regarding the origin of the VO₂(M) polymorph.

To address these controversies, we modeled a VO₂(M) polymorph to theoretically investigate the geometry, energy stability, and electronic and optical properties by first-principle calculations. We used the PBEsol XC functional to elucidate whether it can appropriately describe the correct geometry of the M phase. We also computed phonon softening using different LDA and GGA methodologies to provide information about the dynamical stability of this polymorph. We also combined the Hubbard U value in part of our calculations to explore the electronic properties and demonstrate whether the inclusion of the repulsion parameter has advantages over semi-local functionals. Similar calculations were performed with GGA/PBE to characterize the properties of the VO₂(M) for comparison with those resulting from the PBEsol and PBEsol + U approximations. Additional HSE and PBE0 hybrid functionals were performed to estimate the reliability of the PBE, PBEsol, and PBEsol + U bandgaps and the optical properties of the dielectric function of monoclinic VO₂(M). Finally, we compared the predicted results to those feasible to experimentally measure to demonstrate the theoretical accuracy of the semi-local GGA (PBE and PBEsol), PBEsol + U, hybrid HSE, and PBE0 functionals.

2 Computational methods

All calculations were carried out using Quantum ESPRESSO (QE) (Giannozzi et al., 2009) and QuantumATK (QATK) (Smidstrup et al., 2019) ab initio simulation packages. The polymorph was fully relaxed using the generalized gradient approximations (GGA) and Perdew–Burke–Ernzerhof for solids (PBEsol) XC functional. Compared to the PBE XC functional, the PBEsol XC functional could be important since it handles V–V medium-ranged bonding in VO₂ (M) associated with the smallest mean error relative to the experimental values. Numerical studies have suggested that PBEsol can accurately predict the bulk exchange energies of materials within the pseudopotential approximation. Projector augmented wave (PAW) (Blöchl et al., 1994; Kresse and Hafner, 1994) pseudopotential (PP) types were chosen to treat the V-3d and O-2p as valence orbitals. The valence orbitals were expanded in a plane-wave (PW) basis set with a kinetic energy cut-off of 70 Ry. The Brillouin-zone (BZ) (Brillouin, 1930) integrations were limited to the gamma point mesh, and the lattice constant and internal coordinates were fully optimized until Hellmann–Feynman forces become <0.01 Ry (Vanderbilt, 1990). This set of parameters assured that the total energies converged to 1 × 10⁻⁵ eV/Å. The phonon frequencies were calculated using the local density approximation/Perdew–Wang (LDA/PW), GGA/PBE, and GGA/PBEsol functionals according to the density functional perturbation theory (DFPT) (Baroni et al., 2001) implemented in the QE package.

The electronic properties of VO₂(M) were computed using the semi-local PBE, PBEsol, PBEsol + U, and hybrid HSE and PBE0 functionals with post-processing calculations to allow exhaustive comparisons between functionals. As the strong on-site Coulomb repulsion for V-3d electrons is often adjusted to match existing experimental quantities, the Hubbard parameter U was added to the PBEsol functional. The DFT + U method has been shown to accurately describe the electronic structure and strong correlation of VO₂ (Zayed et al., 2020). As the results of previous studies have underscored that the outcomes are substantially dependent on the magnitude of U, we tested different Hubbard U values for V-3d and O-2p. We set V-3d = 5.20 eV and O-2p = 0.95 eV since these parameters have shown very good agreement with the experimental results, as reported by Mohebbi et al. (2022).

The hybrid XC functionals are constructed by a fraction of non-local exact exchange instead of a fraction of local/semi-local exchange as Eq. 1:

${\mathbf{E}}_{\mathit{X}\mathit{C}}^{\mathit{h}\mathit{y}\mathit{b}\mathit{r}\mathit{i}\mathit{d}}={\mathbf{E}}_{\mathit{X}\mathit{C}}^{\mathit{l}\mathit{o}\mathit{c}\mathit{a}\mathit{l}}+\mathit{\alpha }\left({\mathbf{E}}_{\mathit{X}}^{\mathit{n}\mathit{o}\mathit{n}-\mathit{l}\mathit{o}\mathit{c}\mathit{a}\mathit{l}}-{\mathbf{E}}_{\mathit{X}}^{\mathit{l}\mathit{o}\mathit{c}\mathit{a}\mathit{l}}\right).(1)$

The non-local exact exchange is often computed according to the Hartree–Fock (HF) method. The type of DFT local/semi-local functional and the fraction of non-local exact exchange substituted in ($\mathit{\alpha }$) vary depending on the hybrid functional type.

The hybrid functional HSE (Heyd and Scuseria, 2004; Heyd et al., 2005), using an error-function-screened Coulomb potential, has the following form:

${\mathit{E}}_{\mathit{X}\mathit{C}}^{\mathit{H}\mathit{S}\mathit{E}}={\mathit{\alpha }\mathit{E}}_{\mathit{X}}^{\mathit{H}\mathit{F},\mathit{S}\mathit{R}}\left(\mathit{\omega }\right)+\left(\mathbf{1}-\mathit{\alpha }\right){\mathit{E}}_{\mathit{X}}^{\mathit{P}\mathit{B}\mathit{E},\mathit{S}\mathit{R}}\left(\mathit{\omega }\right)+{\mathit{E}}_{\mathit{X}}^{\mathit{P}\mathit{B}\mathit{E},\mathit{L}\mathit{R}}\left(\mathit{\omega }\right)+{\mathit{E}}_{\mathit{C}}^{\mathit{P}\mathit{B}\mathit{E}},(2)$

where $\alpha$ is a mixing parameter and $\omega$ is an adjustable parameter controlling the short range of the interaction. In this equation, ${\mathrm{E}}_X^{HF,SR}\left(\omega \right)$ and ${\mathrm{E}}_X^{PBE,SR}\left(\omega \right)$ refer to short-range HF and the PBE exchange functional, ${\mathrm{E}}_X^{PBE,LR}\left(\omega \right)$ corresponds to the long-range component of PBE, and $E_C^{PBE}$ refers to the PBE correlation functional. For the HSE calculations in this study, we chose values of [$\omega$ = 0.11 Bohr^-1] and [$\alpha$ = 0.25] as several theoretical papers have demonstrated the accuracy of hybrid functionals with these parameters (Krukau et al., 2006).

The hybrid functional PBE0 has the following formula:

${\mathit{E}}_{\mathit{X}\mathit{C}}^{\mathit{P}\mathit{B}\mathit{E}\mathbf{0}}={\frac{\mathbf{1}}{\mathbf{4}}\mathit{E}}_{\mathit{X}}^{\mathit{H}\mathit{F}}+{\frac{\mathbf{3}}{\mathbf{4}}\mathit{E}}_{\mathit{X}}^{\mathit{P}\mathit{B}\mathit{E}}+{\mathit{E}}_{\mathit{C}}^{\mathit{P}\mathit{B}\mathit{E}}.(3)$

The PBE0 hybrid XC functional degenerates $\mathit{\omega }$ to zero (Perdew et al., 1996; Yang et al., 2018).

The optical properties of the VO₂(M) nanostructure are discussed based on random-phase approximation (RPA) independent-particle (IP) to the dielectric constant using the KS states as a useful tool to calculate the screening and optical response of materials (Das, 1975; Wolterink et al., 2002; De Conti et al., 2001; Paier et al., 2008).

The optical properties can be determined based on two components of the dielectric function $\mathit{\epsilon }\left(\mathit{\omega }\right)={\mathit{\epsilon }}_{\mathbf{1}}\left(\mathit{\omega }\right)+\mathit{i}{\mathit{\epsilon }}_{\mathbf{2}}\left(\mathit{\omega }\right)$.

The imaginary part $\left({\mathit{\epsilon }}_{\mathbf{2}}\left(\mathit{\omega }\right)\right)$ of the dielectric coefficient can be determined from Eq. 4 (Dinh et al., 1996; Mortazavi et al., 2017; Mortazavi et al., 2019):

${\mathit{\epsilon }}_{\mathbf{2}}\left(\mathit{\omega }\right)=\frac{\mathbf{4}{\mathit{\pi }}^{\mathbf{2}}{\mathit{e}}^{\mathbf{2}}}{\mathbf{\Omega }}\underset{\mathit{q}\to \mathbf{0}}{\mathbf{lim}}\frac{\mathbf{1}}{{\left|\mathit{q}\right|}^{\mathbf{2}}}{\displaystyle \sum }_{\mathit{c},\mathit{v},\mathit{k}}\mathbf{2}{\mathit{w}}_{\mathit{k}}\mathit{\delta }$

$\times \left({\mathit{\epsilon }}_{\mathit{c}\mathit{k}}-{\mathit{\epsilon }}_{\mathit{v}\mathit{k}}-\mathit{\omega }\right)\times 〈{\mathit{u}}_{\mathit{c}\mathit{k}+{\mathit{e}}_{\mathit{\alpha }}\mathit{q}}|{\mathit{u}}_{\mathit{v}\mathit{k}}〉$

$\times {〈{\mathit{u}}_{\mathit{c}\mathit{k}+{\mathit{e}}_{\mathit{\beta }}\mathit{q}}|{\mathit{u}}_{\mathit{v}\mathit{k}}〉}^{*},(4)$

where $\mathrm{\Omega }$ and $q$ denote the volume of the unit cell and Bloch vector of the incident wave, respectively, $w_k$ is the weight of the k-point, and $c\mathrm{a}\mathrm{n}\mathrm{d}v$ correspond to the conduction and the valence bands, respectively. The vectors $e_{\alpha }$ refer to the unit vectors of the three Cartesian directions, and $u_{ck}$ is related to the cell periodic part of the orbitals at the k-point mesh.

Moreover, the real part of the dielectric constant can be obtained using Eq. 5:

${\mathit{\epsilon }}_{\mathbf{1}}\left(\mathit{\omega }\right)=\mathbf{1}+\frac{\mathbf{2}}{\mathit{\pi }}\mathit{P}{\int }_{\mathbf{0}}^{\mathit{\infty }}\frac{\overline{\mathit{\omega }}{\mathit{\epsilon }}_{\mathbf{2}}\left(\overline{\mathit{\omega }}\right)}{{\overline{\mathit{\omega }}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}+\mathit{i}\mathit{\eta }}\mathit{d}\overline{\mathit{\omega }},(5)$

where $\mathit{P}$ is the principal value and $\mathit{\eta }$ denotes the complex shift.

The absorption coefficient ($\mathit{\alpha }\left(\mathit{\omega }\right)$) of this structure is determined according to Eq. 6 (Kolwas and Derkachova, 2020):

$\mathit{\alpha }\left(\mathit{\omega }\right)=\frac{\mathit{\omega }\mathit{I}\mathit{m}\left[\mathbf{\varepsilon }\left(\mathit{\omega }\right)\right]}{\mathit{c}\mathit{n}\left(\mathit{\omega }\right)},(6)$

where $\mathit{c}$ is the speed of light and $\mathit{n}\left(\mathit{\omega }\right)$ refers to the refraction index.

The real part of the optical conductivity $Re\left[\sigma \left(\omega \right)\right]$ of the VO₂(M) structure can be determined as follows:

$Re\left[\sigma \left(\omega \right)\right]=\frac{\omega }{4\pi }Im\left[\epsilon \left(\omega \right)\right].(7)$

We next assessed the reflectivity of the VO₂(M) structure using Eq. 8:

$R\left(\omega \right)={\left|\frac{\sqrt{\mathrm{\epsilon }\left(\omega \right)+1}}{\sqrt{\sqrt{\epsilon \left(\omega \right)-1}}}\right|}^2.(8)$

Finally, we evaluated the refractive index ($n$) and extinction coefficient ($k$) of the VO₂(M) based on Eqs 9, 10:

${\epsilon }_1=n^2-k^2,(9)$

${\epsilon }_2=2nk.(10)$

Material visualization was performed using XCrySDen graphical software (Kokalj, 1999).

3 Results and discussion

3.1 Analysis of geometry and stability

The unit cell of the VO₂(M) polymorph consists of a unit cell of 24 atoms, including eight vanadium atoms. The lattice parameters were calculated as follows: a = 5.1836 Å, b = 5.0504 Å, and c = 9.0187 Å. Figure 1 shows the modeled possible planes along the xy, xz, and yz directions. The VO₂(M) nanostructure comprised two layers including the 3D frameworks of VO₆ octahedra (Figure 2). These octahedra packings of VO₆ are only linked by oxygen atoms (plane xy). The octahedra in the VO₂(M) phase are orthorhombically distorted, making it possible to differentiate the apical and equatorial V-O bonds resulting in alternate long and short V-V bonds (plane yc). Plane xc indicates how V atoms in the octahedra frameworks share their edges with oxygen atoms along the zigzag direction. We investigated the atomic positions, cell parameters, and V-V and V-O bonds in this bulk structure. In our DFT calculations, the VO₂(M) nanostructure showed the longest/shortest V-V bond distances of 3.04 and 2.76 Å, respectively. Moreover, the V-O bond lengths in the octahedra VO₆ were 2.10, 1.85, 1.83, 1.81, 1.97, and 2.18 Å. These parameters were in excellent agreement with available experimental observations (Goodenough, 1971; Zylbersztejn and Mott, 1975; Zhang, 2016) and theoretical studies (Wan et al., 2017; Chen et al., 2021). The calculated formation energy of the VO₂ (M) structure in this study by PBEsol (8.00 eV) was in fair agreement with other theoretical values using PBE + U approximation (7.14 eV), HSE functional (8.17 eV (Abdellaoui et al., 2016) and 7.18 eV (Zhang et al., 2011)), and the experimental value of 7.38 eV (Melnik et al., 2012; Lee et al., 2016), indicating that our method for semi-local XC functional calculation is reasonable.

FIGURE 1

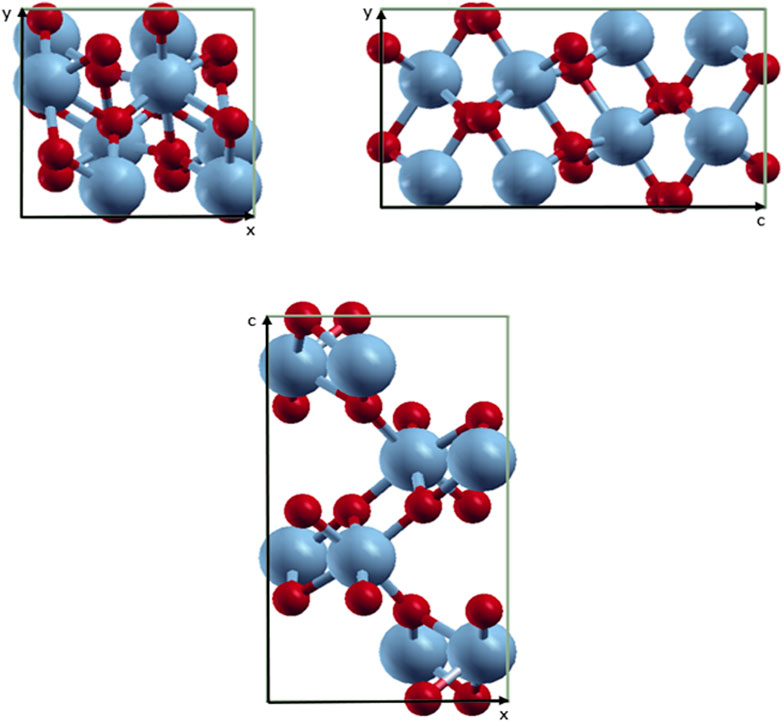
FIGURE 1. Schematic representations of the VO₂(M) unit cell. Color code in the ball and stick model: V = blue and O = red.

FIGURE 2

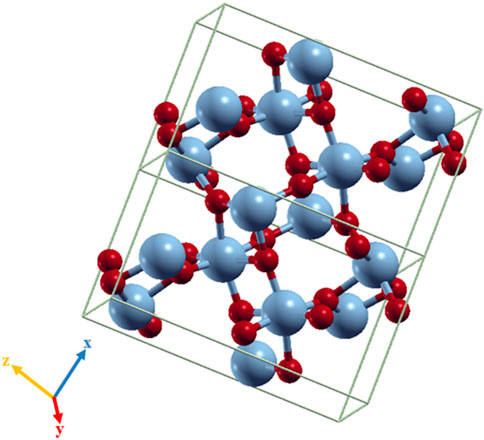
FIGURE 2. Octahedra frameworks (VO₆) in the VO₂(M) nanostructure. Color code in the ball and stick model: V = blue and O = red.

The phonon dispersion of a VO₂(M) polymorph was investigated using the different methodologies of LDA and GGA and the PW, PBE, and PBEsol XC functionals to provide useful information about the dynamic stability of this polymorph. All phonon calculations were performed after full relaxation of the atomic positions and the lattice volume. The phonon bands were computed for the VO₂(M) nanostructure along with the high-symmetry points of G–M-K–G in the first BZ (see Figure 3). Inspection of the dispersion plots in Figure 3 shows that the dynamical matrix has negative frequencies for the three approximations, which indicates the dynamic instability of this polymorph. The most noteworthy was the difference in phonon dispersion curves between different XC functionals. Figure 2 shows that in the graph obtained by LDA/PW functional phonon, softening of the instabilities occurs around −177 and −52 cm^-1 at the G and M points in reciprocal space, while in GGA/PBE, the negative frequencies were suggested to occur around −62 and −86 cm^-1 at the G and K points, respectively. More interestingly, in the case of GGA/PBEsol, the imaginary frequencies at the G point were limited to one acoustic mode, with no additional negative frequencies like those in the LDA/PW (−177 cm^-1) and GGA/PBE (−62 cm^-1) functionals. Since there are no first-principle DFT calculations of phonon dispersions of VO₂(M) for comparison, the results of previous experiments (Li et al., 2017; Wu et al., 2020) confirm the phase instability of this polymorph. According to these experimental observations, among different polymorphs of the VO₂ family, the VO₂(M) and VO₂(B) phases are metastable in their bulk structures; hence, the preparation of phase-pure and high-quality materials has been a major challenge in VO₂ research. These two monoclinic polymorphs can undergo an irreversible phase change into VO₂(R) (rutile phase of VO₂) upon heating, indicating the thermodynamic instability of these non-equilibrium materials (Chernova et al., 2009; Sims et al., 2017). One solution to improve the stability of these materials could be the deposition of VO₂(M) on perovskite substrates like SiTiO₃ (Sims et al., 2017) or sapphire (Jian et al., 2016; Lee et al., 2016).

FIGURE 3

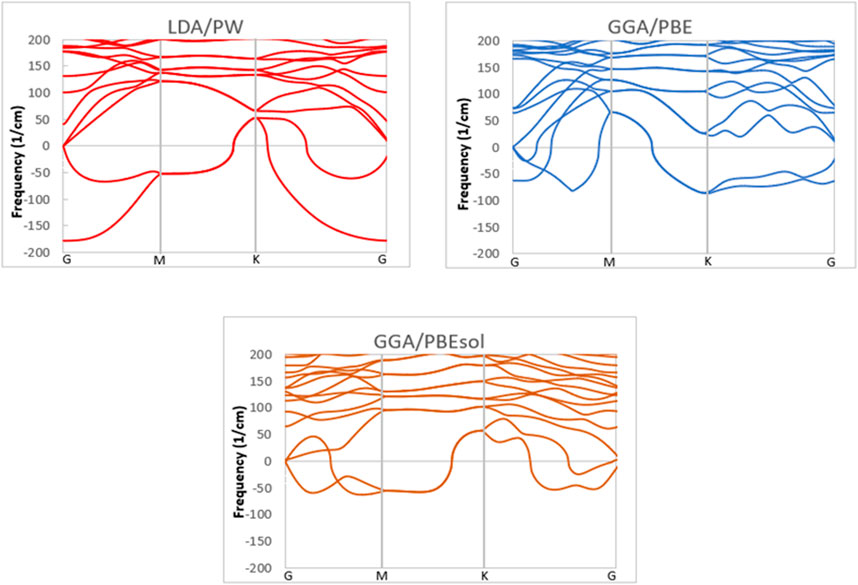
FIGURE 3. Phonon dispersion of the VO₂(M) structure predicted by the LDA, PBE, and PBEsol functionals.

3.2 Band gap properties and state densities

Next, we examined the electronic properties of the VO₂(M) structure. Table 1 summarizes the band gaps for the VO₂(M) polymorph predicted by the PBE, PBEsol, PBEsol + U, HSE, and PBE0 functionals. Our calculation with PBE showed a bandgap of 0.23 eV for bulk VO₂(M), close to the value predicted using PBEsol (0.15 eV) by upshifting of the Fermi level to the higher energies. Thus, the inclusion of the Hubbard U value produced a larger band gap (0.96 eV), while the position of the Fermi level did not change significantly. The electronic structures were also calculated using the QE code based on the hybrid HSE and PBE0 functionals. When the band gap of the semiconducting VO₂ (M) computed using HSE showed excellent agreement with photoemission experiments (E_g∼0.6–0.7 eV) (Verleur et al., 1968; Tanaka, 2003; Haverkort et al., 2005; Pandurang et al., 2017) by 0.60 eV, the hybrid PBE0 approximation yielded an unexpectedly high band gap of 1.39 eV. The HSE calculation produced an accurate band gap, in contrast with the other DFT approximations.

TABLE 1

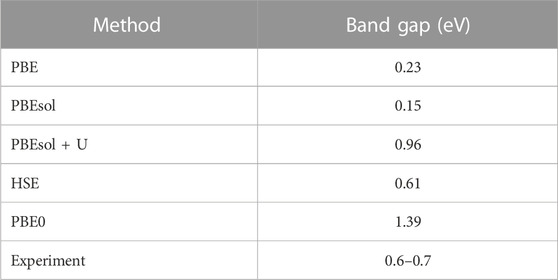
TABLE 1. Calculated electronic band gaps of the VO₂(M) structure predicted by the PBE, PBEsol, and PBEsol + U, HSE, and PBE0 functionals compared to the experimental results.

The electronic band diagram of monoclinic VO₂(M) showed that each V-3d is surrounded by oxygen’s octahedron, resulting in the splitting of the d level to triply degenerate the t₂g and doubly degenerate the $e_g^{\sigma }$ states. The former further splits into $e_g^{\pi }$ (π; ${\mathrm{\pi }}^{*}$) and a_1g ($d_{⫽}$) orbitals. In this polymorph, the dimerization of V atoms causes splitting of the a_1g ($d_{⫽}$) bands into bonding/antibonding states, energetical upshift of ${\pi }^{*}$ bands, and a charge transfer from the $e_g^{\pi }$ orbitals, leading to the separation of the bonding $d_{⫽}$ and $e_g^{\pi }$ sub-bands at the Fermi level with a band gap of approximately 0.7 eV. Figure 4 shows the calculation of the predicted band structure and partial density of states (PDOS) of VO₂(M) using the PBEsol + U functional. The band structure was considered along with the directions of the high-symmetry points of G–M–K–G in the first BZ (Figure 4A). According to the PDOS calculation of this polymorph, the main contribution of total DOS belonged to the V-3d orbitals associated with the lower contribution of the O-2p states (Figure 4B). The DFT + U system shows a semiconducting characteristic due to the a_1g ($d_{⫽}$) bands splitting into bonding/antibonding states and the ${\mathrm{\pi }}^{*}$ states experiencing energetical upshift, leading to strong hybridization with the O-2p states.

FIGURE 4

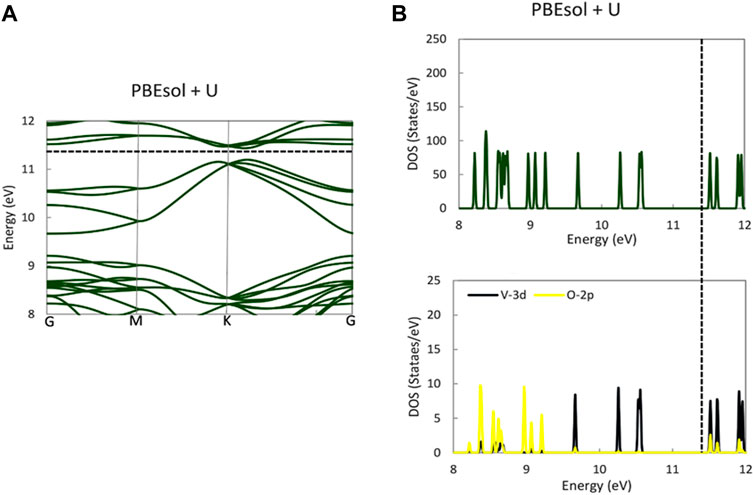
FIGURE 4. Band structure (A) and PDOS (B) of the VO₂(M) structure for V-3d, O-2p, and total DOS predicted by the PBEsol + U functional. The Fermi energy is aligned with the dashed line.

While all previous theoretical studies have reported a metallic property for VO₂(M), with a band gap of 0.0 eV (Tran and Blaha, 2017) using HLE16 (a local Kohn–Sham gradient approximation), 0.07 eV (Zheng and Wagner, 2015) using quantum Monte Carlo (QMC), and 0.06 eV (Varadwaj and Miyake, 2022) using first-principle PBE calculations, our PBE and PBEsol calculations using the QE code revealed the semiconductor properties of this polymorph. Similarly, a DFT study of the geometrical and bandgap properties of VO₂(M) using another semi-local functional in the WIEN2k (Grau-Crespo et al., 2012) package showed the zero band gap of this structure, demonstrating that the Hubbard U value is essentially required to reproduce the experimental band gap. In contrast, in a theoretical study, Tran and Blaha (2017), reported that all semi-local functionals implemented in various first-principle simulation codes all failed to provide a bandgap for monoclinic VO₂, with high band gap values of 1.03 and 1.35 eV obtained by HSE and B3PW91 approximations, respectively. In their recent theoretical study, Varadwaj and Miyake (2022) implemented SCAN, SCAN-rVV10, and G₀W₀ functionals in the VASP package to study the bandgap property of the monoclinic M phase of VO₂. Their results showed that VO₂(M) had semiconductor properties, with band gaps of 0.58, 0.57, and 0.68 eV, respectively. Meanwhile, Grau-Crespo et al. (2012) reported an overestimated band gap value of 0.98 eV from HSE hybrid functional using the same code as that used by Varadwaj and Miyake (2022). The comparison of our results to those of other methodologies implemented in different quantum mechanics packages suggests that the PBE and PBEsol functionals employing PAW PPs in QE code can polarize the Fermi level and open the band gap, resulting in a non-zero band gap and the semiconductor property of this polymorph. Furthermore, the HSE code in QE showed an excellent ability to reproduce the experimental band gap of this polymorph, while PBE0 showed some unacceptable results. Overall, our results reveal that the opening of the band gap in the band structure of VO₂ (M) may first have a strong dependency on the optimized geometry (in our study, we used PBEsol XC functional) and then is more correlated with the functional used to investigate the postprocessing electronic calculations.

3.3 Optical features

In this section, the optical properties of VO₂(M) were calculated, including the imaginary and real parts of the dielectric constant, the absorption coefficient [$\alpha \left(\omega \right)$], the optical conductivity $Re\left[\sigma \left(\omega \right)\right]$, the reflectivity spectra ($r$), the extinction coefficient ($k$), and the refractive index ($n$) which were computed using Eqs 4–9. Figure 5 compares the real and imaginary parts of the dielectric constant of the VO₂(M) polymorph predicted by the PBE, PBEsol, PBEsol + U, and HSE functionals. For the real part of the dielectric function, the ${\epsilon }_1\left(\omega \right)$ for the VO₂(M) geometry showed predicted positive values of 172.57, 77.22, 82.44, and 7.54 for the PBE, PBEsol, PBEsol + U, and HSE functionals, respectively. According to these results, when we apply the PBEsol functional including/excluding the Hubbard U value, the similarity in the ${\epsilon }_1\left(\omega \right)$ spectra between PBEsol and PBEsol + U indicates a nearly unchanged dielectric constant value. The value of the dielectric function approximated by the HSE functional (7.54) was very similar to that for the experimental spectra [${\epsilon }_1\left(\omega \right)$ = ∼7.80] in the study by Verleur et al. (1968). More specifically, the ${\epsilon }_1\left(\omega \right)$ spectrum obtained in their study had a reported maximum value of 12.00 for a static dielectric constant for this material, indicating that other functionals are needed to predict the far values of the dielectric constant.

FIGURE 5

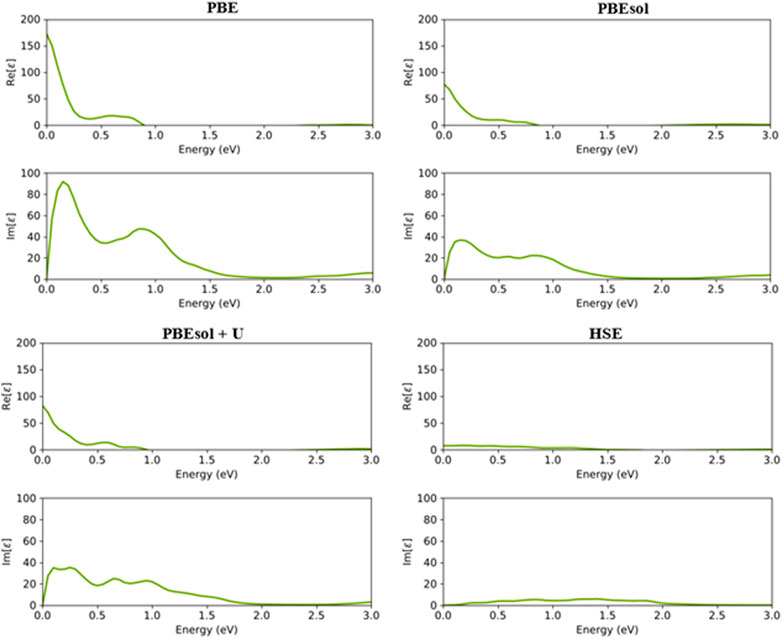
FIGURE 5. Real and imaginary parts of the dielectric constants of the VO₂(M) polymorph as a function of the energy (eV), predicted by the PBE, PBEsol, PBEsol + U, and HSE functionals.

As shown in Figure 5, the first main peak of imaginary of the dielectric constant (${\epsilon }_2\left(\omega \right)$) showed strong absorption in the infrared range in the energy range of 0–0.4 eV for the VO₂(M) nanostructure predicted by the PBE, PBEsol, and PBEsol + U functionals. However, the situation changed remarkably for HSE, which showed a significant low-intensity adsorption peak in the infrared-visible region with a frequency range of 0.15–1.95 eV. Figure 5 also demonstrates that the simulated absorption peaks and shape of the ${\epsilon }_2\left(\omega \right)$ spectrum calculated by HSE functional qualitatively/quantitatively showed excellent consistency with the experimental results (Verleur et al., 1968), especially the optical band gap.

Figure 6 shows the absorption spectra for VO₂(M) calculated using the PBE, PBEsol, PBEsol + U, and HSE functionals. The maximum adsorption spectra approximated by four functionals were 6.1 × 10⁵ cm^-1, 4.0 × 10⁵ cm^-1, 4.8 × 10⁵ cm^-1, and 3.4 × 10⁵ cm^-1 for PBE, PBEsol, PBEsol + U, and HSE, respectively. Based on this figure and the range of photon energy (eV), the prominent main absorption peaks for PBE were located at 0.35 and 1.10 eV, while the corresponding values predicted by PBEsol were 0.25 and 1.05 eV. The outcomes also indicated that the main peaks of absorption spectra of VO₂(M) were situated at 0.35, 0.70, and 1.05 eV based on PBEsol + U, while HSE showed peaks around 0.85, 1.45, 1.8, and 2.2 eV, respectively. Although several peaks were related to optical adsorption data on monoclinic VO₂ (M) at photon energies <2.5 eV, if a band scheme is chosen as the basis for interpretation, it can only be concluded at present that the absorption peaks near 1.0 (0.85 eV predicted by the HSE approximation) can interpret the electronic band gap for this polymorph. Moreover, our results revealed that PBE/HSE showed intense/dropped adsorption peaks for this structure.

FIGURE 6

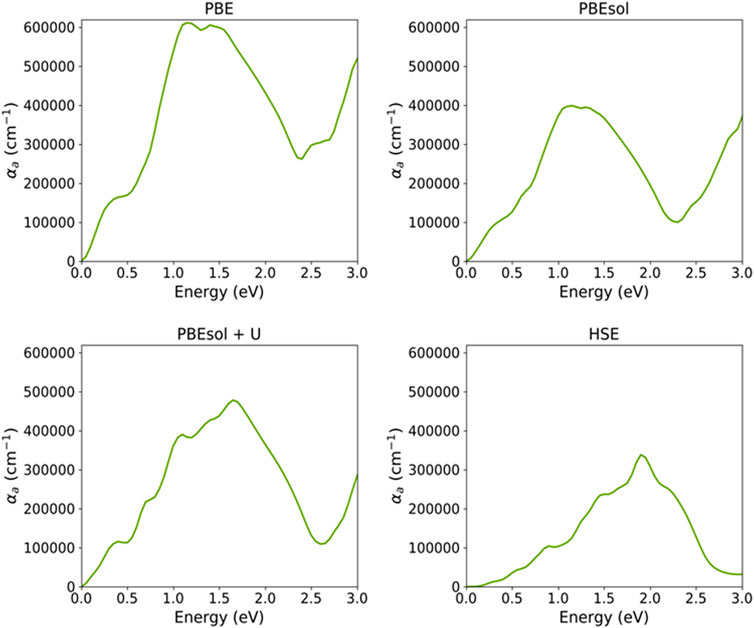
FIGURE 6. Optical absorption spectra of the VO₂(M) polymorph, as a function of energy (eV), predicted by the PBE, PBEsol, PBEsol + U, and HSE functionals.

Figure 6 shows that by employing the functional from PBE to HSE, the adsorption spectrum upshifted to higher energies from the far-infrared to the near-infrared ranges of light, while the corresponding adsorption coefficient decreased from 6.1 × 10⁵ cm^-1 to 3.4 × 10⁵ cm^-1 (Figure 6, adsorption spectra predicted by PBE and HSE), respectively. Overall, the comparison of the four functionals showed that the absorption coefficient was more strengthened by semi-local PBE compared to hybrid functionals, resulting in low reflectivity, as we discuss later. These results indicate that the optical absorption peaks predicted using computationally expensive HSE are more accurate than those of semi-local methods, particularly when the optical spectrum is compared to the experimental observations. The HSE hybrid functional slightly overestimated the lower energy transition 1.3 eV (experimental value) at 1.45 eV (curve in Figure 6), whereas this functional accurately predicted the first transition of 0.85 eV (the same value as the experimental value).

Next, we assessed the optical conductivity spectra of the VO₂(M) polymorph based on the PBE, PBEsol PBEsol + U, and HSE functionals (Figure 7). As expected, the optical conductivities began with a high intensity of 5710 A. V⁻¹. cm^-1 for the PBE calculations, while the intensity of peaks dropped in PBEsol + U and PBEsol (2938 A. V⁻¹. cm^-1 and 2620 A. V⁻¹. cm^-1), respectively. The results in Figure 7 indicate that the optical conductivity of 1056 A. V⁻¹. cm^-1 was predicted by the HSE functional. The VO₂(M) polymorph showed strong conductivity in the infrared range in the non-hybrid calculations, while the HSE calculations indicated intense optical conductivity between visible-infrared regions. The results of our HSE calculations correctly verified the experimental optical observations reported by Cai et al., 2016. According to this study, the VO₂(M) structure showed its first optical conductivity peak in the energy range of 0.3–1.5 eV, with no peak observed below 0.3 eV.

FIGURE 7

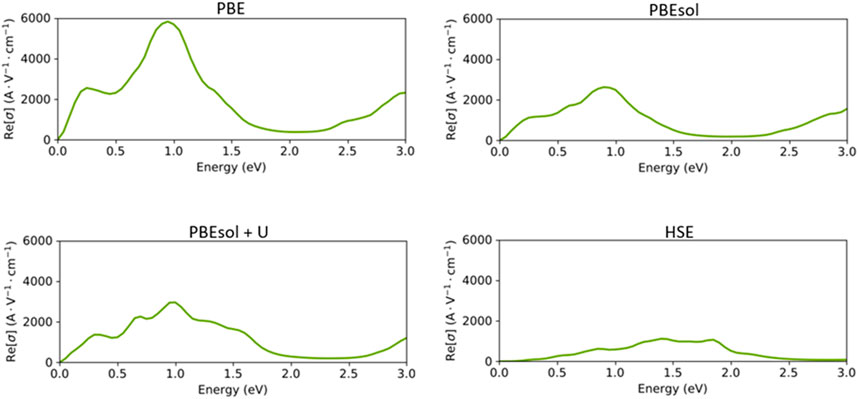
FIGURE 7. Optical conductivity of the VO₂(M) structure as a function of the energy (eV), predicted by the PBE, PBEsol, PBEsol + U, and HSE functionals.

Figure 8 shows the reflectivity spectra of the VO₂(M) nanostructure computed using semi-local and hybrid functionals. The percentages were 73%, 63%, 64%, and 22%, respectively, for the PBE, PBEsol, PBEsol + U, and HSE functionals. Experimentally, Verleur et al. (1968) reported a reflectivity of around 10% for the monoclinic VO₂ monoclinic lattice. Although the calculated reflectivity percentages for the VO₂(M) nanostructure in this study by semi-local functionals excluding and including the U parameter are higher than the experimental value (Verleur et al., 1968), the HSE functional provided a more accurate result compared to previous methodologies. For instance, the theoretical works of Chen et al. (2017 and Chen et al. (2021) reported calculated reflectivity values of this material of 32% and 35% using the same PBE + U functional. Another study by Gatti et al. (2015) based on the Bethe–Salpeter equation (BSE) and G₀W₀ approximations reported reflectivity values of 30% and 28%, respectively.

FIGURE 8

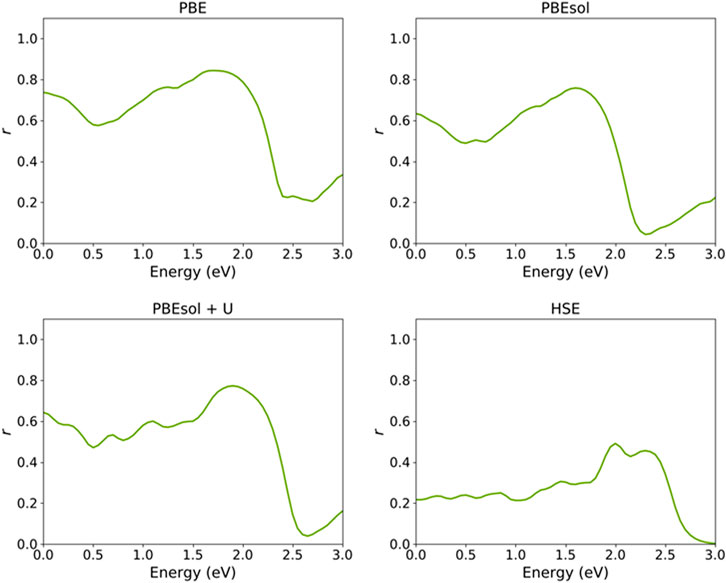
FIGURE 8. Reflectivity spectrum of the VO₂(M) polymorph as a function of the energy (eV), predicted by semi-local PBE, PBEsol, PBEsol + U, and hybrid HSE functionals.

Finally, we calculated the other optical features of the VO₂(M) polymorph, including the extinction coefficient (k) and refractive index (n) (Figures 9, 10), based on the semi-local and hybrid functionals. As shown in Figure 9, the maximum values of the extinction coefficients were about 5.43/3.67 for the energy values of 1.05 and 1.00 eV when the systems were predicted using the PBE and PBEsol functionals, respectively. The corresponding computed extinction coefficient value for PBEsol + U was 3.56 for 1.00 eV, while the value was 1.75 for the HSE functional in the high energy range of 1.85 eV.

FIGURE 9

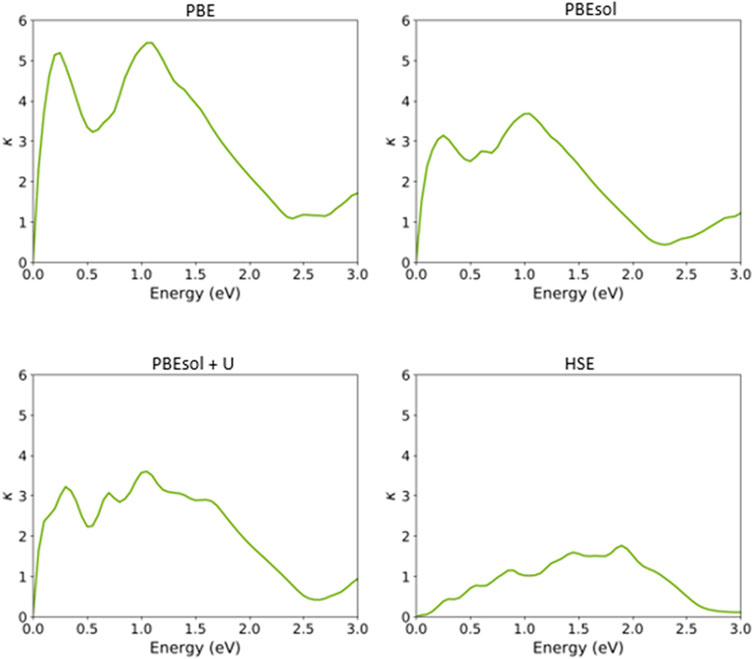
FIGURE 9. Extinction coefficient of the VO₂(M) polymorph as a function of the energy (eV), predicted by the PBE, PBEsol, PBEsol + U, and HSE functionals.

FIGURE 10

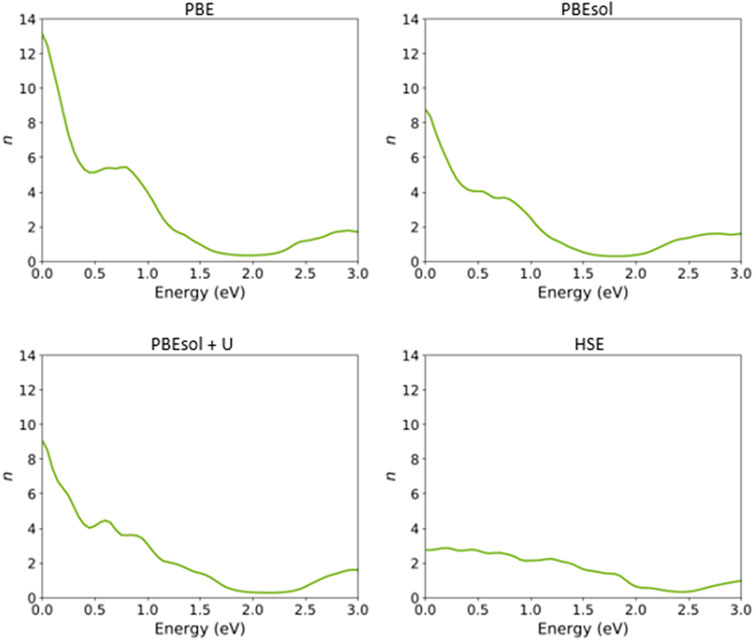
FIGURE 10. Refractive index of the VO₂(M) nanostructure as a function of energy (eV), as predicted by the PBE, PBEsol, PBEsol + U, and HSE functionals.

Figure 10 shows that the refractive index (n) of this nanostructure is dependent on the DFT functional. From Figure 10, the static refractive indices are 13.13, 8.78, and 9.08 by PBE, PBEsol, and PBEsol + U, respectively, whereas the value for the HSE calculation was 2.74, significantly lower than those for the semi-local functionals.

4 Conclusion

In this study, we optimized the geometry of a VO₂(M) polymorph using the PBEsol XC functional. Our results indicated that this approximation accurately reproduced the experimental properties of the lattice constants and structural parameters. The phonon dispersion calculations using LDA and GGA methods predicted some imaginary eigenvalues and instability of this nanostructure, revealing that the low-temperature monoclinic VO₂(M) polymorph lacked dynamical stability, consistent with some experimental observations. We also investigated the electronic band gap calculations for VO₂(M) by applying the PBE, PBEsol, PBEsol + U, HSE, and PBE0 functionals. For the first time, both the PBE and PBEsol functionals confirmed the semiconductor property of the VO₂(M) polymorph, whereas the hybrid HSE functional generated the experimental bandgap of this phase (0.60 eV). The results based on PBE0 revealed the overestimated prediction of 1.39 eV for the electronic band gap of the VO₂(M) structure. In contrast, the HSE functional accurately approximated the optical features of this polymorph. Although the magnitudes differed between the static dielectric constants obtained from the four functionals, the real part of the dielectric constant, with a calculated value of 7.54, showed very good agreement with the experimental value of 7.80. Furthermore, the absorption peaks centered at 0.85 and 1.45 indicated good consistency with the experimental observations of prominent absorption peaks centered near the photon energies of 0.85 and 1.3, respectively.

The excellent electronic and optical properties of the VO₂(M) polymorph suggest its promising advantages and desirable prospects in energy engineering applications. Windows’ materials like VO₂ polymorphs are well-known as among the most energy-efficient building components since they can reduce air-conditioning load to save energy as they can modulate solar radiation passing through the windows of buildings (Wang et al., 2014; Kang et al., 2015). Furthermore, VO₂(M) materials are exploitable in high-performance electronic and photonic device applications like thermoelectric (Byon et al., 2012), field-effect transistor (Liu et al., 2012), terahertz (Luo et al., 2016), and photoelectric devices (Lu et al., 2014).

Data availability statement

The original contributions presented in the study are included in the article Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, EM, EL, and PS; methodology, EM and EL; validation, EM, EL, and PS; investigation, EM; data curation, EM; writing—original draft preparation, EM; writing—review and editing, EM, EL, EP, and PS; visualization, EM; supervision, PS; project administration, EM, EL, PS, LP, and DM. All authors have read and agreed to the published version of the manuscript.

Funding

This work is part of the H2020 research (FETPROACT-EIC-05-2019) “Nanomaterials enabling smart energy harvesting for next-generation Internet-of-Things” (NANO-EH) (grant agreement No. 951761).

Acknowledgments

The authors acknowledge the CINECA-HPC ISCRA MARCONI-100 computer system (NANO-PR project n. HP10CK3EZ0) for the QE calculations.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2023.1145822/full#supplementary-material

References

Abdellaoui, I., Merad, G., Maaza, M., and Abdelkader, H. S. (2016). Electronic and optical properties of Mg-F-doped and Mg∖ F-codoped M1-VO2 via hybrid density functional calculations. J. Alloys Compd. 658, 569–575. doi:10.1016/j.jallcom.2015.10.248

CrossRef Full Text | Google Scholar

Babulanam, S. M., Eriksson, T. S., Niklasson, G. A., and Granqvist, C. G. (1987). Thermochromic VO2 films for energy-efficient windows. Sol. energy Mater. 16 (5), 347–363. doi:10.1016/0165-1633(87)90029-3

CrossRef Full Text | Google Scholar

Bai, L., Li, Q., Corr, S. A., Meng, Y., Park, C., Sinogeikin, S. V., et al. (2015). Pressure-induced phase transitions and metallization inVO2. Phys. Rev. B 91 (10), 104110. doi:10.1103/physrevb.91.104110

CrossRef Full Text | Google Scholar

Baroni, S., De Gironcoli, S., Dal Corso, A., and Giannozzi, P. (2001). Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73 (2), 515–562. doi:10.1103/RevMod.Phys.73.515

CrossRef Full Text | Google Scholar

Blöchl, P. E., Jepsen, O., and Andersen, O. K. (1994). Projector augmented-wave method. Phys. Rev. B 49 (23), 17953–17979. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Brillouin, L. (1930). Les électrons dans les métaux et le classement des ondes de de Broglie correspondantes. Comptes Rendus Hebd. Séances l’Académie Sci. 191, 292. doi:10.1051/jphysrad:01930001011037700

CrossRef Full Text | Google Scholar

Brito, W. H., Aguiar, M. C. O., Haule, K., and Kotliar, G. (2016). Metal-insulator transition inVO2: ADFT+DMFTPerspective. Phys. Rev. Lett. 117 (5), 056402. doi:10.1103/PhysRevLett.117.056402

PubMed Abstract | CrossRef Full Text | Google Scholar

Byon, J. W., Kim, M. B., Kim, M. H., Kim, S. Y., Lee, S. H., Lee, B. C., et al. (2012). Electrothermally induced highly responsive and highly selective vanadium oxide hydrogen sensor based on metal–insulator transition. J. Phys. Chem. C 116 (1), 226–230. doi:10.1021/jp2080989

CrossRef Full Text | Google Scholar

Cai, G., Wang, J., and Lee, P. S. (2016). Next-generation multifunctional electrochromic devices. Accounts Chem. Res. 49 (8), 1469–1476. doi:10.1021/acs.accounts.6b00183

CrossRef Full Text | Google Scholar

Chen, L., Wang, X., Wan, D., Cui, Y., Liu, B., Shi, S., et al. (2017). Energetics, electronic and optical properties of X (X= Si, Ge, Sn, Pb) doped VO2 (M) from first-principles calculations. J. Alloys Compd. 693, 211–220. doi:10.1016/j.jallcom.2016.09.153

CrossRef Full Text | Google Scholar

Chen, L., Xiong, H., Cui, Y., Luo, H., and Gao, Y. (2021). Ru4+-assisted phase transition in VO2 nanoparticles: Electronic structures and optical properties. Vacuum 192, 110495. doi:10.1016/j.vacuum.2021.110495

CrossRef Full Text | Google Scholar

Chernova, N. A., Roppolo, M., Dillon, A. C., and Whittingham, M. S. (2009). Layered vanadium and molybdenum oxides: Batteries and electrochromics. J. Mater. Chem. 19 (17), 2526–2552. doi:10.1039/b819629j

CrossRef Full Text | Google Scholar

Das, A. K. (1975). The relaxation-time approximation in the RPA dielectric formulation. J. Phys. F Metal Phys. 5 (11), 2035–2040. doi:10.1088/0305-4608/5/11/015

CrossRef Full Text | Google Scholar

De Conti, C., Batista, E. F., Carlson, B. V., and Frederico, T. (2001). The relativistic quasi-particle random phase approximation. Relativistic Aspects Nucl. Phys. 2001, 383–386. doi:10.1142/9789812799814_0033

CrossRef Full Text | Google Scholar

Dinh, L. N., Chase, L. L., Balooch, M., Siekhaus, W. J., and Wooten, F. (1996). Optical properties of passivated Si nanocrystals andSiOxnanostructures. Phys. Rev. B 54 (7), 5029–5037. doi:10.1103/PhysRevB.54.5029

CrossRef Full Text | Google Scholar

Eaton, M., Catellani, A., and Calzolari, A. (2018). VO 2 as a natural optical metamaterial. Opt. Express 26 (5), 5342–5357. doi:10.1364/OE.26.005342

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganesh, P., Lechermann, F., Kylänpää, I., Krogel, J. T., Kent, P. R., and Heinonen, O. (2020). Doping a bad metal: Origin of suppression of the metal-insulator transition in nonstoichiometric VO2. Phys. Rev. B 101 (15), 155129. doi:10.1103/PhysRevB.101.155129

CrossRef Full Text | Google Scholar

Gao, Y., Wang, S., Luo, H., Dai, L., Cao, C., Liu, Y., et al. (2012). Enhanced chemical stability of VO 2 nanoparticles by the formation of SiO 2/VO 2 core/shell structures and the application to transparent and flexible VO 2-based composite foils with excellent thermochromic properties for solar heat control. Energy & Environ. Sci. 5 (3), 6104–6110. doi:10.1039/C2EE02803D

CrossRef Full Text | Google Scholar

Gatti, M., Sottile, F., and Reining, L. (2015). Electron-hole interactions in correlated electron materials: Optical properties of vanadium dioxide from first principles. Phys. Rev. B 91 (19), 195137. doi:10.1103/PhysRevB.91.195137

CrossRef Full Text | Google Scholar

Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. matter 21 (39), 395502. doi:10.1088/0953-8984/21/39/395502

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodenough, J. B. (1971). The two components of the crystallographic transition in VO2. J. Solid State Chem. 3 (4), 490–500. doi:10.1016/0022-4596(71)90091-0

CrossRef Full Text | Google Scholar

Grau-Crespo, R., Wang, H., and Schwingenschlögl, U. (2012). Why the Heyd-Scuseria-Ernzerhof hybrid functional description of VO₂ phases is not correct. Phys. Rev. B 86 (8), 081101. doi:10.1103/PhysRevB.86.08110

CrossRef Full Text | Google Scholar

Hattori, A. N., Osaka, A. I., Hattori, K., Naitoh, Y., Shima, H., Akinaga, H., et al. (2020). Investigation of statistical metal-insulator transition properties of electronic domains in spatially confined VO2 nanostructure. Crystals 10 (8), 631. doi:10.3390/cryst10080631

CrossRef Full Text | Google Scholar

Haverkort, M. W., Hu, Z., Tanaka, A., Reichelt, W., Streltsov, S. V., Korotin, M. A., et al. (2005). Orbital-Assisted metal-insulator transition inVO2. Phys. Rev. Lett. 95 (19), 196404. doi:10.1103/PhysRevLett.95.196404

PubMed Abstract | CrossRef Full Text | Google Scholar

He, Z., Jian, J., Misra, S., Gao, X., Wang, X., Qi, Z., et al. (2020). Bidirectional tuning of phase transition properties in Pt: VO 2 nanocomposite thin films. Nanoscale 12 (34), 17886–17894. doi:10.1039/D0NR04008H

PubMed Abstract | CrossRef Full Text | Google Scholar

Heyd, J. E., Peralta, G., Scuseria, E., and Martin., R. L. (2005). Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional. J. Chem. Phys. 123, 174101. doi:10.1063/1.2085170

PubMed Abstract | CrossRef Full Text | Google Scholar

Heyd, J., and Scuseria, G. E. (2004). Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 121 (3), 1187–1192. doi:10.1063/1.1760074

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, J., Zhou, Y., Liu, Y., Lai, Z., Zhou, F., and Zhu, J. (2021). Sensing mechanism and optical properties of H2O on the surface of Pt/VO2: First-principles study. J. Appl. Phys. 129 (13), 134301. doi:10.1063/5.0041583

CrossRef Full Text | Google Scholar

Huang, T., Yang, L., Qin, J., Huang, F., Zhu, X., Zhou, P., et al. (2016). Study of the phase evolution, metal-insulator transition, and optical properties of vanadium oxide thin films. Opt. Mater. Express 6 (11), 3609–3621. doi:10.1364/OME.6.003609

CrossRef Full Text | Google Scholar

Jian, J., Chen, A., Chen, Y., Zhang, X., and Wang, H. (2017). Roles of strain and domain boundaries on the phase transition stability of VO2 thin films. Appl. Phys. Lett. 111, 153102. doi:10.1063/1.4991882

CrossRef Full Text | Google Scholar

Kang, L., Gao, Y., Luo, H., Wang, J., Zhu, B., Zhang, Z., et al. (2011). Thermochromic properties and low emissivity of ZnO: Al/VO2 double-layered films with a lowered phase transition temperature. Sol. Energy Mater. Sol. Cells 95 (12), 3189–3194. doi:10.1016/j.solmat.2011.06.047

CrossRef Full Text | Google Scholar

Kang, M., Kim, S. W., and Ryu, J. W. (2015). Analysis of diverging effective mass extracted from thermoelectric power across the metal–insulator transition in VO2. J. Appl. Phys. 118 (3), 035105. doi:10.1063/1.4926860

CrossRef Full Text | Google Scholar

Kokalj, A. (1999). XCrySDen—A new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 17 (3-4), 176–179. doi:10.1016/s1093-3263(99)00028-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolwas, K., and Derkachova, A. (2020). Impact of the interband transitions in gold and silver on the dynamics of propagating and localized surface plasmons. Nanomaterials 10 (7), 1411. doi:10.3390/nano10071411

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1994). Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter 6 (40), 8245–8257. doi:10.1088/0953-8984/6/40/015

CrossRef Full Text | Google Scholar

Krukau, A. V., Vydrov, O. A., Izmaylov, A. F., and Scuseria, G. E. (2006). Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125 (22), 224106. doi:10.1063/1.2404663

PubMed Abstract | CrossRef Full Text | Google Scholar

Kylänpää, I., Balachandran, J., Ganesh, P., Heinonen, O., Kent, P. R., and Krogel, J. T. (2017). Accuracy of ab initio electron correlation and electron densities in vanadium dioxide. Phys. Rev. Mater., 1(6), 065408. doi:10.1103/PhysRevMaterials.1.065408

CrossRef Full Text | Google Scholar

Lee, S., Ivanov, I. N., Keum, J. K., and Lee, H. N. (2016). Epitaxial stabilization and phase instability of VO2 polymorphs. Sci. Rep. 6 (1), 1–7. doi:10.1038/srep19621

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Zhang, S., Yang, L., Li, X., Chen, J., and Huang, C. (2017). A convenient way to reduce the hysteresis width of VO 2 (M) nanomaterials. New J. Chem. 41 (24), 15260–15267. doi:10.1039/C7NJ02632C

CrossRef Full Text | Google Scholar

Liu, K., Fu, D., Cao, J., Suh, J., Wang, K. X., Cheng, C., et al. (2012). Dense electron system from gate-controlled surface metal–insulator transition. Nano Lett. 12 (12), 6272–6277. doi:10.1021/nl303379t

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, J., Liu, H., Deng, S., Zheng, M., Wang, Y., van Kan, J. A., et al. (2014). Highly sensitive and multispectral responsive phototransistor using tungsten-doped VO2 nanowires. Nanoscale 6 (13), 7619–7627. doi:10.1039/C4NR00898G

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, Y. Y., Su, F. H., Pan, S. S., Xu, S. C., Zhang, C., Pan, J., et al. (2016). Terahertz conductivities of VO2 thin films grown under different sputtering gas pressures. J. Alloys Compd. 655, 442–447. doi:10.1016/j.jallcom.2015.08.254

CrossRef Full Text | Google Scholar

Melnik, V., Khatsevych, I., Kladko, V., Kuchuk, A., Nikirin, V., and Romanyuk, B. (2012). Low-temperature method for thermochromic high ordered VO2 phase formation. Mater. Lett. 68, 215–217. doi:10.1016/j.matlet.2011.10.075

CrossRef Full Text | Google Scholar

Mohebbi, E., Pavoni, E., Mencarelli, D., Stipa, P., Pierantoni, L., and Laudadio, E. (2022). Insights into first-principles characterization of the monoclinic VO 2 (B) polymorph via DFT+ U calculation: Electronic, magnetic and optical properties. Nanoscale Adv. 4 (17), 3634–3646. doi:10.1039/d2na00247g

PubMed Abstract | CrossRef Full Text | Google Scholar

Mortazavi, B., Shahrokhi, M., Makaremi, M., and Rabczuk, T. (2017). Anisotropic mechanical and optical response and negative Poisson’s ratio in Mo2C nanomembranes revealed by first-principles simulations. Nanotechnology 28 (11), 115705. doi:10.1088/1361-6528/aa5c29

PubMed Abstract | CrossRef Full Text | Google Scholar

Mortazavi, B., Shahrokhi, M., Shapeev, A. V., Rabczuk, T., and Zhuang, X. (2019). Prediction of C 7 N 6 and C 9 N 4: Stable and strong porous carbon-nitride nanosheets with attractive electronic and optical properties. J. Mater. Chem. C 7 (35), 10908–10917. doi:10.1039/C9TC03513C

CrossRef Full Text | Google Scholar

Paier, J., Marsman, M., and Kresse, G. (2008). Dielectric properties and excitons for extended systems from hybrid functionals. Phys. Rev. B 78 (12), 121201. doi:10.1103/PhysRevB.78.121201

CrossRef Full Text | Google Scholar

Pandurang, A. (2017). Transition metal oxide thin film based chromogenics and devices. Elsevier.

Google Scholar

Pendse, S., Jiang, J., Zhang, L., Guo, Y., Chen, Z., Hu, Y., et al. (2020). Tuning phase transition kinetics via van der Waals epitaxy of single crystalline VO2 on hexagonal-BN. J. Cryst. Growth 543, 125699. doi:10.1016/j.jcrysgro.2020.125699

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Popuri, S. R., Artemenko, A., Decourt, R., Josse, M., Chung, U. C., Michau, D., et al. (2015). Structurally restricted phase transitions in VO2 (B) and their impact on transport properties. J. Phys. Chem. C 119 (44), 25085–25092. doi:10.1021/acs.jpcc.5b07826

CrossRef Full Text | Google Scholar

Ruzmetov, D., Senanayake, S. D., Narayanamurti, V., and Ramanathan, S. (2008). Correlation between metal-insulator transition characteristics and electronic structure changes in vanadium oxide thin films. Phys. Rev. B 77 (19), 195442. doi:10.1103/PhysRevB.77.195442

CrossRef Full Text | Google Scholar

Sakuma, R., Miyake, T., and Aryasetiawan, F. (2008). First-principles study of correlation effects inVO2. Phys. Rev. B 78 (7), 075106. doi:10.1103/physrevb.78.075106

CrossRef Full Text | Google Scholar

Sasaki, T., Ueda, H., Kanki, T., and Tanaka, H. (2015). Electrochemical gating-induced reversible and drastic resistance switching in VO2 nanowires. Sci. Rep. 5 (1), 17080–17087. doi:10.1038/srep17080

PubMed Abstract | CrossRef Full Text | Google Scholar

Sims, H., Gao, X., Lee, S., Nichols, J. A., Meyer, T. L., Ward, T. Z., et al. (2017). Oxide epitaxy with large symmetry mismatch: Bronze-phase VO2 on SrTiO3. Microsc. Microanal. 23 (S1), 1580–1581. doi:10.1017/S143192761700856X

CrossRef Full Text | Google Scholar

Smidstrup, S., Markussen, T., Vancraeyveld, P., Wellendorff, J., Schneider, J., Gunst, T., et al. (2019). QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 32 (1), 015901. doi:10.1088/1361-648X/ab4007

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanaka, A. (2003). A new scenario on the metal–insulator transition in VO2. J. Phys. Soc. Jpn. 72 (10), 2433–2436. doi:10.1143/JPSJ.72.2433

CrossRef Full Text | Google Scholar

Tran, F., and Blaha, P. (2017). Importance of the kinetic energy density for band gap calculations in solids with density functional theory. J. Phys. Chem. A 121 (17), 3318–3325. doi:10.1021/acs.jpca.7b02882

PubMed Abstract | CrossRef Full Text | Google Scholar

Vanderbilt, D. (1990). Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. 677 rev. B 41 (11), 7892. doi:10.1103/PhysRevB.41.7892

CrossRef Full Text | Google Scholar

Varadwaj, A., and Miyake, T. (2022). Geometrical-, electronic-and optical properties of vanadium dioxide: A theoretical perspective from meta-GGA SCAN. ChemistrySelect 7 (13), e202200171. doi:10.1002/slct.202200171

CrossRef Full Text | Google Scholar

Verleur, H. W., Barker, A. S., and Berglund, C. N. (1968). Optical properties of VO2between 0.25 and 5 eV. Phys. Rev. 172 (3), 788–798. doi:10.1103/PhysRev.172.788

CrossRef Full Text | Google Scholar

Wan, D., Xiong, P., Chen, L., Shi, S., Ishaq, A., Luo, H., et al. (2017). High-performance thermal sensitive W-doped VO2 (B) thin film and its identification by first-principles calculations. Appl. Surf. Sci. 397, 30–39. doi:10.1016/j.apsusc.2016.11.078

CrossRef Full Text | Google Scholar

Wang, J., Zhang, L., Yu, L., Jiao, Z., Xie, H., Lou, X. W. D., et al. (2014). A bi-functional device for self-powered electrochromic window and self-rechargeable transparent battery applications. Nat. Commun. 5 (1), 4921–4927. doi:10.1038/ncomms5921

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolterink, T., Axt, V. M., and Kuhn, T. (2002). Coulomb quantum kinetics beyond RPA and Bornapproximation. Phys. B Condens. Matter 314 (1-4), 132–135. doi:10.1016/S0921-4526(01)01373-4

CrossRef Full Text | Google Scholar

Wu, X., Weng, X., Yuan, L., Zhang, J., Qi, L., and Wei, B. (2020). Phase-and shape-controlled synthesis of VO2 by a hydrothermal-calcination method. Vacuum 176, 109352. doi:10.1016/j.vacuum.2020.109352

CrossRef Full Text | Google Scholar

Xu, K., Liao, N., Zhang, M., and Xue, W. (2021). Selective methane sensing properties of VO2 at different temperatures: A first principles study. Appl. Surf. Sci. 536, 147969. doi:10.1016/j.apsusc.2020.147969

CrossRef Full Text | Google Scholar

Xu, S., Shen, X., Hallman, K. A., Haglund, R. F., and Pantelides, S. T. (2017). Unified band-theoretic description of structural, electronic, and magnetic properties of vanadium dioxide phases. Phys. Rev. B 95 (12), 125105. doi:10.1103/PhysRevB.95.125105

CrossRef Full Text | Google Scholar

Yang, J., Tan, L. Z., and Rappe, A. M. (2018). Hybrid functional pseudopotentials. Phys. Rev. B 97 (8), 085130. doi:10.1103/PhysRevB.97.085130

CrossRef Full Text | Google Scholar

Yuan, X., Zhang, Y., Abtew, T. A., Zhang, P., and Zhang, W. (2012). VO₂: Orbital competition, magnetism, and phase stability. Phys. Rev. B 86 (23), 235103. doi:10.1103/PhysRevB.86.235103

CrossRef Full Text | Google Scholar

Zayed, M. K., Elabbar, A. A., and Yassin, O. A. (2020). Electronic and optical properties of the VO2 monoclinic phase using SCAN meta-GGA and TB-mBJ methods. Phys. B Condens. Matter 582, 411887. doi:10.1016/j.physb.2019.411887

CrossRef Full Text | Google Scholar

Zhang, S., Shang, B., Yang, J., Yan, W., Wei, S., and Xie, Y. (2011). From VO2 (B) to VO2 (A) nanobelts: First hydrothermal transformation, spectroscopic study and first principles calculation. Phys. Chem. Chem. Phys. 13 (35), 15873–15881. doi:10.1039/C1CP20838A

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y. (2016). VO₂(B) conversion to VO₂(A) and VO₂(M) and their oxidation resistance and optical switching properties. Mater. Pol. 34 (1), 169–176. doi:10.1515/msp-2016-0023

CrossRef Full Text | Google Scholar

Zheng, H., and Wagner, L. K. (2015). Computation of the correlated metal-insulator transition in vanadium dioxide from first principles. Phys. Rev. Lett. 114 (17), 176401. doi:10.1103/PhysRevLett.114.176401

PubMed Abstract | CrossRef Full Text | Google Scholar

Zylbersztejn, A. M. N. F., and Mott, N. F. (1975). Metal-insulator transition in vanadium dioxide. Phys. Rev. B 11 (11), 4383–4395. doi:10.1103/PhysRevB.11.4383

CrossRef Full Text | Google Scholar