Sensitivity optical non-linear measurement based on wide-band phase objects

On the basic that the phase object (PO) is the key optical device in the 4f imaging system, a modified high sensitivity optical nonlinear measurement technique with an absorptive homemade phase object (HPO) is reported in order to characterize the value of weak nonlinear refraction material. The absorptive HPO used in this technique is two transparent glass plates on which a liquid film between two pieces of transparent glasses is deposited and added a rotating object at the below HPO to modulate the phase of a PO. The measuring sensitivity can be improved by changing the transmittance of the absorptive HPO. Meanwhile, because the phase retardation of HPO can be continuously adjustable by modulate the rotating object, it makes the sensitivity of measurement at different wavelengths of laser optimal. Results show that the measuring sensitivity is improved 2-4 times compare with the conventional 4f imaging technique. Furthermore, the modified technique can be used to measure the spectrum of nonlinear refraction coefficients of materials at the continuous wavelength. This method further expands the 4f phase coherent imaging measurement technology, not only solves the deficiencies of the conventional phase object, but also improves the accuracy of the measurement. Experiment and theoretical analysis results are presented to validate our technique.

1 Introduction

In recent years, a large number of non-linear optical (NLO) materials have been investigated for their potential use in photoelectronic devices (Zhang et al., 2022), optical information processing (Wu et al., 2020) and optical communication (SOROKINA et al., 2016). In particular, large attention has been paid to the development of simple and accurate measurement techniques, with emphasis on measurement sensitivity. Highly sensitive measurements play a significant role in characterizing optical non-linearities, especially those of weak NLO materials. The Z-scan technique (Pereira and Correia, 2020) is a popular method to obtain information about third- and higher order non-linearities. The method provides estimate of NLO and is based on the analysis of the distortion of a beam passing through non-linear materials. However, high quality Gaussian beams are not readily available. Hence, Zhao et al. reported that the use of the s-called top-hat (Zhao and Palffy-Muhoray, 1993) beams instead of Gaussian beams in Z-scan setups improves the measurement sensitivity by a factor of 2.5. However, the technique requires multiple irradiations by strong laser pulses to obtain the complex non-linear NLO of optical materials and involves measurements at focal plane. This may damage the sample, especially for photo-sensitive materials, and suggests the use of single-shot techniques, which would overcome the above difficulties. One powerful technique is based on single-shot 4f coherent imaging system (Cherukulappurath et al., 2004). The method involves a different spatial distribution of beams compared to Z-scan, and allows one to obtains accurate measurements of the intensity when equipped with a charge-coupled device (CCD) camera. The setup is based on the Zernike spatial filtering principle to transform the phase changes caused by non-linear refraction into light intensity changes in the plane. Other advantages of the method include the simplicity of the alignment, and the high measurement sensitivity. Furthermore, as it happens for Z-scan experiments, sensitivity may be improved using top-hat beams instead of Gaussian beams (Cherukulappurath et al., 2004). Boudebs et al. reported a 4f non-linear-imaging technique with improved sensitivity and involving a phase object (NIT-PO) (Boudebs and Cherukulappurath, 2004) to analyze the sign of non-linear index. Later on, the technique has been modified with considerable effort, see e.g., Yang et al. (​ Yang et al., 2017) about Z-scan technique with absorptive PO. The sensitivity of the technique can be improved by the changing absorption index of PO which, however, cannot be changed arbitrarily. In addition, an important limitation of 4f NIT-PO techniques employed so far, is the impossibility to use the same PO with a continuous spectrum, as the phase retardation of PO cannot be changed arbitrarily. Indeed, it is significant for the 4f imaging technique to modulate phase and there are piezoelectric ceramic and phase modulators to this aim. However, those devices are expensive and their use complex. Therefore, an alternative simple method with high precision would be exceedingly welcome.

In this paper, the use with a homemade phase object (HPO) added to the 4f imaging technique to and put forward a high sensitivity measurement technique. The materials of the HPO are readily available and the manufacturing is simple. Additionally, our HPO may be used with pulses with a continuous spectrum. The non-linearity of CS₂ and absolute ethanol are considered in this new technique in order to assess its sensitivity and verify the enhancement compared to traditional 4f imaging techniques. Our results confirm that the use of a wideband (The phase object is suitable for optical non-linear measurement at multiple wavelengths) HPO improves the sensitivity of 4f imaging systems and may be used with beams characterized by a continuous spectrum.

2 Theoretical analysis and model

Our HPO is composed of two round pieces of transparent glass with a liquid film in between. The liquid film required by the homemade phase object (HPO) in the technique can be any pure absorptive or transparent liquid. The black ink is used to be a liquid film in our method. The radius is $L_p$, and the HPO is fixed on a rotary table (see Figure 1). The working principle is that a micron space gap may be formed between the two pieces of glass and that changing the thickness of the HPO is possible by controlling the angle of the rotary table (Figure 1C). The technique consists of lenses L₃ and L₄ and is schematically shown Figure 2. The HPO is placed on the object plane of the 4f imaging system. After passing through HPO, the incident beam of light is divided into two beams of light by a beam splitter (BS). One beam is detected by D₁ for the energy of the incident light is monitored, whereas the other beam is focused on the non-linear medium through lens L₃.

FIGURE 1

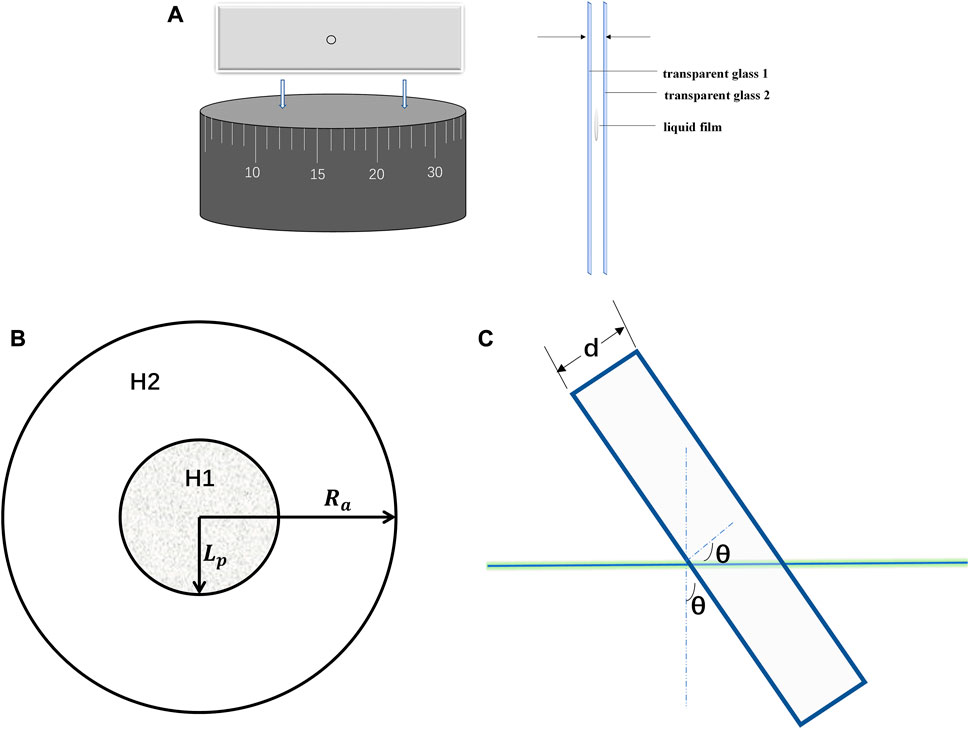
FIGURE 1. (A,B) Schematic of the HPO used in the 4f imaging system. (C) Schematic of the HPO changing the angle of the rotating object.

FIGURE 2

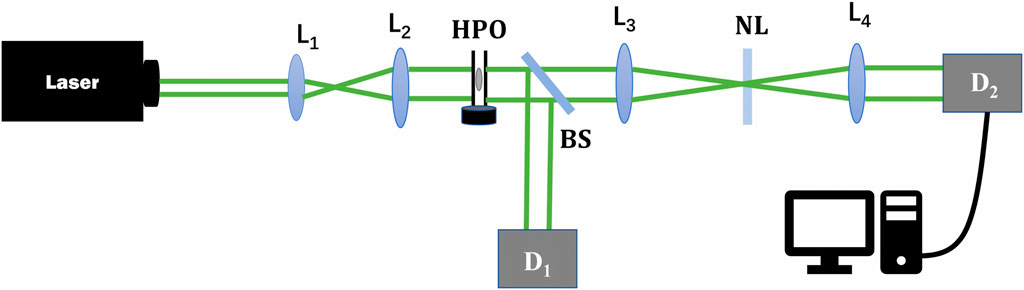
FIGURE 2. Schematic of 4f imaging system with HPO. L₁-L₄, lenses; BS, beam splitter; D₁ is used to detect the reference light, D₂ is used to detect the linear and non-linear images.

In order to analyze the scheme, let us start from a traditional 4f imaging system (see Ref (Cherukulappurath et al., 2004; Boudebs and Cherukulappurath, 2004; Yang et al., 2017; Fedus and Boudebs, 2013). for more details) and assume that we use a top-hat beam and that the HPO is placed on the object plane. Further, we assume for simplicity that a non-linear medium is placed on the focal plane. We refer to Ref (Fedus and Boudebs, 2013). for situations where the non-linear medium is far away from the focus. Finally, we assume that Fourier optics can fully describe the 4f imaging technique. The HPO and the transparent glasses are illuminated at normal incidence by a linearly polarized monochromatic plane wave $E\left(x,y,t\right)=E_0\left(x,y,t\right)\exp \left[-\mathrm{j}\left(\mathrm{w}\mathrm{t}-\mathrm{k}\mathrm{z}\right)\right]+\mathrm{c}.\mathrm{c}.$, where $k$ is the wave vector, $w$ is angular frequency, and $E_0\left(x,y,t\right)$ is amplitude of the electric field containing the temporal envelope of the laser pulse. We use the slowly varying envelope approximation (SVEA) (Bloembergen, 1996; Sutherland, 2003) to investigate the propagation of the electric field in the non-linear sample. Moreover, since we only analyze the intensity of the image, the time term may be omitted. We may also ignore any thermo-optical effect since we are dealing with nanosecond pulses and a low repetition rate (10Hz) (Boudebs and Cherukulappurath, 2004).

The two parts of the HPO, H₁ and H₂, are shown in Figure 1B. The central region H₁ has radius $L_p$ and amplitude transmittance $T_{PO}$ ($0<T_{PO}\le 1$). It induces a uniform shift $\varphi$ and is characterized by a transmittance $t_p=T_{PO}\exp \left[\mathrm{i}\times \mathrm{c}\mathrm{i}\mathrm{r}\left(\mathrm{r}-{\mathrm{L}}_p\right)\times \varphi \right]$, as a function of the radial coordinate, where $\mathrm{c}\mathrm{i}\mathrm{r}\left(x\right)=1$ if $x<0$ and $\mathrm{c}\mathrm{i}\mathrm{r}\left(x\right)=0$ otherwise. The transmittance of the annular region H₂ can be expressed as $t_a=cir\left(\mathrm{r}-{\mathrm{R}}_a\right)-\mathrm{c}\mathrm{i}\mathrm{r}\left(\mathrm{r}-{\mathrm{L}}_p\right)$. If we denote the total transmittance of the HPO by $t_{PO}\left(x,y\right)$, the electric field on the external surface can be written as $O\left(x,y\right)=E\left(x,y\right)t_{PO}\left(x,y\right)$, whereas the field amplitude on the front surface of the non-linear medium (on the focal plane of L₃) is spatial Fourier transform of the $O\left(x,y\right)$:

$S\left(u,v\right)=\frac{1}{\lambda f}\iint o\left(x,y\right)\exp \left[-2\pi j\left(ux+vy\right)\right]dxdy,(1)$

where $f$ is the focal length of L₃, $\mathrm{\lambda }$ is the wavelength of the exciting wave, $u=\frac{x}{\lambda f}$ and $v=\frac{y}{\lambda f}$ are the spatial frequencies on the focal plane. Taking into account the three main features of the non-linear sample, i.e., the linear absorption a (m⁻¹), the non-linear absorption ß (m/W) and the non-linear index ${\mathrm{n}}_2$ (m²/W), the phase shift imposed to the beam by the non-linear sample can be written as

${\phi }_{NL}\left(u,v\right)=\frac{k{n}_2}{\beta }\ln \left[1+\beta L_{eff}I\left(u,v\right)\right],(2)$

where $k=2\pi /\lambda$ is the wave vector, $L_{eff}=\frac{\left[1-\exp \left(-\alpha L\right)\right]}{\alpha }$ is the effective length of a non-linear medium, L is the actual length of a non-linear medium and $I\left(u,v\right)\propto {\left|S\left(u,v\right)\right|}^2$ is the intensity of laser beam exciting a non-linear medium. After modulation through the sample, the complex electric field at the output surface can be defined as

$S_L\left(u,v\right)=S\left(u,v\right)\frac{e^{-\alpha L/2}}{{\left[1+\beta L_{eff}I\left(u,v\right)\right]}^{1/2}}{e}^{j{\phi }_{NL}\left(u,v\right)},(3)$

where $\mathrm{T}\left(u,v\right)$ is the complex amplitude response due to non-linearity, i.e.,

$T\left(u,v\right)=\frac{S_L\left(u,v\right)}{S\left(u,v\right)}=\frac{e^{-\alpha L/2}}{{\left[1+\beta L_{eff}I\left(u,v\right)\right]}^{1/2}}{e}^{j{\phi }_{NL}\left(u,v\right)},(4)$

where, if the sample is a Kerr medium, a and $\mathrm{\beta }$ are both negligible, and Eqs 2, 3 reduce to:

${\phi }_{NL}\left(u,v\right)=k{n}_{2}LI\left(u,v\right),(5)$

$S_L\left(u,v\right)=S\left(u,v\right)e^{j{\phi }_{NL}\left(u,v\right)},(6)$

The technique is described with more details in the following two Subsections.

2.1 Improve sensitivity of 4f imaging system with the absorptive HPO

The non-linear sample in our setup may be regarded as a low-frequency filter. The portion of the incident light passing through the H₂ is spread less than the portion passing through H₁ because R_a is much larger L_P (Shui et al., 2010). Hence, the modulation induced by H₁ may be ignored and we only consider the non-linear modulation induced by H₂. The on-axis field intensity for H₁ is then considered. The complex field amplitude at the output plane of 4f imaging system can be expressed as:

$E=E_1+\Delta E_2,(7)$

The electric field amplitudes coming from the regions H₁ and H₂ of HPO can be written as E₁ and E₂ respectively. The light coming from H₁ is considered a uniform background distribution (regarded as a direct light) because the non-linear modulation is negligible, whereas the light from H₂ is modulated by the non-linear medium at the focal plane and produce a small perturbation of the incident wave (as diffracted light). The second term (∆ $E_2$) in Eq. 7 results from the diffracted light.

The interference induced by the diffracted light is insensitive to phase changes (${\phi }_{NL}$) when $\varphi =0$ and ${\phi }_{NL}\ll 1$ (Boudebs and Cherukulappurath, 2004; Yang et al., 2017). However, if $\varphi =\pi /2$, the intensity at the output of 4f imaging system is given by

$I^{\prime }\left(u,v\right)=\frac{1}{n}{E_1}^2+\Delta {E_2}^2+2\frac{1}{\sqrt{n}}{E}_1\Delta E_2\cos \left(\pi /2+{\phi }_{NL}\right),(8)$

The first term ($\frac{1}{n}{E_1}^2$) in Eq. 8 is the intensity in the linear region on the axis. The transmittance $T_{nor}$ is the normalized peak value of $T_{NL}/T_L$. The variable $\Delta T$ can be defined as an appropriate parameter to estimate the refractive coefficient (${\mathrm{n}}_2$) of non-linear samples.

The difference $\Delta T$ can be written as:

$\begin{array}{l}\Delta T=\frac{2\left(\frac{1}{\sqrt{n}}{E}_1\right)\Delta E_2\cos \left(\pi /2+{\phi }_{NL}\right)+\Delta {E_2}^2}{{\left(\frac{1}{\sqrt{n}}{E}_1\right)}^2}\\ =-\sqrt{n}\frac{2E_1\Delta E_2\sin {\phi }_{NL}}{{E_1}^2}\end{array},(9)$

where $\frac{2E_1\Delta E_2}{{E_1}^2}$ is the sensitivity of the system when $n$ = 1. If the incident field in the HPO region is reduced by a factor of $\frac{1}{\sqrt{n}}$ ($n$ >1), the sensitivity increased by $\sqrt{n}$ times.

In our measurements, the signal received by CCD on the exit plane of the 4f system has been processed using the above analysis (Eqs. 1–9). The extension of the PO region increases if the non-linear sample has a positive phase shift, whereas it decreases otherwise. Here a non-linear sample producing a positive shift has been simulated. In Figure 3A we show the difference transmittance ($\Delta T$) for various transmittance ($T_{PO}$). Figure 3B shows the cross-section views of the normalized linear image and non-linear image amplitudes. The black curve denotes the linear image, the green one denotes the non-linear image as measured by conventional transparent PO ($n$ = 1), and the others denote the non-linear image measured by HPO ($n$ <1).

FIGURE 3

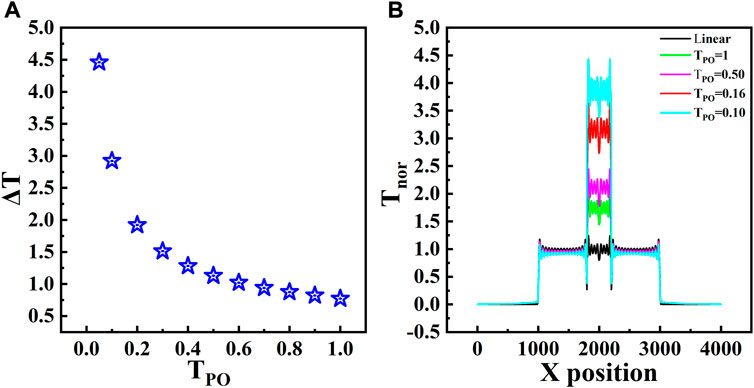
FIGURE 3. (A) Normalized transmittance $\Delta T$ as a function of the transmittance of the HPO. (B) The non-linear imaging curve for various transmittance values.

The simulation results show that when the electric field amplitude (transmittance) in the PO region is less than 50% of the original, the sensitivity is increased by 2–4 times. For example, for $\sqrt{n}=10$ and a HPO with $T_{PO}=0.1$, the sensitivity 4f imaging system is improved by a factor $\sqrt{10}$ compared to that of a conventional transparent PO.

2.2 The use of the HPO in 4f imaging system with light with a continuous spectrum

In Figures 4A, B, we show theoretical results and simulations for the case of the phase shift $\varphi$ of the PO set to $\varphi =2\pi d\left(n^{\prime }-1\right)/\lambda$. Numerical results show that a traditional PO cannot be used to measure the non-linear index with a continuous spectrum. In order to make the phase object conform to the high sensitivity measurement at different wavelengths, the optical path difference between the two beams needs to be changed with high precision, and the required accuracy is up to nm. There are piezoelectric ceramic and phase modulator to match that accuracy, but the devices are expensive and the process is complex. Therefore, a more simple and convenient method ensuring high precision is needed. We consider the scheme in Figure 1A, where a rotating object is added below the HPO in order to modulate the phase $\varphi$ for use with light with a continuous spectrum, and measure the thickness of the HPO. As a function of the angle ($\theta$) of the rotating object we have

$\varphi =2\pi \mathrm{d}\left(n^{\prime }-1\right)/\lambda \cos \theta ,(10)$

FIGURE 4

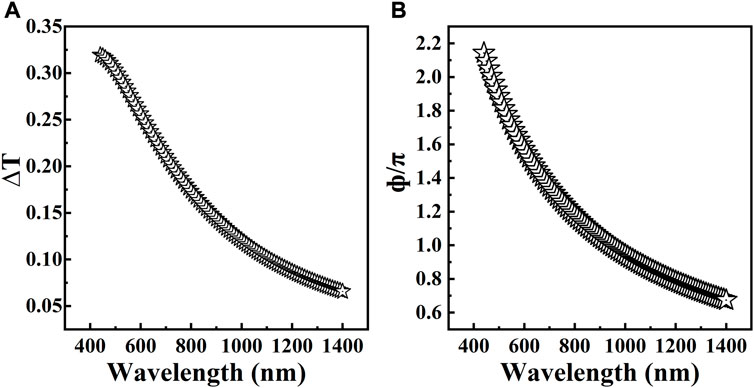
FIGURE 4. (A) Transmittance changes $\left(\Delta T\right)$ as a function of the wavelength $\left(\lambda \right)$. (B) The phase shift in the object as a function of the wavelength $\left(\lambda \right)$.

And the thickness of the HPO can be expressed as:

$\mathrm{d}=\left[\left({\varphi }_1-{\varphi }_2\right)\lambda \right]/\left[2\pi \left(n^{\prime }-1\right)\left(\frac{1}{\cos {\theta }_1}-\frac{1}{\cos {\theta }_2}\right)\right],(11)$

Where $n^{\prime }$ is the refractive index of the used slide, $\theta$ is the angle of the rotating object and $\left({\varphi }_1-{\varphi }_2\right)$ is phase aberration accumulated in a cycle. However, the area of the HPO changes with the angle of rotation and this should be considered to assess the sensitivity of this technique. The dependence of the sensitivity on the area has been investigated numerically and results are shown in Figure 5A: the sensitivity of system is higher when the area of a HPO is smaller ($\mathrm{S}={\left(L_p/R_a\right)}^2$) and the sensitivity is minimum for $\mathrm{S}\approx 0.5$. In Figure 5B we show how the area influences the light intensity from the HPO. The behaviour is similar to that of FIG, i.e., the light intensity is higher when S is smaller and is minimum when $\mathrm{S}\approx 0.5$. Although the light intensity increases when $S>0.5$, the part of the incident light passing through H₂ (diffracted light) decreases. Therefore, the quantity $\Delta T$ increases slowly for $S>0.5$. We use a HPO $L_p$ equal to 0.1 (i.e., $S\approx 0.01$). Figure 5C shows that the area has little effect on $\Delta T$ when the angle is changed ($S<0.01$).

FIGURE 5

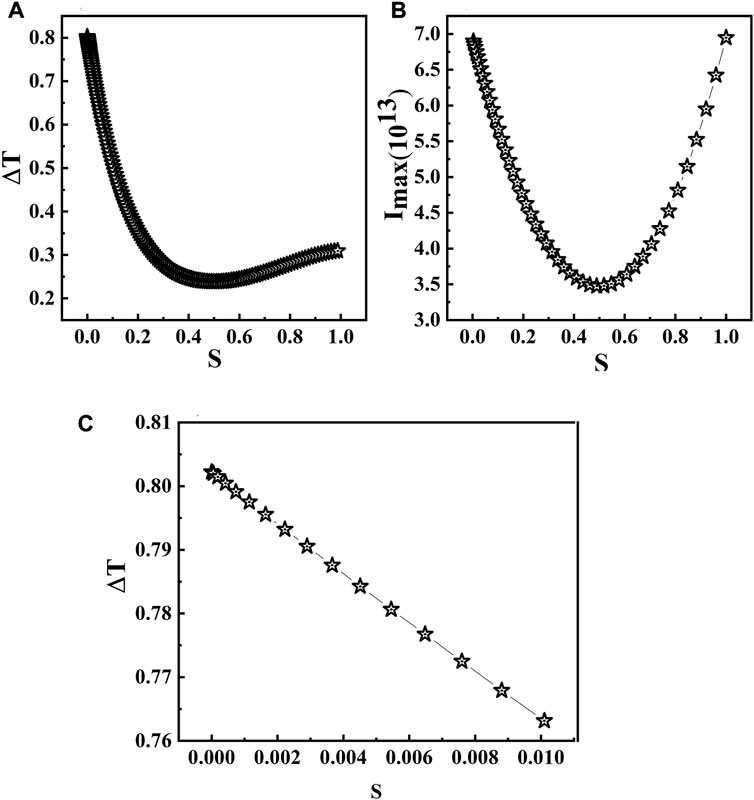
FIGURE 5. (A) Transmittance changes $\left(\Delta T\right)$ as a function of the area ($\mathrm{S}={\left(L_p/R_a\right)}^2$). (B) The intensity I_max (given in GW/cm² inside) of phase object as a function of the area ($\mathrm{S}={\left(L_p/R_a\right)}^2$). (C) Dependence of $\Delta T$ on the HPO area when $\mathrm{S}\le 0.01$.

The sensitivity of 4f phase coherent imaging technology is determined by the phase retardation of PO, and the phase retardation of PO, given a certain thickness, is different at different wavelengths. This means that the sensitivity of the system may be optimized only for a specific wavelength given the thickness of PO. In order to ensure the optimal measurement sensitivity of the system at different wavelengths, it is necessary to continuously change the optical path difference of PO. This also means that conventional transparent PO cannot be used to perform measurements with a continuous spectrum. For example, a conventional transparent PO using light at 400 nm cannot be used to perform measurements at 905 nm. The simulation results also show that the sensitivity is higher when S is smaller ($S<0.5$) (Boudebs and Cherukulappurath, 2004). This is due to the fact that the light intensity depends on the area, whereas the area of HPO has little effect for the $\Delta T$ when $S<0.01$.

3 Experimental results and discussion

In order to order to assess the reliability and precision of our technique we have implemented it to measure the third-order non-linear refraction index of Carbon disulfide (CS₂) and absolute ethanol using an absorptive HPO. Among them, CS₂ is a standard sample to verify the validity of characterization techniques. The solvent CS₂ and the absolute ethanol are loaded into a 2 mm glass sell. The excitation source is a Q-switched and mode-locked Nd: YAG laser which provides 21ps output laser pulses, with a wavelength of 532 nm and a repetition rate of 10-Hz. As a benchmark, the solvent is also measured with a HPO and conventional transparent PO at 905 nm (100 mW) with a continuous laser.

Three kinds of imaging data are needed in experiment. i) No sample: The acquisition is reference light. ii) Linear image: The image acquisition is obtained with low intensity by placing high-density neutral filters before the non-linear samples. iii) Non-linear image: The image is acquired with high intensity by placing the same high-density neutral filters after the non-linear samples. The linear and non-linear images are used to calculate the refraction index n₂ using Eqs 1–9. The non-linear signal processing leads to $\Delta T$ using the normalized peak value of $T_{NL}/T_L$.

The absorptive HPO used in our experiments consists in two transparent glass plates with a liquid film in between. The absorption index can be changed by changing the thickness of the liquid film. The phase $\varphi$ can be changed by controlling the rotation, and the HPO can be rotated to produce a $\mathrm{\pi }/2$ phase at 532 nm. Figures 6A, B show the results of the non-linear refraction of CS₂ with a conventional PO and an absorptive HPO at an energy of about 1.2 $\mu J$. The transmittance of the HPO is approximately 16%. The solid lines in Figures 6C, D are the fitting curves with $\beta =0$; $n_2=3.2\times {10}^{-18}{m}^2/\mathrm{W}$ (Boudebs and Cherukulappurath, 2004; Ganeev et al., 2004). Figures 7A, B show the estimated non-linear refraction of absolute ethanol obtained with a conventional PO and an absorptive HPO at an energy of about 4.5 $\mu J$. The solid line in Figure 7D is the fitting curve with $\beta =0$; $n_2=4.55\times {10}^{-19}{m}^2/\mathrm{W}$ (Ho and Alfano, 1979; Yi et al., 2020). As it can be seen from Figure 6, the normalized transmittance $\Delta T$ measured using this technique with HPO is about 2.5 times higher than that measured using the traditional technique. It shows that the use of absorptive HPO can improve the measure sensitivity in the 4f imaging system. And the experimental results for $\Delta T$ are consistent with the theoretical one from Eq. 9. Meanwhile, the non-linear refraction signal of absolute ethanol is not observed by using the conventional PO, but can be clearly observed by using absorptive HPO. It is further explained that the proposed method can effectively improve the sensitivity of the 4f imaging system. Therefore, our technique has a better advantage for some optical materials which have weak non-linear optical coefficients.

FIGURE 6

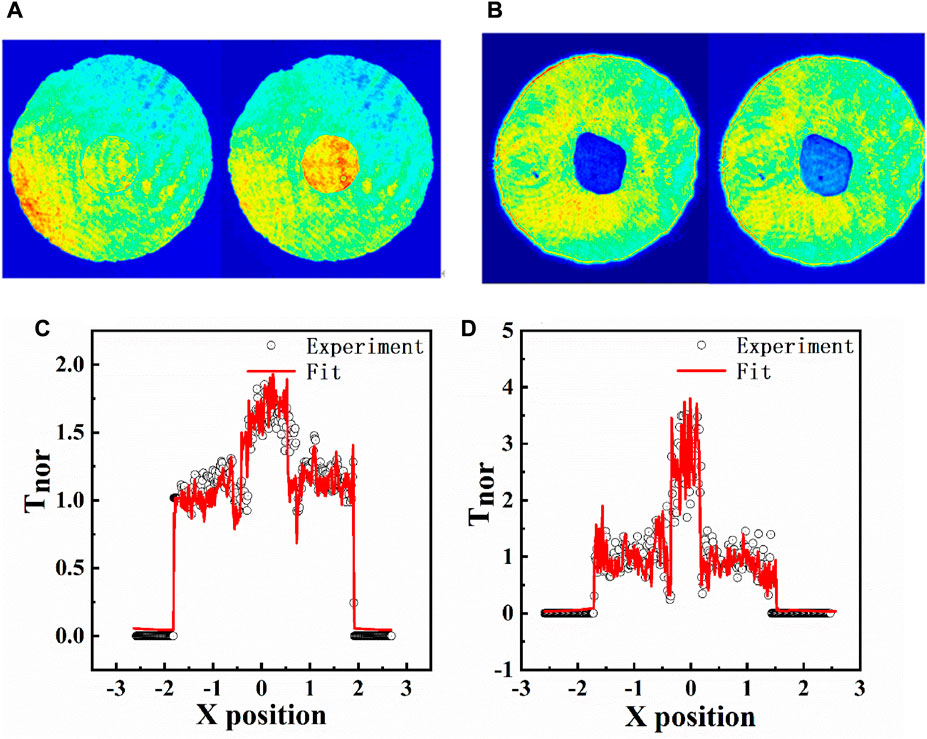
FIGURE 6. (A,B) Linear and non-linear images for CS₂ as acquired by our experimental 4f imaging system with a conventional transparent PO and absorptive (T_PO≈16%) HPOs. (C,D) Profiles of images (A,B) by processing $T_{NL}/T_L$; the red solid lines are theoretical values.

FIGURE 7

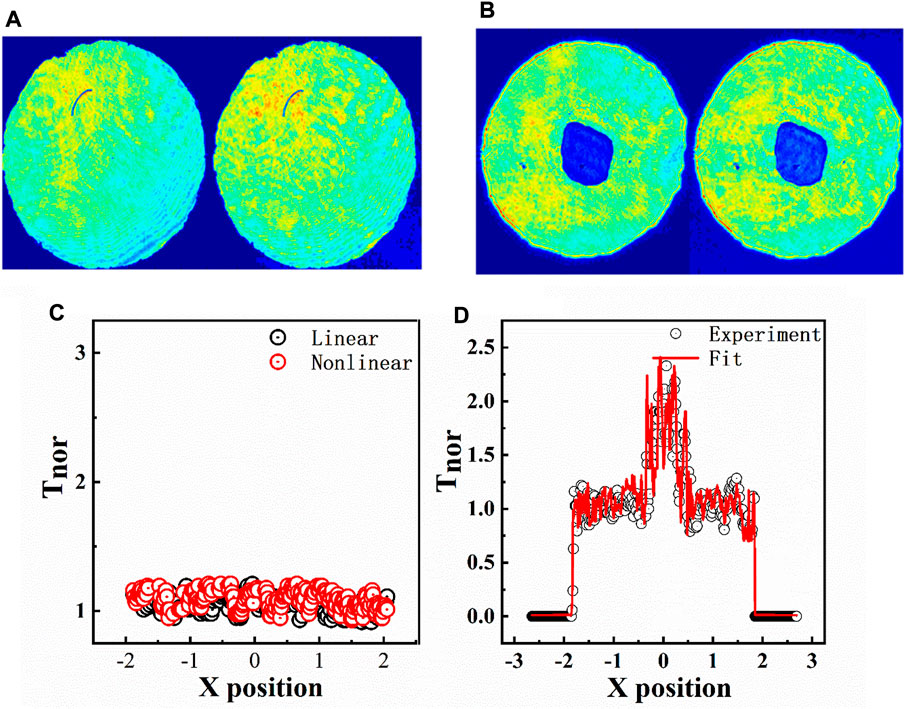
FIGURE 7. (A,B) Linear and non-linear images for ethanol as acquired by our experimental 4f imaging system with a conventional transparent PO and an absorptive (T_PO≈16%) HPO. (C,D) Profiles of images (A,B) by processing $T_{NL}/T_L$; the red solid lines are theoretical values.

Figure 8 is instead the results obtained with conventional transparent POs (a conventional transparent PO of 400 nm, a conventional transparent PO of 532 nm and a conventional transparent PO of 800 nm) and a transparent HPO to measure the solvent using a 905 nm continuous laser at the power of 1 mW. The results shows that the conventional transparent PO cannot be used with a continuous spectrum. The results also shows that the HPO can be modulated to produce a complete cycle and overcome the disadvantage of the conventional transparent PO. Overall, these results confirm the validity of our approach. Furthermore, from our experimental results, the thickness of the HPO is calculated to be approximately 0.634 μm from the Eq. 11. Therefore, if other experimental factors are not considered, it can theoretically be used in a range of about 304 nm–1752 nm by the Eq. 10.

FIGURE 8

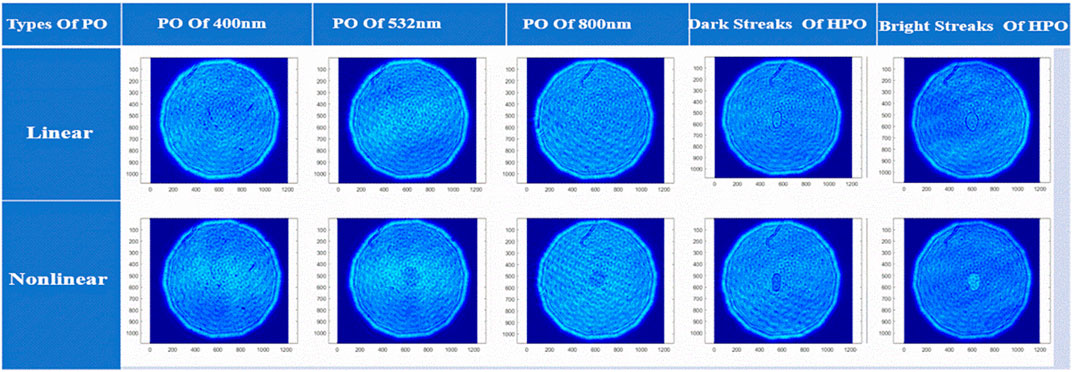
FIGURE 8. Experimental 4f imaging with conventional transparent POs (a conventional transparent PO of 400 nm, a conventional transparent PO of 532 nm and a conventional transparent PO of 800 nm) and linear and non-linear images acquired with a transparent HPO.

4 Conclusion

In summary, a simple and high-sensitive 4f imaging technique has been suggested and demonstrated to measure the non-linear refractive coefficient. In particular, we have illustrated numerically that the use of the low transmittance HPO lead to a higher sensitivity compared to a conventional transparent PO in a 4f imaging system. The sensitivity improves by a factor of ${\left(1/T_{PO}\right)}^{1/2}$ when $0<T_{PO}<1$. In addition, by modulating the phase using a rotating object placed below HPO we made it possible the use of light with a continuous spectrum. In order to verify our technique, the non-linear coefficient of CS₂ (a well-known non-linear material) and that of absolute ethanol have been investigated. The value and sign obtained are agreement with the results obtained by other methods. Furthermore, we have used a HPO in 4f imaging system with continuous spectrum, a technique not available with conventional transparent PO. Our technique retains the advantages of the traditional 4f imaging system (optical alignment is easy, single-shot and no displacement of samples, et.,) and show higher sensitivity in measuring non-linearity. Furthermore, it can be used for non-linearity measurement with 4f imaging systems and continuous spectrum sources.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

ZS: Investigation, writing—Original draft, writing—Review and editing. YY and JY: Provide ideas. And all authors take part in formal analysis.

Funding

This work was supported by National Natural Science Foundation of China (Nos. 11804244, 11704273), Natural Science Foundation of Jiangsu Province (Nos. BK20180965, BK20170375), the National Safety Academic Fund (Grant No. U1630103).

Acknowledgments

We gratefully acknowledge National Natural Science Foundation of China (11704273, 51607119), National Safety Academic Fund (U1630103).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bloembergen, N. (1996). Nonlinear optics. Singapore: World Scientific.

Google Scholar

Boudebs, G., and Cherukulappurath, S. (2004). Nonlinear optical measurements using a4fcoherent imaging system with phase objects. Phys. Rev. A 69 (5), 053813. doi:10.1103/physreva.69.053813

CrossRef Full Text | Google Scholar

Cherukulappurath, S., Boudebs, G., and Monteil, A. (2004). 4f coherent imager system and its application to nonlinear optical measurements. J. Opt. Soc. Am. B 21 (2), 273–279. doi:10.1364/josab.21.000273

CrossRef Full Text | Google Scholar

Fedus, K., and Boudebs, G. (2013). Experimental techniques using 4f coherent imaging system for measuring nonlinear refraction. Opt. Commun. 292, 140–148. doi:10.1016/j.optcom.2012.11.074

CrossRef Full Text | Google Scholar

Ganeev, R. A., Ryasnyansky, A. I., Baba, M., Suzuki, M., Ishizawa, N., Turu, M., et al. (2004). Nonlinear refraction in CS2. Appl. Phys. B 78, 433–438. doi:10.1007/s00340-003-1389-y

CrossRef Full Text | Google Scholar

Ho, P. P., and Alfano, R. R. (1979). Optical Kerr effect in liquids. Phys. Rev. A 20 (5), 2170–2187. doi:10.1103/physreva.20.2170

CrossRef Full Text | Google Scholar

Pereira, M. K., and Correia, R. R. B. (2020). Z-scan and eclipsing Z-scan analytical expressions for third-order optical nonlinearities. J. Opt. Soc. Am. B 37 (2), 478–487. doi:10.1364/josab.376541

CrossRef Full Text | Google Scholar

Shui, M., Luo, X., Zhang, X., Jin, X., Li, C., Yang, J., et al. (2010). Phase filtering in nonlinear-imaging technique with a phase object. J. Opt. Soc. Am. A 27 (11), 2514–2523. doi:10.1364/josaa.27.002514

CrossRef Full Text | Google Scholar

Sorokina, M., Sygletos, S., and Turitsyn, S. (2016). Sparse identification for nonlinear optical communication systems: SINO method. Opt. Express 24 (26), 30433–33044. doi:10.1364/oe.24.030433

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutherland, R. L. (2003). Hand book of nonlinear optics. Boca Raton: CRC Press.

Google Scholar

Wu, J., Li, Z., Luo, J., and Jen, A. K. Y. (2020). High-performance organic second- and third-order nonlinear optical materials for ultrafast information processing. J. Mater. Chem. C 8, 15009–15026. doi:10.1039/d0tc03224g

CrossRef Full Text | Google Scholar

Yang, Y., Yang, J. Y., Li, Z. G., Wu, X. Z., and Song, Y. L. (2017). Sensitive measurement of optical nonlinearity using an absorptive phase object. Appl. Phys. B 123 (9), 248. doi:10.1007/s00340-017-6825-5

CrossRef Full Text | Google Scholar

Yi, J., Miao, L., Li, J., Yi, Q., Huang, J., and Zhao, C. (2020). Self-defocusing of light in ethanol around 1550 nm. IEEE Photonics J. 12 (1), 1–8. doi:10.1109/jphot.2019.2960392

CrossRef Full Text | Google Scholar

Zhang, F., Mi, Z., Hao, W., Chen, H., Zhang, Y., Zhao, J., et al. (2022). Tunable engineering of photo- and electro-induced carrier dynamics in perovskite photoelectronic devices. Sci. China Mater. 65 (4), 855–875. doi:10.1007/s40843-021-1906-5

CrossRef Full Text | Google Scholar

Zhao, W., and Palffy-Muhoray, P. (1993). Z-scan technique using top-hat beams. Appl. Phys. Lett. 63 (12), 1613–1615. doi:10.1063/1.110712

CrossRef Full Text | Google Scholar