Mechanical characteristics of MHD of the non-Newtonian magnetohydrodynamic Maxwell fluid flow past a bi-directional convectively heated surface with mass flux conditions

In engineering and manufacturing industries, stretching flow phenomena have numerous real-world implementations. Real-world applications related to stretched flow models are metalworking, crystal growth processes, cooling of fibers, and plastics sheets. Therefore, in this work, the mechanical characteristics of the magnetohydrodynamics of the non-Newtonian Maxwell nanofluid flow through a bi-directional linearly stretching surface are explored. Brownian motion, thermophoresis, and chemical reaction impacts are considered in this analysis. Additionally, thermal convective and mass flux conditions are taken into consideration. The mathematical framework of the existing problem is constructed on highly non-linear partial differential equations (PDEs). Suitable similarity transformations are used for the conversion of partial differential equations into ordinary differential equations (ODEs). The flow problem is tackled with the homotopy analysis method, which is capable of solving higher-order non-linear differential equations. Different flow profiles against various flow parameters are discussed physically. Heat and mass transference mechanisms for distinct flow factors are analyzed in a tabular form. The outcomes showed that both primary and secondary velocities are the declining functions of magnetic and Maxwell fluid parameters. The heat transfer rate rises with the cumulative values of the Brownian motion and thermal Biot number. In addition, the mass transfer rate decreases with the rising Schmidt number, Brownian motion parameter, and chemical reaction parameter, while it increases with the augmenting thermophoresis parameter. It has been highlighted that streamlines in the current work for Maxwell and Newtonian models are in fact different from one another.

1 Introduction

The fluids that differ from Newtonian fluids in behavior and characteristics in the sense of not obeying Newtonian’s law are termed as non-Newtonian fluids, which include honey, paste, ketchup, and grease lubricant. There are many applications of the non-Newtonian fluid flow in modern industries and technology such as printing technology, biological solution, polymer, braking and damping devices, production of foods, and reduction agents in dragging. These fluids are considered to be the most effective in heat transmission phenomena (Ogunseye, Salawu, Tijani, Riliwan, Sibanda; Salawu and Ogunseye, 2020). Sharma and Shaw (2022) calculated the nanofluid flow over an expanding surface by assuming viscous dissipation and non-linear radiation and have concluded that the drag force has been augmented by an upsurge in the magnetic factor. Kumar and Sahu (2022) inspected the non-Newtonian fluid flow past an elliptical rotary cylinder through a laminar flow stream and have investigated the flow phenomenon numerically. Khalil et al. (2022) inspected the influences of fluctuating fluid properties of the double-diffusive model over the dissipated non-Newtonian liquid flow on a stretched surface. Sneha et al. (2022) appraised the magnetohydrodynamic (MHD) radiated nanoliquid flow toward a stretchy and shrinking sheet subject to the impact of carbon nanotubes and concluded that the velocity of the fluid declined, while the temperature had an upsurge with growing values of the magnetic parameter. Hu et al. (2022) used non-Newtonian fluids in a square channel to discuss the polydispersal, migration, and formation chain of particles. Islam et al. (2020) inspected the impacts of the MHD radiated micropolar fluid flow in a channel with the influence of hybrid nanoparticles. Waini et al. (2022) investigated the thermally radiative flow across an extending sheet by using magnetic field effects.

The branch of science that deals with magnetic characteristics of electrically conducting materials is termed as magnetohydrodynamics (MHD). This field of science provides a basis for many scientific, industrial, and technological applications such as liquid metals, cooling systems for automobiles, cooling of electronic chips, and production of chemicals. Sohail et al. (2020) inspected the MHD Casson fluid flow and entropy production, subject to variable heat conductivities past a non-linear bi-directional stretched surface, and deduced that the upsurge values of the magnetic factor have supported concentration and thermal profiles. Reddy et al. (2022a) used the MHD fluid flow with a porous medium to use the influence of radiation, thermal, and velocity slips and highlighted that the width of the boundary layer weakened with the growth in slip and heat factor parameters. Mishra et al. (2022) numerically explored the Williamson MHD nanofluid flow, subject to variable viscosities over a wedge. Reddy et al. (2016) debated the effect of thermal radiation over the MHD nanoparticle-based liquid flow past an extending surface and compared their results with a fine agreement to those results established in the literature. Bejawada and Yanala (2021) inspected Soret and Dufour impacts upon the time-dependent MHD liquid flow past an inclined surface placed vertically. Reddy et al. (2022b) scrutinized the influence of different slip effects over the MHD liquid flow past a stretchy sheet subject to Soret and Dufour effects. Sandeep et al. (2022) discussed the influence of the non-linearly radiated MHD hybrid nanofluid fluid flow using a heat source and concluded that the fluid flow declined and the thermal flow had an upsurge with a growth in the magnetic factor. Sandeep and Ashwinkumar (2021) studied the impact of different nanoparticles’ shapes upon the MHD fluid flow over a thin movable needle. Ashwinkumar et al. (2021) explained a 2D MHD hybrid nanoparticle flow using two different geometries of a cone and plate and proved that the flow and temperature incrimination are more visible in the case of the plate than that in the case of the cone. Mabood et al. (2022) inspected the influence of the non-linearly radiated 3D time-based MHD hybrid nanofluid flow. Readers can further study about the impact of MHD on mass and heat transmission in Sulochana et al. (2018), Alshehri et al. (2021), Mabood et al. (2021), Bejawada et al. (2022), Kumar et al. (2022), and Nalivela et al. (2022).

The mass and thermal flow problems with the impact of chemical reactions play a pivotal role in numerous fluid flow models. They have captivated more consideration due to its widespread utilization in many engineering and natural phenomena such as refrigeration, aerodynamic extrusions, and human transpiration. Sharma and Mishra (2020) documented the MHD nanoliquid flow using an internal thermal source. Singh et al. (2021) numerically solved the flow of a liquid past an enlarging sheet with the impact of chemical reactions and concluded that an upsurge in the stretching factor declined the diffusivities of heat and mass. Khan et al. (2021) discussed the bioconvection micropolar nanoparticle flow past a thin needle subject to binary chemical reactions and highlighted that mass diffusion declined with an upsurge in the chemical reaction factor and Brownian motion. Kodi et al. (2022) inspected the MHD Casson nanofluid flow past a vertically placed permeable plate subject to the impact of thermal diffusivity and chemical reactions. Kumar and Sharma (2022) discussed the influences of Stefan blowing on a fluid flow past a rotary disc subject to chemical reactions. Raghunath et al. (2022) inspected the time-dependent MHD flow of a liquid over an inclined permeable plate using magnetic impacts and chemical reactions.

Brownian motion and thermophoretic effects are responsible for controlling mass and thermal diffusivities subject to concentration and temperature gradients. Both these effects have numerous applications in different areas of science such as aerosol technology, nuclear safety phenomena, atmospheric pollution, aerospace technology, and hydrodynamics. Irfan (2021) considered the collective influence of Brownian and thermal diffusivity over the nanoparticle flow past a sheet with varying thickness, subject to slip conditions, and concluded that the augmentation of the Brownian number and thermophoresis factor has an upsurge in thermal profiles. Upreti et al. (2022) described the Casson fluid flow past a Riga plate subject to the effects of microorganisms. Saleem et al. (2022) studied the motion of water carrying three different types of nanoparticles subject to thermophoretic effects and the Brownian motion. Kiyani et al. (2022) inspected the MHD micropolar nanoparticle flow past an exponentially radiated surface using thermal radiations, Brownian motion, and thermophoretic effects upon the fluid flow system. Mehta and Kataria (2022) inspected the MHD fluid flow through the shrinking surface along with thermal radiations. Tayyab et al. (2022) have numerically studied the three-dimensional rotary nanoliquid flow subject to bio-convective activation energy.

The boundary-layer flows of nanofluids caused by stretched surfaces have attracted researchers’ attention recently (Andersson et al., 1994; Xu and Liao, 2009; Prasad et al., 2012; Mukhopadhyay, 2013). Their enormous significance in engineering and industrial applications has been the key driver behind this. These uses are particularly common in extrusion operations, paper and glass fiber manufacture, electronic chip manufacturing, paint application, food preparation, and the transfer of biological fluids. There is not a single constitutive connection between stress and the rate of strain that can be used to investigate all non-Newtonian fluids. The diversity of these fluids, their constitutive behavior, and simultaneous viscous and elastic properties make it nearly impossible to distinguish between effects resulting from a fluid’s shear-dependent viscosity and effects resulting from the fluid’s elasticity. A few mathematical models have been explained that closely match the experimental findings (Wu and Thompson, 1996). The Maxwell model is utilized for relaxation time in some highly concentrated polymeric fluids.

In this work, the authors have considered to present a semi-analytical solution of the Maxwell fluid flow over a bi-directional stretching sheet. Additionally, the thermal convective and mass flux conditions are taken into consideration. The mathematical framework of the existing problem is constructed on highly non-linear PDEs. Suitable similarity transformations are used for the conversion of PDEs into ODEs, which is presented in section 2. The flow problem is tackled with a homotopy analysis method, which is capable of solving higher-order non-linear differential equations, presented in section 3. The convergence of the HAM technique is also shown in section 4. Different flow profiles against various flow parameters are discussed physically, as shown in section 5. Finally, the concluding remarks are presented in section 6.

2 Model formulation

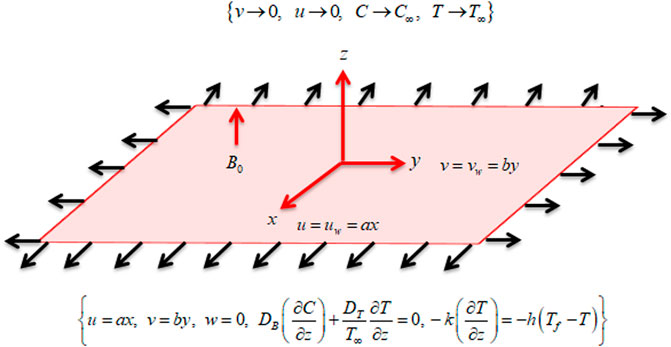
We consider the steady, laminar, and incompressible three-dimensional flow of a Maxwell fluid over a bi-directional linearly extending surface. The surface stretches along $x$ and $y$ directions and with velocity $v_w\left(x\right)=by$, where both $a$ and $b$ are constants. A magnetic field of strength $B_0$ is applied normal to the fluid flow. The surface temperature is denoted by $T_w$, $T_f$ represents the reference temperature, and $T_{\infty }$ shows the ambient temperature. In addition, the surface concentration is denoted by $C_w$ and $C_{\infty }$, showing the ambient concentration. Brownian motion, thermophoresis, and chemical reaction impacts are considered in this analysis. Additionally, the thermal convective and mass flux conditions are taken into consideration, as shown in Figure 1. Under the aforementioned suppositions, the principle equations are as follows (Bilal Ashraf et al., 2016; Dawar et al., 2021):

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0,(1)$

$\begin{array}{l}u\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial z}+v\frac{\partial u}{\partial y}=\nu \frac{{\partial }^{2}u}{\partial z^2}-\frac{\sigma B_0^2}{\rho }\left(u+\lambda w\frac{\partial u}{\partial z}\right)\\ -\lambda \left(u^2\frac{{\partial }^{2}u}{\partial x^2}+w^2\frac{{\partial }^{2}u}{\partial z^2}+v^2\frac{{\partial }^{2}u}{\partial y^2}+2uv\frac{{\partial }^{2}u}{\partial x\partial y}+2uw\frac{{\partial }^{2}u}{\partial x\partial z}+2vw\frac{{\partial }^{2}u}{\partial y\partial z}\right),\end{array}(2)$

$\begin{array}{l}u\frac{\partial v}{\partial x}+w\frac{\partial v}{\partial z}+v\frac{\partial v}{\partial y}=\nu \frac{{\partial }^{2}v}{\partial z^2}-\frac{\sigma B_0^2}{\rho }\left(v+\lambda w\frac{\partial v}{\partial z}\right)\\ -\lambda \left(u^2\frac{{\partial }^{2}v}{\partial x^2}+w^2\frac{{\partial }^{2}v}{\partial z^2}+v^2\frac{{\partial }^{2}v}{\partial y^2}+2uv\frac{{\partial }^{2}v}{\partial x\partial y}+2vw\frac{{\partial }^{2}v}{\partial y\partial z}+2uw\frac{{\partial }^{2}v}{\partial x\partial z}\right),\end{array}(3)$

$u\frac{\partial T}{\partial x}+w\frac{\partial T}{\partial z}+v\frac{\partial T}{\partial y}=\frac{k}{{\left(\rho C_p\right)}_f}\frac{{\partial }^{2}T}{\partial z^2}+\frac{{\left(\rho C_p\right)}_p}{{\left(\rho C_p\right)}_f}\left(D_B\frac{\partial T}{\partial z}\frac{\partial C}{\partial z}\right)+\frac{D_T}{T_{\infty }}{\left(\frac{\partial C}{\partial z}\right)}^2,(4)$

$u\frac{\partial C}{\partial x}+w\frac{\partial C}{\partial z}+v\frac{\partial C}{\partial y}+k_1\left(C-C_{\infty }\right)=D_B\frac{{\partial }^{2}C}{\partial z^2}\frac{D_T}{T_{\infty }}\left(\frac{{\partial }^{2}T}{\partial z^2}\right),(5)$

with boundary conditions, given as follows (Bilal Ashraf et al., 2016; Dawar et al., 2021):

$\left\{\begin{array}{l}u=ax,v=by,w=0,D_B\left(\frac{\partial C}{\partial z}\right)+\frac{D_T}{T_{\infty }}\frac{\partial T}{\partial z}=0,-k\left(\frac{\partial T}{\partial z}\right)=-h\left(T_f-T\right),atz=0,\\ v\to 0,u\to 0,C\to C_{\infty },T\to T_{\infty }asz\to \infty .\end{array}\right\}(6)$

FIGURE 1

FIGURE 1. Geometry of the flow problem.

In the aforementioned equations, $u,v,\mathrm{a}\mathrm{n}\mathrm{d}w$ are the velocity components; $x,y,\mathrm{a}\mathrm{n}\mathrm{d}z$ are the coordinate axes; $\sigma$ is the electrical conductivity; $\rho$ is the density; $\lambda$ is the relaxation time; $B_0$ is the magnetic field strength; $C_p$ is the specific heat; $k$ is the thermal conductivity; $D_B$ is the Brownian diffusion coefficient; $D_T$ is the thermophoretic coefficient; $T$ is the temperature; $C$ is the concentration; $k_1$ is the chemical reaction coefficient; $h$ is the heat transfer coefficient; and $a$ and $b$ are the velocity constants.

The similarity transformations are defined as follows (Bilal Ashraf et al., 2016; Dawar et al., 2021):

$\left.\begin{array}{l}v=ay{g}^{\prime }\left(\eta \right),u=ax{f}^{\prime }\left(\eta \right),w=-\sqrt{a\nu }\left(g\left(\eta \right)+f\left(\eta \right)\right),\\ \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }}=,\eta =z\sqrt{\frac{a}{\nu }}.\end{array}\right\}(7)$

The leading equations are transformed by using similarity transformations defined in (7):

$\begin{array}{l}{f}^{‴}\left(\eta \right)+\left(1+M\beta \right)\left(f\left(\eta \right)f^{″}\left(\eta \right)+g\left(\eta \right)f^{″}\left(\eta \right)\right)-{\left(f^{\prime }\left(\eta \right)\right)}^2-M{f}^{\prime }\left(\eta \right)\\ +\beta \left(\begin{array}{l}2f\left(\eta \right)f^{\prime }\left(\eta \right)f^{″}\left(\eta \right)+2g\left(\eta \right)f^{\prime }\left(\eta \right)f^{″}\left(\eta \right)-\\ f^{‴}\left(\eta \right){\left(f\left(\eta \right)\right)}^2-f^{‴}\left(\eta \right){\left(g\left(\eta \right)\right)}^2-2f^{‴}\left(\eta \right)g\left(\eta \right)f\left(\eta \right)\end{array}\right)=0,\end{array}(8)$

$\begin{array}{l}{g}^{‴}\left(\eta \right)+\left(1+M\beta \right)\left(f\left(\eta \right)g^{″}\left(\eta \right)+g\left(\eta \right)g^{″}\left(\eta \right)\right)-{\left(g^{\prime }\left(\eta \right)\right)}^2-M{g}^{\prime }\left(\eta \right)\\ +\beta \left(\begin{array}{l}2g^{″}\left(\eta \right)f\left(\eta \right)g^{\prime }\left(\eta \right)+2g^{″}\left(\eta \right)g\left(\eta \right)g^{\prime }\left(\eta \right)-\\ g^{‴}\left(\eta \right){\left(f\left(\eta \right)\right)}^2-g^{‴}\left(\eta \right){\left(g\left(\eta \right)\right)}^2-2g^{‴}\left(\eta \right)f\left(\eta \right)g\left(\eta \right)\end{array}\right)=0,\end{array}(9)$

$\frac{1}{\mathit{Pr}}{\theta }^{″}\left(\eta \right)+g\left(\eta \right){\theta }^{\prime }\left(\eta \right)+f\left(\eta \right){\theta }^{\prime }\left(\eta \right)+Nb{\theta }^{\prime }\left(\eta \right){\varphi }^{\prime }\left(\eta \right)+Nt{\left({\theta }^{\prime }\left(\eta \right)\right)}^2=0,(10)$

${\varphi }^{″}\left(\eta \right)+Scf\left(\eta \right){\varphi }^{\prime }\left(\eta \right)+Scg\left(\eta \right){\varphi }^{\prime }\left(\eta \right)+\frac{Nt}{Nb}{\theta }^{″}\left(\eta \right)-ScK\varphi \left(\eta \right)=0,(11)$

with boundary conditions given as follows:

$\left\{\begin{array}{l}f\left(0\right)=0,f^{\prime }\left(0\right)=1,g^{\prime }\left(0\right)=\alpha ,g\left(0\right)=0,{\theta }^{\prime }\left(0\right)=\gamma \left(\theta \left(0\right)-1\right),\\ Nt{\theta }^{\prime }\left(0\right)+Nb{\varphi }^{\prime }\left(0\right)=0,g^{\prime }\left(\infty \right)=0,f^{\prime }\left(\infty \right)=0,\theta \left(\infty \right)=0,\varphi \left(\infty \right)=0.\end{array}\right\}(12)$

The embedded parameters are discussed as follows:

$\left\{\begin{array}{l}M=\frac{\sigma B_0^2}{\rho a},\beta =\lambda a,Sc=\frac{\nu }{D_B},\alpha =\frac{b}{a},\mathrm{Pr}=\frac{\mu {\left(C_p\right)}_f}{k},K=\frac{k_1}{a},\\ \gamma =\frac{h_f}{k}\sqrt{\frac{\nu }{a}},Nt=\frac{{\left(\rho C_p\right)}_p{D}_B\left(T_w-T_{\infty }\right)}{{\left(\rho C_p\right)}_f\nu T_{\infty }},Nb=\frac{{\left(\rho C_p\right)}_p{D}_B\left(C_w-C_{\infty }\right)}{{\left(\rho C_p\right)}_f\nu }.\end{array}\right\}(13)$

Here, $M$ is the magnetic factor, $\beta$ is the Deborah number, $Sc$ is the Schmidt number, $\alpha$ is the stretching constant, $\mathrm{Pr}$ is the Prandtl number, $K$ is the chemical reaction factor, $\gamma$ is the thermal Biot number, $Nt$ is the thermophoresis factor, and $Nb$ is the Brownian motion factor.

The Nusselt, Sherwood, and density numbers are defined as follows:

$\frac{N{u}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-{\left.{\theta }^{\prime }\left(\eta \right)\right|}_{\eta =0},\frac{S{h}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-{\left.{\varphi }^{\prime }\left(\eta \right)\right|}_{\eta =0},(14)$

where ${\mathrm{R}\mathrm{e}}_x=\frac{x{u}_w\left(x\right)}{\nu }$ is the local Reynolds number.

3 HAM solution

For an analytical simulation of the existing model, the HAM technique is considered. The initial guesses are given as follows:

$\left\{f_0\left(\eta \right)=1-e^{-\eta },g\left(\eta \right)=\alpha \left(1-e^{-\eta }\right),{\theta }_0\left(\eta \right)=\frac{\gamma }{\gamma +1}{e}^{-\eta },{\varphi }_0\left(\eta \right)=-\frac{\gamma }{1+\gamma }\frac{Nt}{Nb}{e}^{-\eta }.\right\}(15)$

The linear operators are taken as follows:

${\mathbf{L}}_f\left(\eta \right)=f^{‴}-f^{\prime },{\mathbf{L}}_g\left(\eta \right)=g^{‴}-g^{\prime },{\mathbf{L}}_{\theta }\left(\eta \right)={\theta }^{″}-\theta ,{\mathbf{L}}_{\varphi }\left(\eta \right)={\varphi }^{″}-\varphi ,(16)$

with the following properties:

$\left\{\begin{array}{c}{\mathbf{L}}_f\left({\mho }_1+{\mho }_2\mathit{exp}\left(\eta \right)+{\mho }_3\mathit{exp}\left(-\eta \right)\right)=0,\\ {\mathbf{L}}_g\left({\mho }_4+{\mho }_5\mathit{exp}\left(\eta \right)+{\mho }_6\mathit{exp}\left(-\eta \right)\right)=0,\\ {\mathbf{L}}_{\theta }\left({\mho }_7\mathit{exp}\left(\eta \right)+{\mho }_8\mathit{exp}\left(-\eta \right)\right)=0,\\ {\mathbf{L}}_{\varphi }\left({\mho }_9\mathit{exp}\left(\eta \right)+{\mho }_{10}\mathit{exp}\left(-\eta \right)\right)=0,\end{array}\right\}(17)$

where ${\mho }_i\left(i=\mathrm{1,2,3},\dots ,10\right)$ are the constants.

$\mathfrak{R}\in \left[01\right]$ shows the entrenching factor, and $\mathrm{\hslash }$ shows the auxiliary parameter. Then, the zero-order problems are constructed as follows:

$\left(1-\mathrm{A}\right)L_f\left[f\left(\eta ;\mathrm{A}\right)-f_0\left(\eta \right)\right]=\mathrm{A}{\mathit{\hslash }}_f{N}_f\left[f\left(\eta ;\mathrm{A}\right),g\left(\eta ;\mathrm{A}\right)\right],(18)$

$\left(1-\mathrm{A}\right)L_g\left[g\left(\eta ;\mathrm{A}\right)-g_0\left(\eta \right)\right]=\mathrm{A}{\mathit{\hslash }}_g{N}_g\left[g\left(\eta ;\mathrm{A}\right),f\left(\eta ;\mathrm{A}\right)\right],(19)$

$\left(1-\mathrm{A}\right)L_{\theta }\left[\theta \left(\eta ;\mathrm{A}\right)-{\theta }_0\left(\eta \right)\right]=\mathrm{A}{\mathit{\hslash }}_{\theta }{N}_{\theta }\left[\theta \left(\eta ;\mathrm{A}\right),f\left(\eta ;\mathrm{A}\right),g\left(\eta ;\mathrm{A}\right),\varphi \left(\eta ;\mathrm{A}\right)\right],(20)$

$\left(1-\mathrm{A}\right)L_{\varphi }\left[\varphi \left(\eta ;\mathrm{A}\right)-{\varphi }_0\left(\eta \right)\right]=\mathrm{A}{\mathit{\hslash }}_{\varphi }{N}_{\varphi }\left[\varphi \left(\eta ;\mathrm{A}\right),f\left(\eta ;\mathrm{A}\right),g\left(\eta ;\mathrm{A}\right),\theta \left(\eta ;\mathrm{A}\right)\right],(21)$

$\left\{\begin{array}{c}f\left(0;\mathrm{A}\right)=0,g\left(0;\mathrm{A}\right)=0,f^{\prime }\left(0;\mathrm{A}\right)=1,g^{\prime }\left(0;\mathrm{A}\right)=\alpha ,\\ {\theta }^{\prime }\left(0;\mathrm{A}\right)=\gamma \left(\left(0;\mathrm{A}\right)\theta -1\right),Nt{\theta }^{\prime }\left(0;\mathrm{A}\right)+Nb{\varphi }^{\prime }\left(0;\mathrm{A}\right)=0,\\ f^{\prime }\left(\infty ;\mathrm{A}\right)\to 0,\theta \left(\infty ;\mathrm{A}\right)\to 0,g^{\prime }\left(\infty ;\mathrm{A}\right)\to 0,\varphi \left(\infty ;\mathrm{A}\right),\end{array}\right\}(22)$

$\begin{array}{l}{N}_f\left[f\left(\eta ;\mathrm{A}\right),g\left(\eta ;\mathrm{A}\right)\right]=\frac{{\partial }^{3}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}+\left(1+M\beta \right)\left(f\left(\eta ;\mathrm{A}\right)\frac{{\partial }^{2}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}+g\left(\eta ;\mathrm{A}\right)\frac{{\partial }^{2}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}\right)-\\ M\frac{\partial f\left(\eta ;\mathrm{A}\right)}{\partial \eta }-{\left(\frac{\partial f\left(\eta ;\mathrm{A}\right)}{\partial \eta }\right)}^2+\beta \left(\begin{array}{l}2f\left(\eta \right)\frac{\partial f\left(\eta ;\mathrm{A}\right)}{\partial \eta }\frac{{\partial }^{2}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}+2g\left(\eta ;\mathrm{{\rm A}}\right)\frac{\partial f\left(\eta ;\mathrm{A}\right)}{\partial \eta }\frac{{\partial }^{2}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}\\ -{\left(f\left(\eta ;\mathrm{A}\right)\right)}^2\frac{{\partial }^{3}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}-{\left(g\left(\eta ;\mathrm{A}\right)\right)}^2\frac{{\partial }^{3}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}\\ -2g\left(\eta ;\mathrm{A}\right)f\left(\eta ;\mathrm{A}\right)\frac{{\partial }^{3}f\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}\end{array}\right),\end{array}(23)$

$\begin{array}{l}{N}_g\left[g\left(\eta ;\mathrm{A}\right),f\left(\eta ;\mathrm{A}\right)\right]=\frac{{\partial }^{3}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}+\left(1+M\beta \right)\left(f\left(\eta ;\mathrm{A}\right)\frac{{\partial }^{2}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}+g\left(\eta ;\mathrm{A}\right)\frac{{\partial }^{2}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}\right)-\\ {\left(\frac{\partial g\left(\eta ;\mathrm{A}\right)}{\partial \eta }\right)}^2-M\frac{\partial g\left(\eta ;\mathrm{A}\right)}{\partial \eta }+\beta \left(\begin{array}{l}2f\left(\eta ;\mathrm{A}\right)\frac{\partial g\left(\eta ;\mathrm{A}\right)}{\partial \eta }\frac{{\partial }^{2}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}+2g\left(\eta ;\mathrm{A}\right)\frac{\partial g\left(\eta ;\mathrm{A}\right)}{\partial \eta }\frac{{\partial }^{2}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}\\ -{\left(f\left(\eta ;\mathrm{A}\right)\right)}^2\frac{{\partial }^{3}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}-{\left(g\left(\eta ;\mathrm{A}\right)\right)}^2\frac{{\partial }^{3}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}\\ -2f\left(\eta ;\mathrm{A}\right)g\left(\eta ;\mathrm{A}\right)\frac{{\partial }^{3}g\left(\eta ;\mathrm{A}\right)}{\partial {\eta }^3}\end{array}\right),\end{array}(24)$

$\begin{array}{l}{N}_{\theta }\left[\theta \left(\eta ;\mathrm{A}\right),f\left(\eta ;\mathrm{A}\right),g\left(\eta ;\mathrm{A}\right),\varphi \left(\eta ;\mathrm{A}\right)\right]=\frac{1}{\mathit{Pr}}\frac{{\partial }^2\theta \left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}+g\left(\eta ;\mathrm{A}\right)\frac{\partial \theta \left(\eta ;\mathrm{A}\right)}{\partial \eta }\\ +f\left(\eta ;\mathrm{A}\right)\frac{\partial \theta \left(\eta ;\mathrm{A}\right)}{\partial \eta }+Nb\frac{\partial \theta \left(\eta ;\mathrm{A}\right)}{\partial \eta }\frac{\partial \varphi \left(\eta ;\mathrm{A}\right)}{\partial \eta }+Nt{\left(\frac{\partial \theta \left(\eta ;\mathrm{A}\right)}{\partial \eta }\right)}^2,\end{array}(25)$

$\begin{array}{c}{N}_{\varphi }\left[\varphi \left(\eta ;\mathrm{A}\right),f\left(\eta ;\mathrm{A}\right),g\left(\eta ;\mathrm{A}\right),\theta \left(\eta ;\mathrm{A}\right)\right]=\frac{{\partial }^2\varphi \left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}+\\ Scf\left(\eta ;\mathrm{A}\right)\frac{\partial \varphi \left(\eta ;\mathrm{A}\right)}{\partial \eta }+Scg\left(\eta ;\mathrm{A}\right)\frac{\partial \varphi \left(\eta ;\mathrm{A}\right)}{\partial \eta }+\frac{Nt}{Nb}\frac{{\partial }^2\theta \left(\eta ;\mathrm{A}\right)}{\partial {\eta }^2}-ScK\varphi \left(\eta ;\mathrm{A}\right).\end{array}(26)$

For $\mathrm{{\rm A}}=0$ and $\mathrm{{\rm A}}=1$, we obtain the following:

$\left\{\begin{array}{l}f\left(\eta ;0\right)=f_0\left(\eta \right),f\left(\eta ;1\right)=f\left(\eta \right)\\ g\left(\eta ;0\right)=g_0\left(\eta \right),g\left(\eta ;1\right)=g\left(\eta \right)\\ \theta \left(\eta ;0\right)={\theta }_0\left(\eta \right),\theta \left(\eta ;1\right)=\theta \left(\eta \right)\\ \varphi \left(\eta ;0\right)={\varphi }_0\left(\eta \right),\varphi \left(\eta ;1\right)=\varphi \left(\eta \right)\end{array}\right\}.(27)$

Using the Taylor series, we obtain the following:

$f\left(\eta ;\mathrm{{\rm A}}\right)=f_0\left(\eta \right)+{\displaystyle \sum _{\mathrm{{\rm X}}=1}^{\infty }}{f}_{\mathrm{{\rm X}}}\left(\eta \right){\mathfrak{R}}^{\mathrm{{\rm X}}}as{f}_{\mathrm{{\rm X}}}\left(\eta \right)=\frac{1}{\mathrm{{\rm X}}!}{\left.\frac{{\partial }^{\mathrm{{\rm X}}}f\left(\eta ;\mathrm{A}\right)}{\partial {\mathrm{A}}^{\mathrm{{\rm X}}}}\right|}_{\mathrm{{\rm A}}=0},(28)$

$g\left(\eta ;\mathrm{{\rm A}}\right)=g_0\left(\eta \right)+{\displaystyle \sum _{\mathrm{{\rm X}}=1}^{\infty }}{g}_{\mathrm{{\rm X}}}\left(\eta \right){\mathfrak{R}}^{\mathrm{{\rm X}}}as{g}_{\mathrm{{\rm X}}}\left(\eta \right)=\frac{1}{\mathrm{{\rm X}}!}{\left.\frac{{\partial }^{\mathrm{{\rm X}}}g\left(\eta ;\mathrm{A}\right)}{\partial {\mathrm{A}}^{\mathrm{{\rm X}}}}\right|}_{\mathrm{{\rm A}}=0}.(29)$

$\theta \left(\eta ;\mathrm{{\rm A}}\right)={\theta }_0\left(\eta \right)+{\displaystyle \sum _{\mathrm{{\rm X}}=1}^{\infty }}{\theta }_{\mathrm{{\rm X}}}\left(\eta \right){\mathfrak{R}}^{\mathrm{{\rm X}}}as{\theta }_{\mathrm{{\rm X}}}\left(\eta \right)=\frac{1}{\mathrm{{\rm X}}!}{\left.\frac{{\partial }^{\mathrm{{\rm X}}}\theta \left(\eta ;\mathrm{A}\right)}{\partial {\mathrm{A}}^{\mathrm{{\rm X}}}}\right|}_{\mathrm{{\rm A}}=0}.(30)$

$\varphi \left(\eta ;\mathrm{{\rm A}}\right)={\varphi }_0\left(\eta \right)+{\displaystyle \sum _{\mathrm{{\rm X}}=1}^{\infty }}{\varphi }_{\mathrm{{\rm X}}}\left(\eta \right){\mathfrak{R}}^{\mathrm{{\rm X}}}as{\varphi }_{\mathrm{{\rm X}}}\left(\eta \right)=\frac{1}{\mathrm{{\rm X}}!}{\left.\frac{{\partial }^{\mathrm{{\rm X}}}\varphi \left(\eta ;\mathrm{A}\right)}{\partial {\mathrm{A}}^{\mathrm{{\rm X}}}}\right|}_{\mathrm{{\rm A}}=0}.(31)$

The $\mathrm{{\rm X}}$ th-order deformation problems can be written as follows:

$L_f\left[f_{\mathrm{{\rm X}}}\left(\eta \right)-{\lambda }_{\mathrm{{\rm X}}}{f}_{\mathrm{{\rm X}}-1}\left(\eta \right)\right]={\mathit{\hslash }}_f{R}_{\mathrm{{\rm X}}}^f\left(\eta \right),(32)$

$L_g\left[g_{\mathrm{{\rm X}}}\left(\eta \right)-{\lambda }_{\mathrm{{\rm X}}}{g}_{\mathrm{{\rm X}}-1}\left(\eta \right)\right]={\mathit{\hslash }}_g{R}_{\mathrm{{\rm X}}}^g\left(\eta \right),(33)$

$L_{\theta }\left[{\theta }_{\mathrm{{\rm X}}}\left(\eta \right)-{\lambda }_{\mathrm{{\rm X}}}{\theta }_{\mathrm{{\rm X}}-1}\left(\eta \right)\right]={\mathit{\hslash }}_{\theta }{R}_{\mathrm{{\rm X}}}^{\theta }\left(\eta \right),(34)$

$L_{\varphi }\left[{\varphi }_{\mathrm{{\rm X}}}\left(\eta \right)-{\lambda }_{\mathrm{{\rm X}}}{\varphi }_{\mathrm{{\rm X}}-1}\left(\eta \right)\right]={\mathit{\hslash }}_{\varphi }{R}_{\mathrm{{\rm X}}}^{\varphi }\left(\eta \right),(35)$

$\left\{\begin{array}{l}{f}_{\mathrm{{\rm X}}}\left(0\right)=f_{\mathrm{{\rm X}}}^{\prime }\left(0\right)=f_{\mathrm{{\rm X}}}^{\prime }\left(\infty \right)=0,\\ g_{\mathrm{{\rm X}}}\left(0\right)=g_{\mathrm{{\rm X}}}^{\prime }\left(0\right)=g_{\mathrm{{\rm X}}}^{\prime }\left(\infty \right)=0,\\ {\theta }_{\mathrm{{\rm X}}}^{\prime }\left(0\right)-\gamma \left({\theta }_{\mathrm{{\rm X}}}\left(0\right)-1\right)={\theta }_{\mathrm{{\rm X}}}\left(\infty \right)=0,\\ Nb{\varphi }_{\mathrm{{\rm X}}}^{\prime }\left(0\right)+Nt{\theta }_{\mathrm{{\rm X}}}^{\prime }\left(0\right)={\varphi }_{\mathrm{{\rm X}}}\left(\infty \right)=0,\end{array}\right\},(36)$

$\begin{array}{l}{R}_{\mathrm{{\rm X}}}^f\left(\eta \right)=f_{\mathrm{{\rm X}}-1}^{‴}\left(\eta \right)+\left(1+M\beta \right)\left({\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(f_{\mathrm{{\rm X}}-1-j}\left(\eta \right)f_{\mathrm{{\rm X}}-1}^{″}\left(\eta \right)\right)+{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(g_{\mathrm{{\rm X}}-1-j}\left(\eta \right)f_{\mathrm{{\rm X}}-1}^{″}\left(\eta \right)\right)\right)\\ -{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(f_{\mathrm{{\rm X}}-1-j}^{\prime }\left(\eta \right)f_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right)-M{f}_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)+\beta \left[2{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{f}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{f}_{\mathrm{{\rm X}}-l}^{\prime }\left(\eta \right){\displaystyle \sum _{p=0}^l}{f}_{l-p}^{″}\left(\eta \right)\right.\\ +2{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{g}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{f}_{\mathrm{{\rm X}}-l}^{\prime }\left(\eta \right){\displaystyle \sum _{p=0}^l}{f}_{l-p}^{″}\left(\eta \right)+{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{f}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{f}_{\mathrm{{\rm X}}-l}\left(\eta \right){\displaystyle \sum _{p=0}^l}{f}_{l-p}^{‴}\left(\eta \right)\\ -{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{g}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{g}_{\mathrm{{\rm X}}-l}\left(\eta \right)\left.{\displaystyle \sum _{p=0}^l}{f}_{l-p}^{‴}\left(\eta \right)-2{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{g}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{f}_{\mathrm{{\rm X}}-l}\left(\eta \right){\displaystyle \sum _{p=0}^l}{f}_{l-p}^{‴}\left(\eta \right)\right],\end{array}(37)$

$\begin{array}{l}{R}_{\mathrm{{\rm X}}}^g\left(\eta \right)=g_{\mathrm{{\rm X}}-1}^{‴}\left(\eta \right)+\left(1+M\beta \right)\left({\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(f_{\mathrm{{\rm X}}-1-j}\left(\eta \right)g_{\mathrm{{\rm X}}-1}^{″}\left(\eta \right)\right)+{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(g_{\mathrm{{\rm X}}-1-j}\left(\eta \right)g_{\mathrm{{\rm X}}-1}^{″}\left(\eta \right)\right)\right)\\ -{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(g_{\mathrm{{\rm X}}-1-j}^{\prime }\left(\eta \right)g_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right)-M{g}_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)+\beta \left[2{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{f}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{g}_{\mathrm{{\rm X}}-l}^{\prime }\left(\eta \right){\displaystyle \sum _{p=0}^l}{g}_{l-p}^{″}\left(\eta \right)\right.\\ +2{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{g}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{g}_{\mathrm{{\rm X}}-l}^{\prime }\left(\eta \right){\displaystyle \sum _{p=0}^l}{g}_{l-p}^{″}\left(\eta \right)+{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{f}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{f}_{\mathrm{{\rm X}}-l}\left(\eta \right){\displaystyle \sum _{p=0}^l}{g}_{l-p}^{‴}\left(\eta \right)\\ -{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{g}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{g}_{\mathrm{{\rm X}}-l}\left(\eta \right)\left.{\displaystyle \sum _{p=0}^l}{g}_{l-p}^{‴}\left(\eta \right)-2{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}{g}_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\displaystyle \sum _{l=0}^n}{g}_{\mathrm{{\rm X}}-l}\left(\eta \right){\displaystyle \sum _{p=0}^l}{g}_{l-p}^{‴}\left(\eta \right)\right],\end{array}(38)$

$\begin{array}{l}{R}_{\mathrm{{\rm X}}}^{\theta }\left(\eta \right)=\frac{1}{\mathit{Pr}}{\theta }_{\mathrm{{\rm X}}-1}^{″}\left(\eta \right)+{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(g_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\theta }_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right)+{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(f_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\theta }_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right)\\ +Nb{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left({\theta }_{\mathrm{{\rm X}}-1-j}^{\prime }\left(\eta \right){\varphi }_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right)+Nt{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left({\theta }_{\mathrm{{\rm X}}-1-j}^{\prime }\left(\eta \right){\theta }_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right),\end{array}(39)$

$R_{\mathrm{{\rm X}}}^{\varphi }\left(\eta \right)=\frac{1}{\mathit{Pr}}{\varphi }_{\mathrm{{\rm X}}-1}^{″}\left(\eta \right)+Sc{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(f_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\varphi }_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right)+Sc{\displaystyle \sum _{n=0}^{\mathrm{{\rm X}}-1}}\left(g_{\mathrm{{\rm X}}-1-j}\left(\eta \right){\varphi }_{\mathrm{{\rm X}}-1}^{\prime }\left(\eta \right)\right)+\frac{Nt}{Nb}{\theta }_{\mathrm{{\rm X}}-1}^{″}+-ScK{\varphi }_{\mathrm{{\rm X}}-1}\left(\eta \right),(40)$

where

${\lambda }_{\mathrm{{\rm X}}}=\left\{\begin{array}{l}0,\mathrm{{\rm X}}\le 1,\\ 1,\mathrm{{\rm X}}>1.\end{array}\right.(41)$

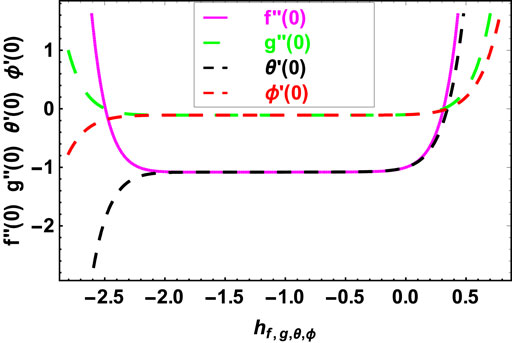
4 HAM convergence

The factors ${\mathrm{\hslash }}_f$, ${\mathrm{\hslash }}_g$, ${\mathrm{\hslash }}_{\theta },$ and ${\mathrm{\hslash }}_{\varphi }$ are called auxiliary factors, regulating the homotopic convergence. At the 23rd order of approximations, convergence regions for primary velocity, secondary velocity, temperature, and concentration distributions are shown in Figure 2. The convergence area of $f^{″}\left(0\right)$ is $-2.1\le {\mathrm{\hslash }}_f\le 0.0$, $g^{″}\left(0\right)$ is $-2.25\le {\mathrm{\hslash }}_g\le 0.2$, ${\theta }^{\prime }\left(0\right)$ is $-2.1\le {\mathrm{\hslash }}_{\theta }\le 0.0,$ and ${\varphi }^{\prime }\left(0\right)$ is $-2.25\le {\mathrm{\hslash }}_{\varphi }\le 0.2$.

FIGURE 2

FIGURE 2. $\mathrm{\hslash }-$ curves for ${\mathrm{\hslash }}_f$, ${\mathrm{\hslash }}_g$, ${\mathrm{\hslash }}_{\theta },$ and ${\mathrm{\hslash }}_{\varphi }$.

5 Results and discussion

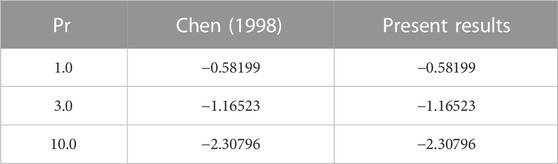
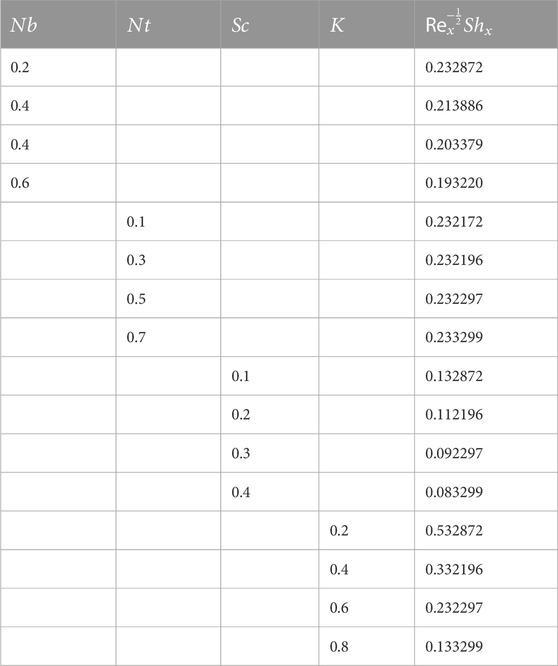
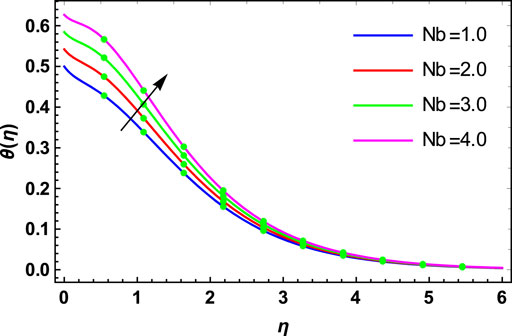
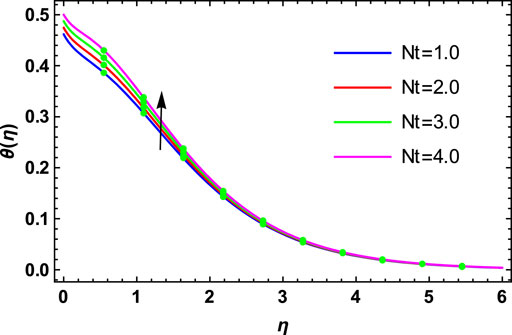
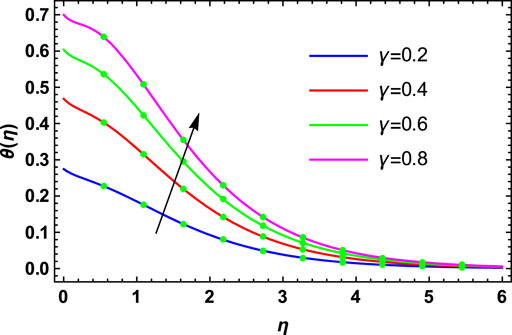
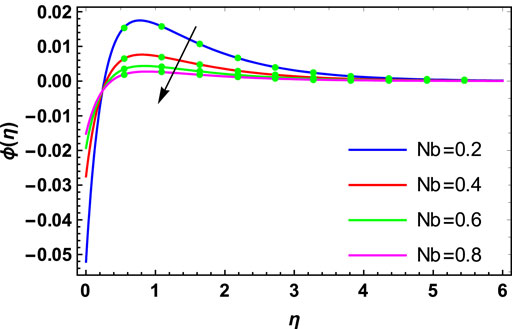
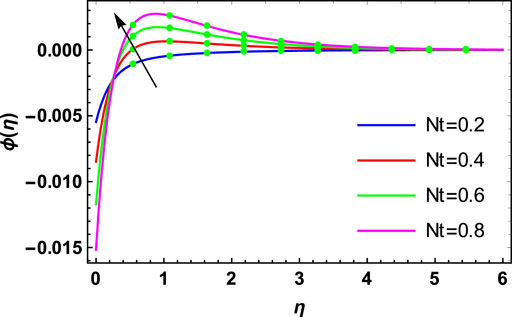
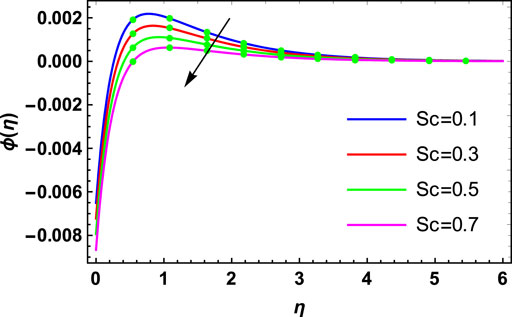
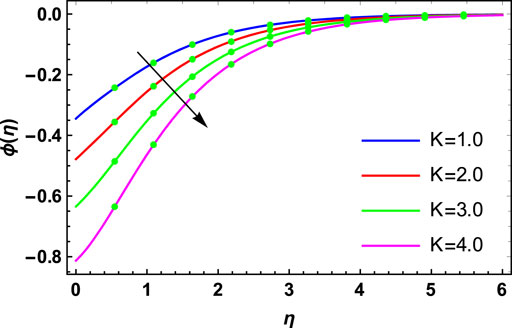
The physical investigation of the flow of the Maxwell fluid with the occurrence of the magnetic effect past an extending surface is explored in this section. With the occurrence of the thermal and mass diffusivity, the role of heat and mass transport is analyzed. The HAM procedure is used for the simulation of the existing model. Impacts of various flow parameters on flow distributions of the nanofluid are computed and discussed. Table 1 shows the validation of the present results with the published results. Here, a close relation between both the results is found, and we can validate our present analysis. The influences of $Nb$, $Nt$, and $\gamma$ on the Nusselt number ${\mathrm{R}\mathrm{e}}_x^{-\frac{1}{2}}N{u}_x$ are investigated in Table 2. Table 2 shows that by increasing $Nb$, $Nt,$ and $\gamma$, ${\mathrm{R}\mathrm{e}}_x^{-\frac{1}{2}}N{u}_x$ also increases. In Table 3, the variation in Sherwood number ${\mathrm{R}\mathrm{e}}_x^{-\frac{1}{2}}S{h}_x$ versus flow constraints such as $Nb$, $Nt$, $Sc,$ and $K$ is examined. In this analysis, it is observed that greater $Nb$, $Sc,$ and $K$ values decrease ${\mathrm{R}\mathrm{e}}_x^{-\frac{1}{2}}S{h}_x$, while increasing $Nt$ augments ${\mathrm{R}\mathrm{e}}_x^{-\frac{1}{2}}S{h}_x$. Figures 3, 4 display variations in the primary velocity distribution of the nanofluid via the increasing Maxwell fluid factor $\beta$ and magnetic parameter $M$, respectively. It is detected that the primary velocity distribution declines with growing values of $\beta$. Incidentally, increasing values of $\beta$ correspond to the higher viscosity of the fluid, which, consequently, reduces the velocity of the fluid flow. Thus, the velocity distribution declines with the increase in $\beta$. Additionally, $\beta =0.0$ corresponds to the Newtonian fluid. Thereafter, it is found that the Newtonian fluid is less viscous than the non-Newtonian fluid. Figure 4 is drawn to determine the role of the primary velocity distribution against augmenting values of $M$. In this observation, a decreased performance in the primary velocity distribution is found for the increasing $M$ value. With the increasing magnetic field, the Lorentz force shows a retarding behavior against the flow behavior. Therefore, the Lorentz force opposes the fluid motion, which, consequently, decreases the boundary layer thickness and velocity distribution of the fluid flow. Furthermore, the increase in the magnetic parameter shows an upsurge of frictional forces between particles of fluids. This explains why velocity distribution is lower for higher magnetic factors. The effects of $\beta$ and $M$ on secondary velocity distributions are analyzed in Figures 5, 6. Since, the surface stretches linearly along both $x-$ and $y-$ directions. Therefore, similar impacts of the Maxwell fluid parameter $\beta$ and magnetic parameter $M$ are also found along the secondary velocity distribution. Figures 7–9 are plotted for the assessment of nanoliquid temperatures against increasing values of $Nb$, $Nt$, and $\gamma$. The consequence of $Nb$ on an energy profile is shown in Figure 7. An increase in the nanofluid temperature is examined for expanding the values of $Nb$. Brownian motion refers to the movement of particles; therefore, an increased production of heat occurs, which raises the energy profile. Figure 8 shows the effect of $Nt$ on the temperature distribution. Figure 8 describes that the nanoliquid temperature is enhanced for intensifying values of $Nt$. In the case of thermophoresis, liquid elements are quickly transformed from the hot region to the cold region with a rising the thermophoresis parameter $Nt$ which, consequently, shows a surge in the temperature distribution. The outcome of the nanoliquid temperature for increasing values of the thermal Biot number $\gamma$ is observed in Figure 9. In this figure, the increasing behavior in the temperature distribution due to $\gamma$ is observed. For greater values of $\gamma$, the heat transfer coefficient is enhanced because the heat transfer coefficient is directly related to the thermal Biot number $\gamma$. Therefore, the temperature distribution of the nanoliquid increases for the higher thermal Biot number $\gamma$. Figures 10–13 are displayed to discuss variations in the nanoliquid concentration distribution with respect to expanding values of $Nb$, $Nt$, $Sc$, and $kr$. The result of $Nb$ on the concentration distribution is shown in Figure 10. It is examined that, a rise in $Nb$ reduces the nanofluid concentration distribution. As $Nb$ increases, the concentration gradually falls. The explanation behind this is because higher values of the Brownian parameter enhance fluid particle collisions and lower the viscosity of nanofluids. Figure 11 explains the role of $Nt$ on the concentration distribution. In this figure, it is perceived that enhancing values of $Nt$ increase the nanofluid concentration distribution. This is because the thermodiffusion coefficient and the thermophoresis parameter are closely related. Increased diffusion coefficients are implied by higher values of $Nt$, which intensify the concentration distribution. The impact of $Sc$ on the concentration distribution is discussed in Figure 12. It is observed that the nanofluid concentration is lower with the expansion of the Schmidt number $Sc$. The Schmidt number $Sc$ is the ratio of momentum diffusivity and mass diffusivity. So, the mass diffusivity of the fluid decreases with the increase of the Schmidt number $Sc$. This is because the Schmidt number and mass diffusivity are inversely related to each other. Thus, a decrease in mass diffusivity decreases the concentration distribution. The consequence of $K$ on the concentration distribution is shown in Figure 13. It should be noted that the growth in the values of $K$ decays the nanofluid concentration. Furthermore, it can be perceived that molecular diffusivity is lower for higher chemical reactions. Therefore, a lower molecular diffusivity decreases the boundary layer thickness and concentration distribution of the nanoliquid. Figures 14, 15 show streamline patterns of Newtonian and Maxwell fluids, respectively. It should be noted that the analysis streamlines for Maxwell and Newtonian models in the current study are indeed distinct from one another.

TABLE 1

TABLE 1. Comparison of the present results of $-\theta \left(0\right)$ with the published results.

TABLE 2

TABLE 2. Impacts of $Nb$, $Nt,$ and $\gamma$ on ${\mathrm{R}\mathrm{e}}_x^{-\frac{1}{2}}N{u}_x$.

TABLE 3

TABLE 3. Impacts of $Nb$, $Nt$, $Sc$, and $K$ on ${\mathrm{R}\mathrm{e}}_x^{-\frac{1}{2}}S{h}_x$.

FIGURE 3

FIGURE 3. Influence of $\beta$ on $f^{\prime }\left(\eta \right)$.

FIGURE 4

FIGURE 4. Influence of $M$ on $f^{\prime }\left(\eta \right)$.

FIGURE 5

FIGURE 5. Influence of $\beta$ on $g^{\prime }\left(\eta \right)$.

FIGURE 6

FIGURE 6. Influence of $M$ on $g^{\prime }\left(\eta \right)$.

FIGURE 7

FIGURE 7. Influence of $Nb$ on $\theta \left(\eta \right)$.

FIGURE 8

FIGURE 8. Influence of $Nt$ on $\theta \left(\eta \right)$.

FIGURE 9

FIGURE 9. Influence of $\gamma$ on $\theta \left(\eta \right)$.

FIGURE 10

FIGURE 10. Influence of $Nb$ on $\varphi \left(\eta \right)$.

FIGURE 11

FIGURE 11. Influence of $Nt$ on $\varphi \left(\eta \right)$.

FIGURE 12

FIGURE 12. Influence of $Sc$ on $\varphi \left(\eta \right)$.

FIGURE 13

FIGURE 13. Influence of $K$ on $\varphi \left(\eta \right)$.

FIGURE 14

FIGURE 14. Streamlines for the Newtonian fluid.

FIGURE 15

FIGURE 15. Streamlines for the Maxwell fluid.

6 Conclusion

This article examines the 3D flow of a Maxwell nanofluid across a bi-directional stretching surface with magnetic field applications. In this approach, the effects of Brownian motion, thermophoresis, and chemical reactions are taken into account. The conditions for mass flux and thermal convection are also taken into account. The modeled problem is solved using the HAM technique. The HAM convergence is also demonstrated. Simulations and detailed discussions are carried out to determine the effects of various physical factors on flow profiles and quantities of interest. Key findings of the current problem are as follows:

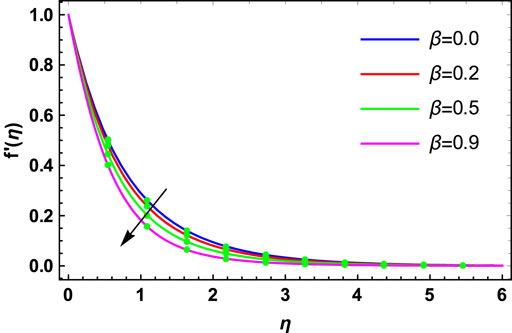
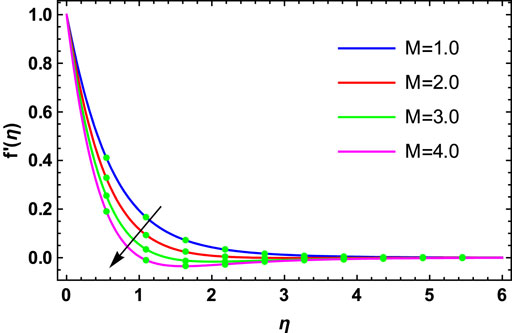
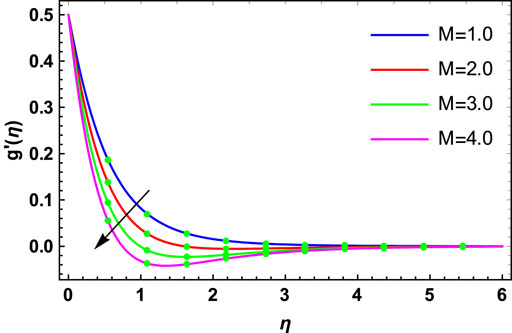
• The magnetic and Maxwell fluid parameters determine the decreasing functions of primary and secondary velocities.

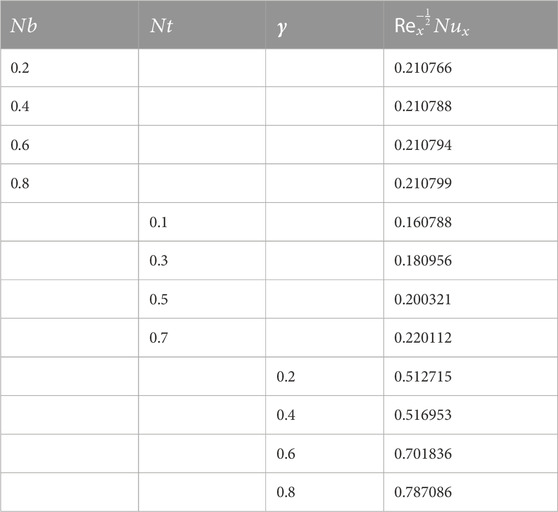
• The thermophoresis parameter, Brownian motion parameter, and thermal Biot number are the enhancing functions of the temperature distribution.

• The thermophoresis parameter has an enhancing effect on the concentration distribution, whereas Brownian motion, the Schmidt number, and chemical reaction parameters have a decreasing effect.

• The Nusselt number rises as the thermal Biot number, thermophoresis parameter, and Brownian motion parameter rise.

• The Sherwood number increases with the increasing thermophoresis parameter, while decreasing with the increasing Schmidt number, Brownian motion parameter, and chemical reaction parameter.

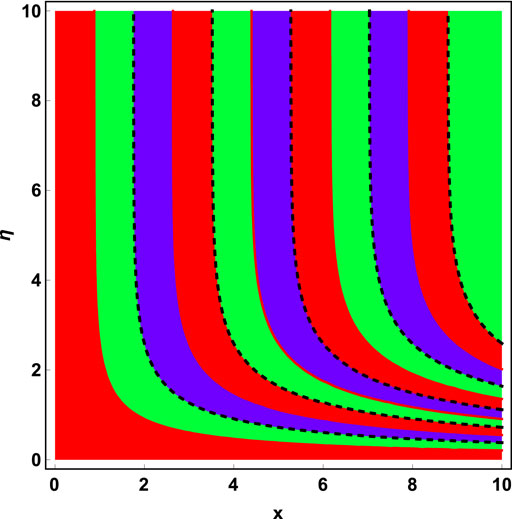
• It has been noted that the analysis streamlines for Maxwell and Newtonian models in the current study are indeed distinct from one another.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

EA and SL: conceptualization, methodology, software, reviewing, and editing. ZR: data curation and writing—original draft preparation. SE: visualization and investigation. AS: software, validation, and supervision. AG: writing—reviewing and editing.

Acknowledgments

The author ZR extends her appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under grant number (RGP.1/334/43).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alshehri, N. A., Abidi, A., Khan, M. R., Reddy, Y. D., Rasheed, S., Alali, E., et al. (2021). Unsteady convective MHD flow and heat transfer of a viscous nanofluid across a porous stretching/shrinking surface: Existence of multiple solutions. Crystals 11, 1359. doi:10.3390/cryst11111359

CrossRef Full Text | Google Scholar

Andersson, H. I., Hansen, O. R., and Holmedal, B. (1994). Diffusion of a chemically reactive species from a stretching sheet. Int. J. Heat. Mass Transf. 37, 659–664. doi:10.1016/0017-9310(94)90137-6

CrossRef Full Text | Google Scholar

Ashwinkumar, G. P., Samrat, S. P., and Sandeep, N. (2021). Convective heat transfer in MHD hybrid nanofluid flow over two different geometries. Int. Commun. Heat. Mass Transf. 127, 105563. doi:10.1016/j.icheatmasstransfer.2021.105563

CrossRef Full Text | Google Scholar

Bejawada, S. G., Reddy, Y. D., Jamshed, W., Nisar, K. S., Alharbi, A. N., and Chouikh, R. (2022). Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium, Alexandria Eng. J. 61, 8207–8220.

Google Scholar

Bejawada, S. G., and Yanala, D. R. (2021). Finite element Soret Dufour effects on an unsteady MHD heat and mass transfer flow past an accelerated inclined vertical plate. Heat. Transf. 50, 8553–8578. doi:10.1002/htj.22290

CrossRef Full Text | Google Scholar

Bilal Ashraf, M., Hayat, T., and Alhuthali, M. S. (2016). Three-dimensional flow of Maxwell fluid with soret and dufour effects. J. Aerosp. Eng. 29, 4015065. doi:10.1061/%28ASCE%29AS.1943-5525.0000551

CrossRef Full Text | Google Scholar

Chen, C. H. (1998). Laminar mixed convection adjacent to vertical continuously stretching sheets. Heat. mass Transf. 33, 471–476. doi:10.1007/s002310050217

CrossRef Full Text | Google Scholar

Dawar, A., Saeed, A., Islam, S., Shah, Z., Kumam, W., and Kumam, P. (2021). Electromagnetohydrodynamic bioconvective flow of binary fluid containing nanoparticles and gyrotactic microorganisms through a stratified stretching sheet. Sci. Rep. 11, 23159–23229. doi:10.1038/s41598-021-02320-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, X., Lin, P., Lin, J., Zhu, Z., and Yu, Z. (2022). On the polydisperse particle migration and formation of chains in a square channel flow of non-Newtonian fluids. J. Fluid Mech. 936, A5. doi:10.1017/jfm.2022.38

CrossRef Full Text | Google Scholar

Irfan, M. (2021). Study of Brownian motion and thermophoretic diffusion on non-linear mixed convection flow of Carreau nanofluid subject to variable properties. Surfaces Interfaces 23, 100926. doi:10.1016/j.surfin.2021.100926

CrossRef Full Text | Google Scholar

Islam, S., Khan, A., Deebani, W., Bonyah, E., Alreshidi, N. A., and Shah, Z. (2020). Influences of Hall current and radiation on MHD micropolar non-Newtonian hybrid nanofluid flow between two surfaces. AIP Adv. 10, 055015. doi:10.1063/1.5145298

CrossRef Full Text | Google Scholar

Khalil, K. M., Soleiman, A., Megahed, A. M., and Abbas, W. (2022). Impact of variable fluid properties and double diffusive cattaneo–christov model on dissipative non-Newtonian fluid flow due to a stretching sheet. Mathematics 10, 1179. doi:10.3390/math10071179

CrossRef Full Text | Google Scholar

Khan, A., Saeed, A., Tassaddiq, A., Gul, T., Mukhtar, S., Kumam, P., et al. (2021). Bio-convective micropolar nanofluid flow over thin moving needle subject to Arrhenius activation energy, viscous dissipation and binary chemical reaction. Case Stud. Therm. Eng. 25, 100989. doi:10.1016/j.csite.2021.100989

CrossRef Full Text | Google Scholar

Kiyani, M. Z., Abbasi, A. M. K., Muhammad, T., Ahmad, I., Waqas, M., and Riaz, S. (2022). Rheology of magneto-micropolar nanoliquid toward radiative exponential surface subjected to Brownian motion, thermal radiation, thermophoresis and viscous dissipation. Waves Random Complex Media 2022, 1–15. doi:10.1080/17455030.2022.2048921

CrossRef Full Text | Google Scholar

Kodi, R., Mopuri, O., Sree, S., and Konduru, V. (2022). Investigation of MHD Casson fluid flow past a vertical porous plate under the influence of thermal diffusion and chemical reaction. Heat. Transf. 51, 377–394. doi:10.1002/htj.22311

CrossRef Full Text | Google Scholar

Kumar, D., and Sahu, A. K. (2022). Non-Newtonian fluid flow over a rotating elliptic cylinder in laminar flow regime. Eur. J. Mech. 93, 117–136. doi:10.1016/j.euromechflu.2022.01.005

CrossRef Full Text | Google Scholar

Kumar, M. A., Reddy, Y. D., Goud, B. S., and Rao, V. S. (2022). An impact on non-Newtonian free convective MHD Casson fluid flow past a vertical porous plate in the existence of Soret, Dufour, and chemical reaction. Int. J. Ambient. Energy 43, 7410–7418. doi:10.1080/01430750.2022.2063381

CrossRef Full Text | Google Scholar

Kumar, S., and Sharma, K. (2022). Impacts of stefan blowing on reiner–rivlin fluid flow over moving rotating disk with chemical reaction. Arab. J. Sci. Eng. 2022, 1–10. doi:10.1007/s13369-022-07008-9

CrossRef Full Text | Google Scholar

Mabood, F., Ashwinkumar, G. P., and Sandeep, N. (2022). Effect of nonlinear radiation on 3D unsteady MHD stagnancy flow of Fe₃O₄/graphene–water hybrid nanofluid. Int. J. Ambient Energy 43, 3385–3395. doi:10.1080/01430750.2020.1831593

CrossRef Full Text | Google Scholar

Mabood, F., Ashwinkumar, G. P., and Sandeep, N. (2021). Simultaneous results for unsteady flow of MHD hybrid nanoliquid above a flat/slendering surface. J. Therm. Anal. Calorim. 146, 227–239. doi:10.1007/s10973-020-09943-x

CrossRef Full Text | Google Scholar

Mehta, R., and Kataria, H. R. (2022). Brownian motion and thermophoresis effects on MHD flow of viscoelastic fluid over stretching/shrinking sheet in the presence of thermal radiation and chemical reaction. Heat. Transf. 51, 274–295. doi:10.1002/htj.22307

CrossRef Full Text | Google Scholar

Mishra, P., Kumar, D., Dharmendar Reddy, Y., and Shankar Goud, B. (2022). Numerical investigation of MHD flow of Williamson nanofluid with variable viscosity pasting a wedge within porous media: A non-Darcy model approach. Heat. Transf. 51 (7), 6071–6086. doi:10.1002/htj.22580

CrossRef Full Text | Google Scholar

Mukhopadhyay, S. (2013). Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B 22, 074701. doi:10.1088/1674-1056/22/7/074701

CrossRef Full Text | Google Scholar

Nalivela, N. R., Vempati, S. R., Ravindra Reddy, B., and Dharmendar Reddy, Y. (2022). Viscous dissipation and thermal radiation impact on MHD mass transfer natural convective flow over a stretching sheet. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 09544089221081339. doi:10.1177/09544089221081339

CrossRef Full Text | Google Scholar

Ogunseye, H. A., Salawu, S. O., Tijani, Y. O., Riliwan, M., and Sibanda, P. (2019). Dynamical analysis of hydromagnetic Brownian and thermophoresis effects of squeezing Eyring–Powell nanofluid flow with variable thermal conductivity and chemical reaction, Multidiscip. Model. Mat. Struct. 15 (6), 1100–1120. doi:10.1108/MMMS-01-2019-0008

CrossRef Full Text | Google Scholar

Prasad, K. V., Santhi, S. R., and Datti, P. S. (2012). Non-Newtonian power-law fluid flow and heat transfer over a non-linearly stretching surface. Appl. Math. 3, 35065. doi:10.4236/am.2012.35065

CrossRef Full Text | Google Scholar

Raghunath, K., Gulle, N., Vaddemani, R. R., and Mopuri, O. (2022). Unsteady MHD fluid flow past an inclined vertical porous plate in the presence of chemical reaction with aligned magnetic field, radiation, and Soret effects. Heat. Transf. 51, 2742–2760. doi:10.1002/htj.22423

CrossRef Full Text | Google Scholar

Reddy, N. N., Reddy, Y. D., Rao, V. S., Goud, B. S., and Nisar, K. S. (2022). Multiple slip effects on steady MHD flow past a non-isothermal stretching surface in presence of Soret, Dufour with suction/injection. Int. Commun. Heat. Mass Transf. 134, 106024. doi:10.1016/j.icheatmasstransfer.2022.106024

CrossRef Full Text | Google Scholar

Reddy, Y. D., Mebarek-Oudina, F., Goud, B. S., and Ismail, A. I. (2022). Radiation, velocity and thermal slips effect toward MHD boundary layer flow through heat and mass transport of Williamson nanofluid with porous medium. Arab. J. Sci. Eng. 47, 16355–16369. doi:10.1007/s13369-022-06825-2

CrossRef Full Text | Google Scholar

Reddy, Y. D., Ramya, D., and Babu, L. A. (2016). Effect of thermal radiation on MHD boundary layer flow of nanofluid and heat transfer over a non-linearly stretching sheet with transpiration. J. Nanofluids 5, 889–897. doi:10.1166/jon.2016.1284

CrossRef Full Text | Google Scholar

Salawu, S. O., and Ogunseye, H. A. (2020). Entropy generation of a radiative hydromagnetic Powell-Eyring chemical reaction nanofluid with variable conductivity and electric field loading. Results Eng. 5, 100072. doi:10.1016/j.rineng.2019.100072

CrossRef Full Text | Google Scholar

Saleem, S., Animasaun, I. L., Yook, S.-J., Al-Mdallal, Q. M., Shah, N. A., and Faisal, M. (2022). Insight into the motion of water conveying three kinds of nanoparticles shapes on a horizontal surface: Significance of thermo-migration and Brownian motion. Surfaces Interfaces 30, 101854. doi:10.1016/j.surfin.2022.101854

CrossRef Full Text | Google Scholar

Sandeep, N., and Ashwinkumar, G. P. (2021). Impact of nanoparticle shape on magnetohydrodynamic stagnation-point flow of carreau nanoliquid: A comparative study. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 236 (3), 09544089211058427. doi:10.1177/09544089211058427

CrossRef Full Text | Google Scholar

Sandeep, N., Ranjana, B., Samrat, S. P., and Ashwinkumar, G. P. (2022). Impact of nonlinear radiation on magnetohydrodynamic flow of hybrid nanofluid with heat source effect. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 236 (4), 09544089211070667. doi:10.1177/095440892110706

CrossRef Full Text | Google Scholar

Sharma, R. P., and Mishra, S. R. (2020). Effect of higher order chemical reaction on magnetohydrodynamic micropolar fluid flow with internal heat source, Int. J. Fluid Mech. Res. Inter. J. Fluid Mech. Res. 47, 121–134. doi:10.1615/interjfluidmechres.2019027201

CrossRef Full Text | Google Scholar

Sharma, R. P., and Shaw, S. (2022). MHD non-Newtonian fluid flow past a stretching sheet under the influence of non-linear radiation and viscous dissipation. J. Appl. Comput. Mech. 8, 949–961. doi:10.22055/JACM.2021.34993.2533

CrossRef Full Text | Google Scholar

Singh, K., Pandey, A. K., and Kumar, M. (2021). Numerical solution of micropolar fluid flow via stretchable surface with chemical reaction and melting heat transfer using Keller-Box method. Propuls. Power Res. 10, 194–207. doi:10.1016/J.JPPR.2020.11.006

CrossRef Full Text | Google Scholar

Sneha, K. N., Mahabaleshwar, U. S., Chan, A., and Hatami, M. (2022). Investigation of radiation and MHD on non-Newtonian fluid flow over a stretching/shrinking sheet with CNTs and mass transpiration. Waves Random Complex Media 2022, 1–20. doi:10.1080/17455030.2022.2029616

CrossRef Full Text | Google Scholar

Sohail, M., Shah, Z., Tassaddiq, A., Kumam, P., and Roy, P. (2020). Entropy generation in MHD Casson fluid flow with variable heat conductance and thermal conductivity over non-linear bi-directional stretching surface. Sci. Rep. 10, 12530–12616. doi:10.1038/s41598-020-69411-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sulochana, C., Ashwinkumar, G. P., and Sandeep, N. (2018). Boundary layer analysis of persistent moving horizontal needle in magnetohydrodynamic ferrofluid: A numerical study. J. 57, 2559–2566. doi:10.1016/j.aej.2017.08.020

CrossRef Full Text | Google Scholar

Tayyab, M., Siddique, I., Jarad, F., Ashraf, M. K., and Ali, B. (2022). Numerical solution of 3D rotating nanofluid flow subject to Darcy-Forchheimer law, bio-convection and activation energy. South Afr. J. Chem. Eng. 40, 48–56. doi:10.1016/j.sajce.2022.01.005

CrossRef Full Text | Google Scholar

Upreti, H., Pandey, A. K., Uddin, Z., and Kumar, M. (2022). Thermophoresis and brownian motion effects on 3D flow of Casson nanofluid consisting microorganisms over a Riga plate using PSO: A numerical study. Phys. 78, 234–270. doi:10.1016/j.cjph.2022.06.019

CrossRef Full Text | Google Scholar

Waini, I., Khashi’ie, N. S., Kasim, A. R. M., Zainal, N. A., Ishak, A., and Pop, I. (2022). Thermal analysis of non-Newtonian fluid flow past a permeable shrinking wedge with magnetohydrodynamic effects: Reiner–Philippoff model. J. Therm. Anal. Calorim. 147, 13561–13571. doi:10.1007/s10973-022-11508-z

CrossRef Full Text | Google Scholar

Wu, J., and Thompson, M. C. (1996). Non-Newtonian shear-thinning flows past a flat plate. J. Nonnewt. Fluid Mech. 66, 127–144. doi:10.1016/s0377-0257(96)01476-0

CrossRef Full Text | Google Scholar

Xu, H., and Liao, S.-J. (2009). Laminar flow and heat transfer in the boundary-layer of non-Newtonian fluids over a stretching flat sheet. Comput. Math. Appl. 57, 1425–1431. doi:10.1016/j.camwa.2009.01.029

CrossRef Full Text | Google Scholar

Nomenclature

Symbol names

$a$ and $b$ positive constants

$C$ concentration of the fluid

$D_B$ Brownian diffusivity

$L_f,L_g,L_{\theta },{\mathrm{a}\mathrm{n}\mathrm{d}L}_{\varphi }$ linear operators ${\mathrm{\hslash }}_f$, ${\mathrm{\hslash }}_g$, ${\mathrm{\hslash }}_{\theta }$, $\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{\hslash }}_{\varphi }$ and auxiliary parameters

$M$ magnetic term

$T$ temperature

$u,v,\mathrm{a}\mathrm{n}\mathrm{d}w$ velocity components

$x,y,\mathrm{a}\mathrm{n}\mathrm{d}z$ coordinates

Greek letters

$\sigma$ electrical conductivity

$\alpha$ stretching parameter

Subscripts

$w$ at the surface

$B_0$ magnetic field

$f_0,g_0,{\theta }_0,{and\varphi }_0$ initial guesses

$K$ chemical reaction parameter

${\mho }_1-{\mho }_{10}$ arbitrary constants

$\mathrm{Pr}$ Prandtl number

$Sc$ Schmidt number

$u_w\left(x\right)=ax$ stretching velocity along the $x-$ direction

$v_w\left(x\right)=by$ stretching velocity along the $y-$ direction

$\beta$ Deborah number

$\rho$ density

$\infty$ free stream