Simple acoustic metagrating for perfect two- and three-beam splitting

Song, Ailing; Sun, Chaoyu; Xiang, Yanxun; Xuan, Fu-Zhen

doi:10.3389/fmats.2023.1127233

ORIGINAL RESEARCH article

Front. Mater., 08 February 2023

Sec. Metamaterials

Volume 10 - 2023 | https://doi.org/10.3389/fmats.2023.1127233

This article is part of the Research Topic Acoustic and Mechanical Metamaterials for Various Applications - Volume II View all 8 articles

Simple acoustic metagrating for perfect two- and three-beam splitting

Ailing Song

Chaoyu Sun

Yanxun Xiang*

Fu-Zhen Xuan

Key Laboratory of Pressure Systems and Safety of MOE, School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai, China

Acoustic metasurfaces have been widely explored and attracted great attention for their extraordinary wavefront manipulation abilities. In this paper, we propose a simple acoustic metagrating with periodic grooves that can split a normally incident beam into two or three reflected beams. The amplitudes and power flows of different reflected beams can be manipulated by changing the groove parameters. The mirror reflected wave is suppressed for equal two-beam splitting case and allowed for three-beam splitting case. Theoretical analysis and numerical simulations are performed to demonstrate the perfect two- and three-beam splitting performances based on local power conservation. Our research work provides a simple method for designing acoustic beam splitters and has extensive applications in acoustic sensing and communication.

Introduction

Acoustic metasurfaces (Cummer et al., 2016; Assouar et al., 2018) are artificially designed structures composed of periodic subwavelength elements including groove structures (Shen et al., 2018), Helmholtz resonators (Li et al., 2018), labyrinthine structures (Xie et al., 2014), space coiling-up structures (Li et al., 2013; Chen et al., 2021), membranes (Ma et al., 2014), etc. In recent years, acoustic metasurfaces have attracted significant attention for their great potential applications in many fields attributed by their interesting and extraordinary acoustic properties (Zhao et al., 2022), such as anomalous reflection and refraction (Memoli et al., 2017; Zhu and Lau, 2019), acoustic focusing (Qi et al., 2017; Lombard et al., 2022), acoustic cloaking (Faure et al., 2016; Jin et al., 2019), sound absorption (Aurégan, 2018; Song et al., 2019), one-way acoustic propagation (Liang et al., 2010; Li et al., 2017; Song et al., 2019), beam splitting (Ding et al., 2021), etc. Particularly, acoustic beam splitters have attracted growing interest recently due to their applications in acoustic communication (Prada et al., 2007) and acoustic sensing (Dowling and Sabra, 2015) fields.

Acoustic beam splitters (Ni et al., 2019) are devices that can effectively split the incident beam into two or more beams. Acoustic metasurfaces capable of manipulating the amplitude and phase of acoustic waves provide a good method for realizing beam splitting. (Díaz-Rubio et al. 2019) proposed a power flow-conformal acoustic beam splitter by manipulating the surface impedance distribution of metasurface to split the incident wave into two reflected beams propagating along two different directions. Beam splitting with arbitrary energy ratios can be realized by non-local grooved metasurfaces by using deep learning algorithms (Ding et al., 2021). Bianisotropic metasurface was developed for near-perfect arbitrary beam splitting by introducing self-induced surface waves into scattered field (Li et al., 2020). In addition, coding acoustic metasurfaces are widely used for designing acoustic beam splitters. Reflection-type coding acoustic metasurfaces were designed for realizing broadband acoustic splitter by encoding the sequence of logical units (Zhang et al., 2022). Coding acoustic metasurfaces composed of hornlike helical unit were theoretically and experimentally demonstrated for realizing acoustic splitting (Fang et al., 2019). However, we can find that the beam splitters based on acoustic metasurfaces are inevitably limited in element resolution, manipulation efficiency, and operating angle. Furthermore, the most commonly used microstructures including resonator structures (Shen et al., 2018) and space coiling-up structures (Jia et al., 2018) have complex configuration, which may result in large intrinsic loss and low efficiency. In order to solve the above-mentioned problems existing in beam splitters based on acoustic metasurfaces, simple and high-efficiency acoustic metagratings (Torrent, 2018; Fan and Mei, 2021) based on diffraction theory provide a reliable method for achieving good acoustic performances. High-efficiency anomalous acoustic splitters based on genetic optimization algorithm and acoustic metagratings are designed to split the incident wave into different directions (Ni et al., 2019). Perfect beam splitting with unitary efficiency (Fan and Mei, 2020) was demonstrated by using acoustic metagrating composed of periodic iron cylinders and a sound soft plane placed in water. Beam splitter based on acoustic binary metagrating was designed to split an acoustic wave into two directions (Liu et al., 2022). A transmitting beam splitter with grooves was designed to split the incident wave into two waves with arbitrary amplitude ratio and phase differences (Cao and Hou, 2019).

From above discussion, we find that the beam splitters based on acoustic metasurfaces suffer from complicated configurations and inevitable intrinsic loss, which greatly limit their wide practical applications of beam splitters. The literature on metagrating-based acoustic beam splitter with changeable beam number also remain scarce. Therefore, it is necessary to explore new realization methods to overcome these limitations and design beam splitters with simplified structures, high efficiency, and good reconfigurability. In this paper, simple acoustic metagrating with periodic grooves is designed for realizing perfect two- and three-beam splitting with high efficiency, broad bandwidth, and easy fabrication, and demonstrating good beam manipulation performance by changing the groove height. The proposed acoustic metagrating has potential applications in the fields of acoustic communication (Prada et al., 2007) and acoustic sensing (Dowling and Sabra, 2015).

Method and design

In this paper, we propose a simple acoustic metagratings for realizing perfect two-beam and three-beam splitting with specified reflected amplitudes and power flows, as shown in Figure 1. As the proposed acoustic metagrating is a periodic structure, the groove number will not greatly affect the beam splitting performances. Without loss of generality, we take the proposed acoustic metagrating containing 22 periodic grooves as an example, and incident wave is perpendicularly incident on the acoustic metagrating. Actually, the groove number can also be set as other values. Compared with the previously reported beam splitters, our proposed metagrating could manipulate the number of reflected beams, the reflected amplitudes, and the power flows by controlling the groove height based on local power conservation. For perfect two-beam splitting case, the acoustic metagrating can split a normally incident beam into two symmetric reflected beams with reflected angles of θ_-1 and θ₊₁, the corresponding amplitudes are p_-1 and p₊₁, respectively. For perfect three-beam splitting case, the acoustic metagrating can split a normally incident beam into three reflected beams with reflected angles of θ_-1, θ₊₁, and θ₀, the corresponding amplitudes are p_-1, p₊₁, and p₀, respectively. The inset in Figure 1 shows the two-dimensional configuration of the proposed metagrating, which contains periodic grooves. Because the reflected beams of −1 and +1 diffraction orders are completely symmetric beams, so it is enough for one unit cell only contains one groove in our design as demonstrated by Torrent (Torrent, 2018). To generate reflected beams with different amplitudes and realize more beam number, one unit cell should contain two or more grooves and the groove parameters should be changed. The groove width is w, the groove height is h, the thickness of acoustic metagrating is d, the period of acoustic metagrating is a. Careful choice of acoustic metagrating geometrical parameters can in principle scattered all acoustic energy into different diffraction orders according to the diffraction theory, so the amplitudes and power flows of reflected beams can be manipulated. As the metagrating with periodic grooves does not contain resonant (Shen et al., 2018) or narrow (Jia et al., 2018) structures, we can expect high efficiency and low intrinsic loss.

FIGURE 1

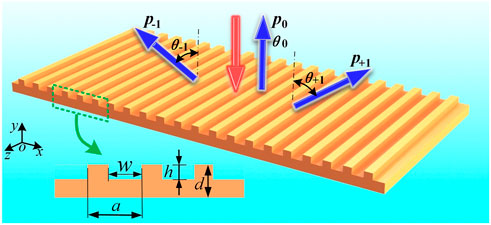
FIGURE 1. Schematic view of the proposed acoustic metagrating for realizing perfect two- and three-beam splitting. The inset shows the two-dimensional configuration of the metagrating with periodic grooves. Red and blue arrows indicate the incident beam and the reflected beams, respectively. The reflected angles of the reflected beams are θ_-1, θ₊₁, and θ₀, the corresponding amplitudes are p_-1, p₊₁, and p₀.

When a plane wave impinges on the periodic acoustic metagrating with the incident angle of θ_i, the incident wave will be diffracted into multiple diffraction orders and the scattered filed can be expressed as (Torrent, 2018):

p_{s} = \sum_{n} p_{n} e^{- j k_{n} \cdot r} (1)

where p_n is the amplitude of nth-order diffracted wave, r is the position vector, k_n is the wave vector of nth-order diffracted wave and can be expressed as $k_{n} = k_{n x} x + k_{n y} y = k \sin θ_{n} x + k \cos θ_{n} y$ , k is the wavenumber in air, θ_n is the reflected angle of nth-order diffracted wave. According to the periodicity of acoustic metagrating and the grating theory, the x-direction wave vector components of incident and reflected waves should satisfy:

k_{n x} = {k_{i}}_{x} + G_{n} (2)

where k_nx = ksinθ_n is x-direction wave vector component of nth-order reflected wave, k_ix = ksinθ_i is x-direction wave vector component of incident wave, G_n = 2πn/a is the nth-order reciprocal vector. Therefore, the y-direction wave vector component of nth-order reflected wave is $k_{n y} = \sqrt{k^{2} - {(k \sin θ_{i} + 2 π n / a)}^{2}}$ , it is noted that k_ny will be a real component only when $k^{2} > k_{n x}^{2}$ and the nth diffraction order corresponds to a propagating wave.

In our design, the incident wave is perpendicularly incident on the acoustic metagrating, so the incident angle is θ_i = 0°. To realize a beam splitting acoustic metagrating, we first calculate the period of the acoustic metagrating based on the Eq. 2 to guarantee the nth diffraction orders are propagating waves. Therefore, the period of acoustic metagrating is a = nλ/|sinθ_±1|, λ is the wavelength in air. By setting a = λ/|sinθ_±1|, the acoustic metagrating will only have −1, 0, and +1 diffraction orders as propagating waves for the case of θ_n > 30°. The n = −1 diffraction order corresponds to the reflected beam with the reflected angle of θ_-1, n = +1 diffraction order corresponds to the reflected beam with the reflected angle of θ₊₁, n = 0 diffraction order corresponds to the reflected beam with the reflected angle of θ₀. As an example, we choose the working frequency is 4,000 Hz and the corresponding wavelength is λ = 85.75 mm, the reflected angles or splitting angles are θ_-1 = −60° and θ₊₁ = 60°, so the period of acoustic metagrating is a = 99 mm. By simultaneously changing the groove width w and groove height h of acoustic metagrating, the amplitudes of different diffracted waves can be effectively manipulated. For simplicity, the groove width is fixed to w = 0.6a = 59.4 mm, the groove height is a variable value. The thickness of acoustic metagrating is d = 50 mm.

As the groove height of acoustic metagrating could influence the amplitudes of different diffracted waves, so it is necessary to determine the groove heights for different beam splitting cases. The amplitude of incident wave is set to be 1. We separately calculate the amplitudes of different reflected beams normalized by the amplitude of normally incident wave, Figure 2A shows the amplitudes of −60°, 60°, and 0° reflected beams when the proposed acoustic metagratings are illuminated by a plane wave of 4,000 Hz, and the groove height gradually increases from 0 to 0.5λ. We can see the amplitudes of −60° (red line) and 60° (cyan circle) reflected beams remain same and gradually increase from 0 to 0.999 at the groove height of h = 0.22λ (point M), then reduce to the minimum amplitude at h = 0.5λ. However, the amplitudes of 0° (blue dotted line) reflected beam presents opposite variation tendency and reaches the minimum amplitude at the groove height of h = 0.22λ (point M′), which means 0° reflected beam is greatly suppressed and two-beam splitting with the same amplitude is achieved at h = 0.22λ. It is worth noting that −60°, 60°, and 0° reflected beams have the same amplitude of 0.707 when the groove height is h = 0.10λ, as denoted by point N in Figure 2A, which means three reflected beams are all effectively excited and perfect three-beam splitting with same amplitude is achieved.

FIGURE 2

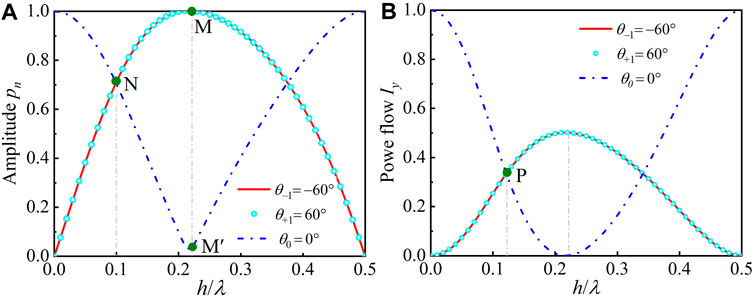
FIGURE 2. (A) Amplitude p_n and (B) y-direction power flow I_y of −60° (red line), 60° (cyan circle), and 0° (blue dotted line) reflected sound beams when the proposed acoustic metagrating with groove height ranging from 0 to 0.5λ is illuminated by a plane wave of 4,000 Hz.

On the other hand, the y-direction power flows of −60°, 60°, and 0° reflected beams are calculated and shown in Figure 2B with the groove height changing from 0 to 0.5λ. The y-direction power flow I_y is normalized by the power flow of normally incident wave. It is observed that the power flows of −60° (red line) and 60° (cyan circle) reflected beams still remain same and reach the maximum value of 0.5 at h = 0.22λ, while the amplitude of 0° (blue dotted line) reflected beam reaches the minimum value, which means two-beam splitting with same power flow is achieved. We can see that −60°, 60°, and 0° reflected beams have same power flow when the groove height is h = 0.12λ, as denoted by point P in Figure 2B, which means all three reflected beams are excited with same power flow and three-beam splitting is achieved. If the local power flow perpendicular to the acoustic metagrating is conserved, the incident amplitude and reflected amplitudes should satisfy ${p_{i}}^{2} = {p_{-}}_{1}^{2} \cos {θ_{-}}_{1} + {p_{+ 1}}^{2} \cos θ_{+ 1} + {p_{0}}^{2} \cos θ_{0}$ , which means the power flow ratio of reflected beams is $I_{- 1} : I_{+ 1} : I_{0} = {p_{-}}_{1}^{2} \cos {θ_{-}}_{1} : {p_{+ 1}}^{2} \cos θ_{+ 1} : {p_{0}}^{2} \cos θ_{0}$ . From above analysis, we predict that equal two-beam splitting ( $p_{- 1} = p_{+ 1} = 1$ or $I_{- 1} : I_{+ 1} = 0.5 : 0.5$ ) can be achieved at h = 0.22λ, three-beam splitting with same amplitude ( $p_{- 1} = p_{+ 1} = p_{0} = \sqrt{2} / 2$ ) can be achieved at h = 0.10λ, and three-beam splitting with same power flow ( $I_{- 1} : I_{+ 1} : I_{0} = \frac{1}{3} : \frac{1}{3} : \frac{1}{3}$ ) can be achieved at h = 0.12λ. Local power flow is conserved in both two- and three-beam splitting cases for realizing perfect beam splitting.

Results and discussion

To intuitively show the two-beam and three-beam splitting performances, numerical simulations of the proposed acoustic metagratings are performed in COMSOL Multiphysics software. The proposed acoustic metagratings are placed in air background and the intrinsic loss is not considered, all boundaries are set to be sound hard boundaries, the air density is 1.21 kg/m³, the sound speed in air is 343 m/s.

Two-beam splitting

Acoustic metagrating for realizing equal two-beam splitting at h = 0.22λ is first investigated, as shown in Figure 3A. One-period scattered sound pressure field distributions in theoretical calculation and in numerical simulation with real acoustic metagrating at h = 0.22λ are shown in Figure 3B. The amplitudes of −1, +1, and 0 diffraction orders are 0.999, 0.999, and 0.001. It can be seen that these two field distributions are almost exactly the same, which means the realized two-beam splitting performance agrees well with the theoretical expectation. Furthermore, when a Gaussian beam of 4,000 Hz normally impinges on the acoustic metagrating with a groove height of 0.22λ, the scattered sound pressure field distribution is shown in Figure 3C. The width of Gaussian beam is 0.4 m. It can be clearly observed that the normally incident beam is completely reflected by the metagrating into two symmetric directions as the white arrows show. As the theoretical analysis, the excitation of mirror reflected wave with 0° reflected angle is effectively suppressed. To better quantitatively analyze the two-beam splitting performance, we plot the far-field radiation pattern with normalized sound intensity of scattered waves, as shown in Figure 3D. The reflected angle can be obtained when the normalized sound intensity of scattered waves takes the maximum value. The reflected angles of two beams are θ_-1 = −60.4° and θ₊₁ = 60.4°, the corresponding amplitudes are 0.999 and 0.998, respectively, which agree well with the theoretical expectation of $p_{- 1} = p_{+ 1} = 1$ . The slight deviation of reflection angle between the theory and numerical simulation is caused by the width variation of incident wave, which can be reduced by increasing the width of Gaussian beam. It should be pointed out that the amplitudes and power flows of 60° and −60° reflected beams are almost same, which means this simple acoustic metagrating can realize equal two-beam splitting.

FIGURE 3

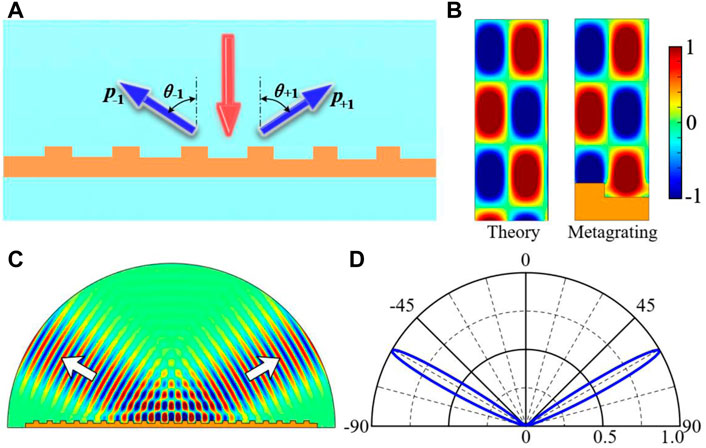
FIGURE 3. (A) Acoustic metagrating with a groove height of 0.22λ for realizing perfect two-beam splitting with same amplitude and power flow. (B) One-period scattered sound pressure fields in theoretical calculation and with real acoustic metagrating. (C) Scattered sound pressure field distribution when a Gaussian beam of 4,000 Hz normally impinges on the proposed acoustic metagrating and white arrows represent the propagation directions of reflected beams. (D) Far-field radiation pattern with normalized sound intensity of scattered waves.

We can see that the proposed acoustic metagrating with a groove height of h = 0.22λ can realize perfect equal two-beam splitting at the frequency of f = 4,000 Hz, it is necessary to investigate the acoustic performances at different working frequencies. The proposed acoustic metagrating can realize two-beam splitting within the frequency range of 3,600∼5,000 Hz. As a few examples, the scattered sound pressure field distributions at the frequencies of f = 3,700 Hz, f = 4,000 Hz, f = 4,300 Hz, f = 4,600 Hz are shown in Figures 4A–D, respectively. It is noted that two-beam splitting effects are obviously observed at different frequencies. For all those working frequencies, the Gaussian beam impinging on the proposed acoustic metagrating is mainly splitted into two reflected beams that propagate along two symmetric directions. With the increase of working frequency, the reflected beams propagating along two symmetric directions gradually approach the normal direction of the metagrating and the reflected angle gradually decreases. This phenomenon can be explained by analyzing the reflected angle of nth-order diffracted wave, which can be expressed as $θ_{n} = \sin^{- 1} (\frac{2 π n}{a k}) = \sin^{- 1} (\frac{n c}{a f})$ . In addition, the mirror reflected waves are slightly excited with small amplitudes at 3,700 Hz, 4,300 Hz, and 4,600 Hz. The amplitude of 0 diffraction order almost keeps zero while the amplitudes of −1 and +1 diffraction orders gradually decreases with the increase of frequency.

FIGURE 4

FIGURE 4. Scattered sound pressure field distributions when the proposed acoustic metagrating with a groove height of h = 0.22λ are normally illuminated by Gaussian beams of different frequencies. (A) f = 3,700 Hz. (B) f = 4,000 Hz. (C) f = 4,300 Hz. (D) f = 4,600 Hz.

Three-beam splitting

Similarly, the acoustic metagrating for realizing three-beam splitting with same amplitude at h = 0.10λ or same power flow at h = 0.12λ are investigated, as shown in Figure 5A. Figures 5B, C show one-period scattered sound pressure field distributions in theoretical calculation and in numerical simulation with real acoustic metagrating at h = 0.10λ and h = 0.12λ, respectively. For h = 0.10λ in Figure 5B, the amplitudes of −1, +1, and 0 diffraction orders are 0.707, 0.707, and 0.706. For h = 0.12λ in Figure 5C, the amplitudes of −1, +1, and 0 diffraction orders are 0.816, 0.816, and 0.577. We can see the scattered sound pressure fields with real acoustic metagrating are almost the same as the theoretical results, which demonstrates the proposed metagrating can realize three-beam splitting as the theory expects. When a normally incident Gaussian beam of 4,000 Hz impinges on the proposed acoustic metagrating with a groove height of 0.10λ or 0.12λ, the corresponding scattered sound pressure field distributions are shown in Figures 5D, E, respectively. We can see that the normally incident beam is effectively splitted by the acoustic metagrating into three beams as the white arrows show. The far-field radiation patterns with normalized sound intensity of scattered waves are shown in Figures 5F, G to help us quantitatively analyze the three-beam splitting performance. All intensities are normalized by the intensity of normally incident wave. When the groove height of acoustic metagrating is 0.10λ, the reflected angles of three reflected beams are θ_-1 = −60.4°, θ₊₁ = 60.4°, and θ₀ = 0.144°, the corresponding amplitudes are 0.706, 0.706, and 0.704, respectively, which means three reflected beams have almost same amplitude as the theoretical expectation of $p_{- 1} = p_{+ 1} = p_{0} = \sqrt{2} / 2$ . When the groove height of acoustic metagrating is 0.12λ, the reflected angles of three reflected beams are θ_-1 = −60.4°, θ₊₁ = 60.4°, and θ₀ = 0.143°, the corresponding normalized y-direction power flow are 0.331, 0.331, and 0.333, respectively, which means three reflected beams have almost same power flow and three-beam splitting with equal power flow is achieved, which agree well with the theoretical expectation of $I_{- 1} : I_{+ 1} : I_{0} = \frac{1}{3} : \frac{1}{3} : \frac{1}{3}$ .

FIGURE 5

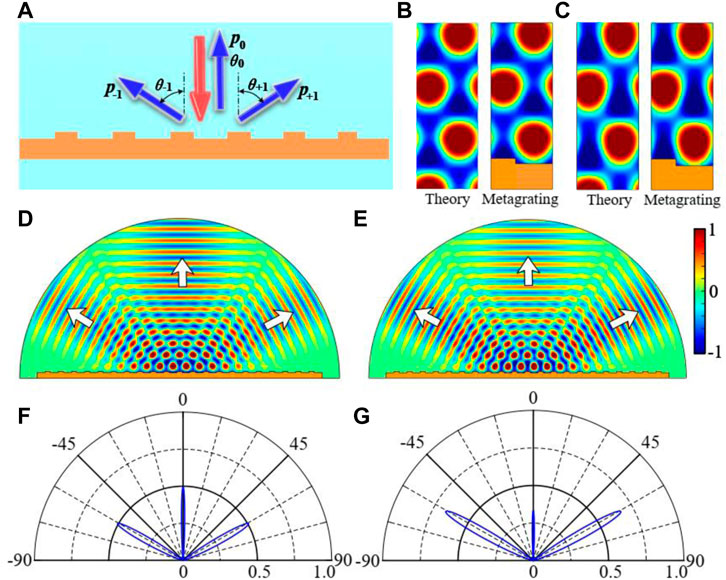
FIGURE 5. (A) Acoustic metagrating for realizing perfect three-beam splitting with same amplitude (h = 0.10λ) or same power flow (h = 0.12λ). One-period scattered sound pressure fields in theoretical calculation and with real acoustic metagrating for three-beam splitting (B) with same amplitude at h = 0.10λ, (C) with same power flow at h = 0.12λ. Scattered sound pressure field distribution when a Gaussian beam of 4,000 Hz normally impinges on the proposed acoustic metagrating with a groove height of (D) h = 0.10λ, (E) h = 0.12λ. Far-field radiation patterns with normalized sound intensity of scattered waves for acoustic metagrating with a groove height of (F) h = 0.10λ, (G) h = 0.12λ.

The proposed acoustic metagrating with a groove height of h = 0.10λ can realize three-beam splitting with same amplitude and that with a groove height of h = 0.12λ can realize three-beam splitting with same power flow, then we investigate the acoustic performances at different working frequencies. The proposed acoustic metagrating can realize three-beam splitting within the frequency range of 3,600∼5,000 Hz. When the acoustic metagrating with a groove height of h = 0.10λ are normally illuminated by a Gaussian beam, the scattered sound pressure field distributions at the frequencies of f = 3,700 Hz, f = 4,000 Hz, f = 4,300 Hz, f = 4,600 Hz are shown in Figures 6A–D respectively. When the acoustic metagrating with a groove height of h = 0.12λ are normally illuminated by a Gaussian beam, the scattered sound pressure field distributions at the frequencies of f = 3,700 Hz, f = 4,000 Hz, f = 4,300 Hz, f = 4,600 Hz are shown in Figures 6E–H, respectively. It can be clearly observed that three-beam splitting effects happen at all different frequencies. The Gaussian beam impinging on the acoustic metagrating is effectively splitted into three reflected beams including mirror reflected beam and two beams propagating along two symmetric directions at all those working frequencies. For three-beam splitting case with same amplitude and same power flow, the reflected angle gradually decreases with the increase of working frequency. The amplitude of 0 diffraction order keep almost unchanged while the amplitudes of −1 and +1 diffraction orders gradually decreases with the increase of frequency.

FIGURE 6

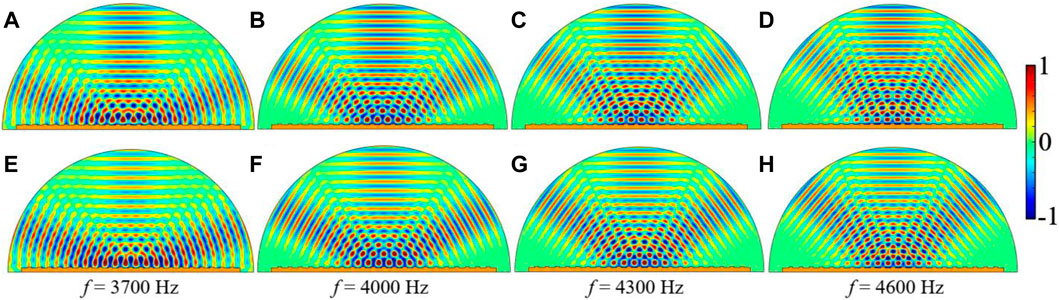
FIGURE 6. Scattered sound pressure field distributions when the proposed acoustic metagratings are normally illuminated by Gaussian beams of different frequencies. When the groove height is h = 0.10λ (upper panel) and the working frequencies are (A) f = 3,700 Hz. (B) f = 4,000 Hz. (C) f = 4,300 Hz. (D) f = 4,600 Hz. When the groove height is h = 0.12λ (lower panel) and the working frequencies are (E) f = 3,700 Hz. (F) f = 4,000 Hz. (G) f = 4,300 Hz. (H) f = 4,600 Hz.

From above numerical simulation results and discussion, we can clearly see that the proposed acoustic metagrating can realize perfect equal two-beam splitting and three-beam splitting with same amplitude or same power flow. In future experiments, we can expect good two- and three-beam splitting performances, but we will possibly encounter problems including fabrication errors, visco-thermal loss, and boundary reflections. The fabrication errors and visco-thermal loss can be reduced by choosing 3D printing technology with higher printing accuracy. The effect of boundary reflections can be appropriately eliminated by using data post-processing method.

Conclusion

In conclusion, we demonstrate an acoustic metagrating with periodic grooves can realize perfect two-beam splitting and three-beam splitting with conserved local power. The proposed acoustic metagrating will only allow −1, 0, and +1 diffraction orders as propagating waves by setting the period of acoustic metagrating. By changing the groove height, the amplitudes and power flows of different reflected beams can be effectively manipulated. Numerical results clearly show that the proposed metagrating can split the normally incident beam into two or three beams by suppressing or exciting the mirror reflected wave. Equal two-beam splitting and three-beam splitting with same amplitude or same power flow are achieved, numerical simulations agree well with the theoretical analysis. The reflected angle gradually decreases with the increase of working frequency. This design method can also be applied to design beam splitters with other splitting angles and working frequencies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AS proposed the idea and performed the metagrating design, numerical simulations, and manuscript writing. CS performed the theoretical calculation. YX and F-ZX contributed to perform the analysis with constructive discussions. All authors contributed to manuscript revision and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12104154, U1930202, 12025403), the Shanghai Pujiang Program (Grant No. 21PJ1402400), the Natural Science Foundation of Shanghai (Grant No. 22ZR1416900), and the Young Elite Scientists Sponsorship Program by CAST (Grant No. 2021QNRC001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Assouar, B., Liang, B., Wu, Y., Li, Y., Cheng, J.-C., and Jing, Y. (2018). Acoustic metasurfaces. Nat. Rev. Mater. 3, 460–472. doi:10.1038/s41578-018-0061-4