Density functional modeling of the binding energies between aluminosilicate oligomers and different metal cations

Interactions between negatively charged aluminosilicate species and positively charged metal cations are critical to many important engineering processes and applications, including sustainable cements and aluminosilicate glasses. In an effort to probe these interactions, here we have calculated the pair-wise interaction energies (i.e., binding energies) between aluminosilicate dimer/trimer and 17 different metal cations Mⁿ⁺ (Mⁿ⁺ = Li⁺, Na⁺, K⁺, Cu⁺, Cu²⁺, Co²⁺, Zn²⁺, Ni²⁺, Mg²⁺, Ca²⁺, Ti²⁺, Fe²⁺, Fe³⁺, Co³⁺, Cr³⁺, Ti⁴⁺ and Cr⁶⁺) using a density functional theory (DFT) approach. Analysis of the DFT-optimized structural representations for the clusters (dimer/trimer + Mⁿ⁺) shows that their structural attributes (e.g., interatomic distances) are generally consistent with literature observations on aluminosilicate glasses. The DFT-derived binding energies are seen to vary considerably depending on the type of cations (i.e., charge and ionic radii) and aluminosilicate species (i.e., dimer or trimer). A survey of the literature reveals that the difference in the calculated binding energies between different Mⁿ⁺ can be used to explain many literature observations associated with the impact of metal cations on materials properties (e.g., glass corrosion, mineral dissolution, and ionic transport). Analysis of all the DFT-derived binding energies reveals that the correlation between these energy values and the ionic potential and field strength of the metal cations are well captured by 2nd order polynomial functions (R² values of 0.99–1.00 are achieved for regressions). Given that the ionic potential and field strength of a given metal cation can be readily estimated using well-tabulated ionic radii available in the literature, these simple polynomial functions would enable rapid estimation of the binding energies of a much wider range of cations with the aluminosilicate dimer/trimer, providing guidance on the design and optimization of sustainable cements and aluminosilicate glasses and their associated applications. Finally, the limitations associated with using these simple model systems to model complex interactions are also discussed.

1 Introduction

The interactions between aluminosilicates and metal cations are important for many engineering processes and applications. One example is the formation of cementitious materials, including alkali-activated materials (AAMs) and blended cements, which bind aggregates together to form concrete. AAM is an important sustainable material technology that is able to convert a solid precursor source (e.g., industrial wastes and calcined clay rich in amorphous aluminosilicates) to a cementitious binder (Provis and van Deventer, 2014). The final AAM binder has many potential applications, including being used as a low-CO₂ cement alternative to Portland cement (PC) (Provis and Van Deventer, 2009; Pacheco-Torgal, 2014), whose production worldwide is currently responsible for ∼8% of global anthropogenic CO₂ emissions (Monteiro et al., 2017). For geopolymers, i.e., AAMs based on low-Ca precursors (e.g., metakaolin and class F fly ash), the main binder gel responsible for most of its engineering properties is an amorphous three-dimensional alkali-alumino-silicate-hydrate (N-A-S(-H), when Na is the alkali) gel mainly consisting of Q⁴(mAl) (m = 0, 1, 2, 3, 4) for the silica units (Provis and Van Deventer, 2009). Alkali cations, for example, Na⁺ and K⁺, charge-balance the negatively charged alumina tetrahedra (Al(O_1/2)₄)⁻¹, thereby stabilizing the aluminosilicate network. This charge-balancing interaction (interaction between negatively charged alumina tetrahedra and metal cations) helps to hinder ionic transport in calcium-alumino-silicate-hydrate (C-(A)-S-H, compared with calcium-silicate-hydrate (C-S-H)) gel (Hou and Li, 2018), stabilize zeolite framework structures (Gatti et al., 2012) and reduce alkali leaching from geopolymer binders (Provis and Van Deventer, 2009). Furthermore, this interaction in geopolymers has been used to immobilize heavy metals (Ji and Pei, 2020; Wang et al., 2021) and treat wastewater (El Alouani et al., 2021). On the other hand, excess alkali metal cations beyond those needed for charge-balancing act as modifiers to depolymerize the aluminosilicate network structure, as has been shown recently for sodium-substituted calcium-alumino-silicate-hydrate (C-(N)-A-S-H) (Garg et al., 2019).

The negatively charged aluminosilicate network can also be charge-balanced by alkaline earth metal cations (e.g., Ca²⁺ and Mg²⁺). In addition to charge-balancing, these alkaline earth metal cations, beyond those required for charge balancing, are also effective network modifiers, causing the aluminosilicate gel network to depolymerize. The resulting binder gels (e.g., C-A-S-H or magnesium-alumino-silicate-hydrate (M-A-S-H)) possess different atomic structures (mainly short aluminosilicate chain structure (Q²) for C-(A)-S-H (Yang et al., 2021) and plane structure (Q³) for M-A-S-H (Bernard et al., 2020)), pore structures (Provis et al., 2012; Blyth et al., 2017; Osio-Norgaard et al., 2018; Yang and White, 2020), mechanical properties (Kim et al., 2022), transport properties (Bernal and Provis, 2014; Blyth et al., 2017; Zhang et al., 2017; Osio-Norgaard et al., 2018) and chemical stability (Zhang et al., 2017; Osio-Norgaard et al., 2018)), compared with the three-dimensional N-A-S(-H) gel.

Another important example where the interactions between metal cations and aluminosilicates are critical is aluminosilicate glass containing alkali and/or alkaline earth metal cations. Aluminosilicate glasses are ubiquitous in many important industrial applications, including nuclear waste encapsulation, high-performance glasses, ceramics, metallurgical processes, and sustainable cement (Jakse et al., 2012; Piovesan et al., 2018; Gong and White, 2021; Gong and Olivetti, 2022). The metal cations in these aluminosilicate glasses play two distinct roles: (i) to charge-balance the negatively charged alumina tetrahedra (i.e., (Al(O_1/2)₄)⁻¹), and (ii) to depolymerize the aluminosilicate network creating non-bridging oxygen (NBO) atoms (i.e., oxygen atoms bonded to only one silica or alumina tetrahedra). Many studies have shown that the type of alkali and alkaline earth metal cations has a dramatic impact on the resulting glasses, affecting both the atomic structure (Taniguchi et al., 1995; Ispas et al., 2010; Baral et al., 2017; Gong et al., 2021; Gong and Olivetti, 2022) and engineering properties (e.g., physical (Inaba et al., 1999; Lv et al., 2022), mechanical (Januchta et al., 2017; Lv et al., 2022), thermal (Atila et al., 2020; Lv et al., 2022) and chemical properties (Karlsson et al., 2017; Mascaraque et al., 2019; Oey et al., 2019)). Furthermore, the type of metal cations also has a significant impact on the dissolution of silicate minerals and glasses (Brantley et al., 2008; Gong and Olivetti, 2022), which is critical to soil fertility, transport and sequestration of contaminants, and global geochemical cycle (including the CO₂ cycle) (Brady and Gíslason, 1997; Kump et al., 2000; Brantley et al., 2008).

However, fundamental studies on the atomic scale interactions between different metal cations and aluminosilicate networks are limited since these detailed interactions are often difficult to elucidate using experiments. For this purpose, atomistic simulations are ideal for simulating their interactions. Recently, we have performed density functional theory (DFT) calculations to determine the pair-wise interaction energies (Gibbs free energies) between different monomeric species (silicate, aluminate, sodium, and calcium ions), gaining insight into the early stage formation mechanisms of different binder gels (i.e., C-S-H, C-A-S-H, and C-(N)-A-S-H gels), where the gels are responsible for most of the engineering properties of modern concrete (Yang and White, 2021). Previously, a similar computational framework has been adopted to calculate the interaction energies between silicate and aluminate species (White et al., 2011), which, when combined with a coarse-grained Monte Carlo (CGMC) model, enables quantitative modeling of the early stages of formation of N-A-S(-H) gel in geopolymers (White et al., 2012; Yang and White, 2016). Similar DFT approaches have been adopted to calculate interaction energies among silicate species (Mora-Fonz et al., 2005), silicate and alkali species (Mora-Fonz et al., 2007; Asaduzzaman et al., 2015), and phosphate species (Tang et al., 2010). They have also been used to calculate interaction energies between different metal cations (e.g., Li⁺, Na⁺, K⁺, Ca²⁺, and Mg²⁺) and zeolitic frameworks (Gatti et al., 2012) and organic matter (e.g., guanine and 6-thioguanine tetrads (Deepa et al., 2011), glutathione (Liu et al., 2013), tetraoxa[8]circulene sheet (Karaush et al., 2015), and cubane, cyclohexane and adamantane (Gopalsamy and Subramanian, 2014)).

A survey of the literature reveals that few computational studies have investigated the interactions between aluminosilicates and different metal cations, in spite of their prevalence in many important applications, as briefly mentioned above. In this study, we have probed the pair-wise interactions between aluminosilicate dimer/trimer and over seventeen metal cations/clusters (e.g., Li⁺, Na⁺, K⁺, Cu⁺, Cu²⁺, Co²⁺, Zn²⁺, Ni²⁺, Mg²⁺, Ca²⁺, Ti²⁺, Fe²⁺, Fe³⁺, Co³⁺, Cr³⁺, Ti⁴⁺ and Cr⁶⁺) that are relevant to the aforementioned applications using DFT calculations. Detailed analysis of the DFT-optimized structures has been carried out to determine their interatomic distances, which were compared with literature data on silicate glasses, minerals, or clusters, to ensure that the cluster structures obtained are reasonable. Their pair-wise interaction energies (or binding energies) were determined and compared in the context of existing literature, where the observed trends in the interaction energies of different cations have been correlated with different literature observations (including the impact of different metal cations on glass corrosion, mineral dissolution, and ionic transport). Furthermore, the correlations between interaction energies and the attributes of different metal cations (e.g., charge, ionic radii, ionic potential, and field strength) have been explored to identify simple empirical equations to enable rapid estimation of interaction energies for unexplored cations. Finally, we have discussed the potential limitations of this study including the use of simple model system. Although we are limited to pair-wise interaction as opposed to simulating large cluster reactions that are more realistic, this investigation illustrates the value of using simple model systems to better understand the impact of metal cations on the properties of aluminosilicate materials, which is critical to many important applications.

2 Methodology

Density functional theory calculations were performed to estimate the pair-wise interaction energies between aluminosilicate dimers and trimers and different charge balancing cations (see Table 1 for all the studied pairs), following procedures similar to our previous studies (White et al., 2011; Yang and White, 2021). Specifically, for each individual species (e.g., “dimer”, “trimer”, and “dimer/trimer + cation”), we first performed simulated annealing on gas-phase clusters using ab initio molecular dynamics (MD) simulations at different temperatures in order to generate proper starting structures for subsequent geometry optimization. We then determined the highest annealing temperature to use for a given cluster based on two considerations: the temperature is (i) not too high to cause the cluster to dissociate into smaller clusters and individual atoms and (ii) high enough to allow different geometrical configurations to be explored. We ran each simulation for 3 ps with a time step of 1 fs, which is comparable to previous studies ((Yang and White, 2021), (Mora-Fonz et al., 2005), (Tang et al., 2010)) and is deemed sufficient for exploring the energy landscape of each cluster based on simulated annealing. From the 3000 structural configurations of each cluster, we selected a number of configurations that correspond to different minima on the potential energy landscape of the MD run. In some cases, the cation position of the exported cluster (i.e., “dimer/trimer + cation”) was manually adjusted to generate new unexplored configurations. Overall, we used this process to generate 5–11 different configurations for each species (except for single cations), ensuring a wide potential energy surface was explored. All the MD simulations were conducted using the NVT ensemble, with the temperature being controlled by a Nose-Hoover thermostat (Nosé, 1984; Hoover, 1985). The DNP basis set and PWC functional were used for the MD simulations to save computational cost (Mora-Fonz et al., 2005; Yang and White, 2021).

TABLE 1

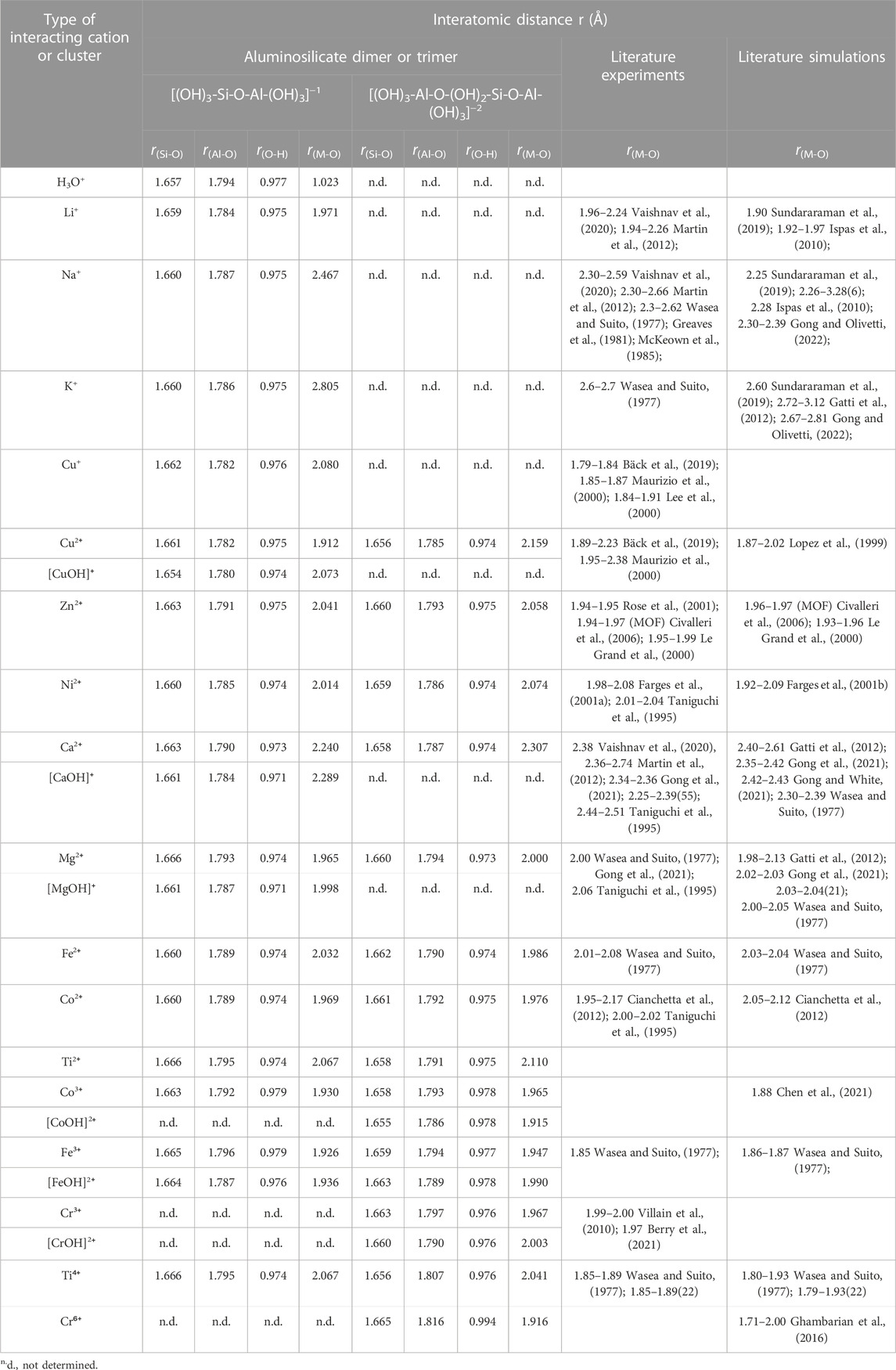
TABLE 1. Average interatomic distances (i.e., Si-O, Al-O, O-H and metal-oxygen (M-O) bond distances) for the DFT-optimized cluster structures (see Figure 2, Figure 3; Supplementary Figures S1, S2 of Supporting Information). Also given in the table are literature data (both experiments and simulations) for Si-O, Al-O, O-H and metal-oxygen (M-O) bond distances in silicate glasses, minerals and clusters.

The generated 5–11 configurations for each species were then geometry-optimized using an orbital cutoff of 8.0 Å for all atoms, the DNP basis set, and the BLYP functional without pseudopotential, similar to our previous study (Yang and White, 2021). The BLYP exchange-correlation functional was adopted here because this functional has been widely used and proven to be effective for silicate-based systems (Mora-Fonz et al., 2007; White et al., 2011; Pegado et al., 2014; Yang and White, 2021). The convergence thresholds for energy, force, and displacement were set at 1 × 10⁻⁶ Hartrees, 2 × 10⁻⁴ Hartrees/Å, and 5 × 10⁻⁴ Å, respectively. For some configurations, a thermal smearing of 0.02 Hartrees has been used to assist convergence. For each geometry-optimized structural configuration, we have performed vibrational frequency analysis to obtain its Gibbs free energy at 298.15 K and, at the same time, ensure that the configuration is located at a local energy minimum. Due to the inclusion of transition metal ions with open-shell electron configuration, we used spin-polarized DFT (spin unrestricted in DMol³). All the simulations (both the ab initio MD and DFT geometry optimization) were performed using the DMol³ v7.0 package, which was part of the Accelrys Materials Studio software.

Once the total energy (i.e., the summation of the ground state energy and Gibbs free energy at 298.15 K) of all configurations for a given species (e.g., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) was determined, we selected the lowest energy value (i.e., the most energetically favorable configuration) and used it to estimate the pair-wise interaction energies (or binding energies) E_b between this negatively charged aluminosilicate species and positively charged cations, as illustrated in Eq. 1.

${\mathit{E}}_{\mathit{b}}={\mathit{E}}_{\mathit{t}}\left({\left[AS+R\right]}^{n-m}\right)–\left({\mathit{E}}_{\mathit{t}}\left(R^{n+}\right)+{\mathit{E}}_{\mathit{t}}\left({\left[AS\right]}^{-m}\right)\right)(1)$

where [AS]^−m and Rⁿ⁺ refer to the aluminosilicate species with a negative charge of m and the cation with a positive charge of n, respectively; E_t(Rⁿ⁺) is the calculated total energy of the cation Rⁿ⁺; E_t([AS]^−m) is the calculated total energy of the aluminosilicate species [AS]^−m; and E_t([AS + R] ^n−m) is the total energy of the reaction product, i.e., the combined cluster of the aluminosilicate species and cation [AS + R] ^n−m. A negative binding energy E_b means that the interaction between the aluminosilicate species and the cation is thermodynamically favorable, with a more negative value indicating a stronger interaction.

As mentioned above, some clusters (e.g., [AS]^−m species with the Fe³⁺, Ni²⁺, and Co³⁺ cations) required thermal smearing of 0.02 to assist convergence. Hence, we have evaluated the impact of thermal smearing on the binding energy calculation (based on Eq. 1) for several clusters (e.g., an aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) balanced with a Li⁺, Na⁺, or Ca²⁺ cation) that do not have convergence problems. The results are shown in Figure 1, where it is clear that the obtained binding energy values for all three clusters remain almost the same (variations smaller than 1%) at a smearing value less than 0.02. This result suggests that the use of thermal smearing at 0.02 to assist convergence with certain clusters should not significantly change the binding energy calculations and alter the findings and conclusions of this study.

FIGURE 1

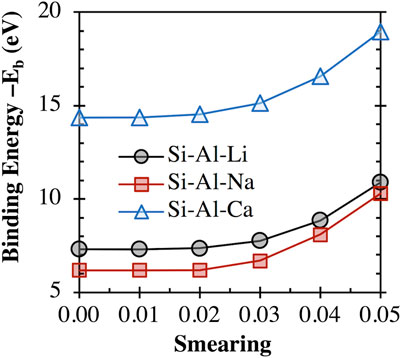
FIGURE 1. Impact of thermal smearing value on the binding energy between an aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) and a Li⁺, Na⁺, or Ca²⁺ cation, calculated using Eq. 1.

3 Results and discussion

3.1 Optimized structures

Figures 2A–D shows the DFT-optimized cluster structures (i.e., an aluminosilicate dimer [(OH)₃-Si-O-Al-(OH)₃]⁻¹ with a metal cation Mⁿ⁺) obtained following the procedures outlined in the Methodology section for a typical monovalent (Na⁺), bivalent (Mg²⁺), trivalent (Fe³⁺) and tetravalent (Ti⁴⁺) cation, respectively. The metal cations are seen to form metal-oxygen (M-O) bonds with oxygen atoms in both the silica and alumina tetrahedra. The distance values in Figure 2 show that the M-O bonds formed with oxygen atoms in alumina tetrahedra are shorter than those in silica tetrahedra. Taking Na⁺ for example (Figure 2A), the average Na-O(Al) distance (∼2.40 Å) is about 0.13 Å shorter than the average Na-O(Si) distance (∼2.53 Å), which is consistent with the trend seen in previous DFT calculations on Na-exchanged zeolitic frameworks (Vayssilov et al., 1999). This observation is also generally true for other cations in Supplementary Figure S1 of the Supporting Information (optimized structures for other investigated (OH)₃-Si-O-Al-(OH)₃ • Mⁿ⁺ species), which can be attributed to the overall negative charge of the alumina tetrahedra (i.e., [Al(O_1/2)₄]⁻¹), leading to higher attractive forces with the positively charged cations and hence shorter M-O(Al) bond distances (compared with M-O(Si) bonds). These attractive forces pull the oxygen atoms away from the connected Si and Al atoms, leading to longer Si-O(M) (∼1.68–1.78 Å) and Al-O(M) (∼1.80–1.87 Å) distances compared with other Si-O (∼1.61–1.65 Å) and Al-O (∼1.69–1.79 Å) bonds away from the metal cations, as clearly seen in Figure 2 and Supplementary Figure S1 of Supporting Information.

FIGURE 2

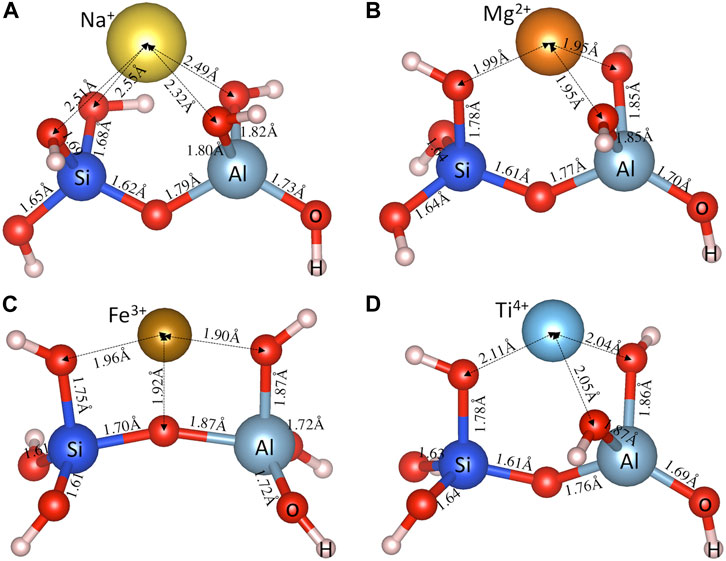
FIGURE 2. DFT-optimized aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) charge balanced by a typical (A) monovalent (Na⁺), (B) bivalent (Mg²⁺), (C) trivalent (Fe³⁺), and (D) tetravalent (Ti⁴⁺) cation. Also shown are the interatomic bond distances (in Å).

Figures 3A–D shows the optimized structures for the aluminosilicate trimer (i.e., [(OH)₃-Al-O-Si-O(-(OH)₂)-Al-(OH)₃]⁻²) charge-balanced by several typical cations (i.e., Ca²⁺, Cr³⁺, [CrOH]²⁺ and Ti⁴⁺), with those for the other investigated cations given in Supplementary Figure S2 of Supporting Information. Figure 3 and Supplementary Figure S2 show that the metal cations also form M-O bonds with oxygen atoms in both the silica and alumina tetrahedra; however, there appears to be a preferential formation of M-O bonds with bridging oxygen (BO, defined as the oxygen connected to two silica and alumina tetrahedra), rather than NBO in the silica tetrahedra. Furthermore, the M-O bonds formed with BO (e.g., ∼2.36 Å for Ca-BO in Figure 3A) are seen to be generally longer than those formed with NBO (e.g., ∼2.26 Å for Ca-NBO in Figure 3A), which is consistent with observations in silicate glasses (Ispas et al., 2010). Another observation from Figure 3 and Supplementary Figure S2 for the aluminosilicate trimer that is consistent with the aluminosilicate dimer (Figure 2; Supplementary Figure S1) is the longer Si-O(M) (∼1.65–1.74 Å) and Al-O(M) (∼1.81–1.88 Å) bonds compared with the other Si-O (∼1.62–1.65 Å) and Al-O (∼1.67–1.76 Å) bonds due to the strong interaction between the oxygen atoms and the metal cations (which pull the oxygen atoms away from the Si and Al atoms).

FIGURE 3

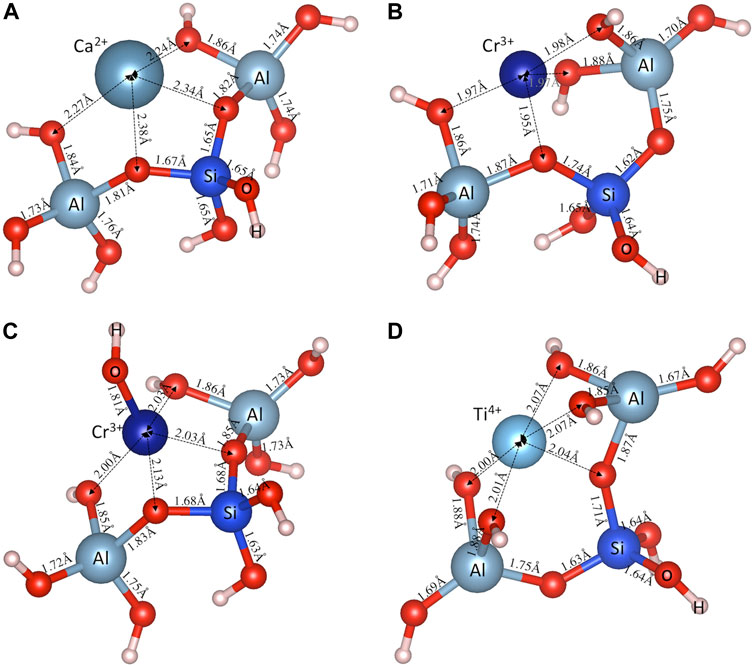
FIGURE 3. DFT-optimized aluminosilicate trimer (i.e., [(OH)₃-Al-O-Si-O(-(OH)₂)-Al-(OH)₃]⁻²), charge-balanced by a typical (A) divalent cation (Ca²⁺), (B) trivalent cation (Cr³⁺), (C) bivalent cluster ([Cr(OH)]²⁺), and (D) tetravalent (Ti⁴⁺) cation. Also shown are the interatomic bond distances (in Å).

The average interatomic distances for all investigated aluminosilicate clusters are summarized in Table 1 and compared with those reported in the literature for aluminosilicate glasses and/or clusters. The results show that the average Si-O and Al-O distances are around 1.65–1.67 Å and 1.78–1.79 Å, respectively, which are slightly longer than those reported in aluminosilicate glasses (Si-O: ∼1.60–1.64 Å (Wasea and Suito, 1977; Ispas et al., 2010; Gong et al., 2021; Gong and White, 2021) and Al-O: ∼1.72–1.77 Å (Wasea and Suito, 1977; Gong and White, 2021)). Nevertheless, they are comparable to Si-O and Al-O distances in aluminosilicate clusters reported in previous DFT calculations (Si-O: ∼1.64–1.67 Å and Al-O: ∼1.76–1.79 Å) (Xu et al., 2004; Yang et al., 2011). The O-H bond distance varies only slightly at around 0.97–0.99 Å, regardless of the type of chemical complex and cation, where the O-H distance values are comparable to previous DFT calculations on silicate dimers and trimers (∼0.95–0.97 Å) (Xiao and Lasaga, 1994). A comparison of the average M-O bond distances in Table 1 shows that the values obtained here in the small aluminosilicate clusters are generally consistent with values reported in the literature on silicate-based glasses and/or clusters. For example, the average Li/Na/K-O distances in our clusters are 1.97, 2.47, and 2.81 Å, respectively, which are within the range reported for silicate glasses in the literature (1.94–2.26, 2.25–2.66, and 2.60–3.12 Å, respectively). The largest deviation is seen for Ti⁴⁺-O and Cu⁺-O, where our DFT-optimized clusters give average Ti⁴⁺-O and Cu⁺-O distances of ∼2.04–2.07 and ∼2.08 Å, slightly larger than those reported in silicate glasses (1.85–1.93 and 1.79–1.91 Å, respectively). Minor deviations (∼0.05 Å) between DFT-derived bond distances and literature data can be observed for Zn²⁺-O, and Fe³⁺-O bond distances (Table 1). These differences may be partially caused by the differences in the coordination states and local atomic arrangements of the cations in the clusters studied here and those in silicate glasses.

3.2 Binding energies

Based on the total energies of the optimized structures for the individual components (e.g., dimer, trimer, Mⁿ⁺, “dimer + Mⁿ⁺”, and “trimer + Mⁿ⁺”, as seen in Supplementary Table S1 of Supporting Information), we have calculated the binding energies between the aluminosilicate dimer/trimer and the different metal cations/clusters using Eq. 1. In this section, we present these energy values and discuss the observations in relation to diverse literature studies on the impact of metal cations on materials properties (e.g., glass corrosion, mineral dissolution, and ionic transport). While the observations illustrate the value of probing pair-wise interaction for simple model systems, we need to keep in mind that the actual interactions in real material systems are much more complex.

3.2.1 Monovalent cations

Figure 4A compares the calculated binding energies between the aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) and monovalent cations/clusters, where we see negative binding energies for all cases, suggesting that their interactions are all energetically favorable. This favorability is expected because of the attractive Coulomb interaction between a negatively and a positively charged species. Figure 4B shows that there is a general increase in binding energy (i.e., becomes more negative) as the effective ionic radius of the corresponding monovalent cation decreases. Similar trends have been observed for the interactions of monovalent cations with different chemical species, including (i) guanine and 6-thioguanine tetrads (Deepa et al., 2011), (ii) glutathione (Liu et al., 2013), (iii) tetraoxa[8]circulene sheet (Karaush et al., 2015), (iv) cubane, cyclohexane and adamantane (Gopalsamy and Subramanian, 2014), and (v) methanol (Vayssilov et al., 2000), where the binding energy (also obtained from DFT calculations in referred studies) increases (i.e., becomes more negative) in the order of K⁺ < Na⁺ < Li⁺. Although these chemical species are very different from the aluminosilicate dimer/trimer, their interaction energies with monovalent cations are highly correlated with each other, as illustrated in Supplementary Figure S3 of Supporting Information. Supplementary Figure S3 shows that R² values of 0.94–1.00 are achieved for linear regressions between binding energies obtained here and those reported in the literature for other chemical species (Vayssilov et al., 2000; Deepa et al., 2011; Liu et al., 2013; Gopalsamy and Subramanian, 2014; Karaush et al., 2015). The trend observed here (increasing interaction energy in the order of K⁺ < Na⁺ < Li⁺) can be attributed to the increase of bond strength (evidenced by bond order) in the order of K-O < Na-O < Li-O, as shown for alkali silicate-based glasses using ab initio calculations (Baral et al., 2017).

FIGURE 4

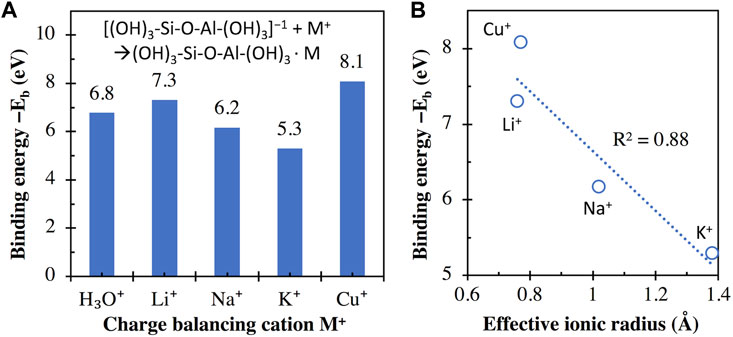
FIGURE 4. (A) Binding energies (in eV) between the aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) and different monovalent cations, calculated using Eq. 1, with the total energies of individual components in Eq. 1 given in Supplementary Table S1 of Supporting Information. (B) Comparison of binding energies in (A) and the effective ionic radius (for VI-coordinated M⁺) of the monovalent metal cations. The R² value for linear regression is also given in (B).

However, we do see considerable differences in binding energy between Li⁺ and Cu⁺, although their effective ionic radius is similar. This discrepancy means that the calculated binding energy of alkali with the aluminosilicate dimer cannot be solely explained by ionic radius. This discrepancy may be related to the difference in the absolute hardness of the two cations (35.1 and 6.3 eV for Li⁺ and Cu⁺, respectively) (Parr and Pearson, 1983), which is a measure of the resistance of the metal cation to lose electrons.

The higher binding energy of Cu⁺ with the aluminosilicate dimer compared with the other three alkalis M⁺ (i.e., Na⁺, K⁺, and Li⁺) could be used to explain the observed trend of Cu⁺⇌M⁺ exchange in alkali aluminosilicate glasses (i.e., 20M₂O-10Al₂O₃-70SiO₂) in an early study (Yoko et al., 1991), where the extent of Cu⁺⇌R⁺ exchange is seen to increase in the order of Li⁺ < Na⁺ < K⁺. The occurrence of this Cu⁺⇌R⁺ exchange can be partially attributed to the higher binding energy of Cu⁺ (or bond strength) with the negatively charged aluminosilicate network than the other three alkalis, which promotes the exchange. The trend in the extent of Cu⁺⇌R⁺ exchange (Li⁺ < Na⁺ < K⁺) can be attributed to the increasing difference in binding energy between Cu⁺ and R⁺ in the order of Li⁺ < Na⁺ < K⁺, which gives an exchange driving force in the order of Li⁺ < Na⁺ < K⁺.

Another observation from Figure 4A is that the binding energy of H₃O⁺ with the aluminosilicate dimer is seen to be higher than K⁺ and Na⁺, yet lower than Li⁺, which can be used to explain the observations in a recent experimental study on alkali aluminosilicate glasses (30M₂O-10Al₂O₃-60SiO₂) (Guo et al., 2014). Corrosion experiments in this study (Guo et al., 2014) showed no obvious H⁺ ⇌ Li⁺ exchange for the lithium aluminosilicate glass, suggesting that this glass is resistant to moisture attack, likely due to the higher binding energy of Li⁺ with the aluminosilicate network than H₃O⁺. In contrast, obvious H⁺ ⇌ Na⁺ and H⁺ ⇌ K⁺ exchange was observed in the sodium- and potassium-containing glasses to a hydrogen penetration depth of 0.4 and 3 μm, respectively, within the same experimental timeframe. This observation is likely due to the lower binding energies of Na⁺ and K⁺ (especially the latter, where the binding energy is the lowest among all monovalent cations considered here) with the aluminosilicate network compared to H₃O⁺, as illustrated in Figure 4A.

3.2.2 Divalent cations

The binding energies of different divalent cations with the aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) and trimer (i.e., [(OH)₃-Al-O-(OH)₂-Si-O-Al-(OH)₃]⁻²) are compared in Figure 5A, which shows that the interaction energy with the trimer is consistently higher than those with the dimer by ∼7.6–8.2 eV. This is expected given that the trimer has a higher negative charge (−2) than the dimer (−1) and hence exhibits stronger attractive Coulomb interactions with the positively charged divalent cations. A comparison of the energy values in Figures 4A and 5A shows that the divalent cations exhibit higher binding energies (∼14.5–22.5 eV) with the dimer than the monovalent cations (∼5.3–8.1 eV). This observation is consistent with previous DFT calculations on other chemical complexes (Deepa et al., 2011; Gatti et al., 2012; Liu et al., 2013; Gopalsamy and Subramanian, 2014; Karaush et al., 2015), where divalent cations (e.g., Ca²⁺ and Mg²⁺) are seen to exhibit higher binding energies than monovalent cations (e.g., K⁺, Na⁺, and Li⁺). Again, the energy values from this study are highly correlated with those reported in refs. (Deepa et al., 2011; Gatti et al., 2012; Liu et al., 2013; Gopalsamy and Subramanian, 2014; Karaush et al., 2015), regardless of the type of chemical complex that the metal cations interact with, as seen by the high R² values (0.94–1.00) achieved with linear regressions in Supplementary Figure S3 of Supporting Information. These high degrees of correlation among binding energies obtained with different chemical complexes suggest that the differences in cationic binding energies for any given complex are mainly controlled by the inherent properties of the cations (e.g., field strength and ionic potential, as will be shown in the subsequent sections).

FIGURE 5

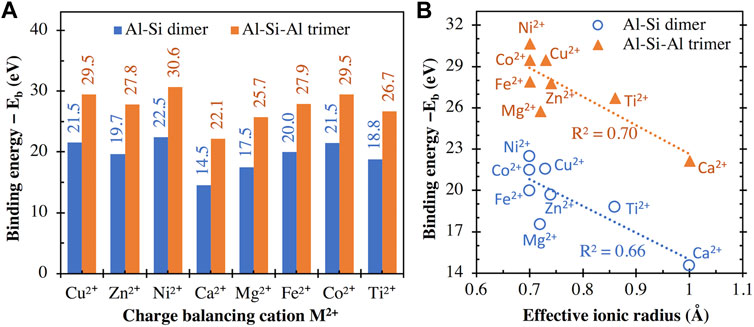
FIGURE 5. (A) Binding energies between (I) the aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) and trimer (i.e., [(OH)₃-Al-O-(OH)₂-Si-O-Al-(OH)₃]⁻²) and (ii) different divalent cations, calculated using Eq. 1, with the total energies of individual components in Eq. 1 given in Supplementary Table S1. (B) Comparison of binding energies in (A) and the effective ionic radius (for VI-coordinated M²⁺) of the divalent metal cations. R² values for linear regression are also given in (B).

Similar to Figure 4B, we have examined the correlation between the binding energy values (Figure 5A) and effective ionic radii of the divalent cations in Figure 5B, where we see approximate inverse correlations. Nevertheless, the R² values achieved with linear regressions (0.66–0.70, Figure 5B) are lower than those in Figure 4B for the monovalent cations (0.88). It is seen in Figure 5B that the calculated binding energy can be noticeably different even when the effective ionic radius is the same (e.g., Ni²⁺, Co²⁺, and Fe²⁺), similar to the case of Li⁺ and Cu⁺ in Figure 4B. Again, this discrepancy may be related to the difference in the absolute hardness of these divalent cations (e.g., 8.5 and 7.3 eV for Ni²⁺, and Fe²⁺, respectively) (Parr and Pearson, 1983), or the acid softness index defined by Xu et al. (e.g., −10.9, −13 and −21.87 kcal/mol for Ni²⁺, Co²⁺, and Fe²⁺, respectively) (Xu et al., 2017).

The binding energy results in Figure 5 can also be used to explain observations in many literature investigations. For example, MD simulations on ionic transport in C-A-S-H gel show that the diffusion coefficient of Ca²⁺ is over twenty times smaller than Na⁺ (Duque-Redondo et al., 2021). The slower diffusion of Ca²⁺, in this case, is likely due to its higher binding strength with the aluminosilicate network (as shown in Figures 4 and 5), which hinders the diffusion of Ca²⁺ in C-A-S-H gel channel (compared with Na⁺). Furthermore, recent investigations on the chemical durability of alkali/alkaline earth aluminoborate glasses show that the initial glass dissolution rate increases in the order of Mg²⁺ < Ca²⁺ < Li⁺ (Oey et al., 2019) and Mg²⁺ < Li⁺ < Na⁺ (Mascaraque et al., 2019). These observations can be attributed to the opposite trend in the ability of these cations to stabilize the negatively charged network and to hinder network dissolution/destruction in the order of Mg²⁺ > Ca²⁺ > Li⁺ > Na⁺ (as suggested by the binding energies in Figures 4 and 5). More recently, the addition of Mg²⁺ (Gevaudan et al., 2021) and Cu²⁺, and Co²⁺ (Gevaudan et al., 2019) in AAMs has been shown to reduce AAM leaching (especially leaching of Al species) in sulfuric acid. This observed reduction in dealumination in cation-doped AAMs in refs. (Gevaudan et al., 2019; Gevaudan et al., 2021) may be partially attributed to the higher binding strength of the doped Mg²⁺, Cu²⁺ and Co²⁺ cations that help better stabilize Al compared with Na⁺ and Ca²⁺ in reference samples (see the binding energy differences in Figures 4 and 5). This stronger Al stabilization effect of Mg²⁺, Cu²⁺ and Co²⁺ (than Na⁺ and Ca²⁺) may have two underlying mechanisms: (i) on the one hand, due to their higher binding strength, the doped divalent cations enhance the stability of the negatively charged aluminosilicate network in AAMs (i.e., the main binding gel in the investigated AAMs) upon acid attack, rending it more resistant to destruction; (ii) on the other hand, the doped cations may better stabilize a passivation layer (rich in Si and Al according to SEM-EDX analysis (Gevaudan et al., 2019)) at the reaction front that slows down diffusion of chemical species.

Figure 6 (and Supplementary Figure S4 of Supporting Information) compares (i) the binding energy of the aluminosilicate dimer (and trimer) with six divalent cations (M²⁺ = Ca²⁺, Mg²⁺, Zn²⁺, Fe²⁺, Co²⁺, and Ni²⁺) and (ii) the measured log dissolution rate of the corresponding M₂SiO₄ and MCO₃ minerals at different pHs and the log water exchange rate from the hydration sphere of the corresponding dissolved cation to the surrounding solvent (data extracted from refs. (Casey and Westrich, 1992; Pokrovsky and Schott, 2002)). Although the R² values achieved using linear regressions are not high (∼0.43–0.56), they appear to be inversely correlated, with higher binding energy associated with generally lower dissolution and water exchange rates (Figure 6; Supplementary Figure S4). These inverse correlations may be due to the same underlying mechanism: a higher M-O bond strength leads to a higher binding energy in the case of the current study and a higher resistance to M-O bond-breaking for M₂SiO₄ and MCO₃ mineral dissolution and water exchange. Nevertheless, we note that the mineral dissolution process is highly complex, and measured dissolution rates may be influenced by other factors (Brantley et al., 2008) in addition to M-O bond strength.

FIGURE 6

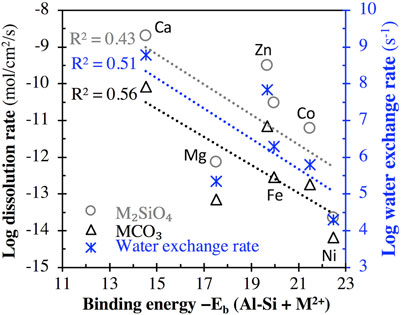
FIGURE 6. Comparison of the binding energy between the aluminosilicate dimer and divalent cation M²⁺ (M²⁺ = Ca²⁺, Mg²⁺, Zn²⁺, Fe²⁺, Co²⁺, and Ni²⁺) with (i) the log dissolution rate (in mol/cm²/s) of M₂SiO₄ minerals at pH = 2°C and 25 °C and MCO₃ minerals at 5< pH < 8°C and 25°C (left axis), and (ii) the log rate constant for water exchange from the hydration sphere of the dissolved cation to the surrounding solvent (right axis). Rate data of M₂SiO₄ minerals are from ref. (Casey and Westrich, 1992), while the rate data of MCO₃ minerals and water exchange are from ref. (Pokrovsky and Schott, 2002). R² values for linear regression are also given.

3.2.3 High valent cations

The calculated binding energy values for the high valent cations (i.e., Co³⁺, Cr³⁺, Fe³⁺, Ti⁴⁺ and Cr⁶⁺) are presented in Figure 7, which shows higher interaction energies with the trimer than with the dimer, consistent with the divalent cations in Figure 5A. Furthermore, these binding energy values are considerably higher (i.e., more negative) than those for the monovalent and divalent cations given in Figures 4A and 5A, respectively. For example, the binding energies of Fe³⁺ (39.6 and 53.0 eV with the dimer and trimer, respectively) are considerably higher than those of Fe²⁺ (20.0 and 27.9 eV, Figure 5A). This may explain the higher strength of Fe³⁺-O bonds compared to Fe²⁺-O bonds (Gong and Olivetti, 2022) and the lower dissolution rate of Fe-containing minerals under oxidative conditions compared with reductive conditions, as has been reported in the literature (Brantley et al., 2008).

FIGURE 7

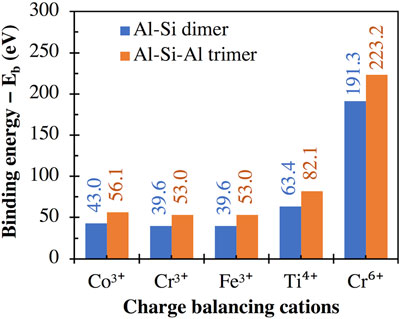
FIGURE 7. Binding energies between (i) the aluminosilicate dimer (i.e., [(OH)₃-Si-O-Al-(OH)₃]⁻¹) and trimer (i.e., [(OH)₃-Al-O-(OH)₂-Si-O-Al-(OH)₃]⁻²) and (ii) different high valent cations, calculated using Eq. 1, with the total energies of individual components in Eq. 1 given in Supplementary Table S1.

In fact, as seen in Figure 8A, there appears to be a general trend of increasing binding energy with both the aluminosilicate dimer and trimer as the charge of the cation/cluster increases (all the cations and cationic clusters containing OH⁻¹ have been included in the figure). These binding energy values are plotted in Figure 8B against the effective ionic radius of the corresponding cations, which shows that they are generally inversely correlated, as already seen in Figures 4B and 5B for monovalent and divalent cations, respectively. Due to these opposite correlations seen in Figures 8A, B, we have plotted in Figure 9A the binding energy values as a function of cation charge/ionic radii, which is defined as the ionic potential (IP) of the cation introduced by Cartledge (Cartledge, 1928) to describe to what extent the cations are electrostatically attracted by oppositely charged ions. Here, we used the effective ionic radii tabulated by Shannon (Shannon, 1976) to calculate the ionic potential of each studied cation (see the values in Table 2). It is clear from Figure 9A that the cationic binding energies with the aluminosilicate dimer/trimer are positively correlated with the IP of the cations, and their correlations can be accurately captured using 2nd order polynomial functions, as evidenced by the high R² values achieved for regressions (0.99–1.00). Previous studies have also attempted to connect the IP of cations to their binding energies with organic species (e.g., glutathione (Liu et al., 2013) and calix[2]furano[2]pyrrole (Teixeira dos Santos and Magalhães, 2010)), as well as to other material properties (e.g., formation enthalpies (Wu et al., 2013; Sun et al., 2016) and cation discharge potential (Cartledge, 1928)).

FIGURE 8

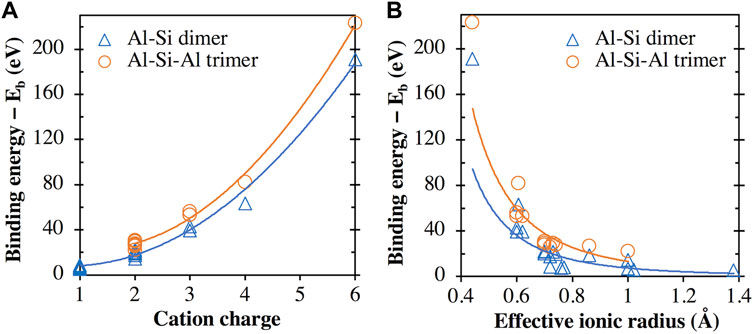
FIGURE 8. Comparison of binding energies of all the metal cations (including all the metal cation + OH clusters, e.g., [Ca(OH)]⁺) with the aluminosilicate dimer/trimer and (A) the cation/cluster charge (B) the cation effective ionic radius. In the case of cation + OH clusters (e.g., [Ca(OH)]⁺), the effective ionic radius of the corresponding cation (i.e., Ca²⁺) is used. The lines are given to guide the eye.

FIGURE 9

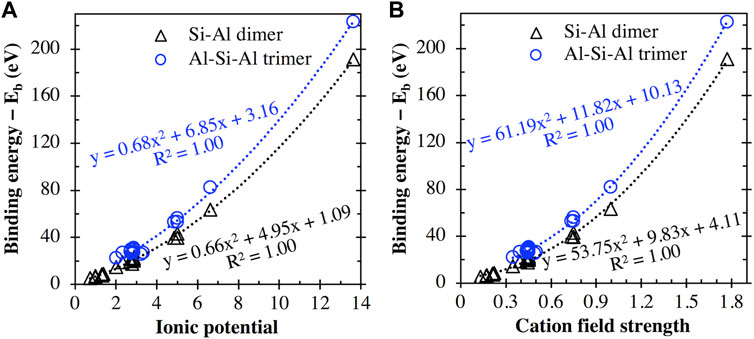
FIGURE 9. Comparison of the cation binding energies (including cation + OH clusters) with the aluminosilicate dimer and trimer with (A) the ionic potential (i.e., charge/effective ionic radius) and (B) the field strength (see Eq. 2) of the metal cations. Data have been fitted using 2nd order polynomial functions, where the equations of best fit and corresponding R² values are provided.

TABLE 2

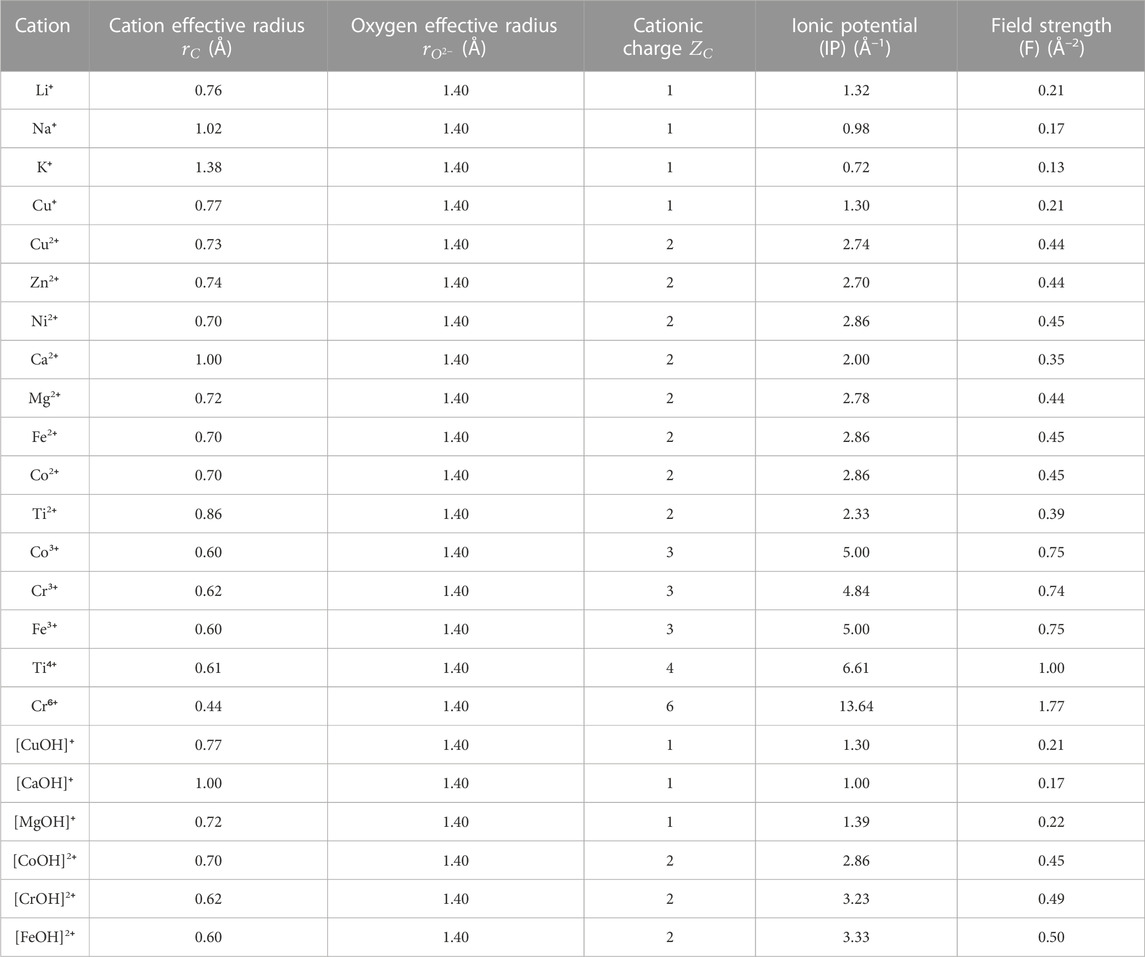
TABLE 2. Summary of effective ionic radii (${\mathit{r}}_{\mathit{C}}$) of the studied cations [obtained from Shannon (Shannon, 1976)], along with calculated ionic potential (${\mathit{Z}}_{\mathit{C}}/{\mathit{r}}_{\mathit{C}}$) and field strength (${\mathit{Z}}_{\mathit{C}}/{\left({\mathit{r}}_{\mathit{C}}+{\mathit{r}}_{{\mathit{O}}^{\mathbf{2}-}}\right)}^{\mathbf{2}}$).

In the glass community, one important term introduced by Dietzel (Dietzel, 1942) to characterize the effect of a single cation on oxide glasses is the cationic field strength ($F$) parameter, which is given by Eq. 2 (Vogel, 2012):

$F=\frac{Z_C}{{\left(r_C+r_{O^{2-}}\right)}^2}(2)$

where $Z_C$ is the charge of the cation; $r_C$ and $r_{O^{2-}}$ are the ionic radii of the cation and oxygen anion, respectively. This field strength parameter has been widely used to classify ions as network modifiers ($F$ $\approx$ 0.1–0.4), network formers ($F$ $\approx$ 1.3–2.1), and intermediates ($F$ $\approx$ 0.5–1) (Vogel, 2012). Again, here we have used the effective ionic radii from Shannon (Shannon, 1976) to calculate the field strength of each cation (see the values in Table 2), where the results are presented in Figure 9B as a function of the calculated binding energies with the aluminosilicate dimer and trimer. The binding energy values are seen to be positively correlated with the cationic field strength, and the correlations can be well captured by 2nd order polynomial functions (R² values of 0.99–1.00), similar to the case of the ionic potential (Figure 9A). In fact, as shown in Supplementary Figure S5, the ionic potential and field strength of the cations are positively and linearly correlated with an R² value of 0.99 for a linear regression. In the glass literature, many studies have attempted to use cationic field strength to draw connections with the properties of silicate-based glasses, including effective ionic diffusion (Karlsson et al., 2017), glass transition temperature (Januchta et al., 2017; Atila et al., 2020; Lv et al., 2022), and network connectivity (e.g., Al and B coordination) (Januchta et al., 2017; Atila et al., 2020; Lv et al., 2022).

With these simple polynomial functions in Figure 9 (also given in Eqs. 3, 4) obtained using regression, we can now provide approximate estimates of the binding energies of different cations with the aluminosilicate dimer/trimer by using either the ionic potential or the field strength of the cations, where the ionic potential and field strength of the cations can be readily estimated from well-tabulated ionic radii available in the literature for a wide range of cations beyond those studied here (Shannon, 1976). For example, we can estimate binding energies of different cations with the aluminosilicate dimer, including cations beyond those included in the DFT calculations here (e.g., Rb⁺, Cs⁺, Be²⁺, Ba²⁺, Sr²⁺, Cd²⁺, Pb²⁺, and Al³⁺), by using Eqs. 3, 4.

$-E_b=0.66\times {IP}^2+4.95\times IP+1.09(3)$

$-E_b=53.75\times F^2+9.83\times F+4.11(4)$

The calculated cationic binding energies with the aluminosilicate dimer (values given in Supplementary Table S2 of Supporting Information) are plotted in Figure 10 against the corresponding cationic binding energies with different organic species reported in the literature (calix[2]furano[2]pyrrole (C₂₀N₂O₂H₉) (Teixeira dos Santos and Magalhães, 2010), β-cyclodextrin (C₄₂H₇₀O₃₅) (Stachowicz et al., 2011) and cucurbit[6]uril (C₃₆H₃₆N₂₄O₁₂) (Sinha and Sundararajan, 2014)), where the binding energies have been obtained using DFT calculations. It is clear from Figure 10 that the cationic binding energies estimated using Eqs. 3, 4 for the aluminosilicate dimer are positively and linearly correlated with the DFT-derived binding energies for all three types of organic species. In spite of the large difference in the types of interacting chemical complexes (see the atomic structures of the three organic species in refs. (Teixeira dos Santos and Magalhães, 2010; Stachowicz et al., 2011; Sinha and Sundararajan, 2014)), these linear correlations (R² values of 0.95–0.99 for linear regressions) in Figure 10 suggest that the relative binding energy values estimated using Eqs. 3, 4 are reasonable, with the overall trend for a range of cations being correctly captured. Nevertheless, we also see that the estimated values from Eqs. 3, 4 are generally more than 30% higher than those from DFT calculations. This discrepancy may be partially attributed to the difference in the charge of the organic complex (neutral) compared with the Al-Si dimer (−1). This is supported by Figure 9, where the interaction energies with the more negatively charged trimer (−2) are consistently higher (∼30–50% higher) than the same cation with the dimer. The linear correlations in Figure 10 and Supplementary Figure S3 also demonstrate the governing effect that the ionic potential and field strength of cations have on the binding energies with a given chemical species.

FIGURE 10

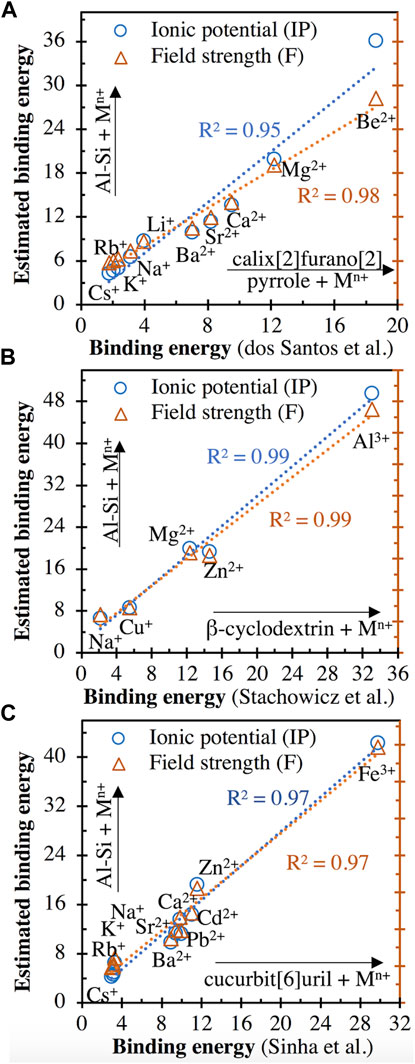
FIGURE 10. Comparison of the cationic binding energies with the aluminosilicate dimer ([(OH)₃-Si-O-Al-(OH)₃]⁻¹) estimated using Eqs. 3, 4 and the DFT-derived binding energies of same cations interacting with three organic species: (A) calix[2]furano[2]pyrrole (C₂₀N₂O₂H₉) (Teixeira dos Santos and Magalhães, 2010), (B) β-cyclodextrin (C₄₂H₇₀O₃₅) (Stachowicz et al., 2011) and (C) cucurbit[6]uril (C₃₆H₃₆N₂₄O₁₂) (Sinha and Sundararajan, 2014). All energies are in units of eV. The range of cation types studied in each of the three literature studies is provided, along with the R² values achieved for linear regressions.

Finally, we have reported the number of unpaired electrons (alpha spin–beta spin) in the DFT-optimized clusters (the explored configurations with the lowest energy) involving transition metal cations based on our Dmol³ calculations. The results, along with the dipole moments, are summarized in Supplementary Table S3 of Supporting Information for the reference of future studies.

3.3 Broader impact and limitations

The interactions of positively charged metal cations with negatively charged aluminosilicate networks are important to many aluminosilicate-based materials (e.g., sustainable cements and aluminosilicate glasses) and their associated applications (e.g., building and construction, waste encapsulation, and durable glasses). Here, we probe this interaction using simple model systems, i.e., calculating the pair-wise interaction energies between aluminosilicate dimer/trimer and different metal cations/clusters using DFT calculations. By covering a wide range of cations, we reveal that simple 2nd order polynomial functions can be used to estimate the binding energy values based on ionic potential or field strength, which can then be estimated using well-tabulated ionic radii available in the literature. With these equations, one can rapidly estimate the binding energies with the aluminosilicate dimer/trimer for a wider range of cations in the periodic table. This presents enormous opportunities for the design and optimization of aluminosilicate-based materials for specific applications, given that there is a strong correlation between the binding energies of cations and their impact on different materials properties (e.g., aluminosilicate glass corrosion, leaching and acid attack of AAMs, ionic transport in AAMs, and mineral dissolution), as seen in the discussion of results in Section 3.2.

For example, microbial-induced sulfuric acid attack represents a major durability issue for concrete sewer pipelines, requiring an estimated 390 billion dollars in the United States alone over the next 20 years for maintenance and replacement (Gutiérrez-Padilla et al., 2010). Recent studies have demonstrated the potential of doping Mg²⁺, Cu²⁺, and Co²⁺ ions to improve the resistance of AAMs to sulfuric acid attack (Gevaudan et al., 2019; Gevaudan et al., 2021). The results of this study suggest that there are cations (e.g., Fe³⁺ and Ti⁴⁺) that may better stabilize the aluminosilicate network in AAMs and hence further improve their resistance to acid attack. A wider range of cations can be quickly evaluated for this application using the semi-empirical equations (as given in Figure 9 for the aluminosilicate dimer and trimer) derived here prior to carrying out validation experiments. However, it is noted that the actual performance of elemental doping also depends on the cost of the doped elements and to what extent the doped cations can be incorporated into the AAM structure while not significantly compromising their other properties (e.g., development of strength). A high extent of cation incorporation (beyond those required to charge-balance [AlO_1/2]₄⁻¹) may cause the AAM aluminosilicate framework to depolymerize (Garg et al., 2019), which could reduce its resistance to acid attack.

Furthermore, in a geopolymer system fully charge-balanced by a cation, intuitively, one may expect cations that give a higher binding energy may better stabilize the geopolymer gel and hence improve its mechanical properties. An early DFT study on calcium silicate-hydrate (C-S-H) gel has shown that C-S-H gel with a Ca replaced by a [Na + H] has a higher bulk modulus than that replaced with a [K + H] (Özçelik and White, 2016), which is consistent with the trend of binding energy calculation seen here for Na and K (Figure 4). A recent force field MD simulation study shows that replacing a small percentage of Na⁺ with Ca²⁺ (<3%) leads to higher modulus of elasticity for a sodium aluminosilicate hydrate (N-A-S-H) gel, where the trend is also consistent with binding energy calculation here for Na and Ca. Nevertheless, the same study shows that replacing Na with Mg (up to 10%) leads to a considerable reduction in the modulus of elasticity of the N-A-S-H gel, where the trend is inconsistent with the binding energy calculation here for Na and Mg. This inconsistency illustrates that further research is needed to evaluate if the binding energy calculation can be used predict the relative impact of metal cations on the mechanical properties of the aluminosilicate gels in AAMs. We note that the mechanical properties of the AAM gels are influenced by other important factors, including porosity in AAMs and the relative amount of metal cations (as they can act as a charge balancer or a network modifier depending on the molar ratio of MO/Al₂O₃ or M₂O/Al₂O₃).

In glass literature, a recent MD study (Sundararaman et al., 2019) shows that 0.15Li₂O-xAl₂O₃-(0.85-x)SiO₂ glasses have higher bulk moduli and Young’s moduli than the corresponding 0.15Na₂O-xAl₂O₃-(0.85-x)SiO₂ glasses. The observation is consistent with the trend of binding energy calculation seen for Na⁺ and Li⁺ in Figure 4. An earlier experimental study (Tiegel et al., 2015) on aluminosilicate glasses with 20 mol% Al₂O₃ and 20 mol% M₂O or MO (M = Na⁺, Li⁺, Ca²⁺, and Mg²⁺) showed that the Young’s modulus increased in the order of Na⁺ < Li⁺ < Ca²⁺ < Mg²⁺, where the trend is also consistent with the trend of binding energy calculation seen here for Na⁺, Li⁺, Ca²⁺, and Mg²⁺.

Similar methods and analysis could be extended to other systems, where binding energy values based on DFT calculations are available, as shown for some organic species (Vayssilov et al., 2000; Teixeira dos Santos and Magalhães, 2010; Deepa et al., 2011; Stachowicz et al., 2011; Liu et al., 2013; Gopalsamy and Subramanian, 2014; Sinha and Sundararajan, 2014; Karaush et al., 2015). Nevertheless, several limitations regarding this work warrant some discussion. First, the interactions between metal cations and the aluminosilicate network are more complex than those with the aluminosilicate dimer/trimer, especially considering the second role of metal cations in aluminosilicates (in addition to charge balancing), i.e., acting as a modifier cation to depolymerize the aluminosilicate network. This impact of depolymerization is opposite to the stabilization effect of cationic charge balancing and hence needs to be considered when using the method and analysis presented here. Furthermore, in real material systems (e.g., AAMs), the metal cation is often coordinated with hydroxide ions and/or water molecules, in addition to the oxygen atom in the aluminosilicate network (Walkley et al., 2018). The presence of hydroxide ions and/or water molecules will change the binding energy, as illustrated for a number of cations with one OH⁻ in Table S1 of the Supporting Information (e.g., [CuOH]⁺, [CaOH]⁺, [MgOH]⁺, [CoOH]²⁺, [FeOH]²⁺ and [CrOH]²⁺). Here we focused on the simple model systems for the purpose of comparing the different cations without needing significantly more computational power, and future investigations should explore more realistic scenarios where the metal cations are fully coordinated. Nevertheless, this study, along with many others in the literature, has demonstrated the benefits of using DFT calculations and simple model systems to gain physical insight into complex material systems.

Second, although Figure 9 shows that the overall trend of binding energy can be well captured by the ionic potential and field strength of the cations with high R² values (0.99–1.00), the correlations for the divalent cations alone are much lower (R² values of 0.65–0.69) as seen in Supplementary Figure S6 of Supporting Information. Furthermore, similar to Supplementary Figure S6, we have correlated the ionic potential and field strength of divalent cations with their binding/adsorption energies with several other chemical species reported in the literature (see Supplementary Figure S7 of Supporting Information). Supplementary Figure S7 shows that although the binding (adsorption) energies for the divalent cations with 1,10-phenanthroline complexes (Nose et al., 2013) (silica-disiloxane cluster (Chang et al., 2003)) are positively correlated with both the ionic potential and field strength of the cations, their levels of correlation are obviously lower than those in Figure 9, but comparable with those shown in Supplementary Figure S6. One possible contribution to the lower levels of correlation seen for the divalent cations is that the effective ionic radii used to calculate ionic potential and field strength are based on the assumption of VI-coordinated cations. However, this assumption is different from the DFT calculations on the model clusters (as seen in Figures 2 and 3), where the cations are not VI-coordinated; and it also deviates from aluminosilicate glass systems where, for example, Fe²⁺ is mainly V-coordinated, and Zn²⁺ is mainly IV- and V-coordinated (Cormier et al., 2021).

Furthermore, as shown in Figures 9 and 10, the interaction energies also depend on the type of chemical species (dimer vs. trimer and inorganic vs. organic complex) interacting with the cations. This means that the equations that capture the relationship between the binding energies and the cationic attributes (e.g., IP and field strength) vary among different interacting species (as seen in Figure 9).

4 Conclusion

In this study, we employed density functional theory (DFT) calculations to calculate the pair-wise interaction energies (i.e., binding energies) between aluminosilicate dimer/trimer and different metal cations Mⁿ⁺ (including Li⁺, Na⁺, K⁺, Cu⁺, Cu²⁺, Co²⁺, Zn²⁺, Ni²⁺, Mg²⁺, Ca²⁺, Ti²⁺, Fe²⁺, Fe³⁺, Co³⁺, Cr³⁺, Ti⁴⁺ and Cr⁶⁺). Comparison with literature data on aluminosilicate glasses shows that the main attributes (e.g., interatomic distances) of DFT-optimized cluster (dimer/trimer + Mⁿ⁺) structures are reasonable. The DFT-derived binding energies are seen to increase (i.e., become more negative) as the charge of the metal cation and aluminosilicate increase, whereas these energies decrease (i.e., become less negative) as the radii of the metal cation increase. Comparison with literature data shows that the cationic binding energy can be used to explain many literature observations on the impact of metal cations on the properties of aluminosilicate materials (including aluminosilicate glass corrosion, leaching and acid attack of alkali-activated materials (AAMs), ionic transport in AAMs, and mineral dissolution). These binding energies are shown to be highly correlated (R² values of 0.94–1.00 for linear regression) with the reported binding energy values in the literature (also obtained using DFT calculations) on the same cations but with different chemical species for interaction (mostly organic complexes), suggesting the presence of certain inherent attributes of the metal cations that control their strength of interaction with a given chemical species.

Analysis of all the DFT-derived binding energies from this study reveals that these energy values can be approximated as a function of two fundamental properties of the metal cations (R² values of 0.99–1.00 are achieved using regression of 2nd order polynomial function), namely the ionic potential (charge/radii) and field strength (Eq. 2). This means that the binding energies of a given metal cation with the aluminosilicate dimer/trimer can be readily estimated using simple polynomial functions since both the ionic potential and field strength of the cation can be computed from ionic radii that are well-tabulated in the literature. This is demonstrated for eight cations (Cs⁺, Rb⁺, Sr²⁺, Ba²⁺, Cd²⁺, Pb²⁺, Be²⁺, and Al³⁺), where the estimated binding energies using these polynomial functions (Eqs. 3, 4) are seen to be linearly correlated (R² values of 0.95–0.99) with DFT-derived interaction energies for different organic species reported in the literature. The differences in the interaction energies among the aluminosilicate dimer and trimer and different organic species with the same cations show that the attribute of the interacting species also has a role to play. The findings in this study present a bottom-up approach (e.g., tailoring the cationic binding energy) toward the design and optimization of sustainable cements and aluminosilicate glasses for specific applications (e.g., improving the resistance of AAM to acid attack, a major durability issue of concrete materials and structures). Similar approaches can be extended to study the binding energies of cations with other chemical species and to derive semi-empirical governing equations that allow rapid estimation of binding energies across a wider range of atoms in the periodic table.

5 Supporting information

1. Optimized dimeric clusters

2. Optimized trimeric clusters

3. Summary of all binding energy values

4. Comparison of binding energies

5. Comparison of binding energy and mineral dissolution rates

6. Comparison of ionic potential and field strength of cations

7. Binding energy values in Figure 10 of the main article

8. Comparison of binding energy and the ionic potential and field strength for divalent cations

9. Number of unpaired electrons and dipole moment

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

KG and CW contributed to conception and design of the study. KG performed the DFT calculations, conducted the analysis and wrote the first draft of the manuscript. KY helped with the DFT calculations. All authors contributed to manuscript revision, read, and approved the submitted version.

Acknowledgments

This material is based on work supported by ARPA-E under Grant No. 1953-1567.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2023.1089216/full#supplementary-material

References

Asaduzzaman, A., Runge, K., Muralidharan, K., Deymier, P. A., and Zhang, L. (2015). Energetics of substituted polyhedral oligomeric silsesquioxanes: A DFT study. MRS Commun. 5 (3), 519–524. doi:10.1557/mrc.2015.58

CrossRef Full Text | Google Scholar

Atila, A., Ouaskit, S., and Hasnaoui, A. (2020). Ionic self-diffusion and the glass transition anomaly in aluminosilicates. Phys. Chem. Chem. Phys. 22 (30), 17205–17212. doi:10.1039/d0cp02910f

PubMed Abstract | CrossRef Full Text | Google Scholar

Bäck, L. G., Ali, S., Karlsson, S., Wondraczek, L., and Jonson, B. (2019). X-ray and UV-Vis-NIR absorption spectroscopy studies of the Cu(I) and Cu(II) coordination environments in mixed alkali-lime-silicate glasses. J. Non-Cryst Solids X. 3, 100029. doi:10.1016/j.nocx.2019.100029

CrossRef Full Text | Google Scholar

Baral, K., Li, A., and Ching, W-Y. (2017). Ab initio modeling of structure and properties of single and mixed alkali silicate glasses. J. Phys. Chem. A 121 (40), 7697–7708. doi:10.1021/acs.jpca.7b06530

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernal, S. A., and Provis, J. L. (2014). Durability of alkali-activated materials: Progress and perspectives. J. Am. Ceram. Soc. 97 (4), 997–1008. doi:10.1111/jace.12831

CrossRef Full Text | Google Scholar

Bernard, E., Lothenbach, B., Cau-Dit-Coumes, C., Pochard, I., and Rentsch, D. (2020). Aluminum incorporation into magnesium silicate hydrate (MSH). Cem. Concr. Res. 128, 105931. doi:10.1016/j.cemconres.2019.105931

CrossRef Full Text | Google Scholar

Berry, A. J., Miller, L. A., O'Neill, H. S. C., and Foran, G. J. (2021). The coordination of Cr²⁺ in silicate glasses and implications for mineral-melt fractionation of Cr isotopes. Chem. Geol. 586, 120483. doi:10.1016/j.chemgeo.2021.120483

CrossRef Full Text | Google Scholar

Blyth, A., Eiben, C. A., Scherer, G. W., and White, C. E. (2017). Impact of activator chemistry on permeability of alkali-activated slags. J. Am. Ceram. Soc. 100, 4848–4859. doi:10.1111/jace.14996

CrossRef Full Text | Google Scholar

Brady, P. V., and Gíslason, S. R. (1997). Seafloor weathering controls on atmospheric CO₂ and global climate. Geochim. Cosmochim. Ac 61 (5), 965–973. doi:10.1016/s0016-7037(96)00385-7

CrossRef Full Text | Google Scholar

Brantley, S. L. (2008). “Kinetics of mineral dissolution,” in Kinetics of water-rock interaction. 168. Editors S. L. Brantley, J. D. Kubicki, and A. F. White (New York: Springer), 151–210.

CrossRef Full Text | Google Scholar

Cartledge, G. H. (1928). Studies on the periodic system. I. The ionic potential as a periodic function. J. Am. Chem. Soc. 50 (11), 2863–63. doi:10.1021/ja01398a001

CrossRef Full Text | Google Scholar

Casey, W. H., and Westrich, H. R. (1992). Control of dissolution rates of orthosilicate minerals by divalent metal–oxygen bonds. Nature 355 (6356), 157–159. doi:10.1038/355157a0

CrossRef Full Text | Google Scholar

Chang, C. M., Jalbout, A. F., and Lin, C. (2003). Novel descriptors based on density functional theory for predicting divalent metal ions adsorbed onto silica—Disiloxane cluster model study. J. Mol. Struc-THEOCHEM 664, 27–35. doi:10.1016/s0166-1280(03)00564-5

CrossRef Full Text | Google Scholar

Chen, Z., Schwarz, B., Zhang, X., Du, W., Zheng, L., Tian, A., et al. (2021). Peroxo species formed in the bulk of silicate cathodes. Angew. Chem. 133 (18), 10144–10151. doi:10.1002/ange.202100730

CrossRef Full Text | Google Scholar

Cianchetta, I., Colantoni, I., Talarico, F., d'Acapito, F., Trapananti, A., Maurizio, C., et al. (2012). Discoloration of the smalt pigment: Experimental studies and ab initio calculations. J. Anal. At. Spectrom. 27 (11), 1941–1948. doi:10.1039/c2ja30132f

CrossRef Full Text | Google Scholar

Civalleri, B., Napoli, F., Noël, Y., Roetti, C., and Dovesi, R. (2006). Ab-initio prediction of materials properties with CRYSTAL: MOF-5 as a case study. CrystEngComm 8 (5), 364–371. doi:10.1039/b603150c

CrossRef Full Text | Google Scholar

Cormier, L., Delbes, L., Baptiste, B., and Montouillout, V. (2021). Vitrification, crystallization behavior and structure of zinc aluminosilicate glasses. J. Non-Cryst Solids 555, 120609. doi:10.1016/j.jnoncrysol.2020.120609

CrossRef Full Text | Google Scholar

Deepa, P., Kolandaivel, P., and Senthilkumar, K. (2011). Structural properties and the effect of interaction of alkali (Li⁺, Na⁺, K⁺) and alkaline earth (Be²⁺, Mg²⁺, Ca²⁺) metal cations with G and SG-tetrads. Comput. Theor. Chem. 974 (1-3), 57–65. doi:10.1016/j.comptc.2011.07.012

CrossRef Full Text | Google Scholar

Dietzel, A. (1942). Die kationenfeldstärken und ihre beziehungen zu entglasungsvorgängen, zur verbindungsbildung und zu den schmelzpunkten von silicaten. Z Elektrochem Angew. Phys. Chem. 48 (1), 9–23.

Google Scholar

Duque-Redondo, E., Yamada, K., Dolado, J. S., and Manzano, H. (2021). Microscopic mechanism of radionuclide Cs retention in Al containing CSH nanopores. Comput. Mater Sci. 190, 110312. doi:10.1016/j.commatsci.2021.110312

CrossRef Full Text | Google Scholar

El Alouani, M., Saufi, H., Moutaoukil, G., Alehyen, S., Nematollahi, B., Belmaghraoui, W., et al. (2021). Application of geopolymers for treatment of water contaminated with organic and inorganic pollutants: State-of-the-art review. J. Environ. Chem. Eng. 9 (2), 105095. doi:10.1016/j.jece.2021.105095

CrossRef Full Text | Google Scholar

Farges, F., Brown, G. E., Petit, P-E., and Munoz, M. (2001). Transition elements in water-bearing silicate glasses/melts. Part I. A high-resolution and anharmonic analysis of Ni coordination environments in crystals, glasses, and melts. Geochim. Cosmochim. Ac 65 (10), 1665–1678. doi:10.1016/s0016-7037(00)00625-6

CrossRef Full Text | Google Scholar

Farges, F., Munoz, M., Siewert, R., Malavergne, V., Brown, G. E., Behrens, H., et al. (2001). Transition elements in water-bearing silicate glasses/melts. Part II. Ni in water-bearing glasses. Geochim. Cosmochim. Ac 65 (10), 1679–1693. doi:10.1016/s0016-7037(00)00624-4

CrossRef Full Text | Google Scholar

Garg, N., Özçelik, V. O., Skibsted, J., and White, C. E. (2019). Nanoscale ordering and depolymerization of calcium silicate hydrates in the presence of alkalis. J. Phys. Chem. C 123 (40), 24873–24883. doi:10.1021/acs.jpcc.9b06412

CrossRef Full Text | Google Scholar

Gatti, C., Ottonello, G., and Richet, P. (2012). Energetics and bonding in aluminosilicate rings with alkali metal and alkaline-earth metal charge-compensating cations. J. Phys. Chem. A 116 (33), 8584–8598. doi:10.1021/jp302839f

PubMed Abstract | CrossRef Full Text | Google Scholar

Gevaudan, J. P., Caicedo-Ramirez, A., Hernandez, M. T., and Srubar III, W. V. (2019). Copper and cobalt improve the acid resistance of alkali-activated cements. Cem. Concr. Res. 115, 327–338. doi:10.1016/j.cemconres.2018.08.002

CrossRef Full Text | Google Scholar

Gevaudan, J. P., Craun, Z., and Srubar III, W. V. (2021). Sulfuric acid degradation of alkali-activated metakaolin cements supplemented with brucite. Cem. Concr. Comp. 121, 104063. doi:10.1016/j.cemconcomp.2021.104063

CrossRef Full Text | Google Scholar

Ghambarian, M., Azizi, Z., and Ghashghaee, M. (2016). Diversity of monomeric dioxo chromium species in Cr/silicalite-2 catalysts: A hybrid density functional study. Comp. Mater Sci. 118, 147–154. doi:10.1016/j.commatsci.2016.03.009

CrossRef Full Text | Google Scholar

Gong, K., and Olivetti, E. A. (2022). Development of structural descriptors to predict dissolution rate of volcanic glasses: Molecular dynamic simulations. J. Am. Ceram. Soc. 105 (4), 2575–2594. doi:10.1111/jace.18265

CrossRef Full Text | Google Scholar

Gong, K., Özçelik, V. O., Yang, K., and White, C. E. (2021). Density functional modeling and total scattering analysis of the atomic structure of a quaternary CaO-MgO-Al₂O₃-SiO₂ (CMAS) glass: Uncovering the local environment of calcium and magnesium. Phys. Rev. Mater 5 (1), 015603. doi:10.1103/physrevmaterials.5.015603

CrossRef Full Text | Google Scholar

Gong, K., and White, C. E. (2021). Predicting CaO-(MgO)-Al₂O₃-SiO₂ glass reactivity in alkaline environments from force field molecular dynamics simulations. Cem. Concr. Res. 150, 106588. doi:10.1016/j.cemconres.2021.106588

CrossRef Full Text | Google Scholar

Gopalsamy, K., and Subramanian, V. (2014). Hydrogen storage capacity of alkali and alkaline earth metal ions doped carbon based materials: A DFT study. Int. J. Hydrogen Energ 39 (6), 2549–2559. doi:10.1016/j.ijhydene.2013.11.075

CrossRef Full Text | Google Scholar

Greaves, G. N., Fontaine, A., Lagarde, P., Raoux, D., and Gurman, S. J. (1981). Local structure of silicate glasses. Nature 293 (5834), 611–616. doi:10.1038/293611a0

CrossRef Full Text | Google Scholar

Guo, X., Pivovarov, A. L., Smedskjaer, M. M., Potuzak, M., and Mauro, J. C. (2014). Non-conservation of the total alkali concentration in ion-exchanged glass. J. Non-Cryst Solids 387, 71–75. doi:10.1016/j.jnoncrysol.2013.12.033

CrossRef Full Text | Google Scholar

Gutiérrez-Padilla, M. G. D., Bielefeldt, A., Ovtchinnikov, S., Hernandez, M., and Silverstein, J. (2010). Biogenic sulfuric acid attack on different types of commercially produced concrete sewer pipes. Cem. Concr. Res. 40 (2), 293–301. doi:10.1016/j.cemconres.2009.10.002

CrossRef Full Text | Google Scholar

Hoover, W. G. (1985). Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 31 (3), 1695–1697. doi:10.1103/physreva.31.1695

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, D., and Li, T. (2018). Influence of aluminates on the structure and dynamics of water and ions in the nanometer channel of calcium silicate hydrate (C–S–H) gel. Phys. Chem. Chem. Phys. 20 (4), 2373–2387. doi:10.1039/c7cp06985e

PubMed Abstract | CrossRef Full Text | Google Scholar

Inaba, S., Fujino, S., and Morinaga, K. (1999). Young's modulus and compositional parameters of oxide glasses. J. Am. Ceram. Soc. 82 (12), 3501–3507. doi:10.1111/j.1151-2916.1999.tb02272.x

CrossRef Full Text | Google Scholar

Ispas, S., Charpentier, T., Mauri, F., and Neuville, D. R. (2010). Structural properties of lithium and sodium tetrasilicate glasses: Molecular dynamics simulations versus NMR experimental and first-principles data. Solid State Sci. 12 (2), 183–192. doi:10.1016/j.solidstatesciences.2009.06.033

CrossRef Full Text | Google Scholar

Jakse, N., Bouhadja, M., Kozaily, J., Drewitt, J. W. E., Hennet, L., Neuville, D. R., et al. (2012). Interplay between non-bridging oxygen, triclusters, and fivefold Al coordination in low silica content calcium aluminosilicate melts. Appl. Phys. Lett. 101 (20), 201903. doi:10.1063/1.4766920

CrossRef Full Text | Google Scholar

Januchta, K., Bauchy, M., Youngman, R. E., Rzoska, S. J., Bockowski, M., and Smedskjaer, M. M. (2017). Modifier field strength effects on densification behavior and mechanical properties of alkali aluminoborate glasses. Phys. Rev. Mater 1 (6), 063603. doi:10.1103/physrevmaterials.1.063603

CrossRef Full Text | Google Scholar

Ji, Z., and Pei, Y. (2020). Immobilization efficiency and mechanism of metal cations (Cd²⁺, Pb²⁺ and Zn²⁺) and anions (AsO₄^3-and Cr₂O₇^2-) in wastes-based geopolymer. J. Hazard Mater 384, 121290. doi:10.1016/j.jhazmat.2019.121290

PubMed Abstract | CrossRef Full Text | Google Scholar

Karaush, N. N., Baryshnikov, G. V., and Minaev, B. F. (2015). Alkali and alkaline-earth metal complexes with tetraoxa[8]circulene sheet: A computational study by DFT and qtaim methods. RSC Adv. 5 (31), 24299–24305. doi:10.1039/c4ra13806f

CrossRef Full Text | Google Scholar

Karlsson, S., Wondraczek, L., Ali, S., and Jonson, B. (2017). Trends in effective diffusion coefficients for ion-exchange strengthening of soda-lime-silicate glasses. Front. Mater 4, 13. doi:10.3389/fmats.2017.00013

CrossRef Full Text | Google Scholar

Kim, G., Im, S., Jee, H., Suh, H., Cho, S., Kanematsu, M., et al. (2022). Effect of magnesium silicate hydrate (MSH) formation on the local atomic arrangements and mechanical properties of calcium silicate hydrate (CSH): In situ X-ray scattering study. Cem. Concr. Res. 159, 106869. doi:10.1016/j.cemconres.2022.106869

CrossRef Full Text | Google Scholar

Kump, L. R., Brantley, S. L., and Arthur, M. A. (2000). Chemical weathering, atmospheric CO₂, and climate. Annu. Rev. Earth Pl. S. C. 28 (1), 611–667. doi:10.1146/annurev.earth.28.1.611

CrossRef Full Text | Google Scholar

Le Grand, M., Ramos, A. Y., Calas, G., Galoisy, L., Ghaleb, D., and Pacaud, F. (2000). Zinc environment in aluminoborosilicate glasses by Zn K-edge extended x-ray absorption fine structure spectroscopy. J. Mater Res. 15 (9), 2015–2019. doi:10.1557/jmr.2000.0289

CrossRef Full Text | Google Scholar

Lee, J., Yano, T., Shibata, S., Nukui, A., and Yamane, M. (2000). EXAFS study on the local environment of Cu⁺ ions in glasses of the Cu₂O–Na₂O–Al₂O₃–SiO₂ system prepared by Cu⁺/Na⁺ ion exchange. J. Non-Cryst Solids 277 (2-3), 155–161. doi:10.1016/s0022-3093(00)00330-6

CrossRef Full Text | Google Scholar

Liu, J., Xia, X., Li, Y., Wang, H., and Li, Z. (2013). Theoretical study on the interaction of glutathione with group IA (Li⁺, Na⁺, K⁺), IIA (Be²⁺, Mg²⁺, Ca²⁺), and IIIA (Al³⁺) metal cations. Struct. Chem. 24 (1), 251–261. doi:10.1007/s11224-012-0031-1

CrossRef Full Text | Google Scholar

Lopez, N., Illas, F., and Pacchioni, G. (1999). Ab initio theory of metal deposition on SiO₂. 1. Cu_n (n=1− 5) clusters on nonbridging oxygen defects. J. Phys. Chem. B 103 (10), 1712–1718. doi:10.1021/jp9840174

CrossRef Full Text | Google Scholar

Lv, P., Wang, C., Stevensson, B., Yu, Y., Wang, T., and Edén, M. (2022). Impact of the cation field strength on physical properties and structures of alkali and alkaline-earth borosilicate glasses. Ceram. Int. 48 (13), 18094–18107. doi:10.1016/j.ceramint.2022.03.022

CrossRef Full Text | Google Scholar

Martin, R. A., Twyman, H. L., Rees, G. J., Smith, J. M., Barney, E. R., Smith, M. E., et al. (2012). A structural investigation of the alkali metal site distribution within bioactive glass using neutron diffraction and multinuclear solid state NMR. Phys. Chem. Chem. Phys. 14 (35), 12105–12113. doi:10.1039/c2cp41725a

PubMed Abstract | CrossRef Full Text | Google Scholar

Mascaraque, N., Januchta, K., Frederiksen, K. F., Youngman, R. E., Bauchy, M., and Smedskjaer, M. M. (2019). Structural dependence of chemical durability in modified aluminoborate glasses. J. Am. Ceram. Soc. 102 (3), 1157–1168. doi:10.1111/jace.15969

CrossRef Full Text | Google Scholar

Maurizio, C., d'Acapito, F., Benfatto, M., Mobilio, S., Cattaruzza, E., and Gonella, F. (2000). Local coordination geometry around Cu and Cu ions in silicate glasses: An X-ray absorption near edge structure investigation. Eur. Phys. J. B 14 (2), 211–216. doi:10.1007/s100510050122

CrossRef Full Text | Google Scholar

McKeown, D. A., Waychunas, G. A., and Brown Jr, G. E. (1985). EXAFS and XANES study of the local coordination environment of sodium in a series of silica-rich glasses and selected minerals within the Na₂O-Al₂O₃-SiO₂ system. J. Non-Cryst Solids 74 (2-3), 325–348. doi:10.1016/0022-3093(85)90078-x

CrossRef Full Text | Google Scholar

Monteiro, P. J. M., Miller, S. A., and Horvath, A. (2017). Towards sustainable concrete. Nat. Mater 16 (7), 698–699. doi:10.1038/nmat4930

PubMed Abstract | CrossRef Full Text | Google Scholar

Mora-Fonz, M. J., Catlow, C. R. A., and Lewis, D. W. (2007). Modeling aqueous silica chemistry in alkali media. J. Phys. Chem. C 111 (49), 18155–18158. doi:10.1021/jp077153u

CrossRef Full Text | Google Scholar

Mora-Fonz, M. J., Catlow, C. R. A., and Lewis, D. W. (2005). Oligomerization and cyclization processes in the nucleation of microporous silicas. Angew. Chem. Int. Ed. 117 (20), 3082–3086. doi:10.1002/anie.200462524

CrossRef Full Text | Google Scholar

Nose, H., Chen, Y., and Rodgers, M. T. (2013). Energy-resolved collision-induced dissociation studies of 1,10-phenanthroline complexes of the late first-row divalent transition metal cations: Determination of the third sequential binding energies. J. Phys. Chem. A 117 (20), 4316–4330. doi:10.1021/jp401711c

PubMed Abstract | CrossRef Full Text | Google Scholar

Nosé, S. (1984). A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52 (2), 255–268. doi:10.1080/00268978400101201

CrossRef Full Text | Google Scholar

Oey, T., Frederiksen, K. F., Mascaraque, N., Youngman, R., Balonis, M., Smedskjaer, M. M., et al. (2019). The role of the network-modifier's field-strength in the chemical durability of aluminoborate glasses. J. Non-Cryst Solids 505, 279–285. doi:10.1016/j.jnoncrysol.2018.11.019

CrossRef Full Text | Google Scholar

Osio-Norgaard, J., Gevaudan, J. P., and Srubar III, W. V. (2018). A review of chloride transport in alkali-activated cement paste, mortar, and concrete. Constr. Build. Mater 186, 191–206. doi:10.1016/j.conbuildmat.2018.07.119

CrossRef Full Text | Google Scholar

Özçelik, V. O., and White, C. E. (2016). Nanoscale charge balancing mechanism in alkali substituted calcium-silicate-hydrate gels. J. Phys. Chem. Lett. 7 (24), 5266–5272. doi:10.1021/acs.jpclett.6b02233

PubMed Abstract | CrossRef Full Text | Google Scholar

Pacheco-Torgal, F. (2014). Handbook of alkali-activated cements, mortars and concretes. Cambridge, UK: Woodhead Publishing.

Google Scholar

Parr, R. G., and Pearson, R. G. (1983). Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 105 (26), 7512–7516. doi:10.1021/ja00364a005

CrossRef Full Text | Google Scholar

Pegado, L., Labbez, C., and Churakov, S. V. (2014). Mechanism of aluminium incorporation into C–S–H from ab initio calculations. J. Mater Chem. A 2 (10), 3477–3483. doi:10.1039/c3ta14597b

CrossRef Full Text | Google Scholar

Piovesan, V., Bardez-Giboire, I., Fournier, M., Frugier, P., Jollivet, P., Montouillout, V., et al. (2018). Chemical durability of peraluminous glasses for nuclear waste conditioning. NPJ Mater Degrad. 2 (1), 7–10. doi:10.1038/s41529-018-0028-3

CrossRef Full Text | Google Scholar

Pokrovsky, O. S., and Schott, J. (2002). Surface chemistry and dissolution kinetics of divalent metal carbonates. Environ. Sci. Technol. 36 (3), 426–432. doi:10.1021/es010925u

PubMed Abstract | CrossRef Full Text | Google Scholar

Provis, J. L., Myers, R. J., White, C. E., Rose, V., and Van Deventer, J. S. J. (2012). X-ray microtomography shows pore structure and tortuosity in alkali-activated binders. Cem. Concr. Res. 42 (6), 855–864. doi:10.1016/j.cemconres.2012.03.004

CrossRef Full Text | Google Scholar

Provis, J. L., and van Deventer, J. S. J. (2014). Alkali activated materials: State-of-the-art report (Dordrecht: Springer/RILEM).

Google Scholar

Provis, J. L., and van Deventer, J. S. J. (2009). Geopolymers: Structures, processing, properties and industrial applications. Cambridge, UK: Woodhead Publishing Limited.

Google Scholar

Rose, J., Moulin, I., Masion, A., Bertsch, P. M., Wiesner, M. R., Bottero, J-Y., et al. (2001). X-ray absorption spectroscopy study of immobilization processes for heavy metals in calcium silicate hydrates. 2. Zinc. Langmuir 17 (12), 3658–3665. doi:10.1021/la001302h

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystall a-crys. 32 (5), 751–767. doi:10.1107/s0567739476001551

CrossRef Full Text | Google Scholar

Sinha, V., and Sundararajan, M. (2014). “Structure and cation binding affinities of cucurbit [6] uril: A DFT Study,” in AIP Conference Proceedings, Vol. 1591, 1708–1710.

CrossRef Full Text | Google Scholar

Stachowicz, A., Styrcz, A., Korchowiec, J., Modaressi, A., and Rogalski, M. (2011). DFT studies of cation binding by β-cyclodextrin. Theor. Chem. Acc. 130 (4), 939–953. doi:10.1007/s00214-011-1014-9

CrossRef Full Text | Google Scholar

Sun, H., Wu, D., Liu, K., Guo, X., and Navrotsky, A. (2016). Energetics of alkali and alkaline earth ion-exchanged zeolite A. J. Phys. Chem. C 120 (28), 15251–15256. doi:10.1021/acs.jpcc.6b04840

CrossRef Full Text | Google Scholar

Sundararaman, S., Huang, L., Ispas, S., and Kob, W. (2019). New interaction potentials for alkali and alkaline-earth aluminosilicate glasses. J. Chem. Phys. 150 (15), 154505. doi:10.1063/1.5079663

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, E., Di Tommaso, D., and de Leeuw, N. H. (2010). Accuracy of the microsolvation–continuum approach in computing the pKa and the free energies of formation of phosphate species in aqueous solution. Phys. Chem. Chem. Phys. 12 (41), 13804–13815. doi:10.1039/c0cp00175a

PubMed Abstract | CrossRef Full Text | Google Scholar

Taniguchi, T., Okuno, M., and Matsumoto, T. (1995). The structural studies of CaMgSi₂O₆, CaCoSi₂O₆ and CaNiSi₂O₆ glasses. Mineral. J. 17 (5), 231–244. doi:10.2465/minerj.17.231

CrossRef Full Text | Google Scholar

Teixeira dos Santos, C. A., and Magalhães, A. L. (2010). DFT study on the ability of calix [2] furano [2] pyrrole to form host–guest type complexes with alkali and alkaline-earth metal ions. J. Mol. Struc-THEOCHEM 956 (1-3), 50–54. doi:10.1016/j.theochem.2010.06.022

CrossRef Full Text | Google Scholar

Tiegel, M., Hosseinabadi, R., Kuhn, S., Herrmann, A., and Rüssel, C. (2015). Young׳ s modulus, Vickers hardness and indentation fracture toughness of alumino silicate glasses. Ceram. Int. 41 (6), 7267–7275. doi:10.1016/j.ceramint.2015.01.144

CrossRef Full Text | Google Scholar

Vaishnav, S., Hannon, A. C., Barney, E. R., and Bingham, P. A. (2020). Neutron diffraction and Raman studies of the incorporation of sulfate in silicate glasses. J. Phys. Chem. C 124 (9), 5409–5424. doi:10.1021/acs.jpcc.9b10924

PubMed Abstract | CrossRef Full Text | Google Scholar

Vayssilov, G. N., Lercher, J. A., and Rösch, N. (2000). Interaction of methanol with alkali metal exchanged molecular sieves. 2. Density functional study. J. Phys. Chem. B 104 (35), 8614–8623. doi:10.1021/jp000195x

CrossRef Full Text | Google Scholar

Vayssilov, G. N., Staufer, M., Belling, T., Neyman, K. M., Knözinger, H., and Rösch, N. (1999). Density functional studies of alkali-exchanged zeolites. Cation location at six-rings of different aluminum content. J. Phys. Chem. B 103 (37), 7920–7928. doi:10.1021/jp991473z

CrossRef Full Text | Google Scholar

Villain, O., Galoisy, L., and Calas, G. (2010). Spectroscopic and structural properties of Cr³⁺ in silicate glasses: Cr³⁺ does not probe the average glass structure. J. Non-Cryst Solids 356 (43), 2228–2234. doi:10.1016/j.jnoncrysol.2010.08.028

CrossRef Full Text | Google Scholar

Vogel, W. (2012). Glass chemistry. Berlin Heidelberg, Germany: Springer.

Google Scholar

Walkley, B., Rees, G. J., San Nicolas, R., van Deventer, J. S., Hanna, J. V., and Provis, J. L. (2018). New structural model of hydrous sodium aluminosilicate gels and the role of charge-balancing extra-framework Al. J. Phys. Chem. C 122 (10), 5673–5685. doi:10.1021/acs.jpcc.8b00259

CrossRef Full Text | Google Scholar

Wang, C., Yang, Z., Song, W., Zhong, Y., Sun, M., Gan, T., et al. (2021). Quantifying gel properties of industrial waste-based geopolymers and their application in Pb²⁺ and Cu²⁺ removal. J. Clean. Prod. 315, 128203. doi:10.1016/j.jclepro.2021.128203

CrossRef Full Text | Google Scholar

Wasea, Y., and Suito, H. (1977). The structure of molten alkali metal silicates. Trans. Iron Steel Inst. Jpn. 17 (2), 82–91. doi:10.2355/isijinternational1966.17.82

CrossRef Full Text | Google Scholar

White, C. E., Provis, J. L., Kearley, G. J., Riley, D. P., and Van Deventer, J. S. J. (2011). Density functional modelling of silicate and aluminosilicate dimerisation solution chemistry. Dalton T 40 (6), 1348–1355. doi:10.1039/c0dt01042a

PubMed Abstract | CrossRef Full Text | Google Scholar

White, C. E., Provis, J. L., Proffen, T., and van Deventer, J. S. J. (2012). Molecular mechanisms responsible for the structural changes occurring during geopolymerization: Multiscale simulation. AIChE J. 58 (7), 2241–2253. doi:10.1002/aic.12743

CrossRef Full Text | Google Scholar

Wu, L., Navrotsky, A., Lee, Y., and Lee, Y. (2013). Thermodynamic study of alkali and alkaline-earth cation-exchanged natrolites. Micropor Mesopor Mat. 167, 221–227. doi:10.1016/j.micromeso.2012.09.003

CrossRef Full Text | Google Scholar

Xiao, Y., and Lasaga, A. C. (1994). Ab initio quantum mechanical studies of the kinetics and mechanisms of silicate dissolution: H⁺ (H₃O⁺) catalysis. Geochim. Cosmochim. Ac 58 (24), 5379–5400. doi:10.1016/0016-7037(94)90237-2

CrossRef Full Text | Google Scholar

Xu, H., Van Deventer, J. S. J., Roszak, S., and Leszczynski, J. (2004). Ab initio study of dissolution reactions of five-membered aluminosilicate framework rings. Int. J. Quantum Chem. 96 (4), 365–373. doi:10.1002/qua.10720

CrossRef Full Text | Google Scholar

Xu, H., Xu, D. C., and Wang, Y. (2017). Natural indices for the chemical hardness/softness of metal cations and ligands. ACS Omega 2 (10), 7185–7193. doi:10.1021/acsomega.7b01039

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C-S., Mora-Fonz, J. M., and Catlow, C. R. A. (2011). Stability and structures of aluminosilicate clusters. J. Phys. Chem. C 115 (49), 24102–24114. doi:10.1021/jp202394w

CrossRef Full Text | Google Scholar

Yang, K., and White, C. E. (2021). Modeling of aqueous species interaction energies prior to nucleation in cement-based gel systems. Cem. Concr. Res. 139, 106266. doi:10.1016/j.cemconres.2020.106266

CrossRef Full Text | Google Scholar

Yang, K., and White, C. E. (2016). Modeling the formation of alkali aluminosilicate gels at the mesoscale using coarse-grained Monte Carlo. Langmuir 32 (44), 11580–11590. doi:10.1021/acs.langmuir.6b02592

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, K., and White, C. E. (2020). Multiscale pore structure determination of cement paste via simulation and experiment: The case of alkali-activated metakaolin. Cem. Concr. Res. 137, 106212. doi:10.1016/j.cemconres.2020.106212

CrossRef Full Text | Google Scholar

Yang, S-Y., Yan, Y., Lothenbach, B., and Skibsted, J. (2021). Incorporation of sodium and aluminum in cementitious calcium-alumino-silicate-hydrate C-(A)-S-H phases studied by ²³Na, ²⁷Al, and ²⁹Si MAS NMR spectroscopy. J. Phys. Chem. C 125 (51), 27975–27995. doi:10.1021/acs.jpcc.1c08419

CrossRef Full Text | Google Scholar

Yoko, T., Nishiwaki, T., Kamiya, K., and Sakka, S. (1991). Copper ⇌ alkali ion exchange of alkali aluminosillcate glasses in copper-containing molten salt: I, monovalent copper salt, CuCl. J. Am. Ceram. Soc. 74 (5), 1104–1111. doi:10.1111/j.1151-2916.1991.tb04349.x

CrossRef Full Text | Google Scholar

Zhang, J., Shi, C., Zhang, Z., and Ou, Z. (2017). Durability of alkali-activated materials in aggressive environments: A review on recent studies. Constr. Build. Mater 152, 598–613. doi:10.1016/j.conbuildmat.2017.07.027

CrossRef Full Text | Google Scholar