Application of phase field model coupled with convective effects in binary alloy directional solidification and roll casting processes

Based on the Kim-Kim-Suzuki (KKS) phase field model coupled with the thermodynamic parameters, the transformation process from columnar dendrites to equiaxed crystals during directional solidification of aluminium alloy was simulated, and the effects of phase field parameters on the growth morphology and dendrite segregation were discussed. Furthermore, considering the effect of the microcosmic flow field, the convection influence gradient term is introduced into KKS formula near the solid-liquid interface, and the phase field model considering flow field was applied to the inherent convective environment of the actual roll casting process, also the multiple dendrites growth behavior of magnesium alloy under the action of microscopic convection was further explored. When coupling calculation of microscopic velocity field and pressure field, the staggered grid method was used to deal with the complex interface. The combined solution of Marker in Cell (MAC) algorithm and phase field discrete calculation was realized. In order to further describe the influence of convection on the solidification process, the roll casting experiments are used to verify the impact growth of multiple dendrites under convection. The results show that the dendrites undergo solute remelting and the dendrites melt into equiaxed crystals, showing the phenomenon of Columnar to Equiaxed Transition (CET).

1 Introduction

The growth process of directionally solidified dendrites was influenced by the interplay of heat, mass and momentum transport as well as interfacial dynamics (Zhao et al. (2019); Shiga et al. (2019)), which ultimately results in a complex and variable structure (Li et al. (2021); Cui et al. (2020)). The use of numerical simulation methods with lower cost than thermal experiments to explore the growth patterns of dendrites under different conditions, which not only provides important guidance for practical production but also helps to gain insight into the solidification characteristics of metallic materials (Lee et al. (2020); Noubary et al. (2017)). The development of computer numerical simulation technology provides a practical method for the quantitative description of complex metal solidification processes (Sinhababu and Bhattacharya, (2022)). By coupling external fields such as temperature field, solute field and flow field, the phase field method can simulate the evolution of metal microstructure in the casting process more accurately (Wei et al. (2020); Li et al. (2020)), which helps people to deeply understand the metal solidification theory and predict the microstructure of metal materials (Wang et al. (2019)), and use it as a basis to optimize the casting process. Pinomaa et al. (Pinomaa and Provatas, (2019)) quantitatively mapped the thin interface behavior of an ideal dilute binary alloy phase field model to CGM dynamics, the simulation results show that the mapping was convergent for different interface widths, and the effect of solute trapping on cell crystal growth in directional solidification was found. Novokreshchenova et al. (Novokreshchenova and Lebedev, (2017)) optimized the local nonequilibrium phase field model and accurately predicted the relationship between interfacial mobility and temperature during directional solidification of pure nickel. Steinmetz, Ghosh et al. (Steinmetz et al. (2018); Ghosh et al. (2019)) conducted a simulation study using a thermodynamically consistent phase field model, the effects of different interfacial energies, diffusivity, lamellar spacing and solidification rate on the growth of the solid phase during directional solidification were studied. The results show that all the factors have significant effects on the growth of dendrites. Lenart et al. (Lenart and Eshraghi, (2020)) used the phase field Boltzmann model (PF-LBM) to simulate the transformation process of Inconel 718 alloy from columnar dendrites to equiaxed crystal, and found that the simulation results were consistent with those obtained in the Inconel 718 solidification experiments. A lot of achievements have also been achieved in the micro simulation of directional solidification in China. Ma et al. (Ma et al. (2020)) proposed a new 3D cellular automata-lattice Boltzmann method (CA-LBM) for simulating the formation of facet and facet dendrites in directional solidification, and reasonably solved the interaction of interfacial energy anisotropy and dynamical anisotropy. Yang et al. (Yang et al. (2017)) investigated the microstructure of a nickel-based superalloy during three-dimensional solidification using the phase field method, and found that the simulated results of dendrites directional solidification were in good agreement with the experimental results. Zhang, Zhu, and Wang et al. (Zhang B. et al. (2019); Zhu et al. (2019); Wang et al. (2020)) used the phase field method to simulate the directional solidification process of Al-Si, Al-Cu, and Mg-Gd binary alloys, all the simulation results show that the increase of anisotropy, cooling rate and temperature gradient can accelerate the solidification rate of columnar dendrites. Based on the above research, in order to simulate the real dendritic growth process more closely in recent years, metallurgical researchers put emphasis on the optimization of phase-field model, but at the same time, the phase-field model becomes more and more complex, which increases the pressure of computer calculation. Therefore, it is very important to find a faster and better calculation method to promote the development of phase-field method.

It is an unquestionable fact that convection has a significant effect on the morphology of solidified dendrites (Nabavizadeh et al. (2020)). Convection can promote or hinder the growth of dendrites, and the microstructure of dendrites is completely different from that of pure diffusion (Geng et al. (2020); Xiong et al. (2022)). The research on the effect of convection on the evolution of solidification organization is relatively fast in China, but there is still scarce of foreign research in this area. Yang et al. (Yang et al. (2020)) combined the multiphase field model with Boltzmann’s method to simulate the dendrites growth process of superalloys under the action of convection, the distribution of solute with the velocity of dendrites tip during solidification was obtained, and the effect of natural convection on the microsegregation and dendrites growth rate was confirmed. Yuan et al. (Yuan and Ding, (2012)) studied the growth morphology of pure nickel dendrites by using a phase field model with coupled flow fields, it was found that the melt flow significantly changes the heat transfer at the solidification front, which affects the dendrites growth. Chen and Wang et al. (Chen et al. (2011); Wang et al. (2012)) simulated the dendritic evolution of Ni-Cu alloy under non-isothermal conditions and found that the nuclei grew into asymmetric dendrites in forced convection. Later, Luo and Zhang et al. (Luo et al. (2020); Zhang A. et al. (2019)) investigated the dendrites growth behavior of Fe-C alloys under forced convection, and also found that the unsymmetrical behavior of dendrites growth was caused by forced convection. In addition, Chen et al. (Chen et al. (2016)) used KKS phase field model to simulate the microstructure evolution of AZ31 magnesium alloy dendrites in the center of roll casting molten pool. The effect of different flow rate values on dendrite evolution was discussed in detail, and it is found that the microstructure was consistent with the actual pattern observed by optical microscopy. Therefore, there is no doubt that micro convection makes the dendrites in the melt grow asymmetrically, but the above research only establishes a phase field model with convective properties and does not consider the actual metallurgical process including the flow field. Moreover, the research on the microstructure evolution of polycrystalline directional solidification with real flow field in the actual process is relatively scarce. Due to the actual production process is complex and changeable, the simulation results should also be different. Based on this, it will be of far-reaching significance to explore the growth behavior of dendrites under actual process conditions.

In this paper, based on the KKS phase field model coupled with the thermodynamic parameters, the transformation process from columnar dendrites to equiaxed crystals during directional solidification of aluminum alloy was simulated. The effects of phase field parameters on the growth morphology and dendrites segregation were discussed. Furthermore, considering the effect of the microcosmic flow field, the convection influence gradient term is introduced into KKS formula near the solid-liquid interface, and the phase field model considering flow field was applied to the inherent convective environment of the actual roll casting process, also the multiple dendrites growth behavior of magnesium alloy under the action of microscopic convection was further explored. The combined solution of MAC algorithm and phase field discrete calculation realized. The dendrites growth behavior of magnesium alloy under the action of microscopic convection in the roll casting was further explored.

2 Phase field model

2.1 Phase field equation

The directional solidification technique can obtain a specific columnar dendrites structure, which is very significant for optimizing the axial mechanical properties of the alloy. Although the traditional experimental has the advantage of being intuitive and operable, it does not reveal the mechanism of dendrites formation. In this paper, the KKS phase field model of the system free energy changing with time was used (Kim et al. (1999)). The control equation of the KKS phase field is:

$\frac{\partial \phi }{\partial t}=M_{\phi }\left({ϵ}^2{\nabla }^2\phi -f\left(c,\phi \right)\right)(1)$

In Eq. 1, the free energy density$f\left(c,\phi \right)$can be expressed as:

$f\left(c,\phi \right)=h\left(\phi \right)f^S\left(c_s\right)+\left(1-h\left(\phi \right)\right)f^L\left(c_L\right)+Wg\left(\phi \right)(2)$

where$Wg\left(\phi \right)$is a specific double potential well function, $h\left(\phi \right)$is the potential function, $g\left(\phi \right)$is the residual free energy function, in this paper: $h\left(\phi \right)={\phi }^3\left(6{\phi }^2-15\phi +10\right)$, $g\left(\phi \right)={\phi }^2\left(1-{\phi }^2\right)$, $f^S\left(c_s\right)$and$f^L\left(c_L\right)$are the free energies of the solid and liquid phases, respectively.

Therefore, the phase field equation can be re-expressed as:

$\frac{\partial \phi }{\partial t}=M_{\phi }\left[{ϵ}^2\left(\theta \right){\nabla }^2\phi +h\left(\phi \right)\left(f^L\left(c_L\right)-f^S\left(c_s\right)\right)-Wg\left(\phi \right)\right](3)$

where$M_{\varphi }$is the interface migration rate, $\epsilon$and$W$are the phase field parameters related to the interface energy and interface thickness.

2.2 Solute field equation

During the numerical simulation of directional solidification, it is also necessary to solve the solute diffusion equation at the same time. The diffusion equation is:

$\frac{\partial c}{\partial t}=\nabla \cdot \left(\frac{D\left(\phi \right)}{f_{cc}}\nabla f_c\right)(4)$

The effect of flow field action on solute diffusion during solidification was considered, and the microscopic flow field was coupled to the solute field equation by modifying the solute gradient term near the solid-liquid interface, it is feasible to simulate dendrite growth by considering a phase field model that incorporates the flow field (Natsume et al. (2005)). Therefore, the solute field equation under forced convection becomes:

$\frac{\partial c}{\partial t}=\nabla \cdot \left(\frac{D\left(\phi \right)}{f_{cc}}\nabla f_c\right)+k\nabla c(5)$

where$D\left(\varphi \right)$is the solute diffusion coefficient, $D\left(\phi \right)=D_L+h\left(\phi \right)\left(D_S-D_L\right)$, $D_S$and$D_L$are the solute diffusion coefficients of the solid and liquid phases, respectively, $f$is the free energy density of the metal system, and the subscript$c$represents the partial derivative of$f$, $k$is a parameter related to the flow velocity.

The solute concentration$c$in the interface region is the sum of the mass fractions of the solid and liquid phases. In addition, the chemical potentials of the solid and liquid phases at any point in the interface region are equal when the solid and liquid phases are in equilibrium:

$c=h\left(\phi \right)c_S+\left(1-h\left(\phi \right)\right)c_L(6)$

${\mu }^S\left(c_S\left(x,t\right)\right)={\mu }^L\left(c_L\left(x,t\right)\right)(7)$

where$c_L$and$c_S$are the solute concentrations in the liquid and solid phases, respectively, ${\mu }^L$and${\mu }^S$are the chemical potentials of the liquid and solid phases, respectively.

2.3 Determination of thermodynamic parameters and boundary conditions

Thermodynamic parameters of the alloy were obtained by the CALPHAD method (Kim et al. (1998); Chen et al. (2016)), as shown in Table 1.

TABLE 1

TABLE 1. Thermophysical data of alloys.

In the numerical simulation of directional solidification of aluminium alloy, the explicit difference solution method was used, and the 2D simulation interface was discretized into a grid space of 750 × 750. Grid size of $1.0\times {10}^{-8}\mathrm{m}$($dx=dy$; $dt=d{x}^2/5D_L$). 50 random nucleus were set underneath the calculation area. The Neumann boundary condition was used in the simulation, and the undercooling value was set to 20 K.

For the 2D simulation interface of the phase field coupled with flow field under conditions of roll casting, three different grid differential forms of$500\times 500$, $750\times 750$, $1000\times 1000$ were used according to the actual calculation needs. Grid size of$1\times {10}^{-6}\mathrm{m}$($dx=dy$; $dt=d{x}^2/5D_L$). The magnitude of anisotropy is$v=0.02$and the magnitude of the noise is $\omega =0.01$. A grid size of$10\times 10$nuclei was set in the center of the simulation plane. The Neumann boundary condition was used in the simulation. Frozen temperature approximation was employed (Langer, (2007)), and the undercooling value was set to 20 K.

3 The N-S equation and pressure Poisson equation were calculated by marker in cell (MAC) algorithm

The dendrites growth behavior of roll casting magnesium alloys was affected by the external field and the structure of the molten pool, which makes the roll casting microstructure show abundant dendrites morphology than ordinary casting and die-casting (Bao et al. (2020); Zhang et al. (2020); Wu et al. (2015)). Among them, the effect of flow field has a great influence on the growth morphology of dendrites. The flow in the molten pool was expressed as turbulent flow, and solving the continuity equation of the flow field was achieved by solving the Navier-Stokes (N-S) equation. The equation is a nonlinear partial differential equation, the solution of which is very difficult and complex, and the exact solution can be obtained only for some very simple flow problems. The N-S equation and the continuity equation are as follows:

$\frac{\partial u}{\partial t}+\frac{\partial \left(u^2\right)}{\partial x}+\frac{\partial \left(uv\right)}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)(8)$

$\frac{\partial v}{\partial t}+\frac{\partial \left(v^2\right)}{\partial y}+\frac{\partial \left(uv\right)}{\partial x}=-\frac{1}{\rho }\frac{\partial p}{\partial y}+\mu \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)(9)$

$\frac{\partial u}{\partial x}+\frac{\partial \nu }{\partial y}=0(10)$

where$u$and$v$indicate the components of the velocity vector in the horizontal and vertical directions, respectively. $\rho$indicates the density of the fluid, and$\mu$is the viscosity coefficient.

There are many algorithms for solving the N-S system of equations, the most famous of which is the Marker in Cell (MAC) algorithm (Zhang, (2010)). Initially, the MAC algorithm was specifically designed to solve for positions with free surfaces, but the MAC algorithm has been improved and extended, and applied to various incompressible viscous flows in recent years (Liu et al. (2019)). Chen et al. (Chen et al. (2016)) used the MAC algorithm to calculate the evolution of dendrites in the center of the roll casting melt pool and found that the microstructure was very similar to that of AZ31 alloy under the microscope. Jinho et al. (Jinho et al. (2007)) used the MAC algorithm to simulate the fluid flow process during the pure metal filling process and the subsequent solidification process. The fluid flow problem with free surface motion was analyzed, making it possible to predict the defects occurring during the filling and solidification processes. The MAC algorithm is a hybrid Eulerian-Lagrangian finite-difference algorithm with pressure and velocity as the original variables. When solving the N-S equation and continuity equation, Eqs 8–10 can be expressed as follows:

$\frac{\partial k}{\partial t}=-k\cdot \nabla k+\mu {\nabla }^{2}k-\frac{\nabla p}{\rho }(11)$

Where$p$is the pressure, $k$is a uniform representation of the velocity$u$in the horizontal direction and the velocity$v$in the vertical direction.

In order to facilitate programming, the above formula can be rewritten into discrete format:

$k^{n+1}=k^n+\mathrm{\Delta }t\left(-{\mathrm{A}}_{i,j}^n+{\mathrm{D}}_{i,j}^n\right)+\mathrm{\Delta }t{\nabla }_h{P}_{i,j}(12)$

${\nabla }_h\cdot k^{n+1}=0(13)$

Where${\mathrm{A}}_{i,j}^n$and${\mathrm{D}}_{i,j}^n$represent the divergence in the$\left(i,j\right)$grid, used to determine whether the iterations have converged, $P=p/\rho$, In the MAC algorithm difference scheme, $h=dx/L$, $L=Lx\cdot dx$, and$Lx$represent grid numbers.

Solving the above equation is divided into two steps: 1. Solving for$k^t$from$k^n$. 2. Solving$k^{n+1}$from$k^t$and satisfy${\nabla }_h\cdot k^{n+1}=0$.

For the numerical calculation, a staggered grid is used, and the x, y directions are designed in a differential format based on nodes$\left(i+\frac{1}{2},\mathrm{j}\right)$and$\left(i,j+\frac{1}{2}\right)$, respectively. The iterative flow and simulation results of multi-crystal phase field in the center of roll casting melt pool were shown in Figure 1.

FIGURE 1

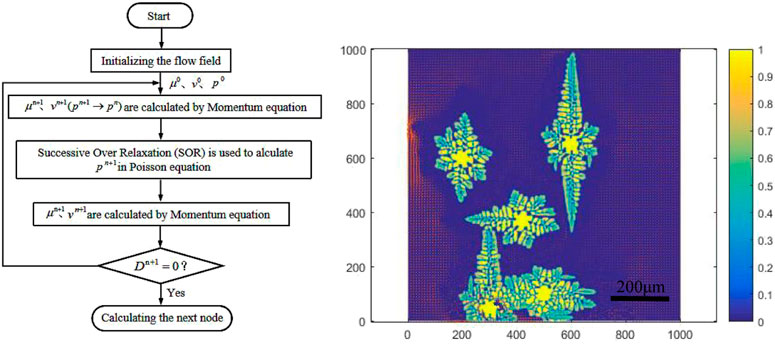
FIGURE 1. The iterative flow and simulation results of multi-crystal phase field in the center of roll casting melt pool.

4 Results and discussion

In order to better illustrate the universality of the KKS model for rare alloys, the KKS model is used to simulate the solidification process of aluminum alloys and directional solidification growth process of magnesium alloy under roll casting conditions at the edge of roll casting molten pool, respectively. In addition, in order to further describe the correctness of the influence of convection on the solidification process when the phase field KKS model is coupled with MAC algorithm, roll casting experiments are used to verify the convection effect.

4.1 Directional solidification of aluminium alloy by KKS model

4.1.1 The transformation process of aluminium alloy flat interface - Cell crystal - columnar dendrites

As shown in Figure 2, the transformation process of aluminium alloy flat interface - cell crystal - columnar dendrites was reproduced by phase field simulation. where the horizontal coordinate represents the grid scale and the different colors of the vertical coordinate describe the diffuse phase field interface. As the solidification progresses, the solutes at the front of the solid-liquid interface were enriched, which lead to the components supercooling. Therefore, the solidification flat interface unstable and evolves into a cellular morphology, resulting in the appearance of cellular crystals. The cellular crystals continue to grow under the action of supercooling, some of the cellular crystals were eliminated due to the phenomenon of competitive growth between dendrites. In addition, as solidification progresses, solutes are largely expelled due to the growth of equiaxed crystals. The solute will be enriched in the root of the main dendrites, inhibiting the growth of the root of the main dendrites. Therefore, the root position of the main dendrites appears to be necked. Overall, the growth of dendrites is consistent under the effect of supercooling degree, and only a small amount of secondary dendrites are found in Figure 2D. At a certain cooling rate, the appearance of secondary dendrite arms during the growth of primary dendrites is normal, but it can be seen from the figure that no secondary dendrites capable of hindering the growth of oriented primary dendrite arms have developed.

FIGURE 2

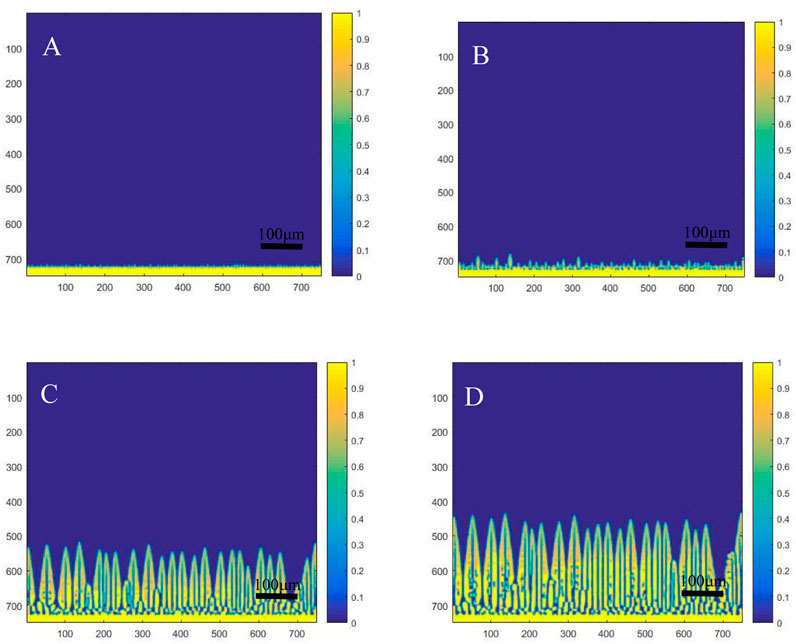
FIGURE 2. The dendrites growth of directional solidification at different stages: (A) 1000 dt; (B) 2000 dt; (C) 4000 dt; (D) 6000 dt.

4.1.2 Effect of anisotropy on interface morphology

The interfacial anisotropy strength has an important effect on the dendrites growth morphology and tip velocity. In this paper, the interfacial anisotropy was introduced into the phase field using Eq 14:

$ϵ\left(\theta \right)=ϵ\left[1+4\cos \gamma \left(\theta -{\theta }_0\right)\right](14)$

Where$\gamma$is the interface anisotropy coefficient, $\theta$is the angle between the normal direction of the interface and the main arms of the dendrites, ${\theta }_0$is the angle between the grain preferential growth direction and the horizontal direction, in this paper: ${\theta }_0=0$.

As shown in Figure 3, the dendrites growth morphology was simulated at the same calculation step for each anisotropy coefficient of 0.04, 0.05 and 0.06, respectively. When the anisotropy coefficient is 0.04, the dendrite arms are thicker, the growth rate is slower, there are no secondary dendrites, and the dendrites show a cytosolic structure. When the anisotropy coefficient increases to 0.05, the dendrites become denser, the radius of the dendrites tip becomes significantly smaller, the dendrites competition growth phenomenon becomes more obvious, and the elimination rate further increases. The growth rate is significantly faster than when the anisotropy coefficient was 0.04. When the anisotropy coefficient increases to 0.06, the growth rate of dendrites was almost constant, but the dendrites become denser. It can also be found from Figure 3 that with the increase of the anisotropy coefficient, the equiaxed crystals at the root of the dendrites are obviously refined. When the anisotropy coefficient is 0.06, the wall of the dendrite arms were unstable and secondary dendrites appear. Because of the accelerated growth of dendrites, the latent heat of solidification cannot be fully released. Therefore, the latent heat causes thermal disturbance on the dendrites surface, which develops secondary dendrites. The research shows that the anisotropy coefficient is proportional to the density of dendrites growth, but the increase of the anisotropy coefficient is not conducive to the growth of directional primary dendrites, and there is a tendency to develop secondary dendrites.

FIGURE 3

FIGURE 3. Effect on dendrites morphology by anisotropy: (A)$\gamma =0.04$; (B)$\gamma =0.05$; (C)$\gamma =0.06$.

4.1.3 Effect of interfacial energy on dendrites segregation and CET

According to the MS theory proposed by Mullins and Sekerka in the 1960s, the existence of interfacial energy has a very significant effect on dendrites growth (Mullins and Sekerka, (1985)). A large number of studies have also proved that interfacial energy can stabilize the solidification interface (Dantzig et al. (2013); Chen and Zhao, (2022)), but the research on the effect of interfacial energy on dendrites segregation and CET is still relatively scarce. In this paper, the effects of interfacial energy on dendrites solute segregation and CET transition were discussed. The relationship between the interface energy$\sigma$and the phase field parameters$M_{\varphi }$, $\epsilon$, and$W$were described by using Eqs 15–17:

$M_{\phi }^{-1}=\frac{{ϵ}^2}{\sigma }\left(\frac{RT}{V}\frac{1-k^e}{m^e}\beta \right)(15)$

$\epsilon =\sqrt{\frac{6\lambda }{2.2}\sigma }(16)$

$W=\frac{6.6\sigma }{\lambda }(17)$

Where$\beta$is the coefficient of interface dynamics, $R$is the gas constant, $T$is the temperature, $V_m$is molar volume, $m^e$is the equilibrium slope of the liquids, $k^e$is the equilibrium partition coefficient.

As shown in Figure 4, the solute field simulation results of directional solidification dendrites growth under the action of different interface energies are shown. When the interface energy was selected to be$0.06J\cdot m^{-2}$or$0.08J\cdot m^{-2}$, the solutes are mostly concentrated in the front of the solidification interface and between the dendrites. With the increase of the interfacial energy, the solute trapping phenomenon becomes more and more obvious. This is because the solute precipitated from the liquid phase during the growth of dendrites does not have time to diffuse, which leads to the solute interception phenomenon. In addition, with the interface energy increasing to$0.09J\cdot m^{-2}$, solute remelting can be observed. The reason is that the slope of liquidus is negative and the accumulation of solute leads to the decrease of melting point, which leads to solute remelting.

FIGURE 4

FIGURE 4. Effect on segregation by interface energy: (A)$\sigma =0.06J\cdot m^{-2}$; (B)$\sigma =0.08J\cdot m^{-2}$; (C)$\sigma =0.09J\cdot m^{-2}$.

Columnar dendrites and equiaxed crystal are two main components of casting solidification microstructure. Although the columnar dendrite structure has more beneficial axial mechanical properties, However, the equiaxed crystal structure will make the material more dense and optimization segregation phenomenon. It is very important to master the mechanism of CET transformation for controlling the solidification structure and predicting the performance of castings. Figure 5 reproduces the transformation process of dendrites to equiaxed crystals. It can be seen from the figure that as the solidification progresses, the dendrites tip grow into the liquid phase under the action of the temperature gradient. However, the dendrites were gradually broken from the root to the tip and transformed into equiaxed crystals, finally, all transformed. This is because the solute was greatly enriched in the solidification dendrites front and between the dendrites during the solidification process, which leads to component supercooling. CET occurs when the solute is sufficient to dissipate the supercooling of the columnar dendrites front. This is consistent with the solute blocking mechanism proposed by Martorano et al. (Martorano et al. (2003)). Based on the above analysis, it can be concluded that the increase of interfacial energy will lead to serious solute segregation. At the same time, the CET phenomenon is easier to occur when the interface energy is larger. Therefore, the effect of interface energy on the morphology of dendrites growth should not only be considered but also the effect of interface energy on the solute segregation of dendrites should be considered in the simulation of directional solidification.

FIGURE 5

FIGURE 5. CET transformation process.

4.2 Roll casting solidification of magnesium alloy by KKS model coupled convection

4.2.1 Effect of forced convection on the segregation and growth morphology of columnar dendrites for directional solidification at the melt pool edge

There is still a paucity of reports exploring dendrite segregation and edge directional solidification dendrite growth under conditions of roll casting. Chen et al. (Chen et al. (2016)) explored the effect of flow rate on grain growth in the center of the melt pool under conditions of roll casting, but did not investigate dendrite segregation and the growth of edge-directed dendrites. Therefore, this article is inspired and started work.

Figure 6 shows the simulation results of dendrites growth phase field and solute field of edge directional solidification under the condition of roll casting. From the phase field results (Figures 6A, B), it can be seen that a large number of cytosol crystals were produced and a thick protective shell was formed driven by the supercooling degree. And continues to transform to equiaxed dendrites. The dendrite grows further into the liquid phase, and at this time the dendrite was influenced by the high flow rate in the center of the roll casting molten pool. The direction of directional dendrites growth shifts upstream and the dendrites growth become more and more dense. In addition, the solute field simulation results show that the solute distribution coincides with the dendrite growth (Figures 6C, D). The concentration of solute in dendrite center is the lowest, which is due to the curvature effect of dendrite tip during solidification. Supercooling causes the solid line to move downwards, and the diffusion rate of solute in the solid phase is slower than the growth rate of Dendrite. In addition, solute enrichment occurs at the dendrite solidification interface, which is caused by the solute redistribution effect during solidification. The solute concentration in the solid phase is lower than the initial concentration, and the solute diffusion rate in the liquid phase is also lower than the dendrite growth rate. The solute can not fully diffuse into the liquid phase, thus enriching in the dendrite front. In the interface region surrounded by secondary dendrite arms, the solute is not easy to diffuse into the liquid phase, so the solute concentration is also relatively high.

FIGURE 6

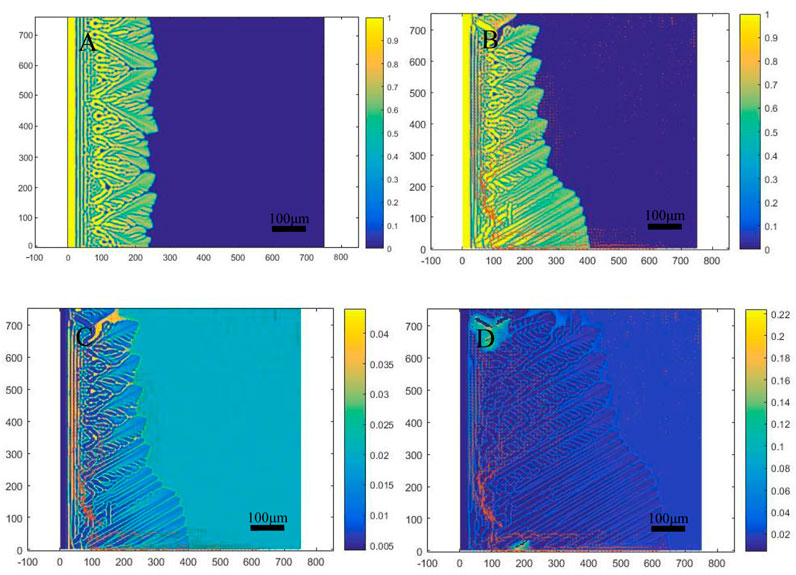
FIGURE 6. The simulation results of dendrites growth phase field and solute field of edge directional solidification under the condition of roll casting. (A,B) The simulation results of phase field. (C,D) The simulation results of solute field.

4.2.2 Effect of forced convection on the CET transition of dendrites in the roll casting melt pool and experimental verification

Figure 7 are the phase field simulation result of magnesium alloys and the actual roll casting experiment result. It can be seen from the diagram that the countercurrent dendrite arms easily induce lateral branching under the condition of rapid cooling roll casting. The dendrites showed obvious anisotropy, and the growth rate was inconsistent in all directions, the symmetry of the dendrites morphology was broken. The dendrites growth in the countercurrent direction was faster than that in the downstream direction under the action of forced convection. In addition, the length of each dendrite arms was different, and the dendrite arms become abnormally thick (Figures 7A, B). For the directional solidification region at the edge, the dendrites undergo solute remelting because of the mutual influence of supercooling and microscopic convection. Furthermore, the dendrites melt into equiaxed crystals, showing the phenomenon of CET (Figures 7C, D. Therefore, it is further proved that the micro flow field has a significant effect on the dendrite’s growth morphology. In addition, it is found by comparison that the dendrites morphology obtained from the simulation and the experiment are very similar, which reflects the accuracy of the simulation results in this paper.

FIGURE 7

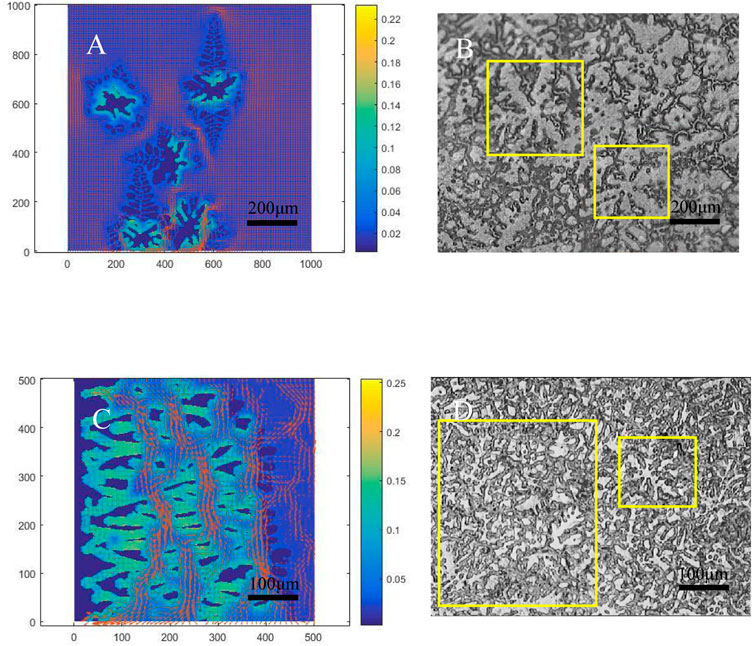
FIGURE 7. Phase field simulation results and microstructure comparison of Magnesium Alloy: (A) Simulation results of solute remelting of equiaxed crystals in the central area of roll casting; (B) Microstructure of central area of roll casting after experiment; (C) Simulation results of dendrites melt in directional solidification region of edge; (D) Microstructure of edge area of roll casting after experiment.

5 Conclusion

In this paper, based on the KKS phase field model coupled with the thermodynamic parameters, the transformation process from columnar dendrites to equiaxed crystal during directional solidification of aluminium alloy was simulated. The effects of phase field parameters on the growth morphology and dendrites segregation were discussed. In addition, considering the inherent convective environment of the actual roll casting process, the dendrite growth behavior of magnesium alloy under the action of microscopic convection in the roll casting was further explored. The conclusion as follows:

(1) The phase field simulation of dendrites morphology and competition growth between dendrites during directional solidification of aluminium alloy was realized, and the crystal growth mode of the flat interface - cell crystal - columnar dendrites - equiaxed crystals was reproduced.

(2) When the anisotropy coefficient is 0.04, the dendrite arms are thicker, the growth rate is slower, there are no secondary dendrites. When the anisotropy coefficient increases to 0.05, the dendrites become denser, the radius of the dendrites tip becomes significantly smaller, the dendrites competition growth phenomenon becomes more obvious. When the anisotropy coefficient increases to 0.06, the growth rate of dendrites was almost constant, and secondary dendrites were developed.

(3) In the process of directional dendrites growth, the solute trapping phenomenon becomes more and more obvious with the increase of the interfacial energy. Solute remelting occurs when the interfacial energy is$0.09J\cdot m^{-2}$. In addition, by reproducing the CET phenomenon of dendrites, it is further proved that the interface energy has a large effect on the CET transition, and it is consistent with the solute blocking mechanism proposed by Martorano et al.

(4) For the multi-crystal growth of magnesium alloy in the center of roll casting molten pool, the dendrites growth behavior exhibits obvious anisotropy under the action of the microscopic flow field. The symmetry of the dendrite’s morphology was destroyed, the dendrites growth in the countercurrent direction was faster than in the downstream direction, and the dendrite arms are thicker.

(5) For the directional solidification region at the edge of roll casting molten pool, directional solidification dendrites were affected by the high flow rate in the center of the roll casting melt pool during the growth process. The direction of directional dendrites growth shifts upstream, and the dendrites become denser. The dendrites undergo solute remelting because of the mutual influence of supercooling and microscopic convection. Furthermore, the dendrites melt into equiaxed crystals, showing the phenomenon of CET. And it was found by comparison that the dendrites morphology obtained from the simulation and the experiment is very similar, which reflects the accuracy of the simulation results in this paper.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding author.

Author contributions

HZ, XA, and MC contributed conception and design of the study. HZ organized the database and analytic result and wrote the first draft of the manuscript. HZ, MC, and XH provided the experimental resources and conducted experimental supervision. HZ, XA, MC, and XH did the writing-review and editing.

Acknowledgments

The authors acknowledge the financial support for this work from the 14th Five-Year National Key R and D Plan (2021YFB3702005), Liaoning Provincial Department of Education Project (LJKZ0281) and General Program of National Natural Science Foundation of China (51774179), as well as Key Technology and Demonstration Application of Steel for Marine Engineering Equipment in Extreme Environment (2020JH1/10100001). And The authors wish to thank the help given by the Roll casting Research Center of Magnesium Alloy in University of Science and Technology Liaoning.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, Y. J., Li, Y., Wei, B. W., Xu, B. Y., and Xu, G. M. (2020). Effect of cast-rolling rate on microstructure of Al-9Si-0.25Mg alloy cast-rolling sheet. Foundry Technol. 41, 974–977+985. doi:10.16410/j.issn1000-8365.2020.10.018

CrossRef Full Text | Google Scholar

Chen, L. Q., and Zhao, Y. H. (2022). From classical thermodynamics to phase-field method. Prog. Mater. Sci. 124, 100868–100869. doi:10.1016/j.pmatsci.2021.100868

CrossRef Full Text | Google Scholar

Chen, M., Hu, X. D., Han, B., Deng, X. H., and Ju, D. Y. (2016). Study on the microstructural evolution of AZ31 magnesium alloy in a vertical twin-roll casting process. Appl. Phys. A 122, 91–10. doi:10.1007/s00339-016-9627-4

CrossRef Full Text | Google Scholar

Chen, Z., Hao, L. M., and Chen, C. L. (2011). Simulation of faceted dendrite growth of non-isothermal alloy in forced flow by phase field method. J. Cent. South Univ. Technol. 18, 1780–1788. doi:10.1007/s11771-011-0902-4

CrossRef Full Text | Google Scholar

Cui, C., Liu, W., Deng, L., Ang, Y. W., Su, H., Wang, S., et al. (2020). Primary dendrite arm spacing and preferential orientations of the Ni–Si hypereutectic composites at different solidification rates. Appl. Phys. A 126, 898–899. doi:10.1007/s00339-020-04080-6

CrossRef Full Text | Google Scholar

Dantzig, J. A., Di Napoli, P., Friedli, J., and Rappaz, M. (2013). Dendritic growth morphologies in Al-Zn alloys-Part II: Phase-field computations. Metall. Mat. Trans. A 44A, 5532–5543. doi:10.1007/s11661-013-1911-8

CrossRef Full Text | Google Scholar

Geng, S., Jiang, P., Shao, X., Guo, L., and Gao, X. (2020). Heat transfer and fluid flow and their effects on the solidification microstructure in full-penetration laser welding of aluminum sheet. J. Mater. Sci. Technol. 46, 50–63. doi:10.1016/j.jmst.2019.10.027

CrossRef Full Text | Google Scholar

Ghosh, S., Karma, A., Plapp, M., Akamatsu, S., Bottin-Rousseau, S., and Faivre, G. (2019). Influence of morphological instability on grain boundary trajectory during directional solidification. Acta Mater. 175, 214–221. doi:10.1016/j.actamat.2019.04.054

CrossRef Full Text | Google Scholar

Jinho, L., Jinho, M., and Hong, C. P. (2007). Straightforward numerical analysis of casting process in a rectangular mold: From filling to solidification. Trans. Iron Steel Inst. Jpn. 39, 1252–1261. doi:10.2355/isijinternational.39.1252

CrossRef Full Text | Google Scholar

Kim, S. G., Kim, W. T., and Suzuki, T. (1998). Interfacial compositions of solid and liquid in a phase-field model with finite interface thickness for isothermal solidification in binary alloys. Phys. Rev. E 58, 3316–3323. doi:10.1103/physreve.58.3316

CrossRef Full Text | Google Scholar

Kim, S. G., Kim, W. T., and Suzuki, T. (1999). Phase-field model for binary alloys. Phys. Rev. E 60, 7186–7197. doi:10.1103/PhysRevE.60.7186

PubMed Abstract | CrossRef Full Text | Google Scholar

Langer, J. S. (2007). Instabilities and pattern formation in crystal growth. Rev. Mod. Phys. 52, 1–28. doi:10.1103/RevModPhys.52.1

CrossRef Full Text | Google Scholar

Lee, W., Jeong, Y., Lee, J. W., Lee, H., Kang, S. H., Kim, Y. M., et al. (2020). Numerical simulation for dendrite growth in directional solidification using LBM-CA (cellular automata) coupled method. J. Mater. Sci. Technol. 49, 15–24. doi:10.1016/j.jmst.2020.01.047

CrossRef Full Text | Google Scholar

Lenart, R., and Eshraghi, M. (2020). Modeling columnar to equiaxed transition in directional solidification of Inconel 718 alloy. Comput. Mater. Sci. 172, 109374–109378. doi:10.1016/j.commatsci.2019.109374

CrossRef Full Text | Google Scholar

Li, L. J., Li, W. M., Chen, M., and Zang, X. M. (2020). Application status of phase field method in metal solidification process. J. Iron Steel Res. 32, 847–859. doi:10.13228/j.boyuan.issn1001-0963.20200079

CrossRef Full Text | Google Scholar

Li, Y., Hong, L., and Han, B. (2021). Microstructure and volume shrinkage during directional solidification of peritectic steel. Mater. Sci. Technol. 37, 395–404. doi:10.1080/02670836.2021.1904600

CrossRef Full Text | Google Scholar

Liu, J. L., Lu, Y. Q., and Xu, B. (2019). Two dimensional debris flow numerical calculation model based on MACcormack-TVD finite difference algorithm. Bull. Sci. Technol. 35, 222–228.

Google Scholar

Luo, S., Wang, P., Wang, W., and Zhu, M. (2020). PF-LBM modelling of dendritic growth and motion in an undercooled melt of Fe-C binary alloy. Metall. Mat. Trans. B 51, 2268–2284. doi:10.1007/s11663-020-01925-6

CrossRef Full Text | Google Scholar

Ma, W., Li, R., and Chen, H. J. (2020). Three-dimensional CA-LBM model of silicon facet formation during directional solidification. Crystals 10, 669–710. doi:10.3390/cryst10080669

CrossRef Full Text | Google Scholar

Martorano, M. A., Beckermann, C., and Gandin, C. A. (2003). A solutal interaction mechanism for the columnar-to-equiaxed transition in alloy solidification. Metall. Mat. Trans. A 34, 1657–1674. doi:10.1007/s11661-003-0311-x

CrossRef Full Text | Google Scholar

Mullins, W. W., and Sekerka, R. F. (1985). On the thermodynamics of crystalline solids. J. Chem. Phys. 82, 5192–5202. doi:10.1063/1.448644

CrossRef Full Text | Google Scholar

Nabavizadeh, S. A., Eshraghi, M., Felicelli, S. D., Tewari, S. N., and Grugel, R. N. (2020). The Marangoni convection effects on directional dendritic solidification. Heat. Mass Transf. 56, 1329–1341. doi:10.1007/s00231-019-02799-4

CrossRef Full Text | Google Scholar

Natsume, Y., Ohsasa, K., and Narita, T. (2005). Investigation of the mechanism of alloy dendrite deflection due to flowing melt by Phase-Field simulation. Mat. Trans. 43, 2228–2234. doi:10.2320/matertrans.43.2228

CrossRef Full Text | Google Scholar

Noubary, K. D., Kellner, M., Steinmetz, P., Hoetzer, J., and Nestler, B. (2017). Phase-field study on the effects of process and material parameters on the tilt angle during directional solidification of ternary eutectics. Comput. Mater. Sci. 138, 403–411. doi:10.1016/j.commatsci.2017.07.006

CrossRef Full Text | Google Scholar

Novokreshchenova, A. A., and Lebedev, V. G. (2017). Determining the phase-field mobility of pure nickel based on molecular dynamics data. Tech. Phys. 62, 642–644. doi:10.1134/s1063784217040181

CrossRef Full Text | Google Scholar

Pinomaa, T., and Provatas, N. (2019). Quantitative phase field modeling of solute trapping and continuous growth kinetics in quasi-rapid solidification. Acta Mater. 168, 167–177. doi:10.1016/j.actamat.2019.02.009

CrossRef Full Text | Google Scholar

Shiga, K., Kawano, M., Maeda, K., Morito, H., and Fujiwara, K. (2019). The in situ observation of faceted dendrite growth during the directional solidification of GaSb. Scr. Mater. 168, 56–60. doi:10.1016/j.scriptamat.2019.04.022

CrossRef Full Text | Google Scholar

Sinhababu, A., and Bhattacharya, A. (2022). A fixed grid based accurate phase-field method for dendritic solidification in complex geometries. Comput. Mater. Sci. 202, 110973–110978. doi:10.1016/j.commatsci.2021.110973

CrossRef Full Text | Google Scholar

Steinmetz, P., Kellner, M., Hoetzer, J., and Nestler, B. (2018). Quantitative comparison of ternary eutectic phase-field simulations with analytical 3D jackson-hunt approaches. Metall. Materi. Trans. B 49, 213–224. doi:10.1007/s11663-017-1142-2

CrossRef Full Text | Google Scholar

Wang, J. W., Wang, Z. P., Yang, L. U., Zhu, C. S., Feng, L., and Xiao, R. Z. (2012). Effect of forced lamina flow on microsegregation simulated by phase field method quantitatively. Trans. Nonferrous Metals Soc. China 22, 391–397. doi:10.1016/S1003-6326(11)61189-8

CrossRef Full Text | Google Scholar

Wang, K., Wang, Y. X., Wei, P., Lu, Y. L., Zhang, J., and Chen, Z. (2019). Microscopic phase-field model and its application for solid-state phase transformation of alloys. Rare Metal Mater. Eng. 48, 3770–3780.

Google Scholar

Wang, Y. B., Wei, M. G., Liu, X. T., Chen, C., Wu, Y. J., Peng, L. M., et al. (2020). Phase-field study of the effects of the multi-controlling parameters on columnar dendrite during directional solidification in hexagonal materials. Eur. Phys. J. E 43, 41–49. doi:10.1140/epje/i2020-11964-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, C., Ke, C. B., Liang, S. B., Cao, S., Ma, H. T., and Zhang, X. P. (2020). An improved phase field method by using statistical learning theory-based optimization algorithm for simulation of martensitic transformation in NiTi alloy. Comput. Mater. Sci. 172, 109292–109298. doi:10.1016/j.commatsci.2019.109292

CrossRef Full Text | Google Scholar

Wu, X. H., Zhao, H. Y., and Hu, X. D. (2015). Microstructure and mechanical properties of twin-roll casting strips of high-Al Magnesium alloy. Special Cast. Nonferrous Alloys 35, 533–536. doi:10.15980/j.tzzz.2015.05.023

CrossRef Full Text | Google Scholar

Xiong, F., Gan, Z., Chen, J., and Lian, Y. (2022). Evaluate the effect of melt pool convection on grain structure of IN625 in laser melting process using experimentally validated process-structure modeling. J. Mater. Process. Technol. 303, 117538–117539. doi:10.1016/j.jmatprotec.2022.117538

CrossRef Full Text | Google Scholar

Yang, C., Xu, Q., and Liu, B. (2017). GPU-accelerated three-dimensional phase-field simulation of dendrite growth in a nickel-based superalloy. Comput. Mater. Sci. 136, 133–143. doi:10.1016/j.commatsci.2017.04.031

CrossRef Full Text | Google Scholar

Yang, C., Xu, Q. Y., and Liu, B. C. (2020). Phase-field-lattice Boltzmann simulation of dendrite growth under natural convection in multicomponent superalloy solidification. Rare Met. 39, 147–155. doi:10.1007/s12598-019-01292-5

CrossRef Full Text | Google Scholar

Yuan, X. F., and Ding, Y. T. (2012). Study on the phase field method of pure Ni dendrite growth under forced convection. Cast. Technol. 33, 913–917.

Google Scholar

Zhang, A., Du, J., Guo, Z., Wang, Q., and Xiong, S. (2019b). Phase-field lattice-Boltzmann investigation of dendritic evolution under different flow modes. Philos. Mag. 99, 2920–2940. doi:10.1080/14786435.2019.1646437

CrossRef Full Text | Google Scholar

Zhang, B., Zhao, Y., Chen, W., Xu, Q., Wang, M., and Hou, H. (2019a). Phase field simulation of dendrite sidebranching during directional solidification of Al-Si alloy. J. Cryst. Growth 522, 183–190. doi:10.1016/j.jcrysgro.2019.06.027

CrossRef Full Text | Google Scholar

Zhang, C., Guo, C., Zhang, S., Feng, H., Chen, Y., Kong, F., et al. (2020). The effect of rolling temperature on the microstructure and mechanical properties of 5 vol.% (TiBw + TiCp)/Ti composites. JOM J. Minerals 72, 1376–1383. doi:10.1007/s11837-019-03972-0

CrossRef Full Text | Google Scholar

Zhang, D. L. (2010). Computational fluid dynamics. BeiJing: Higher Education Press.

Google Scholar

Zhao, Y., Zhang, B., Hou, H., Chen, W., and Wang, M. (2019). Phase-field simulation for the evolution of solid/liquid interface front in directional solidification process. J. Mater. Sci. Technol. 35, 1044–1052. doi:10.1016/j.jmst.2018.12.009

CrossRef Full Text | Google Scholar

Zhu, C. S., Xu, S., Feng, L., Han, D., and Wang, K. M. (2019). Phase-field model simulations of alloy directional solidification and seaweed-like microstructure evolution based on adaptive finite element method. Comput. Mater. Sci. 160, 53–61. doi:10.1016/j.commatsci.2018.12.058

CrossRef Full Text | Google Scholar