Topological states in boron phosphide with zinc-blende structure

Li, Yang

doi:10.3389/fmats.2022.977595

ORIGINAL RESEARCH article

Front. Mater., 20 September 2022

Sec. Quantum Materials

Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.977595

This article is part of the Research Topic Innovators in Quantum Materials View all 5 articles

Topological states in boron phosphide with zinc-blende structure

Yang Li^1,2*

¹Aviation and Automobile School, Chongqing Youth Vocational and Technical College, Chongqing, China
²College of Physics, Chongqing University, Chongqing, China

The field of topological states in phonon of solids have been rapidly developing in recent years. This work examined the phonon dispersion of a compound Boron Phosphide (BP) with a Zinc-Blende structure via first-principle calculation. The results show that BP is a stable compound in theory and hosts rich topological signatures in its phonon dispersion. Specifically, Weyl and quadratic nodal line states can be found in the acoustic branches, and triple point and quadratic contact triple point can be found in the optical branches. It is hoped that the rich topological states in BP can be imaged by inelastic x-ray scattering or neutron scattering in the near future.

Introduction

Topological electronic materials have been one of the most active research fields in the past decade. To this date, many types of topological electronic materials (Wang, 2008; Li et al., 2009; Hasan and Kane, 2010; Moore, 2010; Qi and Zhang, 2011; Gao et al., 2016; Tokura et al., 2019; Wang et al., 2020a; Yue et al., 2020), including topological insulators (Hasan and Kane, 2010; Moore, 2010; Qi and Zhang, 2011; Tokura et al., 2019), spin-gapless semiconductors (Wang, 2008; Li et al., 2009; Gao et al., 2016; He et al., 2017; Wang et al., 2020a; Yue et al., 2020; Yang et al., 2021), topological semimetals (Vazifeh and Franz, 2013; Yang et al., 2015; Chang et al., 2016; Liu et al., 2019a; Wang et al., 2020b; Li and Xia, 2020; Lim et al., 2020; Liu et al., 2022a), (Li et al., 2020b; Li et al., 2020c; Li et al., 2020d), and topological superconducting (Chung et al., 2011; Stoudenmire et al., 2011; Sato and Ando, 2017; Zhang et al., 2018; Frolov et al., 2020), have been predicted in theory; some of them are also confirmed in experiments. For example, some three-dimensional (3D) material databases documented tens of thousands of candidates as topological semimetals. In 2019, Zhang et al. Zhang et al. (2019a) swept through 39,519 materials in the crystal database and proposed that 8,056 of 39,519 materials have topologically nontrivial properties. In the same year, Vergniory et al. Vergniory et al. (2019) performed a high-throughput search of high-quality materials in the Inorganic Crystal Structure Database (ICSD) database and found 4,078 topological semimetals. Tang et al. Tang et al. (2019) listed 692 topological semimetals with symmetry-dominated band crossing points around the Fermi level using symmetry indicators. In 2022, Yu et al. Yu et al. (2022) exhibited an encyclopedia of emergent particles in three-dimensional crystals. They completed a complete list of all possible particles in time-reversal-invariant systems using systematic symmetry analysis.

Very recently, the studies of topological states are intensively generalized to phonons in crystalline materials (Liu et al., 2020a; Chen et al., 2021a; Li et al., 2021). Many realistic solids with diverse topological signatures (Jin et al., 2018a; Jin et al., 2018b; Liu et al., 2019b; Xia et al., 2019; Li et al., 2020a; Liu et al., 2020b; Wang et al., 2020c; Peng et al., 2020; Zheng et al., 2020; Liu et al., 2021a; Wang et al., 2021a; Xie et al., 2021a; Zhou et al., 2021a; Chen et al., 2021b; Liu et al., 2021b; Wang et al., 2021b; Xie et al., 2021b; Zhou et al., 2021b; Liu et al., 2021c; Wang et al., 2021c; Liu et al., 2021d; Wang et al., 2021d; Zheng et al., 2021; Zhong et al., 2021; Ding et al., 2022a; Wang et al., 2022a; Ding et al., 2022b; Liu et al., 2022b; Wang et al., 2022b; Liu et al., 2022c; Yang et al., 2022) are reported via first-principle calculation and symmetry analysis. For example, in theory, solids with Weyl point phonons (Xia et al., 2019; Liu et al., 2020b; Wang et al., 2020c; Liu et al., 2021b), Dirac point phonons (Chen et al., 2021b), nodal chain phonons (Zhou et al., 2021b), nodal box phonons (Zhou et al., 2021b), nodal cage phonons (Ding et al., 2022a; Wang et al., 2022b), and nodal surface phonons (Xie et al., 2021b; Wang et al., 2021d) have been reported. More interestingly, some topological signatures in the phonon spectrum have been confirmed in an experiment with the help of meV-resolution inelastic X-ray scattering. In two consecutive works (Miao et al., 2018; Zhang et al., 2019b), the double Weyl points and the parity-time reversal symmetry-dominated helical nodal lines are realized in the phonon spectrum of FeSi and MoB₂, respectively.

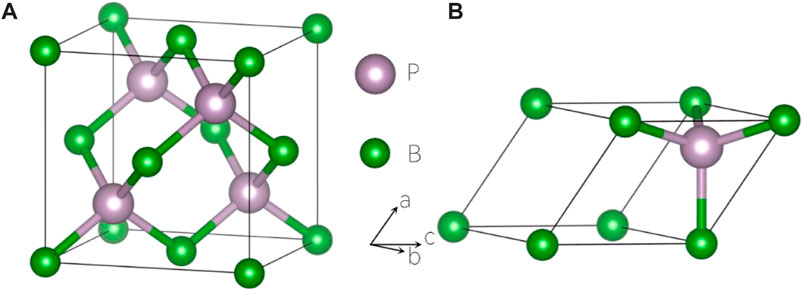
In particular, the coexistence of topological phonons in realistic materials has attracted much attention, such as the coexistence of zero-, one-, and two-dimensional degeneracy phonons (Wang et al., 2021a), hybrid-type nodal-ring and quadratic nodal-line phonons and nodal-net and nodal-link phonons (Zhou et al., 2021b), Dirac nodal line and Weyl nodal line phonons (Wang et al., 2022a). In this work, we focus on a realistic material (Popper and Ingles, 1957), Boron Phosphide (BP), with a Zinc-Blende structure, and study the topological signatures in the phonon dispersion of BP. BP has already been prepared before by the reaction of boron and red phosphorus in an evacuated, sealed silica tube at 1,100°C. BP is with space group F-43m (space group number 216) and contains two atoms, B and P, located at the (0,0,0) and (0.75,0.75,0.75) Wyckoff sites, respectively (see Figure 1A,B). The lattice structure of BP is totally relaxed via first-principle calculation, and the obtained lattice constant is a = b = c = 3.217 Å. To the best of our knowledge, the prosperous topological state has not even been previously reported in the phonon dispersion of BP, and this is the first time to report the topological phonons in the acoustic and optical branches of BP.

FIGURE 1

FIGURE 1. (A,B) crystal structure of unit cell and primitive cell of BP.

Computation methods

The theoretical calculation is performed in the framework of density functional theory (Cohen et al., 2012), which is implemented in the Vienna ab initio Simulation Package (Hafner, 2008). The generalized gradient approximation with Perdew-Burke-Ernzerhof formalism (Perdew et al., 1996) is used for the exchange-correlation energy, and the projector augmented wave method (Blöchl, 1994) is applied for the interactions between the ions and valence electrons. Moreover, a cutoff energy of 500 eV is chosen for the plane wave set, and a Γ-centered k grid of 5 × 5 × 5 is sampled for the Brillouin zone. Based on this optimized lattice of BP, we have computed the phonon dispersion spectrum of 2 × 2 × 2 supercell by the density functional perturbation theory, as implemented within the PHONOPY package (Togo and Tanaka, 2015).

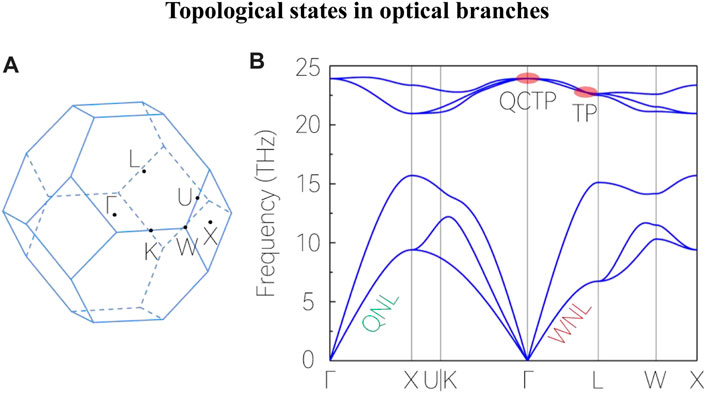
Topological states in optical branches

The phonon dispersion of BP along the $Γ - X - U | K - Γ - L - W - X$ (see Figure 2A) is shown in Figure 2B. BP system contains two atoms, so there should be six branches in the phonon dispersion, i.e., three acoustic branches and three optical branches. As shown in Figure 2B, one finds that there is no imaginary frequency in the phonon dispersion. Moreover, an acoustic-optical branch gap is visible.

FIGURE 2

FIGURE 2. (A) Three-dimensional (3D) Brillouin zone (BZ). (B) Phonon dispersion of BP.

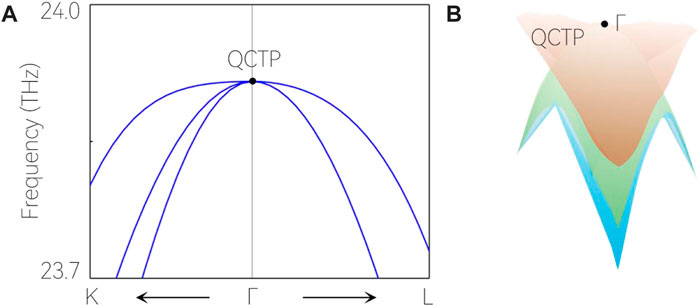
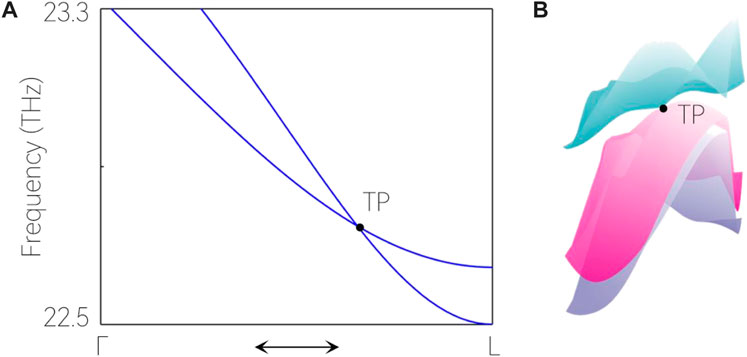
For the three optical branches, one finds two crossing points, one is at $Γ$ , and the other one is on $Γ - L$ path. The crossing point at $Γ$ is actually a quadratic contact triple point (QCTP). The QCTP is a zero-dimensional (0D) three-fold band degeneracy with a topological charge C = 0. The QCTP only occurs at high-symmetry point in spinless systems, and it features a quadratic energy splitting along any direction in momentum space (see the three-dimensional (3D) plot of the QCTP in Figure 3B). Moreover, the QCTP can split into a doubly degenerate band and a non-degenerate band along the certain high-symmetry line(s) (such as $Γ - L$ path in Figure 3A).

FIGURE 3

FIGURE 3. (A) Enlarged phonon dispersions of BP along $K - Γ - L$ path. (B) 3D plots of QTCP at $Γ$ .

As shown in Figure 4A, the crossing point on $Γ - L$ path is a triple point (TP) formed by a doubly degenerate band and a non-degenerate band. The 3D plot of the TP on $Γ - L$ path is shown in Figure 4B). TP on $Γ - L$ path features a linear energy splitting along any direction in momentum space, and is an accidental degeneracy in BZ. We would like to point out that Singh et al. (Singh et al., 2018) also provided evidence of the topological signature in a TP phonon. More interestingly, they (Singh et al., 2018) stated that the appearance of the topological band crossings in phonons could enhance the thermoelectric response in topological metals.

FIGURE 4

FIGURE 4. (A) Enlarged phonon dispersions of BP along $Γ - L$ path. (B) 3D plots of TP on $Γ - L$ path.

Topological states in acoustic branches

Then, we come to study the topological states in acoustic branches in BP. As shown in Figure 1C, one finds two doubly degenerate acoustic phonon bands appear along the $Γ - X$ and $Γ - L$ paths.

The crossing bands along the $Γ - X$ path belong to quadratic nodal line (QNL). The QNL is a 1D two-fold band degeneracy and features a quadratic energy splitting in the plane normal to the line. The QNL only occurs along high-symmetry line in 3D BZ. To prove the quadratic energy splitting features of the QNL, we selected some symmetry points, an (n = 1–4) (see Figure 5A), and calculated the phonon dispersions of BP along the bn-an-bn (n = 1–4). The results are shown in Figure 5B. Obviously, a series of crossing points (with green background) with quadratic energy splitting appear on the above k-paths.

FIGURE 5

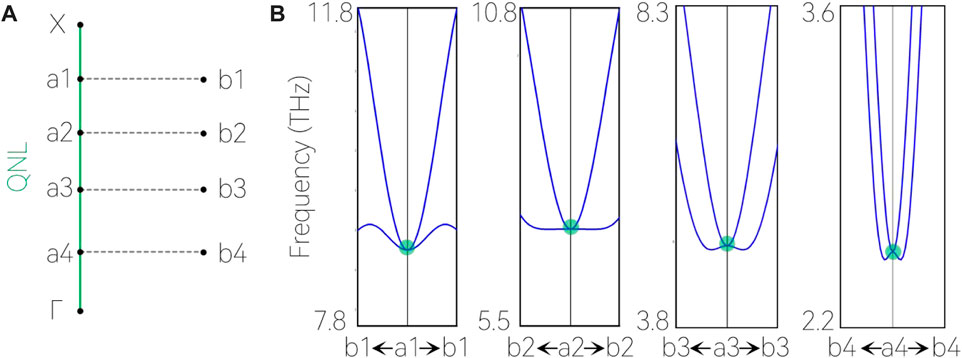
FIGURE 5. (A) Selected symmetry points a1 (0.4, 0.0, 0.4), a2 (0.3, 0.0, 0.3), a3 (0.2, 0.0, 0.2), a4 (0.1, 0.0, 0.1), b1 (0.9, 0.5, 0.4), b2 (0.8, 0.5, 0.3), b3 (0.7, 0.5, 0.2), and b4 (0.6, 0.5, 0.1). (B) Enlarged phonon dispersions of BP along the bn-an-bn (n = 1–4) paths.

Actually, the crossing bands along the $Γ - L$ path belong to Weyl nodal line (WNL). The WNL is a one-dimensional (1D) two-fold band degeneracy. The WNL features a linear energy dispersion in the plane normal to the line. Moreover, the Berry phase for WNL along the $Γ - L$ path equals π, indicating its topologically nontrivial behavior. As shown in Figure 6A, we selected some symmetry points (c1, c2, c3, and c4) on $Γ - L$ path, and c1-c4 points equally divided the line $Γ - L$ . The phonon dispersions of BP along the cn-dn (n = 1–4) are shown in Figure 6B. The band crossings (highlighted by red balls) with a linear band dispersion appear on the selected k paths, i.e., dn-cn-dn (n = 1–4).

FIGURE 6

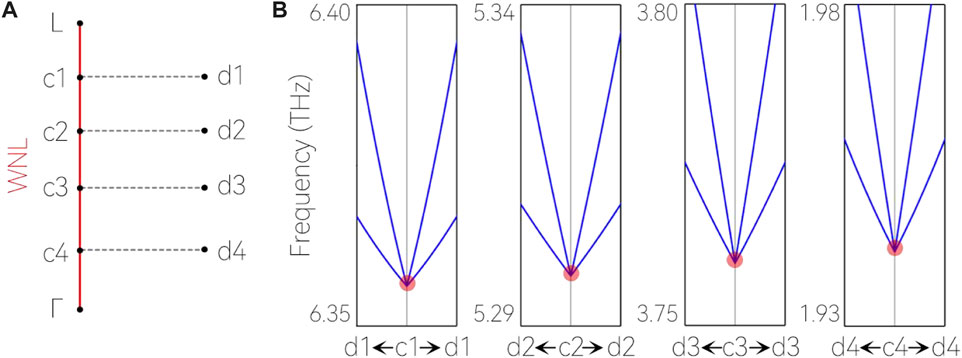
FIGURE 6. (A) Selected symmetry points c1 (0.4, 0.4, 0.4), c2 (0.3, 0.3, 0.3), c3 (0.2, 0.2, 0.2), c4 (0.1, 0.1, 0.1), d1 (0.4, 0.5, 0.4), d2 (0.3, 0.4, 0.3), d3 (0.2, 0.3, 0.2), and d4 (0.1, 0.2, 0.1). (B) Enlarged phonon dispersions of BP along the dn-cn-dn (n = 1–4) paths.

Summary

In this work, based on theoretical calculations, we studied the WNL, QNL, TP, and QTCP in the phononic system BP. The acoustic branches form the WNL and QNL and the optical branches form the TP and QCTP. There is a frequency gap between the acoustic and the optical branches. Furthermore, the rich nodal points and rich nodal lines are distributed at different frequency ranges. The WNL phonons along the $Γ - L$ , the QNL phonons along $Γ - X$ , the TP on $Γ - L$ , and the QCTP at $Γ$ are all symmetry-dominated. That is, to say, one can search these topological signatures in phononic systems with space group number 216. However, the TP is accidental degeneracies in 3D BZ; the other three signatures (QNL, WNL, and QCTP) are essential degeneracies in 3D BZ. The reported topological signatures in BP phonon are very clean, and the following technologies, including the inelastic x-ray scattering and neutron scattering, can be selected to image the bulk phonon dispersion of BP in an experiment. Subsequent experimental works are imminent.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Fundings

This work is supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJZD-K202104101), the Open Project Funding of Theoretical Physics Academic Exchange Platform of Chongqing University (Grant No. 2, in the year of 2021), and the school-level Scientific Research Project of Chongqing Youth Vocational and Technical College (Grant No. CQY2021KYZ03).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B, 50(24), 17953, 17979.doi:10.1103/physrevb.50.17953