Calculation of thermodynamic properties and transport parameters of C6F12O

C₆F₁₂O has good insulating properties and has the potential to be used as an insulating medium in gas-insulated equipment. Previous researches show that thermodynamic properties and transport parameters can reflect the microscopic properties of plasma and evaluate the physical properties of gas during gas discharge. In this paper, the thermodynamic and transport properties of C₆F₁₂O are calculated based on LTE conditions. According to the type of particles participating in the reaction and the thermal parameters, the number density of particles, the thermodynamic properties and transport parameters in the range of 300–30000 K are calculated. The results show that the conductivity of C₆F₁₂O is higher than that of CO₂ and N₂ at lower temperatures, which is consistent with the properties of most electronegative gases. The thermal conductivity of C₆F₁₂O has distinct peaks at 3500, 5500 and 16000 K, respectively. The calculation results can provide a data basis for the subsequent calculation of breakdown and interruption characteristics, which is significant to the design and development of gas insulating equipment.

Introduction

Gas insulation medium has the advantages of safety, reliability, long maintenance period and without aging, therefore, it plays a major role in the field of high voltage insulation (Xiao, 2016). Among various insulating gas media, SF₆ is widely used in electrical insulation equipment. Its insulation strength in uniform electric field is more than 2.5 times that of air (Tian et al., 2019a). Besides, it can recombine under the high temperature arc has excellent arc extinguishing performance. In terms of performance, SF₆ is a gas medium with excellent insulation, however, its global warming potential (GWP) of 23,500 can not be ignored (Hou et al., 2019; Zhang et al., 2020a). With the continuous development of the power industry, the content of SF₆ in the global atmosphere has increased by 20% in the past 5 years, which has a harmful impact on the environment. If it is left alone, it may cause the global average temperature to increase by 4°C or more until 2100 (Zhang et al., 2017a; Obama, 2017). Therefore, it is urgent to find an environmentally friendly insulating gas.

C₆F₁₂O is non-toxic and nonflammable, which is in focus due to the original application of extinguishing agent (Linteris et al., 2013). The molecular structure is shown in Figure 1. Further research shows that its insulation performance is more than twice that of SF₆ and the GWP value is close to 1, which has little impact on the environment. However, the liquefaction temperature of C₆F₁₂O is high, which needs to be mixed with buffer gas to meet the application requirements (Zhang et al., 2017b; Tian et al., 2018; Tian et al., 2019b; Wang et al., 2020a).

FIGURE 1

FIGURE 1. Molecular structure of C₆F₁₂O.

At present, the research on the related properties of C₆F₁₂O has made preliminary progress. In 2014, the experimental studies conducted by ABB show that the mixture of C₆F₁₂O and air or CO₂ has similar insulation performance to SF₆ under AC voltage and lightning impulse voltage (Mantilla et al., 2014). In recent years, some progress has been made in the domestic research on the insulation and decomposition properties of C₆F₁₂O. In 2017, Zhang et al. were the first to study the influence of the mixing ratio on the power frequency breakdown characteristics of C₆F₁₂O/N₂ mixture through experiments. The results show that the power frequency breakdown performance of 3% C₆F₁₂O/N₂ is 1.7 times that of pure N₂ under 0.1 MPa, which is very close to that of to N₂ after adding 10% SF₆ (Tian et al., 2018). Under this condition of pressure and mixing ratio, the products are mainly CF₄, C₂F₆, C3F₈, C₄F₁₀ and C₅F₁₂ after breakdown. When the buffer gas is CO₂, the breakdown voltage of 3% C₆F₁₂O/CO₂ mixture at 0.1–0.2 MPa is slightly higher than that of 10% SF₆/CO₂ mixture (Tian et al., 2019c). In further research, the team also studied the partial discharge characteristics of C₆F₁₂O/CO₂ mixture. Both the initial voltage and extinction voltage are positively correlated with the mixing ratio, and they are greatly influenced by the mixing ratio under the higher the pressure (Zhang et al., 2017b). In addition to the characteristics of the breakdown and decomposition, the team also studied thermal decomposition characteristics of C₆F₁₂O (Yi et al., 2019). The results show that decomposition products are mainly CF₄, C₂F₆, C₃F₈, C₃F₆ and C₅F₁₂ at high temperatures. For the compatibility of C₆F₁₂O and metal, existing studies have shown that the compatibility of C₆F₁₂O-air with aluminum is better than that of copper (Pan, 2021a; Pan, 2021b; Chen and Pan, 2022a; Chen and Pan, 2022b; Pan, 2022).

From a theoretical level, in 2020, Tian et al. calculated the total electron collision ionization cross section of the C₆F₁₂O molecule to evaluate its dielectric strength by using the Deutsch-Märk formula (Tian et al., 2019b). In 2019, Tang et al. analyzed its bond energy and bond angle in detail from the molecular level, then, its thermal stability was preliminarily revealed (Tang et al., 2019). In 2020, Zhong et al. comprehensively analyzed the decomposition mechanism of C₆F₁₂O through advanced quantum chemical calculations of DFT and TST on the basis of experimental research (Wang et al., 2020b). In 2021, Rao et al. calculated the formation process of C₆F₁₂O decomposition products based on DFT, which explained the formation process of decomposition products from a theoretical level (Rao et al., 2021).

The above theoretical and experimental researches on the insulation and decomposition characteristics of C₆F₁₂O have been carried out in a deeply study. Thermodynamic and transport parameters can be used to evaluate the interruption and breakdown characteristics of gas insulating media, now, some relevant calculations have been made in the study of other environmentally friendly insulating media (Zhang et al., 2020b; Zhang et al., 2020c). In this paper, the thermodynamic properties and transport parameters in the range of 300K–30000 K are calculated, which can provide a theoretical basis for the design and development of gas insulation equipment filled with C₆F₁₂O and buffer gases.

Calculation method

Based on the assumption that C₆F₁₂O is in local thermodynamic equilibrium (LTE), it is assumed that the discharge is in an ideal gas environment. Based on the partition function of each particle, the law of mass action, the law of partial pressure of Dolton, the ionization equation and the dissociation equation, electric neutrality, and atomic conservation are combined to calculate the number density of each particle. Then, various thermodynamic parameters can be obtained directly by using standard thermodynamic relations (Wang et al., 2011). The transmission of particle mass, momentum, and energy in the plasma can be described by the Boltzmann equation, therefore, the transport coefficients can be obtained by the Chapman-Enskog expansion of this equation (Wang et al., 2012).

Specifically, the law of mass action is that the rate of chemical reaction is proportional to the effective mass of the reactants. The law of partial pressure of Dolton is that the partial pressure in a gas mixture is equal to the pressure when it occupies the entire region alone at the same temperature, and the sum of the pressures of the components in the mixture is the mixture’s pressure. The Saha ionization equation and Guldberg-Waage dissociation equation indicates that the atomic concentration and ion concentration are keep balance depending on ionization and recombination, which are calculated through formula (1) and (2).

$\frac{n_e\left(T\right)\cdot n_{{\left(z+1\right)}^{+}}\left(T\right)}{n_{z^{+}}\left(T\right)}=\frac{Q_e^{\mathrm{int}}\cdot Q_{{\left(z+1\right)}^{+}}^{\mathrm{int}}\left(T\right)}{Q_{z^{+}}^{\mathrm{int}}\left(T\right)}\cdot {\left(\frac{2\pi m_e{k}_{b}T}{h^2}\right)}^{\frac{3}{2}}\exp \left(-\frac{E_{\text{ion}}}{k_{b}T}\right)(1)$

$\frac{n_A\left(T\right)\cdot n_B\left(T\right)}{n_{AB}\left(T\right)}=\frac{Q_A^{\mathrm{int}}\cdot Q_B^{\mathrm{int}}\left(T\right)}{Q_{AB}^{\mathrm{int}}\left(T\right)}\cdot {\left(\frac{m_A\cdot m_B}{m_A+m_B}\right)}^{\frac{3}{2}}\cdot {\left(\frac{2\pi k_{b}T}{h^2}\right)}^{\frac{3}{2}}\exp \left(-\frac{E_{\text{dis}}}{k_{b}T}\right)(2)$

Q^int is the internal partition function of the particle. n_i is the number density of the particle, m_e is the mass of the electron, K_b is the Boltzmann constant, h is the Planck constant and Eion is the ionization energy of the particle. m_A, m_B, and m_AB are the masses of the particles and E_dis is the dissociation energy.

For the partition function of a particle, it is significant in the calculation. It is the sum of the Boltzmann factors of its possible states in the system, which reflects the structural characteristics and thermal parameters of the particle. According to the molecular structure of C₆F₁₂O and preliminary research, C₆F₁₂O may decompose to a variety of different particles after discharge, which can be divided into monatomic and polyatomic particles to calculate the partition function, respectively. There are 13 kinds of monatomic particles: C, C⁻, C⁺, C²⁺, O, O⁻, O⁺, O²⁺, F, F⁻, F⁺, F²⁺, e. Diatomic particles are 12 types: C₂, C₂⁻, F₂, F₂⁺, O₂, O₂⁻, O₂⁺, CF⁺, CF, FO, CO, CO⁺. Polyatomic particles are 34 types: C₃, CF₂, CF₂⁺, CO₂, CFO, F₂O, C₂O, FO₂, F₂O₂, C₄, C₅, C₂F, C₂F₂, CF₃, C₂F₄, C₃F, C₃F₄, C₃F₆, C₃F₆O, C₃O₂, CF₄, C₂F₆, C₂F₆O, CF₂O, CF₄O, C₃O₂, C₃F₈, C₃F₇, C₄F₈O, C₄F₁₀O, C₅F₈, C₅F₁₀, C₅F₁₀O, C₆F₁₂O.

The calculation methods of different types of particles are slightly different for the partition function. The atoms can be directly calculated according to Formula 1. In the formula: $Q_i^{\mathrm{int}}$ is the internal partition function of particle i; g_n is the degeneracy of the nth electron energy level; ${\epsilon }_n$ is the energy value of the nth electron energy level.

$Q_i^{\mathrm{int}}={\displaystyle \sum _n{g}_n\exp \left(-\frac{{\epsilon }_n}{k_{b}T}\right)}(3)$

When calculating the partition function of diatomic particles, the vibrational energy level and the rotational energy level also need to be considered except the electronic excitation energy level, as shown in Formula 4.

$\begin{array}{c}{Q}_i^{\mathrm{int}}=Q_i^{\mathrm{el}}\cdot Q_i^{vib}\cdot Q_i^{rot}\\ =\frac{1}{\sigma }{\displaystyle \sum _{T_e}\left\{g_e\exp \left(-\frac{T_e}{k_{b}T}\right){\displaystyle \sum _v^{v_{\max }}\left(g_v\exp \left(-\frac{G_v\left(T_e\right)}{k_{b}T}\right){\displaystyle \sum _J^{J_{\max }}\left(g_J\exp \left(-\frac{F_v\left(J\right)}{k_{b}T}\right)\right)}\right)}\right\}}\end{array}(4)$

Where $Q_i^{\text{el}}$ is the electron internal partition function of particle i, $Q_i^{vib}$ is the oscillation partition function of particle i, $Q_i^{rot}$ is the rotational partition function of particle i, T_e is the excitation energy level of the particle, v is the vibrational energy level of the particle, and J is the particle vibration energy level. The spectral data involved can be obtained from the NIST database.

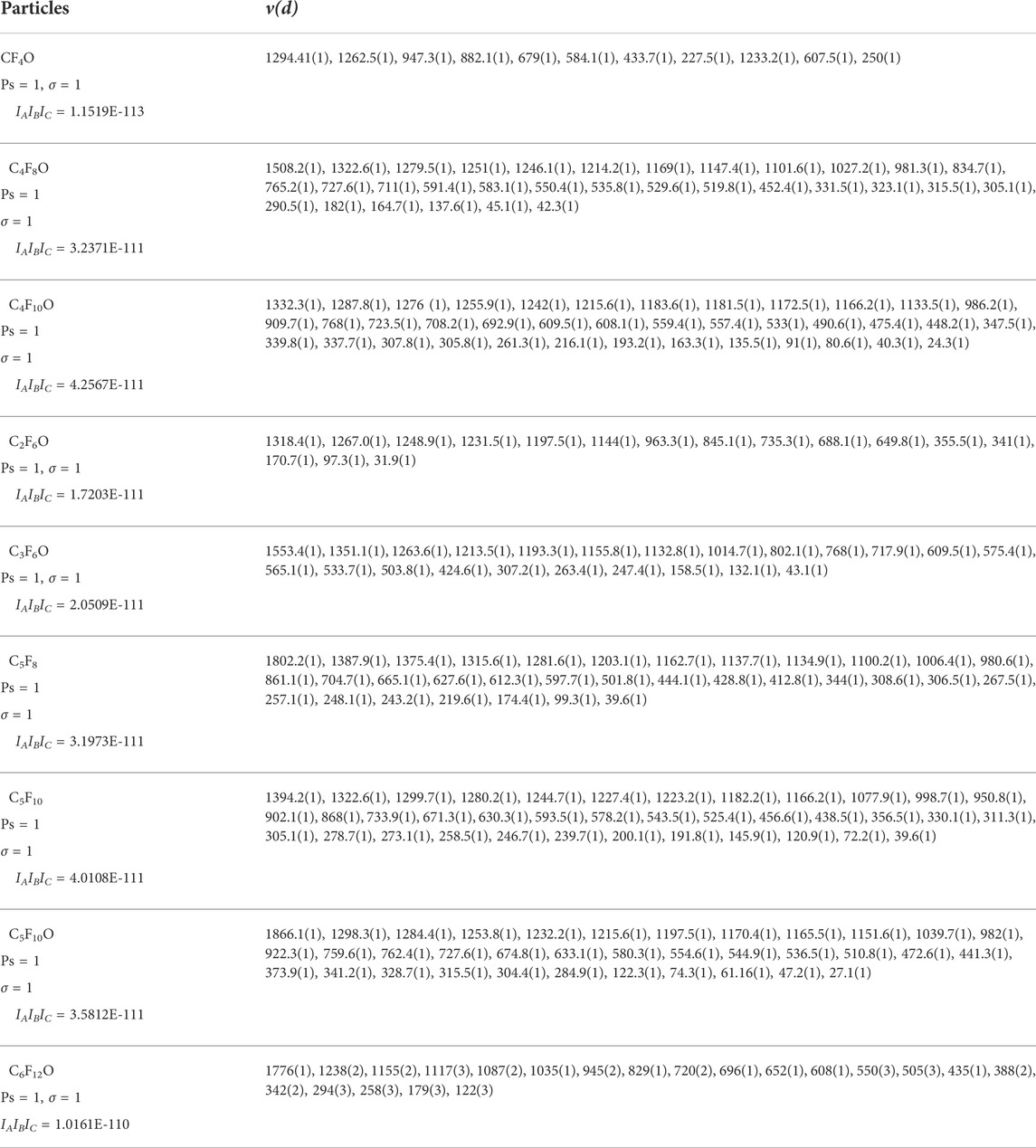
For the calculation of the partition function of polyatomic particles needs to be divided into linear particles and nonlinear particles. During the calculation, some required vibration parameters and rotation parameters can be found in the JANAF thermochemical data manual. In addition, for the macromolecular particles CF₄O, C₄F₈, C₄F₁₀O, C₆F₁₂O, C₅F₈, C₅F₁₀, C₅F₁₀O, C₂F₆O and C₃F₆O, the models of them are built and the geometric optimizations are carried out in Materials Studio. Then, the vibration parameters and rotation parameters with the stable structures are calculated based on the density functional theory, the results are shown in Table 1.

TABLE 1

TABLE 1. Calculated values of vibration parameters and rotation parameters of polyatomic particles.

Based on the partition functions of different particles, the nonlinear equations are obtained in combination with ionization equation, dissociation equation, electric neutrality principle, atomic conservation and Dalton’s partial pressure law. The number density of each particle are calculated through Newton iterative method to get the thermodynamic parameters (Cressault, 2001; Cressault and Gleizes, 2004; Boulos et al., 2013).

The transport parameters of C₆F₁₀O can be calculated based on the mass, momentum and energy transmission of the particles in the plasma. Based on the interaction potential, the collision integrals between different particles at different temperatures are analyzed and calculated, then, the Chapman-Enskog expansion is performed on them to obtain the transport coefficients. During the calculation of the collision effect, the required parameters of the binding energy, the distance between the two particles when the potential energy is zero and the polarization rate of most macromolecules can be obtained from literature (Cressault et al., 2011). In addition, for other macromolecules, the relevant parameters are calculated by quantum chemistry method in Materials Studio, the calculation results are shown in Table 2.

TABLE 2

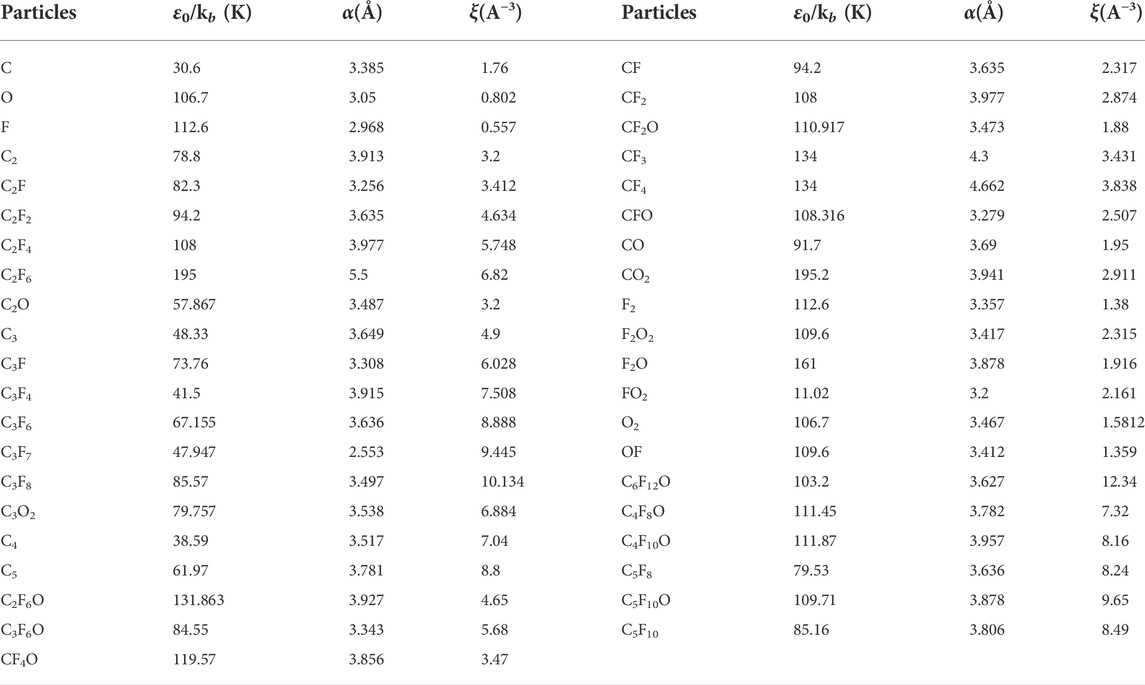
TABLE 2. The key parameters of collision integral the main neutral particle (Yu et al., 2017; Zhong et al., 2017).

Analysis of calculation results

Number density of particles

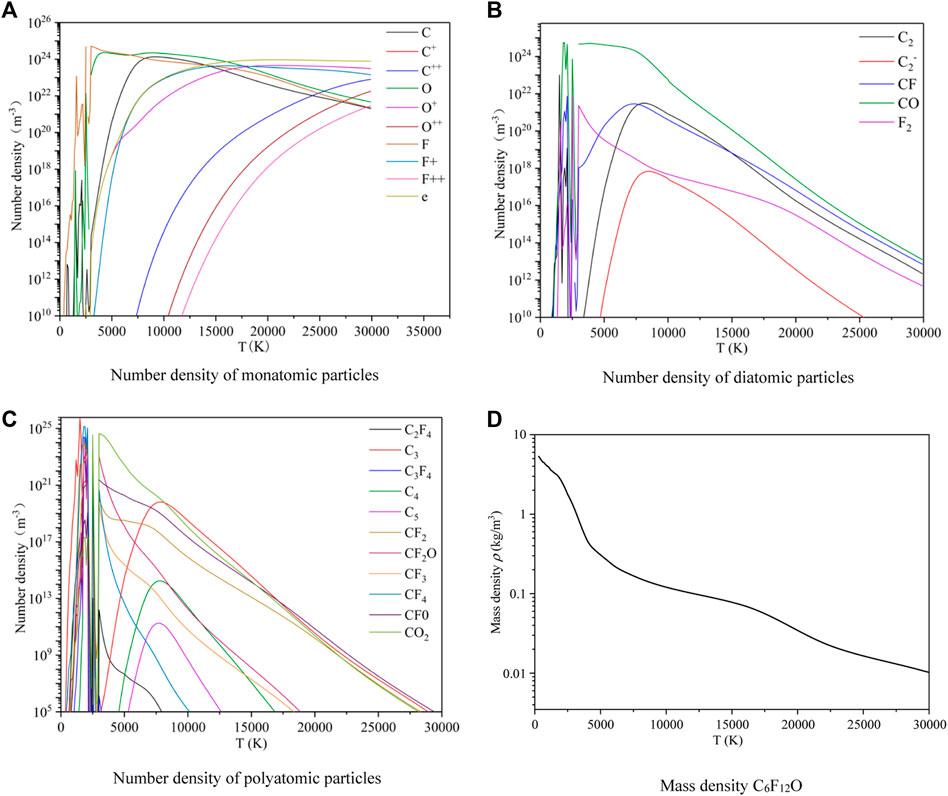
The monatomic, diatomic and polyatomic particles can be produced after the ionization and dissociation of C₆F₁₂O at 0.1 MPa. As shown in Figures 2A–C, it is the change of the number density of each particle at 300 K–30000 K. With a rise of temperature, some small molecular particles such as C₂, C₂F₄, C₃, C₃F₄, C₄, C₅, CF, CF₂, CF₂O, CF₃, CF₄, CFO, CO, CO₂ and F₂ are firstly dissociated from C₆F₁₂O between 300 and 3000 K. At the same time, the appearance of C, F and O are accompanied with ionization. As the temperature continuously rises, the number density of most particles begins to decrease and the secondary ionization process occurs. When the temperature is high enough, there are a large number of monatomic particles C₂⁺, F₂⁺ and O₂⁺ in the plasma. Therefore, the proportion of macromolecules is low at high temperature. For polyatomic particles produced during discharge, the number density is relatively low, which is less than 10¹⁴/m³.

FIGURE 2

FIGURE 2. Number density and mass density of main particles.

As shown in Figure 2D, it is the mass density of C₆F₁₂O, which is obtained by summing the product of the number density and mass corresponding for the above particles. Under the constant pressure, with the increase of the temperature, the total number of particles increases due to the increasing decomposition of the plasma, which can increase the total volume of the system. Therefore, the mass per unit volume continuously decrease. Some small molecular particles appear at 300–3000 K, so the mass density of C₆F₁₂O decreases rapidly in this temperature range.

Thermodynamic parameters

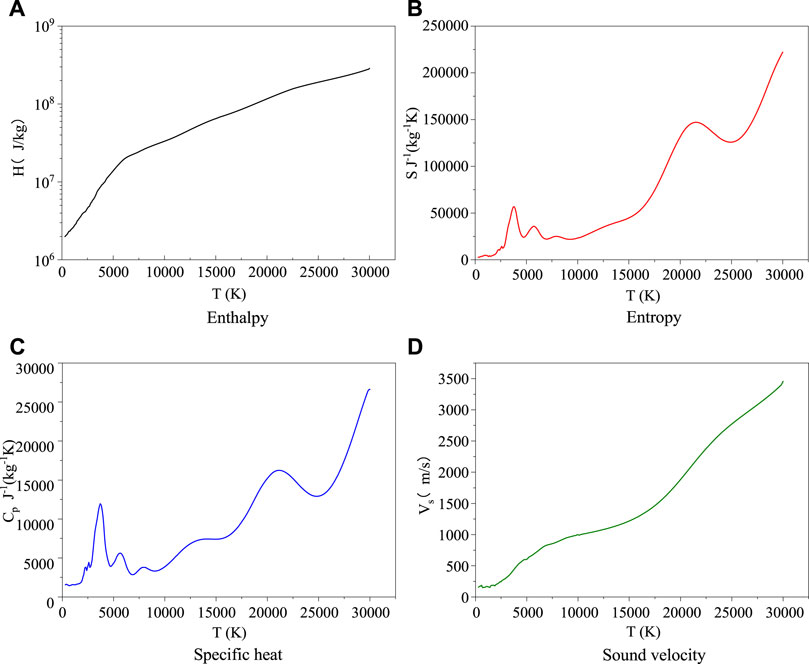
Based on the particle number density obtained above, the main thermodynamic parameters of enthalpy H, entropy S, specific heat C_p and sound velocity V_s of C₆F₁₂O are calculated. As shown in Figure 3, it is the calculation results of main thermodynamic parameters of C₆F₁₂O at 0.10 MPa.

FIGURE 3

FIGURE 3. The calculation results of main thermodynamic parameters of C₆F₁₂O.

As shown in Figure 3, it is the calculation results of main thermodynamic parameters of C₆F₁₂O at 0.10 MPa. Among them, the change trend of enthalpy, entropy and sound velocity is roughly the same as that of most other gases. The specific heat has an obvious peaks in the temperature range of 300–5000 K and 20000–25000 K. The position of the peak is generally considered to be caused by endothermic reaction processes of particles. Therefore, combined with the analysis of the change of particle number density, the peak can be considered to be caused by the dissociation between particles below 1000 K. At higher temperatures, the appearance of the peak is mainly due to the peak change caused by the ionization of atoms.

Transportation parameters

Conductivity

Conductivity σ_e is a physical quantity used to characterize the electron conduction characteristics in plasma, which is closely related to the electron number density and ionization degree. The expression is as follow.

${\sigma }_e=\frac{e^2{n}_e}{\sqrt{2m_e\pi T}\cdot n_a{\sigma }_{en}}(5)$

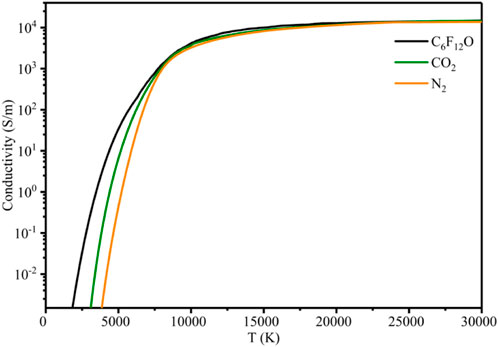
Where e, n_e, m_e, n_a, σ_en are the amount of elementary charge, number density of electron, electronic mass, number density of neutral particles and collision cross section between electrons and neutral particles, respectively. The internal conductivity of σ can be obtained by the calculation of Chapman-Enskog third-order approximation. The conductivity of C₆F₁₂O, CO₂ and N₂ at 0.1 MPa is calculated by the above method, as shown in Figure 4. It can be seen that when the temperature is higher than 10000 K, the conductivity difference of the plasma formed by the three gases is small and the curves of them with temperature almost coincide. When the temperature is low, the curves show obvious differences with the change of temperature. Specifically, the curve of C₆F₁₂O is higher than that of CO₂ and N₂, which is consistent with the properties of most electronegative gases.

FIGURE 4

FIGURE 4. Conductivity of C₆F₁₂O, CO₂ and N₂.

Thermal conductivity

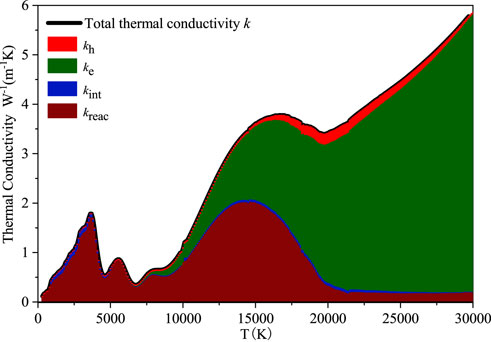
The Thermal conductivity k characterizes the ability of a material to directly conduct heat, which is consisted of heavy particle thermal conductivity k_h, electron thermal conductivity k_e, internal thermal conductivity k_int and reaction thermal conductivity k_reac. The k_h, k_e and k_int are calculated through the second approximation order, the third approximation order and the first approximation order of the Chapman-Enskog method, respectively. The k_reac is obtained from the Butler and Brokaw theory. Among them, the internal thermal conductivity is caused by the change of heat transfer energy due to the internal degrees of freedom of particles. The specific calculation method can refer to Reference (Wang et al., 2020b).

Figure 5 shows the calculation results of each part and total thermal conductivity of C₆F₁₂O. It can be seen that the proportion of thermal conductivity of each part at different temperatures. When the temperature is low, the total thermal conductivity of C₆F₁₂O mainly depends on the reaction thermal conductivity, which is related to the enthalpy of particle reaction. When the temperature is higher than 20000 K, the reaction thermal conductivity decreases to a lower level. When the temperature is higher than 7000 K, the electron thermal conductivity increases significantly with the increase of the temperature, which is mainly because of the enhancement of atomic ionization and the increase of the electron number density at higher temperature. When the temperature continuously rises to higher than 20,000 K, the contribution of electronic thermal conductivity to the total thermal conductivity is dominant.

FIGURE 5

FIGURE 5. Calculation results of thermal conductivity of C₆F₁₂O.

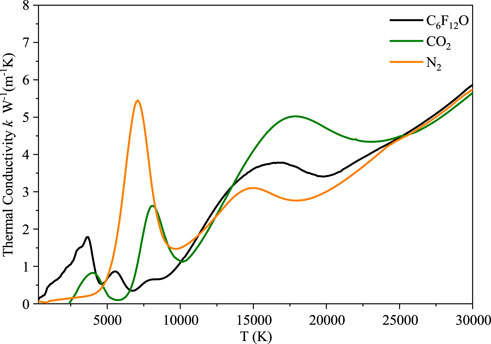
As shown in Figure 6, the thermal conductivities of CO₂ and N₂ are compared with that of C₆F₁₂O. The calculation results of thermal conductivities of CO₂ and N₂ are consistent with those in literature (Cressault and Gleizes, 2004). Since the types and number densities of particles formed by different gases at different temperatures are different, the thermal conductivities of different gases show different amplitudes for the peaks at different temperatures. At the same time, the number density of electron increases significantly with the gradual increase of temperature, and the change of the whole thermal conductivity shows an upward trend. The thermal conductivity of C₆F₁₂O has three obvious peaks, which appear at 3500 K, 5500 K and 16000 K, respectively.

FIGURE 6

FIGURE 6. Thermal conductivity of C₆F₁₂O, CO₂ and N₂.

Conclusion

In this paper, according to all possible particle types, the nonlinear equations are written through the conditions satisfied by LTE to obtain the number density of each particle. Then, the thermodynamic parameters are obtained with partition function and the transport parameters are obtained by calculating the collision cross sections between different particles. The specific conclusions are as follows:

(1) With the increase of temperature, small molecular particles C₂, C₂F4, C₃, C₃F₄, C₄, C₅, CF, CF₂, CF₂O, CF₃, CF₄, CFO, CO, CO₂, F₂, etc. firstly appear between 300 and 3000 K. At the same time, the appearance of C, F and O are accompanied with ionization. As the temperature continuously rises, the number densities of most particles begin to decrease and the secondary ionization process occurs. When the temperature is high enough, there are a large number of C₂⁺, F₂⁺ and O₂⁺ in the plasma.

(2) When the temperature is higher than 10000 K, the conductivities of the plasma formed by C₆F₁₂O, CO₂ and N₂ at different temperatures are almost the same. At low temperature, the difference of the conductivities is obvious. Specifically, the conductivity of C₆F₁₂O is higher than that of CO₂ and N₂, which is consistent with the properties of most electronegative gases.

(3) The thermal conductivity of different gases show peaks with different amplitudes at different temperatures and the overall thermal conductivity shows an upward trend. There are three obvious peaks in the thermal conductivity of C₆F₁₂O, which appear at 3500, 5500 and 16000 K, respectively.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XR, DL, and XZ performed calculations on the data, BP and LZ performed statistical analysis, and YL and SM wrote the first draft of the paper. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of interest

Authors XR, DL, XZ, BP, LZ, YL, and SM were employed by Electric Power Research Institute of Guangxi Power Grid Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boulos, M. I., Fauchais, P., and Pfender, E. (2013). Thermal plasmas: fundamentals and applications[M]. New York, NY: Springer Science & Business Media.

Google Scholar

Chen, Shuang, and Pan, Yong (2022). Enhancing catalytic properties of noble metal@MoS2/WS2 heterojunction for the hydrogen evolution reaction. Appl. Surf. Sci. 591, 153168. doi:10.1016/j.apsusc.2022.153168

CrossRef Full Text | Google Scholar

Chen, Shuang, and Pan, Yong (2022). Mechanism of interlayer spacing on catalytic properties of MoS2 from ab-initio calculation. Appl. Surf. Sci. 599, 154041. doi:10.1016/j.apsusc.2022.154041

CrossRef Full Text | Google Scholar

Cressault, Y., Connord, V., Hingana, H., Teulet, P., and Gleizes, A. (2011). Transport properties of CF3I thermal plasmas mixed with CO₂, air or N₂ as an alternative to SF₆ plasmas in high-voltage circuit breakers[J]. J. Phys. D. Appl. Phys. 44 (49), 495202. doi:10.1088/0022-3727/44/49/495202

CrossRef Full Text | Google Scholar

Cressault, Y. (2001). Propriétés des plasmas thermiques dans des mélanges argon-hydrogene-cuivre [D]. Toulouse: Université Paul Sabatier-Toulouse III.

Google Scholar

Cressault, Y., and Gleizes, A. (2004). Thermodynamic properties and transport coefficients in Ar–H₂–Cu plasmas. J. Phys. D. Appl. Phys. 37 (4), 560–572. doi:10.1088/0022-3727/37/4/008

CrossRef Full Text | Google Scholar

Hou, H., Yan, X., Yu, X., Liu, W., Liu, Z., and Wang, B. (2019). Theoretical investigation on the adsorption of C₄F₇N/CO₂ dielectric gas and decomposition products in zeolite [J]. High Volt. Eng. 45 (04), 1040–1047.

Google Scholar

Linteris, G. T., Babushok, V. I., Sunderland, P. B., Takahashi, F., Katta, V. R., Meier, O., et al. (2013). Unwanted combustion enhancement by C₆F₁₂O fire suppressant[J]. Proc. Combust. Inst. 34 (2), 2683–2690. doi:10.1016/j.proci.2012.06.050

CrossRef Full Text | Google Scholar

Mantilla, J D., Gariboldi, N., Grob, S., and Claessens, M. (2014). “Investigation of the insulation performance of a new gas mixture with extremely low GWP[C],” in IEEE Electrical Insulation Conference, Philadelphia, PA, USA, 08-11 June 2014 (IEEE), 469–473.

Google Scholar

Obama, B. (2017). The irreversible momentum of clean energy. Science 355 (6321), 126–129. doi:10.1126/science.aam6284

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, Yong (2022). First-principles investigation of structural stability, electronic and optical properties of suboxide (Zr3O). Mater. Sci. Eng. B 281, 115746. doi:10.1016/j.mseb.2022.115746

CrossRef Full Text | Google Scholar

Pan, Yong (2021). Influence of N vacancy on the electronic and optical properties of bulk GaN from first principles investigations. Int. J. Energy Res. 45 (10), 15512–15520. doi:10.1002/er.6744

CrossRef Full Text | Google Scholar

Pan, Yong (2021). The influence of Ag and Cu on the electronic and optical properties of ZrO from first-principles calculations. Mater. Sci. Semicond. Process. 135, 106084. doi:10.1016/j.mssp.2021.106084

CrossRef Full Text | Google Scholar

Rao, X., Li, D., Xia, X., Su, Y., Lu, Y., Peng, B., et al. (2021). Study on discharge decomposition characteristics of environmentally friendly gas C₆F₁₂O/CO₂ [J]. Vacuum 186 (5), 110004. doi:10.1016/j.vacuum.2020.110004

CrossRef Full Text | Google Scholar

Tang, J., Lei, Z., Wan, Z., Yao, Q., Gao, K., and Zeng, F. (2019). “Reaction Thermodynamics of Overthermal Decomposition of C₆F₁₂O [J],” in Proceedings of the CSEE, Rome, Italy, April 7-9, 2019 (CSEE), 5257–5262+5306.

Google Scholar

Tian, S., Zhang, X., Song, X., Deng, Z., Yi, L., Tang, J., et al. (2019). Experimental research on insulation properties of C₆F₁₂O/N₂ and C₆F₁₂O/CO₂ gas mixtures[J]. Generation, Transmission & Distribution. IET Gener. Transm. &amp. Distrib. 13 (3), 417–422. doi:10.1049/iet-gtd.2018.5474

CrossRef Full Text | Google Scholar

Tian, S., Zhang, X., Song, X., Ran, Z., Wang, D., Deng, Z., et al. (2018). Breakdown characteristics and decomposition characteristics of C₆F₁₂O and N₂ mixed gas under AC voltage [J]. Proc. CSEE 38 (10), 3125–3132. doi:10.13334/j.0258-8013.pcsee.170886

CrossRef Full Text | Google Scholar

Tian, S., Zhang, X., Wang, Y., Rao, X., Song, X., Li, Y., et al. (2019). Partial discharge characteristics of C₆F₁₂O/CO₂ mixed gas at power frequency AC voltage[J]. AIP Adv. 9 (9), 095057. doi:10.1063/1.5123903

CrossRef Full Text | Google Scholar

Tian, S., Zhang, X., Yann, C., Hu, J., Wang, B., Song, X., et al. (2019). Research status of replacement gases for SF₆ in power industry. AIP Adv. 45 (01), 109–116. doi:10.1063/1.5134727

CrossRef Full Text | Google Scholar

Wang, F., Liu, J., Zhong, L., Hai, B., Zhou, Y., Tang, N., et al. (2020). Theoretical analysis of the decomposition pathways and species of environmentally friendly insulation gas C₆F₁₂O based on the DFT and TST[J]. Plasma Chem. Plasma Process. 41 (5), 1–21. doi:10.1007/s11090-020-10129-4

CrossRef Full Text | Google Scholar

Wang, W. Z., Wu, Y., Rong, M. Z., and Yang, F. (2012). Theoretical computation studies for transport properties of air plasmas[J]. ACTA Phys. SIN. 61 (10), 105201. doi:10.7498/aps.61.105201

CrossRef Full Text | Google Scholar

Wang, W., Rong, M., Murphy, A. B., Xu, W., Haibo, S., and Fei, Y. (2011). Calculation analysis on statistic thermodynamic properties of thermal arc plasmas[J]. Hsi-An Chiao Tung Ta Hsueh/Journal Xi'an Jiaot. Univ. 45 (4), 86–92.

Google Scholar

Wang, Y., Tian, S., Zhang, X., Liu, W., and Zhang, G. (2020). Theoretical calculation of total electron-impact ionization cross section of C₆F₁₂O[J]. AIP Adv. 10 (3), 035217. doi:10.1063/1.5133830

CrossRef Full Text | Google Scholar

Xiao, D. (2016). Development prospect of gas insulation based on environmental protection [J]. High Volt. Eng. 42 (04), 1035–1046. doi:10.13336/j.1003-6520.hve.20160405020

CrossRef Full Text | Google Scholar

Yu, X., Hou, H., and Wang, B. (2017). Prediction on dielectric strength and boiling point of gaseous molecules for replacement of SF₆[J]. J. Comput. Chem. 38 (10), 721–729. doi:10.1002/jcc.24741

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., Ye, M., Lei, P., Zhang, Q., Su, Z., and Xu, X. (2020). Calculation of thermodynamic properties of C₄F₇N mixtures arc plasma [J]. High Volt. Eng. 46 (1), 362–368.

Google Scholar

Zhang, X., Tian, S., Song, X., Deng, Z., Yi, L., Tang, J., et al. (2017). Insulation strength and decomposition characteristics of a C₆F₁₂O and N₂ Gas Mixture[J]. Energies 10 (8), 1170. doi:10.3390/en10081170

CrossRef Full Text | Google Scholar

Zhang, X., Wang, Y., Yi, L., Li, Y., Ye, F., Tian, S., et al. (2020). Thermal compatibility properties of C₆F₁₂O-air gas mixture with metal materials[J]. AIP Adv. 10 (5), 125024. doi:10.1063/1.5131724

CrossRef Full Text | Google Scholar

Zhang, X., Xiao, H., Tang, J., Cui, Z., and Zhang, Y. (2017). Recent advances in decomposition of the most potent greenhouse gas SF₆[J]. Crit. Rev. Environ. Sci. Technol. 47 (18), 1763–1782. doi:10.1080/10643389.2017.1400860

CrossRef Full Text | Google Scholar

Zhang, Z., Lin, X., Yu, W., Xu, J., Zhang, J., and Su, Z. (2020). Thermodynamic calculation of physical properties of C₄F₇N/CO₂ and C₄F₇N/N₂ [J]. High Volt. Eng. 46 (1), 250–256.

Google Scholar

Zhong, L., Rong, M., Wang, X., Wu, J., Han, G., Han, G., et al. (2017). Compositions, thermodynamic properties, and transport coefficients of high-temperature C₅F₁₀O mixed with CO₂ and O₂ as substitutes for SF₆ to reduce global warming potential[J]. AIP Adv. 7 (7), 075003. doi:10.1063/1.4993305

CrossRef Full Text | Google Scholar

Yi, L., Zhang, X., Tian, S., Song, X., Li, Y., and Chen, D. (2019). Insight into the decomposition mechanism of C6F12O-CO2 gas mixture [J]. Chemical Engineering Journal 360, 929–940. doi:10.1016/j.cej.2018.10.167

CrossRef Full Text | Google Scholar