- 1MinesParis, PSL University, Centre for Material Sciences (MAT), UMR7633CNRS, Evry, France
- 2Safran Tech, Rue des Jeunes Bois, Colombes, France
Digital twins in the mechanics of materials usually involve multimodal data in the sense that an instance of a mechanical component has both experimental and simulated data. These simulations aim not only to replicate experimental observations but also to extend the data. Whether spatially, temporally, or functionally, augmentation is needed for various possible uses of the components to improve the predictions of mechanical behavior. Related multimodal data are scarce, high-dimensional and a physics-based causality relation exists between observational and simulated data. We propose a data augmentation scheme coupled with data pruning, in order to limit memory requirements for high-dimensional augmented data. This augmentation is desirable for digital twining assisted by artificial intelligence when performing nonlinear model reduction. Here, data augmentation aims at preserving similarities in terms of the validity domain of reduced digital twins. In this article, we consider a specimen subjected to a mechanical test at high temperature, where the as-manufactured geometry may impact the lifetime of the component. Hence, an instance is represented by a digital twin that includes 3D X-Ray tomography data of the specimen, the related finite element mesh, and the finite element predictions of thermo-mechanical variables at several time steps. There is, thus, for each specimen, geometrical and mechanical information. Multimodal data, which couple different representation modalities together, are hard to collect, and annotating them requires a significant effort. Thus, the analysis of multimodal data generally suffers from the problem of data scarcity. The proposed data augmentation scheme aims at training a recommending system that recognizes a category of data available in a training set that has already been fully analyzed by using high-fidelity models. Such a recommending system enables the use of a ROM-net for fast lifetime assessment via local reduced-order models.
1 Background
A digital twin (DT), of a system or a component, is an ultra-realistic model in geometric details Bellinger et al. (2011). These details include manufacturing anomalies. More precisely, when considering model-based engineering systems, the DT integrates ultra-high fidelity simulations, maintenance history, and all available historical among real data. This information is used to mirror the life of their respective “flying twin,” as proposed in Glaessgen and Stargel (2012) for aeronautical applications. In this article, we consider real instances of mechanical components (RIMC) that undergo thermo-mechanical loadings in an experiment that reflects what an aircraft engine imposes on a high-pressure turbine blade. The as-manufactured geometries are observed by X-Ray computed tomography (CT) which generates accurate 3D digital images of RIMC. A numerical model is a DT only if its corresponding RIMC exists. Making the best use of existing data while exploiting the information with classical mathematical models is an important issue. Data-driven modeling is emerging as a powerful paradigm for physical and biological systems, according to Zhang et al. (2019). In various industrial fields related to structural mechanics, most numerical models incorporate scientific knowledge about the mechanics of materials. Hence, the numerical instance of a DT incorporates multimodal data. Each modality of data has its own ambient space related either to material parameters, geometrical and morphological representation, or boundary and initial conditions for partial differential equations. One important modality is related to the synthetic data forecast by model-based numerical simulations, predicting the lifetime of the RIMC, for instance, upon observational data. Such synthetic data support decisions in engineering for maintenance, operating optimization, or decommission of RIMC. With the development of non-destructive testing (NDT) in the manufacturing industry, we can expect a growing activity on image-based DTs (Seon et al., 2020; Launay et al., 2021a) for accurate descriptions of as-manufactured geometries and microstructural properties of structural components. Such data are crucial for lifetime predictions (Aublet et al., 2022). Unfortunately, image-based DTs in material science are so complex and time-consuming, so in practice, this task does not scale with the frequency of quality inspection in manufacturing. This is a major scaling issue for online DT of as-manufactured structural components, where lifetime prediction is strongly affected by geometrical defects. Another issue is the curse of dimensionality related to the dimension of the geometrical ambient space, so a dense sampling of this space is unaffordable. So, learning regression for lifetime prediction from observational data, as in cross-modal predictions (Launay et al., 2021a), may not be relevant for such image-based modeling. In this work, we augment multimodal data in order to train a ROM-net (Daniel et al., 2020). A ROM-net learns a piecewise linear latent space for model order-reduction. It incorporates a classifier, in its first layers, that recommends the selection of a local reduced-order model (LROM), from a digital image of the RIMC, where each LROM has its own label. In this article, we assume that the latent space has a structure of vector bundle that is locally trivial. This means that LROMs have a validity domain larger than the support of training data (Ryckelynck et al., 2015). In the sequel, DTs that have similar validity domains for their specific LROM are termed ROM-similar. Therefore, ROM-net predictions should be accurate when the input data have ROM-similar data in the dictionary of LROM. Unfortunately, the multimodal data related to image-based DT are very scarce, compared to the dimension of the ambient spaces of these data. Furthermore, we need to prove the efficiency of digital twining assisted by artificial intelligence prior to getting more data related to manufactured components. Hence ROM-net, or more precisely, the classifier of the ROM-net, needs augmented data (Lecun et al., 1998). A review on image-data augmentation schemes is available in Shorten and Khoshgoftaar (2019). Both image warping and oversampling augmentations are proposed in the literature, so labels are preserved. Here, the multimodal data involved in digital twining are required to account for the causality relation that exists between the model-based predictions and observational image data. In data warping augmentation alone, the causality relation between observational data and simulated data is not preserved. Hence, labels that refer to LROM cannot be preserved by data warping. So, we propose a dedicated oversampling procedure based on ROM-similarity. A schematic view of the assumed piecewise linear latent space is shown in Figure 1. In this figure, ROM-similar data are aligned on the same slope. We consider both experimental data and simulated data related to the lifetime of a realistic structural component, composed of CMSX4-PLUS super alloy, undergoing cyclic loading and plastic strains at high temperatures. The next section details the proposed scheme for multimodal data oversampling. In Section 3, two examples are provided. The first one is an augmentation around a defect in a 2D picture which affects the local strain fields. In the second example, we give a detailed description of the considered multimodal data for an academic example and for a mechanical component undergoing cyclic loading at high temperature for its lifetime characterization. The ambient spaces related to the multimodal data in this article are realistic regarding manufactured parts of the aeronautics industry (Aublet et al., 2022).
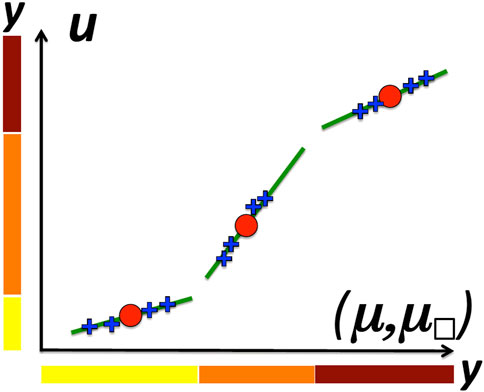
FIGURE 1. Schematic view of augmented data (blue crosses) around digital twins (red points) in a multimodal ambient space (μ, μ□, u). Oversampling assumes a piecewise linear latent space (green slopes). Each linear subset of the latent space has a dedicated label y. The extent of green segments illustrates the validity domain of LROMs.
2 Methods
The multimodal data involved in a DT are denoted by μ for material or metallurgical parameters, μ□ for digital images, p for the lifetime prediction, and a matrix
where
The solution manifold of all u fulfilling Equation 1, for given μ and μ□, is denoted by E. For reduced-order modeling purposes, we assume that E has a structure that the data augmentation scheme has to preserve. This structure is a vector bundle of rank N. It is a family of vector spaces of dimension N parametrized by a base space denoted by M. In the proposed framework, M is the manifold of primal variables u for digital twins. The vector bundle is assumed to be locally trivial, in the sense that the local vector space is constant on subsets of M. In the sequel, these subsets of M have a dedicated label y, and this label refers to a local reduced basis
This admissibility criteria involve, in Equation 3, the usual constrains that preserve labels of original data. We acknowledge that the proposed data augmentation scheme does not improve the sampling of the base space M. Its purpose is to augment the number of instances that share the same labels. Figure 1 is illustrating the structure of manifold E. In this figure, the sampling points on manifold M are the red points. The local vector spaces are represented as green lines. The desired augmented data are represented by blue crosses. The labels have also been represented on each axis of this plot.
Usually,
where Ω is the geometrical domain occupied by the DT, and ξ is the position vector in this domain. In image-based DTs, the finite element shape functions and the domain Ω are specific to each instance of
and
For pruned data, approximation errors in Equation 2 must be tolerated. We propose a two-step augmentation technique that contains 1) a random sampling step of parameters μ, μ□ in the vicinity of
where ‖ ⋅‖F is the Frobenius norm. Here, we assume that
Remark: It is possible to update the vector bundle after the data augmentation. The accuracy of the LROM that we can compute after data augmentation is not directly related to the threshold used here for the ROM-similarity. For instance, after data augmentation, we can aggregate in a matrix
3 Results and discussion
3.1 Modeling the local mechanical response of voids in an elastic material
In a previous work (Ryckelynck et al., 2020), we published 2D DTs of voids in elastic bodies. In this example, we augment the data around two DTs from this previous work. The augmentation ratio is 100 for each DT, prior to fulfilling the constraints for the construction of
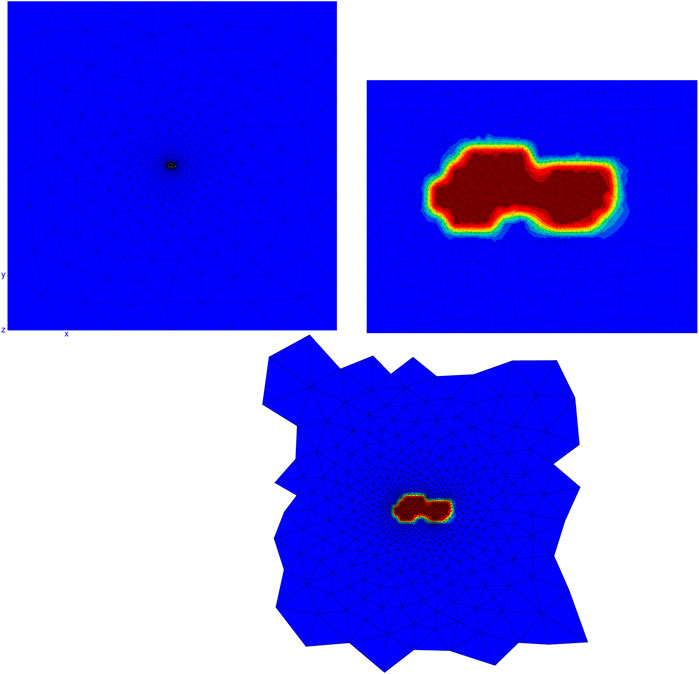
FIGURE 2. The finite element mesh of one digital twin (on the left), a focus on the phase field of the void at the center of this mesh (Right), and the mesh of the reduced domain ΩR (Below).
Multimodal data are the 2D image of the void (i.e., the image of ϕ) and the mechanical shear strain in ΩR. These data are shown in Figure 3 and Figure 4 for digital twins i = 1 and i = 2, respectively. Augmented image data are obtained by usual shear and rotation of the void image. The resulting phase field is denoted by ϕ′. The mechanical expression of the strain tensor is the symmetric part of the gradient of the displacement field u. This strain tensor is denoted by ɛ, ɛ(u) = (∇u + ∇uT)/2. The solution of elastic Equations 11 and 12 forecasts the augmented value for the shear strain ɛ(u′). We can see in the full order simulations, in Figure 3 and Figure 4, that the mechanical strains are highly dependent on the void morphology.
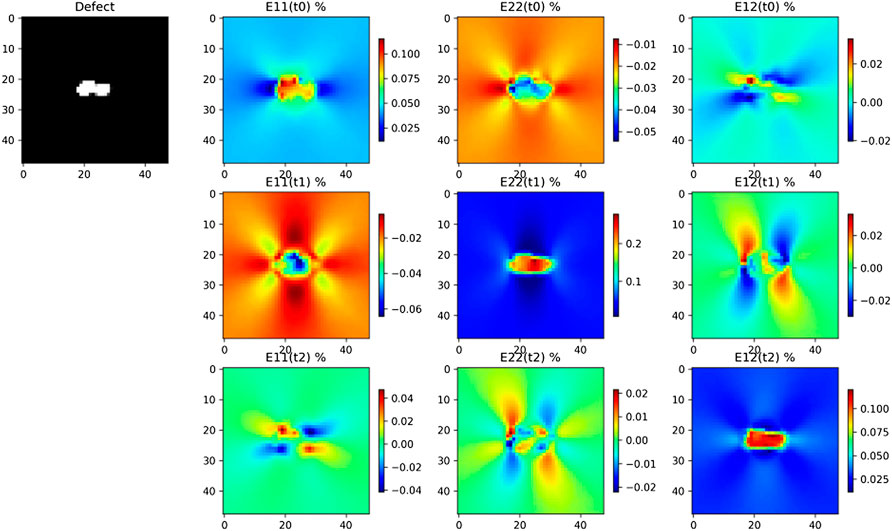
FIGURE 3. Multimodal data for digital twin i = 1, on the top left
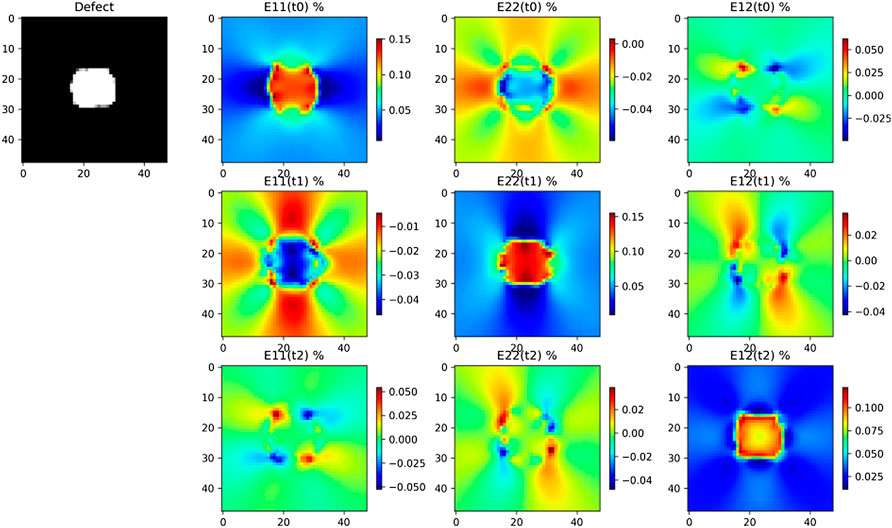
FIGURE 4. Multimodal data for digital twin i = 2, on the top left
Two examples of augmented data are shown in Figure 5 and Figure 6. In these examples, it is clear that the mechanical variables do not follow the warping imposed to μ□, especially far from the void. Local reduced bases have 3 modes. The reduced basis of the first DT is shown in Figure 7. The ROM-similarity of augmented data is shown in Figure 8. Only one set of augmented data in
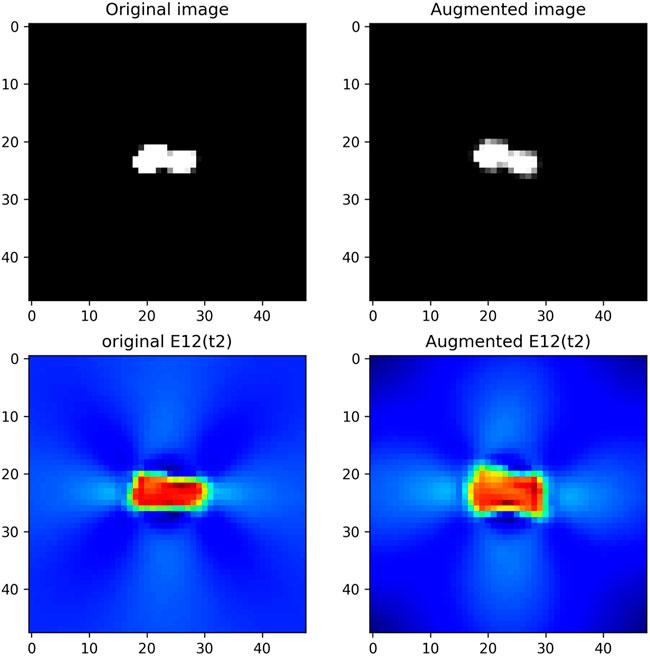
FIGURE 5. Example of augmented multimodal data for digital twin i = 1: on the left, original data; on the right, augmented data; in the first row, μ□; and in the second row, the shear strain at time t2.
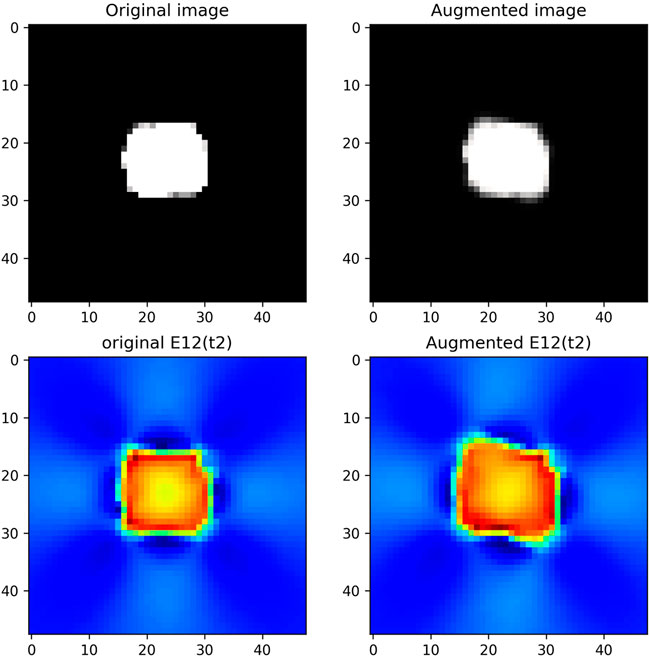
FIGURE 6. Example of augmented multimodal data for digital twin i = 2: on the left, original data; on the right, augmented data; in the first-row, μ□; in the second row, the shear strain at time t2.
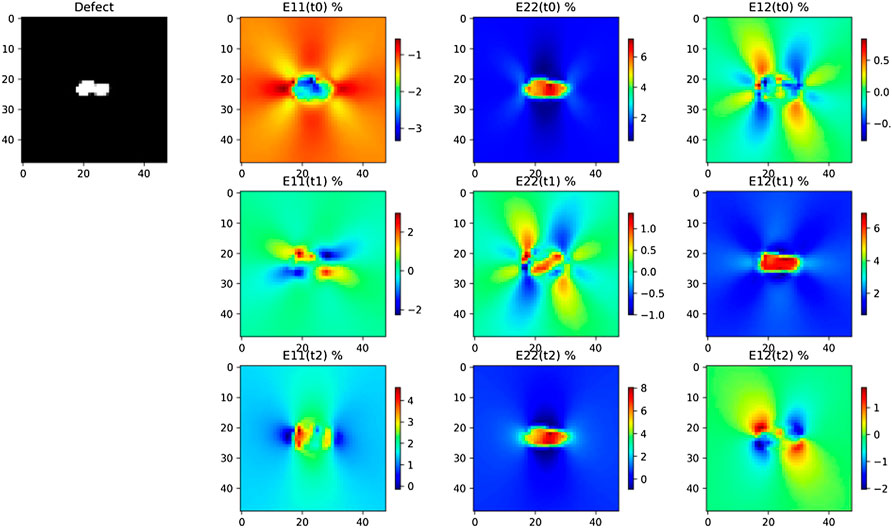
FIGURE 7. Strain components of the LROM for digital twin i = 1: on the top left, μ□; on the right,
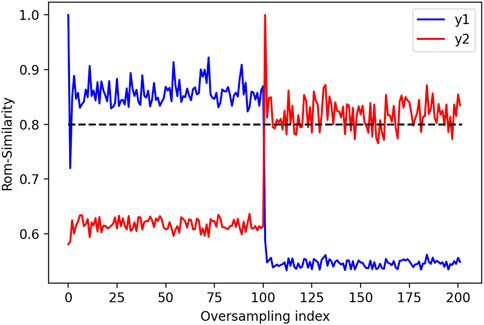
FIGURE 8. ROM-similarity for all instances of augmented data in
3.2 Application on fatigue specimen observed via X-ray computer tomography
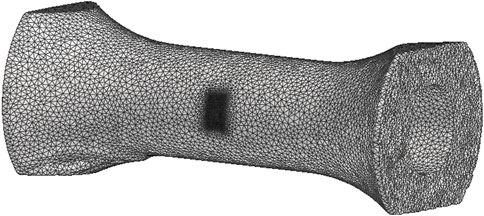
In this subsection, we consider a mechanical specimen subjected to a mechanical test at high temperature, where as-manufactured geometry may impact the lifetime of the specimen. The DT includes a 3D X-Ray tomography of the specimen (Figure 9), the related finite element mesh (Figure 10), and the finite element predictions of thermo-mechanical variables that are modified at several time steps during the test (on the pruned mesh in Figure 13). The problem of data scarcity is particularly pronounced for this kind of DT. In this example,
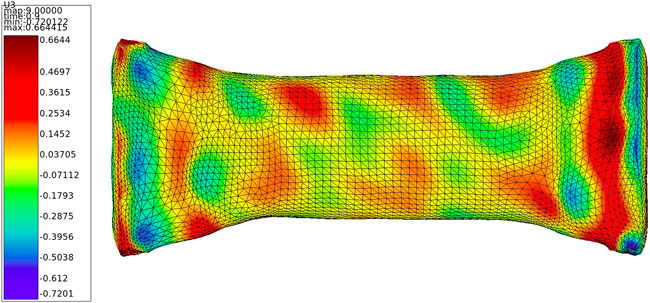
FIGURE 11. Example of node displacements along axial direction for mesh morphing according to augmented data for geometrical variations Δμ□.
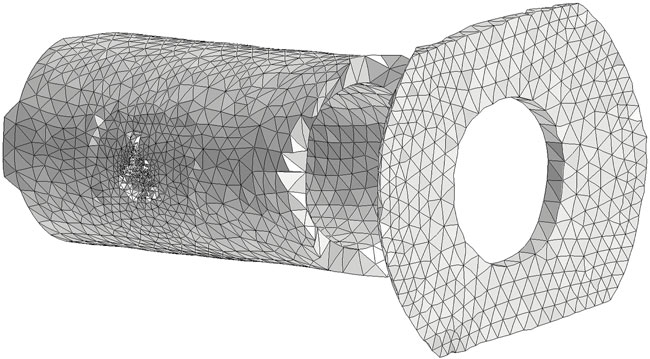
FIGURE 12. Finite element mesh restrained to ΩR
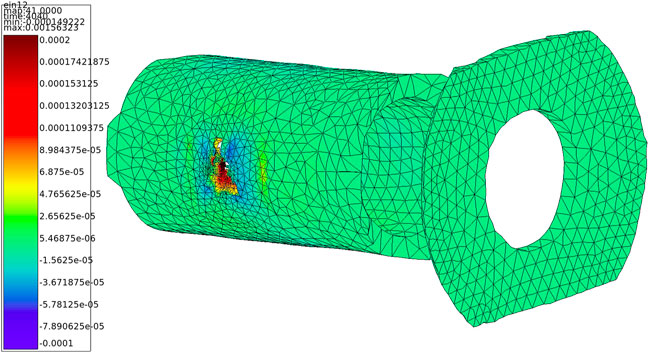
FIGURE 13. Shear strain forecast by the finite element model, in ΩR, at the maximum mechanical loading of the specimen.
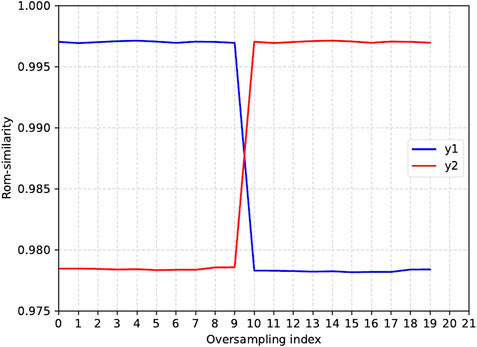
FIGURE 14. ROM-similarity for all instances of augmented data in
Here, we consider a time-dependent problem due to plasticity computed with a crystal plasticity model developed by Méric et al. (1991). This kind of problem implies a temporal analysis with an initial important spread on the domain (low values with importation gradients) the first time, and then, a localization due to a mechanical defect such as a hole as shown in Figure 10. This localization implies local variations of displacement fields around the defect which needs a higher value of N to catch the information in LROM. As we performed a truncature with N = 6, we cannot gather the local information on plasticity. The development of ROM-similarity criteria is still a work in progress in plasticity. Here, V(y(1)) and V(y(2)) seem pretty similar, hence the close ROM-similarities reported in Figure 14.
4 Conclusion
The proposed data augmentation method is very versatile for multimodal data that includes simulated data in the framework of image-based digital twinning. It requires access to the finite element model used for digital twinning. The method assumes that the latent space hidden in the multimodal data is piecewise linear, so the nonlinear model reduction uses local reduced bases. The validity domains of these reduced bases enable the definition of similarities, termed ROM-similarity, between multimodal data. The pruning technique, used to limit memory requirement for high-dimensional augmented data, has a hyper-parameter ΩR. The larger the domain ΩR, the more accurate the evaluation of ROM-similarities. The smaller the ΩR, the higher the memory savings. The development of ROM-similarity criteria is still a work in progress in plasticity.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
AA performed the digital twinnings for the thermo-mechanical specimens and made the X-Ray computed tomographies. FN did all image-based finite element meshes. HP brought his help for the elasto-viscoplastic simulations, and edited and commented on the initial manuscript. DR proposed the augmentation scheme, and he applied it to the numerical results on the 2D example. AA applied the augmentation scheme to the thermo-mechanical specimens.
Funding
AA’s PhD thesis is financially supported by SAFRAN.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aublet, A., Rambaudon, M., N’Guyen, F., Ryckelynck, D., Remacha, C., Cariou, R., et al. (2022). Mechanical fatigue testing under thermal gradient and manufacturing variabilities in nickel-based superalloy parts with air-cooling holes. Exp. Mech. doi:10.1007/s11340-022-00868-0 |
Bellinger, N., Tuegel, E. J., Ingraffea, A. R., Eason, T. G., and Spottswood, S. M. (2011). Reengineering aircraft structural life prediction using a digital twin. Int. J. Aerosp. Eng. 1, 14. doi:10.1155/2011/154798 |
Daniel, T., Casenave, F., Akkari, N., and Ryckelynck, D. (2021). Data augmentation and feature selection for automatic model recommendation in computational physics. Math. Comput. Appl. 26, 17. doi:10.3390/mca26010017 |
Daniel, T., Casenave, F., Akkari, N., and Ryckelynck, D. (2020). Model order reduction assisted by deep neural networks (ROM-net). Adv. Model. Simul. Eng. Sci. 7, 16. doi:10.1186/s40323-020-00153-6 |
Everson, R., and Sirovich, L. (1995). Karhunen-Loeve procedure for gappy data. J. Opt. Soc. Am. A 12, 1657. doi:10.1364/JOSAA.12.001657 |
Glaessgen, E., and Stargel, D. (2012). “The digital twin paradigm for future nasa and u.s. air force vehicles,” in Structures, Structural Dynamics, and Materials Conference (Aerospace Research Central). doi:10.2514/6.2012-1818 |
Hilth, W., Ryckelynck, D., and Menet, C. (2019). Data pruning of tomographic data for the calibration of strain localization models. Math. Comput. Appl. 24, 18. doi:10.3390/mca24010018 |
Launay, H., Ryckelynck, D., Lacourt, L., Besson, J., Mondon, A., and Willot, F. (2021a). Deep multimodal autoencoder for crack criticality assessment. Int. J. Numer. Methods Eng. 1, 1456–1480. doi:10.1002/nme.6905 |
Launay, H., Willot, F., Ryckelynck, D., and Besson, J. (2021b). Mechanical assessment of defects in welded joints: Morphological classification and data augmentation. J. Math. Ind. 11, 18. doi:10.1186/s13362-021-00114-7 |
Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324. doi:10.1109/5.726791 |
Méric, L., Poubanne, P., and Cailletaud, G. (1991). Single crystal modeling for structural calculations: Part 1 — model presentation. J. Eng. Mat. Technol. 113, 162–170. doi:10.1115/1.2903374 |
Ryckelynck, D., Gallimard, L., and Jules, S. (2015). Estimation of the validity domain of hyper-reduction approximations in generalized standard elastoviscoplasticity. Adv. Model. Simul. Eng. Sci. 2, 6. doi:10.1186/s40323-015-0027-7 |
Ryckelynck, D., Goessel, T., and Nguyen, F. (2020). Mechanical dissimilarity of defects in welded joints via Grassmann manifold and machine learning. Preprint.
Seon, G., Nikishkov, Y., Makeev, A., and Ferguson, L. (2020). Towards a digital twin for mitigating void formation during debulking of autoclave composite parts. Eng. Fract. Mech. 225, 106792. doi:10.1016/j.engfracmech.2019.106792 |
Shorten, C., and Khoshgoftaar, T. M. (2019). A survey on image data augmentation for deep learning. J. Big Data 6, 60. doi:10.1186/s40537-019-0197-0 |
Keywords: high-dimensional data, model order-reduction, data pruning, oversampling, computational mechanics, lifetime prediction
Citation: Aublet A, N’Guyen F, Proudhon H and Ryckelynck D (2022) Multimodal data augmentation for digital twining assisted by artificial intelligence in mechanics of materials. Front. Mater. 9:971816. doi: 10.3389/fmats.2022.971816
Received: 17 June 2022; Accepted: 11 August 2022;
Published: 16 September 2022.
Edited by:
Elías Cueto, University of Zaragoza, SpainReviewed by:
Alberto Badias, Polytechnic University of Madrid, SpainReza Abedi, The University of Tennessee, Knoxville, United States
Copyright © 2022 Aublet, N’Guyen, Proudhon and Ryckelynck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Axel Aublet, YXhlbC5hdWJsZXRAbWluZXNwYXJpcy5wc2wuZXU=; David Ryckelynck, ZGF2aWQucnlja2VseW5ja0BtaW5lcy1wYXJpc3RlY2guZnI=
 Axel Aublet1,2*
Axel Aublet1,2* Henry Proudhon
Henry Proudhon David Ryckelynck
David Ryckelynck