Yi Fei Huang
Zhongjin Jiang1
Lu Liu
Hao Chi Zhang- 1The State Key Laboratory of Millimeter Wave, Southeast University, Nanjing, China
- 2School of Ocean Information Engineering, Jimei University, Xiamen, China
A 2-bit wide-angle coding metasurface is proposed to decrease the bistatic radar cross section (RCS) in this study. Each meta-atom of the designed coding metasurface is composed of a wide-beamwidth microstrip antenna whose feeding port is loaded with an open stub. There are globally four phase-coding states, namely, “00,” “01,” “10,” and “11,” which are achieved in a wide-angle range through an elaborate design of the lengths of the open stubs. Simulation results indicate that, for each meta-atom, the reflective amplitude is above −1 dB, and the reflective phase difference between two adjacent coding states is limited in the range of 90° ± 25° at 8 GHz at incident angles, 0°, 20°, 40°, and 60°. In addition, the generalized Rudin–Shapiro (RS) polynomial is applied to design the coding sequence of the metasurface array to reduce bistatic RCS. A 16 × 16 metasurface array is simulated, manufactured, and measured to validate the bistatic RCS reduction. The simulated results perfectly agree with the experimental results when the incidence angle of the 8 GHz plane wave is within 60°, which shows that the coding metasurface is practical and valid.
Introduction
In contrast to natural materials composed of microscopic particles such as molecules and atoms, metamaterials are artificial structures composed of either periodically or nonperiodically arranged subwavelength structural units (VeselagoViktor, 1968; Pendry et al., 1996; Pendry et al., 1999; Smith et al., 2000; Zheludev and Kivshar, 2012; Hajian et al., 2017). Also, metamaterials have abnormal macroscopic medium parameters that are distinct from natural materials, such as negative permittivity (Pendry et al., 1996), negative permeability (Pendry et al., 1999), and permittivity-near-zero (Hajian et al., 2017). Researchers have accomplished many intriguing and unprecedented physical phenomena (Antonoyiannakis and Pendry, 1999; Shelby et al., 2001; Schurig et al., 2006; Liu et al., 2009; Chen et al., 2010). However, electromagnetic (EM) metamaterials are typically three-dimensional structures with large dimensions and massive weights, making integration with other devices challenging. To overcome these drawbacks, metasurfaces, which are two-dimensional forms of metamaterials, have been proposed (Holloway et al., 2009). Moreover, metasurfaces exhibit great size, cost, and integration advantages. By modifying the parameters of metasurfaces, EM wave characteristics such as amplitude (Landy et al., 2008), phase (Yu et al., 2011; Liu et al., 2014), and polarization (Mutlu et al., 2011) are availably manipulated.
In 2014, the concept of coding metasurfaces was proposed (Cui et al., 2014). In contrast to conventional metasurfaces, coding metasurfaces are described by discretized reflective or refractive phases. In general, 1-bit coding metasurfaces consist of two types of unit cells with 0° and 180° phase responses, denoted as “0” and “1,” respectively. Many intriguing applications are performed by designing a metasurface array with different encodings. RCS reduction is one of the most critical applications based on the ability of different coding sequence metasurfaces to manipulate electromagnetic waves.
RCS is widely used in military scenarios as a critical indicator of the target characteristic of the signal, and the RCS value should be as small as possible to be detected. There has been some research on bistatic RCS reduction using metasurfaces. In these research studies, the diffuse reflection property of electromagnetic waves based on the law of energy conservation is widely utilized in RCS reduction (Cui et al., 2014; Wang et al., 2014; Liu et al., 2016; Han et al., 2017; Masaki et al., 2017; Moccia et al., 2017; Zhang et al., 2017; Liaori et al., 2018; Khan et al., 2019). Optimization algorithms are applied to design coding sequences (Wang et al., 2014; Liu et al., 2016; Han et al., 2017; Zhang et al., 2017; Liaori et al., 2018; Khan et al., 2019), and 1-bit coding metasurfaces are adopted to lower bistatic RCS (Liu et al., 2016; Han et al., 2017; Masaki et al., 2017; Liaori et al., 2018). The situation of regular and fixed oblique incident angles is discussed (Liaori et al., 2018). Moreover, the incident angle of bistatic RCS does not exceed 45° (Cui et al., 2014; Wang et al., 2014; Liu et al., 2016; Han et al., 2017; Moccia et al., 2017; Zhang et al., 2017; Liaori et al., 2018; Dong et al., 2019; Khan et al., 2019). However, the ability of RCS reduction has severely deteriorated when radar operates at a wider incident angle. Also, the simulated results of bistatic RCS reduction within 60° are discussed (Masaki et al., 2017). Moreover, there is a big difference between 0° and 60°, indicating that the RCS reduction is not stable at a wide angle. Furthermore, it should also be noted that no related experimental results are provided. The simulation graphs rather than the specific results are displayed (Semenikhin et al., 2021). The RCS reduction researched in the study does not appear to be satisfactory. So far, the stability of the wide angle and the reduction of bistatic RCS remain focused on issues.
To achieve bistatic RCS reduction, a 2-bit wide-angle coding metasurface inspired using the microstrip patch antenna is proposed in this study. For constructing the coding metasurface, open stubs of different lengths are loaded on the feeding port of a microstrip patch antenna with a wide beamwidth. According to the previous research study, meta-atoms “00,” “01,” “10,” and “11,” with phases of 0°–270°, stepping by 90°, can manipulate EM waves effectively. In addition, it is feasible for the proposed meta-atom to realize four coded phases at a wide angle, with a reflection amplitude greater than −1 dB and a reflective phase difference of 90° ± 25° between two adjacent coding meta-atoms. Moreover, the generalized RS polynomial is utilized in the coding sequence design of the 2-bit 16 × 16 metasurface array to achieve bistatic RCS reduction, based on a proposed suboptimal design method (Moccia et al., 2017). The simulated and measured results demonstrate the excellent stability of bistatic RCS within 60° of incidence angles at 8 GHz. The proposed metasurface could facilitate further research and expand more applications to the metasurface system.
Design and analysis
Meta-atom design and analysis
As mentioned previously, the inspiration for the design is mainly using the microstrip patch antenna structure (He and Li, 2020). By adjusting the equivalent impedance at the feeding port, the different phase state of the meta-atom could be constructed accordingly. Commercial simulation software CST Microwave Studio is utilized to design the meta-atom. The proposed coding metasurface unit is illustrated in Figures 1A,B, which show the profile and side view of the meta-atom. Moreover, the meta-atom consists of ten layers with three different materials. From top to bottom, the following layers are present: metal layer 1, substrate layer 1, PP layer 1, substrate layer 2, PP layer 2, substrate layer 3, metal ground layer, PP layer 3, substrate layer 4, and metal layer 2. The metal grids between the second and fourth layers, consisting of 5 × 4 metal blind holes, contact the square metallic patch on the top layer. The feeding point metal blind spot connects the metal patch to the open microstrip line on the bottom metal layer. In addition, the metal material is copper, and the substrate material is F4B with a relative dielectric constant of 2.2 and a loss tangent of 0.001. The PP, whose material is FR4 with a relative dielectric constant of 4.4, is used for bonding the layers together.
FIGURE 1. (A,B) Profile and side view of the meta-atom. (C) Bottom view of four meta-atoms.
In addition, the thickness of copper metal is 0.035 mm, the thickness of dielectric from top to bottom is 0.18, 1.43, 0.18, and 0.18 mm, and the thickness of the PP layer is 0.1 mm. Figure 1C shows the various open microstrip structures on the bottom layer that correspond to the four types of coding meta-atoms, i.e., “00,” “01,” “10,” and “11.” The related geometric parameters of the unit are listed in Table 1. Furthermore, the width of the open microstrip is 0.6 mm, and the diameter of the hole drilled in the metal ground layer is 0.9 mm. Four meta-atoms have an equivalent open microstrip length of 4.4, 16.875, 16.275, and 10.775 mm on the bottom layer.
TABLE 1. Related geometric parameters about meta-atoms.
Furthermore, the simulated results of meta-atom reflective amplitudes and phases of four types of meta-atoms at different incident angles θ are depicted in Figure 2. The periodic boundaries are used in the simulation. In particular, the Floquet ports are set in the z-direction, and the unit-cell boundary conditions are applied in x- and y-directions in CST Microwave Studio to simulate an infinite xy-plane. To characterize the reflective characteristics of the meta-atoms in response to the x-polarized EM wave, the scattering parameters of port Zmax (2) to port Zmax (2) are employed, where Zmax represents the port in the +z-direction and the number in bracket represents the mode that the electric field is x-polarized. In addition, the wave vector k of the incident plane wave is set at the xz-plane, the angle of the wave vector with -z-axis is θ, and the angle between the projection of the wave vector in the xy-plane and the x-axis is φ. Without loss of generality, θ is limited to 60°, and four angles, 0°, 20°, 40°, and 60°, are chosen to verify, and the φ is set to 180°. The lower and upper Z distances are set to 150 mm, along with the frequency from 6 to 10 GHz. It could be seen that the amplitudes of four meta-atoms are above −1 dB, and the phase difference between the two adjacent coding meta-atoms is within 90° ± 25° at 8 GHz in different θ, whose wide-angle stabilization property allows for bistatic RCS reduction using the proposed metasurface array. The details of reflective amplitudes and phases of the proposed meta-atom in different θ at 8 GHz are listed in Table 2.
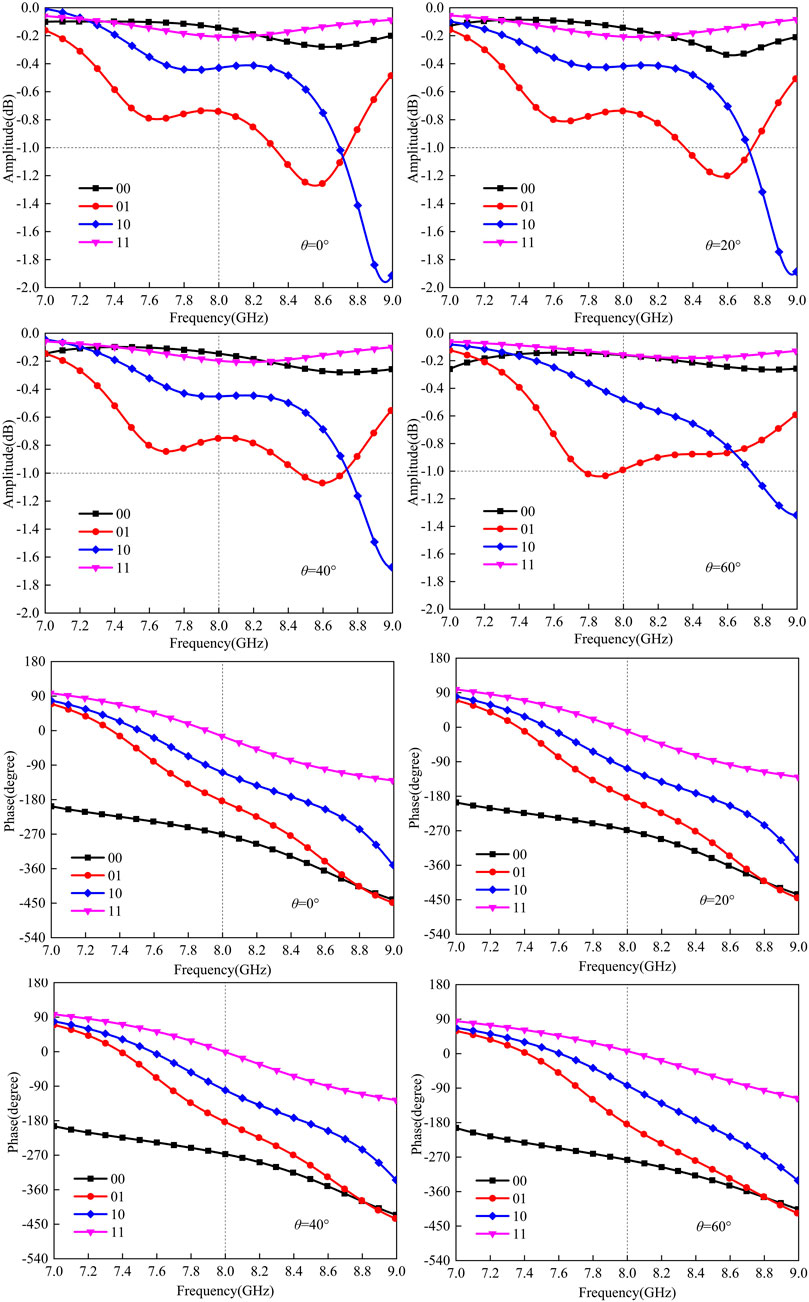
FIGURE 2. Amplitudes and phases of four types of meta-atoms in θ = 0°, 20°, 40°, and 60° from 7 to 9 GHz.
TABLE 2. Reflective amplitudes and phases of meta-atoms in θ = 0°, 20°, 40°, and 60° at 8 GHz.
Metasurface design and analysis of radar cross-section reduction
Compared with other coding metasurfaces, the meta-atom proposed in this study has wide-angle stability, so many fascinating functions are achieved, among which the bistatic RCS reduction is representative. RCS is defined as Eq. 1, where Es and Ei represent the intensity of scattered and incident electric fields, respectively, with angles θ and φ being the same as mentioned previously. Moreover, R denotes the distance between radar to target, while bistatic RCS is defined as max σ(θ, φ) in the upper z-plane. Figure 3 shows the schematic diagrams of a 2-bit coding metasurface array composed of 16 × 16 unit cells, which could reduce bistatic RCS in a wide-angle range. To simplify the simulation of bistatic RCS, the wave vector k of the incident plane wave is always in the xz-plane, the angles are also set as mentioned previously, the magnetic field vector h is parallel to the y-axis, and the projection of the electric field vector e in the xy-plane is parallel to the x-axis. Inspired by the absolute lower bound and IAF bound proposed by Moccia et al. (2017), the suboptimal method of 2-bit coding sequences is further studied. Furthermore, it is found that the generalized RS polynomial (Lei, 1991) is suitable to design array coding sequences, which could be expressed as the following Eqs. 2–5.
FIGURE 3. Diffuse scattering diagram of the metasurface in the plane wave with the incident angle θ.
The generalized RS polynomial method does not require optimization algorithms and extensive simulation, saves computational resources, speeds up the design cycle, and has good results. In addition, considering the array composed of 16 × 16 unit cells, the array factor in two dimensions is separable. The coding sequences along the two dimensions are identical, so only one-dimensional sequence needs to be designed. It is noted that designing a coding sequence is to render the absolute value of the array factor as a constant as possible. Hence, the feature of generalized RS polynomial is well suited. Considering that the meta-atom has four different phase states, which means that the value of q is 4 and that the length of the sequence is 16, the coefficient matrix M with four rows and sixteen columns in Eq. 5 is needed.
In matrix M, different values map different dots of the unit circle in the complex domain, which contains four phase states, namely, 0°, 90°, 180°, and 270°. Moreover, the third-row elements in matrix M are chosen as the coding sequence in one dimension. Then, the whole coding matrix in the array is easily obtained.
The colored sketch matrix of the array is depicted in Figure 4A. Colors yellow, blue, purple, and red represent reflective phases 0°, 90°, 180°, and 270°, respectively. Furthermore, the curves of the absolute lower bound, IAF bound, and algebraic fit (Moccia et al., 2017) are shown in Figure 4B as a reference. Based on the parameters mentioned previously, the RCS ratio γfit (a negative value of RCS reduction) of the metasurface array in Eq. 6 can be obtained, where λ represents wavelength in free space, l represents the length and width of the meta-atom, and N represents the number of units in one dimension. In addition, the metasurface array is designed to meet the results of the RCS reduction approaching the IAF bound as much as possible. In Figure 4B, the value in the cross symbol represents points (4.267, −9.711) owing to that the meta-atom length is in the subwavelength scale at 8 GHz, about 1/3 wavelength in free space, and the RCS reduction is less than 10 dB according to Eq. 6. If the number of the array in the x- or y-direction is increased, the RCS reduction increases further. The RCS reduction comparative results of the metal plate and metasurface, which are of identical sizes in different θ, are shown in Figure 5. Compared with the metal plate, the RCS values of the metasurface are significantly reduced. Since the metasurface could manipulate the EM wave and disperses the energy in all directions, the RCS value is reduced at different incident angles. There are concrete values in Table 3, where the angle θr represents the angle between the wave vector of the maximum scattered wave and the z-axis and φr indicates the angle between the projection of the wave vector of the maximum scattered wave at the xy-plane and the x-axis and θ is defined as previously. The simulated RCS reduction results in different θ are approximate with the calculated algebraic fit value at θ = 0°, which embodies the feasibility of designing the method using the generalized RS polynomial. Moreover, the direction of RCS reduction of the metasurface is not precise in the mirror direction, demonstrating the manipulation of EM waves.
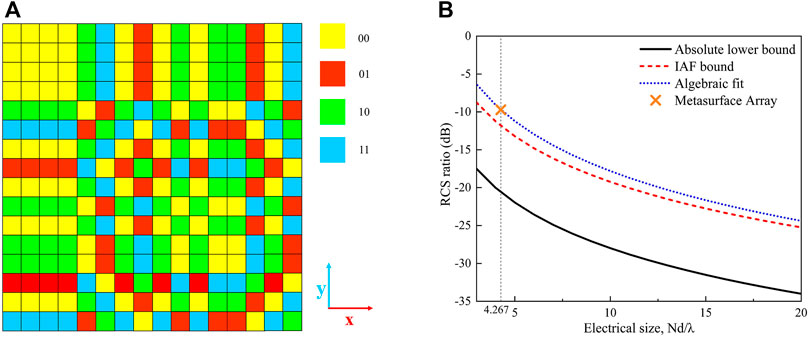
FIGURE 4. (A) Colored coding matrix of the array. (B) RCS-ratio scaling laws in Moccia et al. (2017).
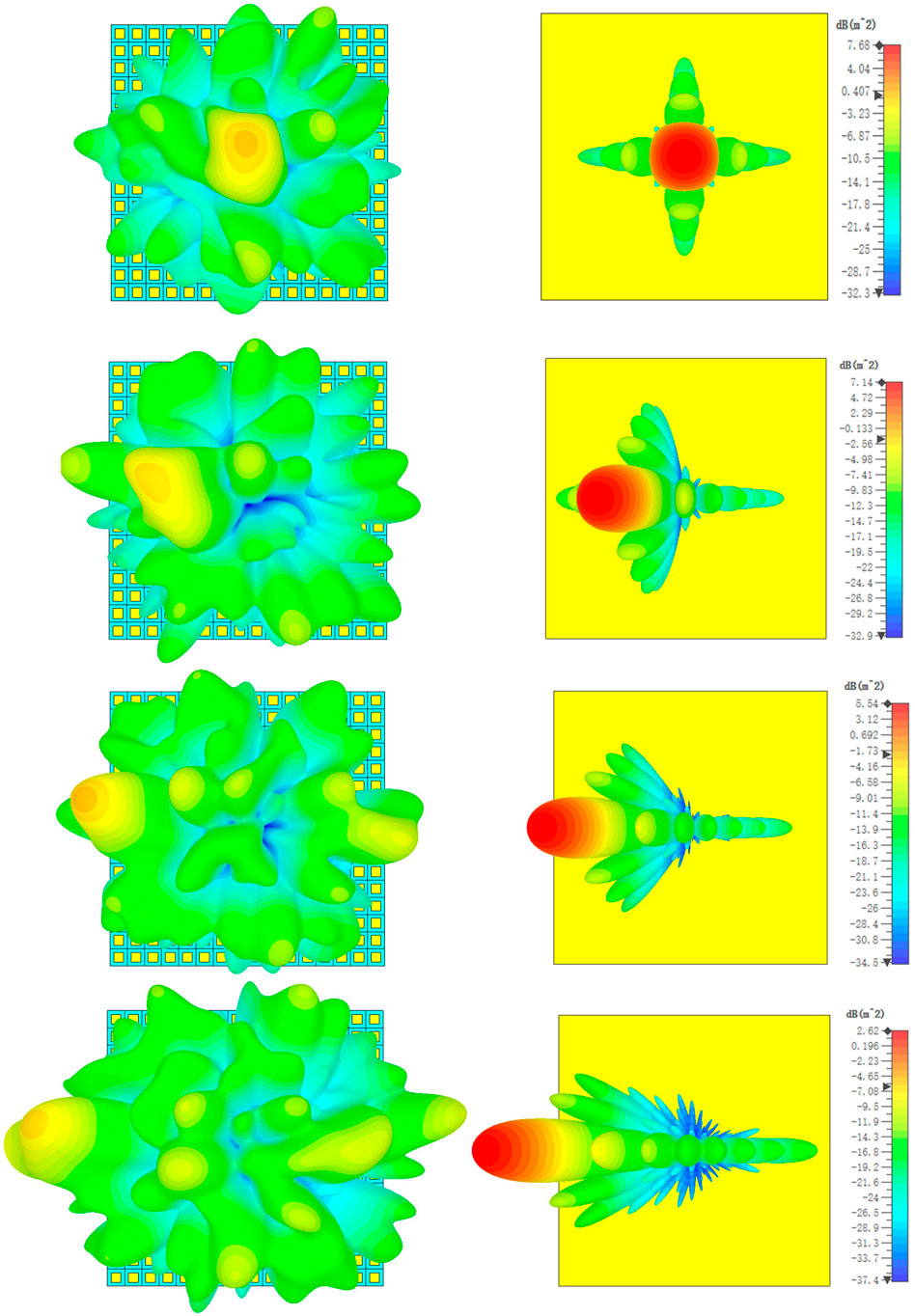
FIGURE 5. Simulated results concerning RCS of the metal plate and the metasurface at different θ in the upper z plane.
TABLE 3. Value and angle of max RCS of the metal plate and metasurface in different incident angles θ.
Results and discussion
A prototype composed of 16 × 16 unit cells is fabricated based on a standard printed-circuited-board fabrication process to validate the aforementioned design method. The whole parameters are identical to the simulated model. The front and back views of the sample and the simulated model are shown in Figure 6A. The whole experiment is performed in the microwave anechoic chamber. Due to the conditions of the microwave anechoic chamber and the difficulty of bistatic RCS measurement, the measurement method is illustrated in Figure 6B to measure RCS of the sample and the metal plate in the mirror direction and use the data for comparison with the simulation results. Specifically, two horizontally polarized horn antennas are located at the same height as the device under test (DUT). Moreover, two horns connect with port 1 and port 2 of a vector network analyzer. Horn antenna 1 transmits EM waves, while horn antenna 2 receives EM waves. To better accomplish measurement in the microwave anechoic chamber, work fixture 1 with a length of 200 mm connects horn 1 to DUT, which guarantees that the angle between the transmitting horn and DUT is unchanged when measuring. Moreover, it has bearings on work fixture 2 in DUT, and the incident angle between horn 1 and DUT could regulate through the tools. The work fixture’s surroundings are covered with absorbing materials to prevent the interference of EM waves. In specific measurements, DUT, referring to sample 1, sample 2, and the stainless steel plate, is fixed on the turntable, which could rotate at the azimuthal plane. The incident angle is changed from 20° to 50°, stepping by 10°, as well as the angle of the turntable in azimuthal synchronously, while horn 2 is always immobile, the normal direction is perpendicular to the wall. Figure 6C illustrates the related measurement scenarios. For the case of θ = 0°, the measured method refers to the monostatic measured method in most of the articles. Figure 6D shows the simulated and experimental results of the aforementioned measured method. It should be noted that θ = 60° and the degrees below 20° are not measured due to the limitations of the microwave anechoic chamber and the horn antenna’s main lobe beamwidth. The detailed results are displayed in Table 4. Compared with the simulated results, the experimental results are better except for some individual points, for example, sample 2 in θ = 0° and 20°, and sample 1 in θ = 30°. Moreover, the RCS reduction of sample 1 is about 1.5 dB larger than that of the simulated one in θ = 40°. The scatter diagram variation tendency of sample 2 and the simulated results are exactly similar from 0° to 50°, and the trend of sample 1 is almost the same as well except θ = 30°. In different θ, the mean value of bistatic RCS reduction of mirror direction of the simulated model is 9.806 dB. In comparison, the values for samples 1 and 2 are 10.524 and 10.05 dB, respectively. The measured results are better than the simulated results. Furthermore, the standard deviations are 0.711, 1.067, and 1.401 dB, which demonstrate the excellent stability of bistatic RCS reduction in a wide angle compared with the results in Masaki et al.(2017). Compared with the RCS reduction of the metasurface with normal incidence (Cui et al., 2014), the maximum incidence angle of bistatic RCS has been raised to 60°, and the experimental results validate the design in this study.
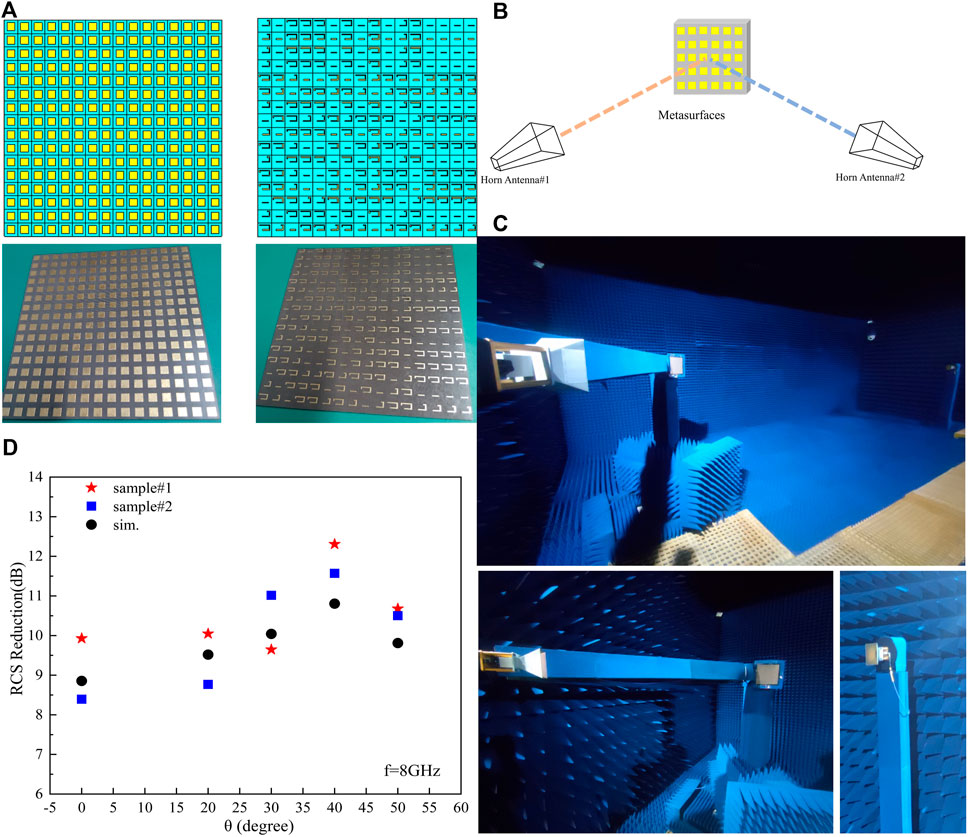
FIGURE 6. (A) Front and back view of the prototype and simulated model. (B) Schematic diagram of the bistatic RCS measured method. (C) Experimental environment of bistatic RCS measurement. (D) Results of RCS reduction in mirror direction of the simulated models, sample 1 and sample 2.
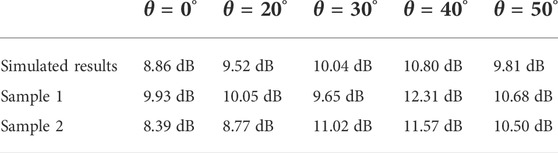
TABLE 4. Bistatic RCS reduction in mirror direction of the simulated model and samples 1 and 2 in different θ.
Conclusion
In this study, we propose a 2-bit wide-angle coding metasurface to reduce the bistatic radar cross section (RCS). Four phase-coding states with 90° phase differences, namely, “00,” “01,” “10,” and “11” states, are designed, which are achieved in a wide-angle range by different lengths of open stubs in the bottom layer. Moreover, the generalized RS polynomial is used in the coding sequence of the metasurface array without complex optimized algorithms. The simulated results have validated that the mean value of bistatic RCS reduction by 2-bit metasurface is 8.381 dB within 60° at 8 GHz. Also, the experimental results show that bistatic RCS reduction is about 10 dB in the mirror direction within 50°, and that the standard deviations of the prototypes with the simulated model are no more than 1 dB. The proposed metasurface design could facilitate further research on metasurface systems and other significant engineering practical applications such as wide-angle radar stealth.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
YFH, ZJ, LL, and HCZ conceived the idea of the wide-angle coding metasurface for bistatic RCS reduction. YFH, LL, and HCZ conducted the theoretical analysis. YFH conducted the simulations and performed the fabrication and measurements. YFH wrote the manuscript. All authors discussed the results and commented on the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant No. 62101122, the Natural Science Foundation of Jiangsu Province of China under Grant No. BK20210212, and the Fundamental Research Funds for the Central Universities under Grant No. 2242021R10107, the Natural Science Foundation of Fujian Province of China under Grant Nos. 2021J05179.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Antonoyiannakis, M. I., and Pendry, J. B. (1999). Electromagnetic forces in photonic crystals. Phys. Rev. B 60 (4), 2363–2374. doi:10.1103/PhysRevB.60.2363
Chen, H., Chan, C. T., and Sheng, P. (2010). Transformation optics and metamaterials. Nat. Mat. 9 (5), 387–396. doi:10.1038/nmat2743
Cui, T. J., Qi, M. Q., Wan, X., Zhao, J., and Cheng, Q. (2014). Coding metamaterials, digital metamaterials and programmable metamaterials. Light. Sci. Appl. 3 (10), e218. doi:10.1038/lsa.2014.99
Dong, G., Li, X., Liu, Y., Zhu, S., He, Y., and Zhang, A. (2019). Multi-polarization, polarization-independent, wide-angle RCS reduction metasurface based on random phase gradients. Appl. Opt. 58 (4), 764–771. doi:10.1364/AO.58.000764
Hajian, H., Ozbay, E., and Caglayan, H. (2017). Beaming and enhanced transmission through a subwavelength aperture via epsilon-near-zero media. Sci. Rep. 7 (1), 4741–4748. doi:10.1038/s41598-017-04680-y
Han, T., Cao, X., Gao, J., and Zhao, Y. (2017). “Broadband and wide-angle RCS reduction based on an optimal-arranged metasurface,” in 2017 sixth asia-pacific conference on antennas and propagation (APCAP) (IEEE), 1–3.
He, Y., and Li, Y. (2020). Dual-polarized microstrip antennas with capacitive via fence for wide beamwidth and high isolation. IEEE Trans. Antennas Propag. 68 (7), 5095–5103. doi:10.1109/TAP.2020.2975269
Holloway, C. L., Dienstfrey, A., Kuester, E. F., O’Hara, J. F., Azad, A. K., and Taylor, A. J. (2009). A discussion on the interpretation and characterization of metafilms/metasurfaces: The two-dimensional equivalent of metamaterials. Metamaterials 3 (2), 100–112. doi:10.1016/j.metmat.2009.08.001
Khan, T. A., Li, J., Chen, J., Raza, M. U., and Zhang, A. (2019). Design of a low scattering metasurface for stealth applications. Materials 12 (18), 3031. doi:10.3390/ma12183031
Landy, N. I., Sajuyigbe, S., Mock, J. J., Smith, D. R., and Padilla, W. J. (2008). Perfect metamaterial absorber. Phys. Rev. Lett. 100 (20), 207402. doi:10.1103/PhysRevLett.100.207402
Lei, Z. (1991). Several properties about generalized Rudin-Shpiro polynomials. Chin. Ann. Math. Ser. A (02).
Liaori, J. I. D. I., Xiangyu, C. A. O., Yao, T. A. N. G., Siming, W. A. N. G., Yi, Z. H. A. O., and Xuewen, Z. H. U. (2018). A new coding metasurface for wideband RCS reduction. Radioengineering 27 (2), 394–401. doi:10.13164/RE.2018.0394
Liu, L., Zhang, X., Kenney, M., Su, X., Xu, N., Ouyang, C., et al. (2014). Broadband metasurfaces with simultaneous control of phase and amplitude. Adv. Mat. 26 (29), 5031–5036. doi:10.1002/adma.201401484
Liu, R., Ji, C., Mock, J. J., Chin, J. Y., Cui, T. J., and Smith, D. R. (2009). Broadband ground-plane cloak. Science 323 (5912), 366–369. doi:10.1126/science.1166949
Liu, X., Gao, J., Xu, L., Cao, X., Zhao, Y., and Li, S. (2016). A coding diffuse metasurface for RCS reduction. IEEE Antennas Wirel. Propag. Lett. 16, 724–727. doi:10.1109/LAWP.2016.2601108
Masaki, T., Ishii, Y., Michishita, N., Morishita, H., and Hada, H. (2017). International symposium on antennas and propagation (ISAP). IEEE, 1–2.Bistatic RCS reduction characteristics of flat and curved metasurfaces
Moccia, M., Liu, S., Wu, R. Y., Castaldi, G., Andreone, A., Cui, T. J., et al. (2017). Coding metasurfaces for diffuse scattering: Scaling laws, bounds, and suboptimal design. Adv. Opt. Mater. 5 (19), 1700455. doi:10.1002/adom.201700455
Mutlu, M., Akosman, A. E., Serebryannikov, A. E., and Ozbay, E. (2011). Asymmetric chiral metamaterial circular polarizer based on four U-shaped split ring resonators. Opt. Lett. 36 (9), 1653–1655. doi:10.1364/OL.36.001653
Pendry, J. B., Holden, A. J., Robbins, D. J., and Stewart, W. J. (1999). Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 47 (11), 2075–2084. doi:10.1109/22.798002
Pendry, J. B., Holden, A. J., Stewart, W. J., and Youngs, I. (1996). Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 76 (25), 4773–4776. doi:10.1103/physrevlett.76.4773
Schurig, D., Mock, J. J., Justice, B. J., Cummer, S. A., Pendry, J. B., Starr, A. F., et al. (2006). Metamaterial electromagnetic cloak at microwave frequencies. Science 314 (5801), 977–980. doi:10.1126/science.1133628
Semenikhin, A. I., Semenikhina, D. V., Blagovisnyy, P. V., and Ilyin, I. V. (2021). “Broadband reduction of monostatic and bistatic RCS using blocks of 2-bit anisotropic meta-coatings,” in 2021 radiation and scattering of electromagnetic waves (RSEMW) (IEEE), 253–256.
Shelby, R. A., Smith, D. R., and Schultz, S. (2001). Experimental verification of a negative index of refraction. science 292 (5514), 77–79. doi:10.1126/science.1058847
Smith, D. R., Padilla, W. J., Vier, D. C., Nemat-Nasser, S. C., and Schultz, S. (2000). Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 84 (18), 4184–4187. doi:10.1103/physrevlett.84.4184
Veselago, V. G. (1968). The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Usp. 10 (4), 509–514. doi:10.1070/pu1968v010n04abeh003699
Wang, K., Zhao, J., Cheng, Q., Dong, D. S., and Cui, T. J. (2014). Broadband and broad-angle low-scattering metasurface based on hybrid optimization algorithm. Sci. Rep. 4 (1), 5935–5936. doi:10.1038/srep05935
Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J. P., Capasso, F., et al. (2011). Light propagation with phase discontinuities: Generalized laws of reflection and refraction. science 334 (6054), 333–337. doi:10.1126/science.1210713
Zhang, L., Wan, X., Liu, S., Yin, J. Y., Zhang, Q., Wu, H. T., et al. (2017). Realization of low scattering for a high-gain Fabry–Perot antenna using coding metasurface. IEEE Trans. Antennas Propag. 65 (7), 3374–3383. doi:10.1109/TAP.2017.2700874
Keywords: coding metasurface, wide-angle, bistatic RCS reduction, 2-bit phase, microstrip antenna
Citation: Huang YF, Jiang Z, Liu L and Zhang HC (2022) Design of a 2-Bit wide-angle coding metasurface for bistatic RCS reduction. Front. Mater. 9:956061. doi: 10.3389/fmats.2022.956061
Received: 30 May 2022; Accepted: 22 July 2022;
Published: 01 September 2022.
Edited by:
Hai Lin, Central China Normal University, ChinaReviewed by:
Shi-Wang Fan, Shijiazhuang Tiedao University, ChinaHodjat Hajian, Bilkent University, Turkey
Copyright © 2022 Huang, Jiang, Liu and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hao Chi Zhang, MTAxMDEyOTEwQHNldS5lZHUuY24=