Effects of Ca substitution on the local structure and oxide–ion behavior of layered perovskite lanthanum nickelate

La₂NiO_4+δ-based materials with a layered perovskite structure have attracted significant attention as air–electrode materials for use in solid oxide fuel cells. In particular, Ca-substituted materials, La_2-xCa_xNiO_4+δ, have been investigated, as the partial substitution of La with Ca can improve oxide–ion conduction in crystals. However, the local structures around the conducting oxide ion and Ca dopant are not been well understood because their distributions cannot be characterized by a general structure analysis only using Bragg peaks. Therefore, we examine the atomic structure of La_1.75Ca_0.25NiO_4+δ by a combination of molecular dynamics simulations and a reverse Monte Carlo modeling using the Faber–Ziman structure factor, real-space function, and the Bragg profile simultaneously. The results indicate that conducting oxide ions are introduced into rocksalt layers in the crystal and are present around La but not Ca. Furthermore, it is found that ionic diffusion is accompanied by a change in the rocksalt layer volume, which can be suppressed by the partial substitution with Ca. This can be regarded as a major reason why Ca substitution improves oxide–ion diffusion in the La₂NiO_4+δ layered perovskite.

Introduction

Solid oxide fuel cells (SOFCs) are high-efficiency clean energy conversion devices that have drawn significant attention for realizing a low-carbon society. To enable the widespread use of SOFCs, their operating temperature must be reduced to an intermediate-temperature range, i.e., below 700°C. To satisfy this requirement, many researchers have focused on developing novel air–electrode materials with oxide–ion conduction in addition to electronic conduction, as this mixed conduction expands the area available for the oxygen-reduction reaction. In the last few decades, La₂NiO_4+δ-based materials with a layered perovskite structure can be regarded as promising candidates as electrode materials owing to their excellent mixed conductions (Kharton et al., 1999; Skinner and Kilner, 2000; Kharton et al., 2001; Boehm et al., 2005; Mauvy et al., 2006; Shen et al., 2010; Gu et al., 2020; Li et al., 2020; Wu et al., 2020). The previous reports showed that excess oxide ions can be introduced into interstitial spaces in the rocksalt layers due to the oxidation of Ni²⁺, and result in high oxide–ion conduction. Furthermore, previous studies successfully improved the electrical conduction properties of La₂NiO_4+δ by partial substitution with other cations. For example, Ca²⁺ substitution for La³⁺ can enhance oxide-ion conduction (Shen et al., 2010; Li et al., 2020), although this partial substitution (acceptor doping) decreases the excess oxide–ion amount, δ, based on electroneutrality conditions. The improved conduction properties must be related to the atomic structures of the materials, prompting the study of La_2-xCa_xNiO_4+δ crystal structures by Rietveld refinement using diffraction patterns (Bragg peaks) (Ruck et al., 1997; Shen et al., 2010; Gu et al., 2020; Li et al., 2020; Wu et al., 2020). However, the relationship between the atomic structure and oxide–ion conduction mechanism remains unclear. This uncertainty arises from the fact that a structural analysis only using Bragg peaks cannot distinguish local environments around La and Ca which occupy the same crystallographic site in the layered perovskite structure.

Therefore, the atomic structure of La_1.75Ca_0.25NiO_4+δ with a layered perovskite structure was investigated in this study to clarify the effects of partial Ca substitution on the local structure around the interstitial oxide ion, which can diffuse in the crystal. The oxide–ion distribution was equilibrated using molecular dynamics (MD) simulations, and the cation arrangement and local structure around each cation were determined via Monte Carlo modeling with experimental data, referred to as reverse Monte Carlo (RMC) modeling (McGreevy and Pusztai, 1988; Tucker et al., 2007). Neutron and X-ray total scattering data were used in addition to the Bragg profile, as the total scattering data provided us information on local structures without translational symmetry, such as the local environment around the dopant (Ca). The analysis of a snapshot of the atomic configuration allowed for a detailed investigation of the local structure around the interstitial oxide ion and the effects of Ca substitution on the oxide–ion behavior in La_2–xCa_xNiO_4+δ.

Materials and methods

La_1.75Ca_0.25NiO_4+δ with a layered perovskite structure was synthesized using a solution method with subsequent heat treatment. La(NO₃)₃·6H₂O, Ca(NO₃)₂·4H₂O, and Ni(NO₃)₂·6H₂O were dissolved in ethanol in appropriate proportions, and citric acid was added to the solution to achieve a molar ratio of citric acid to the total amount of cations of 1.1:1. The solution was heated above 140°C, and the obtained product was calcined at 350°C for 2 h. The calcined powder was finally fired at 950°C for 8 h in air. As for the sample, the valence of Ni was evaluated by analyzing the X-ray absorption near-edge structure (XANES) with Athena (Ravel and Newville, 2005). This measurement was performed at BL14B2 (SPring-8) in the transmission mode.

The atomic structure was investigated to clarify the effect of Ca substitution on the oxide–ion behavior in the crystal. To precisely determine the lattice parameters and average atomic positions, the neutron Bragg profile was obtained with iMATERIA installed at J-PARC and Rietveld refinement was performed using the profile with a Z-Rietveld program (Oishi et al., 2009). From the refined crystal structure (average structure), a simulation box with 1,031 atoms was prepared for MD-RMC modeling.

Total scattering data were also obtained to further investigate the local structure. Neutron total scattering measurement was performed at NOVA (J-PARC). The sample powder was loaded in a V–Ni alloy container, and the total scattering pattern was recorded. The scattering pattern was normalized into a Faber–Ziman structure factor, S(Q), and then converted to a real-space function using a Fourier transform (Keen, 2001). X-ray S(Q) was obtained via X-ray total scattering measurement with an incident beam of 61 keV at BL04B2 (SPring-8) (Kohara et al., 2007). The incident X-ray intensity was monitored using an ionization chamber filled with Ar gas, and the scattered beam was monitored using CdTe and Ge detectors. To investigate the effect of Ca substitution on the atomic structure, the X-ray total correlation functions, T(r), of La₂NiO_4+δ as well as La_1.75Ca_0.25NiO_4+δ were derived from the structure factors.

In this study, the atomic configuration of La_1.75Ca_0.25NiO_4+δ was determined by combining MD simulation and RMC modeling. The MD simulation was performed with the LAMMPS program (Thompson et al., 2022) using a simulation box after the optimization of the La/Ca arrangement via preliminary RMC modeling (RMCProfile (Tucker et al., 2007)) with the swapping of La and Ca positions. In the MD simulation, a short-range Buckingham potential with a cutoff value of 10.5 Å and a long-range Coulombic potential were applied to express the interaction between atoms i and j. Therefore, the lattice energy, E_L, can be described as follows:

$E_{\text{L}}={\displaystyle \sum _{\text{j}>\text{i}}{\displaystyle \sum \left[A_{\text{ij}}\exp \left(-\frac{r_{\text{ij}}}{{\rho }_{\text{ij}}}\right)-\frac{C_{\text{ij}}}{r_{\text{ij}}^6}+\frac{q_{\text{i}}{q}_{\text{j}}}{4\pi {\epsilon }_0{r}_{\text{ij}}}\right]}}(1)$

In Eq. 1, r_ij, q_i, and ε₀ represent the interatomic distance, a charge of atom (ion) i, and vacuum permittivity, respectively. A_ij, ρ_ij, and C_ij are the parameters of the Buckingham potential, and the values utilized here are summarized in Table 1. It should be noted that the Ni–O interaction was assumed by considering the Ni valence. The simulation was run at 800°C for 800 ps with a constant number of the atoms–pressure–temperature (NPT) ensemble to optimize the distribution of interstitial oxide ions. The system was subsequently equilibrated at room temperature (27°C) for 200 ps using the constant number of the atoms–volume–temperature (NVT) ensemble.

TABLE 1

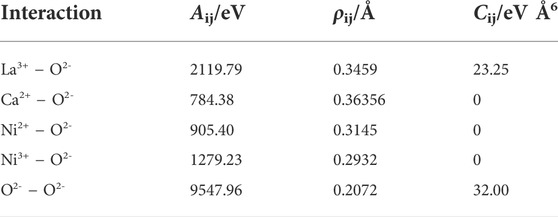
TABLE 1. Buckingham potential parameters (Minervini et al., 2000; Atkinson et al., 2003; Chroneos et al., 2010; Kitamura et al., 2020).

After the MD simulation, RMC modeling was performed without swapping La and Ca using the final snapshot obtained with the MD simulation as an initial structure. For the experimental data, a complementary dataset of neutron and X-ray S(Q), neutron real-space function, and a neutron Bragg profile was utilized. In the modeling, the S(Q) was convolved by considering the simulation-box size to eliminate the translational symmetry contribution. The convolved structure factors are denoted as S_box(Q) hereafter.

Results and discussion

Figure 1A shows the XANES spectrum at the Ni K-edge of the synthesized La_1.75Ca_0.25NiO_4+δ, along with those of NiO, LiNiO₂, and La_1.75Sr_0.25NiO_4+δ as references. The Ni valence of La_1.75Ca_0.25NiO_4+δ is considered to be between divalent and trivalent by comparing the absorption energy of the white line with those of NiO (divalent) and LiNiO₂ (trivalent) references. Moreover, it is supposed that the electronic state of Ni is almost independent of the substituted alkaline–earth metal. According to the literature (Inprasit et al., 2015; Kitamura et al., 2020), Ni in the Sr-substituted sample can be regarded as approximately +2.58; hence, the Ni valence in the Ca-substituted sample synthesized in this study should be essentially equal to +2.58. Since the excess oxide ions are introduced into the crystal interstitial space due to Ni²⁺ oxidation, the associated amount, δ, can be estimated to be 0.16 based on the electroneutrality condition.

FIGURE 1

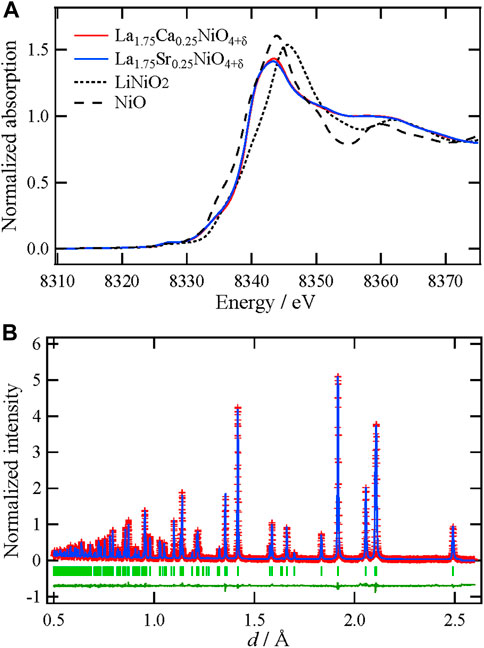
FIGURE 1. (A) XANES spectra at the Ni K-edge of La_1.75Ca_0.25O_4+δ with reference materials (B) The Rietveld refinement pattern of La_1.75Ca_0.25O_4+δ using a neutron Bragg profile. Red plus marks show the observed intensities, and the blue solid line represents the calculated intensities. The vertical bars indicate the positions of allowed Bragg reflections. The green curve at the bottom is the difference between the observed and calculated intensities at the same scale.

To refine the average structure of La_1.75Ca_0.25NiO_4+δ, Rietveld refinement was performed using the neutron Bragg profile. The refinement pattern and structural parameters are shown in Figure 1B and Supplementary Table S1, respectively. Although different space groups have been proposed for La₂NiO_4+δ-based materials, I4/mmm was used for the refinement (Ruck et al., 1997; Shen et al., 2010; Gu et al., 2020; Li et al., 2020; Wu et al., 2020). In this refinement, the average position of the interstitial oxide ions was not considered because their distribution was determined by a combination of MD and RMC. As can be seen in this figure, the average structure, except for the interstitial oxide ions, was successfully refined under these hypotheses. It is noteworthy that the bond valence sum, which is regarded as a valence indicator for Ni is +2.57, and this value is almost the same as the Ni valence estimated from the XANES spectrum (Figure 1A). Therefore, it is concluded that the refined average structure is reasonable.

To examine the differences in the local environments between La and Ca, the X-ray T(r) of La_2–xCa_xNiO_4+δ (x = 0, 0.25) are compared in Figure 2 along with the refined average structure and representative interatomic distances. It is found that interatomic distances become shorter by apparently substituting Ca for La. This phenomenon is supposed to reflect that an ionic radius of Ca²⁺ is slightly smaller than that of La³⁺ (Shannon, 1976). In addition, Ca²⁺ substitution (acceptor doping) is considered to oxidize the Ni ion, and then the oxidation might decrease the interatomic distances. The lattice contraction upon Ca substitution should affect oxide–ion conduction through the interstitial space in the crystal. For a better understanding of this effect, a detailed local structural analysis was performed.

FIGURE 2

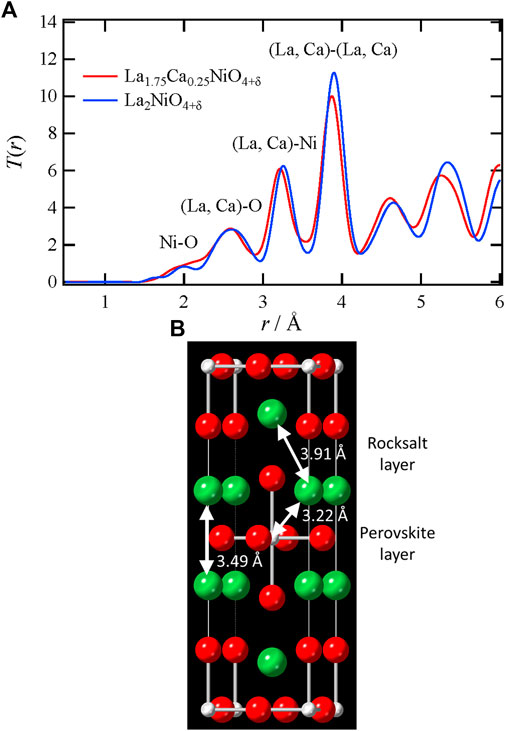
FIGURE 2. (A) X-ray total correlation functions, T(r), of La_1.75Ca_0.25NiO_4+δ and La₂NiO_4+δ (B) Representative interatomic distances in the crystal of La_1.75Ca_0.25NiO_4+δ. Color code (La, Ca) site, green; Ni site, gray; O site, red.

For the MD-RMC modeling on La_1.75Ca_0.25NiO_4+δ, an initial simulation box was generated by expanding the average structure (Supplementary Table S1), and interstitial oxide ions were distributed randomly in the rocksalt layers according to the literature (Shen et al., 2010; Gu et al., 2020; Li et al., 2020). In this structural modeling, the La and Ca arrangement was optimized by swapping atoms in RMC, and the distribution of the interstitial oxide ions was equilibrated via MD calculation. To enhance accuracy, this modeling procedure was repeated several times and the local structures were interrogated using the atomic-configuration snapshots. Figure 3 shows the MD-RMC modeling result. As can be seen in this figure, we could succeed in making an atomic configuration of La_1.75Ca_0.25NiO_4+δ, which can reproduce all the experimental data, i.e., neutron and X-ray S_box(Q), neutron reduced pair distribution function, G(r), and the neutron Bragg profile. This indicates that the atomic configuration is reasonable from the perspective of theoretical calculations (MD) and experimental data (RMC). The obtained atomic-configuration snapshot of La_1.75Ca_0.25NiO_4+δ and the condensed view (atomic distribution within the unit cell) are presented in Figures 4A,B, respectively. Figure 4A shows that the interstitial oxide ions are present in the rocksalt layer even after the MD calculation, indicating that this layer is the main diffusion path for the oxide ions. It is also demonstrated from the condensed view that the interstitial oxide ions are distributed toward the apex oxide ions of NiO₆ octahedra (O2 site) in the perovskite layer. This is consistent with the ionic conduction mechanism proposed for La₂NiO_4+δ-based materials in previous reports (Minervini et al., 2000; Yashima et al., 2010; Kitamura et al., 2020), which state that the interstitial oxide ions can diffuse through the O2 site.

FIGURE 3

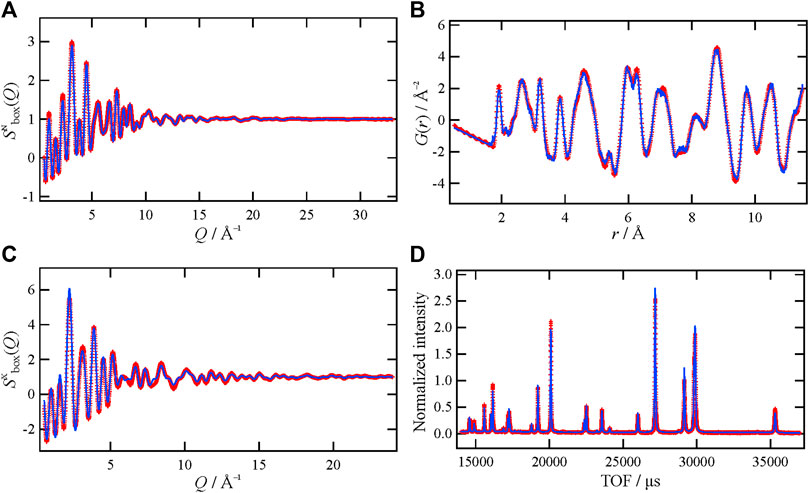
FIGURE 3. (A) Neutron and (B) X-ray S_box(Q), (C) neutron G(r), and (D) neutron Bragg profile of La_1.75Ca_0.25NiO_4+δ. The red marks and blue lines represent the experimental data and MD-RMC model, respectively.

FIGURE 4

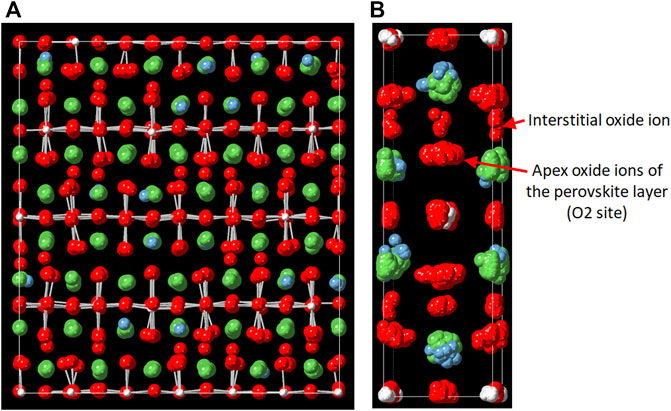
FIGURE 4. (A) Snapshot of the atomic configuration of La_1.75Ca_0.25NiO_4+δ and (B) the condensed view (atomic distribution within the unit cell). Color code: La, green; Ca, blue; Ni, gray; O, red.

Figure 5A shows the partial pair distribution functions, g_ij(r), of La–O and Ca–O. The functions demonstrate that the distribution of the Ca–O distance is significantly relative to that of the La–O distance, indicating a large distortion around the dopant. In addition, the interatomic distances around Ca are slightly shorter than those around La, and this tendency can be observed even in the second coordination shell. This result indicates that the local structures around Ca ions are key for the lattice compression in La_1.75Ca_0.25NiO_4+δ. From partial pair distribution functions, the coordination numbers of O around La and Ca were calculated; these are plotted as a function of distance in Figure 5B. With increasing distance, the coordination number initially increases around Ca and subsequently around La at longer distances. This trend is consistent with the ionic radii differences between the cations. It should be noted that the coordination number around Ca in the first coordination shell is almost nine and is lower than that around La. In the La₂NiO₄ (A₂BO₄)-type layered perovskite structure without interstitial oxide ions, the coordination number of O around the A-site cation must be 9 (Supplementary Figure S1). Therefore, the larger coordination number of O around La originates from the interstitial oxygen ions. In this material, an effective charge of Ca²⁺ at the La³⁺ site can be regarded as negative (−1) and this Ca can be expressed as $C{a}_{La}^{\prime }$ with a Körger–Vink notation. Therefore, this oxide–ion behavior should originate from an effective electrostatic repulsion between Ca and O. This suggests that the oxide–ion conduction path in La_1.75Ca_0.25NiO_4+δ is dominated by the La arrangement.

FIGURE 5

FIGURE 5. (A) Partial pair distribution function, g_ij(r), of La–O and Ca–O and (B) coordination numbers of O around La and Ca in La_1.75Ca_0.25NiO_4+δ.

Particular attention was devoted to the local environments around the interstitial oxide ions in the rocksalt layer because they directly affect the oxide–ion diffusion in La_1.75Ca_0.25NiO_4+δ. In the crystal, the interstitial oxide ions are basically surrounded by four A-site cations (La and Ca), and thus form tetrahedra as depicted in Figure 6. Table 2 summarizes the tetrahedral volume with an interstitial oxide ion as the central ion. Considering the average position of the interstitial oxide ion (Yashima et al., 2010), the tetrahedral volumes were also calculated from the result of the Rietveld refinements of the Ca-substituted sample (Supplementary Table S1) and La₂NiO_4+δ (Supplementary Table S2). For La_1.75Ca_0.25NiO_4+δ, the tetrahedra with interstitial oxide ions exhibit smaller volumes than those exhibited by the tetrahedra in the structure refined by the Rietveld analysis. Because the latter volume includes contribution of the tetrahedra without the interstitial oxide ions, the volume differences indicate that oxide–ion diffusion is accompanied by the rocksalt layer shrinkage. It is also demonstrated that the tetrahedral volume estimated by the Rietveld refinement is smaller in the Ca-substituted sample compared to that in La₂NiO_4+δ. Therefore, it can be concluded that the volume change due to the oxide–ion diffusion becomes less significant by the partial substitution with Ca. The structural change that occurs with Ca substitution can be considered as one of the reasons why La_1.75Ca_0.25NiO_4+δ could exhibit a larger diffusion coefficient of the oxide ions in comparison with La₂NiO_4+δ (Shen et al., 2010; Li et al., 2020).

FIGURE 6

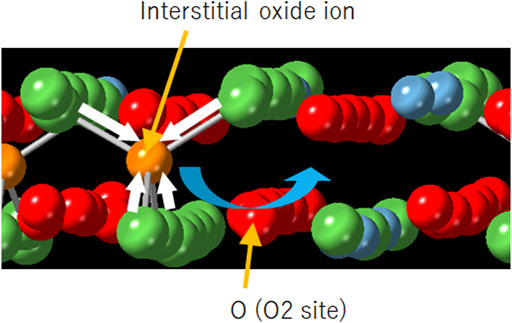
FIGURE 6. Schematic illustration of the local structure around the interstitial oxide ion in the rocksalt layer. The blue and white arrows indicate the diffusion path (Supplementary Figure S2) and local shrinkage around the interstitial oxide ion, respectively. Color code: La, green; Ca, blue; Ni, gray; O (O2 site), red; interstitial oxide ion, orange.

TABLE 2

TABLE 2. Volumes of (La, Ca)₄ tetrahedra with the interstitial oxide ion as the central ion. This table also lists the tetrahedral volumes estimated from the average structure refined via the Rietveld analysis, which represents the average values of (La, Ca)₄ tetrahedra with and without the interstitial oxide ion.

Conclusion

In this study, the local structure in layered perovskite La_1.75Ca_0.25NiO_4+δ is comprehensively investigated. Based on the analytical results, the effect of the partial substitution of La³⁺ with Ca²⁺ on the local environment around the excess interstitial oxide ions is discussed with respect to oxide–ion diffusion. The oxide ion prefers to exist around La³⁺ in the rocksalt layer due to electrostatic interactions. Moreover, it is demonstrated that the volume of the rocksalt layer decreases around the conducting ion, and this volume change due to the ionic diffusion becomes less significant by Ca substitution. Thus, it is concluded that the local structural features considerably influence the oxide–ion behavior in La₂NiO_4+δ-based materials.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KK synthesized the samples. NK, NI, CI, and YI performed total scattering (diffraction) and X-ray absorption measurements. NK and KK analyzed the data and wrote the manuscript. All authors discussed and commented on the final manuscript.

Funding

This research was financially supported by the JSPS Grant-in-Aid for Transformative Research Areas (A) “Hyper-Ordered Structures Science” (Grant No. 20H05880).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are grateful to K. Ohara (JASRI) for his support with the X-ray total scattering measurements at SPring-8, Japan (Proposal Nos. 2017A1290 and 2020A1134). We appreciate T. Honma and H. Ofuchi (JASRI) for their support with the X-ray absorption measurements at SPring-8, Japan (Proposal No. 2014B1932). We thank T. Ishigaki, A. Hoshikawa, and K. Ikeda (KEK) for their support with the neutron diffraction and total scattering measurements at J-PARC, Japan (Proposal Nos. 2021PM2001 and 2020B0095).

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.954729/full#supplementary-material

References

Atkinson, K. J. W., Grimes, R. W., Levy, M. R., Coull, Z. L., and English, T. (2003). Accommodation of impurities in α-Al₂O₃, α-Cr₂O₃ and α-Fe₂O₃. J. Eur. Ceram. Soc. 23, 3059–3070. doi:10.1016/s0955-2219(03)00101-8

CrossRef Full Text | Google Scholar

Boehm, E., Bassat, J., Dordor, P., Mauvy, F., Grenier, J., and Stevens, P. (2005). Oxygen diffusion and transport properties in non-stoichiometric Ln_2–xNiO_4+δ oxides. Solid State Ionics 176, 2717–2725. doi:10.1016/j.ssi.2005.06.033

CrossRef Full Text | Google Scholar

Chroneos, A., Parfitt, D., Kilner, J. A., and Grimes, R. W. (2010). Anisotropic oxygen diffusion in tetragonal La₂NiO_4+δ: molecular dynamics calculations. J. Mat. Chem. 20, 266–270. doi:10.1039/b917118e

CrossRef Full Text | Google Scholar

Gu, C.-Y., Wu, X.-S., Cao, J.-F., Hou, J., Miao, L.-N., Xia, Y.-P., et al. (2020). High performance Ca-containing La_2–xCa_xNiO_4+δ (0≤x≤0.75) cathode for proton-conducting solid oxide fuel cells. Int. J. Hydrogen Energy 45, 23422–23432. doi:10.1016/j.ijhydene.2020.06.106

CrossRef Full Text | Google Scholar

Inprasit, T., Wongkasemjit, S., Skinner, S. J., Burriel, M., and Limthongkul, P. (2015). Effect of Sr substituted La_2–xSr_xNiO_4+δ (x = 0, 0.2, 0.4, 0.6, and 0.8) on oxygen stoichiometry and oxygen transport properties. RSC Adv. 5, 2486–2492. doi:10.1039/c4ra11672k

CrossRef Full Text | Google Scholar

Keen, D. A. (2001). A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Cryst. 34, 172–177. doi:10.1107/s0021889800019993

CrossRef Full Text | Google Scholar

Kharton, V. V., Viskup, A. P., Naumovich, E. N., and Marques, F. M. B. (1999). Oxygen ion transport in La₂NiO₄-based ceramics. J. Mat. Chem. 9, 2623–2629. doi:10.1039/a903276b

CrossRef Full Text | Google Scholar

Kharton, V. V., Viskup, A. P., Kovalevsky, A. V., Naumovich, E. N., and Marques, F. M. B. (2001). Ionic transport in oxygen-hyperstoichiometric phases with K₂NiF₄-type structure. Solid State Ionics 143, 337–353. doi:10.1016/s0167-2738(01)00876-1

CrossRef Full Text | Google Scholar

Kitamura, N., Ishizaki, K., Ishida, N., and Idemoto, Y. (2020). Defect structure and oxide-ion conduction in (La, Sr)₂NiO_4+δ with layered perovskite structure. Chem. Lett. 49, 1071–1074. doi:10.1246/cl.200344

CrossRef Full Text | Google Scholar

Kohara, S., Itou, M., Suzuya, K., Inamura, Y., Sakurai, Y., Ohishi, Y., et al. (2007). Structural studies of disordered materials using high-energy x-ray diffraction from ambient to extreme conditions. J. Phys. Condens. Matter 19, 506101-1–506101-15. doi:10.1088/0953-8984/19/50/506101

CrossRef Full Text | Google Scholar

Li, X., Huan, D., Shi, N., Yang, Y., Wan, Y., Xia, C., et al. (2020). Defects evolution of Ca doped La₂NiO_4+δ and its impact on cathode performance in proton-conducting solid oxide fuel cells. Int. J. Hydrogen Energy 45, 17736–17744. doi:10.1016/j.ijhydene.2020.04.150

CrossRef Full Text | Google Scholar

Mauvy, F., Lalanne, C., Bassat, J.-M., Grenier, J.-C., Zhao, H., Huo, L., et al. (2006). Electrode properties of Ln₂NiO_4+δ (Ln = La, Nd, Pr) AC impedance and DC polarization studies. J. Electrochem. Soc. 153, A1547–A1553. doi:10.1149/1.2207059

CrossRef Full Text | Google Scholar

McGreevy, R. L., and Pusztai, L. (1988). Reverse Monte Carlo simulation: a new technique for the determination of disordered structures. Mol. Simul. 1, 359–367. doi:10.1080/08927028808080958

CrossRef Full Text | Google Scholar

Minervini, L., Grimes, R. W., Kilner, J. A., and Sickafus, K. E. (2000). Oxygen migration in La₂NiO_4+δ. J. Mat. Chem. 10, 2349–2354. doi:10.1039/b004212i

CrossRef Full Text | Google Scholar

Oishi, R., Yonemura, M., Nishimaki, Y., Torii, S., Hoshikawa, A., Ishigaki, T., et al. (2009). Rietveld analysis software for J-PARC. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 600, 94–96. doi:10.1016/j.nima.2008.11.056

CrossRef Full Text | Google Scholar

Ravel, B., and Newville, M. (2005). ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 12, 537–541. doi:10.1107/s0909049505012719

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruck, K., Ruck, M., and Krabbes, G. (1997). Crystal structure of La_1.7Ca_0.3NiO₄. Mater. Res. Bull. 32, 933–938. doi:10.1016/s0025-5408(97)00059-7

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. Sect. A 32, 751–767. doi:10.1107/s0567739476001551

CrossRef Full Text | Google Scholar

Shen, Y., Zhao, H., Liu, X., and Xu, N. (2010). Preparation and electrical properties of Ca-doped La₂NiO_4+δ cathode materials for IT-SOFC. Phys. Chem. Chem. Phys. 12, 15124–15131. doi:10.1039/c0cp00261e

PubMed Abstract | CrossRef Full Text | Google Scholar

Skinner, S., and Kilner, J. A. (2000). Oxygen diffusion and surface exchange in La_2–xSr_xNiO_4+δ. Solid State Ionics 135, 709–712. doi:10.1016/s0167-2738(00)00388-x

CrossRef Full Text | Google Scholar

Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., et al. (2022). LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171-1–108171-34. doi:10.1016/j.cpc.2021.108171

CrossRef Full Text | Google Scholar

Tucker, M. G., Keen, D. A., Dove, M. T., Goodwin, A. L., and Hui, Q. (2007). RMCProfile: reverse Monte Carlo for polycrystalline materials. J. Phys. Condens. Matter 19, 335218-1–335218-16. doi:10.1088/0953-8984/19/33/335218

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X., Gu, C., Cao, J., Miao, L., Fu, C., and Liu, W. (2020). Investigations on electrochemical performance of La₂NiO_4+δ cathode material doped at A site for solid oxide fuel cells. Mat. Res. Express 7, 065507-1–065507-8. doi:10.1088/2053-1591/ab9c60

CrossRef Full Text | Google Scholar

Yashima, M., Sirikanda, N., and Ishihara, T. (2010). Crystal structure, diffusion path, and oxygen permeability of a Pr₂NiO₄-based mixed conductor (Pr_0.9La_0.1)₂(Ni_0.74Cu_0.21Ga_0.05)O_4+δ. J. Am. Chem. Soc. 132, 2385–2392. doi:10.1021/ja909820h

PubMed Abstract | CrossRef Full Text | Google Scholar