A phase-field model with irradiation-enhanced diffusion for constituent redistribution in U-10wt%Zr metallic fuels

Constituent redistribution is a unique phenomenon to metal fuels that threatens the safety of such fuel forms. Therefore, it is imperative to establish models to understand the intrinsic mechanisms and predict the redistribution kinetics. In this work, we derived the conservative field equations of the phase-field model from near-equilibrium thermodynamic theory. A macroscopic constituent redistribution phase-field model was developed by introducing the effect of irradiation on the atom mobility and the effect of temperature on the interface mobility. An expression of phase boundary width, applicable to both microscopic and macroscopic scenarios was proposed. The interfacial parameters of the model and the Zr concentration distribution near the fuel surface were discussed at last. These works may help understand constituent redistribution characteristics and promote the application of the phase-field method in studying constituent redistribution in macroscopic scenarios.

Introduction

Metal fuels are ideal for fast reactors due to their higher fissile and fertile densities, and they possess high thermal conductivity and inherent safety features as demonstrated by the EBR-II (Experimental Breeder Reactor II) ULOF (Unprotected Loss-Of-Flow) and ULOHS (Unprotected Loss-Of-Heat-Sink) experiments (Feldman et al., 1987; Mohr et al., 1987). However, constituent redistribution in metal fuels is a significant threat to fuels’ safety. The initial uniform radial constituent distribution of metal-fuel transforms to an inhomogeneous counterpart due to the redistribution phenomenon driven by thermodynamics. Inhomogeneous distribution of ingredients and fission products significantly impacts fuels’ mechanical and physical properties (Murphy et al., 1969; Kim et al., 2004; Rahn et al., 2021). Therefore, it is crucial to understand and predict the redistribution kinetics.

Murphy et al. first observed the redistribution phenomenon in irradiated U-Pu-Zr fuel rods (Murphy et al., 1969). Thereafter, constituent redistribution was observed in U-Zr alloys at elevated temperatures (Hofman et al., 1996). Researchers have been establishing thermodynamic models to describe the constituent redistribution process. One of the most popular models was a U-10wt%Zr redistribution model (Hofman et al., 1996) based on a thermal diffusion mechanism. In addition, similar models were also established (Nam and Hwang, 1998; Kim et al., 2006) to analyze the constituent redistribution process. More innovatively, a quantitative constituent redistribution model for U-10wt%Zr alloy using the phase-field method was developed recently (Hirschhorn et al., 2019a; Hirschhorn et al., 2021). Phase-field method is good at dealing with thermodynamic problems and interface behaviour issues (Hu et al., 2009; Hu et al., 2010; Millett and Tonks, 2011a; Millett et al., 2011; Ahmed et al., 2014; Tonks et al., 2014; Liang et al., 2016; Mei et al., 2016). This method has been increasingly used for modelling and simulation in the field of nuclear materials in recent years, including U-Zr and U-Pu-Zr (Millett and Tonks, 2011b; Mohanty et al., 2011; Li et al., 2017; Tonks et al., 2018; Hirschhorn et al., 2019b; Hirschhorn et al., 2020). In all the above-described models, chemical diffusion coefficients, which control the diffusion of atoms and determine the final constituent distribution, were artificially enlarged several times by multiple a number, because the original chemical diffusion coefficients were not enough large to satisfy the simulation results. If key parameters in model cannot be theoretically and accurately determined, the subsequent prediction and design of materials in engineering will have a vital threat.

In this work, we have developed a more accurate phase field model than before. To obtain a more accurate diffusion coefficient, we introduced the irradiation-enhanced diffusion theory into the phase-field model of constituent redistribution and discussed the effects of irradiation on both chemical and thermal diffusion in U-10wt%Zr in this work. It has become an accepted fact that the additional vacancies introduced by irradiation will accelerate the diffusion of atoms, and such acceleration is particularly important at lower temperatures where thermal diffusion becomes limited. We also considered the effect of temperature on the interface mobility, which was overlooked by the previous phase-field model. This will also further improve the accuracy of the phase-field model. Besides, element concentration gradient free energy was added into the total free energy expression to make the free energy expression more comprehensive. In addition to making the model more accurate, the interfacial parameters related to phase boundary in our model were redefined and interpreted because the definition of grain boundary under microscopic conditions is unsuitable for phase boundaries under macroscopic conditions (Faulkner et al., 1996; Moelans et al., 2008). Finally, the interfacial parameters of the model and the Zr concentration distribution near the fuel surface were discussed.

Model development

The phase-field equations

Constituent redistribution is an irreversible process associated with material transport, which is essentially a near-equilibrium thermodynamic phenomenon. During U-Zr constituent redistribution, the Soret phenomenon, also called thermal diffusion, which is driven by the temperature gradient, was observed in the EBR-II X447 irradiation experiment (Hofman et al., 1996). The linear phenomenological law can derive the expression of diffusion flux caused by temperature gradient $J_i={\displaystyle \sum }_j{L}_{ij}{X}_j$(Kreuzer, 1981). Where $J_i$ is the $i^{th}$ thermodynamic flux; the coefficient $L_{ij}$satisfies Onsager’s reciprocal relationship $L_{ij}=L_{ji}$ and $X_j$ is the $j^{th}$thermodynamic force stemming from a kind of gradient, such as temperature gradient, chemical potential gradient, etc. In the constituent redistribution of U-Zr, the thermodynamic flux refers to the Zr diffusion flux, and the thermodynamic force contains two parts. One is produced by the temperature gradient, and the other is generated by the chemical potential gradient. Thus, the term which represents the contribution of a temperature gradient to the Zr diffusion flux (Kreuzer, 1981; Mohanty et al., 2009) was added into the model based on the original phase-field model which only considered the contribution from a chemical potential gradient.

$J_T=M_T\frac{\nabla T}{T}$(1)

$J_T$ represents the Zr diffusion flux induced by the temperature gradient, $M_T$ is the thermal mobility, and $T$is the temperature. The Zr diffusion flux generated by chemical potential gradient can be expressed as,

$J_c=-M_c^I\nabla \frac{\delta F}{\delta c}$(2)

where $M_c^I$ is the chemical mobility with the effect of irradiation; $F$is the system’s free energy, and $c$ is the Zr atomic fraction, and here we use it to represent the Zr concentration. The variation of free energy versus concentration is precisely the chemical potential. According to Fick’s second law, we have,

$\frac{\partial c}{\partial t}=-\nabla \cdot \left(J_T+J_c\right)$(3)

By substituting Eq. 1 and 2 into Eq. 3, the equation of the evolution of concentration with respect to time can be derived,

$\frac{\partial c}{\partial t}=\nabla \cdot \left(M_c^I\nabla \frac{\delta F}{\delta c}-M_T\frac{\nabla T}{T}\right)$(4)

That is actually one part of the phase-field model.

In the previous U-Zr component redistribution models, only the pure thermodynamic models were used, and the phase distributions needed to be determined a priori without considering phase evolutions (Hofman et al., 1996; Nam and Hwang, 1998; Kim et al., 2006). Determining the spatial distribution of phases followed by calculating the concentration can cause great inconvenience to deal with phase boundaries. Though phase interfaces are always complicated subjects, they can be effectively dealt with by introducing the phase diffusion equation into the phase-field model. Ever since the beginning of the development of phase-field method, the method has always been proven to have unique advantages in dealing with boundary problems (Millett et al., 2012; Ahmed et al., 2014; Biner, 2017). Another advantage of using phase-field model is that the specific distributions of each phase can be seen intuitively, which is not available in traditional thermodynamic models. Based on these considerations, the Allen-Cahn equation (Allen and Cahn, 1972; Allen and Cahn, 1973) was introduced into the phase-field model to describe the diffusion evolution of phases:

$\frac{\partial \gamma }{\partial t}=-L\frac{\delta F}{\delta \gamma }$(5)

Where, $\gamma$is the phase fraction of γ phase, and can be seen as the order parameter, ranging from 0 to 1. $L$is the kinetic coefficient of phase boundary mobility led by the evolution of the multi-phase region. Though $L$ can be seen as a constant under isothermal conditions, the effect of temperature on $L$ should be explicitly considered if temperature plays a vital role in the system. It has been verified that temperature significantly impacts grain-boundary mobility in previous studies (Tonks et al., 2014). Consequently, in this case, the Arrhenius formula should be taken into account (Wen et al., 2006; Mei et al., 2016),

$L=L_0{e}^{-\frac{Q_{\gamma }}{RT}}$(6)

Where, $L_0$ is a constant. $Q_{\gamma }$is the activation energy of phase boundary diffusion (Wang et al., 2009; Mei et al., 2016). Since the essence of phase boundary diffusion is the atomic diffusion, it is suggested that $Q_{\gamma }$ can take the value of activation energy of the diffusion of Zr, namely$Q_{\gamma }=128000-107000c_{\gamma }+174000{\left(c_{\gamma }\right)}^2$ (Kim et al., 2006); $R$is the gas constant.

The constituent redistribution of U-Zr mainly involves three single phases, γ, a and β. We inherited the idea of Hirschhorn et al. (Hirschhorn et al., 2019a) for the co-evolution of three phases. One order parameter $\gamma$ was used to simplify the three-phase model to a two-phase counterpart because phase-field can easily handle two-phase problems while it encounters a lot more difficulties dealing with three-phase issues. Due to the unique distribution of the three phases in the U-Zr phase diagram, the a and β phases can be reasonably regarded as one phase (α-β phase) independent of the γ phase. Then they can be distinguished through the phase transition temperature $T_{\alpha \beta }=935$K of a phase and β phase. Here, we introduce the interpolation functions:

$h_{\alpha \beta }=\frac{1}{2}+\frac{1}{2}\tanh \left(\frac{T_{\alpha \beta }-T}{2}\right)$(7)

$\alpha =\left(1-h_{\alpha \beta }\right)\left(1-\gamma \right)\beta =h_{\alpha \beta }\left(1-\gamma \right)$(8)

Where, $\alpha$ is the phase fraction of the a phase, and $\beta$ is the phase fraction of the β phase. In the non-γ phase area where the temperature is higher than $T_{\alpha \beta }$, β phase is present; and where the temperature is lower than $T_{\alpha \beta }$, a phase is present.

Free energy

The selection and discussion of free energy and migration coefficient are manifested below. In the phase-field model, total free energy generally contains volume free energy and gradient free energy (Kim et al., 1999; Chen et al., 2017). The volume free energy is composed of γ phase, a phase, and β phase, and the gradient free energy is composed of the concentration gradient and phase fraction gradient. The expression is as follows:

$F=\underset{V}{{\displaystyle \int }}\left\{\frac{1}{V_m}\left[\left(1-h\left(\gamma \right)\right)f_{\alpha \beta }+h\left(\gamma \right)f_{\gamma }\right]+\omega g+\frac{1}{2}{\kappa }_c{\left(\nabla c\right)}^2+\frac{1}{2}{\kappa }_{\gamma }{\left(\nabla \gamma \right)}^2\right\}dV$(9)

Where, $f_{\alpha \beta }$ represents the bulk free energy in a-β phase; $f_{\gamma }$is the free energy of the γ phase, $h\left(\gamma \right)$is an interpolation function of $\gamma$, $h\left(\gamma \right)={\gamma }^3\left(6{\gamma }^2-15\gamma +10\right)$, $V_m$ is defined as the fractional volume $V_m=\raisebox{1ex}{$N_A{a}^3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, $N_A$is the Avogadro’s constant, and $a$ is the lattice parameter of U-10wt%Zr, which is 0.3462; $g$is a barrier function, expressed as $g={\gamma }^2{\left(1-\gamma \right)}^2$; $\omega$ is the height of the double potential well function; ${\kappa }_c$ is the concentration gradient energy coefficient, and it needs to be in the 10⁻⁹ order of magnitude; ${\kappa }_{\gamma }$is the energy coefficient of the phase fraction gradient; $\omega$ and ${\kappa }_{\gamma }$ determine the shape and width of the phase diffusion interface, which will be discussed in the following. The expression of the thermodynamic free energy of a-β phase and γ phase comes from references (Dinsdale, 1991; Quaini et al., 2018; Hirschhorn et al., 2019a) and is given by:

$\begin{array}{l}{f}_{\alpha \beta }=\left(1-c_{\alpha \beta }\right)G_0^{\gamma -U}+c_{\alpha \beta }\left(38000+G_0^{\alpha -Zr}\right)+RT\left[\left(1-c_{\alpha \beta }\right)\ln \left(1-c_{\alpha \beta }\right)+c_{\alpha \beta }\ln c_{\alpha \beta }\right]+\\ \left(1-c_{\alpha \beta }\right)c_{\alpha \beta }\left(-7000\right)-23500.0+24.0T\end{array}$(10)

$\begin{array}{l}{f}_{\gamma }=\left(1-c_{\gamma }\right)G_0^{\gamma -U}+c_{\gamma }{G}_0^{\beta -Zr}+R988.4\left[\left(1-c_{\gamma }\right)\ln \left(1-c_{\gamma }\right)+c_{\gamma }\ln c_{\gamma }\right]+\\ \left(1-c_{\gamma }\right)c_{\gamma }\left\{28369.0639-14.741714*998.4+4992.02639\left(1-2c_{\gamma }\right)+2609.10711{\left(1-2c_{\gamma }\right)}^2\right\}\end{array}$(11)

Where $c_{\alpha \beta }$ is the equilibrium atomic fraction of Zr in the a-β phase; $c_{\gamma }$is the equilibrium atomic fraction of Zr in the γ phase; $G_0^{\alpha -U}$, $G_0^{\alpha -Zr}$, $G_0^{\gamma -U}$, $G_0^{\beta -Zr}$are the intrinsic free energy, and all of them can be found in the SGTE database (Scientific Group Thermodata Europe) (Dinsdale, 1991), corresponding to each component described therein, respectively. The KKS (Kim-Kim-Suzuki) model (Kim et al., 1999) was adopted to deal with phase boundaries in pursuit of accuracy. According to the KKS model, there should be a mutually restrictive relationship between Zr concentration, phase, and equilibrium concentration, as shown below:

$c=\left(1-h\right)c_{\alpha \beta }+h{c}_{\gamma }$(12)

$\frac{\partial f_{\alpha \beta }}{\partial c_{\alpha \beta }}=\frac{\partial f_{\gamma }}{\partial c_{\gamma }}$(13)

It should be noted that it is required that not only the above equations be satisfied near the interface, but also the equilibrium relationship be satisfied at each location point in the system. $c_{\alpha \beta }$ and $c_{\gamma }$ are not compositions of the phase interface, but compositions of different phases, respectively, at a certain infinitesimal point which is assumed to be a mixture of a phase, β phase, and γ phase. Thus, Eq. 13 does not imply a constant chemical potential throughout the interfacial region. It is consistent across the interface only at a thermodynamic equilibrium state. The chemical potential can vary across the moving interface from the γ phase side to the a-β phase side, which results in the solute trapping effect (Aziz, 1982; Aziz and Kaplan, 1988; Aziz, 1996). Eq. 12 and 13 are a transcendental system of equations and have no analytical solution, so the equations were discretized using the explicit finite difference method. Then Newton’s method was used to solve the discrete equations. We set the accuracy as ${10}^{-15}$ to ensure enough iterations to obtain a satisfactory numerical solution.

Migration coefficient accelerated by radiation

The diffusion coefficient of atoms in a crystal matrix $D_i$can be given by (Shewmon, 1989),

$D_i=\theta w{p}_v$(14)

Where $\theta$ is a constant determined by material, $w$ is the probability that an atom jumps into a vacant nearest-neighbour lattice site, and $p_v$ is the probability that any given nearest-neighbour lattice site is vacant and it is approximately equal to the vacancy concentration $C_v$. $w$ can be obtained from

$w=v\exp \left(-\frac{G_m}{kT}\right)$(15)

Where $v$ is the vibrational frequency of the atoms, $G_m$is the free energy required for an atom to migrate from an equilibrium position to the nearest neighbour site and is a function of absolute temperature $T$, and $k$ is the Boltzmann constant. By substituting Eq. 15 into Eq. 14, the diffusion coefficient of atoms can be rewritten as

$D_i=\theta v\exp \left(-\frac{G_m}{kT}\right)C_v$(16)

Where we define $\delta \left(T\right)=\theta v\exp \left(-\frac{G_m}{kT}\right)$, which is not influenced by irradiation. Under irradiation condition, the vacancy concentration is the sum of the thermal equilibrium vacancy concentration $C_v^e$ and the remaining free vacancy concentration created by irradiation $C_v^r$

$C_v=C_v^e+C_v^r$(17)

Then the irradiation-enhanced diffusion coefficient can be rewritten as

$D_i^{*}=\delta \left(T\right)\left(C_v^e+C_v^r\right)$(18)

$D_i^{*}$ is equal to the intrinsic diffusion coefficient $D_i^0$, in the absence of irradiation. According to Eq. 16, $\delta \left(T\right)$ is given by

$\delta \left(T\right)=D_i^0/C_v^e$(19)

Thus, the irradiation-enhanced solute diffusion coefficient $D_i^{*}$can be obtained as,

$D_i^{*}=\xi D_i^0$(20)

where,

$\xi =\left(\frac{C_v^e+C_v^r}{C_v^e}\right)$(21)

and

$D_i^0=D_{oi}\exp \left(-\frac{E_i}{kT}\right)$(22)

$C_v^e=A_v\exp \left(-\frac{E_f^v}{kT}\right)$(23)

Where $E_i$ is the activation energy and $D_{oi}$ is the pre-exponential constant for solute diffusion in the matrix; $A_v$ is a constant correlating with the vibrational entropy of atoms around the vacancy; the value can be taken as 1. $E_f^v$is the vacancy formation energy, and it is 1.20eV in U-10Zr (Vizoso and Deo, 2021).

By introducing the relationship of intrinsic diffusion and irradiation-enhanced diffusion, as shown in Eq. 20, into the phase-field model of constituent redistribution, we can get the diffusion mobility enhanced by irradiation,

$M_c^I=M_c\xi$(24)

Where $M_c$ is the chemical diffusion coefficient caused by the chemical potential gradient. According to the research of R. G. Faulkner (Faulkner et al., 1997), after 350 °C, the radiation enhanced diffusion coefficient is equal to the thermal diffusion coefficient in the a-Fe matrix, thermal diffusion starts to become significant and dominate at higher temperatures. Therefore, the value of $\xi$ here should be as small as possible though we do not know the exact value without experimental data. Thermal equilibrium vacancy concentration can be obtained easily using Eq. 23. In contrast, the value of the vacancy concentration in an irradiated material is more challenging to calculate as it is a function of the radiation flux, the vacancy formation energy, the dislocation density, etc. Here, rate theory (Olander, 1976) was used to get an approximate reference value of vacancy concentration (7.04 × 10⁻⁷) in the condition that the power was 30 kW/m and the temperature was about 1000K (Hofman et al., 1996). The vacancy concentration was derived from the vacancy created minus the vacancy absorbed, as calculated by a computer program developed based on the rate theory model of J. Rest (Rest, 1993). The other relevant parameters needed in this calculation can be found in the reference (Rest, 1993).

$M_c$is expressed by the three-phase chemical diffusion coefficient (Mohanty et al., 2009),

$M_c=\left(1-h_{\alpha \beta }\right)\left(1-h\right)M_c^{\alpha }+h_{\alpha \beta }\left(1-h\right)M_c^{\beta }+h{M}_c^{\gamma }$(25)

Where $M_c^{\alpha }$is the chemical diffusion coefficient in the a phase, and $M_c^{\beta }$ is the chemical diffusion coefficient in the β phase. The specific expressions of $M_c^i$are given below. The chemical diffusion coefficient in the a-β phase is:

$M_c^i=\frac{D_0^i{V}_m}{RT}\exp \left(\frac{-Q_i}{RT}\right),\left(i=\alpha ,\beta \right)$(26)

The chemical diffusion coefficient in the γ phase (Mohanty et al., 2011) is,

$M_c^{\gamma }=V_m{c}_{\gamma }\left(1-c_{\gamma }\right)\left[c_{\gamma }{\beta }_U+\left(1-c_{\gamma }\right){\beta }_{Zr}\right]$(27)

Where,

${\beta }_i={\beta }_0\exp \left(\frac{-H_i}{RT}\right)$(28)

Where $D_0^i$is the pre-exponential factor of the diffusion coefficient, and $Q_i$ is the activation energy of the mutual migration of U and Zr in the i phase (i stands for α, β, and γ); ${\beta }_U$ and ${\beta }_{Zr}$ are the atomic mobility of U and Zr in the γ phase, $H_i$ is the activation energy for the migration of U and Zr in the $i$ phase, and ${\beta }_0$ is the pre-exponential factor of the diffusion coefficient.

$M_T$ is similarly composed of the three parts, and it is expressed as follows:

$M_T=\left(1-h_{\alpha \beta }\right)\left(1-h\right)M_T^{\alpha }+h_{\alpha \beta }\left(1-h\right)M_T^{\beta }+h{M}_T^{\gamma }$(29)

The thermal migration coefficient in the a-β phase is:

$M_T^i=\frac{D_0^i{Q}_i^{*}}{RT}\exp \left(\frac{-Q_i}{RT}\right)$(30)

The thermal migration coefficient in the γ phase is:

$M_T^{\gamma }=c_{\gamma }\left(1-c_{\gamma }\right)\left(Q_U^{*}{\beta }_U+Q_{Zr}^{*}{\beta }_{Zr}\right)$(31)

Where $Q_i^{*}$ is an experimentally determined parameter describing the heat transport effect. Its sign determines whether the material migrates to the high-temperature region or the low-temperature region, and its value determines the amount of migration. In Table 1, the values of all the required parameters used above are summarized.

TABLE 1

TABLE 1. Parameters required in calculating the diffusion coefficients.

Simulation methods

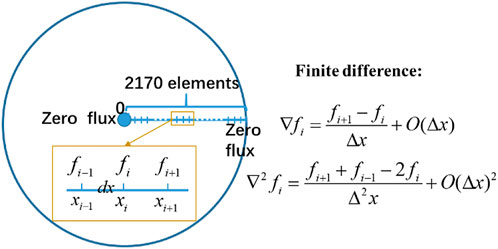
The thermodynamic parameters used in our simulation were all inherited from the DP-81 fuel. The DP-81 fuel element was irradiated at the EBR-II reactor by Argonne National Laboratory. The experimental data of the DP-81 pin provided a typical example for verification of this work because there exists not only the temperature profile but also measured data which indicates significant migration of zirconium. The experimental data about Zr concentration we used here were from Figure 7 of Hofman et al.’s article (Hofman et al., 1996). The fuel surface temperature was 900K, while the central temperature was about 988K, and the temperature distribution profile used here was from A. M. Yacout et al. (Yacout et al., 1996). All the simulations were conducted using the explicit finite difference method on the Matlab platform in this work. 1D simulations with 2170 μm long axisymmetric domain discretized into 2,170 elements were used in the current work to represent the DP-81 fuel, as shown in Figure 1. The left side of the 1-D linear segment represents the centerline, and the right side represents the outer surface of the fuel. Zero-flux boundary conditions were applied to all the centerline and the external surface variables. The time step was chosen to be 1s, and a total time length of 1.3 × 10⁵ s was conducted in all simulations.

FIGURE 1

FIGURE 1. Schematic diagram of finite difference method simulation.

Simulation results

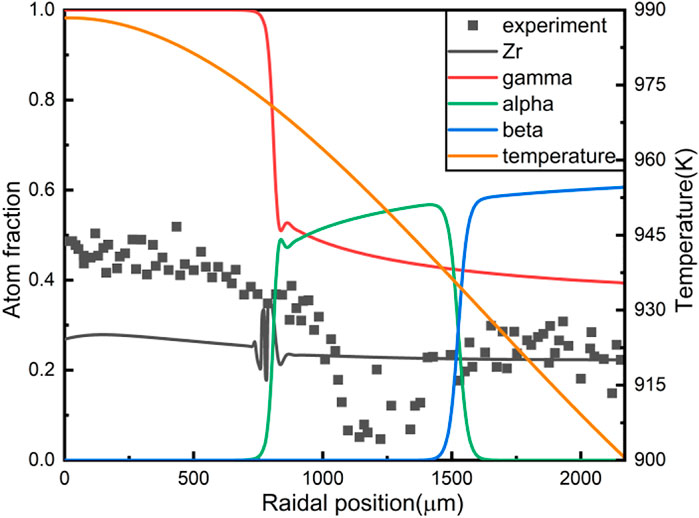
As described before, the driving forces acting on the Zr migration can be divided into two parts, i.e., heat transport term due to the temperature gradient and chemical potential gradient term which tends to equalize the concentration distribution. The diffusion coefficient controls the amount of Zr relocated, and heat transport and chemical potential gradient control the direction and the trend of the redistribution. To highlight the importance of radiation-accelerated diffusion in constituent redistribution models, we compared the simulation results between redistribution without the effect of irradiation and redistribution with the effect of irradiation, as shown inFigure 2, 3. Figure 2 shows the simulation results without considering the accelerated diffusion of irradiation. It can be seen that although Zr still tends to move to the high-temperature region due to the existence of the temperature gradient, there is almost no constituent redistribution. While the simulation results of Figure 3 are much in good agreement with the experimental data.

FIGURE 2

FIGURE 2. The results of U-10wt%Zr constituent redistribution without the effect of irradiation.

FIGURE 3

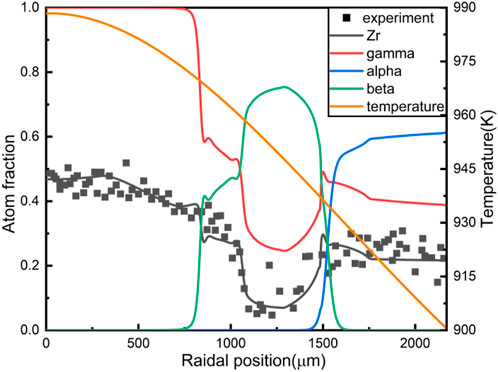
FIGURE 3. The results of U-10wt%Zr constituent redistribution with introducing the radiation-enhanced diffusion.

A noticeable feature of the Zr redistribution in Figure 3 is that a “Zr well” formed in the middle radial region of the fuel slug. Zr atoms migrate towards the fuel centre at high temperatures, causing the Zr concentration in the fuel centre to increase and U concentration to decline correspondingly. Consequently, the concentration of Zr in the middle radial region is relatively low. Phase distribution is also in line with the experimental results. The red line is the γ phase fraction, and the γ phase is mainly located in the central region of the fuel, coexisting with the β phase in the middle radial region, and coexisting with the a phase near the outer fuel surface.

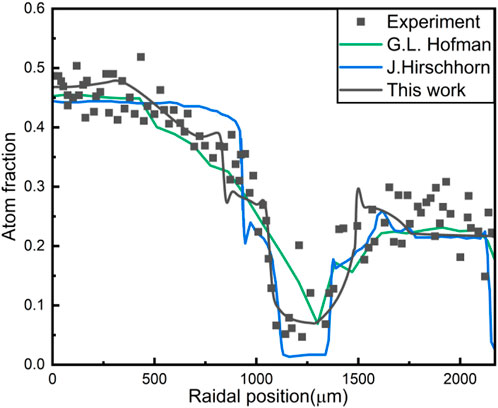
The comparison of the Zr concentration redistribution simulated by different models, including the model in this work, are shown in Figure 4. It is found that the introduction of the radiation-enhanced diffusion coefficient into the existing phase-field model seems to be able to replace reasonably the artificial increase of the diffusion coefficient. And by improving the rationality of some parameters of the phase-field model, such as the influence of temperature on the interface mobility, the accuracy of the simulation is significantly improved.

FIGURE 4

FIGURE 4. The U-10%Zr constituent redistribution obtained by different models.

Discussion

Discussion of interfacial parameters

The interface energy and the interface width occupy extraordinary significance in the phase-field model. The model parameters are often phenomenological and don’t possess the essence of natural physical properties (Moelans et al., 2008). Therefore, it is necessary to analyze the parameters and their effects on the simulation results. In this section, we first discussed the interface energy and then discussed the interface width by defining the macro phase boundary width.

For the KKS model, the chemical energy is decoupled from the interfacial energy, and the interfacial energy is only provided by the potential well term and the gradient term (Aagesen et al., 2018). It should be noted that the interface energy is not a specific phase boundary energy but rather a homogenized parameter describing all the phase boundaries in the two-phase region. The interface energy of phase boundaries in the two-phase areas in the discrete system model can thus be written as:

${\sigma }_{pb}={\displaystyle \sum }_x\left[\omega g\left(\gamma \right)+\frac{{\kappa }_{\gamma }}{2}{\left(\left|\frac{d\gamma }{dx}\right|\right)}^2\right]$(32)

Where $x$ is the axial coordinate of the phase boundaries in the two-phase regions. $\omega$ is the height of the double potential well function and ${\kappa }_{\gamma }$ is the energy coefficient of the phase fraction gradient in Eq. 9.

It is well known that the interfacial width is chosen mainly based on computational consideration in interface growth models. The phase boundary, which refers to the boundary between different phases, will be discussed in the following, referencing the definition of the grain boundary. Strictly speaking, there are many possibilities to define a measure for the boundary once the diffusion surface thickness reaches infinity. For example, Moelans et al. (Faulkner et al., 1996; Moelans et al., 2008) described the grain boundary based on the absolute value of the gradient.

$l_{gb}=\frac{1}{\left|{(d\gamma \left(x\right)/dx)}_{x=x_{\mathrm{i}\mathrm{n}\mathrm{t}er}}\right|}$(33)

Where $x_{\mathrm{i}\mathrm{n}\mathrm{t}er}$ is the position where the interface gradient is the greatest. The gradient term is expressed using the finite difference method,

$\frac{d\gamma \left(x\right)}{dx}=\frac{\gamma \left(x_2\right)-\gamma \left(x_1\right)}{x_2-x_1}$(34)

Since the profiles are steepest at the middle of the diffuse boundary region, a grain boundary width defined in this way can be used as numerical criteria for stability and accuracy. However, the description of the boundary in the microscopic situation does not apply to the situation of the macroscopic edge. Here, we proposed a new definition of boundary width based on Moelans et al., as shown in Eq. 35.

$l_{pb}=\frac{{\left|d\gamma \left(x\right)\right|}_{x=x_{\mathrm{i}\mathrm{n}\mathrm{t}er}}}{\left|{(d\gamma \left(x\right)/dx)}_{x=x_{\mathrm{i}\mathrm{n}\mathrm{t}er}}\right|}\propto \sqrt{\frac{{\kappa }_{\gamma }}{\omega }}$(35)

This equation is an extension of Eq. 34. In phase-field method, it can be used to express the phase boundaries and make the boundaries describable and discussible in macroscopic scenarios. For example, in a microscopic system with grain boundaries, two crystal grains can be distinguished by $\eta =0$ and $\eta =1$, and the value of $d\eta$ at the grain boundary always equals 1. Under this circumstance, Eq. 33 is applicable. However, in a macroscopic system, it is not enough to distinguish different phase regions based on whether the value of $\gamma$ is 0 or 1. For example, in the γ phase area, $\gamma$ is equal to 1, while in the γ+ß phase area, $\gamma$ is not equal to 0, but the γ phase area and the γ+ß phase area are two-phase regions, which are also needed to be distinguished. Similarly, γ+ß phase area and γ+α phase area are also two different phases, as shown by the yellow rectangles in Figure 5. One boundary between two-phase areas is shown as the white areas in Figure 5. The values of $d\gamma$ at boundaries between two-phase areas are also not equal to 1, and in most cases, they are not fixed values. Therefore, we flexibly defined the area where the phase fraction $\gamma$ has obvious saltation as the phase boundary. Its width is the interface width, which can describe the actual situation more accurately.

FIGURE 5

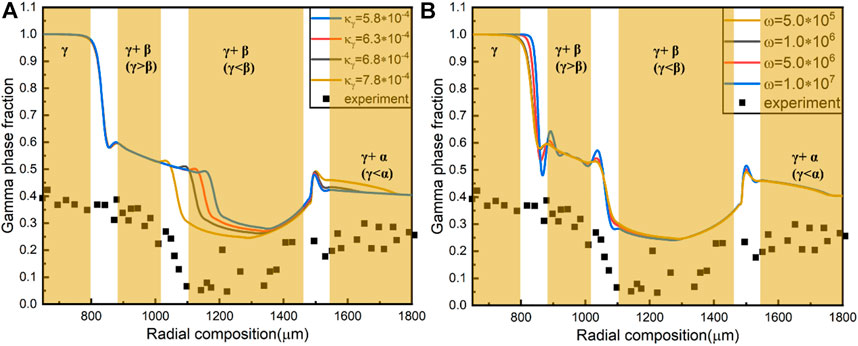
FIGURE 5. (A) γ Phase fraction as a function of ${\kappa }_{\gamma }$, with $\omega$ = 5.0 × 10⁵J/m³; (B) The curve of γ phase fraction concerning the $\omega$ at the interface, with${\kappa }_{\gamma }$ = 7.8 × 10⁻⁴J/m. Rectangular areas are different phase areas divided according to the yellow curves.

To get the values of interface energy ${\sigma }_{pb}$ and interface width $l_{pb}$, ${\kappa }_{\gamma }$ and $\omega$ should be first determined. By comparing the Zr concentration, obtained with different values of ${\kappa }_{\gamma }$ and $\omega$ with the experimental data, we locked the order of magnitude of the two parameters and then continuously refined and finally determined the values. In Figure 5, the evolution of γ at a flat boundary is shown for different values of the parameters ${\kappa }_{\gamma }$ and $\omega$. The variation of the phase fraction is concentrated in the 700–1300 μm region along the radial direction. Comparisons among these profiles were helpful to analyze the effects of $\omega$ and ${\kappa }_{\gamma }$. In Figure 5A, the value of $\omega$ was fixed to observe the impact of ${\kappa }_{\gamma }$. It can be found that the role of ${\kappa }_{\gamma }$ is primarily reflected by the size of the “Zr well”. The larger the value of ${\kappa }_{\gamma }$, the deeper and broader the well becomes. By comparing the experimental data (Zr concentration) with the simulation results and regarding the “Zr well” as an apparent reference, it is found that the yellow curve is mostly in good agreement. Either too large or too small values of ${\kappa }_{\gamma }$ can distort the simulation results. In Figure 5B, the predicted $\gamma$ profiles show that the value of $\omega$ can vary across two orders of magnitude. Within this range, variations of $\omega$ produce minor local variations in the predicted $\gamma$ profiles. With the increase of $\omega$, the interface width decreases gradually, and the interfaces between different phase regions are getting sharper, which can also degrade the computational efficiency.

The interfacial energy ${\sigma }_{pb}$ and the interfacial width $l_{pb}$ can be calculated by numerical computation from Eq. 32 and 35. Their values are shown in Table 2, corresponding to the different interfacial parameter values. The values in the grey background line are found to be the most appropriate values for the model by trial-and-error type of calculations.

TABLE 2

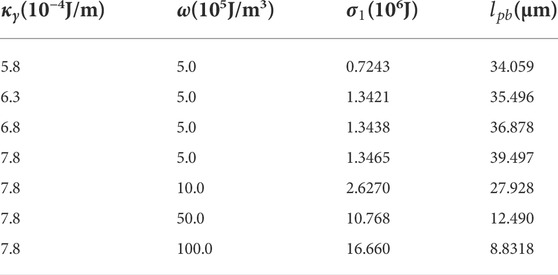
TABLE 2. Different ${\kappa }_{\gamma }$ and $\omega$ corresponding to different interfacial energy and interface width. ${\sigma }_1$ is the interfacial energy between γ phase and γ+ β (γ>ß) phase.

Discussion of the results near the fuel surface

Obviously, there is a distinct difference between the simulation results and the experimental data near the fuel surface among all constituent redistribution models, shown as Figure 4. Some Zr atoms migrate to the region between 1700 and 2000μm, making the Zr concentration higher than the initial concentration (0.225). Under normal circumstances, there is hardly Zr migration due to the small atom diffusion coefficient in the a-U phase. The specific reason is unknown, but it shall not be interpreted to be caused by temperature because the heat of transport parameter $Q^{*}$ analysis by G. L. Hofman (Hofman et al., 1996) has shown that Zr concentration at this position has nothing to do with $Q^{*}$. According to Thaddeus et al. (Rahn et al., 2021), it seems that the Zr rind can form during fabrication. But we cannot rule out that the increased atom diffusion coefficient due to irradiation effects made Zr gather locally in a long time-scale. Another possibility is that the structural change causes the free energy of the initial a-U phase to no longer apply. If so, the high fuel consumption effect cannot be ruled out. These will need to be clarified with further research.

Conclusion

Combined with traditional thermodynamics, the phase-field model coupling the radiation-enhanced diffusion model was constructed in this work. Firstly, the results of Zr redistribution simulated by the phase-field model were given and compared with the results of the model without the effect of radiation, which demonstrated the importance and necessity of introducing the radiation-enhanced diffusion model. Secondly, the influence of temperature on the kinetic coefficients was also imported to improve the rigour of the model. The computational results of the improved model appear to be in better agreement with the experimental data, compared to the previous models. Thirdly, an expression of boundary width applied to the macroscopic scenario was proposed to analyse the phase distribution. Through the analysis of phase interfacial parameters, the magnitude of the potential barrier played an essential role in forming a sharp interface and the energy coefficients had few effects on the redistribution results. This model may further help extend the application of phase-field in the constituent redistribution.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

CW: The realization of the phase-field model; Manuscript writing WL: Study conception and design; Model modification idea DY: Study conception and design; The manuscript revised ZQ: Calculation of rate theory.

Funding

This work was supported by the NSAF Joint Fund (No. U2130105), the National Natural Science Foundation of China (No. 11675126) and the Innovative Scientific Program of CNNC.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aagesen, L. K., Gao, Y., Schwen, D., and Ahmed, K. (2018). Grand-potential-based phase-field model for multiple phases, grains, and chemical components. Phys. Rev. E 98 (2), 023309. doi:10.1103/physreve.98.023309 | |

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmed, K., Pakarinen, J., Allen, T., and El-Azab, A. (2014). Phase field simulation of grain growth in porous uranium dioxide. J. Nucl. Mater. 446 (1-3), 90–99. doi:10.1016/j.jnucmat.2013.11.036 |

CrossRef Full Text | Google Scholar

Allen, S. M., and Cahn, J. W. (1973). A correction to the ground state of FCC binary ordered alloys with first and second neighbor pairwise interactions. Scr. Metall. 7 (12), 1261–1264. doi:10.1016/0036-9748(73)90073-2 |

CrossRef Full Text | Google Scholar

Allen, S. M., and Cahn, J. W. (1972). Ground state structures in ordered binary alloys with second neighbor interactions. Acta Metall. 20 (3), 423–433. doi:10.1016/0001-6160(72)90037-5 |

CrossRef Full Text | Google Scholar

Aziz, M. J. (1996). Interface attachment kinetics in alloy solidification. Metallurgical Mater. Trans. A 27 (3), 671–686. doi:10.1007/bf02648954 |

CrossRef Full Text | Google Scholar

Aziz, M. J., and Kaplan, T. (1988). Continuous growth model for interface motion during alloy solidification. Acta Metall. 36 (8), 2335–2347. doi:10.1016/0001-6160(88)90333-1 |

CrossRef Full Text | Google Scholar

Aziz, M. J. (1982). Model for solute redistribution during rapid solidification. J. Appl. Phys. 53 (2), 1158–1168. doi:10.1063/1.329867 |

CrossRef Full Text | Google Scholar

Biner, S. B. (2017). An overview of the phase-field method and its formalisms. Cham, Switzerland: Springer International Publishing, 1–7. Programming Phase-Field Modeling. |

CrossRef Full Text | Google Scholar

Chen, W., Peng, Y., Li, X. A., Chen, K., Ma, J., Wei, L., et al. (2017). Phase-field study on geometry-dependent migration behavior of voids under temperature gradient in UO₂ crystal matrix. J. Appl. Phys. 122 (15), 154102. doi:10.1063/1.4996692 |

CrossRef Full Text | Google Scholar

Dinsdale, A. (1991). SGTE data for pure elements. Calphad 15 (4), 317–425. doi:10.1016/0364-5916(91)90030-n |

CrossRef Full Text | Google Scholar

Faulkner, R. G., Song, S., and Flewitt, P. E. J. (1996). A model describing neutron irradiation-induced segregation to grain boundaries in dilute alloys. Metallurgical Mater. Trans. A 27 (11), 3381–3390. doi:10.1007/bf02595431 |

CrossRef Full Text | Google Scholar

Faulkner, R. G., Song, S., Flewitt, P. E. J., and Fisher, S. B. (1997). Irradiation-enhanced solute diffusion in alloys. J. Mat. Sci. Lett. 16 (14), 1191–1194. doi:10.1007/bf02765407 |

CrossRef Full Text | Google Scholar

Feldman, E. E., Mohr, D., Chang, L. K., Planchon, H., Dean, E., and Betten, P. (1987). EBR-II unprotected loss-of-heat-sink predictions and preliminary test results. Nucl. Eng. Des. 101 (1), 57–66. doi:10.1016/0029-5493(87)90150-6 |

CrossRef Full Text | Google Scholar

Galloway, J., Unal, C., Carlson, N., Porter, D., and Hayes, S. (2015). Modeling constituent redistribution in U-Pu-Zr metallic fuel using the advanced fuel performance code BISON. Nucl. Eng. Des. 286, 1–17. doi:10.1016/j.nucengdes.2015.01.014 |

CrossRef Full Text | Google Scholar

Hirschhorn, J., Aitkaliyeva, A., Adkins, C., and Tonks, M. (2019). The microstructure and thermodynamic behavior of as-cast U-24Pu-15Zr: Unexpected results and recommendations for U-Pu-Zr fuel research methodology. J. Nucl. Mater. 518, 80–94. doi:10.1016/j.jnucmat.2019.02.039 |

CrossRef Full Text | Google Scholar

Hirschhorn, J., Tonks, M., Aitkaliyeva, A., and Adkins, C. (2020). Reexamination of a U-Zr diffusion couple experiment using quantitative phase-field modeling and sensitivity analysis. J. Nucl. Mater. 529, 151929. doi:10.1016/j.jnucmat.2019.151929 |

CrossRef Full Text | Google Scholar

Hirschhorn, J., Tonks, M., and Matthews, C. (2021). A CALPHAD-informed approach to modeling constituent redistribution in Zr-based metallic fuels using BISON. J. Nucl. Mater. 544, 152657. doi:10.1016/j.jnucmat.2020.152657 |

CrossRef Full Text | Google Scholar

Hirschhorn, J., Tonks, M. R., Aitkaliyeva, A., and Adkins, C. (2019). A study of constituent redistribution in U-Zr fuels using quantitative phase-field modeling and sensitivity analysis. J. Nucl. Mater. 523, 143–156. doi:10.1016/j.jnucmat.2019.05.053 |

CrossRef Full Text | Google Scholar

Hofman, G. L., Hayes, S. L., and Petri, M. C. (1996). Temperature gradient driven constituent redistribution in U- Zr alloys. J. Nucl. Mater. 227 (3), 277–286. doi:10.1016/0022-3115(95)00129-8 |

CrossRef Full Text | Google Scholar

Hu, S., Henager, C. H., Heinisch, H. L., Stan, M., Baskes, M. I., and Valone, S. M. (2009). Phase-field modeling of gas bubbles and thermal conductivity evolution in nuclear fuels. J. Nucl. Mater. 392, 292–300. doi:10.1016/j.jnucmat.2009.03.017 |

CrossRef Full Text | Google Scholar

Hu, S., Li, Y., Sun, X., Gao, F., Devanathan, R., Henager, C. H., et al. (2010). Application of the phase-field method in predicting gas bubble microstructure evolution in nuclear fuels. Int. J. Mater. Res. 101, 515–522. doi:10.3139/146.110304 |

CrossRef Full Text | Google Scholar

Kim, S. G., Kim, W. T., and Suzuki, T. (1999). Phase-field model for binary alloys. Phys. Rev. E 60 (6), 7186–7197. doi:10.1103/physreve.60.7186 | |

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y. S., Hayes, S. L., Hofman, G. L., and Yacout, A. (2006). Modeling of constituent redistribution in U-Pu-Zr metallic fuel. J. Nucl. Mater. 359 (1-2), 17–28. doi:10.1016/j.jnucmat.2006.07.013 |

CrossRef Full Text | Google Scholar

Kim, Y. S., Hofman, G. L., Hayes, S. L., and Sohn, Y. (2004). Constituent redistribution in U-Pu-Zr fuel during irradiation. J. Nucl. Mater. 327 (1), 27–36. doi:10.1016/j.jnucmat.2004.01.012 |

CrossRef Full Text | Google Scholar

Kreuzer, H. J. (1981). Nonequilibrium thermodynamics and its statistical foundations. London, United Kingdom: Clarendon Press, 438.

Google Scholar

Li, Y., Hu, S., Sun, X., and Stan, M. (2017). A review: Applications of the phase field method in predicting microstructure and property evolution of irradiated nuclear materials. NPJ Comput. Mat. 3 (1), 16–17. doi:10.1038/s41524-017-0018-y |

CrossRef Full Text | Google Scholar

Liang, L., Mei, Z. G., Kim, Y. S., Ye, B., Hofman, G., Anitescu, M., et al. (2016). Mesoscale model for fission-induced recrystallization in U-7Mo alloy. Comput. Mater. Sci. 124, 228–237. doi:10.1016/j.commatsci.2016.07.033 |

CrossRef Full Text | Google Scholar

Mei, Z. G., Liang, L., Kim, Y. S., Wiencek, T., O'Hare, E., Yacout, A. M., et al. (2016). Grain growth in U-7Mo alloy: A combined first-principles and phase field study. J. Nucl. Mater. 473, 300–308. doi:10.1016/j.jnucmat.2016.01.027 |

CrossRef Full Text | Google Scholar

Millett, P. C., El-Azab, A., and Wolf, D. (2011). Phase-field simulation of irradiated metals Part II: Gas bubble kinetics. Comput. Mater. Sci. 50, 960–970. doi:10.1016/j.commatsci.2010.10.032 |

CrossRef Full Text | Google Scholar

Millett, P. C., and Tonks, M. (2011). Application of phase-field modeling to irradiation effects in materials. Curr. Opin. Solid State Mater. Sci. 15 (3), 125–133. doi:10.1016/j.cossms.2010.10.002 |

CrossRef Full Text | Google Scholar

Millett, P. C., and Tonks, M. (2011). Phase-field simulations of gas density within bubbles in metals under irradiation. Comput. Mater. Sci. 50, 2044–2050. doi:10.1016/j.commatsci.2011.02.006 |

CrossRef Full Text | Google Scholar

Millett, P. C., Tonks, M. R., Biner, S. B., Zhang, L., Chockalingam, K., and Zhang, Y. (2012). Phase-field simulation of intergranular bubble growth and percolation in bicrystals. J. Nucl. Mater. 425 (1-3), 130–135. doi:10.1016/j.jnucmat.2011.07.034 |

CrossRef Full Text | Google Scholar

Moelans, N., Blanpain, B., and Wollants, P. (2008). Quantitative analysis of grain boundary properties in a generalized phase field model for grain growth in anisotropic systems. Phys. Rev. B 78 (2), 024113. doi:10.1103/physrevb.78.024113 |

CrossRef Full Text | Google Scholar

Mohanty, R. R., Bush, J., Okuniewski, M. A., and Sohn, Y. (2011). Thermotransport in γ (bcc) U-Zr alloys: A phase-field model study. J. Nucl. Mater. 414 (2), 211–216. doi:10.1016/j.jnucmat.2011.03.028 |

CrossRef Full Text | Google Scholar

Mohanty, R. R., Guyer, J. E., and Sohn, Y. H. (2009). Diffusion under temperature gradient: A phase-field model study. J. Appl. Phys. 106 (3), 034912. doi:10.1063/1.3190607 |

CrossRef Full Text | Google Scholar

Mohr, D., Chang, L. K., Feldman, E. E., Betten, P., and Planchon, H. (1987). Loss-of-primary-flow-without-scram tests: Pretest predictions and preliminary results. Nucl. Eng. Des. 101 (1), 45–56. doi:10.1016/0029-5493(87)90149-x |

CrossRef Full Text | Google Scholar

Murphy, W. F., Beck, W. N., Brown, F. L., Koprowski, B. J., and Neimark, L. A. (1969). Postirradiation examination of U-Pu-Zr fuel elements irradiated in EBR-II to 4.5 atomic percent Burnup. Illinois, United States: Argonne National Laboratory.

Google Scholar

Nam, C., and Hwang, W. (1998). A calculation model for fuel constituent redistribution and temperature distribution on metallic U-10Zr fuel slug of liquid metal reactors. Nucl. Eng. Technol. 30 (6), 507–517.

Google Scholar

Olander, D. R. (1976). Fundamental aspects of nuclear reactor fuel elements. TID-26711-P1. Berkeley (USA): California University.

Google Scholar

Quaini, A., Guéneau, C., Gossé, S., Dupin, N., Sundman, B., Brackx, E., et al. (2018). Contribution to the thermodynamic description of the corium-the U-Zr-O system. J. Nucl. Mater. 501, 104–131. doi:10.1016/j.jnucmat.2018.01.023 |

CrossRef Full Text | Google Scholar

Rahn, T., Capriotti, L., Di Lemma, F., Trowbridge, T. L., Harp, J. M., and Aitkaliyeva, A. (2021). Investigation of constituent redistribution in U-Pu-Zr fuels and its dependence on varying Zr content. J. Nucl. Mater. 557, 153301. doi:10.1016/j.jnucmat.2021.153301 |

CrossRef Full Text | Google Scholar

Rest, J. (1993). Kinetics of fission-gas-bubble-nucleated void swelling of the alpha-uranium phase of irradiated U-Zr and U-Pu-Zr fuel. J. Nucl. Mater. 207, 192–204. doi:10.1016/0022-3115(93)90261-v |

CrossRef Full Text | Google Scholar

Shewmon, P. (1989). Diffusion in solids. The minerals, Metals & Materials Series (Cham, Switzerland: Springer), 53–130.

Google Scholar

Tonks, M. R., Cheniour, A., and Aagesen, L. (2018). How to apply the phase field method to model radiation damage. Comput. Mater. Sci. 147, 353–362. doi:10.1016/j.commatsci.2018.02.007 |

CrossRef Full Text | Google Scholar

Tonks, M. R., Zhang, Y., Bai, X., and Millett, P. C. (2014). Demonstrating the temperature gradient impact on grain growth in UO₂ using the phase field method. Mater. Res. Lett. 2, 23–28. doi:10.1080/21663831.2013.849300 |

CrossRef Full Text | Google Scholar

Vizoso, D., and Deo, C. (2021). Determination of vacancy formation energies in binary UZr alloys using special quasirandom structure methods. Front. Mat. 8, 243. doi:10.3389/fmats.2021.692660 |

CrossRef Full Text | Google Scholar

Wang, M., Zong, B., and Wang, G. (2009). Grain growth in AZ31 Mg alloy during recrystallization at different temperatures by phase field simulation. Comput. Mater. Sci. 45, 217–222. doi:10.1016/j.commatsci.2008.09.010 |

CrossRef Full Text | Google Scholar

Wen, Y. H., Wang, B., Simmons, J. P., and Wang, Y. (2006). A phase-field model for heat treatment applications in ni-based alloys. Acta Mater. 54, 2087–2099. doi:10.1016/j.actamat.2006.01.001 |

CrossRef Full Text | Google Scholar

Yacout, A. M., Yang, W. S., Hofman, G. L., and Orechwa, Y. (1996). Average irradiation temperature for the analysis of in-pile integral measurements. Nucl. Technol. 115 (1), 61–72. doi:10.13182/nt96-a35275 |

CrossRef Full Text | Google Scholar