Flexible Beam Manipulations by Reconfigurable Intelligent Surface With Independent Control of Amplitude and Phase

Reconfigurable intelligent surfaces (RISs) have attracted extensive attention in recent years due to their strong ability to improve and customize electromagnetic wave propagation channels in wireless communications. In this article, we propose a design procedure for an RIS and its programmable element, whose reflection phase and amplitude can be jointly controlled by adjusting the states of the varactor and PIN-diode. In addition, by introducing metallic vias in the RIS element, the programmable element can maintain the stable reflection amplitude and phase responses under the illumination of transverse magnetic (TM) wave with the incident angle of 0–60°. In order to verify the beam steering performance of the RIS, theoretical calculations and full-wave simulations of single beam and dual beams are carried out according to the addition theorem of the complex reflection coefficient. The amplitude- and phase-coding patterns on the RIS array are well designed so that the deflection angles and power intensities of the scattered beams can be manipulated independently.

Introduction

Reconfigurable intelligent surfaces (RISs), which developed from metasurfaces, are two-dimensional artificial electromagnetic materials which can be assembled in the wireless channel to improve or even customize the wireless channel by changing the environment of electromagnetic (EM) wave propagation in space (Basar et al., 2019) (Wu and Zhang, 2019) (Di Renzo et al., 2020) (Dai et al., 2020) (Sur and Bera, 2021). In recent years, RISs have attracted great research interest in the wireless communication community due to their great application potential. Metasurfaces, which have strong abilities to manipulate the EM waves, have also experienced a rapid development from analog to digital and from untunable to programmable (Cui et al., 2014) (Jing et al., 2019) (Ma et al., 2019) (Jing et al., 2019) (Cui et al., 2020). Therefore, the digital and programmable metasurfaces are important platforms to realize RIS-based wireless communication.

The proposal of the convolution theorem (Cui et al., 2016a) and the addition theorem (Wu et al., 2018) make it possible for RISs to form more advanced beam patterns. However, only the phase responses of the elements are considered while their amplitude responses are ignored in these metasurface designs (Cui et al., 2014) (Cui et al., 2016b) (Chen et al., 2018) (Wu et al., 2018) (Chen et al., 2019) (Liu et al., 2020) (Zhang et al., 2020) (Zhao et al., 2020) (Chen et al., 2021) (Huang et al., 2021) (Gao et al., 2021). In Ref. (Bao et al., 2019) (Rajabalipanah et al., 2019), both the amplitude and phase responses of the element are taken into consideration at the same time, thus forming a more complex multiple beams with controllable deflection angles and power intensities.

However, most of the reported metasurfaces with independent control of amplitude and phase are not programmable (Bao et al., 2019) (Rajabalipanah et al., 2019). Liao et al. (2021) proposed a PIN-diode-based 1-bit programmable element in which one PIN-diode was used to achieve two states with a 180° phase difference, and one PIN-diode was used to achieve variable attenuation of reflection amplitude. The proposed element in Liao et al. (2021) only realized symmetrical beams with large sidelobes due to the 1-bit phase accuracy. Li et al. (2022) proposed a programmable element with independent controls of transmission amplitude and phase, but its complicated structure makes manufacturing difficult. And Dai et al. (2018) realized the independent control of the amplitude-phase by introducing time dimension into the coding sequences, which is only effective for high-order harmonics.

In this article, we propose a programmable element whose reflection amplitude and phase can be jointly controlled by its own embedded PIN-diode and varactor. Three states of reflection amplitude and four states of reflection phase can be obtained by changing the operating states of the PIN-diode and varactor. In addition, numerous metallic vias are introduced in the programmable element to maintain a stable reflection amplitude and phase responses under the illumination of transverse magnetic (TM) waves with the incident angle of 0°–60°. Finally, in order to verify the performance of the proposed RIS element, the independent control of the deflection angles and power intensities of the dual-beam scattering patterns is realized by the addition theorem of complex reflection coefficients.

The Design Procedure of the Programmable Element

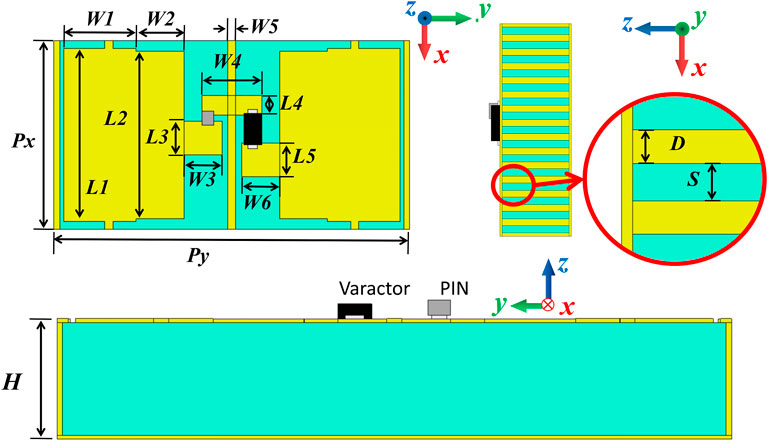
The proposed programmable element is a typical double-layered metal structure and can be fabricated by Print Circuit Board (PCB) technology. Figure 1 shows the schematic of the RIS array and its close-up view of programmable elements. Figure 2 shows the three-view of the programmable element labeled with structure parameters. F4B substrate ($\text{tan}\delta =0.001$, ${\epsilon }_r=2.65$) with a thickness of 3 mm is used to isolate the top and bottom metal layers. The bottom layer with a complete metal ground is used as a reflector plate. The top metal layer of the element is mainly composed of three patches with a thickness of 0.035 mm.

FIGURE 1

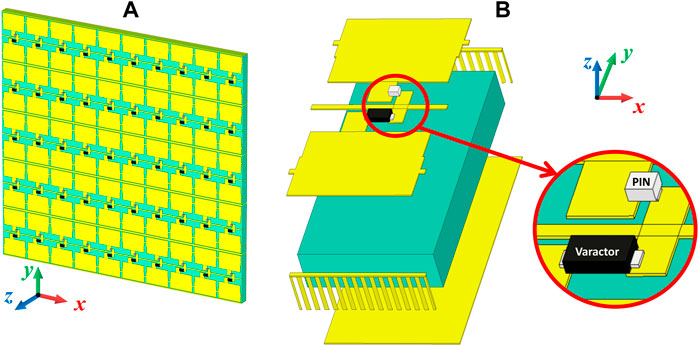
FIGURE 1. (A) Schematic diagram of the RIS array and (B) its close-up view of programmable elements integrated with a PIN-diode and a varactor.

FIGURE 2

FIGURE 2. The three-view of the proposed programmable element.

A PIN-diode and a varactor connect the patches over the narrow slot between the three main surface patches. The PIN-diode (SMP1321-040LF) can be modeled as a series connection of a tunable resistor R_PIN and an inductor L_PIN (0.27–0.36 nH). When the forward direct current (DC) decreases from 100 mA to 100 uA, the R_PIN increases from 0.46 to 19.7 Ω. The varactor (SMV1405-079LF) can be modeled as a series connection of a tunable capacitor C_Var, a resistor R_Var (0.63 Ω), and an inductor L_Var (0.7 nH). When the reverse DC voltage increases from 0 to 30 V, C_Var decreases from 2.6 to 0.6 pF. The DC feeding lines are designed for the PIN-diode and varactor to set desired working states. The thin metallic strip on the top layer serves as a DC ground, which crosses the element and connects the adjacent element. There are also thin metal strips going through the two larger patches. In such a design of DC feeding lines, all elements along the x-axis direction work in the same state for simplifying the DC control circuit to some extent.

Liang et al. (2021) proposed a method to decrease angular sensitivity by introducing metallic vias between adjacent elements. The dielectric discontinuity caused by the metallic vias destroys the original EM wave propagation mode and builds a more stable propagation mode. Considering the machining accuracy and approximate effect, metallic vias with a diameter (D) of 0.3 mm and a spacing (S) of 0.3 mm are drilled in the dielectric substrate. Other dimensional parameters in Figure 2 are Px = 9.5 mm, Py = 17.6 mm, L1 = 8.7 mm, L2 = 8.4 mm, L3 = 1.7 mm, L4 = 1 mm, L5 = 1.7 mm, W1 = 3.7 mm, W2 = 2.4 mm, W3 = 1.9 mm, W4 = 3 mm, W5 = 0.4 mm, W6 = 1.9 mm, and H = 3 mm.

The equivalent circuit model theory can be used to explain the operating mechanism of the proposed programmable element (Liang et al., 2021) (Vendik and Nikol, 2001). As shown in Figure 3, the element can be regarded as the load terminal when it is illuminated by a plane wave. The internal resistance of free space is ${\eta }_0=377$ Ohm. Three parallel capacitors, C₁, C_2, and C₃, are formed between the three main surface patches. The grounded dielectric substrate operates as a transmission line with a terminal short-circuit, and its equivalent impedance can be calculated as (Pozar, 2005) (Yu et al., 2011):

$Z_a=j\frac{{\eta }_0}{\sqrt{{\epsilon }_r}}\tan \frac{2\pi f\sqrt{{\epsilon }_r}H}{c}(1)$

FIGURE 3

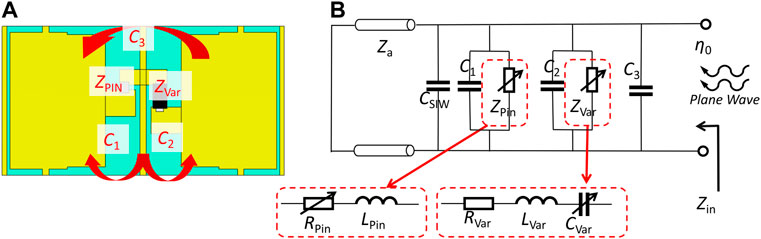
FIGURE 3. (A) Equivalent capacitance between the surface patches. (B) The equivalent circuit model of the proposed programmable element.

in which j is the imaginary unit. ${\epsilon }_r$ and H are the relative permittivity and the thickness of the dielectric substrate, respectively. f is the frequency of the incident EM wave, and c is the velocity of light in the vacuum. A capacitor C_SIW is formed by metallic vias between adjacent elements. The PIN-diode and the varactor are in parallel connection with C₁ and C_2, respectively. The overall input admittance $Y_{\text{in}}$ can be easily achieved as:

$Y_{\text{in}}=\frac{1}{Z_a}+j\omega C_{\text{SIW}}+\left(j\omega C_1+\frac{1}{R_{\text{PIN}}+j\omega L_{\text{PIN}}}\right)+\left(j\omega C_2+\frac{1}{R_{\text{Var}}+j\omega L_{\text{Var}}+\frac{1}{j\omega C_{\text{Var}}}}\right)+j\omega C_3(2)$

The reflection coefficient in the far-field is given as:

$\Gamma =\frac{\frac{1}{{\eta }_0}-Y_{\text{in}}}{\frac{1}{{\eta }_0}+Y_{\text{in}}}(3)$

Eq. 3 indicates that the amplitude and phase of the reflection coefficient can be jointly controlled by adjusting $R_{\text{PIN}}$ and $C_{\text{Var}}$ in the model of PIN-diode and the varactor together.

Numerical Results of the Programmable Element

The commercial EM simulation software, CST Microwave Studio 2021, is employed to calculate the EM responses of the programmable element. To simulate an infinite array, Floquet periodic boundaries are set along the x- and y-axes, and a Floquet port along the z-axis is used as an excitation to simulate the incidence of a plane wave. The excited electric field is set along the y-axis.

Figure 4 shows the numerical full-wave simulation results of the element at the normal incidence. “A⁰A¹A²A³B⁰B¹B²B³C⁰” is defined as nine coding states, which can be roughly divided into three groups. In the first group of states, the amplitude of states “A⁰A¹A²A³” is about 0.85, and there is a 90° phase shift among adjacent states. Different PIN states are employed to obtain the same reflection amplitude between states of A⁰∼A³. In the second group, the amplitude of states “B⁰B¹B²B³” is about 0.6, also with a 90° phase shift interval. The state “C⁰” has the lowest amplitude of about 0.2. The nine coding states corresponding to R_PIN and C_Var are listed in Table 1.

FIGURE 4

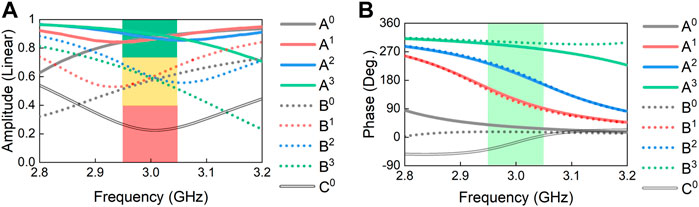
FIGURE 4. Numerical simulation results for the (A) amplitude and (B) phase responses of the programmable element. “A⁰A¹A²A³B⁰B¹B²B³C⁰” is defined as nine coding states with different reflection amplitude and phase.

TABLE 1

TABLE 1. The nine coding states of the proposed programmable element.

Wu et al. (2018) mentioned a special situation of “indefinite coding addition” when applying the addition theorem for RIS. This situation is caused by a 180° phase difference between the corresponding digits in the two sets of coding sequences before the addition operation. (Wu et al. (2018) makes artificial interventions for this special situation by introducing more coding states for the programmable element. However, it is not very friendly to the RIS loaded with tunable devices when balancing phase shift range and EM wave loss. Thus, the low-amplitude state (“C⁰”) is designed to deal with this indefinite situation. Due to its low amplitude, the error caused by its phase can be negligible.

To visually display the EM response of the programmable element, Figure 5A shows the reflection coefficients of nine coding states on the complex plane at normal incidence at 3 GHz. The position of the reflection coefficient $A\cdot {\text{e}}^{\text{j}\phi }$ of each state is determined by its amplitude A and phase φ simultaneously. To investigate the impact of oblique incidence, Figures 5B, C show the reflection coefficient at TM incidence angles of 30 and 60°. The reflection coefficients of nine coding states exhibit stable amplitude and phase responses at different incident angles, which is very important to ensure angular reciprocity in wireless communications (Liang et al., 2021).

FIGURE 5

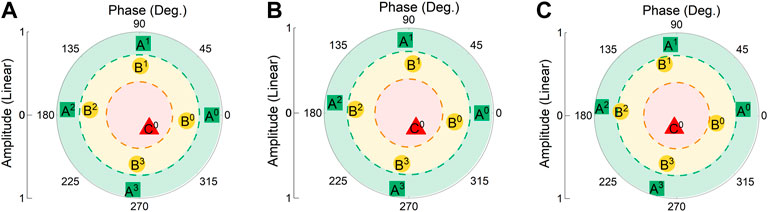
FIGURE 5. The reflection coefficients on the complex plane at incident angles of (A) 0° (B) 30°, and (C) 60°. Stable amplitude and phase responses are obtained due to the introduction of the numerous metallic vias at 3 GHz.

Numerical Results of RIS for Beam Steering

According to the generalized Snell’s law, anomalous reflection or refraction of EM waves will occur when there is a phase discontinuity on the material interface [30]. A phase gradient along the RIS can be set to realize beam steering. In addition, since the coding states “A⁰A¹A²A³” and “B⁰B¹B²B³” exhibit similar phase responses but different amplitude responses, they can be directly used to generate beams in the same direction but with different power intensities.

As a proof-of-principle example, an RIS array with 12 × 24 elements is considered, which has more elements in the direction of phase gradient, that is y-axis, to reduce the influence of truncated boundaries on the array simulation. The RIS array is illuminated by a normal incident uniform plane wave. For an array consisting of $M\times N$ elements, its scattering pattern in the far-field can be calculated as (Cui et al., 2014):

$f\left(\theta ,\phi \right)={\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{n=1}^N{f}_{mn}\left(\theta ,\phi \right)e^{-j\cdot {\phi }_{mn}-j\cdot k\cdot d\cdot \sin \theta \left(\left(m-\frac{1}{2}\right)\cos \phi +\left(n-\frac{1}{2}\right)\sin \phi \right)}(4)$

in which $f_{mn}\left(\theta ,\phi \right)$ is the scattering pattern of the mn-th element. k is the wavenumber of the EM wave in the vacuum. d is the period of the element.

Figures 6A–C shows the scattering patterns of two set of coding sequences “A⁰A⁰A⁰A¹A¹A¹A²A²A²A³A³A³...” and “B⁰B⁰B⁰B¹B¹B¹B²B²B²B³B³B³...ˮ. The two sets of coding sequences form the same phase gradient on the RIS and thus deflect the beam in the same direction $\theta =-27°$. However, since the reflection amplitudes of the elements in the first coding sequence are larger than that in the second coding sequence, the beam intensity of the first coding sequence is larger than that of the second coding sequence. Figures 6D–F shows the simulation results of another two set of coding sequences “A³A³A²A²A¹A¹A⁰A⁰...” and “B³B³B²B²B¹B¹B⁰B⁰...ˮ, it can be observed that two beams are pointed to the same direction of $\theta =47°$ with different power intensities.

FIGURE 6

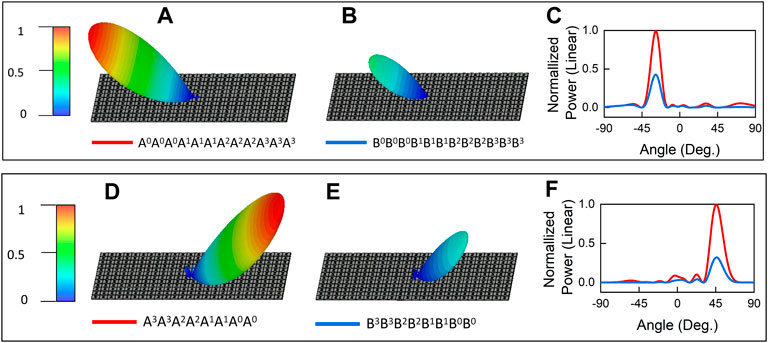
FIGURE 6. The 3D scattering patterns of coding sequences (A) “A⁰A⁰A⁰A¹A¹A¹A²A²A²A³A³A³...ˮ (B) “B⁰B⁰B⁰B¹B¹B¹B²B²B²B³B³B³...ˮ (D) “A³A³A²A²A¹A¹A⁰A⁰...ˮ (E) “B³B³B²B²B¹B¹B⁰B⁰...” and (C,F) their corresponding 2D scattering patterns.

According to the addition theorem of the complex reflection coefficient in Bao et al. (2019) and Rajabalipanah et al. (2019), the proposed programmable element with independent control of amplitude and phase can also be used to generate dual beams with independent control of deflection angles and power intensities. In this theorem, two sets of coding arrays S1 and S2 are considered. The complex coding sequences of S1 and S2 are set as $\left[A_1\right]\cdot e^{j\left[{\phi }_1\right]}$ and $\left[A_2\right]\cdot e^{j\left[{\phi }_2\right]}$, in which $\left[A\right]$ and $\left[\phi \right]$ represent the amplitude and phase distribution in the coding array, respectively. The coding array S1 and S2 can redirect the incident EM waves to two angles θ₁ and θ₂, with power intensities A₁ and A₂, respectively. According to the theorem, the composite coding sequences S can be obtained by

$S=\left[A_3\right]\cdot e^{j\left[{\phi }_3\right]}=\left[A_1\right]\cdot e^{j\left[{\phi }_1\right]}+\left[A_2\right]\cdot e^{j\left[{\phi }_2\right]}(5)$

The coding sequence S will redistribute the incident wave into two main beams pointing at angles θ₁ and θ₂ simultaneously, with a power intensity ratio of A₁/A₂. Theoretically, the proposed element can be used to form the arbitrary shape of dual or multiple beams.

To verify the ability to generate the arbitrary shape of dual beams, two groups of simulations are carried out. In the first simulation, two sets of coding sequences with different intensities pointing to −27° and 47° are arranged on the RIS array. The vector sums of the two sets of coding sequences are quantized according to the coding states in Table 1. Figures 7A–E shows the dual beams pointing at −27° and 47° simultaneously, with power intensity ratios of 0:1, 0.5:1, 1:1, 1:0.5, and 1:0, respectively. Both 3D and 2D far-field scattering patterns are displayed. Similarly, in the second group of simulations, the dual beams pointing at −21 and 37° simultaneously with different power intensity ratios are achieved, as shown in Figures 8A–E. The simulation results are well consistent with those calculated by Eq. 4.

FIGURE 7

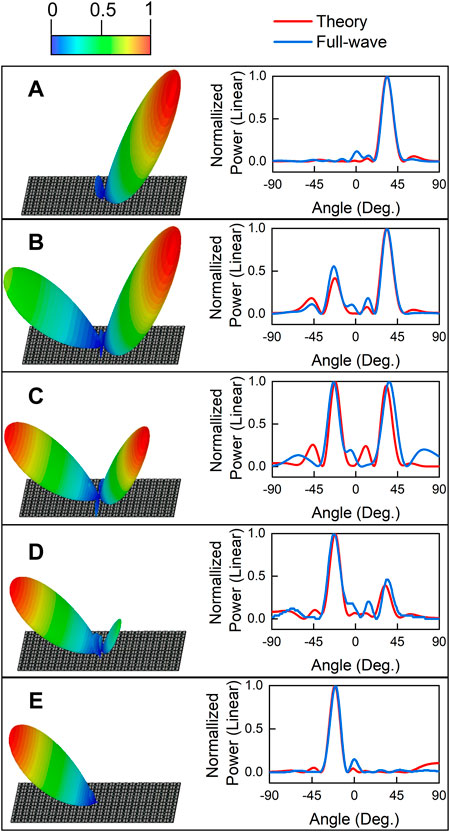
FIGURE 7. The 3D scattering patterns of dual beams pointing at -27° and 47° simultaneously, with power intensity ratios of (A) 0:1 (B) 0.5:1 (C) 1:1 (D) 1: 0.5 (E) 1:0 and their corresponding 2D scattering patterns.

FIGURE 8

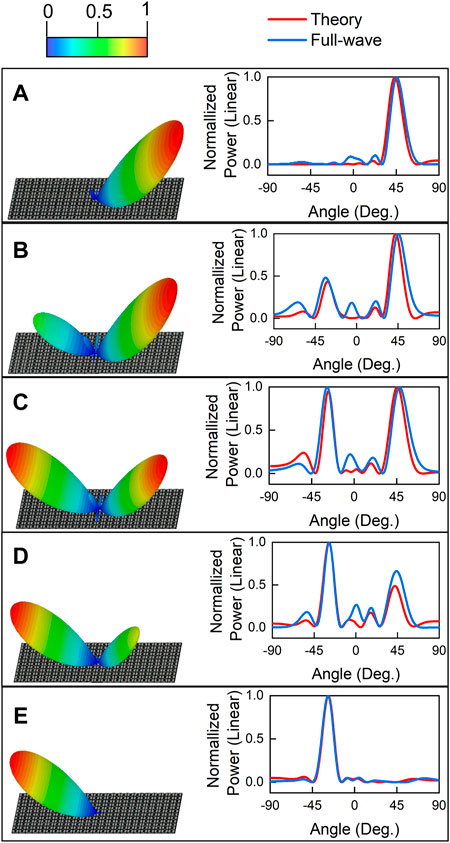
FIGURE 8. The 3D scattering patterns of dual beams pointing at -21° and 37° simultaneously, with power intensity ratios of (A) 0:1 (B) 0.5:1 (C) 1:1 (D) 1: 0.5 (E) 1:0 and their corresponding 2D scattering patterns.

It should be noted that in some sets of coding sequences, sidelobes appear at some unexpected angles. One of the reasons for this phenomenon is quantization errors. The amplitude and phase of the RIS array after the addition are not the precise preset coding states in Table 1 in some situations, and this approximation leads to quantization errors. In addition, truncating the boundaries also contributes to side lobes for the limited size of the RIS array.

In Bao et al. (2019) and Rajabalipanah et al. (2019), a freer intensity distribution for arbitrary multiple beams can be realized. However, due to the limitation of bit width, there will be more side lobes when realizing multiple beams by the proposed element, which is one of the problems that needs to be solved in the future.

Conclusion

In this article, a programmable element with independent control of amplitude and phase is designed and is applied to construct RIS arrays to generate scattered beams with controllable deflection angles and power intensities. A PIN-diode and a varactor are loaded into the programmable element simultaneously, and nine coding states with different reflection amplitudes and phases are obtained. The well-designed element exhibits good angular stability by introducing numerous metallic vias in the substrate. Numerical simulations of a single beam in the same directions but with different power intensities are performed by applying different coding states. Furthermore, under the guidance of the addition theorem of complex reflection coefficients, dual beams with independently controllable deflection angles and power intensities are investigated with theoretical calculations and full-wave simulations. All simulation results are basically consistent with the theoretical ones. This design of RIS with independent control of amplitude and phase has potential applications in next-generation wireless communications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

JL, LZ, ZC, PZ, and TC conceived the idea. JL, ZC, and LZ discussed the theoretical analysis, and JL performed numerical simulations. JL and LZ wrote the manuscript. All authors discussed the results and reviewed the manuscript.

Funding

This work is supported by the National Key Research and Development Program of China (2017YFA0700201, 2017YFA0700202, 2017YFA0700203, and 2018YFA0701904), the National Natural Science Foundation of China (62101123, 61722106, 61731010, and 11227904), the Major Project of Natural Science Foundation of Jiangsu Province (BK20212002), and the 111 Project (111-2-05), the National Postdoctoral Program for Innovative Talents (BX2021062), the China Postdoctoral Science Foundation (2020M680062), the Jiangsu Planned Projects for Postdoctoral Research Funds (2021K058A), the Jiangsu Province Frontier Leading Technology Basic Research Project (BK20212002), and the Fundamental Research Funds for the Central Universities (2242022k30004).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, L., Wu, R. Y., Fu, X., Ma, Q., Bai, G. D., Mu, J., et al. (2019). Multi-Beam Forming and Controls by Metasurface with Phase and Amplitude Modulations. IEEE Trans. Antennas Propagat. 67 (10), 6680–6685. doi:10.1109/tap.2019.2925289

CrossRef Full Text | Google Scholar

Basar, E., Di Renzo, M., De Rosny, J., Debbah, M., Alouini, M.-S., and Zhang, R. (2019). Wireless Communications through Reconfigurable Intelligent Surfaces. IEEE Access 7, 116753–116773. doi:10.1109/access.2019.2935192

CrossRef Full Text | Google Scholar

Chen, L., Shao, R. W., Dai, J. Y., Cheng, Q., Castaldi, G., Galdi, V., et al. (2019). Breaking Reciprocity with Space-Time-Coding Digital Metasurfaces. Adv. Mater 31 (41), e1904069. doi:10.1002/adma.201904069

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Tang, W., Dai, J. Y., Miao, L., Zhou, X. Y., Jin, S., et al. (2021). A Wireless Communication Scheme Based on Space- and Frequency-Division Multiplexing Using Digital Metasurfaces. Nat. Electron 4 (3), 218–227. doi:10.1038/s41928-021-00554-4

CrossRef Full Text | Google Scholar

Chen, L. X. Q., Liu, S., Zhang, Q., Zhao, J., Dai, J. Y., Bai, G. D., et al. (43342018). Space-time-coding Digital Metasurfaces. Nat. Commun. 9 (1), 4334. doi:10.1038/s41467-018-06802-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, S. T. J., Xu, Q., Bao, D., Du, L., Wan, X., Tang, W. X., et al. (2016a). Anisotropic Coding Metamaterials and Their Powerful Manipulation of Differently Polarized Terahertz Waves. Light Sci. Appl. 5 (5), e16076. doi:10.1038/lsa.2016.76

CrossRef Full Text | Google Scholar

Cui, S., Zhang, L., Xu, Q., Wang, Q., Wan, X., Gu, J. Q., et al. (2016b). Convolution Operations on Coding Metasurface to Reach Flexible and Continuous Controls of Terahertz Beams. Adv. Sci. (Weinh) 3 (10), 1600156. doi:10.1002/advs.201600156

CrossRef Full Text | Google Scholar

Cui, T. J., Li, L., Liu, S., Ma, Q., Zhang, L., Wan, X., et al. (2020). Information Metamaterial Systems. iScience 23 (8), 101403. doi:10.1016/j.isci.2020.101403

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, T. J., Qi, M. Q., Wan, X., Zhao, J., and Cheng, Q. (2014). Coding Metamaterials, Digital Metamaterials and Programmable Metamaterials. Light Sci. Appl. 3 (10), e218. doi:10.1038/lsa.2014.99

CrossRef Full Text | Google Scholar

Dai, J. Y., Zhao, J., Cheng, Q., and Cui, T. J. (2018). Independent Control of Harmonic Amplitudes and Phases via a Time-Domain Digital Coding Metasurface. Light Sci. Appl. 7, 90. doi:10.1038/s41377-018-0092-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, W., Chen, M. Z., Wong, K.-K., Li, X., Zhao, X., Jin, S., et al. (2020). MIMO Transmission through Reconfigurable Intelligent Surface: System Design, Analysis, and Implementation. IEEE J. Sel. Areas Commun. 38 (11), 2683–2699. doi:10.1109/jsac.2020.3007055

CrossRef Full Text | Google Scholar

Di Renzo, M., Zappone, A., Debbah, M., Alouini, M.-S., Yuen, C., de Rosny, J., et al. (2020). Smart Radio Environments Empowered by Reconfigurable Intelligent Surfaces: How it Works, State of Research, and the Road Ahead. IEEE J. Sel. Areas Commun. 38 (11), 2450–2525. doi:10.1109/jsac.2020.3007211

CrossRef Full Text | Google Scholar

Gao, W. H., Chen, M., Cheng, Q., Shao, E. W., Liang, J. C., Gao, V. Y., et al. (2021). 1-bit Reconfigurable Transmitarray with Low Loss and Wide Bandwidth. New J. Phys. 23 (6), 065006. doi:10.1088/1367-2630/ac02de

CrossRef Full Text | Google Scholar

Huang, C. X., Zhang, J., Cheng, Q., and Cui, T. J. (2021). Polarization Modulation for Wireless Communications Based on Metasurfaces. Adv. Funct. Mater. 31 (36). doi:10.1002/adfm.202103379

CrossRef Full Text | Google Scholar

Jing, H. B., Ma, Q., Bai, G. D., and Cui, T. J. (2019). Anomalously Perfect Reflections Based on 3‐Bit Coding Metasurfaces. Adv. Opt. Mater. 7 (9), 1801742. doi:10.1002/adom.201801742

CrossRef Full Text | Google Scholar

Li, H., Gong, C. Y., Dong, S. Y., Wang, S. Y., Wang, H. P., and Cui, T. J. (2022). Design of Programmable Transmitarray Antenna with Independent Controls of Transmission Amplitude and Phase. IEEE Trans. Antennas Propagat. (IEEE), 1. doi:10.1109/TAP.2022.3168278

CrossRef Full Text | Google Scholar

Liang, J. C., Gao, Y., Xiao, C., Gao, S., Zhang, L., Jin, S., et al. (2021). An Angle-Insensitive 3-Bit Reconfigurable Intelligent Surface. IEEE Trans. Antennas Propagat. (IEEE), 1. doi:10.1109/TAP.2021.3130108

CrossRef Full Text | Google Scholar

Liao, J., Guo, S., Yuan, L., Ji, C., Huang, C., and Luo, X. (2021). Independent Manipulation of Reflection Amplitude and Phase by a Single‐Layer Reconfigurable Metasurface. Adv. Opt. Mater. 10 (4), 2101551. doi:10.1002/adom.202101551

CrossRef Full Text | Google Scholar

Liu, B., He, Y., Wong, S., and Li, Y. (2020). Multifunctional Vortex Beam Generation by a Dynamic Reflective Metasurface. Adv. Opt. Mater. 9, 2001689. doi:10.1002/adom.202001689

CrossRef Full Text | Google Scholar

Ma, Q., Bai, G. D., Jing, H. B., Yang, C., Li, L., and Cui, T. J. (2019). Smart Metasurface with Self-Adaptively Reprogrammable Functions. Light Sci. Appl. 8, 98. doi:10.1038/s41377-019-0205-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Pozar, D. M. (2005). Microwave Engineering. Hoboken, NJ: John Wiley & Sons, 59–60.

Google Scholar

Rajabalipanah, H., Abdolali, A., Shabanpour, J., Momeni, A., and Cheldavi, A. (2019). Asymmetric Spatial Power Dividers Using Phase-Amplitude Metasurfaces Driven by Huygens Principle. ACS Omega 4 (10), 14340–14352. doi:10.1021/acsomega.9b02195

PubMed Abstract | CrossRef Full Text | Google Scholar

Sur, S. N., and Bera, R. (2021). Intelligent Reflecting Surface Assisted MIMO Communication System: A Review. Phys. Commun. 47 (1), 101386. doi:10.1016/j.phycom.2021.101386

CrossRef Full Text | Google Scholar

Vendik, O. G., and Nikol, M. A. (2001). Simulation of a Multilayer Planar Capacitor. Tech. Phys. 46 (1), 112–116. doi:10.1134/1.1340895

CrossRef Full Text | Google Scholar

Wu, Q., and Zhang, R. (2019). Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 18 (11), 5394–5409. doi:10.1109/twc.2019.2936025

CrossRef Full Text | Google Scholar

Wu, R. Y., Shi, C. B., Liu, S., Wu, W., and Cui, T. J. (2018). Addition Theorem for Digital Coding Metamaterials. Adv. Opt. Mater. 6 (5), 1701236. doi:10.1002/adom.201701236

CrossRef Full Text | Google Scholar

Yu, N., Genevent, P., Kats, M. A., Aieta, F., Capasso, F., Gaburro, Z., et al. (2011). Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334 (6054), 333–337. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X. G., Yu, Q., Jiang, W. X., Sun, Y. L., Bai, L., Wang, Q., et al. (2020). Polarization-Controlled Dual-Programmable Metasurfaces. Adv. Sci. (Weinh) 7 (11), 1903382. doi:10.1002/advs.201903382

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., Huang, C., Yang, J., Song, J., Guan, C., and Luo, X. (2020). Broadband Polarization-Insensitive Tunable Absorber Using Active Frequency Selective Surface. Antennas Wirel. Propag. Lett. 19 (6), 982–986. doi:10.1109/lawp.2020.2985710

CrossRef Full Text | Google Scholar