A Photovoltaic Power Predicting Model Using the Differential Evolution Algorithm and Multi-Task Learning

The rapid growth of photovoltaic installed capacity exacerbates the power management challenges faced by photovoltaic power stations, emphasizing the importance of accurate and stable photovoltaic generation forecasting. As a result, researchers conducted research and developed several photovoltaic power prediction models. However, many prediction models focus exclusively on the algorithm structure in order to improve model accuracy, oblivious to how the dataset is constructed and divided for the prediction model. This paper proposes a comprehensive model to address this gap. To be more precise, the differential evolution algorithm is constantly looking for optimal values between different populations and determining the best way to construct datasets for prediction tasks. Multi-task learning enables the transfer of knowledge between related tasks via parameter sharing layers, referring to the accuracy and stability of prediction models. Overall, the proposed model achieves high prediction accuracy and stability. The prediction error of the proposed model is less than 450W in RMSE, NRMSE is less than 2.5%, and R-Square is greater than 99% in multiple prediction tasks. Additionally, when compared to other single-task prediction models with an R-Square greater than 96%, the proposed model further reduces the root mean squared error by an average of 28% and the standard deviation of root mean squared error by 54%.

Introduction

Background

With the continuous improvement of people’s awareness of green energy, the photovoltaic generation has garnered widespread attention worldwide due to its mature technology (Mitrašinović, 2021). Regrettably, it also brings significant uncertainty due to environmental factors (such as weather, wind speed, and sunshine intensity) (Ramli et al., 2016), which is detrimental to the power grid’s stability and reliability (Liang, 2017). As a result, accurate photovoltaic power forecasting research is critical to the power grid and energy utilization industries.

The prediction period mainly divides photovoltaic power prediction research into two models: ultra-short-term early photovoltaic power prediction (predicting photovoltaic power from minutes to hours) and short-term early photovoltaic power prediction (predicting photovoltaic power from a day to weeks) (Rana et al., 2016). They are critical for real-time grid dispatch and the formulation of daily power generation plans in advance (Al-Shetwi and Sujod, 2018).

Literature Review and Motivation

Numerous researchers have previously proposed various models for forecasting photovoltaic energy generation. Physical, statistical, and integrated methods are the most frequently used prediction techniques (Sobri et al., 2018). Physical methods directly calculate photovoltaic energy generation based on the efficiency of photovoltaic components (such as photovoltaic modules and inverters) and environmental variables (such as sunlight intensity) (Ogliari et al., 2017). They are primarily influenced by the efficiency of various components involved in the photoelectric conversion process and the physical location of photovoltaic power plants (Humada et al., 2020). Previous studies have researched the modeling of the photovoltaic modules to confirm the operating conditions of solar cells and to determine their effective parameters (Humada et al., 2016). However, not only the accuracy of the model is related to the choice of the model type and the number of parameters, but also the balance between the accuracy and complexity of the model has always been challenging for researchers.

Statistical methods extract the internal relationships between historical data and establish a specific mapping relationship between prediction model input and output. Specifically, statistical methods include the persistence model, the autoregressive moving average (ARMA) model (Boland et al., 2016), the regression method (Trapero et al., 2015), the exponential smoothing method (Dong et al., 2013), the support vector machine (SVM) (Jufri et al., 2019), and the artificial neural network (ANN) (Shahsavar et al., 2021). Integrated methods incorporate multiple models into physical or statistical methods (Abdel-Nasser and Mahmoud, 2019), effectively circumventing the limitations of a single model and increasing the model’s predictive accuracy. Because of its superior nonlinear fitting ability, ANN is frequently used as a fundamental model in the appealing model.

Due to the exceptional ability of recurrent neural network (RNN) models to extract timing features, researchers have proposed variant models based on the RNN model to forecast photovoltaic power generation in ANN (Lin et al., 2018). The long short-term memory (LSTM) model is frequently used in time series prediction as a variant of the RNN model (Qu et al., 2021). However, the method by which datasets are divided has a significant impact on the model’s prediction performance and accuracy (Wang et al., 2020). Additionally, the prediction of the single-task prediction model will be highly unstable. When a single-task prediction model makes multiple predictions for distinct prediction tasks, the prediction errors fluctuate wildly, reducing the predictability of the photovoltaic power generation prediction model, which is detrimental to photovoltaic power generation prediction.

This paper aims to address the problem that the division and construction of datasets rely heavily on the experience of researchers, as well as the poor prediction and stability of traditional prediction models. Given these issues, the priori model consisting of a differential evolution algorithm and LSTM is proposed for the dataset construction of concrete prediction tasks. The prediction performance and stability are further improved by the multi-task learning mechanism through the process of knowledge transfer between related and target tasks. Verified on a variety of concrete prediction tasks, the proposed model further reduces root mean squared error by an average of 28% and the standard deviation of root mean squared error by 54% when compared to other single-task prediction models with an R-Square greater than 96%.

Theories and Motivation

Long Short-Term Memory Networks

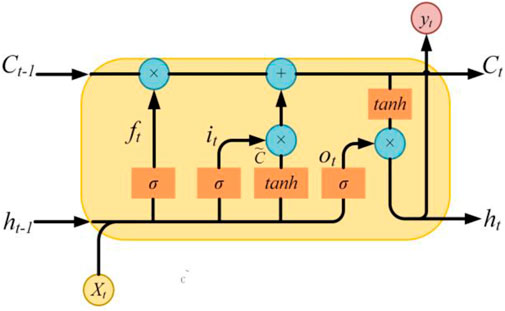
Long short-term memory (LSTM) is a subtype of recurrent neural network (RNN). Due to its atypical structure, it is capable of grasping the timing characteristics of photovoltaic power and resolving the gradient disappearance and explosion problems associated with long sequence training.

The LSTM introduced the concept of cell state, and three gate structures (input gate, forget gate, and output gate) are used to maintain and control the flow of timing information, as illustrated in Figure 1. Assume that C_t-1 and h_t-1 represent the current state of the cell and hidden layer, respectively. The LSTM’s status update process for each gate per unit time step is illustrated in Eqs. 1–6.

$f_t=\sigma \left(W_f·\left[h_{t-1},x_t\right]+b_f\right)(1)$

$i_t=\sigma \left(W_i·\left[h_{t-1},x_t\right]+b_i\right)(2)$

$C_t=\tanh \left(W_C·\left[h_{t-1},x_t\right]+b_C\right)(3)$

$C_t=f_t\odot C_{t-1}+i_t\odot C_t(4)$

$O_t=\sigma \left(W_O·\left[h_{t-1},x_t\right]+b_O\right)(5)$

$h_t=O_t\odot \tanh \left(C_t\right)(6)$

where $f_t$ is the current state of the forget gate, $i_t$ is the current state of the update gate, ${\tilde{C}}_t$ is the cell candidate state, $C_t$ is the current state of the cell state, and $O_t$ is the current state of the output gate. The output is calculated by the fully connected layer whose activation function is the sigmoid function and is uniformly represented as a function $\sigma$ (·)

FIGURE 1

FIGURE 1. The structure of the LSTM cell.

Differential Evolution Algorithm

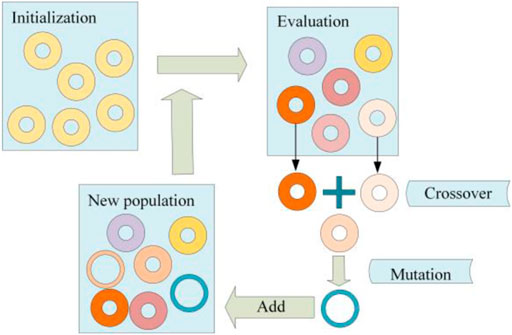
As illustrated in Figure 2, the differential evolution (DE) algorithm is a global optimization algorithm based on populations (Bilal et al., 2020). DE algorithm is divided into two phases: initialization and evolution. The populations are generated randomly in the first phase. The second phase, evolution, involves the repeated mutation, crossover, and selection processes of the generated populations until the termination criteria are met. Finally, the optimal value is discovered through evolution.

FIGURE 2

FIGURE 2. Schematic diagram of differential evolution algorithm.

Multi-Task Learning With Homoscedastic Uncertainty

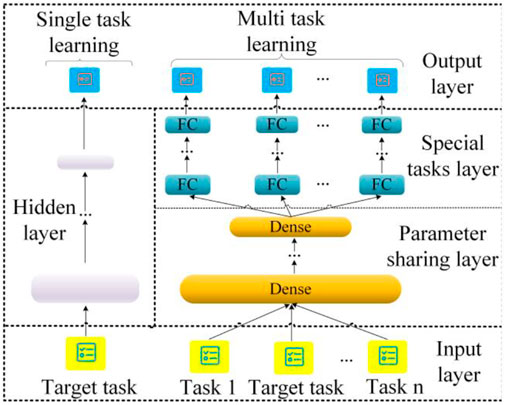
Multi-task learning is a type of machine learning in which multiple related tasks are learned concurrently via parameter sharing layers. As illustrated in Figure 3, multi-task learning uses multiple loss functions during the model training process to improve the models’ generalization ability, whereas single-task learning uses a single loss function. There are numerous advantages to multi-task learning over single-task learning, two of which are particularly significant. Multi-task learning mitigates the overfitting problem and increases the stability of models during training. On the other hand, multi-task learning enhances the predictive accuracy of models through the process of knowledge transfer, as illustrated in Figure 4.

FIGURE 3

FIGURE 3. Comparison between single-task and multi-task learning.

FIGURE 4

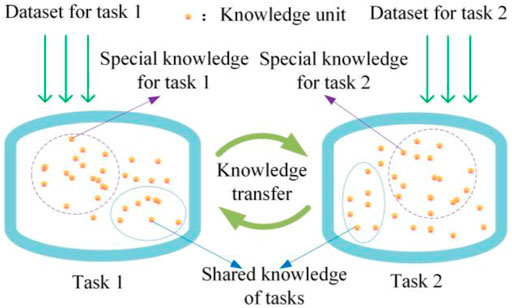
FIGURE 4. The graph of knowledge transfer in multi-task learning. The chart only shows the process of knowledge transfer between two tasks.

The weights of each loss function have a significant effect on the accuracy of multi-task learning models during the training process. The simplistic approach to combining multi-objective losses would be to perform a weighted linear sum for each task illustrated in Eq. 7.

$L_{total}={\displaystyle \sum _i{w}_i\cdot L_i}(7)$

where $L_{total}$ is the total loss function in model training, $L_i$ is the loss function of each subtask, $w_i$ is the weight of each subtask’s loss function. The $w_i$ is a fixed value set artificially.

However, model performance is highly dependent on weight selection, resulting in a high cost of manual parameter adjustment. Alex Kendall and his colleagues proposed a method for determining the weight of each task loss function shown in Eq. 8 by utilizing homoscedastic uncertainty (Cipolla et al., 2018).

$L_{total}={\displaystyle \sum _i\left[\frac{1}{2{\sigma }_i^2}{l}_i\left(w\right)+\log \left({\sigma }_i\right)\right]}(8)$

where $L_{total}$ is the total loss function in model training, $l_i\left(w\right)$ is the loss function of each subtask, ${\sigma }_i$ is the weight of each subtask’s loss function. Different from $w_i$ in Eq. 7, the ${\sigma }_i$ is a parameter in the loss function layer and changes autonomously with model training.

In the model training process, ${\sigma }_i$ is a parameter within the model structure and changes with each iteration to train the optimal value of each subtask loss function of multi-task learning. It significantly saves the time of manual parameter adjustment. However, there is a disadvantage in Eq. 8. When ${\sigma }_i$ is a value from 0 to 1, $log\left({\sigma }_i\right)$ is negative, so L_total may become negative, which will make the model unable to converge and the prediction performance worse. Therefore, a modified formula is proposed, shown in Eq. 9 based on (8), to make sure $L_{total}$ is not negative in any case.

$L_{total}={\displaystyle \sum _i\left[\frac{1}{2{\sigma }_i^2}{l}_i\left(w\right)+\log \left(1+{\sigma }_i\right)\right]}(9)$

The Priori and Prediction Models: Their Motivation and Implementation

In data mining, the division of datasets frequently has a significant effect on the model’s predictive performance. Historically, researchers have typically divided the entire dataset into a training set, a verification set, and a test set based on their proportions (e.g., 80% of the data set is used as the training set, 10% as the verification set, and 10% as the test set). While the method of proportionally dividing datasets is widely used in various data mining competitions, it is impractical in the context of photovoltaic power prediction. In contrast to other competitions, the datasets required for photovoltaic power prediction models must be collected independently by researchers, which means that the raw datasets collected by researchers may differ from their experience. Additionally, datasets constructed from historical data from different days have a significant effect on model predictions (Graditi et al., 2016). As a result, an acute problem arises: how to scientifically select data for the purpose of constructing datasets with less empirical interference when performing specific photovoltaic power prediction tasks?

Additionally, many engineers incorporate historical data from the previous time period into the feature quantity to aid in model training, which may result in the predicted value curve lagging behind the actual value curve due to the series’ autocorrelation. The conventional method for removing autocorrelation is to use difference calculation: set the regression target to the difference between the current and previous times. However, the strategy is not effective or efficient.

To construct rational and intelligent datasets, we define the photovoltaic power prediction on a date as the prediction tasks and the photovoltaic power prediction of the day before the prediction tasks as priori tasks. Actively discover appropriate dataset construction rules for the priori task from back to front on the timeline using a priori model composed of LSTM and DE algorithms. Additionally, we believe that by incorporating multiple historical power data sets to improve the data’s quality, we can eliminate autocorrelation and obtain the optimal values via the priori model.

We obtain the dataset composition method based on the rules extracted from the priori model. The law is primarily composed of two parameters: the size of the training sets and verification sets, and the number of historical power data points used to bolster the dataset in the past. And apply the rules discovered in the priori tasks to the prediction tasks.

During priori model experiments, the rules derived from the priori model can be used to improve prediction accuracy across a variety of different prediction models with varying structures. However, the errors of single-task prediction models vary significantly across prediction tasks, which makes practical application of photovoltaic power prediction difficult. To enhance the stability and reliability of photovoltaic power prediction models, we propose a prediction model with lower prediction error fluctuation through the use of a multi-task learning mechanism.

To be more precise, the proposed prediction model takes the photovoltaic power predictions of multiple single-task prediction models on the same date as target tasks and related tasks and trains the model using the multi-task learning hard-sharing mechanism. Additionally, we use homoscedastic uncertainty to determine the weight of the loss function for each task and apply 9) to ensure that the prediction model converges quickly and accurately during training.

On the whole, a combined photovoltaic power prediction model is proposed, as illustrated in Figure 5. To begin, we filter out the characteristics of the public photovoltaic output dataset that have the most significant impact on photovoltaic power. Following that, the power-related data is compressed and normalized using the normalization layers. Then, we define the photovoltaic power prediction of the day before the prediction tasks as priori tasks. We can find the laws suitable for constructing the priori tasks dataset using the priori model composed of the DE algorithm and LSTM and apply them to the construction of the prediction tasks dataset. In the prediction model, we combine predictions of photovoltaic power on the same day from multiple single-task prediction models with varying structures for target and related tasks that can be adjusted flexibly. The parameter sharing layers combine all tasks (related and target tasks) in order to achieve parallel knowledge transfer and noise balance between tasks, thereby implementing the multi-task learning mechanism via the hard sharing mechanism. Finally, each associated task and target task independently output the photovoltaic power prediction results via their respective single-task prediction models.

FIGURE 5

FIGURE 5. The training process of the combined photovoltaic power prediction model.

Experiment and Result Analysis

It is necessary to introduce the working platform and experimental equipment prior to beginning the experiments. Our models were trained on laptops equipped with an AMD R5-5600H processor, a Radeon RTX3050 graphics card, the TensorFlow 2.4 deep learning framework, Keras 2.4, and a 64-bit version of Windows 10.

Data Collection and Processing

Dataset Introduction

We begin with the public photovoltaic output dataset (PVOD) from the scientific data bank. PVOD is a high-quality dataset collected and maintained on a regular basis by Tiechui Yao et al. (Yao et al., 2021). It is constructed from two data sources separated by a 15-min interval: numerical weather prediction (NWP) from meteorological services and local measurement data (LMD) from photovoltaic power stations. The NWP is composed of seven components: global irradiance, direct irradiance, temperature, humidity, wind speed, wind direction, and pressure. Local Measurements Data consists of seven parts: global irradiance, diffuse irradiance, temperature, pressure, wind direction, and wind speed, as well as photovoltaic output records. PVOD, in general, contains historical data on solar photovoltaic energy generation and the major environmental factors affecting energy generation, making it ideal for photovoltaic power prediction experiments.

Feature Selection

Photovoltaic energy is extremely dependent on environmental factors. Each environmental factor, however, has a unique effect on photovoltaic power. To conserve resources and increase the efficiency of models, we must first identify the significant ecological characteristics affecting photovoltaic energy generation using Spearman’s rank correlation coefficient shown in Eq. 10. We choose environmental factors with absolute correlation coefficients greater than 0.3 in the original dataset as the characteristic quantity for our model training, as shown in Table 1. Besides, because photovoltaic power is time-dependent, we encode weekly and hourly photovoltaic power data, respectively (For details, please refer to Supplementary Appendix A).

$r=\frac{{\displaystyle \sum _{i=1}^n\left(y_i-\overline{y}\right)\left(M_i-\overline{M}\right)}}{\sqrt{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}\sqrt{{{\displaystyle \sum _{i=1}^n\left(M_i-\overline{M}\right)}}^2}}(10)$

Where r represents the calculation results of the correlation coefficient, and y_i represents the actual photovoltaic power values in the prediction tasks. M_i represents the actual values of each environmental factor. $\overline{y}$ and $\overline{\text{M}}$ are the average values of y_i and M_i, respectively. Specifically, the closer the absolute value of r is to 1, the stronger the correlation is.

TABLE 1

TABLE 1. Correlation coefficients of the environmental factors.

The Padding of Missed Data

PVOD is a collection of open datasets devoted to the photovoltaic industry. It is routinely maintained and managed by professionals and has an excellent dataset quality, eliminating the need to fill in missing values.

Model Evaluation

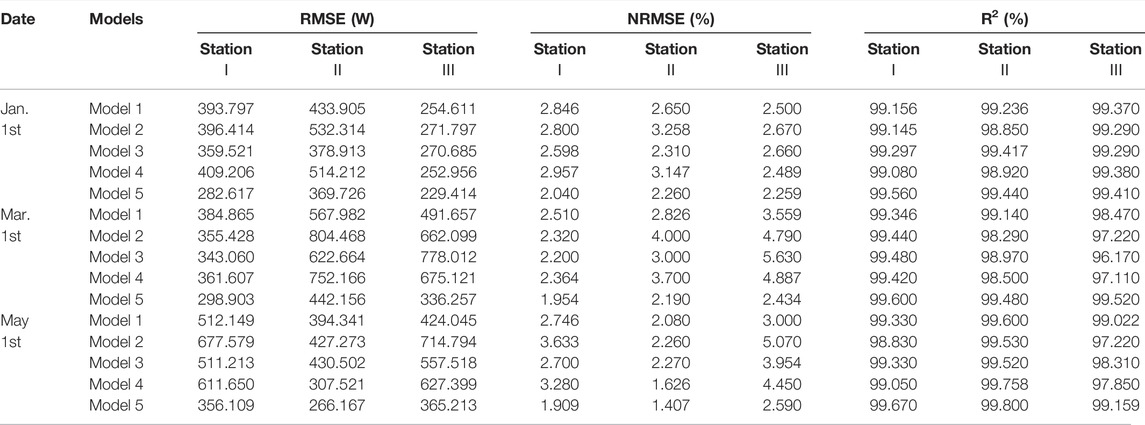
To comprehensively test the rationality and correctness of the priori model’s laws, we use the photovoltaic power predictions of three photovoltaic power stations on 1 January 2019, 1 March 2019, and 1 May 2019 as prediction tasks 1 to 9 and conduct experiments on several prediction models with various structures. The main form of the models is shown in Table 2 (For details, please refer to Supplementary Appendix B). Additionally, we maintain the same number of network layers and neurons across all prediction models to mitigate the effect of the basic structure of prediction models. The optimizer opts for RAdam, while the activate function opts for the swish.

TABLE 2

TABLE 2. The main structure of models.

We use six evaluation indexes to reflect the prediction accuracy and stability of each model thoroughly: Root Mean Squared Error (RMSE), Normalized Root Mean Squared Error (NRMSE), R-Square (R²), and the standard deviations of RMSE, NRMSE, and R², as shown in Eqs. 11–16.

$RMSE=\sqrt{\frac{1}{m}{\displaystyle \sum _{q=1}^m{\left(y_i-{\widehat{y}}_i\right)}^2}}(11)$

$NRMSE=\frac{RMSE\left(\widehat{y},y\right)}{\max \left(y\right)}(12)$

$R^2=1-\frac{MSE\left(\widehat{y},y\right)}{\mathrm{var}\left(y\right)}(13)$

${\sigma }_{RMSE}=\sqrt{\frac{{\displaystyle \sum _{i=1}^N{\left[RMS{E}_i\left(\stackrel{⌢}{y},y\right)-{\mu }_{RMSE}\right]}^2}}{N}}(14)$

${\sigma }_{NRMSE}=\sqrt{\frac{{\displaystyle \sum _{i=1}^N{\left[NRMS{E}_i\left(\stackrel{⌢}{y},y\right)-{\mu }_{NRMSE}\right]}^2}}{N}}(15)$

${\sigma }_{R^2}=\sqrt{\frac{{\displaystyle \sum _{i=1}^N{\left[R_i^2\left(\stackrel{⌢}{y},y\right)-{\mu }_{R^2}\right]}^2}}{N}}(16)$

where $y_i$, $y$ and ${\widehat{y}}_i$, $\widehat{y}$ are the actual and predicted values of the prediction tasks; ${\mu }_{RMSE}$, ${\mu }_{NRMSE}$ and ${\mu }_{R^2}$ are the mathematical expectations of RMSE, NRMSE, and R², respectively.

Experiments and Results Analysis

The Necessity Verification of the Priori Model

Aiming to reveal the influence of the features extracted by the priori model on the accuracy of the models, we conducted a series of comparative experiments with different characteristics on prediction Model 5 on 1 January 2019, and the experimental results are shown in Tables 3 and 4. The W (Watt) is the power unit in the international system of units.

TABLE 3

TABLE 3. Comparison of prediction errors of training sets with different days.

TABLE 4

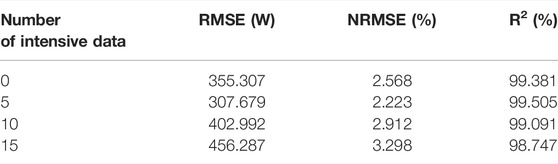
TABLE 4. Comparison of Prediction Errors of Training Sets by Adding different Historical Photovoltaic Power Data.

Tables 3 and 4 demonstrate that datasets of varying lengths and historical photovoltaic power data added to the characteristic quantity have a significant effect on the accuracy of prediction models. When the number of days and the amount of intensive data increases, the prediction errors initially decrease and then increase. When the number of days is 20, the prediction errors are the smallest in Table 3. By incorporating intensive data, the prediction error is further reduced by 13.4% in RMSE when the number of intensive data is five, as shown in Table 4. There are two potential explanations. From the process of model training, one possible reason for this is that insufficient or excessive data may result in underfitting or overfitting, respectively, during the model training process.

On the other hand, when predicting the photovoltaic power of the next day, the models may pay more attention to the regularity between the historical data of the previous week or month, while the regularity of the historical information of half a year or even a year ago may have little impact on the prediction of the model that day, or even the opposite. In general, it is necessary to construct different data sets for specific prediction tasks.

Experiments on Model Performance

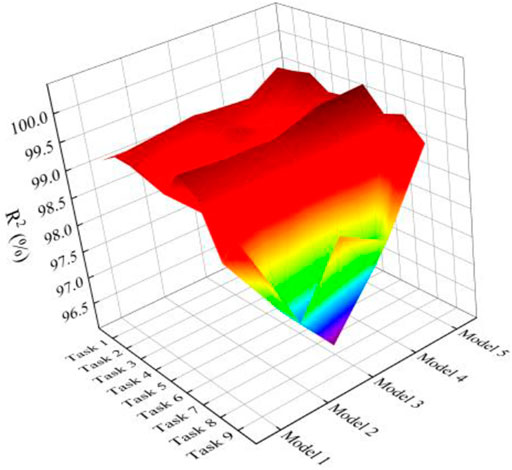
As a result, we set the number of days of historical data used for model training and the number of historical photovoltaic power data used to improve the dataset’s quality as two variables affecting the prediction models’ accuracy. In the priori model, the prediction error R² of Model 1 on priori tasks is set as the objective function. The DE algorithm then determines the optimal value suitable for constructing the priori tasks dataset. We are surprised to discover that the optimal values obtained from priori tasks fluctuate within a small range (the optimal values in the adjacent week are nearly unchanged), indicating that the rule obtained by the priori model is robust to changing prediction tasks in a short time. As a result, we directly apply the rules learned from the priori tasks to the prediction tasks. The results of the prediction models are shown in Table 5 and Figure 6. In Table 5, the darker the color (red), the smaller the prediction error; the lighter the color (white), the larger the prediction error.

TABLE 5

TABLE 5. RMSE, NRMSE, and R² of models on different prediction tasks.

FIGURE 6

FIGURE 6. The corresponding prediction results of each model on different tasks. Specifically, (A–I) show the prediction results of prediction tasks 1 to 9, respectively. Models 1 to 5 can achieve good prediction results in different prediction tasks.

The R² value for each model on different prediction tasks is greater than 96% in Table 5, indicating that prediction models perform well across multiple prediction tasks. As a result, the rules extracted from the priori model exhibit a high degree of robustness when applied to prediction models with varying structures. This is demonstrated in Figure 6 (a) to (i), where each prediction model fits well between the prediction curve and the actual curve for various prediction tasks, thereby validating the correctness and rationality of the underlying theory of the priori model that selecting the appropriate dataset for model training and adding a moderate amount of historical power data to enhance the dataset can significantly improve the prediction performance of the prediction model.

Experiments on Prediction Stability and Accuracy

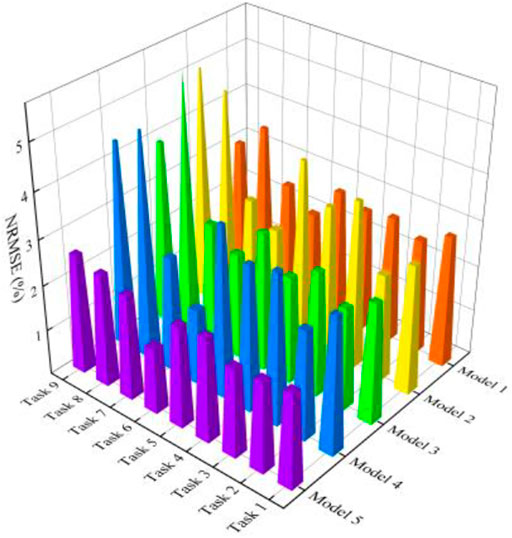
However, while the prediction errors of each model are already small, the prediction errors of Models 1 to 4 on different prediction tasks exhibit significant fluctuations, increasing the prediction models’ instability and unreliability. Thus, in the experiments with prediction models, multi-task learning facilitates knowledge transfer between related tasks by sharing parameter layers, improving the prediction model’s accuracy and stability. As illustrated in Figure 7 and Figure 8, the R² and NRMSE values for Model 5 are lower than those for Models 1 to 4, indicating that multi-task learning models are more accurate than single-task prediction models. This is also demonstrated in Table 5 by the prediction error indicators. Model 5’s RMSE is less than 450W, its NRMSE is less than 2.5%, and its R² is greater than 99%. Additionally, when comparing the evaluation indexes in Table 5, Model 5 reduces RMSE and NRMSE by an average of 28% and 56%, respectively, when comparing Models 1 to 4.

FIGURE 7

FIGURE 7. R² of models in different prediction tasks.

FIGURE 8

FIGURE 8. NRMSE of models in different prediction tasks.

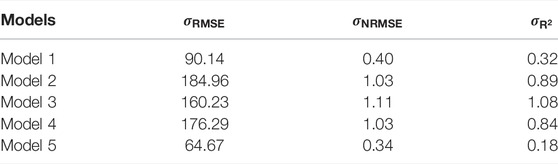
The standard deviations of the prediction model are shown in Table 6 as ${\sigma }_{RMSE}$, ${\sigma }_{NRMSE}$, ${\sigma }_{R^2}$. Clearly, the standard deviations of each evaluation index for Model 5 are lower than those for Models 1 to 4, indicating that the multi-task learning model is more robust and stable in predicting photovoltaic power than single-task prediction models.

TABLE 6

TABLE 6. Standard deviations of evaluation indices of prediction models between prediction tasks.

Additionally, as illustrated in Figure 7 and Figure 8, Model 5 exhibits more minor variations in prediction errors across different prediction tasks. In concrete terms, when compared to Models 1 to 4, Model 5’s standard deviations in RMSE, NRMSE, and R² are reduced by 54%, 54%, and 71%, respectively.

In general, when validated on multiple prediction tasks using various datasets, the combined model’s R² value is greater than 99 percent, with a standard deviation R² of 0.18, indicating that the combined model composed of the priori model and the prediction model based on multi-task learning accurately and consistently predict various photovoltaic power prediction tasks.

Policy and Environmental Impact

As the prediction accuracy and stability of the photovoltaic power prediction model are greatly improved, it would significantly enhance the power management efficiency of photovoltaic power stations and create more economic value for grid-connected power grids. Photovoltaic power stations with larger installed capacity can be further developed, conducive to relieving employment problems and the environment.

To be more precise, improving the prediction accuracy and stability of the photovoltaic power prediction model promotes the development of photovoltaic installed capacity tremendously. This will provide new jobs during the energy transformation period in the context of the gradual introduction of environmental policies and the improvement of energy security issues. On the other hand, with the increase of photovoltaic installed capacity, the proportion of solar power generation in the total power generation has been further increased, significantly reducing the combustion of fossil energy and carbon emissions.

Conclusion

The paper proposes a combined model composed of a priori and multi-task learning prediction models to solve how to construct the dataset scientifically and effectively improve the stability and prediction accuracy of the prediction model, which has reduced the uncertain impact of the photovoltaic power station grid connection on the power grid. If properly utilized, the accurate photovoltaic power prediction model would significantly promote the development of the photovoltaic industry and reduce carbon emissions. The following is the conclusion to this paper:

• Numerous evaluation indices for various prediction tasks have been proposed to assess the prediction performance and stability of prediction models comprehensively. In detail, the RMSE, NRMSE, and R² values reflect the accuracy of prediction models, while the standard deviations of the RMSE, NRMSE, and R² values reflect the stability of prediction models.

• A priori model based on the DE algorithm and LSTM was developed to construct datasets for various prediction tasks efficiently. The priori model’s rule can significantly improve the accuracy of prediction models with varying structures (R² of prediction models on different prediction tasks is greater than 96%).

• A model for accurate and stable prediction has been proposed that makes use of the multi-task learning mechanism. The multi-task learning mechanism enables the transfer of knowledge between related tasks, thereby increasing the accuracy and generalizability of photovoltaic power prediction models. In comparison to other single-task prediction models, the multi-task learning prediction model improves prediction accuracy and stability by an average of 28% and 54%, respectively.

Future Work

Although the model we proposed has outstanding prediction performance, there are still many areas to be improved for the efficiency and applicability of the prediction model. Specific discussions about future work are as follows:

1. The differential evolution algorithm is a single objective optimization algorithm. Although it can obtain an excellent solution-set in most cases, it is easy to fall into the local optimal solution in the process of optimization. This is not conducive to the accurate prediction of the photovoltaic power prediction model. In the following research work, we will consider using a multi-objective optimization algorithm to reduce or avoid the probability of falling into the local optimal solution in the optimization process.

2. Multi-task learning can relieve the problem of overfitting in the process of model training by using knowledge transfer in the process of model training. However, selecting target tasks and related tasks is still a problem worthy of further study. How to determine the target task will also be the focus of our subsequent research. In addition, the selection of the number of related tasks affects the running time of the whole model. The more the number of related tasks, the longer the running time of the model. Therefore, in the following research work, we will also carry out corresponding research to find the least number of related tasks without affecting the model’s prediction performance to reduce the running time of the model.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

SP and JL: Writing-original draft preparation, software, writing-review editing. ZZ: Software, writing-review editing. YZ and DZ: Writing-review editing, supervision. GH and XF: Investigation, supervision.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors gratefully acknowledge the public photovoltaic output dataset (PVOD) from the scientific data bank.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.938167/full#supplementary-material

References

Abdel-Nasser, M., and Mahmoud, K. (2019). Accurate Photovoltaic Power Forecasting Models Using Deep LSTM-RNN. Neural Comput. Applic 31, 2727–2740. doi:10.1007/s00521-017-3225-z

CrossRef Full Text | Google Scholar

Al-Shetwi, A. Q., and Sujod, M. Z. (2018). Grid-connected Photovoltaic Power Plants: A Review of the Recent Integration Requirements in Modern Grid Codes. Int. J. Energy Res. 42, 1849–1865. doi:10.1002/er.3983

CrossRef Full Text | Google Scholar

Bilal, B., Pant, M., Zaheer, H., Garcia-Hernandez, L., and Abraham, A. (2020). Differential Evolution: A Review of More Than Two Decades of Research. Eng. Appl. Artif. Intell. 90, 103479. doi:10.1016/J.ENGAPPAI.2020.103479

CrossRef Full Text | Google Scholar

Boland, J., David, M., and Lauret, P. (2016). Short Term Solar Radiation Forecasting: Island versus Continental Sites. Energy 113, 186–192. doi:10.1016/j.energy.2016.06.139

CrossRef Full Text | Google Scholar

Cipolla, R., Gal, Y., and Kendall, A. (2018). Multi-task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics. Proceeding IEEE Computer Soc Conference Computer Vision Pattern Recognition, Salt Lake City, UT, USA. 18-23 June 2018. 7482–7491. doi:10.1109/CVPR.2018.00781

CrossRef Full Text | Google Scholar

Dong, Z., Yang, D., Reindl, T., and Walsh, W. M. (2013). Short-term Solar Irradiance Forecasting Using Exponential Smoothing State Space Model. Energy 55, 1104–1113. doi:10.1016/j.energy.2013.04.027

CrossRef Full Text | Google Scholar

Graditi, G., Ferlito, S., and Adinolfi, G. (2016). Comparison of Photovoltaic Plant Power Production Prediction Methods Using a Large Measured Dataset. Renew. Energy 90, 513–519. doi:10.1016/j.renene.2016.01.027

CrossRef Full Text | Google Scholar

Humada, A. M., Darweesh, S. Y., Mohammed, K. G., Kamil, M., Mohammed, S. F., Kasim, N. K., et al. (2020). Modeling of PV System and Parameter Extraction Based on Experimental Data: Review and Investigation. Sol. Energy 199, 742–760. doi:10.1016/j.solener.2020.02.068

CrossRef Full Text | Google Scholar

Humada, A. M., Hojabri, M., Mekhilef, S., and Hamada, H. M. (2016). Solar Cell Parameters Extraction Based on Single and Double-Diode Models: A Review. Renew. Sustain. Energy Rev. 56, 494–509. doi:10.1016/j.rser.2015.11.051

CrossRef Full Text | Google Scholar

Jufri, F. H., Oh, S., and Jung, J. (2019). Development of Photovoltaic Abnormal Condition Detection System Using Combined Regression and Support Vector Machine. Energy 176, 457–467. doi:10.1016/j.energy.2019.04.016

CrossRef Full Text | Google Scholar

Liang, X. (2017). Emerging Power Quality Challenges Due to Integration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 53, 855–866. doi:10.1109/TIA.2016.2626253

CrossRef Full Text | Google Scholar

Lin, P., Peng, Z., Lai, Y., Cheng, S., Chen, Z., and Wu, L. (2018). Short-term Power Prediction for Photovoltaic Power Plants Using a Hybrid Improved Kmeans-GRA-Elman Model Based on Multivariate Meteorological Factors and Historical Power Datasets. Energy Convers. Manag. 177, 704–717. doi:10.1016/j.enconman.2018.10.015

CrossRef Full Text | Google Scholar

Mitrašinović, A. M. (2021). Photovoltaics Advancements for Transition from Renewable to Clean Energy. Energy 237, 121510. doi:10.1016/j.energy.2021.121510

CrossRef Full Text | Google Scholar

Niu, Z., Yu, Z., Tang, W., Wu, Q., and Reformat, M. (2020). Wind Power Forecasting Using Attention-Based Gated Recurrent Unit Network. Energy 196, 117081. doi:10.1016/j.energy.2020.117081

CrossRef Full Text | Google Scholar

Ogliari, E., Dolara, A., Manzolini, G., and Leva, S. (2017). Physical and Hybrid Methods Comparison for the Day Ahead PV Output Power Forecast. Renew. Energy 113, 11–21. doi:10.1016/j.renene.2017.05.063

CrossRef Full Text | Google Scholar

Qu, J., Qian, Z., and Pei, Y. (2021). Day-ahead Hourly Photovoltaic Power Forecasting Using Attention-Based CNN-LSTM Neural Network Embedded with Multiple Relevant and Target Variables Prediction Pattern. Energy 232, 120996. doi:10.1016/j.energy.2021.120996

CrossRef Full Text | Google Scholar

Ramli, M. A. M., Prasetyono, E., Wicaksana, R. W., Windarko, N. A., Sedraoui, K., and Al-Turki, Y. A. (2016). On the Investigation of Photovoltaic Output Power Reduction Due to Dust Accumulation and Weather Conditions. Renew. Energy 99, 836–844. doi:10.1016/j.renene.2016.07.063

CrossRef Full Text | Google Scholar

Rana, M., Koprinska, I., and Agelidis, V. G. (2016). Univariate and Multivariate Methods for Very Short-Term Solar Photovoltaic Power Forecasting. Energy Convers. Manag. 121, 380–390. doi:10.1016/j.enconman.2016.05.025

CrossRef Full Text | Google Scholar

Shahsavar, M. M., Akrami, M., Gheibi, M., Kavianpour, B., Fathollahi-Fard, A. M., and Behzadian, K. (2021). Constructing a Smart Framework for Supplying the Biogas Energy in Green Buildings Using an Integration of Response Surface Methodology, Artificial Intelligence and Petri Net Modelling. Energy Convers. Manag. 248, 114794. doi:10.1016/j.enconman.2021.114794

CrossRef Full Text | Google Scholar

Sobri, S., Koohi-Kamali, S., and Rahim, N. A. (2018). Solar Photovoltaic Generation Forecasting Methods: A Review. Energy Convers. Manag. 156, 459–497. doi:10.1016/j.enconman.2017.11.019

CrossRef Full Text | Google Scholar

Trapero, J. R., Kourentzes, N., and Martin, A. (2015). Short-term Solar Irradiation Forecasting Based on Dynamic Harmonic Regression. Energy 84, 289–295. doi:10.1016/j.energy.2015.02.100

CrossRef Full Text | Google Scholar

Wang, F., Xuan, Z., Zhen, Z., Li, K., Wang, T., and Shi, M. (2020). A Day-Ahead PV Power Forecasting Method Based on LSTM-RNN Model and Time Correlation Modification under Partial Daily Pattern Prediction Framework. Energy Convers. Manag. 212, 112766. doi:10.1016/j.enconman.2020.112766

CrossRef Full Text | Google Scholar

Wang, Y., Liao, W., and Chang, Y. (2018). Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting. Energies 11, 2163–2214. doi:10.3390/en11082163

CrossRef Full Text | Google Scholar

Yang, T., Li, B., and Xun, Q. (2019). LSTM-Attention-Embedding Model-Based Day-Ahead Prediction of Photovoltaic Power Output Using Bayesian Optimization. IEEE Access 7, 171471–171484. doi:10.1109/ACCESS.2019.2954290

CrossRef Full Text | Google Scholar

Yao, T. C., Wang, J., Wu, H. Y., Zhang, P., Li, S. G., Wang, Y. G., et al. (2021). PVOD v1.0: A Photovoltaic Power Output Dataset. V4. Science Data Bank. Available at: https://datapid.cn/31253.11.sciencedb.01094.

Google Scholar

Zhang, J., Chi, Y., and Xiao, L. (2018). Solar Power Generation Forecast Based on LSTM. Proceeding IEEE International Conference Software Engineering Service Science ICSESS 2018-November, Beijing, China. 23-25 November 2018. 869–872. doi:10.1109/ICSESS.2018.8663788

CrossRef Full Text | Google Scholar