Xuli Zhu
Shanshan Ma
Haidong Huang1
Guirong Teng- 1School of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qingdao, China
- 2Qingdao Metro Group Co., Ltd, Qingdao, China
- 3School of Energy and Mining Engineering, Shandong University of Science and Technology, Qingdao, China
The capacitance characteristics of magnetorheological fluids (MRFs) were studied experimentally based on simulation analysis. The nonlinear relationship between the capacitance of MRFs and electric field frequency was measured by the self-made circuit device. The effects of magnetic induction intensity and particle volume fraction on the capacitance characteristics of MRFs were investigated. The results show that the nonlinear dependence of the capacitance of an MRF on frequency induced by the effect of tunnel current decreases with the increase in frequency. The capacitance of an MRF is directly related to the particle structures. The capacitance of the MRF with a chain particle structure is greater than that of the MRF with a random particle distribution. The smaller the clearance between the adjacent particles, the greater the capacitance of the MRF. The network particle structure and particle contact will reduce the capacitance of an MRF. The capacitance of an MRF increases with the increment of external magnetic field. The capacitance of an MRF with higher particle volume fraction is smaller than that of an MRF with lower particle volume fraction.
Introduction
Magnetorheological fluids (MRFs) are a class of controllable smart materials characterized by fast, tunable, and reversible changes in their rheological properties, which are suspensions of micron-size magnetizable particles in a viscous carrier fluid enriched with additives (Rabinow, 1948; Ashour, 1996). Magnetorheological effects occur in magnetorheological fluids under the action of an applied magnetic field, which makes the soft magnetic particles magnetize to form a chain-like structure, called a particle chain (Chen, et al., 2013; He, et al., 2013; Mahesh, et al., 2021). The particles are ferromagnetic with good conductivity, and the particle chains can form conductive channels to make the MRFs conductive. The conductive mechanism of magnetorheological materials is relatively complicated. The proposed models are mostly based on the conductive channel theory and tunneling effect theory (Zhu, et al., 2010b; Wang, 2017). Conductive channel theory is usually used to describe the mechanism of composite polymers with fillers inside. The tunnel effect theory is used to explain the movement of the electrons inside the composite material based on quantum mechanics, that is, to analyze the conductivity of the material from the microscopic perspective.
MRFs, similar to conductive polymer composites, can be used widely with high practical value in various sensors, capacitors, and other fields (Wang, 2012; Kaluvan and Choi, 2014). The magneto-conductive properties of MRFs and their solid-state analogs and magnetorheological elastomers are currently receiving increasing attention. Yang et al. (2017) demonstrated that the appropriate amount of ferromagnetic particles is beneficial in improving the electrical conductivity of MRFs. Ruan et al. (2017) analyzed the effect of magnetic field, volume fraction of carbonyl iron powder particles, and applied oscillatory shear force on the conductivity of MRFs and modeled the resistance between particles to explain the resistance changes of MRFs. Wang et al. (2011) deduced the formula between magnetorheological capacitance and dielectric constant and experimentally verified the conclusion that the increase in MRF capacitances induced by the dielectric constant increases when the magnetic field increases. Bica (2009) studied the capacitance of a flat plate capacitor with magnetorheological elastomer as the dielectric as a function of magnetic field strength, and the results showed that the capacitance gradually increases and eventually remains constant when the magnetic field was applied. Huang et al. (2016) prepared MRFs with silver-coated carbonyl iron particles dispersed in silicone oil. The experimental results showed a significant improvement in the electrical properties of MRFs. It can be seen that the current research mainly focuses on the static conductivity properties of MRFs. The dynamic conductivity properties and the interfering factors should be studied further.
The capacitance characteristics of MRFs under an external magnetic field were investigated experimentally in this paper. Firstly, the capacitance of inter-particles was simulated and analyzed according to the dispersing state of particles inside of MRFs. A tunable AC experimental device was designed and assembled, which was used to measure the effects of the applied magnetic field and the particle volume fraction on the capacitive characteristics of MRFs. The conclusions are helpful to understand the state of particle structures in MRFs, to deepen the understanding of the relationship between particle structures and capacitance characteristics of MRFs, and to contribute to the development of MRF application devices in complex working modes.
Simulation Analysis
Magnetizable particles are distributed randomly inside the matrix liquid without the appearance of an external magnetic field. Adjacent particles are close to each other and gradually form chain-like structures when an external magnetic field is applied (Donado, et al., 2017; Wang, et al., 2020). There would be a capacitance between two adjacent particles when every particle seems to be an equipotential body. The equivalent capacitance of an MRF comes from the actions of all micro-capacitance between particles. The capacitance of a particle chain is the sum of the capacitance between particles because the micro-capacitance is connected in parallel, and a larger capacitance can be obtained. The reciprocal of total capacitance of an MRF is equal to the sum of the reciprocal of the capacitance of each particle chain, and the total capacitance will be smaller than the capacitance of a particle chain.
The capacitance characteristics of an MRF containing several particles were investigated using COMSOL Multiphysics according to the mechanism mentioned above. The 2D geometric model was created by the Model Wizard module of the package. Three models of random distribution, loose chain, and tight chain were created to correspond to the state of zero magnetic field, low magnetic field, and high magnetic field, respectively. The capacitance of the three models was simulated and calculated using the physical field of electrostatics of the AC/DC module. The area ratio of the circle in the three models was consistent, which represented the consistent particle volume fraction inside the MRF.
A simple ideal model was established to simulate the effect of particle structures on the capacitance of MRFs qualitatively. The spherical particle size was set to 3.14 μm according to a commercial carbonyl iron powder (MRF-R35, Jiangsu Tianyi Ultrafine Metal Powder Co., Ltd.). The magnetic conductivity of the particles and the matrix liquid were defined, respectively. The particle clearances in the loose chain and the tight chain are 1.54 and 0.5 μm respectively. A 20 V potential was applied to the upper boundary of the model, the lower boundary was defined as grounding, and a suspension potential boundary condition was defined for each particle. The simulation results of the distribution of electric fields are shown in Figure 1.
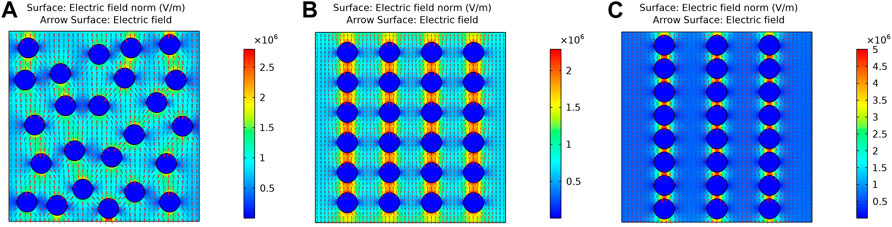
FIGURE 1. Capacitance simulation results. (A) Random distribution; (B) Loose chain; (C) Tight chain.
The capacitance values were obtained through the global calculation of capacitance in COMSOL Multiphysics, and the values were recorded. The capacitances of the three models were calculated by the package. They are 13.734 pF of the random distribution, 14.531 pF of the loose chain, and 18.567 pF of the tight chain, respectively. The simulation results show that the capacitance of an MRF under the action of a magnetic field is larger than that of a zero field condition, and the capacitance value increases with the increase of the magnetic field strength.
Experiment
The schematic of the self-made circuit device is shown in Figure 2. 220 V 50 Hz AC was transformed by a transformer (Zhengzhou Xinxing Electronics Co., Ltd.) to 24 V AC to provide power to the amplifier (FPA1016, FeelTech Co., Ltd.). The amplifier and a bench-type digit multimeter (Agilent Co., Ltd.) were connected in series in the circuit, along with the MRFs. The maximum frequency of the signal generator (FY2302, Zhengzhou Feiyi Technology Co.) is 100 kHz, the full power sinusoid bandwidth of the amplifier is also 100 kHz, and the accuracy of the multimeter is 1 μA. The photo of the circuit device is shown in Figure 3.
FIGURE 2. Schematic of the circuit device.
FIGURE 3. Photo of the circuit device.
MRF samples with different particle volume fractions were prepared, as shown in Table 1. The carbonyl iron powder (MRF-R35, Jiangsu Tianyi Ultrafine Metal Powder Co., Ltd.) was used as magnetizable particles and the dimethyl silicone oil with a viscosity of 20 centistoke was used as the matrix liquid. The prepared MRFs sample is placed between two copper plates. The diameter of the polar plates and the distance between them are 20 and 4 mm, respectively. Permanent magnets were used as the external magnetic field. Different magnetic field strengths were obtained by adjusting the gap between the permanent magnets. The magnetic induction intensity between permanent magnets is measured by using a Tesla meter (HT20, Shanghai Hengtong Magnetoelectric Technology Co., Ltd.), and the magnetic field direction is perpendicular to the plate surfaces.
TABLE 1. MRF sample numbers.
During the experiments, the AC voltage in the circuit was set to 20 V, the frequency of the output sinusoidal wave was adjusted to change from 0 to 100 kHz, and the corresponding current values displayed by the digit multimeter in the circuit were observed and recorded. The above experiments were repeated by changing the magnitude of the applied magnetic induction strength and the particle volume fraction, respectively. The recorded data were used to analyze the dependence of MRF capacitance characteristics on frequency with the controlled parameters.
Results and Discussion
The current values of MRFs at 0–100 kHz are measures by a desktop multimeter (34410A, Agilent Technology Co., Ltd.). The capacitive values of the MRFs were calculated by the following formula:
where I and U are RMS current and voltage respectively, and f is the frequency of the supply power. Based on the theoretical analysis of the conductivity mechanism of MRFs, the current consists of resistance current, tunnel current, and capacitive current. The resistance current can be omitted because of the very low conductivity of the matrix fluid. It is difficult to measure the tunnel current and the capacitive current, respectively. Thus, the measured current in the experiment is the sum of the capacitive current and the tunnel current. The variation curve of capacitance with frequency is plotted and analyzed.
Effect of External Magnetic Field
Three comparable experiments of the MRF samples with the same particle volume fraction were carried out under the condition of different magnetic induction intensity. The samples were A, D, and G. The calculated dependence of MRF capacitance on frequency is shown in Figure 4. It can be seen that the capacitances of the MRFs have a similar trend with frequency under different external magnetic fields. The trends are roughly downward and have a large slope when the frequency is less than 25 kHz. Samples D and G have a rising range from about 25 to 35 kHz, and the decreasing trend of sample A becomes slow. The capacitances of all the three samples are relatively stable in the range from 35 to 75 kHz, and then decreases slowly as the frequency increases . It can also be seen that capacitances of MRFs increase with the increase in magnetic induction intensity at the same frequency, which is consistent with the simulation results.
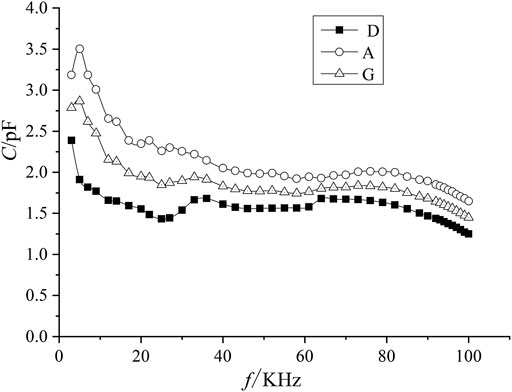
FIGURE 4. The dependence of capacitance of MRFs on frequency under the action of different applied magnetic fields.
The magnetizable particles align themselves to form chain structures inside MRFs under the action of magnetic field. The clearance between two adjacent particles decreases to increase the capacitance of an MRF. Under the action of a strong magnetic field, the particle gap becomes smaller and then makes the capacitance larger. The current in the circuit consists of capacitive current and tunnel current. The capacitances in Figure 4 are calculated from the total current. Tunnel current is the main reason for the variation of capacitance with frequency. Theoretically, the tunnel current is proportional to the square of the voltage and is independent of frequency. Thus, the effect of tunnel current on capacitance becomes weaker with the increase of frequency.
Effect of Particle Volume Fraction
Three groups of samples with different particle volume fractions, A, B, and C, were used to carry out the comparable experiments under a constant applied magnetic field. The results of the variation of capacitance versus frequency for three MRF samples are shown in Figure 5. It can be seen that the capacitance of MRFs with different particle volume ratios have different trends with frequency under the same magnetic induction intensity. The capacitance of the MRF with a particle volume fraction of 1% has an overall decreasing trend and is relatively smooth in the range from 35 to 75 kHz. The capacitance of the MRFs with the large particle volume fraction fluctuates greatly before about 40 kHz. The capacitance of the MRF with a particle volume fraction of 5% shows a stable and slow decline when the frequency is greater than 35 kHz, while that of the MRF with a particle volume fraction of 10% undergoes an increase, flattening and decreasing the processes when the frequency is larger than 40 kHz. It can also be seen that the capacitance of the MRF with a larger particle volume fraction is lower than that of the MRF with a smaller particle volume fraction at the same frequency.
FIGURE 5. Dependence of capacitance of MRFs with different particle volume fractions on frequency.
When the particle volume fraction is relatively small, the particle structures are mostly independent single chains inside the MRFs. As the particle volume fraction increases, the particle structures become more and more complex to be column structure and network structure (Zhu, et al., 2010a), which leads to the capacitances of the MRFs being similar to the random particle distribution model in the zero-field state, and some adjacent particles will contact each other and destroy the capacitive structure. These reasons lead to the negative correlation between MRF capacitance and particle volume fraction. The reason why the capacitance is not constant is that the effect of tunnel current decreases with the increase of frequency.
To study the effect of particle aggregation on the capacitance of MRFs, the capacitances of MRFs with single chain structure and column-like structure were further simulated and analyzed, as shown in Figure 6. The capacitance is 21.437 pF when the particle structure is an independent single chain and 17.254 pF when the particle structure is column-like. The capacitance decreases significantly from structures of single chain to column-like. Figure 6 shows that the more micro-capacitances formed between the particles in a column-like structure and these micro-capacitances connect in series. The more the micro-capacitances, the smaller the equivalent capacitance. Therefore, when the particle volume fraction is large, the particles form a column-like structure and induce the smaller capacitance of MRFs.
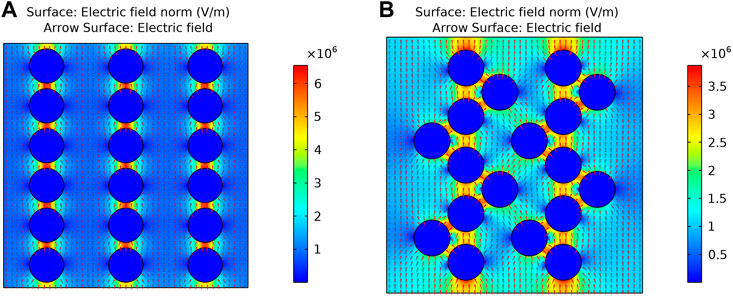
FIGURE 6. Effect of particle aggregation on capacitance. (A) Single chain structure; (B) Column-like structure.
Conclusion
The capacitance characteristics of MRFs were experimentally analyzed in this paper. Considering the effect of external magnetic field and the particle volume fraction, the dependences of capacitance of MRFs on frequency were summarized. The work provides an accurate reference for the measurement of capacitance characteristics, and lays a foundation for further study on the evolution process of the particle structures inside MRFs under complex working modes. The main conclusions are:
(1) The capacitance of an MRF is related to the particle structures. The capacitance of the MRF with chain particle structure is greater than that of the MRF with random particle distribution.
(2) The dependence of capacitance of an MRF on frequency is not constant. The reason is that the effect of tunnel current decreases with the increase in frequency.
(3) The clearance between two adjacent particles decreases to increase the capacitance of an MRF when an external magnetic field is applied. The particle gap becomes smaller and then the capacitance increases when the magnetic field becomes stronger.
(4) The capacitance of MRF is negatively correlated with particle volume fraction. The network particle structure and particle contact will reduce the capacitance of MRF.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
XZ and GT conceptualized the idea. XZ and SM performed the methodology. SM and HS ran the software. SM, HH, ZL, and HS performed the experiment. SM, HH, ZL, and HS wrote the original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China, grant number 51575323.
Conflict of Interest
HS was employed by Qingdao Metro Group Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank the National Natural Science Foundation of China for the research grant support.
References
Ashour, O., Rogers, C. A., and Kordonsky, W. (1996). Magnetorheological Fluids: Materials, Characterization, and Devices. J. Intelligent Material Syst. Struct. 7, 123–130. doi:10.1177/1045389X9600700201
Bica, I. (2009). Influence of Magnetic Field upon the Electric Capacity of a Flat Capacitor Having Magnetorheological Elastomer as a Dielectric. J. Industrial Eng. Chem. 15, 605–609. doi:10.1016/j.jiec.2009.02.005
Chand, M., Shankar, A., Pratap Singh, A., Chandra Mathpal, M., Prasad Pant, R., and Deperyot, J. (2021). Mechanism of Chain Formation under Shearing Forces in Magneto-Rheological Fluids. Mater. Today Proc. 47, 1575–1579. doi:10.1016/J.MATPR.2021.03.675
Chen, X., Zhu, X., Xu, Z., Lin, Y., and He, G. (2013). The Research of the Conductive Mechanism and Properties of Magnetorheological Fluids. Phys. B Condens. Matter 418, 32–35. doi:10.1016/j.physb.2013.02.042
Donado, F., Sausedo-Solorio, J. M., and Moctezuma, R. E. (2017). Dynamical and Structural Properties of a Granular Model for a Magnetorheological Fluid. Phys. Rev. E 95, 022601. doi:10.1103/PhysRevE.95.022601
He, J., Gao, L. X., Long, Z., Liu, Y. Z., and Liu, X. M. (2013). Theoretic and Experimental Study of Chain-Formation Mechanism for MRF. J. Funct. Mater. 44, 522–526. doi:10.1016/j.jmmm.2010.11.046
Huang, Y., Jiang, Y., Yang, X., Sun, H., Piao, H., and Xu, R. (2016). Enhanced Conductivity of Magnetorheological Fluids Based on Silver Coated Carbonyl Particles. J. Mater Sci. Mater Electron 27, 255–259. doi:10.1007/s10854-015-3748-y
Kaluvan, S., and Choi, S.-B. (2014). Design of Current Sensor Using a Magnetorheological Fluid in Shear Mode. Smart Mat. Struct. 23, 127003. doi:10.1088/0964-1726/23/12/127003
Rabinow, J. (1948). The Magnetic Fluid Clutch. Trans. Am. Inst. Electr. Eng. 67, 1308–1315. doi:10.1109/t-aiee.1948.5059821
Ruan, X., Wang, Y., Xuan, S., and Gong, X. (2017). Magnetic Field Dependent Electric Conductivity of the Magnetorheological Fluids: the Influence of Oscillatory Shear. Smart Mat. Struct. 26, 035067. doi:10.1088/1361-665X/aa5fe5
Wang, N., Liu, X., Sun, S., Królczyk, G., Li, Z., and Li, W. (2020). Microscopic Characteristics of Magnetorheological Fluids Subjected to Magnetic Fields. J. Magnetism Magnetic Mater. 501, 166443. doi:10.1016/j.jmmm.2020.166443
Wang, S., He, G. T., Wang, P., Song, L., Ran, Y. C., and Zhang, D. S. (2011). The Research of Capacitance Characteristics of MRF. J. Funct. Mater. 42, 1386–1389.
Wang, S. (2012).The Research of MR's Electromagnetic Characteristics and its Sensor Technology. Chongqing: Chongqing normal university. [dissertation/master’s thesis]. [Chongqing].
Wang, Y. (2017). Study on Mechanical-Electro-Magnetic Coupling Properties of Magnetorheological Elastomers [dissertation/master’s thesis]. [Hefei (Anhui)]. China: University of Science and Technology of China.
Yang, X., Huang, Y., Hou, Y., Wu, H., Xu, R., and Chu, P. K. (2017). An Experimental Study of Magnetorheological Fluids on Electrical Conductivity Property. J. Mater Sci. Mater Electron 28, 8130–8135. doi:10.1007/s10854-017-6519-0
Zhu, X. L., Meng, Y. G., and Tian, Y. (2010a). Effects of Particle Volume Fraction and Magnetic Field Intensity on Particle Structure of Magnetorheological Elastomers. J. Tsinghua Univ. Technol. 50, 167552. doi:10.16511/j.cnki.qhdxxb.2010.02.006
Keywords: magnetorheological fluids, capacitance, frequency, particle structures, magnetic field
Citation: Zhu X, Ma S, Huang H, Liu Z, Sun H and Teng G (2022) Experimental Analysis on the Dependence of the Capacitance of Magnetorheological Fluids on Frequency. Front. Mater. 9:932079. doi: 10.3389/fmats.2022.932079
Received: 29 April 2022; Accepted: 17 June 2022;
Published: 22 July 2022.
Edited by:
Miao Yu, Chongqing University, ChinaReviewed by:
Qing Ouyang, Jiaxing University, ChinaXufeng Dong, Dalian University of Technology, China
Copyright © 2022 Zhu, Ma, Huang, Liu, Sun and Teng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guirong Teng, dGdyenhsQHNpbmEuY29t