Acoustic Hologram Reconstruction With Unsupervised Neural Network

An acoustic hologram is crucial in various acoustics applications. The reconstruction accuracy of the acoustic field from the hologram is important for determining the performance of the acoustic hologram system. However, challenges remain in acoustic hologram reconstruction where the conventional reconstruction methods generally lack accuracy, complexity, and flexibility. Although the deep learning (DL)–based method has been used to overcome these limitations, it needs the labeled training data to optimize the network with a supervised strategy. To address the problem, we put forward a new unsupervised DL-based reconstruction method in this work, termed PhysNet-AH, which is implemented by integrating a convolutional neural network with a physical model representing the process of acoustics hologram formation. The results demonstrate that we only need to provide PhysNet-AH with a single acoustic field recorded from the hologram, the network parameters can be optimized automatically without the labeled training data, and finally implement the acoustic hologram reconstruction with high accuracy, in terms of SSIM and mean squared error indicators. Furthermore, with the trained model, the robustness and generalization capability of PhysNet-AH have also been well-demonstrated by reconstructing the acoustic fields from different diffraction distances or different datasets. As a result, PhysNet-AH opens the door for fast, accurate, and flexible acoustic hologram–based applications.

1 Introduction

Recently, the acoustic hologram has gained extensive attention in acoustics applications, for example, bio-medicine (Sapozhnikov et al., 2015; Jiménez-Gambín et al., 2019; Baudoin et al., 2020; Ma et al., 2020), particle manipulation (Melde et al., 2016; Baudoin et al., 2019; Baresch and Garbin 2020), 3-D display (Kruizinga et al., 2017; Fushimi et al., 2019), acoustic metasurface/metamaterial (Fan et al., 2020; Zhu et al., 2021), etc. Briefly, the acoustic hologram is a technique that allows recording and reconstructing information of the desired acoustic field. The accurate reconstruction of the hologram is important for an acoustic hologram system. Currently, various methods have been proposed for acoustic hologram reconstruction. However, these methods generally have some limitations in computation complexity, reconstruction accuracy, flexibility of implementation (Marzo et al., 2015; Sapozhnikov et al., 2015; Melde et al., 2016; Marjan et al., 2018; Michael 2019; Fushimi et al., 2021), etc.

Currently, deep learning (DL) has been successfully used to solve inverse problems in imaging fields, for example, scattered image recovery (Sinha et al., 2017; Li et al., 2018; Yang et al., 2019), phase imaging (Rivenson et al., 2018), and digital hologram reconstruction (Wang et al., 2018; Wu et al., 2018; Ren et al., 2019; Francesc et al., 2020; Yin et al., 2020). Especially, a DL method based on U-Net has been introduced to generate a hologram for the desired acoustic field, as demonstrated by Lin et al., (2021). Nevertheless, it is noteworthy that the DL method requires large paired data (the raw data and the labeled data) for training a good network. However, in many conditions, it is hard or impossible to acquire enough labeled data. In addition, the computational cost for the network training is generally high because of the amount of the used training data. These factors limit the practicability and flexibility of the DL-based method in acoustic holograms.

To overcome the limitations, here, we put forward a new DL-based method to reconstruct acoustic holograms with an unsupervised strategy, termed PhysNet-AH, which is achieved by combining a convolutional neural network (CNN) with a physical model representing the process of acoustic hologram formation. The main superiority of the PhysNet-AH method is that it can be achieved without the need for a training label. That is, we only need to input a single acoustic field intensity from the hologram into the PhysNet-AH model, and the network parameters will be automatically optimized and eventually implement acoustic hologram reconstructions with high accuracy. As a result, we can eliminate the need for a great quantity of the labeled data in the training stage of the network. To our knowledge, similar methods have not yet been reported previously in the acoustic hologram field.

Briefly, this method uses an end-to-end network combining the CNN and Transformer (Khan et al., 2021; Liu et al., 2021) to learn the local and the global features of the acoustic hologram. Together, referring to the study by Wang F et al., (2020), a physical model is constructed and used during network training. Here, the physical model enables the calculation of the diffracted acoustic field from the network output by the angular spectrum approach, which is sequentially utilized to calculate loss with input data for optimizing the network parameters. In this work, PhysNet-AH is evaluated with a series of acoustic structures, such as digits, letters, and some symbols, acquired from different public datasets (MNIST and Chars74K). The results confirm that even though only a single unlabeled data source is utilized to train the model, PhysNet-AH makes the possibility of reconstructing the diffracted fields from the holographic structure with high accuracy, robustness, and generalization.

The organization of the rest of this study is as follows. In Section 2, the unsupervised DL method containing network framework, loss function, optimization strategy and angular spectral approach is introduced. Section 3 verifies the effectiveness of the method for acoustic holographic reconstruction in different conditions and analyzes the results. Finally, in Section 4, the relevant results are discussed and summarized.

2 Methods

The framework of the proposed unsupervised PhysNet-AH method is shown in Figure 1. Briefly, when using the proposed method, we only need to provide PhysNet-AH a single acoustic field intensity $\wp (x,y;z=d)$ from the hologram, which is a diffracted pattern of a target object $\aleph (x,y;z=0)$, with a holographic recording distance z = d. The network parameters can be automatically optimized, and finally the acoustic hologram reconstruction can be implemented. Especially, when training the network, the proposed PhysNet-AH method does not require the ground truth $\aleph (x,y;z=0)$. Instead, a physical model H is constructed and then used to calculate the acoustic field intensity $\tilde{\wp }(x,y;z=d)$ from $\tilde{\aleph }(x,y;z=0)$ by the angular spectrum approach. Sequentially, the error between the calculated $\tilde{\wp }(x,y;z=d)$ and the measured $\wp (x,y;z=d)$ is calculated to update the network parameters. Comparably, in the conventional DL-based methods, the ground truth $\aleph (x,y;z=0)$ must be known and the network is optimized by calculating the error between $\aleph (x,y;z=0)$ and $\tilde{\aleph }(x,y;z=0)$. The angular spectral approach used for data generation and physical model is detailed in Section 2.1. The proposed unsupervised neural network method integrated with the physical mode is described in Section 2.2.

FIGURE 1

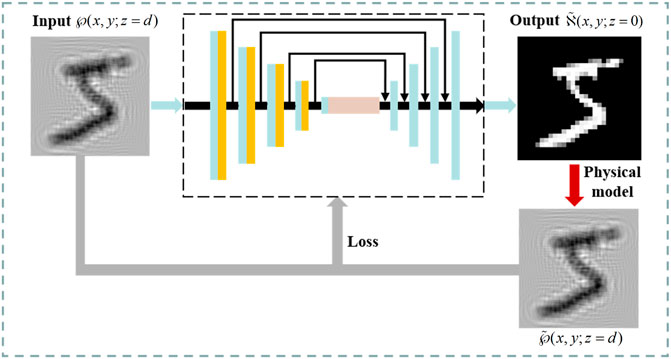
FIGURE 1. Flowchart of the PhysNet-AH method for acoustic hologram reconstruction. Measured acoustic field intensity $\wp \left(x,y;z=d\right)$ from the hologram at the distance of d is the input of the network. The output of the network is the estimated target object $\tilde{\aleph }\left(x,y;z=0\right)$, which is then numerically propagated by physical model H to synthesize the acoustic field intensity $\tilde{\wp }\left(x,y;z=d\right)$. The mean square error, l₁ loss, and structure similar loss between $\wp \left(x,y;z=d\right)$ and $\tilde{\wp }\left(x,y;z=d\right)$ are calculated as the loss to optimize the model.

2.1 Data Generation Based on the Angular Spectral Approach

In this work, we adopt the angular spectral approach (ASA) to synthesize the training and testing dataset. The ASA is an effective method to calculate the diffraction propagation of waves, which can calculate the acoustics fields parallel to the initial plane from a holographic recording by spreading each spatial frequency component of the diffraction wave (Zeng and McGough 2008; Zeng and McGough 2009). In detail, the acoustics field in an initial plane is defined as the input of the angular spectrum approach, and the output from the angular spectrum approach is the acoustics fields at the hologram recording distance of d. The spatial frequency domain propagation of acoustic waves in a linear homogeneous medium is described as follows:

$P\left(k_x,k_y,z\right)=P_0\left(k_x,k_y,0\right)e^{j\text{z}\sqrt{k^2-k_x^2-k_y^2}},(1)$

where $k_x$ and $k_y$ represent the discretized transverse wavenumbers and $k_x^2+k_y^2+k_z^2=k^2$. Here, $k=\omega /c$, $\omega$ denotes the angular frequency, and $c$ denotes the sound speed in the medium. $z$ is the diffraction distance, that is, the hologram recording distance from the initial plane. $P_0\left(k_x,k_y,0\right)$ represents the angular spectrum of the input acoustics field $p_0\left(x,y,0\right)$ at the initial plane, which is the 2-D Fourier transform of the field with regard to x and y. $P\left(k_x,k_y,z\right)$ is the angular spectrum of the acoustics field in $z$ plane parallel to the initial plane.

The acoustics field in each subsequent plane is then obtained by applying a 2-D inverse Fourier transform to $P\left(k_x,k_y,z\right)$, with respect to $k_x$ and $k_y$, as follows:

$p\left(x,y,z\right)=\frac{1}{4{\pi }^2}{\displaystyle \iint P\left(k_x,k_y,z\right)}d{k}_{x}d{k}_y.(2)$

The resulting intensity map $\wp =\Vert p\left(x,y,z\right)\Vert$ is utilized as the diffraction data to train the network.

2.2 Network Architecture

To implement the unsupervised learning strategy, in this work, PhysNet-AH is constructed by integrating a neural network with a physical model. Considering that U-Net is an effective end-to-end convolutional neural network used for solving various image tasks, here, U-Net is used as the main structure of the network, as shown in the black dotted rectangle of Figure 1. In detail, the network consists of four downsampling blocks, three multiple sequence alignment (MSA) Transformers (Rao et al., 2021), and four upsampling blocks. Also,the skipped connections are applied between every two blocks between downsampling and upsampling layers to achieve residual learning. The input to the network is a measured diffracted acoustic field intensity from the holographic recording at the distance of d, and the corresponding output is the estimate of the acoustics target object at the initial plane. Sequentially, the output is numerically propagated by the physical model to synthesize the acoustic field intensity at the distance of d, which is further used to calculate the loss for optimizing the network parameters during training. Details about the network are described as follows:

First, two 3 × 3 convolution layers, each followed by batch normalization (BN) and a ReLU, are adopted to extract the shallow feature maps of the input. In each downsampling block, a 2 × 2 maximum pooling with a stride of 2, two 3 × 3 convolution layers followed by BN and ReLU, and a Channel Attention (CA) layer are stacked sequentially to encode the shallow features into the more abstract and meaningful features. Then, three MSA Transformers are used as the bottleneck to enrich the extracted features and achieve the global information feature extraction. After encoding, four upsampling blocks, where each block contains a transposed convolution and two convolution layers with BN and ReLU, are utilized to enlarge the feature size and decode the abstract feature to the output. Furthermore, skip connections are adopted between the features of the same size (see the black arrows in Figure 1). Here, the feature of the downsampling blocks and the corresponding upsampling feature are concatenated by these skip connections to achieve feature reuse.

A transformer based on the self-attention mechanism is recently proposed, which is capable of learning and extracting information among any position of data. Inspired by the global information extraction of the transformer, researchers gradually apply it to computer vision tasks and have achieved remarkable performance (Ho et al., 2019; Wang H et al., 2020; Khan et al., 2021; Liu et al., 2021; Rao et al., 2021). So, in this work, the MSA Transformer block is utilized at the bottleneck of the network. The MSA Transformer block considers the features obtained by downsampling blocks as aligned sequences, where rows of features correspond to sequences and columns are positioned in the aligned sequences. For the core of this block, the axial attention and multi-head self-attention are adopted for row attention implementation and column attention implementation, respectively, which have high computational efficiency and enable the model to capture the full feature map context (Ho et al., 2019; Wang H et al., 2020; Rao et al., 2021). The structure of this block is demonstrated in Figure 2.

FIGURE 2

FIGURE 2. Architecture of the MSA Transformer block. Here, the residual connection is used between the adjacent sub-modules. The first sub-module is used to achieve a single attention map of all rows by using an axial attention layer. The second sub-module is used to extract the feature for columns of input feature maps by using a multihead self-attention layer. The last sub-module is implemented by using a multilayer perceptron layer.

The design of the loss function is extremely important in the unsupervised method. To more effectively update network parameters (weights and bias), here, the loss function is calculated by combining mean squared error loss, l₁ loss, and structural similarity (SSIM) loss (Wang et al., 2004). The formula is described as follows:

$\ell \left(\wp ,\tilde{\wp }\right)={\Vert \wp -\tilde{\wp }\Vert }_2^2+{\lambda }_1{\Vert \tilde{\wp }\Vert }_1^1+{\lambda }_2\left(1-\text{SSIM}\left(\wp ,\tilde{\wp }\right)\right),(3)$

where $\wp$ is the input of the network, $\tilde{\wp }$ denotes the diffracted acoustic field calculated by propagating the network output with physical model H, and ${\lambda }_1$ and ${\lambda }_2$ denote the weight coefficients. Here, referring to the study by Zhao et al., (2017), ${\lambda }_1=0.2$ and ${\lambda }_2=0.8$.

During the training process, Adam optimization is adopted, and the maximum training epoch is 500. The decay strategy is used for the learning rate in order to ensure that the training quickly and stably converges. In detail, the attenuation is set to 0.5 for every 200 epochs, with the initial learning of 0.001. The proposed unsupervised PhysNet-AH method is implemented by Pytorch, and the training process is executed on equipment with a 16-GB NVidia Tesla V100 GPU, 2 Intel Xeon Gold 6130, and 192 G DDR4 REG ECC. In this work, the computational time for the training procedure is about 10 min.

3 Experiments and Results

In this work, the numerical simulation of the acoustic hologram is realized by the angular spectrum approach. In detail, the target image with the size of 256 × 256 pixels is placed in the x–y plane at z = 0 mm (the initial plane) and is then illuminated by a plane wave. Here, the excitation frequency is set as 2 MHz, the sound speed is set as 1,500 m/s, and the wavelength is 750 μm. The diffracted pattern is recorded at z = 10 mm ($13.33\lambda$), 20 mm ($26.67\lambda$) and 30 mm ($39.99\lambda$) from the initial plane. The size of the recorded acoustics field from the hologram is set as 38.4 × 38.4 mm² ($51.2\lambda$ x $51.2\lambda$), with a resolution of 256 × 256 pixels. Here, the acoustics target images are acquired from the Modified National Institute of Standards and Technology (MNIST) database including the handwritten digits and the letters (Deng 2012) and the Chars74K database containing the symbols used in both English and Kannada (Campos et al., 2009). These data are sequentially used to generate the training and testing data by the ASA method.

3.1 Evaluating the Feasibility of PhysNet-AH in Acoustic Hologram Reconstruction

First, we verify the feasibility of PhysNet-AH in implementing acoustic hologram reconstruction, which is demonstrated by using unseen target images randomly selected from the test dataset. Figure 3 shows the corresponding reconstruction results. The 1st row of Figure 3 shows the diffraction-limited acoustic field intensity from the holograms for different target digits (2, 5, and 6) at the distance (z = 10 mm), which are utilized as the input of the network. The 2nd row of Figure 3 shows the holographic reconstruction of the abovementioned acoustics fields, which are acquired by the proposed PhysNet-AH method. The last row of Figure 3 describes the merged images of the target digits (ground truth) and the reconstructed images. Here, the true digits are represented in red, and the reconstructed images are shown in green. Correspondingly, the overlapping parts of the two images are shown in yellow.

FIGURE 3

FIGURE 3. Acoustic hologram reconstruction results of different acoustic targets are utilized to evaluate the feasibility of the PhysNet-AH. The first row shows the diffraction-limited acoustic field intensity from the holograms for digits 2, 5, and 6 at z = 10 mm, which are used as the input of the network. The second row shows the holographic reconstruction of the abovementioned acoustics fields, which are obtained by PhysNet-AH. The last row shows the merged images of the target digits (ground truth) and the corresponding reconstructed images. Red displays the ground truth, green corresponds to the reconstructed results of PhysNet-AH, and yellow represents their overlaps.

The results demonstrate that there is a high overlap (see the yellow color in the last row of Figure 3) between the ground truth and the result reconstructed by PhysNet-AH, indicating that high reconstruction accuracy can be acquired by the proposed method. Furthermore, to quantitatively evaluate the acoustics field reconstruction quality of PhysNet-AH, two quantitative indicators, that is, mean squared error (MSE) and structural similarity index (SSIM) are calculated. In this case, the normalized MSEs between the reconstruction images and the true target images (ground truth) of the digits 2, 5, and 6 are 0.013, 0.013, and 0.019, respectively. The corresponding SSIMs of digits 2, 5, and 6 are all above 0.8. These quantitative results further confirm that the proposed unsupervised PhysNet-AH method enables effectively implementing holographic reconstruction by the network model trained only with a single unlabeled sample.

3.2 Evaluating the Robustness of PhysNet-AH in Acoustic Hologram Reconstruction

To evaluate the robustness of the PhysNet-AH in acoustic hologram reconstruction, the rotated acoustic fields are incorporated into the trained model and the corresponding results are shown in Figure 4. The 1st row of Figure 4 depicts the diffracted acoustic field from the hologram of the rotated digit 4 at z = 10 mm. The 2nd row of Figure 4 depicts the corresponding reconstruction results from the abovementioned diffracted acoustic fields. The true target images are described in the 3rd row of Figure 4.

FIGURE 4

FIGURE 4. Acoustic hologram reconstructed results for the rotated target images of digit 4 which are used to evaluate the robustness of PhysNet-AH. The first row shows the diffracted acoustic field intensity from the hologram of the rotated images of 4 at z = 10 mm. The second row shows the corresponding reconstruction results. The last row shows the target images (ground truth).

The results show that as expected, PhysNet-AH can effectively reconstruct the diffracted acoustic field from the holographic structure, even if the test image is the transformation of the original target image. Furthermore, to quantitatively evaluate the robustness of the model, SSIM and MSE indicators are calculated for each case. Here, a high average SSIM of 0.83 with a standard deviation of 0.005 and a low average MSE of 0.015 with a standard deviation of 0.0007 are obtained, indicating that good stability and anti-disturbance capability can be obtained by PhysNet-AH.

Moreover, we also demonstrate the reconstruction capability of PhysNet-AH at different diffraction distances, which is used to further evaluate the robustness of PhysNet-AH. Figure 5 depicts the corresponding reconstruction results. The 1st row of Figure 5 depicts the diffracted acoustic fields from the holograms of digits 3 at different distances (z = 10, 20, and 30 mm). We can observe that the diffracted images have more self-interference–related spatial patterns with the increase in distance, which results in a blur and is hard to distinguish the true structure. The 2nd row of Figure 5 depicts the reconstruction images obtained by PhysNet-AH. Comparably, the last row of Figure 5 depicts the merged images with the true target digit and the reconstructed image, where red corresponds to the ground truth, green corresponds to the reconstructed results, and yellow represents their convergence.

FIGURE 5

FIGURE 5. Acoustic hologram reconstruction results of digit 3 at different holographic recording distances (z = 10, 20, and 30 mm) are used to evaluate the robustness of PhysNet-AH. The first row shows the diffracted acoustic field intensity from the holograms of digit 3 at z = 10, 20, and 30 mm. The second row shows the corresponding reconstruction results from the abovementioned acoustics fields. The last row shows the merged images of the target digits (ground truth) and the reconstructed images. Red represents the ground truth, green represents the reconstructed results of PhysNet-AH, and yellow represents their overlaps.

The results show that even though only single unlabeled data is utilized to train the network model, and the proposed PhysNet-AH method can also effectively reconstruct the acoustic field at different diffraction distances. In addition, we also quantitatively evaluate the reconstruction quality of PhysNet-AH at z = 10, z = 20, and z = 30 mm, in terms of SSIM and MSE indicators. Table 1 summarizes the corresponding quantitative results calculated from 100 independent trials at each distance. These quantitative results further confirm the reconstruction robustness of PhysNet-AH. In addition, we can also observe that although PhysNet-AH can effectively implement acoustic hologram reconstruction for different diffraction distances, the reconstruction performance decreases slightly with the increase in the distance.

TABLE 1

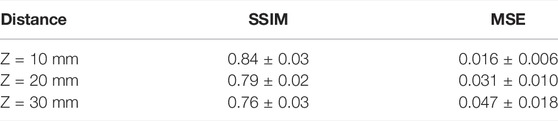
TABLE 1. Quantitative results of acoustic hologram reconstruction at different diffraction distances (z = 10 mm, z = 20 mm, and z = 30 mm). For each distance, 100 independent trials are used and calculated.

3.3 Evaluating the Generalization of PhysNet-AH in Acoustic Hologram Reconstruction

To further validate the generalization of PhysNet-AH, we test the trained model with the MNIST and the Chars74K datasets, which are different from the training data. The 1st row of Figure 6 depicts the diffracted acoustic field intensities of different letters and symbols from different datasets. The 2nd row of Figure 6 depicts the reconstructed acoustic field. Comparably, the last row of Figure 6 depicts the ground truth in different datasets.

FIGURE 6

FIGURE 6. Generalization evaluation of the proposed unsupervised PhysNet-AH method with different datasets. The first row shows the diffracted acoustic field intensities from different datasets at z = 10 mm. The second row shows the corresponding reconstruction results from the abovementioned acoustic fields. The last row shows the target images (ground truth) of the two English letters “m” and “Q” in the MNIST dataset, one English letter B, and two symbols of Kannada in the Chars74K dataset.

The results show that although the model is trained only with a single digit from the MNIST dataset, PhysNet-AH can also effectively reconstruct the acoustic fields from a different database, for example, the MNIST letters and the symbols used in both English and Kannada with an overall satisfactory reconstruction quality. However, there are still some divergences between the reconstruction results and ground truth, especially for the complex structure (see the 4th and 5th columns in Figure 6). The main reason maybe the lack of enough information for unseen data because the network model of PhysNet-AH is trained only by single unlabeled data without the training label.

4 Discussion

Challenges remain in acoustic hologram reconstruction. The conventional reconstruction methods generally lack computation complexity, reconstruction accuracy, and flexibility of implementation. Although the DL-based method has been used to overcome these limitations, it needs large labeled data to optimize the network with a supervised strategy. This work puts forward a new unsupervised DL-based reconstruction method (PhysNet-AH), which is realized by integrating a convolutional neural network with a physical model. Different from the conventional DL-based methods, the proposed unsupervised method is trained to learn the underlying relations between the acoustic field domain and target domain only from a single unlabeled sample. Then, the trained model can be used to effectively reconstruct the acoustic field from the hologram without human intervention.

The results demonstrate that PhysNet-AH can effectively reconstruct the diffracted acoustics fields from a holographic recording, even though only single unlabeled data is adopted to train the network (see Figures 3–6). Furthermore, the diffracted acoustic field generated from different transformations/distances (see Figure 4 and Figure 5) or the diffracted acoustic field generated from different datasets (see Figure 6) can also be effectively reconstructed by the trained model, indicating good robustness and generalization capability of PhysNet-AH in practical applications. Moreover, the quantitative results from SSIM and MSE indicators further confirm the reconstruction capability of PhysNet-AH, where a high SSIM and low MSE are obtained, respectively. Based on the previous results, we believe that the proposed PhysNet-AH method can effectively implement acoustic field reconstruction only using one sample without the need for the labeled data and make it possible to implement acoustic hologram reconstruction in an unsupervised way, without reducing the reconstruction performance, which greatly extends the practicability of PhysNet-AH in applications.

However, it should be noted that in this work, the reconstruction capability of PhysNet-AH is validated based on the simulated data. As a data-driven method, the performance of PhysNet-AH might have limitations in practical applications. In addition, in this work, U-Net is selected and used as the main framework of the network. Considering that the network architecture may affect the hologram reconstruction quality, the reconstruction accuracy may be further improved by using more effective networks. Furthermore, as a proof of concept, here, the angular spectral approach is used to construct the acoustic hologram physical model. For simplification, the reconstruction results from the more complex physical model (e.g., including scattering, attenuation, etc.) are not demonstrated. Moreover, our current work mainly focuses on implementing single acoustics field reconstruction, and the reconstruction of multiple acoustics fields from one hologram has not been investigated. The systemic study will be performed in future work.

In conclusion, PhysNet-AH as an unsupervised learning method paves the way for implementing acoustic hologram reconstruction with high accuracy, robustness, and generalization, which extends the flexibility in various acoustic hologram–based applications.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

BL and ML performed the analysis and drafted the manuscript. CL and XL supported the analysis design and made constructive discussions. XL and DT supervised the project, made critical revisions, and approved the final version.

Funding

This work was supported in part by the National Natural Science Foundation of China (61871263, 12034005, 11827808), in part by the Explorer Program of Shanghai (21TS1400200), in part by the Natural Science Foundation of Shanghai (21ZR1405200, 20S31901300), and in part by the China Postdoctoral Science Foundation (2021M690709).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baresch, D., and Garbin, V. (2020). Acoustic Trapping of Microbubbles in Complex Environments and Controlled Payload Release. Proc. Natl. Acad. Sci. U.S.A. 117 (27), 15490–15496. doi:10.1073/pnas.2003569117

PubMed Abstract | CrossRef Full Text | Google Scholar

Baudoin, M., Gerbedoen, J. C., Riaud, A., Matar, O. B., Smagin, N., and Thomas, J. L. (2019). Folding a Focalized Acoustical Vortex on a Flat Holographic Transducer: Miniaturized Selective Acoustical Tweezers. Sci. Adv. 5 (4), eaav1967–7. doi:10.1126/sciadv.aav1967

PubMed Abstract | CrossRef Full Text | Google Scholar

Baudoin, M., Thomas, J. L., Sahely, R. A., Gerbedoen, J. C., Gong, Z., Sivery, A., et al. (2020). Spatially Selective Manipulation of Cells with Single-Beam Acoustical Tweezers. Nat. Commun. 11 (4244), 4244–4310. doi:10.1038/s41467-020-18000-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Campos, T., Babu, B. R., and Varma, M. (2009). “Character Recognition in Natural Images,” in Proceedings of the International Conference on Computer Vision Theory and Applications.

Google Scholar

Deng, L. (2012). The MNIST Database of Handwritten Digit Images for Machine Learning Research [Best of the Web]. IEEE Signal Process. Mag. 29 (6), 141–142. doi:10.1109/msp.2012.2211477

CrossRef Full Text | Google Scholar

Fan, S.-W., Zhu, Y., Cao, L., Wang, Y.-F., Li Chen, A., Merkel, A., et al. (2020). Broadband Tunable Lossy Metasurface with Independent Amplitude and Phase Modulations for Acoustic Holography. Smart Mat. Struct. 29 (10), 105038. doi:10.1088/1361-665x/abaa98

CrossRef Full Text | Google Scholar

Francesc, L., Pablo, M., Martin, B., and Sven, E. (2020). Sound Field Reconstruction in Rooms: Inpainting Meets Super-resolution. J. Acoust. Soc. Am. 148, 649–659. doi:10.1121/10.0001687

PubMed Abstract | CrossRef Full Text | Google Scholar

Fushimi, T., Marzo, A., Drinkwater, B. W., and Hill, T. L. (2019). Acoustophoretic Volumetric Displays Using a Fast-Moving Levitated Particle. Appl. Phys. Lett. 115, 064101. doi:10.1063/1.5113467

CrossRef Full Text | Google Scholar

Fushimi, T., Yamamoto, K., and Ochiai, Y. (2021). Acoustic Hologram Optimisation Using Automatic Differentiation. Sci. Rep. 11, 12678. doi:10.1038/s41598-021-91880-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ho, J., Kalchbrenner, N., Weissenborn, D., and Salimans, T. (2019). Axial Attention in Multidimensional Transformers. arXiv 1912.12180. doi:10.48550/arXiv.1912.12180

CrossRef Full Text | Google Scholar

Jiménez-Gambín, S., Jiménez, N., Benlloch, J. M., and Camarena, F. (2019). Holograms to Focus Arbitrary Ultrasonic Fields through the Skull. Phys. Rev. Appl. 12 (1), 014016. doi:10.1103/PhysRevApplied.12.014016

CrossRef Full Text | Google Scholar

Khan, S., Naseer, M., Hayat, M., Zamir, S. W., Khan, F. S., and Shah, M. (2021). Transformers in Vision: a Survey. arXiv 2101.01169v4. doi:10.48550/arXiv.2101.01169

CrossRef Full Text | Google Scholar

Kruizinga, P., van der Meulen, P., Fedjajevs, A., Mastik, F., Springeling, G., de Jong, N., et al. (2017). Compressive 3D Ultrasound Imaging Using a Single Sensor. Sci. Adv. 3 (12), e1701423. doi:10.1126/sciadv.1701423

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Xue, Y., and Tian, L. (2018). Deep Speckle Correlation: a Deep Learning Approach toward Scalable Imaging through Scattering Media. Optica 5 (10), 1181–1190. doi:10.1364/optica.5.001181

CrossRef Full Text | Google Scholar

Lin, Q., Wang, J., Cai, F., Zhang, R., Zhao, D., Xia, X., et al. (2021). A Deep Learning Approach for the Fast Generation of Acoustic Holograms. J. Acoust. Soc. Am. 149, 2312–2322. doi:10.1121/10.0003959

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Lin, Y., Cao, Y., Hu, H., Zhang, Z., Lin, S., et al. (2021). Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. arXiv: 2103.14030v1. doi:10.48550/arXiv.2103.14030

CrossRef Full Text | Google Scholar

Ma, Z., Holle, A. W., Melde, K., Qiu, T., Poeppel, K., Kadiri, V. M., et al. (2020). Acoustic Holographic Cell Patterning in a Biocompatible Hydrogel. Adv. Mat. 32 (4), 1904181. doi:10.1002/adma.201904181

PubMed Abstract | CrossRef Full Text | Google Scholar

Marjan, B., Ahmed, E., Muhammad, R., and Shima, S. (2018). Acoustic Holograms in Contactless Ultrasonic Power Transfer Systems: Modeling and Experiment. J. Appl. Phys. 124, 244901. doi:10.1063/1.5048601

CrossRef Full Text | Google Scholar

Marzo, A., Seah, S. A., Drinkwater, B. W., Sahoo, D. R., Long, B., and Subramanian, S. (2015). Holographic Acoustic Elements for Manipulation of Levitated Objects. Nat. Commun. 6, 8661. doi:10.1038/ncomms9661

PubMed Abstract | CrossRef Full Text | Google Scholar

Melde, K., Mark, A. G., Qiu, T., and Fischer, P. (2016). Holograms for Acoustics. Nature 537, 518–522. doi:10.1038/nature19755

PubMed Abstract | CrossRef Full Text | Google Scholar

Michael, D. (2019). Phase and Amplitude Modulation with Acoustic Holograms. Appl. Phys. Lett. 115, 053701. doi:10.1063/1.5110673

CrossRef Full Text | Google Scholar

Rao, R., Liu, J., Verkuil, R., Meier, J., Canny, J. F., Abbeel, P., et al. (2021). MSA Transformer. bioRxiv 2021.02.12.430858. doi:10.1101/2021.02.12.430858

CrossRef Full Text | Google Scholar

Ren, Z., Xu, Z., and Lam, E. Y. (2019). End-to-end Deep Learning Framework for Digital Holographic Reconstruction. Adv. Phot. 1 (1), 016004. doi:10.1117/1.ap.1.1.016004

CrossRef Full Text | Google Scholar

Rivenson, Y., Zhang, Y., Günaydın, H., Teng, D., and Ozcan, A. (2018). Phase Recovery and Holographic Image Reconstruction Using Deep Learning in Neural Networks. Light Sci. Appl. 7, 17141. doi:10.1038/lsa.2017.141

PubMed Abstract | CrossRef Full Text | Google Scholar

Sapozhnikov, O. A., Tsysar, S. A., Khokhlova, V. A., and Kreider, W. (2015). Acoustic Holography as a Metrological Tool for Characterizing Medical Ultrasound Sources and Fields. J. Acoust. Soc. Am. 138 (3), 1515–1532. doi:10.1121/1.4928396

PubMed Abstract | CrossRef Full Text | Google Scholar

Sinha, A., Lee, J., Li, S., and Barbastathis, G. (2017). Lensless Computational Imaging through Deep Learning. Optica 4 (9), 1117–1125. doi:10.1364/optica.4.001117

CrossRef Full Text | Google Scholar

Wang, F., Bian, Y., Wang, H., Lyu, M., Pedrini, G., Osten, W., et al. (2020). Phase Imaging with an Untrained Neural Network. Light Sci. Appl. 9, 77. doi:10.1038/s41377-020-0302-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Zhu, Y., Green, B., Adam, H., Yuille, A., and Chen, L. C. (2020). Axial-deeplab: Stand-Alone Axial-Attention for Panoptic Segmentation. arXiv 2003.07853. doi:10.48550/arXiv.2003.07853

CrossRef Full Text | Google Scholar

Wang, H., Lyu, M., and Situ, G. (2018). eHoloNet: A Learning-Based End-To-End Approach for In-Line Digital Holographic Reconstruction. Opt. Express 26 (18), 22603–22614. doi:10.1364/oe.26.022603

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P. (2004). Image Quality Assessment: from Error Visibility to Structural Similarity. IEEE Trans. Image Process. 13 (4), 600–612. doi:10.1109/tip.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Rivenson, Y., Zhang, Y., Wei, Z., Günaydin, H., Lin, X., et al. (2018). Extended Depth-Of-Field in Holographic Imaging Using Deep-Learning-Based Autofocusing and Phase Recovery. Optica 5 (6), 704–710. doi:10.1364/optica.5.000704

CrossRef Full Text | Google Scholar

Yang, M., Liu, Z.-H., Cheng, Z.-D., Xu, J.-S., Li, C.-F., and Guo, G.-C. (2019). Deep Hybrid Scattering Image Learning. J. Phys. D. Appl. Phys. 52 (11), 115105. doi:10.1088/1361-6463/aafa3c

CrossRef Full Text | Google Scholar

Yin, D., Gu, Z., Zhang, Y., Gu, F., Nie, S., Ma, J., et al. (2020). Digital Holographic Reconstruction Based on Deep Learning Framework with Unpaired Data. IEEE Photonics J. 12 (2), 1–12. doi:10.1109/jphot.2019.2961137

CrossRef Full Text | Google Scholar

Zeng, X., and McGough, R. J. (2008). Evaluation of the Angular Spectrum Approach for Simulations of Near-Field Pressures. J. Acoust. Soc. Am. 123 (1), 68–76. doi:10.1121/1.2812579

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, X., and McGough, R. J. (2009). Optimal Simulations of Ultrasonic Fields Produced by Large Thermal Therapy Arrays Using the Angular Spectrum Approach. J. Acoust. Soc. Am. 125, 2967–2977. doi:10.1121/1.3097499

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, H., Gallo, O., Frosio, I., and Kautz, J. (2017). Loss Functions for Image Restoration with Neural Networks. IEEE Trans. Comput. Imaging 3 (1), 47–57. doi:10.1109/tci.2016.2644865

CrossRef Full Text | Google Scholar

Zhu, Y., Gerard, N. J., Xia, X., Stevenson, G. C., Cao, L., Fan, S., et al. (2021). Systematic Design and Experimental Demonstration of Transmission‐Type Multiplexed Acoustic Metaholograms. Adv. Funct. Mat. 31 (27), 2101947. doi:10.1002/adfm.202101947

CrossRef Full Text | Google Scholar