
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 14 June 2022
Sec. Computational Materials Science
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.908952
This article is part of the Research Topic Modeling of structural and chemical disorders: From metallic glasses to high entropy alloys View all 9 articles
Tailoring heterogeneities in amorphous alloys is a promising strategy for promoting the strength-ductility synergy. Here, molecular dynamics simulations are performed to investigate the effects of grains size and heterogeneous chemical composition on the mechanical properties of Mg-Cu nanoglasses (NGs). The reduced grain size in single-phase NGs improves the plasticity but at the expense of strength. In addition, the mechanical properties of dual-phase NGs composed of two chemical compositions depend critically upon the fraction of softer phase. In particular, the plasticity is improved for the low fraction of the softer phase, but is deteriorated for the high fraction of the softer phase, which is in striking contrast to the observations of the plasticity improvement reported in the traditional nanostructured metals/alloys. This is because that heterogeneities at the glass-glass interfaces intentionally introduce more stress concentration sites which are easier to accelerate the shear band formation. For an appropriate fraction of heterogeneous composition, a balance among strength and plasticity can be realized, which is useful for the design of novel NGs with high strength and superior ductility.
Metallic glass (MG) is a unique type of glassy alloy obtained by melting multi-component metallic alloys and then cooling it at a high rate (Klement et al., 1960). MGs possess some outstanding properties such as high strength and high elastic limit compared to their crystalline counterparts due to the intrinsic amorphous structures (Cyrot-Lackmann, 1980; Boudreaux and Frost, 1981; Greer, 1995; Zhang et al., 2004). Although MGs are considered to be one of the structural materials with great potential of engineering applications (Ashby and Greer, 2006; Shan et al., 2008; Cheng et al., 2009a; Chen et al., 2011; Liu et al., 2011), they suffer from certain challenging issues, especially the lack of macroscopic tensile plasticity at room temperature due to the fact that the plastic deformation of MGs under tensile loading is concentrated in a narrow shear band (SB) region (Zhang et al., 2003; Greer et al., 2013).
Nanoglass (NG) is a new type of structural material which was first proposed by Herbert Gleiter (Gleiter, 2008). It is composed of nanometer-sized glassy grain and a large number of glass-glass interfaces (GGIs) with high free volume and low density relative to the glassy grains, which hence has the potential to tune the macroscopical plastic behavior (Şopu et al., 2011; Fang et al., 2012). Previous work in the past decade has shown that the plasticity of NGs is effectively improved compared with MGs, due to the introduced GGIs which can induce multiple SBs formation (Adibi et al., 2013; Wang et al., 2015; Wang et al., 2016; Brink and Albe, 2018). However, improved plasticity in NGs is at the expense of strength, which is a common dilemma in nanostructured materials (Şopu et al., 2011; Adibi et al., 2013; Wang et al., 2015; Ivanisenko et al., 2018).
One of the common methods to promote the strength-ductility synergy is to tailor heterogeneities such as the introduction of secondary phases in form of nanoprecipitates (Hofmann et al., 2008; Greer et al., 2013). For example, by adding a small amount of Nb to Zr-Cu-Ni-Al MG matrix, the formation of dual-phase MGs results in the improved plasticity without sacrificing strength (Chen and Todd, 2015). Inspired by this observation, a great deal of research has been dedicated to the preparation of heterogeneous nanostructured MGs (Pan et al., 2009; Kuan et al., 2010; Kim et al., 2013; Sha et al., 2015; Yao and Jin, 2015; Sha et al., 2017; Liu et al., 2018; Sun et al., 2018; Wu et al., 2020). In addition, Jian et al. have demonstrated that it is an effective way to balance strength and plasticity by controlling the heterogeneous structure, through the investigation of the mechanical behaviors of crystalline/amorphous nanocomposites (Jian et al., 2016; Jian et al., 2018a, 2018b). Therefore, it is of both great scientific and technological significance to provide an atomic-scale understanding of the deformation and failure mechanism of NGs with heterogeneous chemical compositions.
To this end, we perform molecular dynamics (MD) simulations on the NGs composed of heterogeneous chemical compositions, with focus on the effects of grain size and heterogeneous composition. Here, we choose Mg33Cu67 and Mg85Cu15 NGs due to their large differences in shear modulus. Our results reveal that, as the grain size decreases from 15 to 5 nm, the plasticity of single-phase Mg33Cu67 and Mg85Cu15 NGs are improved, accompanied by a decrease in strength, while a transition from catastrophic fracture to super-plasticity occurs. On the other hand, by introducing softer Mg85Cu15 NGs into the Mg33Cu67 NGs, the strength of dual-phase NGs decreases, while the plasticity improves at first and then deteriorates with the increase of the fraction of softer Mg85Cu15 NGs. Our results show that the mechanical properties of dual-phase NGs can be tuned by controlling the content ratio of soft to hard phase, providing an effective design approach for NGs architectures.
MD simulations are performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) (Plimpton, 1995). The atomic interactions are described by using an embedded atom model (EAM) potential fitted to Mg-Cu alloys (Ding et al., 2012). The system pressure and temperature are controlled by a Parrinello-Rahman barostat (Parrinello and Rahman, 1982) and a Nose-Hoover thermostat (Nosé, 1984), respectively. An integration time step of 2 fs is used in all simulations. Mg33Cu67 and Mg85Cu15 NG samples containing ∼2.0 million atoms are prepared in a slab with dimensions of 6.1 (x) × 48.8 (y) × 97.6 (z) nm3. In constructing the NG samples, a small MG cube with a side length of 6.1 nm is first equilibrated at 2000 K for 2 ns with periodic boundary conditions (PBCs) along all three dimensions, and then cooled to 50 K at a quenching rate of 1010 K/s under the condition of zero external pressure (Ding et al., 2012; Sha et al., 2014). The large MG samples are constructed by replications of the small cubes, then annealed at a temperature near the glass transition temperature (
The NG samples are generated by using the Poisson-Voronoi tessellation method implemented in the Atomsk code (Hirel, 2015) and the MG structure as a source of material for the glassy grains. By setting the number of grains to change the grain size (d) in the sample, columnar glassy grains with average d of 5, 10, and 15 nm are prepared to study the grain size effect. For dual-phase NGs, the d is fixed at 10 nm, and some Mg33Cu67 grains are randomly replaced by Mg85Cu15 grains, as shown in Figure 1. There is a total of 50 grains. And the dual-phase NGs with replaced 15, 25, and 35 grains are used to investigate the effect of heterogeneous composition, and are hereafter referred to as NGI, NGII, and NGIII, respectively. In the work of Adjaoud and Albe (2018), spherical grains were equilibrated in the liquid state (above
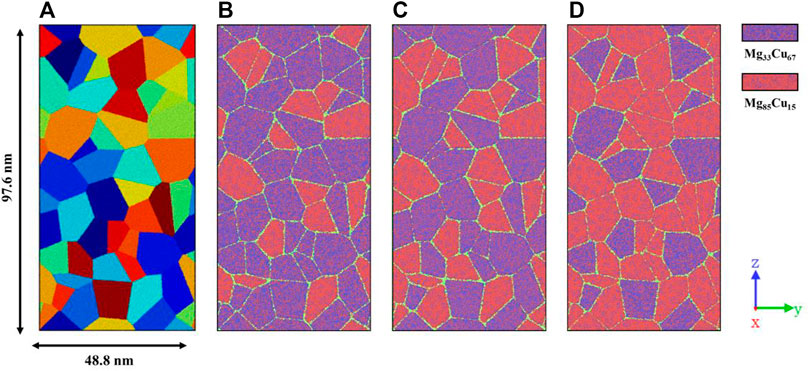
FIGURE 1. (A) Atomic configuration of single-phase NG sample with d = 10 nm. Grains are shown in different colors to highlight the architectures. (B–D) Atomic configurations of dual-phase NGs composed of Mg33Cu67 grains and Mg85Cu15 grains, i.e., NGI, NGII, and NGIII, respectively.
For uniaxial tensile tests, the MD simulations are carried out in isothermal-isobaric (NPT) ensembles at 50 K and zero pressure. A constant tensile strain rate of 1 × 108 s−1 along the z-direction is applied (Cao et al., 2009). PBCs are applied in all three dimensions directions to eliminate the surface effects (Şopu et al., 2011; Albe et al., 2013). The stress is calculated from the normal tensor component of the virial stress along the loading direction (Cao and Wei, 2007). The generation and evolution of local inelastic deformations are analyzed by calculating the atomic local von Mises shear strain
We first investigate the effect of grain size d of the single-phase Mg33Cu67 and Mg85Cu15 NGs. Figures 2A,B depict the tensile engineering stress-strain curves for Mg33Cu67 and Mg85Cu15 NGs with different d values in comparison with the MG specimen. For MGs, the peak stress for Mg33Cu67 MG is 3.3 GPa, which is higher than 1.4 GPa for Mg85Cu15 MG. In addition, a colossal drop in the stress is observed, corresponding to a rapid localization of the plastic strain into the SB region. For NGs, the peak stresses are lower than those of the MGs and decrease with grain size. For a fixed grain size, the peak stress of Mg33Cu67 NG is higher compared to the Mg85Cu15 NG. In other words, Mg85Cu15 NG is softer than Mg33Cu67 NG.
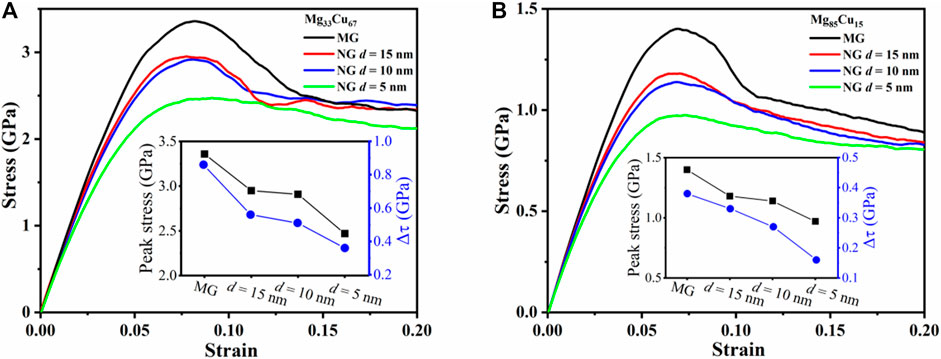
FIGURE 2. Engineering tensile stress-strain curves for (A) Mg33Cu67 and (B) Mg85Cu15 NGs with d = 15, 10, and 5 nm. MG counterparts are also plotted for comparison. The inset shows the peak stress and
The stress drop is defined as
To understand the mechanism underlying the above-mentioned failure transition, we probe the atomic deformation processes by examining the local atomic shear strain
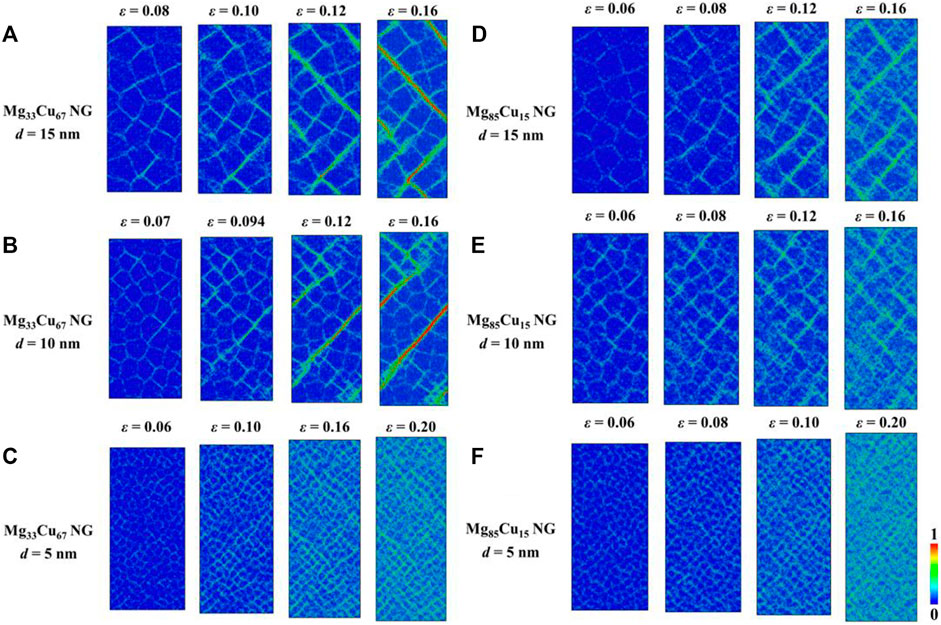
FIGURE 3. Sequence of snapshots capturing the atomic deformation processes for (A–C) Mg33Cu67 NGs with d = 15, 10, and 5 nm, respectively, and (D–F) Mg85Cu15 NGs with d = 15, 10, and 5 nm, respectively. The colors indicate the atomic shear strain.
To further quantify the fraction of the atoms involved in the plastic deformation during the tensile loading, the fraction of atoms with relatively high
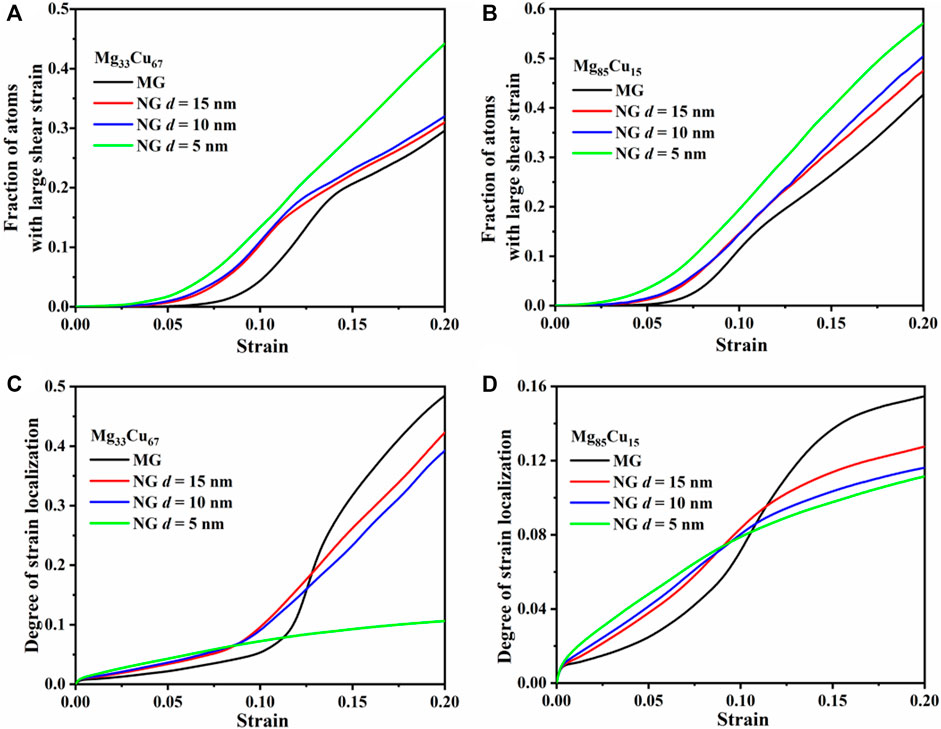
FIGURE 4. (A,B) The fraction of atoms with large
Figure 5A depicts the tensile engineering stress-strain curves for NGI, NGII, NGIII, together with single-phase NGs for comparison. Two features, i.e., the peak stress and the stress drop
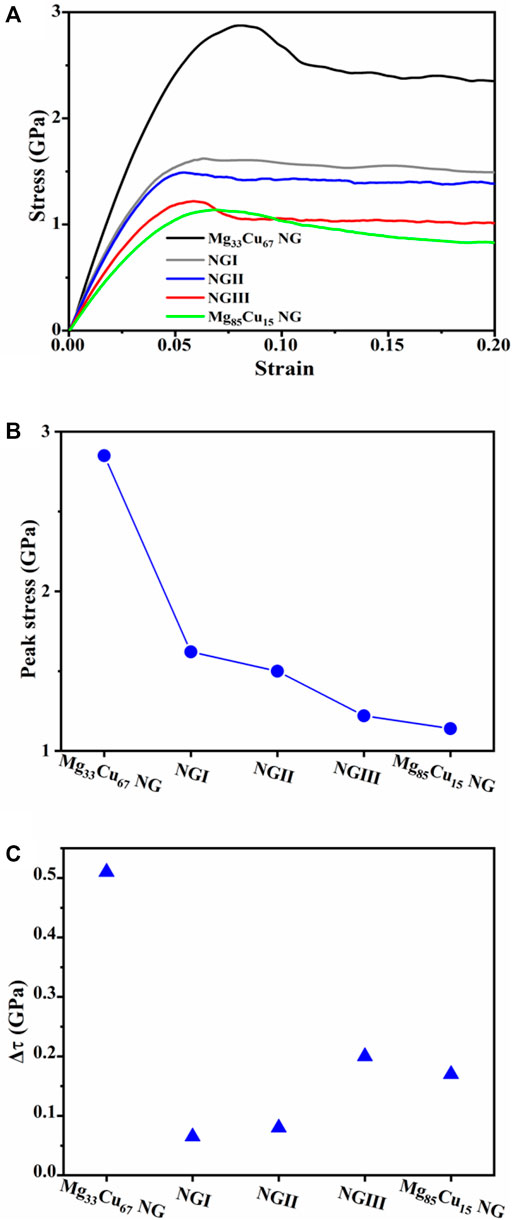
FIGURE 5. (A) Engineering tensile stress-strain curves, (B) peak stress, and (C)
To unravel the conflict, a sequence of snapshots capturing the atomic deformation processes for NGI, NGII, and NGIII is shown in Figures 6A–C, respectively. For NGI, the plastic deformation takes place at the softer regions, including the GGIs and the Mg85Cu15 nanograins. Upon further tensile loading, the STZs are constrained in the softer Mg85Cu15 grains, and the development of a mature SB is possibly blocked by the harder Mg33Cu67 grains. In contrast to NGI, the network of STZs grows into a mature SB for NGII when the fraction ratio of soft to hard phase exceed 1.0 (i.e., NGIII), a mature predominant SB develops. This is because that more free volume at the softer Mg85Cu15/Mg85Cu15 interfaces introduces more stress concentration sites, and void nucleation at these GGIs can develop into cracks and propagate along interfaces, as shown in Figure 6C. Our simulation results thus highlight that the more addition of the softer second phase in MGs deteriorates the overall plasticity.
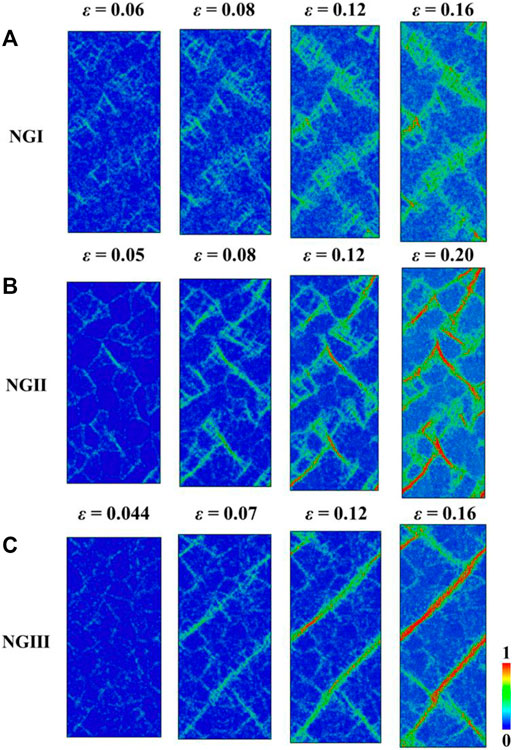
FIGURE 6. (A–C) Sequence of snapshots capturing the atomic deformation processes for NGI, NGII, and NGIII, respectively. The colors indicate the atomic shear strain.
To better understand the failure transition mechanism in dual-phase NGs with different grain ratios, five identical grains are selected and we compare the evolution of the local structure during deformation, as shown in Figure 7. It is found that the vast majority of STZs initially decorate the GGIs among grains with different compositions, referred to as soft-hard GGIs hereafter. For NGI with few soft phases, the STZs are difficult to propagate, because the soft Mg85Cu15 grains are completely surrounded by the hard Mg33Cu67 grains. In comparison with NGI, the incorporation of more soft phases in NGII increases the opportunity of the STZs to penetrate or propagate. For NGIII with overwhelming soft phases, it is intriguing to observe the rapid propagation of the STZs initiated at the soft-hard GGIs, and the other STZs do not participate in the development of the mature SB.
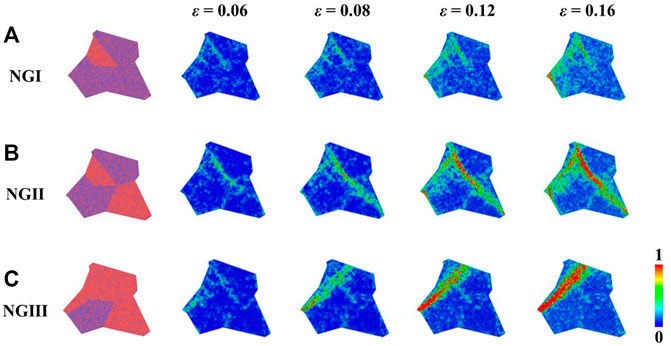
FIGURE 7. (A–C) Deformation snapshots of the selected grains capturing the atomic deformation processes for NGI, NGII, and NGIII, respectively. The colors indicate the atomic shear strain.
Figure 8A shows the fraction of atoms with
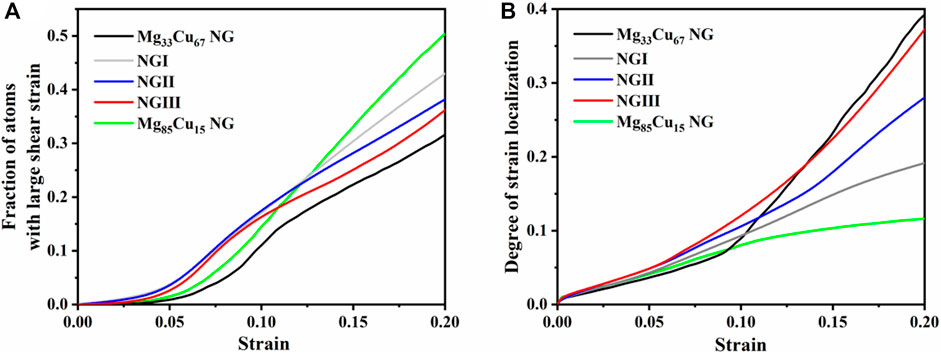
FIGURE 8. (A) The fraction of atoms with large
In summary, atomistic simulations are performed on the single-phase NGs and dual-phase NGs, aiming at the effects of grain size and heterogeneous composition on the mechanical properties. Compared to MGs, single-phase NGs show decreased strength but improved plasticity. The failure mode switches from localized shear banding to homogeneous plastic deformation with decreasing grain size. The existence of GGIs is the main reason for the strength reduction and the plasticity enhancement. For dual-phase NGs, by adding the appropriate content of the softer second phase, the plasticity is improved. Another key finding is that for dual-phase NGs with the content ratio of soft to hard phase larger than 1.0, the plasticity is deteriorated, which is quite different from the improvement in plasticity reported in the traditional nanostructured metals/alloys. The physical origin of this conflict is attributed to the increased free volume or voids at the softer GGIs accelerate the SB formation. The present work provides an in-depth understanding of the mechanical properties and deformation mechanism of dual-phase NGs with heterogeneous chemical compositions.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
YC ran the simulations, performed the analysis, and wrote the first draft of the manuscript; JD and ZDS supervised the work and reviewed and edited the manuscript.
The authors would like to acknowledge financial support from the National Natural Science Foundation of China (NSFC) through Grant Nos. 11790293 and 11972278. Z-DS is also grateful for the support from the Science and Technology Developing Project of Shaanxi (No. 2019JC-03). JD acknowledges support from National Natural Science Foundation of China (12004294), National Youth Talents Program and the HPC platform of Xian Jiaotong University.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Adibi, S., Sha, Z.-D., Branicio, P. S., Joshi, S. P., Liu, Z.-S., and Zhang, Y.-W. (2013). A Transition from Localized Shear Banding to Homogeneous Superplastic Flow in Nanoglass. Appl. Phys. Lett. 103, 211905. doi:10.1063/1.4833018
Adjaoud, O., and Albe, K. (2018). Microstructure Formation of Metallic Nanoglasses: Insights from Molecular Dynamics Simulations. Acta Mater. 145, 322–330. doi:10.1016/j.actamat.2017.12.014
Albe, K., Ritter, Y., and Şopu, D. (2013). Enhancing the Plasticity of Metallic Glasses: Shear Band Formation, Nanocomposites and Nanoglasses Investigated by Molecular Dynamics Simulations. Mech. Mater. 67, 94–103. doi:10.1016/j.mechmat.2013.06.004
Ashby, M., and Greer, A. (2006). Metallic Glasses as Structural Materials. Scr. Mater. 54, 321–326. doi:10.1016/j.scriptamat.2005.09.051
Boudreaux, D. S., and Frost, H. J. (1981). Short-range Order in Theoretical Models of Binary Metallic Glass Alloys. Phys. Rev. B 23, 1506–1516. doi:10.1103/PhysRevB.23.1506
Brink, T., and Albe, K. (2018). From Metallic Glasses to Nanocrystals: Molecular Dynamics Simulations on the Crossover from Glass-like to Grain-Boundary-Mediated Deformation Behaviour. Acta Mater. 156, 205–214. doi:10.1016/j.actamat.2018.06.036
Cao, A. J., Cheng, Y. Q., and Ma, E. (2009). Structural Processes that Initiate Shear Localization in Metallic Glass. Acta Mater. 57, 5146–5155. doi:10.1016/j.actamat.2009.07.016
Cao, A., and Wei, Y. (2007). Atomistic Simulations of Crack Nucleation and Intergranular Fracture in Bulk Nanocrystalline Nickel. Phys. Rev. B 76, 024113. doi:10.1103/PhysRevB.76.024113
Chen, C. Q., Pei, Y. T., Kuzmin, O., Zhang, Z. F., Ma, E., and De Hosson, J. T. M. (2011). Intrinsic Size Effects in the Mechanical Response of Taper-free Nanopillars of Metallic Glass. Phys. Rev. B 83, 180201. doi:10.1103/PhysRevB.83.180201
Chen, S. S., and Todd, I. (2015). Enhanced Plasticity in the Zr-Cu-Ni-Al-Nb Alloy System by In-Situ Formation of Two Glassy Phases. J. Alloys Compd. 646, 973–977. doi:10.1016/j.jallcom.2015.05.140
Cheng, Y. Q., Cao, A. J., and Ma, E. (2009b). Correlation between the Elastic Modulus and the Intrinsic Plastic Behavior of Metallic Glasses: The Roles of Atomic Configuration and Alloy Composition. Acta Mater. 57, 3253–3267. doi:10.1016/j.actamat.2009.03.027
Cheng, Y. Q., Cao, A. J., Sheng, H. W., and Ma, E. (2008). Local Order Influences Initiation of Plastic Flow in Metallic Glass: Effects of Alloy Composition and Sample Cooling History. Acta Mater. 56, 5263–5275. doi:10.1016/j.actamat.2008.07.011
Cheng, Y. Q., Han, Z., Li, Y., and Ma, E. (2009a). Cold versus Hot Shear Banding in Bulk Metallic Glass. Phys. Rev. B 80, 134115. doi:10.1103/PhysRevB.80.134115
Cyrot-Lackmann, F. (1980). Elastic Properties of a Metallic Glass Relative to the Crystal. Phys. Rev. B 22, 2744–2748. doi:10.1103/PhysRevB.22.2744
Ding, J., Cheng, Y.-Q., Sheng, H., and Ma, E. (2012). Short-range Structural Signature of Excess Specific Heat and Fragility of Metallic-Glass-Forming Supercooled Liquids. Phys. Rev. B 85, 060201. doi:10.1103/PhysRevB.85.060201
Fang, J. X., Vainio, U., Puff, W., Würschum, R., Wang, X. L., Wang, D., et al. (2012). Atomic Structure and Structural Stability of Sc75Fe25 Nanoglasses. Nano Lett. 12, 458–463. doi:10.1021/nl2038216
Gleiter, H. (2008). Our Thoughts Are Ours, Their Ends None of Our Own: Are There Ways to Synthesize Materials beyond the Limitations of Today? Acta Mater. 56, 5875–5893. doi:10.1016/j.actamat.2008.08.028
Greer, A. L., Cheng, Y. Q., and Ma, E. (2013). Shear Bands in Metallic Glasses. Mater. Sci. Eng. R Rep. 74, 71–132. doi:10.1016/j.mser.2013.04.001
Hirel, P. (2015). Atomsk: A Tool for Manipulating and Converting Atomic Data Files. Comput. Phys. Commun. 197, 212–219. doi:10.1016/j.cpc.2015.07.012
Hofmann, D. C., Suh, J.-Y., Wiest, A., Duan, G., Lind, M.-L., Demetriou, M. D., et al. (2008). Designing Metallic Glass Matrix Composites with High Toughness and Tensile Ductility. Nature 451, 1085–1089. doi:10.1038/nature06598
Ivanisenko, Y., Kübel, C., Nandam, S. H., Wang, C., Mu, X., Adjaoud, O., et al. (2018). Structure and Properties of Nanoglasses. Adv. Eng. Mat. 20, 1800404. doi:10.1002/adem.201800404
Jian, W. R., Wang, L., Li, B., Yao, X. H., and Luo, S. N. (2016). Improved Ductility of Cu64Zr36metallic glass/Cu Nanocomposites via Phase and Grain Boundaries. Nanotechnology 27, 175701. doi:10.1088/0957-4484/27/17/175701
Jian, W. R., Wang, L., Yao, X. H., and Luo, S. N. (2018a). Balancing Strength, Hardness and Ductility of Cu64Zr36 Nanoglasses via Embedded Nanocrystals. Nanotechnology 29, 025701. doi:10.1088/1361-6528/aa994f
Jian, W. R., Wang, L., Yao, X. H., and Luo, S. N. (2018b). Tensile and Nanoindentation Deformation of Amorphous/crystalline Nanolaminates: Effects of Layer Thickness and Interface Type. Comput. Mater. Sci. 154, 225–233. doi:10.1016/j.commatsci.2018.07.054
Kim, D. H., Kim, W. T., Park, E. S., Mattern, N., and Eckert, J. (2013). Phase Separation in Metallic Glasses. Prog. Mater. Sci. 58, 1103–1172. doi:10.1016/j.pmatsci.2013.04.002
Klement, W., Willens, R. H., and Duwez, P. (1960). Non-crystalline Structure in Solidified Gold-Silicon Alloys. Nature 187, 869–870. doi:10.1038/187869b0
Kuan, S. Y., Chou, H. S., Liu, M. C., Du, X. H., and Huang, J. C. (2010). Micromechanical Response for the Amorphous/amorphous Nanolaminates. Intermetallics 18, 2453–2457. doi:10.1016/j.intermet.2010.09.001
Li, J., Lu, W., Chen, S., and Liu, C. (2020). Revealing Extra Strengthening and Strain Hardening in Heterogeneous Two-phase Nanostructures. Int. J. Plasticity 126, 102626. doi:10.1016/j.ijplas.2019.11.005
Liu, A. C. Y., Paganin, D. M., Bourgeois, L., Nakashima, P. N. H., Ott, R. T., and Kramer, M. J. (2011). Quantitative Microscopic Measurement of Void Distribution in Shear Bands in Zr66.7Cu33.3metallic Glass. Phys. Rev. B 84, 094201. doi:10.1103/PhysRevB.84.094201
Liu, W.-H., Sun, B. A., Gleiter, H., Lan, S., Tong, Y., Wang, X.-L., et al. (2018). Nanoscale Structural Evolution and Anomalous Mechanical Response of Nanoglasses by Cryogenic Thermal Cycling. ₹ Lett. 18, 4188–4194. doi:10.1021/acs.nanolett.8b01007
Nandam, S. H., Ivanisenko, Y., Schwaiger, R., Śniadecki, Z., Mu, X., Wang, D., et al. (2017). Cu-Zr Nanoglasses: Atomic Structure, Thermal Stability and Indentation Properties. Acta Mater. 136, 181–189. doi:10.1016/j.actamat.2017.07.001
Nosé, S. (1984). A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 52, 255–268. doi:10.1080/00268978400101201
Pan, J., Liu, L., and Chan, K. C. (2009). Enhanced Plasticity by Phase Separation in CuZrAl Bulk Metallic Glass with Micro-addition of Fe. Scr. Mater. 60, 822–825. doi:10.1016/j.scriptamat.2009.01.032
Parrinello, M., and Rahman, A. (1982). Strain Fluctuations and Elastic Constants. J. Chem. Phys. 76, 2662–2666. doi:10.1063/1.443248
Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039
Ritter, Y., Şopu, D., Gleiter, H., and Albe, K. (2011). Structure, Stability and Mechanical Properties of Internal Interfaces in Cu64Zr36 Nanoglasses Studied by MD Simulations. Acta Mater. 59, 6588–6593. doi:10.1016/j.actamat.2011.07.013
Sha, Z.-D., Branicio, P. S., Lee, H. P., and Tay, T. E. (2017). Strong and Ductile Nanolaminate Composites Combining Metallic Glasses and Nanoglasses. Int. J. Plasticity 90, 231–241. doi:10.1016/j.ijplas.2017.01.010
Sha, Z. D., Branicio, P. S., Pei, Q. X., Liu, Z. S., Lee, H. P., Tay, T. E., et al. (2015). Strong and Superplastic Nanoglass. Nanoscale 7, 17404–17409. doi:10.1039/C5NR04740D
Sha, Z. D., He, L. C., Pei, Q. X., Pan, H., Liu, Z. S., Zhang, Y. W., et al. (2014). On the Notch Sensitivity of CuZr Nanoglass. J. Appl. Phys. 115, 163507. doi:10.1063/1.4873238
Shan, Z. W., Li, J., Cheng, Y. Q., Minor, A. M., Syed Asif, S. A., Warren, O. L., et al. (2008). Plastic Flow and Failure Resistance of Metallic Glass: Insight Fromin Situcompression of Nanopillars. Phys. Rev. B 77, 155419. doi:10.1103/PhysRevB.77.155419
Shimizu, F., Ogata, S., and Li, J. (2007). Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mat. Trans. 48, 2923–2927. doi:10.2320/matertrans.MJ200769
Şopu, D., and Albe, K. (2015). Influence of Grain Size and Composition, Topology and Excess Free Volume on the Deformation Behavior of Cu-Zr Nanoglasses. Beilstein J. Nanotechnol. 6, 537–545. doi:10.3762/bjnano.6.56
Şopu, D., Albe, K., Ritter, Y., and Gleiter, H. (2009). From Nanoglasses to Bulk Massive Glasses. Appl. Phys. Lett. 94, 191911. doi:10.1063/1.3130209
Şopu, D., Ritter, Y., Gleiter, H., and Albe, K. (2011). Deformation Behavior of Bulk and Nanostructured Metallic Glasses Studied via Molecular Dynamics Simulations. Phys. Rev. B 83, 100202. doi:10.1103/PhysRevB.83.100202
Stukowski, A. (2009). Visualization and Analysis of Atomistic Simulation Data with OVITO-The Open Visualization Tool. Model. Simul. Mat. Sci. Eng. 18, 015012. doi:10.1088/0965-0393/18/1/015012
Sun, M., Rauf, A., Zhang, Y., Sha, G., Peng, G., Yu, Z., et al. (2018). Enhanced Inter-diffusion of Immiscible Elements Fe/Cu at the Interface of FeZr/CuZr Amorphous Multilayers. Mater. Res. Lett. 6, 55–60. doi:10.1080/21663831.2017.1389773
Wang, X., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2016). Sample Size Effects on Strength and Deformation Mechanism of Sc75Fe25 Nanoglass and Metallic Glass. Scr. Mater. 116, 95–99. doi:10.1016/j.scriptamat.2016.01.036
Wang, X. L., Jiang, F., Hahn, H., Li, J., Gleiter, H., Sun, J., et al. (2015). Plasticity of a Scandium-Based Nanoglass. Scr. Mater. 98, 40–43. doi:10.1016/j.scriptamat.2014.11.010
Wu, G., Zhang, J., Liu, C., Wang, Q., and Lu, J. (2020). Ductility of an Ultrastrong Glass-Crystal Nano-dual-phase Alloy in Sub-micron. Scr. Mater. 183, 17–21. doi:10.1016/j.scriptamat.2020.03.002
Yao, L., and Jin, Z.-H. (2015). Stagnation Accommodated Global Plasticity in Nanoglass Composites. Scr. Mater. 106, 46–51. doi:10.1016/j.scriptamat.2015.05.002
Zhang, B., Wang, R. J., Zhao, D. Q., Pan, M. X., and Wang, W. H. (2004). Properties ofCe-Based Bulk Metallic Glass-Forming Alloys. Phys. Rev. B 70, 224208. doi:10.1103/PhysRevB.70.224208
Keywords: nanoglass, glass-glass interface, heterogeous nanocomposite, mechanical property, molecular dynamics
Citation: Chen Y, Ding J and Sha Z-D (2022) Grain Size and Heterophase Effects on Mechanical Properties of Mg-Cu Nanoglasses. Front. Mater. 9:908952. doi: 10.3389/fmats.2022.908952
Received: 31 March 2022; Accepted: 24 May 2022;
Published: 14 June 2022.
Edited by:
Shijun Zhao, City University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Luo Sheng-Nian, Southwest Jiaotong University, ChinaCopyright © 2022 Chen, Ding and Sha. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jun Ding, ZGluZ3NuQHhqdHUuZWR1LmNu; Zhen-Dong Sha, emhlbmRvbmdzaGFAbWFpbC54anR1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.