Nonlinear Instability Behavior and Buckling of Shallow Arches Under Gradient Thermo-Mechanical Loads

This paper investigates the nonlinear behavior and buckling of shallow arches under gradient thermal and mechanical loading. The gradient temperature varies continuously along the thickness of the cross section of the arch but uniformly distributes over the entire length of the arch. The principle of virtual work and mid-plane plane formulations are employed to derive analytical solutions for the structural responses, internal force and critical buckling loads of the arch. Subsequently, the phenomenon of the buckling mode switching are also identified and discussed. It is found that the fixed arch under gradient thermo-mechanical loading can buckle in a symmetric instability mode or an anti-symmetric instability mode, namely limit point buckling or bifurcation buckling, which depend on its geometric parameter and the gradient temperature. The effects of the gradient temperature change on the radial displacement, axial displacement, axial compressive force and bending moment as well as critical buckling loads of the arch are investigated through parametric studies comprehensively.

Introduction

Arches have been used extensively in civil and ocean engineering load-bearing structures. The stability of arch structures has attracted considerable attention from both research and engineering communities, and numerous studies on the nonlinear instability behavior of arches can be found in the open literature (Pi and Bradford, 2004a; Pi and Bradford, 2004b; Pi et al., 2011; Liu et al., 2018a; Liu et al., 2018b; He et al., 2020; Liu et al., 2020). In practical engineering, a steel arch may be subjected to thermo-mechanical load that leads to instability of the arch. It is well known that the material property of the steel is dependent on the temperature (Standard Australia, 1998; Heidarpour et al., 2010a; Maruschak et al., 2012; Moghaddasie and Stanciulescu, 2013; Yasniy et al., 2013; Heidarpour et al., 2014; Wang et al., 2020). When the applied temperature is uniformly distributed over the whole arch, the variations of the material property of steels caused by the temperature is uniform, and the steel arch is still isotropic structure. So the classical analysis method can be used to determine the structural behavior of the arch. A considerable amount of literature has been published on the linear or nonlinear behavior of arches subjected to uniform thermal load. Bradford et al. (Bradford, 2006a; Bradford, 2006b; Bradford, 2010) studied nonlinear instability behavior of a pinned arch under uniform thermal loading only. They found that the axial force in the arch produced by temperature is uniform along the arch axis. Pi et al. (Pi and Bradford, 2010a; Pi and Bradford, 2010b; Pi and Bradford, 2014) conducted a series of studies regarding the nonlinear in-plane thermo-elastic behavior of the crown-pinned, pin-ended and fixed steel arch. Heidarpour et al. (2010b) proposed a generic model to investigate the nonlinear elastic behavior of steel-concrete arches subjected to sustained loading at elevated temperatures. Lu et al. (2019) derived the exact solutions for the out-of-plane buckling load of the steel arch in a thermal environment incorporating shear deformations. The dynamic buckling of an arch subjected to transient thermal loading is studied by Keibolahi et al. (2018), from which they verified that the dynamic snap through buckling of the arch may occur when under rapid surface heating. Virgin et al. (2014) considered the influence of temperature and proved that temperature had a great influence on the extreme point of instability of arch. Malekzadeh et al. (2009) investigated the in-plane free vibrations of FGM arches under thermal environment by adopting two-dimensional elasticity theory and first-order shear deformation theory (FSDT). Yang and Huang (Yang et al., 2019a; Yang et al., 2019b; Yang et al., 2020a; Yang et al., 2020b; Yang et al., 2020c). presented an analytical solution of nonlinear in-plane buckling for a novel graphene reinforced composite arch/beam under mechanical/thermal loading, and determined the special parameter switching the buckling mode of the arch.

However, when the applied temperature is gradient distributed along one or two direction of the arch, the variations of the material property of steels caused by the temperature is non-uniform, and so the arch becomes anisotropic structure. The existence of anisotropy and involvement of geometric nonlinearity makes the problem of structural stability of the steel arch more complicated. So far, there has been very limit research investigating the nonlinear instability behavior of arches under gradient thermo-mechanical loadings. Cai et al. (2012) studied the elastic buckling of parabolic arches with rotational constraint under a vertical uniform load and uniform/gradient temperature changes. Pi et al. (Pi and Bradford, 2010c) developed a research on the nonlinear thermo-elastic buckling of pinned arches under temperature gradient field, and they also studied the out-of-plane buckling of fixed and rotationally restrained slender beam under linear gradient thermal action (Pi and Bradford, 2008; Pi and Bradford, 2010a; Pi and Bradford, 2015). Bateni and Eslami. (2014) discussed the effects of temperature gradient on the buckling of FGM arches and concluded that the temperature gradient enhances the buckling resistance of arches under a lateral mechanical load. Similar researches were also observed from Babaei’s report for the Thermo-mechanical nonlinear in-plane analysis of fix-ended FMG shallow arches (Babaei et al., 2018a; Babaei et al., 2018b). Song et al. (2019) carried out a linear analysis on the instability of steel arch under linear temperature gradient field and uniformly distributed radial load according to the effective centroid method and the principle of virtual work. To the best of authors knowledge, no work has been done on the nonlinear behavior and buckling of steel arches under gradient thermal and uniform radial loading.

Therefore, an analytical study is carried out in this paper to investigate the structural responses and specifically the buckling behavior of arches under gradient thermo-mechanical loadings. The principle of virtual work and mid-plane plane formulations are employed to derive the nonlinear equilibrium paths and critical buckling loads. The temperature-dependent geometric parameters determining the buckling modes of the arch are also obtained. The effects of gradient on the structural response, such as radial and axial displacement, internal force and critical buckling loads are discussed.

Nonlinear Equilibrium

As shown in Figure 1, a fixed arch with center angle $2\Theta$, arc length S and radius R is subjected to gradient thermal load and uniform radial load, where v and w are the radial and axial displacements in the mid-plane of the arch, respectively. By introducing the linear gradient temperature field, a temperature field T(z) varies continuously along the thickness of the cross section of the arch but uniform over the entire length of the arch.

FIGURE 1

FIGURE 1. An arch under gradient temperature and uniform radial load.

Before the structural analysis, the following assumptions are adopted as: 1) deformations of the arch satisfy the Euler-Bernoulli hypothesis; 2) expansions of the cross section are ignored; 3) the states of temperature is treated as time-independent; 4) the coefficient of thermal expansion $\alpha$ is independent of the temperature.

According to classic shallow arch theory, the nonlinear strain-displacement relation of the arch is given as

$\epsilon ={\tilde{w}}^{\prime }-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}-z\frac{{\tilde{v}}^{″}}{R}(1)$

where $({)}^{\prime }\equiv d\left(\right)/d\theta$, $\tilde{v}$ = v/R and $\tilde{w}$ = w/R.

Therefore, the nonlinear stress of the arch under gradient temperature T(z) is

$\sigma =E\left(z\right)\left\{\epsilon -\alpha \left[T\left(z\right)-20\right]\right\}(2)$

where the reference temperature is 20°C, the linear gradient temperature T(z) is formulated as

$T\left(z\right)=\frac{T_1+T_2}{2}+z\frac{\mathrm{\Delta }T}{h}\mathrm{with}\mathrm{\Delta }T=T_2-T_1(3)$

where T₁ and T₂ are the temperature at the top and bottom of cross section. E(z) is the temperature-dependent elasticity modulus of steel according to the Australian Code AS4100 (Heidarpour et al., 2010a) which is given as

$E\left(z\right)=\{\begin{array}{l}{E}_{20}+\frac{E_{20}T\left(z\right)}{2000\ln \left[T\left(z\right)/1100\right]}\text{for}0{}^{\text{o}}\text{C}<\text{Δ}T\le 600{}^{\text{o}}\text{C}\\ E_{20}\frac{690\left[1-T\left(z\right)/1100\right]}{T\left(z\right)-53.5}\text{for}600{}^{\text{o}}\text{C}<\text{Δ}T\le 1000{}^{\text{o}}\text{C}\end{array}(4)$

where E₂₀ is the elastic modulus of steel at 20°C.

According to the principle of virtual work and mid-plane plane formulations, the nonlinear equilibrium equation of the arch is stated as

$\delta K={\displaystyle {\int }_{-\mathrm{\Theta }}^{\mathrm{\Theta }}\left[-NR\left(\delta {\tilde{w}}^{\prime }-\delta \tilde{v}+{\tilde{v}}^{\prime }\delta {\tilde{v}}^{\prime }\right)-M\delta {\tilde{v}}^{″}-q{R}^2\delta \tilde{v}\right]}d\theta =0(5)$

in which, axial compressive force N and bending moment M are formulated as

$N=-A_{11}\left[{\tilde{w}}^{\prime }-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}-\alpha \left(\frac{T_1+T_2}{2}-20\right)\right]+B_{11}\left(\frac{{\tilde{v}}^{″}}{R}+\frac{\alpha \text{Δ}T}{h}\right)(6)$

$M=B_{11}\left[{\tilde{w}}^{\prime }-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}-\alpha \left(\frac{T_1+T_2}{2}-20\right)\right]-D_{11}\left(\frac{{\tilde{v}}^{″}}{R}+\frac{\alpha \text{Δ}T}{h}\right)(7)$

where A₁₁, B₁₁ and D₁₁ are the stiffness components defined as

$\left\{A_{11}{B}_{11}{D}_{11}\right\}=b{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}E\left(z\right)\left\{1z{z}^2\right\}\text{dz}}(8)$

By substituting Eq. 6 into Eq. 7 leads to a new expression of Eq. 7 as

$M=-\left(\frac{{\tilde{v}}^{″}}{R}+\frac{\alpha \mathrm{\Delta }T}{h}\right)\kappa -\frac{B_{11}}{A_{11}}N\mathrm{with}\kappa =D_{11}-\frac{B_{11}^2}{A_{11}}(9)$

Integrating Eq. 5 by parts obtains the equilibrium equation as

${\left(NR\right)}^{\prime }=0(10)$

$NR+{\left(NR{\tilde{v}}^{\prime }\right)}^{\prime }-M^{″}-q{R}^2=0(11)$

and also obtains the boundary conditions of the fixed arch as $\tilde{v}=\tilde{w}={\tilde{v}}^{\prime }=0$ when $\theta =\pm \Theta$.

By substituting Eqs 9, 10 into Eq. 11, the equilibrium equation of arches is rewritten as

$\frac{{\tilde{v}}^{iv}}{{\mu }^2}+{\tilde{v}}^{″}=Q\mathrm{with}Q=\frac{qR-N}{N}(12)$

where μ is defined as

${\mu }^2=\frac{N{R}^2}{\kappa }(13)$

By solving Eq. 12 and considering the fixed-end boundary conditions, obtains

$\tilde{v}=\frac{Q}{{\mu }^2}\left[\frac{{\mu }^2{\theta }^2-{\beta }^2}{2}+\frac{\beta \left(\cos \mu \theta -\cos \beta \right)}{\sin \beta }\right]\mathrm{with}\beta =\mu \mathrm{\Theta }(14)$

By substituting Eq. 14 into Eq. 10, the axial displacement $\tilde{w}$ is solved as

$\begin{array}{l}\tilde{w}=\frac{Q\theta \left(1-Q\right)\left({\theta }^2-{\mathrm{\Theta }}^2\right)}{6}+\frac{Q{B}_{11}}{A_{11}R}\left(\theta -\frac{\text{Θ}\sin \mu \theta }{\sin \beta }\right)+\frac{Q\left(1+Q\right)}{{\mu }^2}\left(\frac{\text{Θ}\sin \mu \theta }{\sin \beta }-\theta \right)\\ +\frac{Q^2{\text{Θ}}^2\sin \mu \theta \cos \mu \theta }{4\mu {\sin }^2\beta }+\frac{Q^2\text{Θ}\left(3\cos \beta -4\cos \mu \theta \right)\theta }{4\mu \sin \beta }\end{array}(15)$

Substituting Eqs 14, 15 into Eqss 6, 7, the exact expression of the axial compressive force N and bending moment M of the arch are determined as

$N=-\frac{A_{11}{Q}^2{\text{Θ}}^2}{4{\sin }^2\beta }-\frac{A_{11}Q\left(2+Q\right){\text{Θ}}^2}{6}+\frac{A_{11}Q\left(1+Q\right)}{{\mu }^2}-\frac{A_{11}Q\left(3P+4\right)\mathrm{\Theta }}{4\mu \tan \beta }+\alpha A_{11}\left(\frac{T_1+T_2}{2}-20\right)+\frac{B_{11}\alpha \mathrm{\Delta }T}{h}(16)$

$\begin{array}{l}M=\frac{B_{11}{Q}^2{\text{Θ}}^2}{4{\sin }^2\beta }+\frac{B_{11}Q\left(2+Q\right){\text{Θ}}^2}{6}+\frac{B_{11}^{2}Q}{A_{11}R}\left(1-\frac{\beta \cos \mu \theta }{\sin \beta }\right)+\frac{B_{11}Q\left(3P+4\right)\text{Θ}}{4\mu \tan \beta }\\ -\frac{B_{11}Q\left(1+Q\right)}{{\mu }^2}+\frac{D_{11}Q}{R}\left(\frac{\beta \cos \mu \theta }{\sin \beta }-1\right)-\alpha B_{11}\left(\frac{T_1+T_2}{2}-20\right)-\frac{D_{11}\alpha \text{Δ}T}{h}\end{array}(17)$

Eqs 10, 16 shows that the axial compressive force of the arch is constant through the arch when the gradient temperature is given.

By substituting Eq. 14 into Eq. 6 and integrating it over the entire length of the arch, the nonlinear equilibrium equation is obtained as

$A_1{Q}^2+B_{1}Q+C_1=0(18)$

where

$A_1=\frac{5}{12{\sin }^2\beta }-\frac{{\cos }^2\beta }{6{\sin }^2\beta }+\frac{3\cos \beta }{4\beta \sin \beta }-\frac{1}{{\beta }^2}(19)$

$B_1=\frac{1}{3}+\frac{1}{\beta \tan \beta }-\frac{1}{{\beta }^2}(20)$

$C_1=\frac{r_{11}^2{\beta }^2}{{\lambda }^2}-\frac{\alpha S^2}{4{\lambda }^2{h}^2}\left(\frac{T_1+T_2}{2}-20+\frac{B_{11}\text{Δ}T}{A_{11}h}\right)(21)$

where $r_{11}=\sqrt{\kappa /A_{11}}/h$, $\lambda$ is a geometrical parameter defined as

$\lambda =\frac{S}{h}\frac{\text{Θ}}{2}(22)$

By combining Eqs 14, 18, the solutions of the nonlinear equilibrium conditions of the fixed arch under gradient thermo-mechanical loadings.

Buckling Analysis

Typical symmetric limit point buckling may occur when the arch is subjected to a gradient thermal and uniform radial load. When this happens, the arch reaches a limit point load and buckle in a limit point instability mode. The limit point loads are located at the local extrema of the nonlinear equilibrium path defined in Eq. 18, and the equation of equilibrium between limit point loads and axial force parameter $\beta$ can be determined by using partial derivative method as

$A_2{Q}^2+B_{2}Q+C_2=0(23)$

where

$A_2=\frac{\beta \partial A_1}{\partial \beta }-4A_1,B_2=-4A_1+\frac{\beta \partial B_1}{\partial \beta }-2B_1,C_2=-2B_1+\frac{\beta \partial C_1}{\partial \beta }(24)$

Solving Eqs 18, 23 simultaneously, the critical axial force parameter $\beta$ and the limit point buckling load Q can be obtained, respectively.

Beyond symmetric limit point buckling, the anti-symmetric bifurcation buckling may also occur to the arch under gradient thermal and uniform radial load. The differential equation for bifurcation equilibrium of the arch is determined by the author previous research as (Heidarpour et al., 2010b)

$\frac{{\tilde{v}}_b^{iv}}{{\mu }^2}+{{\tilde{v}}^{″}}_b=0(25)$

where ${\tilde{v}}_b$ is the bifurcation buckling displacement. Then, a characteristic equation can be determined by solving Eq. 25 incorporating the fixed-ended boundary conditions of the arch as

$\left(\sin \beta -\beta \cos \beta \right)\sin \beta =0(26)$

When $\sin \beta -\beta \cos \beta =0$ in Eq. 26, leads to a critical axial force ${\beta }_b$ parameter for bifurcation buckling as

${\beta }_b={\mu }_b\text{Θ}=1.4303\pi (27)$

Substituting ${\beta }_b$ into Eq. 13 leads to the axial compressive force N_b of the arch as

$N_b=\frac{{\left(1.4303\pi \right)}^2\kappa }{{\left(S/2\right)}^2}(28)$

and substituting ${\beta }_b$ into Eq. 18 leads to the nonlinear equilibrium equation for bifurcation buckling as

$0.416664Q^2+0.333331Q+\frac{{\left(1.4303\pi \right)}^2{r}_{11}^2}{{\lambda }^2}-\frac{\alpha S^2}{4{\lambda }^2{h}^2}(\frac{T_1+T_2}{2}-20+\frac{B_{11}\text{Δ}T}{A_{11}h})=0(29)$

which is a mono basic quadratic equation, and the existence of real solutions for Eq. 29 requires that

${0.333331}^2-4\times 0.416664\times \left[\frac{{\left(1.4303\pi \right)}^2{r}_{11}^2}{{\lambda }^2}-\frac{\alpha S^2}{4{\lambda }^2{h}^2}\left(\frac{T_1+T_2}{2}-20+\frac{B_{11}\text{Δ}T}{A_{11}h}\right)\right]\ge 0(30)$

from which a critical parameter ${\lambda }_{b1}$ defined as the minimum geometric parameter triggering bifurcation buckling of the arch is solved as

${\lambda }_{b1}=\sqrt{302.8644722r_{11}^2-\frac{3\text{.}750026\alpha S^2}{h^2}\left(\frac{T_1+T_2}{2}-20+\frac{B_{11}\text{Δ}T}{A_{11}h}\right)}(31)$

When $\sin \beta =0$ in Eq. 26, leads to a critical axial force parameter ${\beta }_s$ for lowest buckling of the arch as

${\beta }_s={\mu }_s\text{Θ}=\pi (32)$

Substituting ${\beta }_s$ into Eq. 18 and solving the lowest buckling load as

$qR=\frac{{\pi }^2\kappa }{{\left(S/2\right)}^2}(33)$

When the axial force parameter $\beta$ approaches to critical axial force parameter ${\beta }_s$ and leads to a real solutions for the lowest buckling load given by Eq. 33, the condition need to be satisfied as

$\underset{\beta \to {\beta }_s}{\lim }\left(B_1^2-4A_1{C}_1\right)=\frac{4{\pi }^4{r}_{11}^2}{{\lambda }^2}-\frac{\alpha {\pi }^2{S}^2}{{\lambda }^2{h}^2}\left(\frac{T_1+T_2}{2}-20+\frac{B_{11}\text{Δ}T}{A_{11}h}\right)-4\ge 0(34)$

Similarly, a critical parameter ${\lambda }_s$ triggering lowest buckling of the arch can be solved from Eq. 34 as

${\lambda }_s=\sqrt{r_{11}^2{\pi }^4-\frac{\alpha S^2{\pi }^2}{4h^2}\left(\frac{T_1+T_2}{2}-20+\frac{B_{11}\text{Δ}T}{A_{11}h}\right)}(35)$

When the arch having $\lambda <{\lambda }_s$ under a given gradient temperature, there is no buckling for the arch instead of nonlinear bending.

Parametric Study

Comparisons

The finite element (FE) results are presented in this section to validate the proposed method. For conveniently and accurately, the FE analyses are performed by ANSYS 14.0 (Pi and Bradford, 2015) with using SHELL181 elements. In the ANSYS modeling, the dimension of cross section is b× h = 0.03 m × 0.025 m, and the cross section is subdivided into multiple layers in the thickness direction for simulating the material variation where the material properties of each layers are determined by Eq. 4. According to the convergence study, the difference between the results with 10 layers and 1,000 layers is less than 0.3%, which means that 10 layers adopted in the finite element model is sufficiently accurate to model a beam with continuous gradient varying material properties. Thus, 10 layers are adopted in the following FE analyses.

The result verification of the radial displacement at arch crown (v_c/f, $\theta =0$) and the axial displacement at quarter point (w_q/f, $\theta =0.5\Theta$) are shown in Figure 2A, where the applied radial load is qR = 0.25N_b20. Note that N_b20 is the value of N_b at 20°C given by Eq. 28, and f is the rise of the arch. Moreover, the verification of the load-displacement curve of the arch is presented in Figure 2B. From the comparisons, the proposed analytical result agrees well with the FE results.

FIGURE 2

FIGURE 2. Results validation of (A) structural displacements, (B) load-displacement curve.

Nonlinear Structural Responses and Buckling Loads

Figure 3 displays the variations of the structural responses (Figures 3A,B) and internal actions (Figures 3C,D) due to the gradient temperature change $\Delta T$ without applied external load (qR = 0) along the arch axis, and the gradient temperature change $\Delta T$ shows a significant effect on the nonlinear structural behavior of the arch. It is observed from Figure 3A that the value of the radial displacement is negative, which means that the deformation of the arch under the gradient temperature change $\Delta T$ is in the upward direction. It is also observed that the radial displacements are symmetric about the crown of the arch (Figure 3A), while the axial displacements are anti-symmetric about the crown of the arch (Figure 3B). Moreover, the temperature-induced axial force N and bending moment M are presented in Figures 3C,D. It shows that the structural internal forces increase as the gradient temperature change $\Delta T$ increase, and the effects of the gradient temperature change $\Delta T$ on the structural internal actions of arches are indeed significant.

FIGURE 3

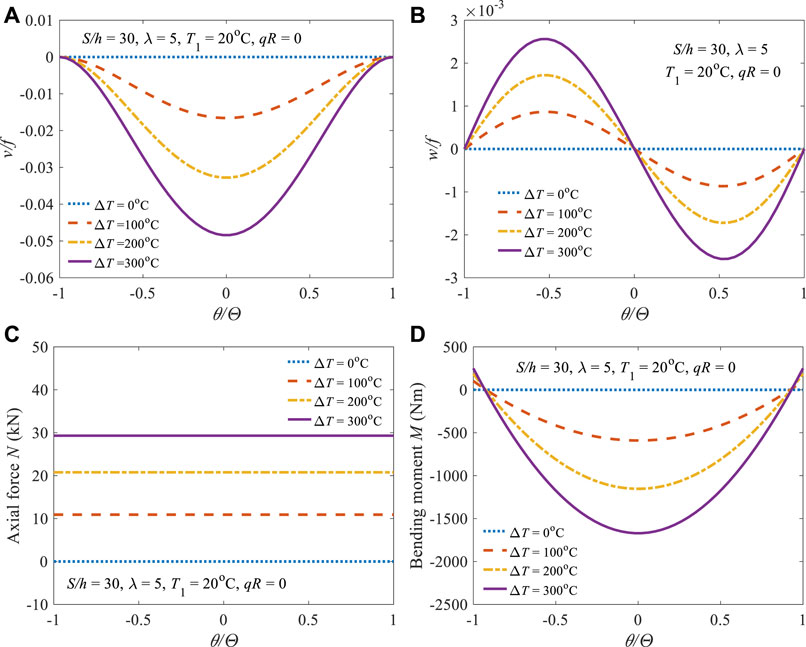
FIGURE 3. Structural responses of (A) dimensionless radial displacement, (B) dimensionless axial displacement, and internal actions of (C) axial force, (D) bending moment.

The combining effects of the gradient temperature change and uniform radial load on the dimensionless radial displacement and bending moment are shown in Figures 4A,B, respectively with qR = 0.25N_b20. From the observation, the directions of the force-induced radial displacement and bending moment are opposite to that of temperature-induced, and the increasing temperature-induced structural responses are counteracting the responses produced by the applied uniform radial load as the gradient temperature change increasing.

FIGURE 4

FIGURE 4. Variations of (A) radial displacements and (B) bending moment along the arch axis.

Figure 5 illustrates the influence of gradient temperature on the limit point buckling load (P_L) and bifurcation buckling load (P_B) of the arch. As can be seen from Figure 5 that the effects are related significantly to the geometrical parameter $\lambda$ of the arch. For the arch with $\lambda =6$, the buckling loads of the arch first increases slightly until $\Delta T=250{}^{\text{o}}\text{C}$ and then decreases. However, the buckling loads of the arch with $\lambda =13$ decreases monotonically with an increase of gradient temperature. This is consistent with the observation in Table 1, where buckling loads of arches with different geometric parameter $\lambda$ under different gradient temperature change $\Delta T$ are tabulated.

FIGURE 5

FIGURE 5. Influences of gradient temperature on buckling loads of the arch with (A) $\lambda =6$, (B) $\lambda =13$.

TABLE 1

TABLE 1. Buckling loads of arches with different geometric parameter (S/h = 30, T₁ = 20 °C).

Nonlinear Equilibrium Paths and Buckling Mode Switching

In addition to the investigation on the nonlinear structural responses and buckling loads, the nonlinear equilibrium paths and the buckling mode of the arch under gradient thermal and uniform radial load are explored in this section. Figure 6 depicts the nonlinear equilibrium paths of the arch with $\lambda =5.3$ under gradient temperature $\Delta T=0{}^{\text{o}}\text{C}$ in Figures 6A,B, and $\Delta T=600{}^{\text{o}}\text{C}$ in Figures 6C,D, respectively.

FIGURE 6

FIGURE 6. Nonlinear equilibrium paths of the arch under (A) and (B) $\Delta T=0{}^{\text{o}}\text{C}$, (C) and (D) $\Delta T=600{}^{\text{o}}\text{C}$.

Noted from Figures 6A,B, when the gradient temperature change is equal to zero, the limit point buckling occur to the arch because the bifurcation point is located behind the limit point. However, as shown in Figures 6C,D, when the temperature applied to the arch is higher than a certain value (i.e. $\Delta T=600{}^{\text{o}}\text{C}$), the bifurcation point of the arch is located before the limit point, so the bifurcation buckling of the arch occurs. Therefore, a specific gradient temperature change $\Delta T$ switching the buckling mode of the arch is found, and its value can be determined by setting the limit point load obtained from Eq. 23 to be equal to the bifurcation buckling load obtained from Eq. 29 at $\beta =1.4303\pi$, from which a critical parameter ${\lambda }_{b2}$ that is switching the buckling mode can also be solved when a gradient temperature is given.

As previously discussed, there are critical parameters ${\lambda }_{b1}$, ${\lambda }_{b2}$, and ${\lambda }_s$ that switch the buckling mode of the arch. For an arch with $\lambda >{\lambda }_{b2}$, the arch buckles in a bifurcation buckling mode; For an arch with ${\lambda }_{b1}<\lambda \le {\lambda }_{b2}$, the limit point buckling mode or the bifurcation buckling mode may occur to the arch; For an arch with ${\lambda }_s<\lambda \le {\lambda }_{b1}$, the arch buckles in a limit point buckling mode; For an arch with $\lambda <{\lambda }_s$, the arch becomes a curved beam and does not display typical buckling behavior. Noted from Eqs 31, 35, the critical parameters are quite related to the gradient temperature change $\Delta T$ and the slenderness S/h. Thus, the variations of critical parameters ${\lambda }_{b1}$, ${\lambda }_{b2}$, and ${\lambda }_s$ with the gradient temperature change $\Delta T$ is shown in Figure 7A, and with the slenderness S/h is shown in Figure 7B. It can be seen that the value of critical parameters ${\lambda }_{b1}$, ${\lambda }_{b2}$, and ${\lambda }_s$ decreases with an increase of the gradient temperature change $\Delta T$ or slenderness S/h.

FIGURE 7

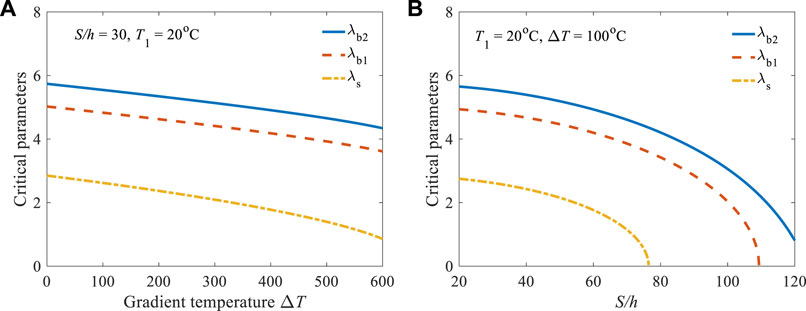
FIGURE 7. Variations of critical parameters ${\lambda }_{b1}$, ${\lambda }_{b2}$, and ${\lambda }_s$ (A) with the gradient temperature change $\Delta T$ and (B) with the slenderness S/h.

Conclusion

The nonlinear elastic behavior and buckling of shallow arch under gradient thermal and uniform radial loading has been studied in this paper. Exact solutions for the structural responses, internal force and critical buckling loads of the arch have been derived by adopting the principle of virtual work and mid-plane plane formulations. The effects of gradient temperature on the radial displacement, axial displacement, internal force and critical buckling loads have been discussed comprehensively. From the numerical discussion, the effects of the gradient temperature are quite significantly on the structural behavior of the arch. The arch deflects in its concave direction and buckles when a critical temperature gradient and external load are reached. It is also found that the arch under gradient thermal and uniform radial loadings can buckle in a limit point instability mode or a bifurcation mode. The critical gradient temperature change $\Delta T$ can be determined by setting the limit point load obtained from Eq. 23 to be equal to the bifurcation buckling load obtained from Eq. 29 at $\beta =1.4303\pi$, from which a critical parameter ${\lambda }_{b2}$ that is switching the buckling mode can also be solved when a gradient temperature is given. The value of three critical parameters ${\lambda }_{b1}$, ${\lambda }_{b2}$, and ${\lambda }_s$ decreases with an increase of the gradient temperature change $\Delta T$ or slenderness S/h.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

RR: Conceptualization, writing—review and editing, funding acquisition, Software, methodology ZY: Data curation, writing—original draft preparation JL: Software, methodology YH: Validation, supervision AL: Conceptualization, Funding acquisition, validation.

Funding

This work was financially supported by the 111 Project (Grant No. D21021), Municipal Science and Technology Planning Project of Guangzhou (Grant No. 20212200004).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This research is financially supported by the National Natural Science Foundation of China (No. 51925802, 11972123 and 51878188), Technology Planning Project of Guangzhou City (No. 201807010021), China-Australia Joint Research Centre for Resilient Material and Structures (No. 2020A050519002). The authors are grateful for these supports.

References

ANASYS, C. F. X. (2012). Introduction of CFX Ver. 14.0. Pennsylvania, US: ANASYS Inc, 36.

Google Scholar

Babaei, H., Kiani, Y., and Eslami, M. R. (2018b). Geometrically Nonlinear Analysis of Functionally Graded Shallow Curved Tubes in Thermal Environment. Thin-Walled Struct. 132, 48–57. doi:10.1016/j.tws.2018.08.008

CrossRef Full Text | Google Scholar

Babaei, H., Kiani, Y., and Eslami, M. R. (2018a). Thermomechanical Nonlinear In-Plane Analysis of Fix-Ended FGM Shallow Arches on Nonlinear Elastic Foundation Using Two-step Perturbation Technique. Int. J. Mech. Mat. Des. 15, 225–244. doi:10.1007/s10999-018-9420-y

CrossRef Full Text | Google Scholar

Bateni, M., and Eslami, M. R. (2014). “Effect of Temperature Gradient on the Mechanical Buckling Resistance of FGM Shallow Arches,” in ASME 2014 12th Biennial Conference on Engineering Systems Design and Analysis (New York, United States: American Society of Mechanical Engineers (ASME)). doi:10.1115/esda2014-20363

CrossRef Full Text | Google Scholar

Bradford, M. A. (2006). Elastic Analysis of Straight Members at Elevated Temperatures. Adv. Struct. Eng. 9, 611–618. doi:10.1260/136943306778827484

CrossRef Full Text | Google Scholar

Bradford, M. A. (2006). In-plane Nonlinear Behaviour of Circular Pinned Arches with Elastic Restraints under Thermal Loading. Int. J. Str. Stab. Dyn. 06, 163–177. doi:10.1142/s0219455406001897

CrossRef Full Text | Google Scholar

Bradford, M. A. (2010). Long-span Shallow Steel Arches Subjected to Fire Loading. Adv. Struct. Eng. 13, 501–511. doi:10.1260/1369-4332.13.3.501

CrossRef Full Text | Google Scholar

Cai, J., Xu, Y., Feng, J., and Zhang, J. (2012). In-plane Elastic Buckling of Shallow Parabolic Arches under an External Load and Temperature Changes. J. Struct. Eng. 138, 1300–1309. doi:10.1061/(asce)st.1943-541x.0000570

CrossRef Full Text | Google Scholar

He, H., Yuan, B., Chen, H., and Wei, Y. (2020). In-plane Failure Mechanism and Stability Bearing Capacity Design of Planar Plate-Tube-Connected Circular Steel Arches. Mech. Based Des. Struc., 1–16. doi:10.1080/15397734.2020.1713157

CrossRef Full Text | Google Scholar

Heidarpour, A., Abdullah, A. A., and Bradford, M. A. (2010). Non-linear Inelastic Analysis of Steel Arches at Elevated Temperatures. J. Constr. Steel Res. 66, 512–519. doi:10.1016/j.jcsr.2009.10.003

CrossRef Full Text | Google Scholar

Heidarpour, A., Cevro, S., Song, Q. Y., and Zhao, X. L. (2014). Behaviour of Stub Columns Utilising Mild-Steel Plates and VHS Tubes under Fire. J. Constr. Steel Res. 95, 220–229. doi:10.1016/j.jcsr.2013.12.007

CrossRef Full Text | Google Scholar

Heidarpour, A., Pham, T. H., and Bradford, M. A. (2010). Nonlinear Thermoelastic Analysis of Composite Steel-Concrete Arches Including Partial Interaction and Elevated Temperature Loading. Eng. Struct. 32, 3248–3257. doi:10.1016/j.engstruct.2010.06.014

CrossRef Full Text | Google Scholar

Keibolahi, A., Kiani, Y., and Eslami, M. R. (2018). Dynamic Snap-Through of Shallow Arches under Thermal Shock. Aerosp. Sci. Technol. 77, 545–554. doi:10.1016/j.ast.2018.04.003

CrossRef Full Text | Google Scholar

Liu, A., Yang, Z., Bradford, M. A., and Pi, Y. L. (2018). Nonlinear Dynamic Buckling of Fixed Shallow Arches under an Arbitrary Step Radial Point Load. J. Eng. Mech. 144, 04018012. doi:10.1061/(asce)em.1943-7889.0001425

CrossRef Full Text | Google Scholar

Liu, A., Yang, Z., Lu, H., Fu, J., and Pi, Y.-L. (2018). Experimental and Analytical Investigation on the In-Plane Dynamic Instability of Arches Owing to Parametric Resonance. J. Vib. Control 24, 4419–4432. doi:10.1177/1077546317726210

CrossRef Full Text | Google Scholar

Liu, D., Sun, J., and Lan, L. (2020). Elasticity Solutions for In-Plane Free Vibration of FG-GPLRC Circular Arches with Various End Conditions. Appl. Sci. 10, 4695. doi:10.3390/app10144695

CrossRef Full Text | Google Scholar

Lu, H., Liu, A., Pi, Y.-L., Bradford, M. A., and Fu, J. (2019). Lateral-torsional Buckling of Arches under an Arbitrary Radial Point Load in a Thermal Environment Incorporating Shear Deformations. Eng. Struct. 179, 189–203. doi:10.1016/j.engstruct.2018.10.071

CrossRef Full Text | Google Scholar

Malekzadeh, P., Atashi, M. M., and Karami, G. (2009). In-plane Free Vibration of Functionally Graded Circular Arches with Temperature-dependent Properties under Thermal Environment. J. Sound Vib. 326, 837–851. doi:10.1016/j.jsv.2009.05.016

CrossRef Full Text | Google Scholar

Malekzadeh, P. (2009). Two-dimensional In-Plane Free Vibrations of Functionally Graded Circular Arches with Temperature-dependent Properties. Compos. Struct. 91, 38–47. doi:10.1016/j.compstruct.2009.04.034

CrossRef Full Text | Google Scholar

Maruschak, P. O., Konovalenko, I. V., and Bishchak, R. T. (2012). Effect of Thermal Fatigue Cracks on Brittle-Ductile Deformation and Failure of Cbcm Roller Surface Layers. Metallurgist 56 (1-2), 30–36. doi:10.1007/s11015-012-9532-9

CrossRef Full Text | Google Scholar

Moghaddasie, B., and Stanciulescu, I. (2013). Equilibria and Stability Boundaries of Shallow Arches under Static Loading in a Thermal Environment. Int. J. Non-Linear Mech. 51, 132–144. doi:10.1016/j.ijnonlinmec.2013.01.001

CrossRef Full Text | Google Scholar

Pi, Y. L., Andrew Bradford, M., and Qu, W. (2011). Long-term Non-linear Behaviour and Buckling of Shallow Concrete-Filled Steel Tubular Arches. Int. J. Non-Linear Mech. 46, 1155–1166. doi:10.1016/j.ijnonlinmec.2011.05.003

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2014). Effects of Nonlinearity and Temperature Field on In-Plane Behaviour and Buckling of Crown-Pinned Steel Arches. Eng. Struct. 74, 1–12. doi:10.1016/j.engstruct.2014.05.006

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2004). Effects of Prebuckling Deformations on the Elastic Flexural-Torsional Buckling of Laterally Fixed Arches. Int. J. Mech. Sci. 46, 321–342. doi:10.1016/j.ijmecsci.2004.02.012

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2010). In-plane Thermoelastic Behaviour and Buckling of Pin-Ended and Fixed Circular Arches. Eng. Struct. 32, 250–260. doi:10.1016/j.engstruct.2009.09.012

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2010). Nonlinear In-Plane Elastic Buckling of Shallow Circular Arches under Uniform Radial and Thermal Loading. Int. J. Mech. Sci. 52, 75–88. doi:10.1016/j.ijmecsci.2009.10.011

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2010). Nonlinear Thermoelastic Buckling of Pin-Ended Shallow Arches under Temperature Gradient. J. Eng. Mech. 136, 960–968. doi:10.1061/(asce)em.1943-7889.0000134

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2008). Thermoelastic Lateral-Torsional Buckling of Fixed Slender Beams under Linear Temperature Gradient. Int. J. Mech. Sci. 50, 1183–1193. doi:10.1016/j.ijmecsci.2008.04.004

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2004). Experimental and Analytical Modal Analysis of Steel Arch Bridge. J. Struct. Eng. 130, 1022–1031. doi:10.1061/(ASCE)0733-9445(2004)130:7(1022)

CrossRef Full Text | Google Scholar

Pi, Y. L., and Bradford, M. A. (2015). Out-of-plane Buckling of Beams Having In-Plane Elastic Restraints under Gradient Thermal Action. J. Eng. Mech. 142, 04015080.

Google Scholar

Song, X., Lu, H., Liu, A., and Huang, Y. (2019). In-plane Instability of Fixed Arches under Linear Temperature Gradient Field and Uniformly Distributed Radial Load. Math. Probl. Eng.2019, 1–12. doi:10.1155/2019/5938030

CrossRef Full Text | Google Scholar

Standard Australia (1998). AS4100-1998 Steel Structures. Ablis.

Google Scholar

Virgin, L. N., Wiebe, R., Spottswood, S. M., and Eason, T. G. (2014). Sensitivity in the Structural Behavior of Shallow Arches. Int. J. Non-Linear Mech. 58, 212–221. doi:10.1016/j.ijnonlinmec.2013.10.003

CrossRef Full Text | Google Scholar

Wang, Q., Ji, B., Fu, Z., and Wang, H. (2020). Effect of High-Temperature Pavement Paving on Fatigue Durability of Bearing-Supported Steel Decks. Appl. Sci. 10, 7196. doi:10.3390/app10207196

CrossRef Full Text | Google Scholar

Yang, Z., Feng, C., Yang, J., Wang, Y., Lv, J., Liu, A., et al. (2020b). Geometrically Nonlinear Buckling of Graphene Platelets Reinforced Dielectric Composite (GPLRDC) Arches with Rotational End Restraints. Aerosp. Sci. Technol. 107, 106326. doi:10.1016/j.ast.2020.106326

CrossRef Full Text | Google Scholar

Yang, Z., Huang, Y., Liu, A., Fu, J., and Wu, D. (2019a). Nonlinear In-Plane Buckling of Fixed Shallow Functionally Graded Graphene Reinforced Composite Arches Subjected to Mechanical and Thermal Loading. Appl. Math. Model. 70, 315–327. doi:10.1016/j.apm.2019.01.024

CrossRef Full Text | Google Scholar

Yang, Z., Liu, A., Yang, J., Fu, J., and Yang, B. (2019b). Dynamic Buckling of Functionally Graded Graphene Nanoplatelets Reinforced Composite Shallow Arches under a Step Central Point Load. J. Sound. Vib. 465, 115019. doi:10.1016/j.jsv.2019.115019

CrossRef Full Text | Google Scholar

Yang, Z., Tam, M., Zhang, Y., Kitipornchai, S., Lv, J., and Yang, J. (2020a). Nonlinear Dynamic Response of FG Graphene Platelets Reinforced Composite Beam with Edge Cracks in Thermal Environment. Int. J. Str. Stab. Dyn. 20, 2043005. doi:10.1142/s0219455420430051

CrossRef Full Text | Google Scholar

Yang, Z., Zhao, S., Yang, J., Lv, J., Liu, A., and Fu, J. (2020c). In-plane and Out-Of-Plane Free Vibrations of Functionally Graded Composite Arches with Graphene Reinforcements. Mech. Adv. Mat. Struc., 1–11. doi:10.1080/15376494.2020.1716420

CrossRef Full Text | Google Scholar

Yasniy, V., Maruschak, P., Yasniy, O., and Lapusta, Y. (2013). On Thermally Induced Multiple Cracking of a Surface: An Experimental Study. Int. J. Fract. 181, 293–300. doi:10.1007/s10704-013-9826-3

CrossRef Full Text | Google Scholar