Impact of the Scatterer Type on Ultrasound Wave Propagation in Microstructure Composites: Calculation and Application

This study is motivated to quantitatively analyze the differences among various multiple scattering models to determine the role played by the scatterer type in ultrasonic wave propagation. By calculating the transmission and reflection coefficients of the composites, the results of multiple scattering theoretical models of different scatterer types have been evaluated. The problem of acoustic properties in a fluid matrix containing different types of micron-scale scatterers operating in the ultrasound frequency range is considered. Theoretical calculations are conducted for composites with different mechanical properties. Meanwhile, the theoretical results have been compared with numerical finite element method simulations, which can be regarded as a benchmark to verify the validity of different theoretical models. The results show that the composites can achieve negative acoustic properties by selecting appropriate resonant scatterers, paving the way for searching ultrasonic metamaterials with desired negative acoustic properties. We further explored the application of microstructure ultrasonic metamaterials by enhancing the ultrasound transmitted energy through the high-impendence skull layer, having the potential for non-invasive ultrasound brain imaging and therapy.

Introduction

Acoustic metamaterials (AMMs) are special composite structures with exotic properties that natural materials do not possess (Lee et al., 2017; Liu et al., 2020). In recent years, the studies of AMMs have paved the way for diverse applications such as acoustic cloaking (Zigoneanu et al., 2014), sound absorption (Yang and Sheng, 2017; Xiao et al., 2022), acoustic imaging (Deng et al., 2009; Zhu et al., 2011; Dong et al., 2018), impedance matching (D’Aguanno et al., 2012), focusing (Zhang et al., 2009; Page, 2016), and canceling out aberrating layers (Shen et al., 2014; Craig et al., 2019). However, the current research study on AMMs mostly focuses on audible sound frequency. The successful application of ultrasonic metamaterials still faces considerable challenges due to the long-wavelength limitation, therefore insisting the need to design, simulate, and fabricate micrometer-scale size AMM resonant scatterers.

Current studies of ultrasonic metamaterials mainly utilize strong Mie-type resonances (Brunet et al., 2013) to exhibit negative acoustic properties, using scatterers randomly suspended in a fluid matrix phase. For over a century, numerous models of multiple scattering of randomly suspended scatterers in composites for inhomogeneous media have been studied. Foldy first proposed the multiple scattering theory (MST) to calculate the effective wavenumber in composites with isotropic scatterers in a fluid matrix (Foldy, 1945). The MST model was further extended to anisotropic scatterers by Waterman and Truell (Waterman and Truell, 1961), Lloyd and Berry (Lloyd and Berry, 1967), Linton and Martin (Linton and Martin, 2005), and Luppé and Conoir (Luppé and Conoir, 2011). This prompted us to investigate whether these models are still efficient for calculating ultrasound wave propagation in composites with randomly suspended microstructure scatterers.

In this study, the acoustic properties of two-dimensional micron-scale scatterers randomly immersed in a fluid matrix have been considered. The role played by the type of scatterers in the propagation of ultrasound waves is investigated. The transmission and reflection coefficients have been analyzed via the effective wavenumber and the effective impedance of the composites. Meanwhile, the acoustic properties of the microstructure composites have been further addressed by the finite element method (FEM) model. Therefore, the numerical simulation benchmark allows us to specify the validity domains for each of these analytical methods under study. Another aspect of this work is to figure out the potential application of the microstructure ultrasonic metamaterials. With the capacity of enhancing the transmitted energy through the skull, this type of ultrasonic metamaterials has the potential for non-invasive ultrasound brain imaging and therapy.

Theoretical Calculation and Numerical Simulation of Composites

For a clear presentation of the computational approach for the calculation and simulation of transmission and reflection coefficients, a random distribution of two-dimensional scatterers immersed in a fluid matrix was considered in this study. We suppose N scatterers are suspended in the slab region of thickness d. The scatterers have identical cylindrical geometry and are uniformly and randomly distributed. The screen of scatterers is insonified by a normal incident plane wave from the left, as shown in Figure 1A; the multiple scattering of ultrasound can be considered as energy transport; some energy from the forward wave is dissipated within the scatterers, while the other portion is transferred to the back wave. The MST theoretical model (Figures 1B,C) is used to obtain the transmission and reflection coefficients of random distributions of scatterers and then compared with the benchmark value from the FEM numerical simulation (Figure 1D).

FIGURE 1

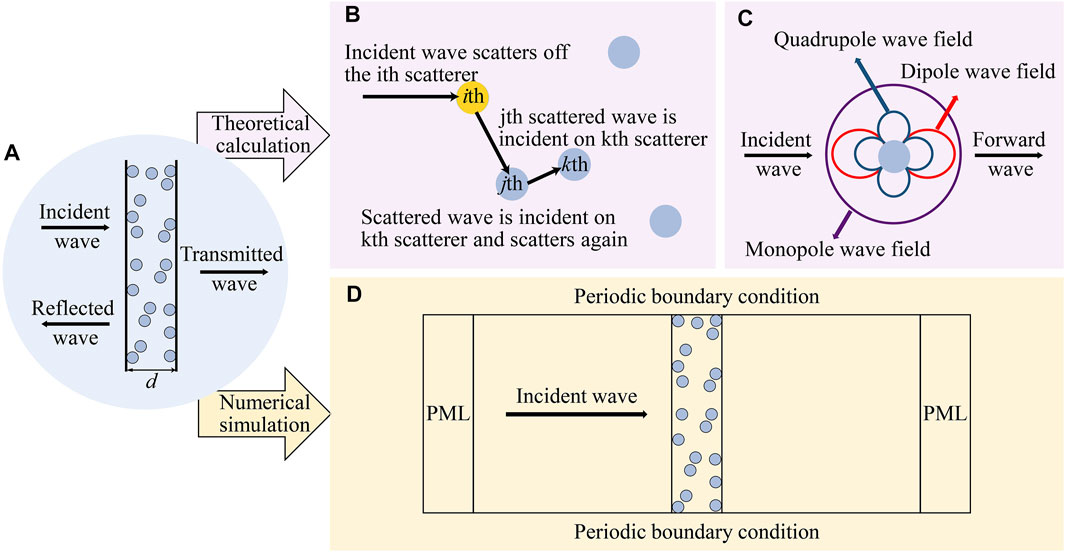
FIGURE 1. (A) Random distribution of scatterers immersed in a fluid matrix. (B) Schematic diagram demonstrating multiple scattering of the incident wave by several scatterers. (C) Monopole, dipole, and quadrupole resonances due to the mechanical contrast between a single scatterer and the fluid matrix. (D) Schematic diagram showing the geometry and boundary conditions used in the numerical simulation FEM model.

Under the influence of an incident wave, multiple scattering occurs inside the scatterers, as shown in Figure 1B. Depending on the MST, the scattered wave generated by the ith scatterer will affect its adjacent scatterers. For an adjacent jth scatterer, the scattered wave excited by the ith scatterer can be regarded as an incident wave, which interacts with the jth scatterer to excite a scattered wave; it can also be regarded as an incident wave of the kth scatterer and so on (Waterman and Truell, 1961). The MST mainly focuses on calculating the effective dynamic properties of random distributions of scatterers, and its basic problem is the scattering of a single scatterer, as shown in Figure 1C. When the scatterer radius is much smaller than the wavelength, multiple resonance modes arise due to the mechanical contrast between a single scatterer and the fluid matrix, which creates movement of the scatters relative to the fluid matrix (Kafesaki et al., 2000), a monopole resonance due to the velocity contrast, a dipole resonance due to the density contrast, and a quadrupole resonance due to the shear modulus contrast. In particular, when the velocity within the scatterers is much slower than that of the fluid matrix, multiple Mie-type resonances can be exhibited. The effective properties of random composites are deeply altered close to the particle frequency resonances, opening up possibilities to achieve ultrasonic metamaterials with negative acoustic properties. In the long-wavelength limit region, the corresponding possible scatterer size is reduced to the micrometer size in water for ultrasound frequency (Povey, 2013). The fact that whether the MST can analyze the acoustic properties of ultrasonic metamaterials with low-velocity micron-scale scatterers randomly immersed in a fluid matrix is also discussed in this article.

To verify the applicability of the MST for composites operating in the ultrasound frequency region, numerical FEM simulation values of the transmission and reflection coefficients are used as the benchmark, as shown in Figure 1D. The numerical simulation results are compared with the theoretical model predictions to analyze different analytical MST methods.

Theoretical Calculation

Multiple scattering by scatterers suspended in composites is a fundamental topic with the extensive literature. The estimation of the effective properties of composites is very significant for the design and preparation of composites. So far, many related approaches and predictive models have been proposed. As early as 1945, Foldy et al. proposed the MST for waves that are isotropically scattered by randomly distributed scatterers. Since the specific configuration of the amorphously distributed scatterers is not important, the configuration of the obstacles can be considered as the average of one state in an ensemble. Foldy considered the first order of the scattering coefficient for a single scattering and obtained Eq. 1 to calculate the frequency-dependent complex wavenumber$K$, where $K_0$ is the wavenumber of the matrix phase, and $N$ is the number of the scatterers (Foldy, 1945). Lax generalized Foldy’s results to anisotropic scatterers by inducing a quantum-mechanical viewpoint and using the quasi-crystalline approximation (Lax, 1951; 1952). However, in both Foldy’s and Lax’s studies, the effective wavenumber is expressed in terms $N$ and the cumulative effect of the only forward far-field scattering amplitude, without considering the important role of the backscattered amplitude.

$K^2=K_0^2-i4Nf\left(\theta \right).(1)$

Waterman and Truell further improved Foldy’s method by introducing quadratic terms for the number of scatterers, laying a foundation for other multiple scattering theories. Their most important result is that the wave propagation in the scattering medium can be described by the far-field amplitude $f\left(\theta \right)$ of a single scatterer, which is an essential parameter of the scattering medium. As observed from Eq. 2, the Waterman and Truell framework has taken both forward $\left(\theta =0\right)$ and backscattered $\left(\theta =\pi \right)$ far-field scattering amplitudes into consideration (Waterman and Truell, 1961).

${\left(K/K_0\right)}^2=1-4iNf\left(0\right)/K_0^2-4N^2[f{\left(0\right)}^2-f{\left(\pi \right)}^2]/K_0^4,(2)$

$f\left(\theta \right)={\displaystyle \sum }_{n=0}^{\infty }{\epsilon }_n{T}_n\text{cos}\left(n\theta \right),(3)$

where ${\epsilon }_n=1$ for $n=0$ and ${\epsilon }_n=2$ for $n\ge 1$. The expansion coefficients $T_n$ are determined by the boundary conditions of the particular problem considered. By comparing Eq. 1 and Eq. 2, it is noted that when the far-field amplitude is equal to the forward far-field amplitude in the Waterman and Truell framework, Eq. 2 is simplified to Eq. 1 in Foldy’s framework. Twersky considered different incidence field angles and expanded the normal incidence formula in the Waterman and Truell framework into a random incidence angle ${\alpha }_{in}$ for two dimensions (Twersky, 1962).

${\left(K/K_0\right)}^2=1-4iNf\left(0\right)/K_0^2-4N^{2}co{s}^2{\alpha }_{in}[f{\left(0\right)}^2-f{\left(\pi -2{\alpha }_{in}\right)}^2]/K_0^4,(4)$

where ${\alpha }_{in}$ is the incidence angle, and $f\left(0\right)$ and $f\left(\pi -2{\alpha }_{in}\right)$ can be obtained from Eq. 3. If the normal incident to the slab (${\alpha }_{in}=0$) is considered, Eq. 4 in the Twersky framework is equal to Eq. 2 in the Waterman and Truell framework. Lloyd and Berry (Lloyd and Berry, 1967) further extended and corrected the work by Waterman and Truell, and they showed that the formula for calculating the wavenumber should be

${\left(K/K_0\right)}^2=1-4iNf\left(0\right)/K_0^2+4N^2\{f{\left(0\right)}^2-f{\left(\pi \right)}^2+\underset{0}{\overset{\pi }{{\displaystyle \int }}}1/\text{sin}\left(\theta /2\right)\frac{d}{d\theta }\left[f{\left(\theta \right)}^2\right]d\theta \}/K_0^4.(5)$

Eq. 5 is different from Eq. 2 by the Waterman and Truell framework, both in the signs of the forward and backscattered terms and in the additional modified term of$N^2$. Linton and Martin also presented a two-dimensional model for circular cylinders inspired and based on the hole correction, assuming that the exclusion distance is small compared to the wavelength (Linton and Martin, 2005):

${\left(K/K_0\right)}^2=1-4iNf\left(0\right)/K_0^2+\left(8N^2/\pi K_0^4\right)\underset{0}{\overset{\pi }{{\displaystyle \int }}}\text{cot}\left(\theta /2\right)\frac{d}{d\theta }\left[f{\left(\theta \right)}^2\right]d\theta .(6)$

Based on the effective wavenumber in the Waterman and Truell framework, Angel and Aristégui further described the effective medium by the reflection coefficient and the transmission coefficient (Angel and Aristégui, 2005; Aristégui and Angel, 2007).

$R=-Qexp\left(-i{K}_{0}d\right)\times \left[1-exp\left(2i{K}_{0}d\right)\right]/ \left[1-Q^{2}exp\left(2iKd\right)\right],(7)$

$T=\left(1-Q^2\right)\times \text{exp}\left[i\left(K-K_0\right)d\right]/ \left[1-Q^{2}exp\left(2iKd\right)\right],(8)$

where $Q=\left(Z_0-Z\right)/\left(Z_0+Z\right),Z$, indicates the effective impedance of the composite, and $Z_0$ indicates the impedance of the matrix phase; from the formula $Z=\rho \omega /K$, we can obtain

$Z/Z_0=\left(K_0/K\right)\times \left(\rho /{\rho }_0\right),(9)$

where $\rho /{\rho }_0$ is the effective mass density (EMD) of the composite, and ${\rho }_0$ indicates the mass density of the matrix phase. Angel and Aristégui also obtained the EMD in Eq. 10 and effective bulk modulus (EBM) as $M/M_0$ in Eq.11.

$\rho /{\rho }_0=1-2iN\left[f\left(0\right)-f\left(\pi \right)\right]/K_0^2,(10)$

$M/M_0=\left[1-2iN[f\left(0\right)+f\left(\pi \right)\right]/K_0^2{]}^{-1},(11)$

where $M_0={\rho }_0{c}_0^2,c_0$, indicates the sound velocity of the matrix phase. Obtaining Eq. 12 by taking Eq. 10 into Eq. 9, then the transmission and reflection coefficients can be calculated.

$Z/Z_0=\left(K_0/K\right)\times \left\{1-2iN\left[f\left(0\right)-f\left(\pi \right)\right]/K_0^2\right\}.(12)$

Recently, Luppé and Conoir further obtained the EMD, EBM, and effective impedance as

$\rho /{\rho }_0=1-2iN(f\left(0\right)-f\left(\pi \right))/K_0^2+(4N^2/K_0^4)\{f{\left(0\right)}^2/2-f{\left(\text{π}\right)}^2/2 + J\left(0\right)[f\left(\pi \right)-T_0-f\left(0\right)]/f\left(0\right)+T_{0}I\left(\text{π}\right)[f\left(0\right)-T_0]/f\left(0\right)$

$+ T_{0}J\left(\pi \right)/f\left(0\right) - T_{0}I\left(0\right)[2f\left(\text{π}\right)-f\left(0\right)-T_0]/f\left(0\right)\},(13)$

$M/M_0=\left(\rho /{\rho }_0\right)\left(K_0^2/K^2\right),(14)$

$Z/Z_0=K_0/K\times \{1-2iN(f\left(0\right)-f\left(\pi \right))/K_0^2+(4N^2/K_0^4)\{f{\left(0\right)}^2/2-f{\left(\text{π}\right)}^2/2 + J\left(0\right)[f\left(\pi \right)-T_0-f\left(0\right)]/f\left(0\right)+T_{0}I\left(\text{π}\right)[f\left(0\right)-T_0]/f\left(0\right) + T_{0}J\left(\pi \right)/f\left(0\right) - T_{0}I\left(0\right)[2f\left(\text{π}\right)-f\left(0\right)-T_0]/f\left(0\right)\},(15)$

with

$J\left(\alpha \right)=-1/\left(2\pi \right)\times \underset{0}{\overset{\pi }{{\displaystyle \int }}}\text{cot}(\theta /2)\left\{\frac{d}{d\theta }\left[f\left(\theta \right)f\left(\alpha -\theta \right)+f\left(-\theta \right)f\left(\alpha +\theta \right)\right]\right\}d\theta ,(16)$

$I\left(\alpha \right)=-1/\left(2\pi \right)\times \underset{0}{\overset{\pi }{{\displaystyle \int }}}\text{cot}(\theta /2)\left\{\frac{d}{d\theta }\left[f\left(\alpha -\theta \right)+f\left(\alpha +\theta \right)\right]\right\}d\theta .(17)$

The effective mass density and effective impedance in the Angel and Aristégui framework and Luppé and Conoir framework are equal when only the first order of $N^2$ is considered. The reasons for the differences of the aforementioned formulas are worth discussing, and errors will occur when different boundary regions are selected during integration. Table 1 summarizes the assumptions, abbreviations, and calculation formulas of the previously mentioned five MST models.

TABLE 1

TABLE 1. Assumption theory, abbreviations, and calculation equations of five different MST models.

Numerical Simulation

Multiple scattering signals are composed of coherent parts and incoherent parts. Since enough scatterer position configurations are averaged, the incoherent part vanishes in MST theoretical calculations. In practice, it is not easy to obtain coherent wave characteristics by using only one sample of random composite because it requires a large number of local measurements along the composite to restore the averaging procedure. Therefore, numerical simulations are a good choice.

The numerical simulations were finished by COMSOL Multiphysics software in the pressure acoustic frequency domain. The designed numerical simulation geometric model is shown in Figure 1D. A slab of screen $S$ contains $N$ identical scatterers with same radius$a$, so the fraction is$\varphi =N\pi a^2/S$. Their positions are selected by a random draw function. The periodicity of the model in the direction perpendicular to sound propagation is simulated by applying periodic boundary conditions on both sides of the screen. Using perfectly matched layer (PML) boundary conditions to simulate the outer boundary of the fluid domain, the incident plane wave is insonified on the left boundary of the model. The reflection coefficient and transmission coefficient of an incident plane wave passing through the screen of scatterers are calculated by using acoustic boundary conditions. We have made 100 simulations to achieve the convergence of the averaged field.

Results and Discussion

It is necessary to establish a precise framework to limit the study field and focus on the role played by microstructures. The purpose of this part is to study the influence of the scatterer type on the ultrasound wave propagation in composites. In the previous section, we summarized the aforementioned five theoretical models of characterizing the scattering medium; now, we compared the results obtained by five different MST theoretical models under the benchmark of the FEM simulations.

To go further into the analysis of the impact of the microstructure scatterers type in general, we studied two different types of scatterers. Case I: steel scatterers are immersed in the water matrix. Case II: rubber scatterers are suspended in the water matrix. In both cases, the radius of the scatterers is set at 60 μm with ϕ = 20.94% to satisfy the long-wavelength limit in ultrasound frequency. Parameters of the used materials are listed in Table 2.

TABLE 2

TABLE 2. Acoustic properties of the materials.

Case 1: Steel Scatterers in Water

We considered the propagation of coherent waves through steel scatterers randomly immersed in water. Figure 2A and Figure 2B present the modulus of complex transmission and reflection coefficients corresponding to steel scatterers in water, according to MST frameworks (Table 1) and FEM simulations. Both in Figure 2A and Figure 2B, the transmission coefficients obtained by four MST frameworks (WT, LB, LM, and LC) agree with each other, except the Foldy framework (F) as expected. It indicates that Foldy only considered the forward far-field scattering amplitude without considering the important role of the backscattered amplitude. Therefore the scattering amplitude of $\left|R\right|$ is significantly lower, and the scattering amplitude of $\left|T\right|$ is higher than the other four MST models. We observed that the calculation results of the four frameworks qualitatively correspond with the FEM simulation results, especially at a low frequency (0–1.0 MHz). At a low frequency, we also observed that the FEM simulation value is between the theoretical value of LC and WT frameworks and more close to the LC framework. In the LC framework, the quadratic coefficient of the scatterer number is modified, and the results show the difference when compared with the WT framework, indicating the correction to $N^2$ is necessary. Depending on the long-wavelength limit, only considering the lowest-order truncation coefficient of $T_n$ in the expansion of the scattering fields can be sufficient. Simpler formulas for calculating the effective wavenumber in the LB framework Eq. 18 and LM framework Eq. 19 can be obtained by using the zero and first orders of $T_n \left(\text{n}\le 2\right)$

${(K/K_0)}^2=1-4iN(T_0+2T_1+2T_2)/K_0^2-32N^2(4T_1^2/3+ 304T_2^2/105+T_0{T}_1+8T_0{T}_2/3+78T_1{T}_2/15)/K_0^4,(18)$

${\left(K/K_0\right)}^2=1-4iN\left(T_0+2T_1+2T_2\right)/K_0^2-32N^2\left(T_1^2+ 2T_2^2+T_0{T}_1+2T_0{T}_2+4T_1{T}_2\right)/K_0^4.(19)$

FIGURE 2

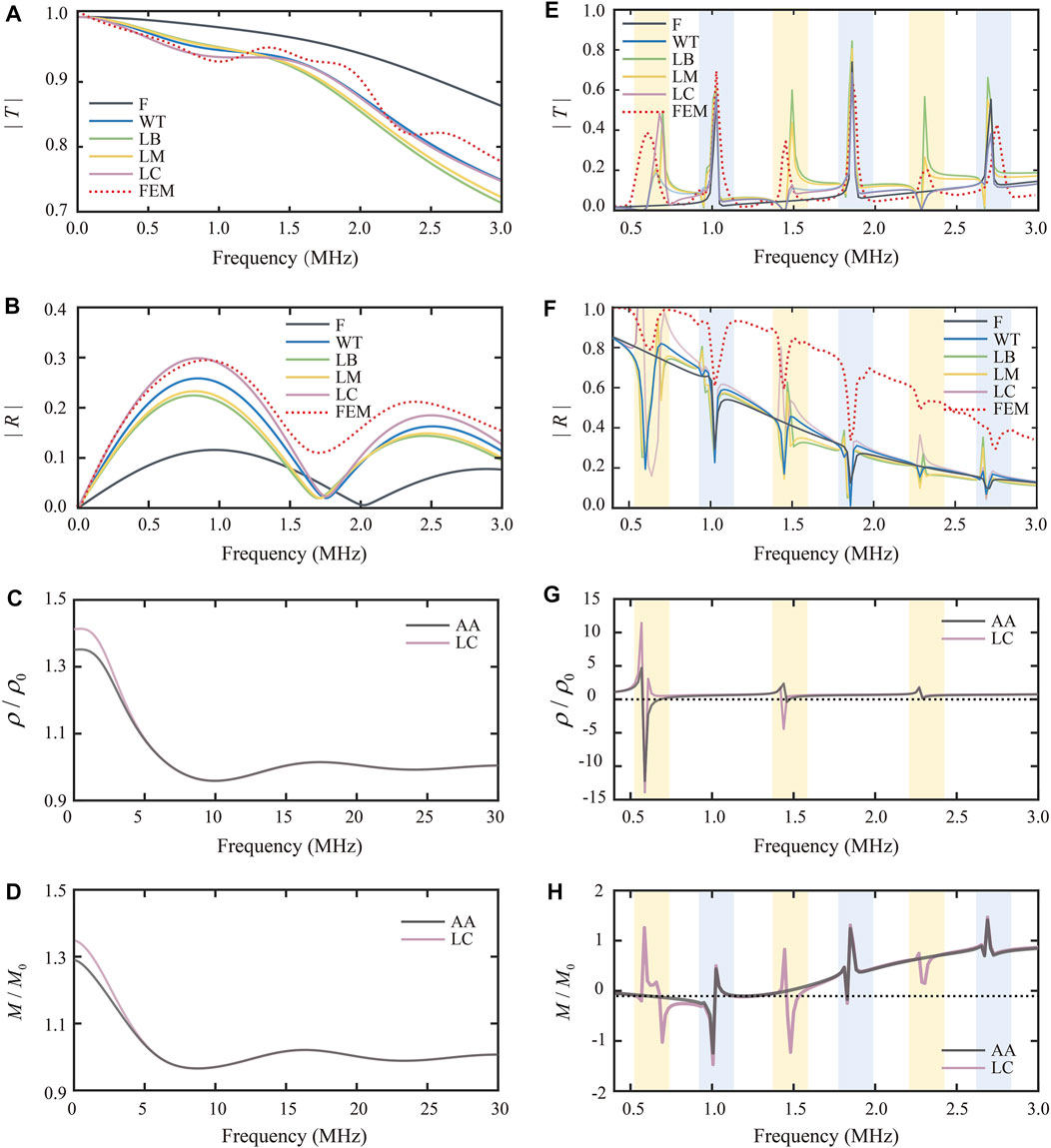
FIGURE 2. Comparison of transmission and reflection coefficients moduli for different types of scatterers suspended in water by MST models and FEM simulations and calculation results of the real parts of the EMD and EBM corresponding to different type scatterers. (A) Modulus of the transmission coefficient versus frequency corresponding to steel scatterers in water. (B) Modulus of the reflection coefficient versus frequency corresponding to steel scatterers in water. (C) Real part of the EMD versus frequency corresponding to steel scatterers in water. (D) Real part of the EBM versus frequency corresponding to steel scatterers in water. (E) Modulus of the transmission coefficient versus frequency corresponding to rubber scatterers in water. (F) Modulus of the reflection coefficient versus frequency corresponding to rubber scatterers in water. (G) Real part of the EMD versus frequency corresponding to rubber scatterers in water. (H) Real part of the EBM versus frequency corresponding to rubber scatterers in water.

It is worth noting that the approximation formulas for LB and LM frameworks are very similar, which is also evidenced by the fact that the LM framework curves are particularly close to the LB framework curves, as shown in Figure 2A and Figure 2B.

AMMs with negative EMD and/or EBM have been studied extensively, which can cause a lot of exotic acoustic properties. To enhance our analysis, we have investigated the EMD and EBM for the microstructure composites. Figure 2C and Figure 2D show the real parts of the EMD and EBM, according to two different MST frameworks, the Angel and Aristégui framework (Eq. 10 and Eq. 11) and LC framework (Eq. 13 and Eq. 14). As observed in Figure 2A and Figure 2B, the transmission and reflection coefficients of steel scatterers in water display no resonance peaks. Therefore, the real parts of the EMD and EBM are decreasing from the static limit to unit one with increasing frequency. At a high frequency, the real parts of the EMD and EBM approach unity, and the imaginary parts of the EMD and EBM tend to zero. These results demonstrate that the EMD and EBM tend to reach that of water at a high frequency; in other words, there is no contribution in the density and modulus from the steel scatterers.

Case 2: Rubber Scatterers in Water

For the second case, rubber scatterers in water, it is notable to see resonances at specific frequency regions. Figure 2E and Figure 2F show the moduli of transmission and reflection coefficients corresponding to rubber scatterers in water. For transmission coefficients (Figure 2E), the frequency regions of the resonances peaks in the MST models are consistent with those in FEM simulation, except the Foldy framework misses three main resonance peaks in 0.4–3 MHz. Once again, it indicates that Foldy only considered the forward far-field scattering amplitude. However, out of resonant frequency regions (around 1.02 and 1.87 MHz), MST models provide results significantly different from FEM simulations. It can be explained that the scatterers reach a steady state at the specific narrow resonant frequency, and a large amount of energy is stored at this frequency region. As less energy is transmitted in the fluid, this reduces the intensity of interactions between scatterers meanwhile. Once out of the steady state, MST models only calculate the coherent part but the incoherent part superposition decreases the amplitude of the transmitted wave. We also noticed that the oscillation of the WT framework at resonance frequency regions appeared visibly smoother than that of LB, LM, and LC frameworks, which can be regarded as the influence of the microstructure type. LB, LM, and LC frameworks have an additional term of $N^2$ compared to the WT framework. When using rubber as scatterers, the velocity within the scatterers is very low in comparison with that of the matrix phase, exhibiting strong Mie-type resonance (Leighton, 1997). In other words, the additional term of $N^2$ causes more oscillations at resonant frequency regions due to the type of microstructure. As for the reflection coefficient (Figure 2F), the calculation results of MST models have the same trend line of change with FEM simulations but provide a lower value. The possible reason is that the incoherent part superposition decreases the amplitude of the transmitted wave and increases the amplitude of the reflected wave, but the multiple scattering theory only calculates the coherent part. For Mie-type scatterers, the results based on MST models and FEM simulations are inconsistent in the non-resonant frequency region, compared with hard-type scatterers. It indicated that the MST models are only suitable for observing the trend change and resonant frequency regions of Mie-type scatterers.

Figure 2G and Figure 2H show the real parts of the EMD and EBM corresponding to rubber scatterers in water. We noted that in six particular frequency regions, the moduli of transmission and reflection coefficients show obvious resonance peaks, which are around 0.57, 1.02, 1.44, 1.87, 2.28, and 2.75 MHz, respectively, within the ultrasound frequency range of 0.4–3 MHz. At six resonance peak frequencies, most of the incident energy is transmitted. As shown in Figure 3, rubber scatterers exhibit a variety of resonance modes at these specific frequencies, whereas at the non-resonant frequencies (Figure 3A), most of the energy is reflected by the composites. In the aforementioned narrow frequency regions, the EMD or EBM also show a negative value. There are negative resonant peaks in the EMD near 0.57 and 1.44 MHz (Figure 2G). For the Angel and Aristégui framework (AA framework), negative resonant peaks are formed in the EBM near 1.02 and 1.87 MHz. For the LC framework, negative resonant peaks in the EBM are observed near 0.57, 1.02, 1.44, and 1.87 MHz (Figure 2H). In the LC framework, the quadratic coefficient of the scatterer number is modified, which results in the difference compared with the AA framework. We can see that EBM results exhibit three more peaks compared to the AA framework (Figure 2H), but these are not shown in Figure 2D. Once again, it can be considered to be influenced by the type of the microstructure. When using ultra-slow Mie-type microstructure scatterers, the correction to $N^2$ term of the effective wavenumber should be considered. In summary, Figure 2 illustrates that both the EMD and EBM can be made negative near the resonance frequency by choosing appropriate soft resonant scatterers, opening the possibility for searching ultrasonic metamaterials with desired negative properties. These narrow resonance frequency regions depend on the scatterer mechanism, size, and fraction. In this work, we mainly discussed the influence of the microstructure type (scatterer mechanism) and illustrated that soft rubber scatterers can show negative acoustic parameters compared with hard steel scatterers.

FIGURE 3

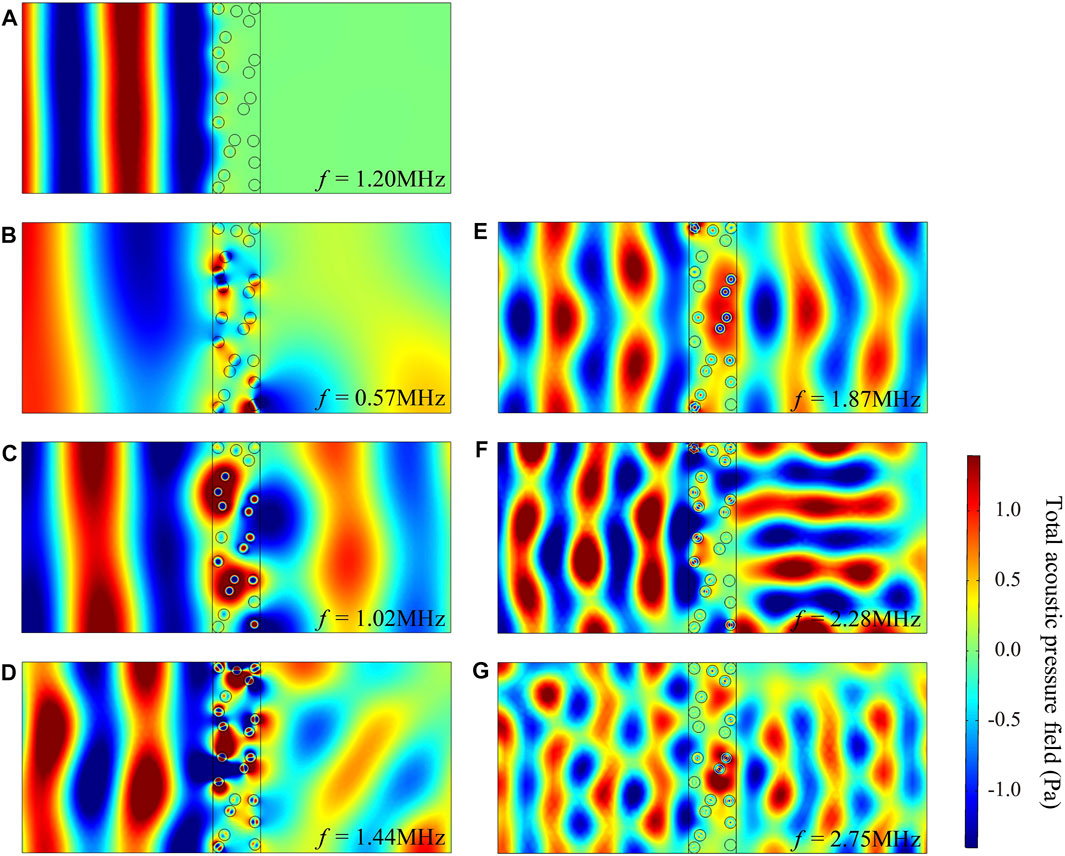
FIGURE 3. Total acoustic pressure field at seven different frequencies corresponding to rubber scatterers in water. (A) Total acoustic pressure field at non-resonant frequency 1.20 MHz. (B)–(G) Total acoustic pressure field at six different resonant frequencies: 0.57, 1.02, 1.44, 1.87, 2.28, and 2.75 MHz, respectively.

Application

The aforementioned results illustrate that the MST theoretical calculation models are capable of analyzing ultrasonic metamaterials with negative effective properties. We chose soft rubber scatterers with low velocity and density suspended in water and a high fraction of scatterers to exhibit strong Mie-type resonances to recognize negative effect properties (Ba et al., 2017). In addition, the application of this ultrasonic metamaterial is further explored, depending on the research on complementary acoustic metamaterials (Shen et al., 2014); the imaging aberration skull layer is used to demonstrate whether the ultrasonic metamaterial in this study can enhance the ultrasound transmission through the skull. A numerical model was further achieved by using FEM simulations by COMSOL Multiphysics software. As shown in Figure 4, after the ultrasonic metamaterial layer is added in front of the skull layer $\left(\rho =2000kg/m^3, c=2500m/s\right)$, the ultrasound energy through the skull was significantly increased at 1.02 MHz. By analyzing the ultrasound intensity magnitude along the axis of ultrasound, it is found that the transmitted ultrasound intensity increases by up to 200% when the ultrasonic metamaterial layer is added. It is worth noting that the ultrasonic metamaterial exhibits negative EBM at 1.02 MHz, indicating that the EBM is the main factor affecting ultrasound wave penetration through the skull layer.

FIGURE 4

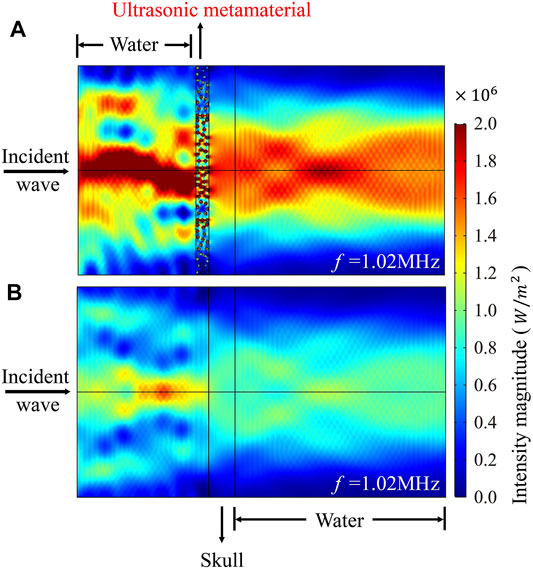
FIGURE 4. Ultrasound intensity distribution under two conditions. (A) Ultrasonic metamaterial is placed in front of the skull layer. (B) Only skull layer without the ultrasonic metamaterial.

Conclusion

In this study, the transmission and reflection coefficients calculating results of five MST theoretical frameworks (Foldy, Waterman & Truell, Lloyd & Berry, Linton & Martin, and Luppé & Conoir) are compared with the FEM simulations. Hard steel scatterers and soft Mie-type scatterers randomly suspended in water operating at the ultrasound frequency region are taken into consideration. In the calculation of soft scatterers with a low velocity immersed in water, the resonances became sharp due to the contrast between the scatterers and the matrix. MST models can still analyze this type of ultrasonic metamaterials with negative properties. The application of this ultrasonic metamaterial is also simulated, and this ultrasonic metamaterial can counteract the attenuation of ultrasound transmission by the high-impedance layer. The intensity of ultrasound through the skull layer is increased by 200% when the ultrasonic metamaterial layer is added, paving the way for further non-invasive ultrasound imaging and therapy through the skull.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YY, HD, and YZ initiated the project. YY wrote the manuscript, carried out the theoretical calculations, and numerical simulations. All the authors contributed to the editing of the manuscript.

Funding

This work was supported by the National Key R&D Program of China (2018YFC0114900). The Zhejiang Provincial Key R&D Program of China (2022C01002). The National Major Scientific Research Instrument Development Project (81827804).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Angel, Y. C., and Aristégui, C. (2005). Analysis of Sound Propagation in a Fluid through a Screen of Scatterers. The J. Acoust. Soc. America 118 (1), 72–82. doi:10.1121/1.1931088

CrossRef Full Text | Google Scholar

Aristégui, C., and Angel, Y. C. (2007). Effective Mass Density and Stiffness Derived from P-Wave Multiple Scattering. Wave Motion 44 (3), 153–164. doi:10.1016/j.wavemoti.2006.08.005

CrossRef Full Text | Google Scholar

Ba, A., Kovalenko, A., Aristégui, C., Mondain-Monval, O., and Brunet, T. (2017). Soft Porous Silicone Rubbers with Ultra-low Sound Speeds in Acoustic Metamaterials. Sci. Rep. 7 (1), 1–6. doi:10.1038/srep40106

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunet, T., Leng, J., and Mondain-Monval, O. (2013). Soft Acoustic Metamaterials. Science 342 (6156), 323–324. doi:10.1126/science.1241727

PubMed Abstract | CrossRef Full Text | Google Scholar

Craig, S. R., Welch, P. J., and Shi, C. (2019). Non-Hermitian Complementary Acoustic Metamaterials for Lossy Barriers. Appl. Phys. Lett. 115 (5), 051903. doi:10.1063/1.5110501

CrossRef Full Text | Google Scholar

D’Aguanno, G., Le, K. Q., Trimm, R., Alù, A., Mattiucci, N., Mathias, A. D., et al. (2012). Broadband Metamaterial for Nonresonant Matching of Acoustic Waves. Sci. Rep. 2 (1), 1–5. doi:10.1038/srep00340

CrossRef Full Text | Google Scholar

Deng, K., Ding, Y., He, Z., Zhao, H., Shi, J., and Liu, Z. (2009). Theoretical Study of Subwavelength Imaging by Acoustic Metamaterial Slabs. J. Appl. Phys. 105 (12), 124909. doi:10.1063/1.3153976

CrossRef Full Text | Google Scholar

Dong, H.-W., Zhao, S.-D., Wang, Y.-S., and Zhang, C. (2018). Broadband Single-phase Hyperbolic Elastic Metamaterials for Super-resolution Imaging. Sci. Rep. 8 (1), 1–10. doi:10.1038/s41598-018-20579-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Foldy, L. L. (1945). The Multiple Scattering of Waves. I. General Theory of Isotropic Scattering by Randomly Distributed Scatterers. Phys. Rev. 67 (3-4), 107–119. doi:10.1103/PhysRev.67.107

CrossRef Full Text | Google Scholar

Kafesaki, M., Penciu, R. S., and Economou, E. N. (2000). Air Bubbles in Water: A Strongly Multiple Scattering Medium for Acoustic Waves. Phys. Rev. Lett. 84 (26), 6050–6053. doi:10.1103/PhysRevLett.84.6050

PubMed Abstract | CrossRef Full Text | Google Scholar

Lax, M. (1951). Multiple Scattering of Waves. Rev. Mod. Phys. 23 (4), 287–310. doi:10.1103/RevModPhys.23.287

CrossRef Full Text | Google Scholar

Lax, M. (1952). Multiple Scattering of Waves. II. The Effective Field in Dense Systems. Phys. Rev. 85 (4), 621–629. doi:10.1103/PhysRev.85.621

CrossRef Full Text | Google Scholar

Lee, D., Nguyen, D. M., and Rho, J. (2017). Acoustic Wave Science Realized by Metamaterials. Nano Convergence 4 (1), 1–15. doi:10.1186/s40580-017-0097-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Leighton, T. G. (1997). The Acoustic Bubble. Academic Press.

Google Scholar

Linton, C. M., and Martin, P. A. (2005). Multiple Scattering by Random Configurations of Circular Cylinders: Second-Order Corrections for the Effective Wavenumber. J. Acoust. Soc. America 117 (6), 3413–3423. doi:10.1121/1.1904270

CrossRef Full Text | Google Scholar

Liu, J., Guo, H., and Wang, T. (2020). A Review of Acoustic Metamaterials and Phononic Crystals. Crystals 10 (4), 305. doi:10.3390/cryst10040305

CrossRef Full Text | Google Scholar

Lloyd, P., and Berry, M. V. (1967). Wave Propagation through an Assembly of Spheres: IV. Relations between Different Multiple Scattering Theories. Proc. Phys. Soc. 91 (3), 678–688. doi:10.1088/0370-1328/91/3/321

CrossRef Full Text | Google Scholar

Luppé, F., and Conoir, J.-M. (2011). “Multiple Scattering by Cylinders Randomly Located in a Fluid: Effective Properties,” in Journal of Physics: Conference Series (Bristol, England: IOP Publishing),

Google Scholar

Page, J. H. (2016). Focusing of Ultrasonic Waves by Negative Refraction in Phononic Crystals. AIP Adv. 6 (12), 121606. doi:10.1063/1.4972204

CrossRef Full Text | Google Scholar

Povey, M. J. W. (2013). Ultrasound Particle Sizing: A Review. Particuology 11 (2), 135–147. doi:10.1016/j.partic.2012.05.010

CrossRef Full Text | Google Scholar

Shen, C., Xu, J., Fang, N. X., and Jing, Y. (2014). Anisotropic Complementary Acoustic Metamaterial for Canceling Out Aberrating Layers. Phys. Rev. X 4 (4), 041033. doi:10.1103/PhysRevX.4.041033

CrossRef Full Text | Google Scholar

Twersky, V. (1962). On Scattering of Waves by Random Distributions. I. Free‐Space Scatterer Formalism. J. Math. Phys. 3 (4), 700–715. doi:10.1063/1.1724272

CrossRef Full Text | Google Scholar

Waterman, P. C., and Truell, R. (1961). Multiple Scattering of Waves. J. Math. Phys. 2 (4), 512–537. doi:10.1063/1.1703737

CrossRef Full Text | Google Scholar

Xiao, H., Yuan, T., Song, X., Chen, J., Zhou, J., Sui, D., et al. (2022). Broadband Sound Absorption of Subwavelength Porous Meta-Liner. Front. Mater. 9. doi:10.3389/fmats.2022.845597

CrossRef Full Text | Google Scholar

Yang, M., and Sheng, P. (2017). Sound Absorption Structures: From Porous media to Acoustic Metamaterials. Annu. Rev. Mater. Res. 47, 83–114. doi:10.1146/annurev-matsci-070616-124032

CrossRef Full Text | Google Scholar

Zhang, S., Yin, L., and Fang, N. (2009). Focusing Ultrasound with an Acoustic Metamaterial Network. Phys. Rev. Lett. 102 (19), 194301. doi:10.1103/PhysRevLett.102.194301

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, J., Christensen, J., Jung, J., Martin-Moreno, L., Yin, X., Fok, L., et al. (2011). A Holey-Structured Metamaterial for Acoustic Deep-Subwavelength Imaging. Nat. Phys 7 (1), 52–55. doi:10.1038/nphys1804

CrossRef Full Text | Google Scholar

Zigoneanu, L., Popa, B.-I., and Cummer, S. A. (2014). Three-dimensional Broadband Omnidirectional Acoustic Ground Cloak. Nat. Mater 13 (4), 352–355. doi:10.1038/nmat3901

PubMed Abstract | CrossRef Full Text | Google Scholar