Two-dimensional (2D) magnetic materials have recently attracted a great attention due to their potential applications in information processing and storage. It was observed in an experiment that the CrGeTe₃/NiO heterostructure shows a higher Curie temperature and a stronger perpendicular anisotropy. This suggests that antiferromagnet NiO can be coupled with ferromagnetic CrGeTe₃ by the proximity effect, which enhances ferromagnetism. However, the mechanism behind the coupling is unknown. In this work, we built a CrGeTe₃/NiO heterostructure model and investigated the electronic structure and magnetic properties of the CrGeTe₃/NiO interface by first-principles calculations. It is shown that the intralayer exchange interaction between the Cr atoms is ferromagnetic, and the interlayer exchange interaction between the Ni atoms and Cr atoms at the interface is antiferromagnetic. The interlayer interaction is equivalent to a magnetic field as strong as $B=100.3 \text{T}$ applied by the NiO substrate to the CrGeTe₃ layer, which results in the higher Curie temperature of CrGeTe₃ observed in the experiment.

Introduction

Since the discovery of graphene (Novoselov et al., 2004; Geim and Novoselov, 2007; Geim, 2009), two-dimensional materials, such as hexagonal BN (Kubota et al., 2007) and transition metal dihalides (TMDs), have attracted considerable attention due to their novel properties and potential applications (Mak et al., 2010; Fang et al., 2012). Since a van der Waals heterostructure (Geim and Grigorieva, 2013) was proposed, the types of two-dimensional materials have been greatly enriched. The two-dimensional magnetic materials can be used in new spintronic devices with the advantages of high sensitivity and high storage density (Pesin and MacDonald, 2012; Han et al., 2014; Han, 2016). In the traditional isotropic Heisenberg model, any thermal fluctuation caused by finite temperature will destroy the long-range magnetic order in one- or two-dimensional systems, as stated in the so-called Mermin–Wagner theorem. However, recent studies have shown that magnetic anisotropy can bypass the Mermin–Wagner theorem and result in a long-range ferromagnetic order at finite temperature (Mermin and Wagner, 1966).

Both CrGeTe₃ and CrSiTe₃ monolayers are 2D ferromagnetic semiconductors, which makes them promising candidates for further applications in spintronics (Žutić et al., 2004; MacDonald et al., 2005; Geim and Grigorieva, 2013; Liu et al., 2016). The intrinsic ferromagnetism of CrGeTe₃ and CrSiTe₃ monolayers is due to the ferromagnetic superexchange interaction via the 90° Cr-Te-Cr path, which is mediated by the t_2g orbital exchange interaction of adjacent high-spin Cr³⁺ (Casto et al., 2015; Chen et al., 2015; Williams et al., 2015; Liu et al., 2016; Gong et al., 2017). The bulk of CrGeTe₃ belongs to the van der Waals crystal, and the layers are bonded together along the c-axis by van der Waals force. This structure makes it easy to peel off a monolayer and combines it with other materials to form a heterostructure. By stacking two-dimensional material layers, the properties of materials can be improved and enhanced. For example, the Curie temperature of the CrI₃/MoTe₂ heterostructure is higher than that of CrI₃ alone (Chen et al., 2019). The Curie temperature of CrX₃ can be boosted by the heterostructure of CrX₃ and Mene (M = Si, Ge) (Li et al., 2019). Conversely, the band degeneracy at KK′ point of WSe₂ can be eliminated by using the neighbor exchange of CrI₃ (Zhong et al., 2017).

Recently, an experimental work found that CrGeTe₃ on the NiO substrate showed higher Curie temperature and stronger perpendicular magnetic anisotropy (Idzuchi et al., 2019). A CrGeTe₃/NiO heterojunction was prepared by depositing NiO on CrGeTe₃ flakes. Compared with the free-standing CrGeTe₃ flake, the hysteresis loop of the CrGeTe₃/NiO heterojunction became a square with a larger coercivity field (Idzuchi et al., 2019). When the thickness of NiO was 50 nm, the Curie temperature of CrGeTe₃/NiO heterojunction was as high as 115 K, while the maximum Curie temperature of CrGeTe₃ alone is only about 60K. In the experiment, CrGeTe₃ with a thickness of 5–200 nm was selected, and the Curie temperature of CrGeTe₃/NiO increased. Even if the thickness of the CrGeTe₃ flake reached 200 nm, the Curie temperature of CrGeTe₃/NiO was higher than that of bulk CrGeTe₃. It can be speculated that the antiferromagnet NiO is coupled with CrGeTe₃ through the proximity effect, which enhances the ferromagnetism of CrGeTe₃. However, the experiment neither gave further analysis nor clarified the micro mechanism of this phenomenon. Therefore, it is necessary to carry out theoretical calculation to explore the microcosmic mechanism behind the experimental phenomena.

In this study, we investigated the electronic structure and magnetism of the CrGeTe₃/NiO (111) interface atomistic model by the first-principles calculations and analyzed the interfacial exchange interaction of the CrGeTe₃/NiO (111) heterojunction.

Approach

The structure and electronic properties of the CrGeTe₃/NiO heterojunction are calculated by the density functional theory (DFT) and the projector-augmented wave (PAW) method implemented in the VASP code (Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b; Kresse and Joubert, 1999; Yu et al., 2009). The Perdew–Burke–Ernzerhof (PBE) parameterization of generalized gradient approximation (GGA) (Perdew et al., 1996) is applied as the exchange correlation functional. The on-site Coulomb interaction of 3d electrons in transition metalions strongly impacts the calculated electronic properties. In order to consider the strong localization effect of the d electrons in Cr and Ni atoms, the GGA + U method (Liechtenstein et al., 1995; Dudarev et al., 1998; Han and van Veenendaal, 2012) is applied to tune the spin properties of Cr and Ni atoms. The Hubbard U of Cr and Ni atoms are set to be 3.0 and 5.0 eV, respectively. In order to reduce the interference of the periodic interaction in the perpendicular direction, a vacuum region of 15 Å is added along the c-axis. The atomic positions are completely relaxed until the error of total energy and the residual force within 10^–5 eV and 0.05 eV/Å, respectively. The energy cutoff of the plane wave basis is 520 eV. The Brillouin zone integral is performed on a Monkhorst–Pack k-mesh of 2 × 2 × 1 size (Monkhorst and Pack, 1976). Along the high symmetry line Γ (0, 0, 0) → M (1/2, 0, 0) → K (1/3, 1/3, 0) → Γ (0, 0, 0), the band structure is calculated.

Results and Discussion

According to the experimental results (Idzuchi et al., 2019), the thickness of CrGeTe₃ is 5.5–8 nm, while the thickness of NiO is 20–100 nm. Therefore, when building the model, the thickness of the NiO layer should be relatively large, while the thickness of the CrGeTe₃ layer is relatively small. In this work, four layers of NiO are used to simulate the substrate. For simplicity, a single layer of CrGeTe₃ is put on the NiO layers. In order to make the lattice match better, we selected the NiO (111) plane. In order to have stronger exchange at the interface, we set the Ni layer right at the interface. The optimized lattice constants of NiO (111) and CrGeTe₃ (001) surfaces are 5.895 Å and 6.913 Å, respectively. In the CrGeTe₃/NiO heterostructure model, CrGeTe₃ (001) ($\sqrt{3}$ × $\sqrt{3}$) is stacked on top of NiO (111) (2 × 2), and the lattice mismatch is about 1.6%. The thickness of the CrGeTe₃ (001) monolayer is 3.502 Å, where a unit cell includes 6 Cr, 6 Ge, and 18 Te atoms. The thickness of NiO (111) layers is 8.505 Å, where a unit cell includes 64 Ni and 64 O atoms. In addition, the lattice parameter of the heterojunction is a = b = 11.944 Å and c = 30.697 Å, and the initial interlayer distance (d) is 3.69 Å. The lower most Ni and O layers are fixed to simulate the NiO substrate, and other atoms are relaxed. Figure 1A shows the atomistic model of the CrGeTe₃/NiO heterojunction. In order to obtain the most stable magnetic ordering, two kinds of ferromagnetic (FM1 and FM2) and two kinds of antiferromagnetic (AFM1 and AFM2) orders of CrGeTe₃ are considered, as shown in Figure 1B. The magnetization direction of all Cr atoms in the FM1 order is upward, and the magnetization direction of all Cr atoms in the FM2 order is downward. The magnetization directions of the four Ni layers, from top to down, are ↑↓↑↓, and the magnetic order in the same layer of Ni atoms are ferromagnetic. This is the so-called “AFM II” magnetic order of bulk NiO. In the FM1 and FM2 orders, the magnetic coupling between CrGeTe₃ layer and NiO layer is ferromagnetic and antiferromagnetic, respectively.

FIGURE 1

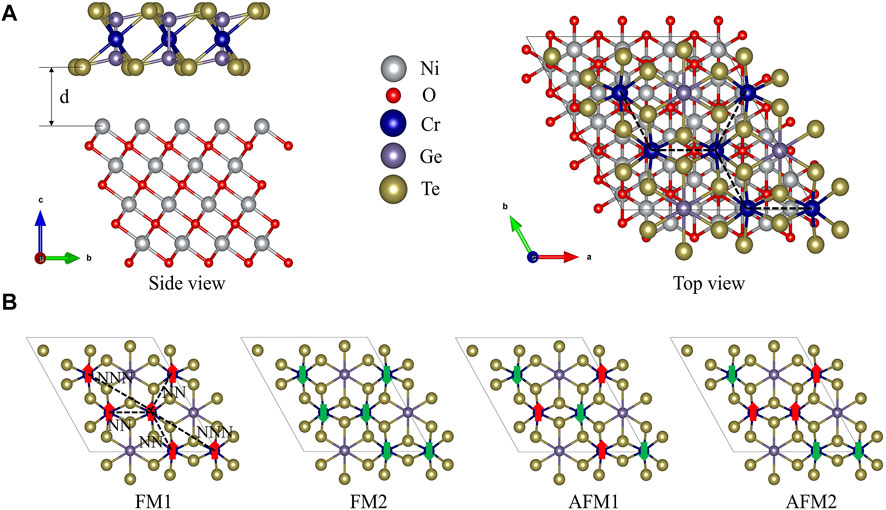
FIGURE 1. (A) Top and side views of the CrGeTe₃/NiO heterostructure. (B) Four possible magnetic states of CrGeTe₃: FM1, FM2, AFM1, and AFM2.

The total energies of FM1, FM2, AFM1, and AFM2 are −744.05, −744.26, −743.97, and −744.14 eV, respectively. It is obvious that the total energy of FM2 state is the lowest. Its total magnetic moment is −18 μ_B. Therefore, the ground state of CrGeTe₃/NiO heterojunction is the FM2 state, where the exchange interaction in the CrGeTe₃ monolayer is ferromagnetic and that between the CrGeTe₃ monolayer and the NiO layers is antiferromagnetic. In order to investigate the stability of the FM2 interface system, we further calculated the binding energy, which is defined as $E_f=E_{tot}-E_{CrGeT{e}_3}-E_{NiO}$. Here, $E_{tot}$ is the total energy of the heterostructure, $E_{CrGeT{e}_3}$ ($E_{NiO}$) is the total energy of the isolated CrGeTe₃ (NiO). The binding energy of the FM2 state is −0.067 eV/Ų. The negative binding energy of the FM2 state shows that the heterostructure is energetically preferred and can be realized in the experiment. We calculated the phonon spectra (Xie et al., 2021) of NiO (111) and CrGeTe₃ (001) surfaces in the FM2 state. The results showed that there is no virtual frequency, which means that the structures of NiO (111) and CrGeTe₃ (001) surfaces are stable.

In order to obtain the detailed charge transfer information of the interface, the charge density difference and Bader charge of the CrGeTe₃/NiO heterojunction in the FM2 state are calculated. Charge density difference is the redistribution of charge as the CrGeTe₃ monolayer is bound to the NiO substrate. In the interface calculation, the bonding of each atom at the interface can be intuitively shown by the charge density difference. The charge density difference can be expressed as $\Delta \rho ={\rho }_{CrGeT{e}_3/NiO}-{\rho }_{CrGeT{e}_3}-{\rho }_{NiO}$. Among them, $\Delta \rho$ is the difference of charge density, ${\rho }_{CrGeT{e}_3/NiO}$ is the total charge density of the heterojunction system, and ${\rho }_{CrGeT{e}_3}$ (${\rho }_{NiO}$) is the charge density of CrGeTe₃ (NiO) slab alone.

Figure 2A shows the charge density difference of the CrGeTe₃/NiO interface in the FM2 state, and Figure 2B zooms in the details of Figure 2A. The cyan area in Figure 2 indicates that the charge density difference is negative, and the yellow region indicates the charge density difference is positive. In Figure 2, the charge transfer results in Ni and Te weak covalent bonds across the interface. In order to further analyze the mechanism of charge transfer, Bader charge analysis is carried out for the system. The results showed that about 1.166 electron is transferred from NiO to CrGeTe₃. The charge transfer mainly occurs between the Ni, Te, and Cr atoms near the interface. In the binding process, a Te atom near the interface gets 0.098 electron in average, a Cr atom gets 0.060 electron in average, and the charge change of each Ge atom is negligible. However, the charge redistribution of the atoms away from the interface is negligible as they do not participate in the binding process.

FIGURE 2

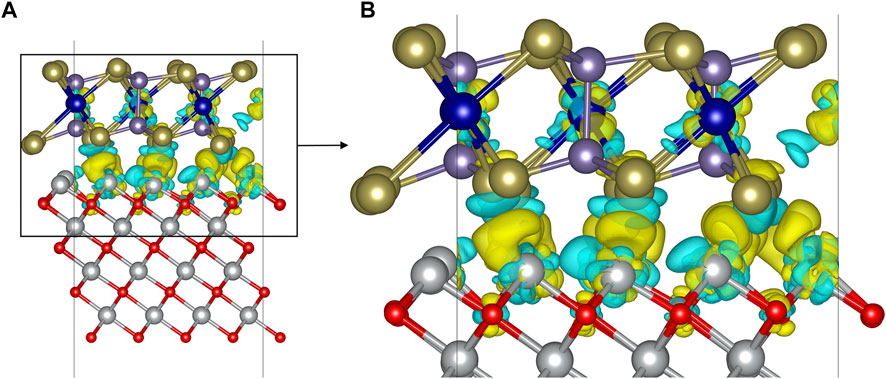
FIGURE 2. Differential charge density (A) and its local enlarged view (B) of the CrGeTe₃/NiO interface in the FM2 state. The isosurface is set to 0.021 e/ų.

In order to study the electronic properties of the CrGeTe₃/NiO interface in the FM2 state, the band structure and density of states of the model are calculated. The band structure of the CrGeTe₃/NiO heterojunction in the FM2 state is shown in Figure 3. The spin-up and spin-down band gaps are 0.578 and 0 eV, respectively. The total band gap is 0 eV. As a comparison, the band gaps of NiO and CrGeTe₃ bulk are calculated to be 2.026 and 0.236 eV, respectively, and those of the NiO (111) surface and CrGeTe₃ (001) monolayer are 0.003 and 0.256 eV, respectively. It is obvious that the band gap of the NiO (111) surface is much smaller than that of NiO bulk, and the band gap of the CrGeTe₃ (001) monolayer is very close to that of CrGeTe₃ bulk. The band gap of the CrGeTe₃/NiO heterojunction in the FM2 state is 0 eV, which is smaller than the NiO (111) surface band gap and CrGeTe₃ (001) monolayer.

FIGURE 3

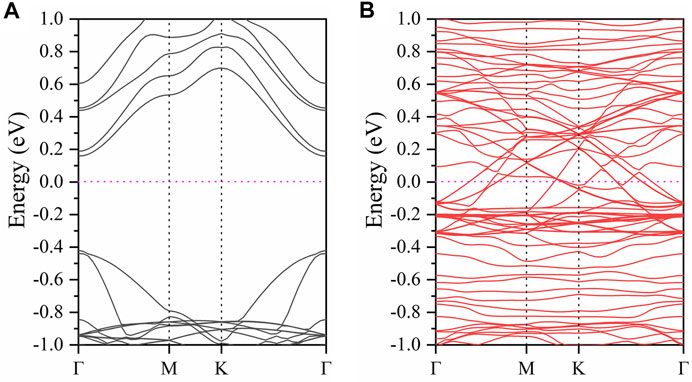
FIGURE 3. Band structure of the CrGeTe₃/NiO heterojunction in the FM2 state. (A) and (B) represent the spin-up and spin-down channels, respectively. The Fermi level is set to zero.

The projected density of states of Ni, Te, and Cr atoms near the interface of the CrGeTe₃/NiO heterojunction in the FM2 state is shown in Figure 4A. The projected density of states of Te and Cr atoms of the CrGeTe₃ alone is shown in Figure 4B. From Figure 4A, it is clear that the state near Fermi level is mainly contributed by the orbitals of Ni, Te, and Cr atoms. Among them, the contribution of the Cr-3d orbital is the largest. The Cr 3d state, the Ni 3d state, and the Te 5p state all pass through the Fermi level. From Figure 4B, it is clear that the state near Fermi level is mainly contributed by the orbitals of Te and Cr atoms. The band gap of CrGeTe₃ alone is 0.236 eV, which is significantly larger than that of CrGeTe₃/NiO heterojunction.

FIGURE 4

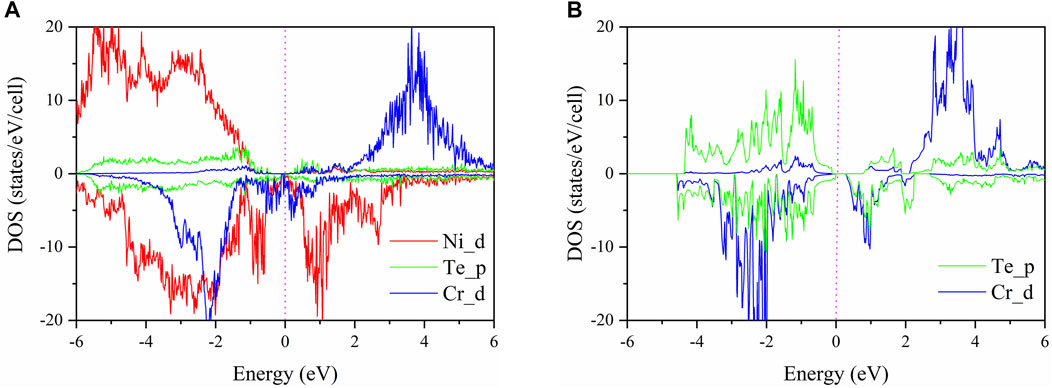
FIGURE 4. (A) Projected density of states (PDOS) for the CrGeTe₃/NiO interface in the FM2 state. (B) Projected density of states (PDOS) for CrGeTe₃ alone. The Fermi level is set to zero.

By comparing the PDOS in Figures 4A,B, for the spin-up state, it is seen that some new electronic states appear on the CrGeTe₃/NiO interface from 0.104 to 0.774 eV nearby the Fermi level. Some electronic states disappear from −0.394 to −0.114 eV nearby the Fermi level. These new electronic states lead to the downward movement of the top of the valence band and the bottom of the conduction band. The final result is that the band gap of the spin-up state of the CrGeTe₃/NiO heterojunction becomes smaller. For the spin-down state, it is seen that some new electronic states appear on the CrGeTe₃/NiO interface from −0.002 to 0.236 eV nearby the Fermi level. The appearance of these new electronic states leads to the upward movement of the top of the valence band and the downward movement of the bottom of the conduction band. The end result is that the band gap of the spin-down state of the CrGeTe₃/NiO heterojunction is reduced to zero.

The occupied Cr-3d orbital cannot appear in both spin-up and spin-down directions. For example, when it is found in the spin-down direction, the spin-up Cr-3d orbital is completely unoccupied. These results can be understood by crystal field theory. Cr³⁺ ions are located in an octahedral environment coordinated by six Te anions. The Cr-3d orbital splits into three low energy t_2g orbitals and two high energy e_g orbitals. According to Pauli’s exclusion principle and Hund’s rule, Cr³⁺ ions will present a high-spin t_2g³e_g⁰ electronic configuration, which means that all occupied 3d orbits must be in one spin direction. Among them, the Cr 3d state also contributes to the spin-down state. Also, higher than the Fermi level, the spin-up state is almost occupied by the Cr 3d state, and the spin-down state is almost occupied by the Ni 3d state.

In order to estimate the magnetic couplings in the CrGeTe₃/NiO heterojunction, we started from the Heisenberg model:

$\begin{array}{c}H=-{\displaystyle \sum _{i<j}{J}_{ij}{\mathit{S}}_i\cdot {\mathit{S}}_j}\end{array},(1)$

and it can be rewritten for our specific model:

$\begin{array}{c}H=-{\displaystyle \sum _{i<j}{J}_1{\mathit{S}}_i\cdot {\mathit{S}}_j}-{\displaystyle \sum _{k<l}{J}_2{\mathit{S}}_k\cdot {\mathit{S}}_l}-{\displaystyle \sum _{m<n}{J}_0{\mathit{S}}_m\cdot {\mathit{S}}_n}\end{array},(2)$

where $J_1$ is the intralayer exchange interaction between a Cr atom and its nearest-neighbors (NN), $J_2$ is the intralayer exchange interaction between a Cr atom and its next-nearest-neighbors (NNN), and $J_0$ is the interlayer exchange interaction parameter between a Cr atom and its NN Ni atoms in the top layer of NiO. The Ni atoms in the lower three layers of NiO are not considered in this model because of their weak exchange interaction with the Cr atoms. $S_i$-$S_m$ is the spin of a Cr atom ($S$) equal to 3/2. $S_n$ is the spin of a Ni atom ($S_{Ni}$) equal to 1.

In the CrGeTe₃ layer, there are three NN and six NNN Cr atoms for a Cr atom. In FM1 and FM2 structures, there are three NN spin parallel Cr atoms and six NNN spin parallel Cr atoms for a Cr atom. For the interlayer exchange interaction with the NiO substrate, the exchange interaction between a Cr atom and three nearest neighbor Ni atoms is considered. Because the spin directions of Cr and Ni atoms are the same, the interlayer coupling in the FM1 structure is ferromagnetic. Because the spin direction of Cr atom and Ni atom is opposite, the interlayer coupling in the FM2 structure is antiferromagnetic. For an AFM1 structure, there are three NN antiparallel spin Cr atoms and six NNN parallel spin Cr atoms for each Cr atom. In addition, because the sum of the spin of Cr atoms is zero, the summation of the exchange interaction between Cr and Ni atoms is also zero. For the AFM2 structure, the situation is complicated. The interlayer magnetic coupling is the same as AFM1, which is zero. For intralayer magnetic coupling, there are four Cr atoms with one NN parallel spin and two NN antiparallel spin Cr atoms. At the same time, these four Cr atoms also have three NNN parallel spin and three NNN antiparallel spin Cr atoms. The other two Cr atoms have two NN parallel spin and one NN antiparallel spin Cr atoms. At the same time, these two Cr atoms also have six NNN antiparallel spin Cr atoms. Therefore, the total energies of the CrGeTe₃/NiO heterojunction in four magnetic states can be written as follows:

$\begin{array}{c}\{\begin{array}{c}{E}_{FM1}=E_0-9J_1{\left|\mathit{S}\right|}^2-18J_2{\left|\mathit{S}\right|}^2-18J_0\left|\mathit{S}\cdot {\mathit{S}}_{Ni}\right|,\\ E_{FM2}=E_0-9J_1{\left|\mathit{S}\right|}^2-18J_2{\left|\mathit{S}\right|}^2+18J_0\left|\mathit{S}\cdot {\mathit{S}}_{Ni}\right|,\\ E_{AFM1}=E_0+9J_1{\left|\mathit{S}\right|}^2-18J_2{\left|\mathit{S}\right|}^2,\\ E_{AFM2}=E_0+J_1{\left|\mathit{S}\right|}^2+6J_2{\left|\mathit{S}\right|}^2,\end{array}\end{array}(3)$

where $E_0$ is the total energy excluding the magnetic coupling that is insensitive to the magnetic states. By eliminating $E_0$, the exchange constants are solved as follows:

$\begin{array}{c}\{\begin{array}{c}{J}_0=\frac{E_{FM2}-E_{FM1}}{36\left|\mathit{S}\cdot {\mathit{S}}_{Ni}\right|},\\ J_1=\frac{E_{AFM1}-\frac{E_{FM1}+E_{FM2}}{2}}{18{\left|\mathit{S}\right|}^2},\\ J_2=\frac{J_1}{3}-\frac{E_{AFM1}-E_{AFM2}}{24{\left|\mathit{S}\right|}^2}.\end{array}\end{array}(4)$

Substituting the calculated total energies of the four magnetic states into Eq. 4, we can get the following exchange interaction parameters: $J_0=-3.87 meV,$ $J_1=+4.76 meV,$ and $J_2=-1.73 meV.$ It is clear that the intralayer exchange interaction between the NN Cr atoms is ferromagnetic, which is consistent with the previous experimental result that the CrGeTe₃ monolayer is a two-dimensional intrinsic ferromagnet (Gong et al., 2017). In addition, the interlayer exchange interaction between the Ni and Cr atoms is antiferromagnetic. An intralayer ferromagnetic interaction between the nearest Cr atoms is produced close to the 90° Cr-Te-Cr superexchange channel. At the same time, the interlayer antiferromagnetic interaction between Cr and Ni atoms is produced by approaching the 120° Cr-Te-Ni superexchange channel.

Magnets with large magnetic anisotropy energy (MAE) have potential applications in magnetic storage. Magnetic anisotropy can avoid the Mermin–Wagner theorem and make a detour to long-range magnetic order in two-dimensional magnets at a non-zero temperature (Mermin and Wagner, 1966; Torelli et al., 2019). MAE is defined as the energy difference when magnetization is in-plane and out-of-plane, respectively ($MAE=E_{\parallel }-E_{\perp }$), where $E_{\parallel }$ is the total energy with the in-plane magnetization direction, and $E_{\perp }$ is that with out-of-plane magnetization direction. The positive (negative) value of MAE represents that the out-of-plane (in-plane) is energetically preferred. The MAE of the CrGeTe₃/NiO heterojunction is calculated by enabling spin-orbit coupling (SOC). The easy axis is in-plane with a MAE of −0.094 meV/Ų.

The previous experimental result indicates that the CrGeTe₃/NiO heterostructure shows a higher Curie temperature than the free-standing CrGeTe₃ monolayer (Idzuchi et al., 2019). Therefore, we showed that the Ni–Cr interlayer exchange leads to the increase in Curie temperature of CrGeTe₃.

The total exchange energy (Zhong et al., 2017) between the Cr and Ni atoms is $\Delta E=\frac{E_{FM1}-E_{FM2}}{2}=104.54 meV$ by the ab initio calculations. Because there are six Cr atoms in the cell, the average exchange energy of each Cr atom is $\overline{E}=17.42 meV$.

In the Zeeman effect, it is written as follows:

$\begin{array}{c}\overline{E}=-g{\mu }_B\mathit{S}\cdot \mathit{B}\end{array},(5)$

where $g$ is the g factor ($g\approx 2$), ${\mu }_B$ is the Bohr magneton, $S$ is the spin of Cr³⁺ ion ($S=3/2$), and $B$ is the magnetic induction intensity. Substituting the ab initio value into Eq. 5, we obtained $B=100.3 \text{T}$, which is the equivalent magnetic field exerted by the NiO substrate on to the CrGeTe₃ layer. The influence of the NiO substrate on the Curie temperature of the CrGeTe₃ monolayer by the interlayer magnetic coupling is analyzed by means of mean field theory.

Brillouin function is defined by Yosida (1996) as follows:

$\begin{array}{c}{B}_S\left(x\right)=\frac{2S+1}{2S}\coth \left(\frac{2S+1}{2S}x\right)-\frac{1}{2S}\coth \left(\frac{1}{2S}x\right)\end{array},(6)$

where $S$ is the spin of Cr atom, and the value of $x$ is as follows:

$\begin{array}{c}x=\frac{2S\sigma \mathcal{J}\left(0\right)+g{\mu }_{B}SB}{k_{B}T}\end{array},(7)$

where $\sigma$ is the thermo average magnetic moment of Cr atom, $k_B$ is Boltzmann’s constant, $T$ is temperature, and $J\left(0\right)$ is defined by

$\begin{array}{c}\mathcal{J}\left(\mathit{q}\right)={\displaystyle \sum _{n}J\left({\mathit{R}}_{\mathit{n}}\right)e^{-\mathit{i}\mathit{q}\cdot {\mathit{R}}_{\mathit{n}}}}\end{array},(8)$

where $J\left(R_n\right)$ is the exchange interaction between the lattice sites, and $q$ is the vector in the reciprocal space. Substituting the exchange constant obtained before, the value of $\mathcal{J}\left(0\right)$ is approximately calculated as follows: $\mathcal{J}\left(0\right)={\displaystyle \sum _{n}J\left({\mathrm{R}}_n\right)}=3J_1+6J_2=3.90 meV=6.25\times {10}^{-22} J.$

At thermo equilibrium, the following equation can be obtained as follows:

$\begin{array}{c}\sigma =S{B}_S\left(\frac{2S\mathcal{J}\left(0\right)}{k_{B}T}\sigma +\frac{g{\mu }_{B}SB}{k_{B}T}\right)\end{array}.(9)$

The left and right sides of Eq. 9 are two functions, respectively, as follows:

$\begin{array}{c}\{\begin{array}{c}y=\sigma ,\\ y=S{B}_S\left(\frac{2S\mathcal{J}\left(0\right)}{k_{B}T}\sigma +\frac{g{\mu }_{B}SB}{k_{B}T}\right).\end{array}\end{array}(10)$

At fixed temperature $T$ and magnetic induction intensity $B$, the solutions of Eq. 9 are the intersection points of the two curves of Eq. 10, as shown in Figure 5.

FIGURE 5

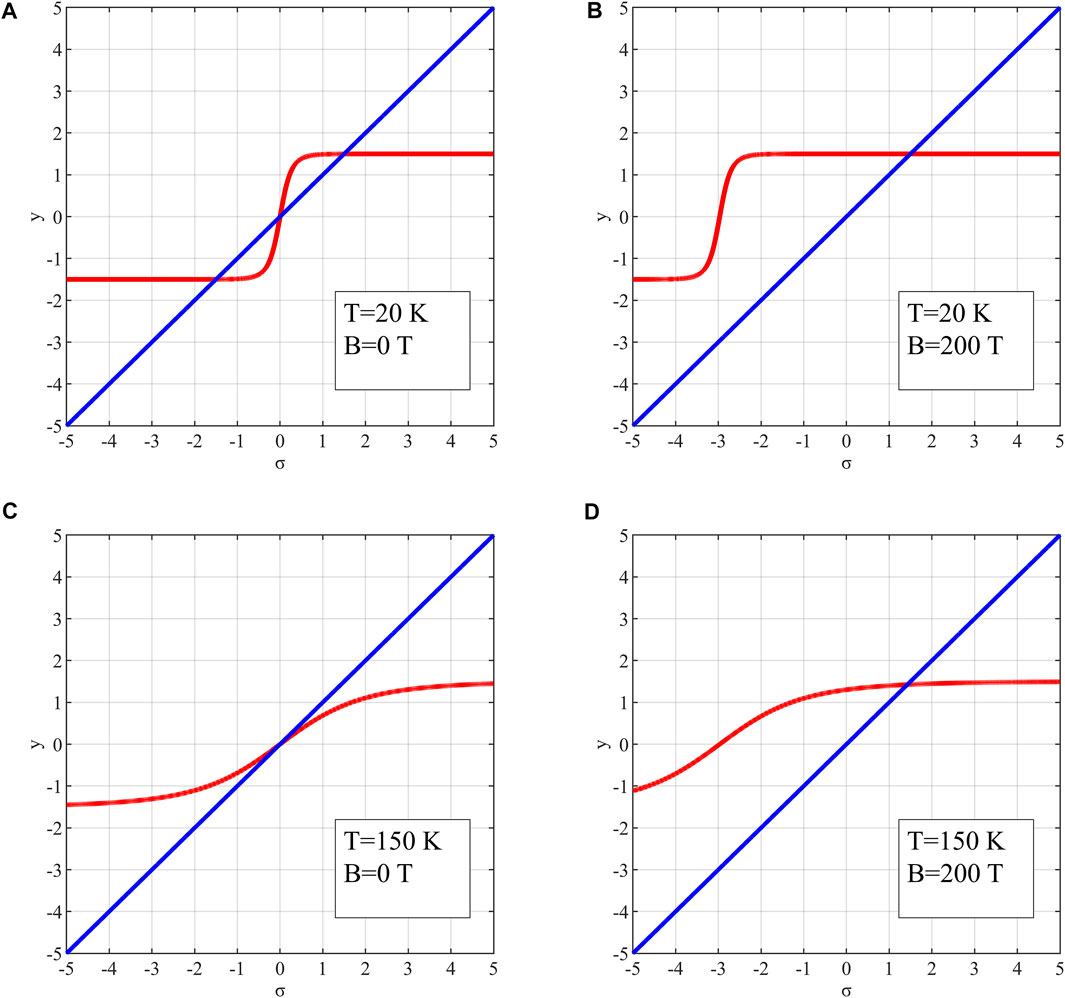
FIGURE 5. Two functions in Eq. 10 with different parameter sets: (A) $T=20 K,$ $B=0 T;$ (B) $T=20 K,$ $B=200 T;$ (C) $T=150 K,$ $B=0 T;$ (D) $T=150 K,$ $B=200 T.$ The red line represents $y=S{B}_S\left(\frac{2S\mathcal{J}\left(0\right)}{k_{B}T}\sigma +\frac{g{\mu }_{B}SB}{k_{B}T}\right)$, and the blue line represents $y=\sigma$.

In Figures 5A,C, there is no equivalent external field, while there is in Figures 5B,D. In Figure 5A, two functions crossover in the first quadrant, indicating that Eq. 9 has a non-zero solution of $\sigma$, which is the average magnetic moment of Cr atom below Curie temperature. In Figure 5C, there is only one intersection point at the origin, which indicates that the spontaneous magnetization vanishes when the temperature is above the Curie temperature. However, when the external field is not zero, as shown in Figures 5B,D, even if the temperature is higher than the Curie temperature at zero extra field, there is still a non-zero solution of $\sigma$, which implies the rise of Curie temperature.

By taking different $T$ values under $B=0 T$, $10 T$, $100 T$, and $200 T$ and solving Eq. 9, the $\sigma -T$ figure is platted in Figure 6:

FIGURE 6

FIGURE 6. $\sigma -T$ curves at different values of $B$.

It is noticeable that the decrease of $\sigma$ with the increase of $T$ is much slower at $B=100 T$ than at $B=0 T$. It indicates that the heterostructure of CrGeTe₃ and NiO is equivalent to applying a strong magnetic field on the CrGeTe₃ monolayer. Thus, the Curie temperature is boosted.

Conclusion

In summary, we built the CrGeTe₃/NiO heterojunction model and discovered that the interlayer exchange interaction between the Cr atoms and Ni atoms is antiferromagnetic using the first-principles calculations. We further calculated the electrical and magnetic properties of the CrGeTe₃/NiO interface. We inferred that the NiO substrate is equivalent to applying a strong magnetic field of $B=100.3\text{ T}$ on the CrGeTe₃ layer, which is the reason for the increase of Curie temperature. In addition, the easy axis is in-plane with a MAE of −0.094 meV/Ų.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

XuL and XZ conceived and implemented the review process. XuL was responsible for the main writing of the manuscript. XZ was responsible for the modification of the manuscript. ZL helped process and check the data part. WZ and HZ helped to build the structure model and provide ideas on magnetic calculation. PY and XiL provided ideas on electronic structure calculation. All authors contributed to the manuscript and approved the submitted version.

Funding

This research is supported by the Science Challenge Project (Grant No. TZ2016003-1-105), the Tianjin Natural Science Foundation (Grant No. 20JCZDJC00750), and the Fundamental Research Funds for the Central Universities-Nankai University (Grant No 63211107 and 63201182).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Casto, L. D., Clune, A. J., Yokosuk, M. O., Musfeldt, J. L., Williams, T. J., Zhuang, H. L., et al. (2015). Strong Spin-Lattice Coupling in CrSiTe3. Apl. Mater. 3, 041515. doi:10.1063/1.4914134

CrossRef Full Text | Google Scholar

Chen, S., Huang, C., Sun, H., Ding, J., Jena, P., and Kan, E. (2019). Boosting the Curie Temperature of Two-Dimensional Semiconducting CrI3 Monolayer through van der Waals Heterostructures. J. Phys. Chem. C 123, 17987–17993. doi:10.1021/acs.jpcc.9b04631

CrossRef Full Text | Google Scholar

Chen, X., Qi, J., and Shi, D. (2015). Strain-engineering of Magnetic Coupling in Two-Dimensional Magnetic Semiconductor CrSiTe3: Competition of Direct Exchange Interaction and Superexchange Interaction. Phys. Lett. A 379, 60–63. doi:10.1016/j.physleta.2014.10.042

CrossRef Full Text | Google Scholar

Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J., and Sutton, A. P. (1998). Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 57, 1505–1509. doi:10.1103/PhysRevB.57.1505

CrossRef Full Text | Google Scholar

Fang, H., Chuang, S., Chang, T. C., Takei, K., Takahashi, T., and Javey, A. (2012). High-Performance Single Layered WSe2 P-FETs with Chemically Doped Contacts. Nano Lett. 12, 3788–3792. doi:10.1021/nl301702r

PubMed Abstract | CrossRef Full Text | Google Scholar

Geim, A. K. (2009). Graphene: Status and Prospects. Science 324, 1530–1534. doi:10.1126/science.1158877

PubMed Abstract | CrossRef Full Text | Google Scholar

Geim, A. K., and Grigorieva, I. V. (2013). Van der Waals heterostructures. Nature 499, 419–425. doi:10.1038/nature12385

PubMed Abstract | CrossRef Full Text | Google Scholar

Geim, A. K., and Novoselov, K. S. (2007). The Rise of Graphene. Nat. Mater 6, 183–191. doi:10.1038/nmat1849

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, C., Li, L., Li, Z., Ji, H., Stern, A., Xia, Y., et al. (2017). Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269. doi:10.1038/nature22060

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, M. J., and van Veenendaal, M. (2012). Spin-moment Formation and Reduced Orbital Polarization in LaNiO3/LaAlO3superlattice:LDA+Ustudy. Phys. Rev. B 85, 195102. doi:10.1103/PhysRevB.85.195102

CrossRef Full Text | Google Scholar

Han, W., Kawakami, R. K., Gmitra, M., and Fabian, J. (2014). Graphene Spintronics. Nat. Nanotech 9, 794–807. doi:10.1038/nnano.2014.214

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, W. (2016). Perspectives for Spintronics in 2D Materials. Apl. Mater. 4, 032401. doi:10.1063/1.4941712

CrossRef Full Text | Google Scholar

Idzuchi, H., Llacsahuanga Allcca, A. E., Pan, X. C., Tanigaki, K., and Chen, Y. P. (2019). Increased Curie Temperature and Enhanced Perpendicular Magneto Anisotropy of Cr2Ge2Te6/NiO Heterostructures. Appl. Phys. Lett. 115, 232403. doi:10.1063/1.5130930

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Kubota, Y., Watanabe, K., Tsuda, O., and Taniguchi, T. (2007). Deep Ultraviolet Light-Emitting Hexagonal Boron Nitride Synthesized at Atmospheric Pressure. Science 317, 932–934. doi:10.1126/science.1144216

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Xu, Y.-K., Lai, K., and Zhang, W.-B. (2019). The enhanced ferromagnetism of single-layer CrX3 (X = Br and I) via van der Waals engineering. Phys. Chem. Chem. Phys. 21, 11949–11955. doi:10.1039/C9CP01837A

PubMed Abstract | CrossRef Full Text | Google Scholar

Liechtenstein, A. I., Anisimov, V. I., and Zaanen, J. (1995). Density-functional Theory and Strong Interactions: Orbital Ordering in Mott-Hubbard Insulators. Phys. Rev. B 52, R5467–R5470. doi:10.1103/PhysRevB.52.R5467

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, B., Zou, Y., Zhang, L., Zhou, S., Wang, Z., Wang, W., et al. (2016). Critical Behavior of the Quasi-Two-Dimensional Semiconducting Ferromagnet CrSiTe3. Sci. Rep. 6, 33873. doi:10.1038/srep33873

PubMed Abstract | CrossRef Full Text | Google Scholar

MacDonald, A. H., Schiffer, P., and Samarth, N. (2005). Ferromagnetic Semiconductors: Moving beyond (Ga,Mn)As. Nat. Mater 4, 195–202. doi:10.1038/nmat1325

CrossRef Full Text | Google Scholar

Mak, K. F., Lee, C., Hone, J., Shan, J., and Heinz, T. F. (2010). Atomically ThinMoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 105, 136805. doi:10.1103/PhysRevLett.105.136805

PubMed Abstract | CrossRef Full Text | Google Scholar

Mermin, N. D., and Wagner, H. (1966). Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 17, 1133–1136. doi:10.1103/physrevlett.17.1133

CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B 13, 5188–5192. doi:10.1103/physrevb.13.5188

CrossRef Full Text | Google Scholar

Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Pesin, D., and MacDonald, A. H. (2012). Spintronics and Pseudospintronics in Graphene and Topological Insulators. Nat. Mater 11, 409–416. doi:10.1038/nmat3305

PubMed Abstract | CrossRef Full Text | Google Scholar

Torelli, D., Thygesen, K. S., and Olsen, T. (2019). High Throughput Computational Screening for 2D Ferromagnetic Materials: the Critical Role of Anisotropy and Local Correlations. 2D Mat. 6, 045018. doi:10.1088/2053-1583/ab2c43

CrossRef Full Text | Google Scholar

Williams, T. J., Aczel, A. A., Lumsden, M. D., Nagler, S. E., Stone, M. B., Yan, J.-Q., et al. (2015). Magnetic Correlations in the Quasi-Two-Dimensional Semiconducting ferromagnetCrSiTe3. Phys. Rev. B 92, 144404. doi:10.1103/physrevb.92.144404

CrossRef Full Text | Google Scholar

Xie, C., Liu, Y., Zhang, Z., Zhou, F., Yang, T., Kuang, M., et al. (2021). Sixfold Degenerate Nodal-point Phonons: Symmetry Analysis and Materials Realization. Phys. Rev. B 104, 045148. doi:10.1103/PhysRevB.104.045148

CrossRef Full Text | Google Scholar

Yosida, K. (1996). Theory of Magnetism. Berlin: Springer.

Google Scholar

Yu, J., Lin, X., Wang, J., Chen, J., and Huang, W. (2009). First-principles Study of the Relaxation and Energy of Bcc-Fe, Fcc-Fe and AISI-304 Stainless Steel Surfaces. Appl. Surf. Sci. 255, 9032–9039. doi:10.1016/j.apsusc.2009.06.087

CrossRef Full Text | Google Scholar

Zhong, D., Seyler, K. L., Linpeng, X., Cheng, R., Sivadas, N., Huang, B., et al. (2017). Van der Waals engineering of ferromagnetic semiconductor heterostructures for spin and valleytronics. Sci. Adv. 3, e1603113. doi:10.1126/sciadv.1603113

PubMed Abstract | CrossRef Full Text | Google Scholar

Žutić, I., Fabian, J., and Das Sarma, S. (2004). Spintronics: Fundamentals and Applications. Rev. Mod. Phys. 76, 323–410. doi:10.1103/RevModPhys.76.323

CrossRef Full Text | Google Scholar