Arrangement and Decomposition of Grain Boundary Dislocations: Two-Mode Phase-Field Crystal Simulation

The grain-boundary dislocation arrangement and decomposition during constant-volume deformation of a nanoscale bi-crystal system in fcc-structured materials were studied by using the two-mode phase-field crystal (2PFC) method. The effects of different grain boundary misorientations (GBMs) and tensile deformation directions on the dislocation arrangement and decomposition are analyzed. In three different symmetrical tilt grain boundaries evaluated by PFC, the atomic density profile of grain boundaries changed periodically at equilibrium. The initial grain boundary dislocation arrangement of the three samples is almost the same when tensile deformation is applied to the samples in the x- or y- direction, and all are symmetrically arranged in a “bowknot ”structure. The stress at the grain boundary is concentrated with the increase of strain, and dislocation decomposition can effectively reduce the stress concentration. The time steps of dislocation decomposition at grain boundaries decreases with increasing strain rate. This work facilitates the application of PFC in the analysis of grain-boundary mechanics in an extended range of materials.

Introduction

The mechanical behavior of materials is affected by defects such as dislocations and grain boundaries, which are related to atomic structure (Hirouchi et al., 2010). The study of the grain-boundary structure and dislocation movement mechanism is conducive to understanding the evolution law of material microstructure and can provide some theoretical support for optimizing processes and improving material properties to a certain extent (Kumar et al., 2003; Hou et al., 2020; Park et al., 2021; Roy et al., 2022).

The study of material properties has become more and more thorough with the progress of experimental technology. The tensile deformation behaviors under different conditions were studied by experiments. For example, tensile response and fracture behavior (Mahabadi et al., 2014), dislocation configuration near the tensile fracture (Liu et al., 2012), the change of grain orientation before and after tensile deformation, and the yield strength of the alloy can be observed by using a scanning electron microscope (SEM), orientation imaging microscopy (OIM), transmission electron microscope (TEM), and electron backscattered diffraction (EBSD) (Suh et al., 2017; Xia et al., 2019; Li et al., 2020; Yan et al., 2021). The high-resolution transmission electron microscope (HRTEM) (Bian et al., 2017) was used to observe the microstructure on a smaller scale (Yang et al., 2020; Volnistem et al., 2021; Guo et al., 2021). However, experimental inquiry alone is not enough in scientific research. Because the process of material microstructure formation and its performance characteristics are essentially multi-scale coupling. So far, the experimental study of the microstructure of materials has some limitations. Atomic simulation can supplement it, especially in the study of scale (Xin et al., 2021; Kuang et al., 2018; Zhao et al., 2018; Guo et al., 2019). With the rapid development of computer simulation, such as the phase-field method (PF) (Peng et al., 2021), molecular dynamics (MD) (Song et al., 2014), and phase-field crystal method (PFC) (Zhao et al., 2014). The evolution morphology of multi-scale material microstructure is vividly given (Zhang et al., 2018; Zhao et al., 2019). Combined with EBSD (Nielsen et al., 2020; Zhao et al., 2021) and HRTEM (Zhang et al., 2019; Shuai et al., 2021) technology, the research efficiency is greatly improved. It is worth mentioning that the phase-field crystal method is more suitable for studying the microstructure defects of crystals. Because the PF method generally studies mesoscopic scale, it is difficult to provide atomic-scale information, and the time scale $\left({10}^{-14}\sim {10}^{-12}\text{s}\right)$ in MD simulations is much smaller than the diffusion scale $\left({10}^{-6}s\right)$ of the microcosmic defects.

Elder et al. (2002) proposed the PFC method which closely a coupled model between atom and microscale according to Ginzburg Landau's theory. The evolution of crystal patterns simulated (Qi et al., 2020; Chen and Zhao, 2021), which can quantitatively reproduce some key characteristics affecting the evolution of microstructure (Tian et al., 2021), and clearly describe the dislocation structure of grain boundary (Qi et al., 2019). The model is expressed in terms of experimentally measurable physical quantities such as liquid structure factors (Hu et al., 2020). Now it has successfully simulated dislocation movement, grain-boundary pre-melting, growth of crystals. The model cannot describe the dislocation motion in a two-dimensional square lattice. Therefore, Wu et al. (2010) and Asadi and Zaeem (2015) modified the free energy function and proposed the 2PFC model. The study of phase diagrams makes the experiment and simulation more closely combined (Greenwood et al., 2010; Can et al., 2013). The 2PFC model studies the deformation and morphology of small-angle asymmetric grain boundaries (Zhang et al., 2014), the migration and dislocation reaction of grain boundaries under deviatoric deformation (Hu et al., 2016a), and the solidification law (Yang et al., 2014) of square phase grains under low, medium, and high driving force during phase transformation. These simulation studies reveal the microstructure phenomena under different conditions on a smaller atomic scale.

In this work, we focus on the dislocation decomposition and dislocation arrangement of low-angle symmetrically tilt grain boundaries under different tensile deformation directions. In the following, we will first describe the model and method in Section 2. The tensile response of grain boundary at x and y tensile deformation directions are presented in Section 3, followed by strain rate, deformation direction, and misorientation angle that affect the critical strain value for grainboundary dislocation decomposition discussed in Section 4. The final conclusion is presented in Section 5.

Models and Methods

Two-Mode Phase-Field Crystal Model

The two-mode PFC model (Wu et al., 2010) simulates the crystal structure and the free energy of a system is as

$\begin{array}{c}\mathcal{F}={\displaystyle \int \left\{\frac{\varphi }{2}\left[a+\lambda {\left({\nabla }^2+q_0^2\right)}^2\right]\left[{\left({\nabla }^2+q_1^2\right)}^2+r_1\right]\varphi +g\frac{{\varphi }^4}{4}\right\}}d\mathit{x}\end{array},(1)$

where $a$ is the lattice parameter. $r_1$ is related to the relative amplitude of density wave, $q_0$ and $q_1$ represents the wavelengths of the first and second density waves. $\lambda$ and $g$ are phenomenological parameters to fit the properties of the material (Blixt et al., 2022).

To minimize the number of parameters, we define the dimensionless parameters

$\begin{array}{cccccc}ϵ=-\frac{a}{\lambda q_0^8},& R_1=\frac{r_1}{q_0^4},& Q_1=\frac{q_1}{q_0},& \psi =\sqrt{\frac{g}{\lambda q_0^8}}\varphi ,& F=\frac{g}{{\lambda }^2{q}_0^{13}}\mathrm{ℱ},& \mathit{r}=q_0\mathit{x}\end{array}.(2)$

substituting the abovementioned definitions into Eq. 1 yields the dimensionless form

$\begin{array}{c}F={\displaystyle \int \left\{\frac{\psi }{2}\left[-ϵ+{\left({\nabla }^2+1\right)}^2\left[{\left({\nabla }^2+Q_1^2\right)}^2+R_1\right]\psi +\frac{{\psi }^4}{4}\right]\right\}}d\mathit{r}\end{array},(3)$

where $\mathit{ϵ}$ controls the size of the solid-liquid coexistence regions as a function of density. $Q_1$ is determined by the selection of crystal structure. $R_1$ controls the relative stability of mode structures. In this word, $Q_1=\sqrt{2}$, $R_1=0$.

The Fourier amplitudes of the first and second reciprocal lattice vectors (RLV) denote by $A_i$ and $B_i$. It is assumed that all density waves in solid-state have the same amplitudes, $\left|A_i\right|=A_s$, $\left|B_i\right|=B_s$. The solid-state density field of FCC crystal is as follows

$\begin{array}{c}{\psi }_s={\psi }_0+2A_s\left[\cos \left(q_{s}x\right)+\cos \left(q_{s}y\right)\right]+4B_s\cos \left(q_{s}x\right)\cos \left(q_{s}y\right)\end{array},(4)$

where $q_s=1$.

The free energy density in the solid-state is

$f_s=2\left(-\mathit{ϵ}+3{\psi }_0^2\right)A_s^2+2\left(-\mathit{ϵ}+3{\psi }_0^2\right)B_s^2+24{\psi }_0{A}_s^2{B}_s$

$\begin{array}{c}+36A_s^2{B}_s^2+9A_s^4+9B_s^4-\frac{\mathit{ϵ}}{2}{\psi }_0^2+2{\psi }_0^2+\frac{1}{4}{\psi }_0^4\end{array},(5)$

where $A_s=\frac{1}{9M}{\left[{\mathit{ϵ}}^2+75{\psi }_0^4-2{\psi }_{0}N+4\mathit{ϵ}{\psi }_0^2+\left(5\mathit{ϵ}-31{\psi }_0^2\right)M^2+M^4-10{\psi }_0^3-2\mathit{ϵ}{\psi }_{0}M\right]}^{\frac{1}{2}}$

$\begin{array}{c}+\frac{1}{9M}{\left[\sqrt{3}\left({\mathit{ϵ}}^2+75{\psi }_0^4-2{\psi }_{0}N+4\mathit{ϵ}{\psi }_0^2-M^4+10{\psi }_0^{3}M+2\mathit{ϵ}{\psi }_0\text{M}\right)i\right]}^{\frac{1}{2}}\end{array},(6)$

$\begin{array}{c}{B}_s=-\frac{1}{18M}\left[\mathit{ϵ}+5{\psi }_0^2+8{\psi }_{0}M+M^2+\sqrt{3}\left(M^2-5{\psi }_0^2-\mathit{ϵ}\right)i\right]\end{array},(7)$

$\begin{array}{c}M={\left(3\mathit{ϵ}{\psi }_0+\sqrt{-{\mathit{ϵ}}^3-6{\mathit{ϵ}}^2{\psi }_0^2-225\mathit{ϵ}{\psi }_0^4+500{\psi }_0^6}-25{\psi }_0^3\right)}^{\frac{1}{3}}\end{array},(8)$

$\begin{array}{c}N=-{\mathit{ϵ}}^3-6{\mathit{ϵ}}^2{\psi }_0^2-225\mathit{ϵ}{\psi }_0^4+500{\psi }_0^6\end{array}.(9)$

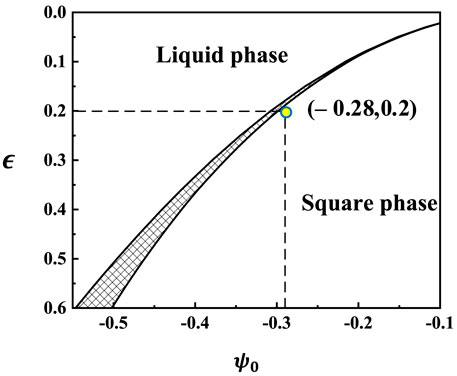
The phase diagram is derived by taking the derivative of free energy for the density field of the square phase and liquid phase respectively and using the common tangent rule, as shown in Figure 1.

FIGURE 1

FIGURE 1. Two-dimensional phase diagram of two-mode approximate calculation.

Application of Applied Stress

First, we apply tensile stress along the x-direction to the system. We employ the isovolumetric numerical scheme (Hirouchi et al., 2009; Berry et al., 2015) during the deformation process:

$\begin{array}{c}S=\mathrm{\Delta }{x}_0\mathrm{\Delta }{y}_0=\mathrm{\Delta }x\mathrm{\Delta }y\end{array}.(10)$

The grid sizes after $n$ time steps are shown as follows:

$\begin{array}{c}\mathrm{\Delta }x=\mathrm{\Delta }{x}_0\left(1+n\dot{\epsilon }\mathrm{\Delta }t\right)\end{array}.(11)$

$\begin{array}{c}\mathrm{\Delta }y=\frac{\mathrm{\Delta }{y}_0}{1+n\dot{\epsilon }\mathrm{\Delta }t}\end{array}.(12)$

similarly, when tensile stress along the y-direction to the system, we have

$\begin{array}{c}\mathrm{\Delta }x=\frac{\mathrm{\Delta }{x}_0}{1+n\dot{\epsilon }\mathrm{\Delta }t}\end{array},(13)$

$\begin{array}{c}\mathrm{\Delta }y=\mathrm{\Delta }{y}_0\left(1+n\dot{\epsilon }\mathrm{\Delta }t\right)\end{array},(14)$

where $\mathrm{\Delta }{x}_0$ and $\mathrm{\Delta }{y}_0$ are initial grid sizes; $\mathrm{\Delta }x$ and $\mathrm{\Delta }y$ are grid sizes after deformation.

Numerical Calculation Method and Parameter Setting

Since the atomic density field is a conserved value, the dimensionless time evolution equation $\psi$ can be expressed by the following Cahn-Hilliard equation (Wu et al., 2010):

$\begin{array}{c}\frac{\partial \psi }{\partial t}={\nabla }^2\frac{\delta F}{\delta \psi }={\nabla }^2\left\{\left[-\mathit{ϵ}+{\left({\nabla }^2+1\right)}^2+{\left({\nabla }^2+2\right)}^2\right]\psi +{\psi }^3\right\}\end{array}.(15)$

By transforming the partial differential equation into a sequence of ordinary differential equations in Fourier space, we apply a Fourier-spectral approximation to Equation 10, we have

$\begin{array}{c}{\psi }_{\mathit{k},t+\mathrm{\Delta }t}=\frac{{\psi }_{\mathit{k},t}-k^2\mathrm{\Delta }t{\psi }_{\mathit{k},t}^3}{1+k^2\mathrm{\Delta }t\left[\left(4-r\right)-12k^2+13k^4-6k^6+k^8\right]}\end{array},(16)$

Where ${\psi }_{\mathit{k},t}$ and ${\psi }_{\mathit{k},t+\mathrm{\Delta }t}$ represents the atomic density at a time $t$ and $t+\mathrm{\Delta }t$ in Fourier space, respectively. $k^2=\left|k^2\right|$ represents the wave vector in Fourier space.

The parameters of the simulation system in this work are set as follows: the simulation region of periodic boundary conditions in all directions is $L_x\times L_y=256\mathrm{\Delta }x\times 256\mathrm{\Delta }y$. The time step and space step are $\mathrm{\Delta }t=0.5$ and $\mathrm{\Delta }x=\mathrm{\Delta }y=\pi /4$, respectively. We set a sandwich simulation structure, $0<x<L_x/4$, $L_x/4<x<3L_x/4$, and $3L_x/4<x<L_x$. Grain orientation angle is set respectively ${\theta }_1$, ${\theta }_{2 }$, and ${\theta }_1$ The misorientation angle $\theta ={\theta }_1-{\theta }_2$ , which is the angle between two adjacent grains. The selection of other simulation parameters is shown in Table 1. The reason for choosing the atomic density parameter is that it is located in the coexistence region of a liquid phase and square phase, so the solid and liquid phases can coexist stably without phase transition (Hu et al., 2016b).

TABLE 1

TABLE 1. Parameters for sample preparation.

We let the system relax for a period of ${10}^4$ time steps to acquire structure equilibrium. The bi-crystal structure with GBM of $6^{°}$ and $7^{°}$ under x-direction tensile strain is applied, as shown in Figure 2. There are two symmetric tilt GBs and every GB consists of four edge dislocations arranged symmetrically. The grain orientation angle ${\theta }_1=b/2D_1$, where $b$ is the amount of Burgers vector and $D_1$ is the spacing of the arrangement of the edge dislocation (Gao et al., 2020). Because the difference in grain orientation angle is very small, the number of edge dislocations in the equilibrium structure of the two systems is the same. At the same time, we find that the atomic density distribution curves of the upper and lower grain boundaries of the two systems change periodically.

FIGURE 2

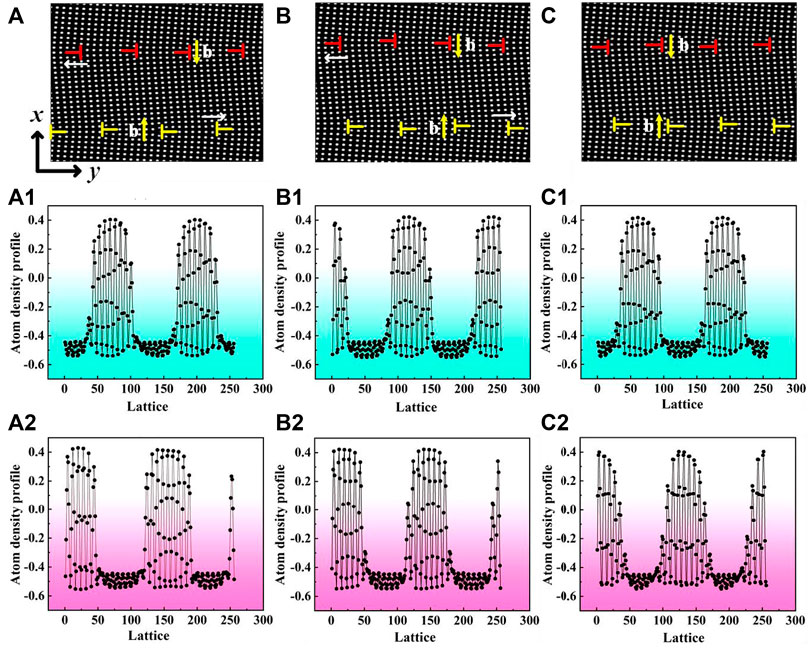
FIGURE 2. (A), (B) Bi-crystal structure with grain boundary misorientation angles of $6^{°}$ and $7^{°}$ under x-direction tensile strain, and the time steps is 5,000. (C) The bi-crystal structure with grain boundary misorientation angles of $7^{°}$ under y-direction tensile strain, and the time steps is 5,000. (A1–C1) The atomic density profile of the upper grain boundary corresponding to the misorientation angle, respectively. (A2–C2) The atomic density profile of the down grain boundary corresponding to the misorientation angle. The white arrow indicates the climbing direction of the edge dislocation. The yellow arrow indicates the direction of Burgers vector of the edge dislocation.

Results and Analysis

The Arrangement and Movement of Edge Dislocations Under X-Direction Tensile Strain

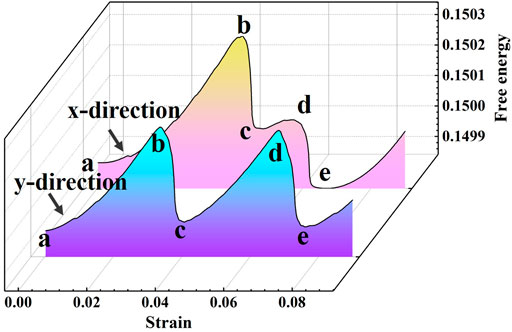
The detailed arrangement and movement process of GBDs under x-direction tensile strain is illustrated in Figures 3, 4. The free energy curve of the system during the deformation process is illustrated in Figure 5.

FIGURE 3

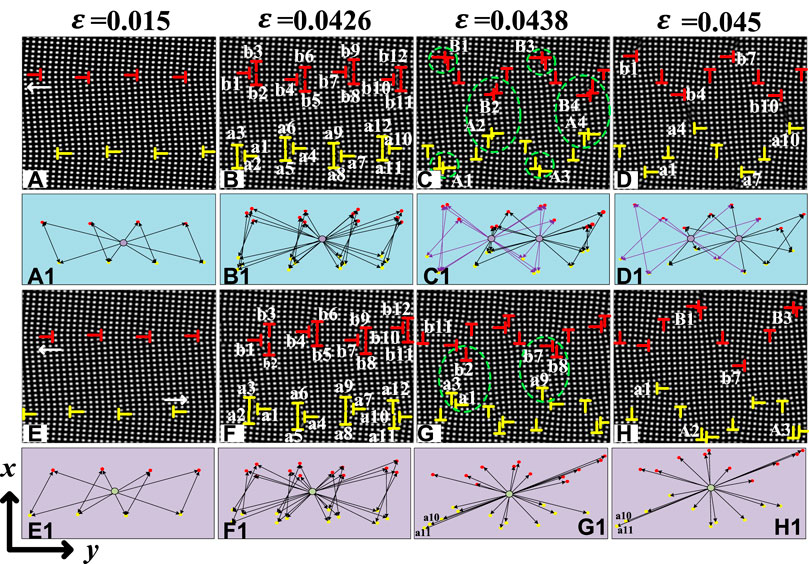
FIGURE 3. (A–D), (A1-D1) The evolution and arrangement of grain boundary dislocations when the GBM are $7^{°}$, respectively. (E–H), (E1–H1) The evolution and symmetry arrangement of grain boundary dislocations when the GBM are $6^{°}$, respectively. The strain $\epsilon$ is $0.015$, $0.0426$, $0.0438$, and $0.045$.

FIGURE 4

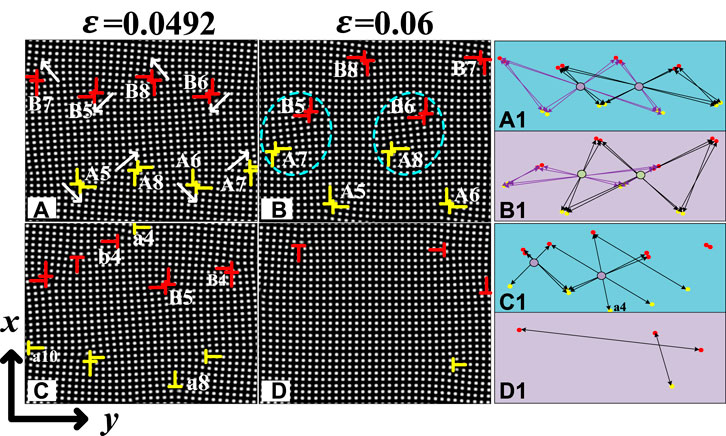
FIGURE 4. (A–D) The dislocation evolution of $7^{°}$ and $6^{°}$ and the corresponding strains are both $0.0492$ and $0.06$. (A1, B1), (C1, D1) The arrangement of $7^{°}$ and $6^{°}$ with strains are both $0.0492$ and $0.06$.

FIGURE 5

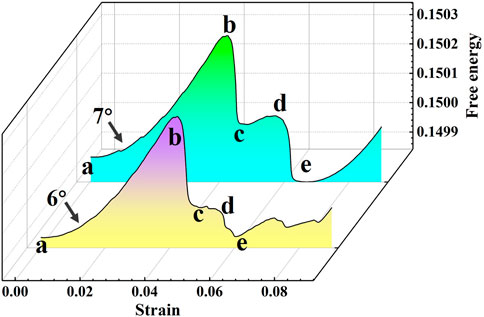
FIGURE 5. The free energy curve of $6^{°}$ and $7^{°}$ grain boundary dislocation evolution process during the x-direction tensile deformation.

As shown in Figures 3A–H, all-grain boundary dislocations are arranged in symmetrical structure from $\epsilon =0.015$ and $\epsilon =0.0426$. The grain-boundary dislocations are completely decomposed when the strain reaches the critical value of dislocation decomposition. This process consumes energy and the free energy is reduced, (b∼c) in Figure 5. With the increase of deformation, the dislocation movement and the symmetry are changed due to different misorientation angles and different resolved shear stresses. When $\epsilon =0.0438$ there are dislocation pairs formed in Figures 3C, G. For example, a4, and a6 in Figure 3B will form dislocation pair A2. We found that the dislocation arrangement and reaction forms $6^{°}$ and $7^{°}$ are different after the formation of dislocation pairs. From Figures 3C,D, dislocation pairs react with dislocation pairs and the dislocations arrangement structure presents a “double bowknot”. From Figures 3G,H, dislocation reacts with the dislocation pair and a single edge dislocation and the dislocations arrangement structure is “fireworks”.

At $\epsilon =0.0492$, it is observed that the system with the GBMs $7^{°}$ is all dislocation pairs as shown in Figure 4A. At this time, the dislocation pairs arrangement is highly symmetrical showing a “double bowknot” structure. The energy consumed by dislocation pairs on the slip is less than that increased by system deformation. Thus, the energy curve rises again corresponding to the rising part in Figures 5C,D. When the GBMs of $6^{°}$, both dislocation pairs and single edge dislocations exist and the dislocations arrangement is chaotic, as shown in Figure 4C1. Four sub-grain boundaries appear in Figure 4B when the strain increases to 0.06. The existence of dislocation pairs reduces the lattice distortion energy and makes the sub-grain boundaries more stable. The dislocations are arranged in a “double bowknot” structure. Subsequently, annihilation occurs concurrently between all dislocation pairs such as A7 and B5 (blue dotted circle in Figure 4B), and finally, the lattice distortion disappears completely into a single crystal. However, we find that there are single edge dislocations and the dislocation arrangement is asymmetric in Figure 4D.

In Figure 5, we found that the energy trend of Figures 5A–C stage in the evolution of the two systems from bi-crystal to single crystal is the same, and the peak value with large GBMs is higher. From Figures 5C,D, the energy curve of the GBMs $7^{°}$ is relatively smooth while there is two small-amplitude torsions (black box) which are caused by dislocation annihilation and dislocation pair formation. The lattice distortion completely disappears in the system with the GBMs $7^{°}$ after point d. If the deformation continues to increase, the system energy increases again. Meanwhile, there are still dislocations in the system with the GBMs $6^{°}$, the remaining single edge dislocations annihilate one after another. Therefore, there are two torsions in Figure 5D,E stage, the lattice distortion of point e disappears completely, and the system energy increases with deformation.

Relationship Between the Direction of Tensile Strain and the Symmetry of Dislocations Arrangement

Different tensile deformation directions of samples affect the dislocation movement direction and dislocation arrangement symmetry in the system. The y-direction tensile strain is applied to sample B. The evolution and symmetrical distribution of grain boundary dislocations of the same strain are shown in Figure 6, and the corresponding change of free energy is shown in Figure 7.

FIGURE 6

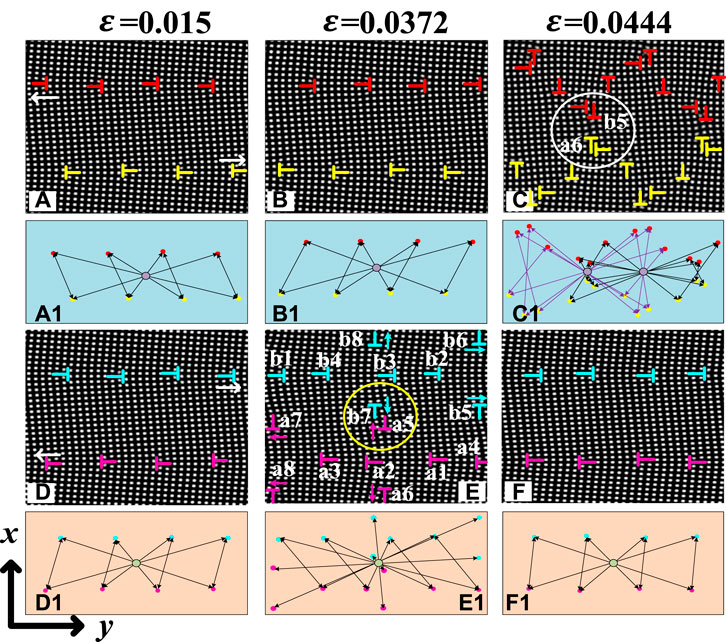
FIGURE 6. (A–C), (D–F) The evolution process of grain boundary dislocations under tensile deformation in x-direction and y-direction with $7^{°}$, respectively, and the corresponding tensile strain $\epsilon$ is $0.015$, $0.0372$, and $0.0444$. (A1–F1) The arrangement of grain boundary dislocations corresponding to the dislocation evolution diagram, respectively.

FIGURE 7

FIGURE 7. Free energy curve of misorientation angle of $7^{°}$ under x-and y-direction tensile deformation.

In the system of grain-boundary misorientation 7°, the number of grain-boundary dislocations doesn’t change but the climbing direction of grain-boundary dislocations is opposite, as shown in Figures 6A,D. In the meantime, the grain-boundary dislocations arrangement is a highly symmetrical “bowknot” structure, as shown in Figures 6A1,D1. At $\epsilon =0.0372$, some dislocations in the y-direction tensile strain system decomposition first, as shown in Figure 6E. The GBDs arrangement is still symmetrical Figure 6E1, but the structure is not completely the same as that in Figure 6D1. While in the system with the tensile deformation direction of x, there is no dislocations decomposition, as shown in Figure 6B. At this time, all edge dislocations climb and the arrangement of grain boundary dislocations is still a “bowknot” structure. Different tensile deformation directions can affect the new dislocations climbing direction after edge dislocations decomposition, the detailed schematic diagram is shown in Figure 8. We know that the free energy of the system with the tensile deformation direction of the y-direction will reach the maximum first by observing the energy Figure 7.

FIGURE 8

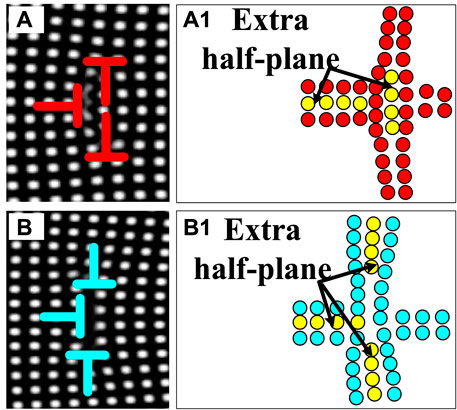
FIGURE 8. (A), (A1) Dislocation decomposition under x-direction tensile strain and its atomic structure diagram. (B), (B1) Dislocation decomposition under y-direction tensile strain and its atomic structure diagram.

With the increase of strain, there is no formation of dislocation pairs in the y-direction tensile strain system and the dislocation reactions are between single edge dislocations. In the x-direction tensile strain system, there are the formations and reactions of dislocation pairs and the annihilations of dislocations reduce the system energy, corresponding to the stage (b∼c) in Figure 7. Two-grain boundaries are re-observed in Figure 6F when $\epsilon =0.0444$. The GBDs arrangement is exactly the same as in Figure 6D1 and the system energy reaches the peak again at point d in Figure 7. Concurrently, the grain boundary is not obvious, all of which are single edge dislocations arranged in a “double bowknot” symmetrical structure Figure 6C1.

Discussion

The effect of different strain rates $\dot{\epsilon }$, grain boundary misorientations $\theta$, and tensile deformation direction on the critical strain value of dislocations decomposition analyzed, as shown in Figure 9. It should be pointed out that the grain boundary with misorientation angle $9^{°}$ does not emerge dislocations decomposition under x-direction tensile deformation. Therefore, there isno corresponding critical strain values of dislocations decomposition in Figure 9. But there are dislocation movement, dislocation reaction, and dislocation annihilation in the process of grain boundary evolution.

FIGURE 9

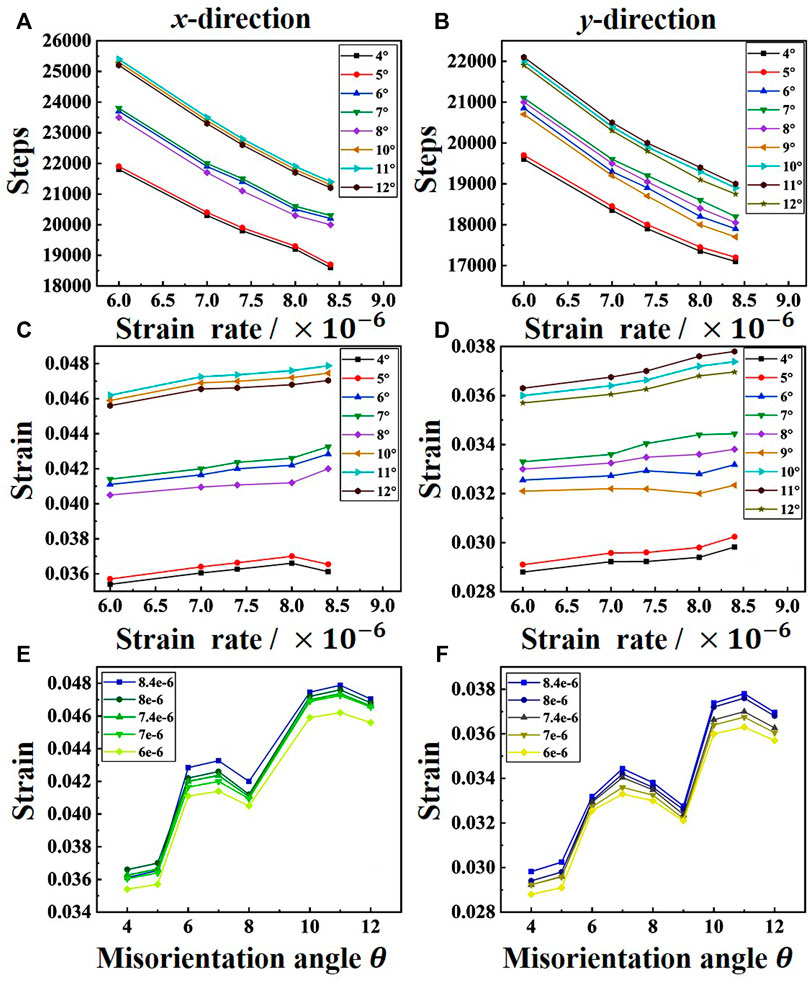
FIGURE 9. Critical strain distribution of dislocations decomposition under different strain rates and GBMs conditions. (A), (C), (E) The critical strain distribution of tensile deformation in the x-direction; (B) (D), (F) the critical strain distribution of tensile deformation in the y-direction.

Through Figure 9A,B, we can find that when the grain boundary misorientations remain unchanged, the critical time steps of dislocation decomposition decrease with the increase of strain rate. This is because the critical strain required for dislocation decomposition in the same system is fixed. It can be seen from the formula $\epsilon =n\dot{\epsilon }\mathrm{\Delta }t$ that when $\dot{\epsilon }$ increases, $n$ decreases. In addition, the critical time steps of dislocations decomposition under y-direction tensile deformation is smaller than x-direction. This requires a larger strain since all-grain boundary dislocations decomposes simultaneously under x-direction tensile deformation while grain boundary dislocations do not decomposes simultaneously when tensile deformation is applied in the y-direction.

In Figure 9C, we found that the critical strain value of grain boundary dislocation decomposition increases with the increase of grain boundary misorientations. This is because grain boundary dislocations increase with the grain boundary misorientations increase, thus the required critical strain value is larger. What we need to pay attention to is that $8^{°}$ and ${12}^{°}$ do not strictly follow this law. Similarly, we can analyze Figure 9D. It can be clearly observed that $8^{°}$, $9^{°}$, and ${12}^{°}$ are special when applying y-direction tensile deformation. In order to better study the grain boundary misorientations and critical strain, we can analyze Figures 9E,F. It is obvious that no matter which direction of tensile strain is applied, $8^{°}$ , $9^{°}$, and ${12}^{°}$ are special angles. In addition, the critical strain value becomes larger with the increase of GBMs when the strain rate remains the same. This result is consistent with Figures 9A,B.

In summary, the critical strain $\text{ε}$ increases with the increase of GBMs except for the special angle. Otherwise, decreasing the critical time steps of dislocations decomposition can be achieved by increasing the strain rate.

Conclusion

In this study, the phase-field crystal model of two modes is used to study the symmetry of grain boundary dislocation arrangement and the critical strain of grain boundary dislocation decomposition under different grain boundary misorientations and tensile strain directions. The results show that:

1) The x-direction tensile deformation is applied to the simulated samples with GBMs $6^{°}$ and $7^{°}$. The grain boundary dislocations arrangement of the two systems is very similar from the equilibrium state to the complete decomposition, which shows a “bowknot” symmetrical structure. The dislocation arrangement in the two systems differs as the strain increases. Sub-grain boundaries appear in the larger GBM system, and the dislocation arrangement always shows asymmetrical structure of “ bowknot ” or “double bowknot.” However, no sub-grain boundary is formed in the smaller GBM system under the same strain and the dislocation arrangement is no longer symmetrical.

2) The y-direction tensile deformation is applied to the $7^{°}$. The easiest to observe is the climbing direction of edge dislocations is opposite to x-direction tensile deformation. The initial grain boundary dislocations arrangement is basically the same and arranged symmetrically in a “bowknot” under x- and y-direction tensile deformation. With the increase of strain and under the same tensile strain, some grain boundary dislocations in the system with y-direction tensile strain will decomposition first and the dislocations arrangement is “like bowknot” symmetrical structure, while the dislocations under x-direction tensile strain do not decomposition and the arrangement unchanged.

3) The critical strains of dislocations decomposition are related to strain rate and GBM. The critical strain can be reached preferentially by increasing the strain rate appropriately or reducing the GBM.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

HL: writing—original draft and editing. XW: writing—original draft, and formal analysis. HZ: writing—original draft, and formal analysis. XT: methodology and visualization. HH: conceptualization and formal analysis. YZ: editing, supervision, and project administration.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52074246).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.875519/full#supplementary-material

References

Asadi, E., and Zaeem, M. A. (2015). A Modified Two-Mode Phase-Field Crystal Model Applied to Face-Centered Cubic and Body-Centered Cubic Orderings. Comput. Mater. Sci. 105, 110–113. doi:10.1016/j.commatsci.2015.04.004

CrossRef Full Text | Google Scholar

Berry, J., Rottler, J., Sinclair, C. W., and Provatas, N. (2015). Atomistic Study of Diffusion-Mediated Plasticity and Creep Using Phase Field Crystal Methods. Phys. Rev. B 92, 134103. doi:10.1103/physrevb.92.134103

CrossRef Full Text | Google Scholar

Bian, M. Z., Sasaki, T. T., Suh, B. C., Nakata, T., Kamado, S., and Hono, K. (2017). A Heat-Treatable Mg-Al-Ca-Mn-Zn Sheet Alloy with Good Room Temperature Formability. Scr. Mater. 138, 151–155. doi:10.1016/j.scriptamat.2017.05.034

CrossRef Full Text | Google Scholar

Blixt, K. H., and Hallberg, H. (2022). Evaluation of Grain Boundary Energy, Structure and Stiffness from Phase Field Crystal Simulations. Model. Simul. Mat. Sci. Eng. 30, 014002. doi:10.1088/1361-651x/ac3ca1

CrossRef Full Text | Google Scholar

Can, G., Zhi-Jun, W., Jin-Cheng, W., Yao-Lin, G., and Sai, T. (2013). Effect of the Direct Correlation Function on Phase Diagram of the Two-Mode Phase Field Crystal Model. Acta Phys. Sin. 62, 108104. doi:10.7498/aps.62.108104

CrossRef Full Text | Google Scholar

Chen, L., and Zhao, Y. (2021). From Classical Thermodynamics to Phase-Field Method. Prog. Mat. Sci. 122, 100868. doi:10.1016/j.pmatsci.2021.100868

CrossRef Full Text | Google Scholar

Elder, K. R., Katakowski, M., Haataja, M., and Grant, M. (2002). Modeling Elasticity in Crystal Growth. Phys. Rev. Lett. 88, 245701. doi:10.1103/physrevlett.88.245701

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Y.-J., Deng, Q.-Q., Liu, Z.-y., Huang, Z.-J., Li, Y.-X., and Luo, Z.-R. (2020). Modes of Grain Growth and Mechanism of Dislocation Reaction under Applied Biaxial Strain: Atomistic and Continuum Modeling. J. Mater. Sci. Technol. 49, 236–250. doi:10.1016/j.jmst.2020.01.030

CrossRef Full Text | Google Scholar

Greenwood, M., Provatas, N., and Rottler, J. (2010). Free Energy Functionals for Efficient Phase Field Crystal Modeling of Structural Phase Transformations. Phys. Rev. Lett. 105 (4), 045702. doi:10.1103/PhysRevLett.105.045702

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, H., Zhao, Y., Sun, Y., Tian, J., Hou, H., Qi, K., et al. (2019). Phase Field Crystal Study of Grain Boundary Structure and Annihilation Mechanism in Low-Angle Grain Boundary. Superlattices Microstruct. 129, 163–175. doi:10.1016/j.spmi.2019.03.020

CrossRef Full Text | Google Scholar

Guo, S., Chen, H., and Wang, M. (2021). Research on the Dislocation Differences of CoCrFeMnNi with Different Local Chemical Orders during Room Temperature Tensile Test. J. Alloys Compd. 868, 159215. doi:10.1016/j.jallcom.2021.159215

CrossRef Full Text | Google Scholar

Hirouchi, T., Takaki, T., and Tomita, Y. (2009). Development of Numerical Scheme for Phase Field Crystal Deformation Simulation. Comput. Mater. Sci. 44, 1192–1197. doi:10.1016/j.commatsci.2008.08.001

CrossRef Full Text | Google Scholar

Hirouchi, T., Takaki, T., and Tomita, Y. (2010). Effects of Temperature and Grain Size on Phase-Field-Crystal Deformation Simulation. Int. J. Mech. Sci. 52, 309–319. doi:10.1016/j.ijmecsci.2009.09.036

CrossRef Full Text | Google Scholar

Hou, X.-W., Tang, X.-Z., Zu, Q., and Guo, Y.-F. (2020). Plastic Deformation Mechanisms of Hierarchical Double Contraction Nanotwins in Mg. J. Mat. Sci. 55, 11701–11713. doi:10.1007/s10853-020-04789-y

CrossRef Full Text | Google Scholar

Hu, S., Chen, Z., Peng, Y.-Y., Liu, Y.-J., and Guo, L.-Y. (2016b). Modeling and Simulation of Microcrack Propagation Behavior under Shear Stress Using Phase-Field-Crystal. Comput. Mater. Sci. 121, 143–150. doi:10.1016/j.commatsci.2016.04.035

CrossRef Full Text | Google Scholar

Hu, S., Chen, Z., Yu, G.-G., Xi, W., and Peng, Y.-Y. (2016a). Phase-field-crystal Study on the Reaction Mechanisms of Opposite Sign Edge Dislocations Appearing in the Deformation Processes of Asymmetric Tilt Sub-grain Boundary System. Comput. Mater. Sci. 124, 195–203. doi:10.1016/j.commatsci.2016.07.030

CrossRef Full Text | Google Scholar

Hu, S., Fan, J., Liu, Q., Li, J., and Wang, J. (2020). Phase-field-crystal Study on Shear-Induced Coupled Evolution of Intragranular Crack and Grain Boundary in Nanoscale Bicrystal System. Eur. Phys. J. B 93 (11), 212. doi:10.1140/epjb/e2020-10349-1

CrossRef Full Text | Google Scholar

Kuang, W., Wang, H., Li, X., Zhang, J., Zhou, Q., and Zhao, Y. (2018). Application of the Thermodynamic Extremal Principle to Diffusion-Controlled Phase Transformations in Fe-C-X Alloys: Modeling and Applications. Acta Mater. 159, 16–30. doi:10.1016/j.actamat.2018.08.008

CrossRef Full Text | Google Scholar

Kumar, K. S., Van Swygenhoven, H., and Suresh, S. (2003). Mechanical Behavior of Nanocrystalline Metals and alloys11The Golden Jubilee Issue-Selected Topics in Materials Science and Engineering: Past, Present and Future, Edited by S. Suresh. Acta Mater. 51, 5743–5774. doi:10.1016/j.actamat.2003.08.032

CrossRef Full Text | Google Scholar

Li, X., Sha, A., Chen, B., and Chu, J. (2020). Effect of Microstructure on Tensile Deformation Behavior of Ti-3Al-4.5V-5Mo Titanium Alloy. J. Aeronaut. Mater 40, 45–52. doi:10.11868/j.issn.1005-5053.2020.000111

CrossRef Full Text | Google Scholar

Liu, Y., Wang, L., He, S., Eng, F., Lv, X., and Zhang, B. (2012). Effect of Long-Term Aging on Dynamic Tensile Deformation Behavior of GH4169 Alloy. Acta Metall. Sin. 48, 49–55. doi:10.3724/sp.j.1037.2011.00435

CrossRef Full Text | Google Scholar

Mahabadi, O. K., Tatone, B. S. A., and Grasselli, G. (2014). Influence of Microscale Heterogeneity and Microstructure on the Tensile Behavior of Crystalline Rocks. J. Geophys. Res. Solid Earth 119, 5324–5341. doi:10.1002/2014jb011064

CrossRef Full Text | Google Scholar

Nielsen, B. F., Linga, G., Christensen, A., and Mathiesen, J. (2020). Substrate Curvature Governs Texture Orientation in Thin Films of Smectic Block Copolymers. Soft Matter 16, 3395–3406. doi:10.1039/c9sm02389e

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J. M., Yang, D. C., Kim, H.-J., Kim, D. G., Lee, S., Kim, H. S., et al. (2021). Ultra-strong and Strain-Hardenable Ultrafine-Grained Medium-Entropy Alloy via Enhanced Grain-Boundary Strengthening. Mater. Res. Lett. 9, 315–321. doi:10.1080/21663831.2021.1913768

CrossRef Full Text | Google Scholar

Peng, F., Huang, W., Zhang, Z. Q., Guo, T. F., Ma, Y. E., and Zhang, Y. (2021). Conservational Integrals of the Fourth-Order Phase Field Model for Brittle Fracture via Noether Theorem. Eng. Fract. Mech. 245, 107590. doi:10.1016/j.engfracmech.2021.107590

CrossRef Full Text | Google Scholar

Qi, K., Zhao, Y., Guo, H., Tian, X., and Hua, H. (2019). Phase Field Crystal Simulation of the Effect of Temperature on Low-Angle Symmetric Tilt Grain Boundary Dislocation Motion. Acta Phys. Sin-Ch Ed. 68, 80–89. doi:10.7498/aps.68.20190051

CrossRef Full Text | Google Scholar

Qi, K., Zhao, Y., Tian, X., Peng, D., Sun, Y., and Hua, H. (2020). Phase Field Crystal Simulation of Effect of Misorientation Angle on Low-Angle Asymmetric Tilt Grain Boundary Dislocation Motion. Acta Phys. Sin-Ch Ed. 69, 69–78. doi:10.7498/aps.69.20200133

CrossRef Full Text | Google Scholar

Roy, A., Devanathan, R., Johnson, D. D., and Balasubramanian, G. (2022). Grain-size Effects on the Deformation in Nanocrystalline Multi-Principal Element Alloy. Mater. Chem. Phys. 277, 125546. doi:10.1016/j.matchemphys.2021.125546

CrossRef Full Text | Google Scholar

Shuai, X., Wang, Z. J., Mao, H., Tang, S., Kong, Y., and Du, Y. (2021). Atomic-scale Study of Compositional and Structural Evolution of Early-Stage Grain Boundary Precipitation in Al-Cu Alloys through Phase-Field Crystal Simulation. J. Mat. Sci. 56, 12700–12715. doi:10.1007/s10853-021-06064-0

CrossRef Full Text | Google Scholar

Song, H. Y., Li, Y. L., and An, M. R. (2014). Atomic Simulations of the Effect of Twist Grain Boundaries on Deformation Behavior of Nanocrystalline Copper. Comput. Mater. Sci. 84, 40–44. doi:10.1016/j.commatsci.2013.11.052

CrossRef Full Text | Google Scholar

Suh, B.-C., Kim, J. H., Bae, J. H., Hwang, J. H., Shim, M.-S., and Kim, N. J. (2017). Effect of Sn Addition on the Microstructure and Deformation Behavior of Mg-3Al Alloy. Acta Mater. 124, 268–279. doi:10.1016/j.actamat.2016.11.020

CrossRef Full Text | Google Scholar

Tian, X.-l., Zhao, Y.-h., Peng, D.-w., Guo, Q.-w., Guo, Z., and Hou, H. (2021). Phase-field Crystal Simulation of Evolution of Liquid Pools in Grain Boundary Pre-melting Regions. Trans. Nonferrous Metals Soc. China 31, 1175–1188. doi:10.1016/s1003-6326(21)65570-x

CrossRef Full Text | Google Scholar

Volnistem, E. A., Macková, L., Muniz, R. F., Estrada, F. R., de Nóbrega, S. M., Dias, G. S., et al. (2021). On the Effects of Dislocations on the Magnetism of BiFeO3 Nanoparticles. J. Alloys Compd. 887, 161421. doi:10.1016/j.jallcom.2021.161421

CrossRef Full Text | Google Scholar

Wu, K. A., Adland, A., and Karma, A. (2010). Phase-field-crystal Model for Fcc Ordering. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 81, 061601. doi:10.1103/PhysRevE.81.061601

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, Q., Liang, Y., Yang, C., Zhang, S., and Ou, M. (2019). Tensile Deformation Behavior of TC4 Titanium Alloy. RATE Met. 43, 765–773. doi:10.13373/j.cnki.cjrm.xy18040023

CrossRef Full Text | Google Scholar

Xin, T., Zhao, Y., Mahjoub, R., Jiang, J., Yadav, A., Nomoto, K., et al. (2021). Ultrahigh Specific Strength in a Magnesium Alloy Strengthened by Spinodal Decomposition. Sci. Adv. 7, 1–9. doi:10.1126/sciadv.abf3039

CrossRef Full Text | Google Scholar

Yan, M., Yuan, F., and Wu, X. (2021). Dynamic Shear Behaviors and Microstructural Deformation Mechanisms in FeNiAlC Dual-phase High Strength Alloy. Explos. Shock Waves 41 (1), 34–45. doi:10.11883/bzycj-2020-0224

CrossRef Full Text | Google Scholar

Yang, T., Zhang, J., Long, J., Long, Q.-H., and Chen, Z. (2014). Phase Field Crystal Study of the Crystallization Modes within the Two-phase Region. Chin. Phys. B 23, 088109. doi:10.1088/1674-1056/23/8/088109

CrossRef Full Text | Google Scholar

Yang, Y., Zhao, Y., Tian, X., and Hou, H. (2020). Microscopic Phase-Field Simulation for Precipitation Process of Ni₆₀Al₂₀V₂₀ Medium Entropy Alloy. Acta Phys. Sin-Ch Ed. 69, 29–38. doi:10.7498/aps.69.20200154

CrossRef Full Text | Google Scholar

Zhang, J., Wang, H., Kuang, W., Zhang, Y., Li, S., Zhao, Y., et al. (2018). Rapid Solidification of Non-stoichiometric Intermetallic Compounds: Modeling and Experimental Verification. Acta Mater. 148, 86–99. doi:10.1016/j.actamat.2018.01.040

CrossRef Full Text | Google Scholar

Zhang, S., Chen, Z., and Yang, Y. (2014). Simulation of Structure and Deformation of Asymmetrical Tilt Grain Boundaries with Small Misorientation Angles by Two-Mode Phase Field Crystal Method. Rare Metal. Mat. Eng. 43, 610–614. 1002-185X(2014)03-0610-05.

Google Scholar

Zhang, X., Huang, L. K., Zhang, B., Chen, Y. Z., Duan, S. Y., Liu, G., et al. (2019). Enhanced Strength and Ductility of A356 Alloy Due to Composite Effect of Near-Rapid Solidification and Thermo-Mechanical Treatment. Mater. Sci. Eng. A 753, 168–178. doi:10.1016/j.msea.2019.03.039

CrossRef Full Text | Google Scholar

Zhao, Y.-H., Tian, X.-L., Zhao, B., Sun, Y., Guo, H., Dong, M., et al. (2018). Precipitation Sequence of Middle Al Concentration Alloy Using the Inversion Algorithm and Microscopic Phase Field Model. Sci. Adv. Mater 10, 1793–1804. doi:10.1166/sam.2018.3430

CrossRef Full Text | Google Scholar

Zhao, Y., Chen, Z., Long, J., and Yang, T. (2014). Influence of Temperature on the Inverse Hall-Petch Effect in Nanocrystalline Materials: Phase Field Crystal Simulation. Acta Metall. Sin. Engl. Lett.) 27, 81–86. doi:10.1007/s40195-014-0027-5

CrossRef Full Text | Google Scholar

Zhao, Y., Jing, J., Chen, L., Xu, F., and Hou, H. (2021). Current Research Status of Interface of Ceramic-Metal Laminated Composite Material for Armor Protection. Acta Metall. Sin. 57, 1107–1125. doi:10.11900/0412.1961.2021.00051

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, B., Hou, H., Chen, W., and Wang, M. (2019). Phase-field Simulation for the Evolution of Solid/Liquid Interface Front in Directional Solidification Process. J. Mater. Sci. Technol. 35, 1044–1052. doi:10.1016/j.jmst.2018.12.009

CrossRef Full Text | Google Scholar