Structural Principles in Liquids and Glasses: Bottom-Up or Top-Down

The conventional approach to elucidate the atomic structure of liquid and glass is to start with local structural units made of several atoms, and to use them as building blocks to form a global structure, the bottom-up approach. We propose to add an alternative top-down approach in which we start with a global high-temperature gas state and then apply interatomic potentials to all atoms at once. This causes collective density wave instability in all directions with the same wavelength. These two driving forces, local and global, are in competition and are mutually frustrated. The final structure is determined through the compromise of frustration between these two, which creates the medium-range-order. This even-handed approach on global and local potential energy landscapes explains the distinct natures of short-range order and medium-range order, and strong temperature dependence of various properties of liquid.

Introduction

Liquids and glasses have strongly disordered atomic structures which are difficult to characterize with precision. Explaining the origin of such structures is an even more daunting task, which has been a subject of discussion for a long time (Egelstaff, 1967; Croxton, 1974; Hansen and McDonald, 1976; Debenedetti and Stillinger, 2001; March and Tosi, 2002; Parisi and Zamponi, 2010). In the absence of symmetry, the most popular approach is the bottom-up approach, starting with local structural units, such as the nearest neighbors of an atom (short-range order—SRO) and building up the global structure with preferred local structures (Miracle, 2004; Sheng, et al., 2006; Robinson et al., 2019). The preferred structures, such as icosahedral clusters, are often geometrically frustrated as a building unit (Sadoc, 1981; Nelson, 1983; Sethna, 1983; Tarjus, et al., 2005), resulting in a disordered global structure. However, in this approach the frustration condition depends on details of the cluster geometry, and the universal principle of structure formation remains deeply hidden.

We propose a holistic concept to depict this frustration through global and local features of potential energy landscape, by going beyond the idea of geometrical frustration. On top of the bottom-up approach we add a top-down approach, in which we start with a high-density gas state and apply interatomic potentials to all atoms at once. We show that a high-density gas state is unstable against the global density wave state, once the interatomic potential is introduced in reciprocal space. The local force to form atomic units and the global force to form density waves are in conflict against each other. The real structure results from the competition and compromise between these two frustrated driving forces. The medium-range order (MRO) in the oscillation in density correlations beyond the nearest neighbors reflects this competition. The competition depends on temperature. At high temperatures the local forces are dominant, whereas as temperature is reduced the importance of global force increases. This change in their roles explains strong temperature dependence in various properties of liquid.

Nature of the Medium-Range-Order

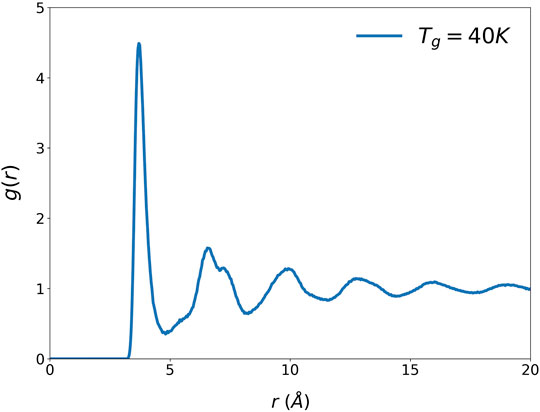
The atomic structure of liquid and glass is usually described in terms of the pair-distribution function (PDF), g(r), which shows the distribution of distances between two atoms. The PDF is obtained by Fourier-transforming the structure function, S(Q), where Q is the momentum transfer in scattering, determined by x-ray or neutron diffraction (Warren, 1969). Figure 1 shows an example of the PDF, that of Argon liquid model with the Lennard-Jones (LJ) potential (Rowley, et al., 1975), with 34,461 atoms in the cubic supercell of the edge size, L = 112.01 Å. The first peak of the PDF describes the distribution of the distances to the nearest neighbor atoms from a central atom and describes the radial SRO. The oscillations in the PDF beyond the first peak describes the MRO, and they decay with the form,

$G\left(r\right)=4\pi r{\rho }_0\left[g\left(r\right)-1\right]=G_0\left(r\right)\exp \left(-r/{\xi }_s\right)(1)$

where ρ₀ is the macroscopic number density of atoms and ξ_s is the structural coherence length, as shown in Figure 2.

FIGURE 1

FIGURE 1. The PDF, g(r), of liquid Argon at T_g = 40 K.

FIGURE 2

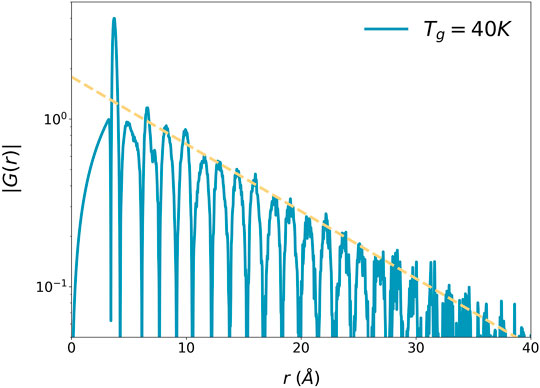
FIGURE 2. The absolute values of the reduced PDF, $\left|G\left(r\right)\right|$, of liquid Argon at T_g = 40 K. The dashed line shows the exponential decay by Eq. 1.

The form of Eq. 1 was first suggested by Ornstein and Zernike. (1914), but it can be derived by a more general argument (Ryu and Egami, 2021). Also, whereas the OZ theory connects the SRO directly to the MRO and regards the MRO as a consequence of the SRO, we found that the nature of the MRO is substantially distinct from that of the SRO. For instance, the variation of the MRO with temperature shows a clear change at the glass transition temperature, T_g, but the SRO is continuous through T_g (Ryu and Egami, 2021). The first peak of the PDF is relatively narrow (<1 Å) and describes the atom-atom distances to the nearest neighbors, which number in the order of ten. But the MRO peaks are wider (∼1 Å), and cover hundreds of atomic distances. Therefore, they describe the correlation between the center atom and aggregates of atoms, or density fluctuations (Egami, 2020). In other words, the SRO describes the point-to-point correlation, whereas the MRO describes the point-to-set correlation (Berthier and Kob, 2012).

For metallic liquids the structural coherence length, ξ_s, which characterizes the MRO, obeys the Curie-Weiss law (Ryu, et al., 2019),

${\xi }_s\left(T\right)=\frac{aC}{T-T_{IG}}(2)$

where a is the nearest neighbor distance, and T_IG (<0) is the ideal glass temperature. At T = T_IG, ξ_s diverges and G (r, T_IG) = G₀(r). Therefore, G₀(r), Figure 3, describes the structure of an ideally coherent glass state (Ryu, et al., 2019), which has long-range positional correlation without periodicity. Its Fourier-transform, the structure function S₀(Q) shown in Figure 4, has a Bragg-like sharp first peak at Q₁, of which height depends on the model size. Small sharp peaks are noise due to the finite model size. Because the structure is isotropic, in three-dimensions the first peak forms a Bragg sphere.

FIGURE 3

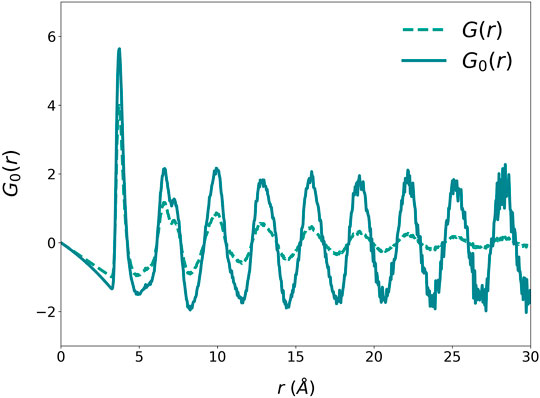
FIGURE 3. The G₀(r) of liquid Argon at T_g = 40 K obtained by Eq. 1.

FIGURE 4

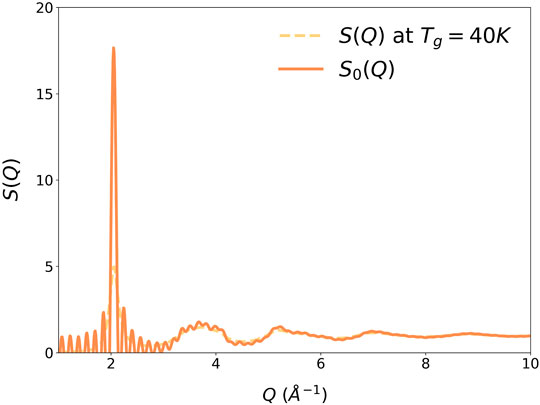
FIGURE 4. The S(Q) of liquid Argon at T_g = 40 K. The height of the first peak depends on the model size, and extrapolates to a δ-function for a macroscopic model.

Interatomic Pseudo-Potential and Density Wave

The ideally coherent glass state exists only in extrapolation, because T_IG is negative and the structure freezes at T_g. However, the Curie-Weiss temperature dependence of the structural coherence length, ξ_s, suggests that there is a driving force for a liquid towards this state. We suggest that the origin of such a force is the attractive interatomic potential. Let us consider a simple monoatomic liquid of atoms interacting with a two-body spherical potential, ϕ(r). We express the local atomic density, ρ(r), in terms of the density waves,

$\rho \left(\mathit{r}\right)={\displaystyle \int \rho \left(\mathit{q}\right)\mathit{exp}\left(i\mathit{q}\cdot \mathit{r}\right)d\mathit{q}}(3)$

In order to make the density real, we assume, $\rho \left(-\mathit{q}\right)=\rho *\left(\mathit{q}\right)$. The ρ(q) is a complex number,

$\rho \left(\mathit{q}\right)=\left|\rho \left(\mathit{q}\right)\right|\mathit{exp}\left(i\delta \left(\mathit{q}\right)\right)(4)$

and the phase factor, δ(q), has a nearly random distribution to avoid wave pile-up which would put more than one atom at a place. The total potential energy is given by

$U={\displaystyle \int {\left|\rho \left(\mathit{q}\right)\right|}^2}\varphi \left(\mathit{q}\right)d\mathit{q}={\rho }_0^2{\displaystyle \int S\left(\mathit{q}\right)\varphi \left(\mathit{q}\right)d\mathit{q}}(5)$

where ϕ(q) is the Fourier-transform of ϕ(r),

$\varphi \left(\mathit{q}\right)={\displaystyle \int \varphi \left(\mathit{r}\right)\mathit{exp}\left(-i\mathit{q}\cdot \mathit{r}\right)d\mathit{r}}(6)$

For a spherical potential, ϕ(r) = ϕ(r), $\mathit{r}=\left|\mathit{r}\right|$, and ϕ(q) = ϕ(q), $\mathit{q}=\left|\mathit{q}\right|$. The ϕ(q) is dominated by the strong repulsive part of ϕ(r) at small r. However, the strongly repulsive part of the potential with the energy much larger than k_BT is irrelevant, because atoms never come so close to each other. Therefore, we define a “pseudopotential,” ϕ_pp(r), in which the strongly repulsive part of ϕ(r) is removed and ${\varphi }_{pp}\left(\mathit{r}\right)=\varphi \left({\mathit{r}}_c\right)$ is assumed for r < r_c, where r_c is the cut-off distance. This is equivalent to disregarding the inaccessible high energy states from the potential energy landscape. It is also similar to the concept of the pseudopotential in the quantum scattering theory: A strong attractive potential simply adds a multiple of 2π to the scattering phase shift, and taking just the principal part of the phase shift corresponds to replacing it with the pseudopotential (Wu and Ohmura, 1962). For electrons removing the redundant phase shift is equivalent to reinforcing orthogonality to the core states (Phillips and Kleinman, 1959). For a repulsive potential we remove the strongly repulsive part. We separate ϕ(r) into two parts; ϕ_pp(r) and the repulsive part, ϕ_R(r),

$\varphi \left(\mathit{r}\right)={\varphi }_R\left(\mathit{r}\right)+{\varphi }_{pp}\left(\mathit{r}\right)(7)$

then, the potential energy is,

$U=U_R+U_{pp}(8)$

$U_R=\frac{1}{V}{\displaystyle \iint {\varphi }_R\left(\mathit{r}\right)\rho \left({\mathit{r}}^{\prime }\right)\rho \left(\mathit{r}+{\mathit{r}}^{\prime }\right)d\mathit{r}d{\mathit{r}}^{\prime }}(9)$

$U_{pp}=\frac{1}{V}{\displaystyle \iint {\varphi }_{pp}\left(\mathit{r}\right)\rho \left({\mathit{r}}^{\prime }\right)\rho \left(\mathit{r}+{\mathit{r}}^{\prime }\right)d\mathit{r}d{\mathit{r}}^{\prime }}(10)$

where V is volume. The ρ(r) of the ground state is determined by minimizing U. However, for the range r < r_c where ϕ_R(r) is non-zero, there is no pair of atoms with such small separations because of the strong repulsion. Therefore,

$U_R=0, U=U_{pp},(11)$

and the structure is determined by minimizing U_pp with,

${\varphi }_{pp}\left(\mathit{q}\right)={\displaystyle \int {\varphi }_{pp}\left(\mathit{r}\right)\mathit{exp}\left(-i\mathit{q}\cdot \mathit{r}\right)d\mathit{r}}(12)$

The pseudopotentials of the Lennard-Jones potential for Argon with various cut-off values and their Fourier-transforms are shown in Figure 5. Interestingly ϕ_pp(q) has a minimum at q₁, which is not too far from the position of the maximum in S(Q) at T_g, Q₁ = 2.06 Å^-1. The dependence of q₁ on $\varphi \left({\mathit{r}}_c\right)$ is shown in Figure 6. The value of Q₁ decreases with increasing temperature, down to 1.93 Å⁻¹ at T = 100 K. A minimum in ϕ_pp(q) at q₁ implies that a density wave with q₁ would be energetically preferred. Because both S(Q) and ϕ(q) are dominated by the region in q around Q₁ (q₁), a density wave which minimize U must be that with q close to q₁. Thus, in the zero-th order the structure is dominated by the global density waves with q₁. In other words, a high-density gas state is unstable against the global density wave state with q₁.

FIGURE 5

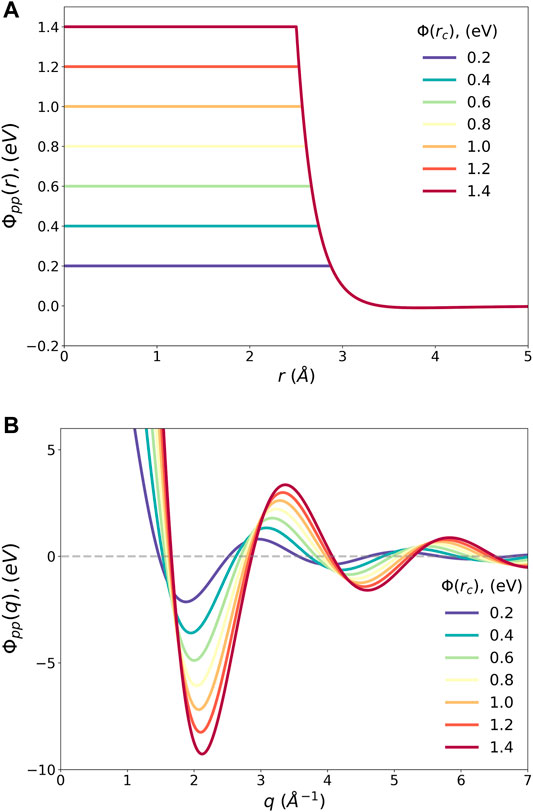
FIGURE 5. (A) The pseudopotential of the Lennard-Jones potential with various cut-off levels, ϕ_pp(r), and (B) their Fourier transforms, ϕ_pp(q).

FIGURE 6

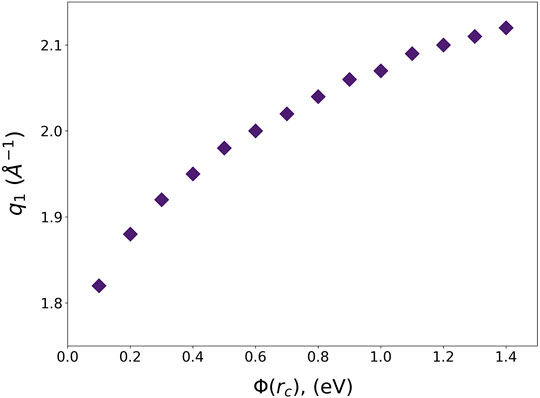
FIGURE 6. The q₁ of liquid Argon pseudopotential as a function of the cut-off energy. Q₁ = 2.06 Å^-1.

However, the density wave with q₁ has a fairly long wavelength, which results in a wide first peak of the PDF, as wide as the higher order PDF peaks. This is in conflict with the real-space requirement that the first peak of g(r) should be narrow around the bottom of ϕ(r) at r = a to reduce the potential energy. Thus, the requirement to reduce the potential energy in q space by density waves and the same requirement in real space by better SRO are orthogonal, resulting in frustration. This is a more general energetic statement of the geometrical frustration discussed by many in more specific forms, such as formation of icosahedral clusters (Sadoc, 1981; Nelson, 1983; Sethna, 1983). This conflict also explains the distinct natures of the MRO and SRO (Ryu and Egami, 2021). The final structure results from the compromise between the two, requiring additional density waves with high q values.

Discussion

The conventional approach to elucidate the structure of liquid is the bottom-up approach, in which the interatomic potential is applied to a small number of atoms to form a good local cluster, and the structure is extended by adding more clusters (Miracle, 2004; Sheng, et al., 2006; Robinson, et al., 2019). A major problem of this approach is that by starting with good clusters the boundaries between good clusters become strongly strained. This heterogeneous strain concentration increases the total strain energy. Actually, in an extended structure the peripheral atoms in one cluster are also central atoms in other clusters, thus the clusters are overlapping. Focusing just on “good” clusters is biased and dangerous. An orthogonal top-down approach is to consider all atoms at once, and to apply the potential simultaneously to all atoms. This can be done more effectively in reciprocal space. By removing the irrelevant strongly repulsive part of the interatomic potential to form the pseudopotential, the Fourier-transform of the potential, ϕ_pp(q), was found to have a minimum at q₁, close to the position of the maximum in S(Q) at Q₁. This means that there is a driving force to form a density wave at q₁. A small set of coherent density waves can form the basis for a crystal structure (Alexander and McTague, 1978), but a large set of density waves with random phase factors can form a state with long-range correlation without periodicity, the structurally coherent ideal glass state. The nature of such a state will be discussed elsewhere. Quasicrystal was the first of such state with long-range correlation without periodicity, which has a periodic crystalline lattice in six-dimensions (Levine and Steinhardt, 1984). The ideal glass forms a crystal in infinite dimensions.

A model of the coherent ideal glass state can be constructed by using G₀(r) as a guide. It was found the model has very diverse local structures (Ryu et al., 2019). For instance, the fraction of the icosahedral local environment is only 0.7%. Apparently, in order to maintain long-range density correlation the local structure is sacrificed. This is another proof of the conflict between the force to produce long-range density wave state and the force to create short-range atomic order. The final structure is determined through the compromise between these two conflicting forces. The balance between the two is reflected to the coherence length; the stronger the SRO is, for instance because of covalency, the shorter the ξ_s is. The extent of this balance can be expressed as the ideality of the structure (Ryu, et al., 2020). Furthermore, temperature also affects this balance. Local density fluctuations due to the atomic-level pressure fluctuations reduces the coherence of the density wave. This argument quantitatively explains the Curie-Weiss law, Eq. 2 (Egami and Ryu, 2021).

The idea of geometric frustration is based on the hard-sphere (HS) packing argument (Nelson, 1983). In the DRP-HS model dynamics is controlled by jamming, because no potential energy is involved. To keep the density constant external pressure is applied, which plays the role of the attractive potential. It is interesting to note, however, if we use the pseudopotential, ϕ_HS(q) has a minimum at q_1,HS as shown in Figure 7, with D_HSq_1,HS = 5.76, where D_HS = 2R_HS and R_HS is the hard-sphere radius. This value is not far from the value of D_HSQ_1,HS = 6.9 for the hard-sphere model, where Q_1,HS is the Q₁ for hard-spheres (Lange, et al., 2009). It could also be related to the long-range oscillation found recently (Rissone et al., 2021), but its value, D_HSQl = 7.5, is considerably higher. If the pseudopotential concept applies even for the hard-sphere mode, it means that the mere action of exclusion on a gas under pressure may induce a density wave state. The height of the pseudopotential is irrelevant as long as it is substantially larger than k_BT. The ϕ_HS(q) has a long oscillating tail, and it influences the structure through the high Q part of S(Q). However, the strong minimum of ϕ_HS(q) has a dominant effect on the first peak of S(Q), producing the density wave and the MRO even in the hard-sphere model.

FIGURE 7

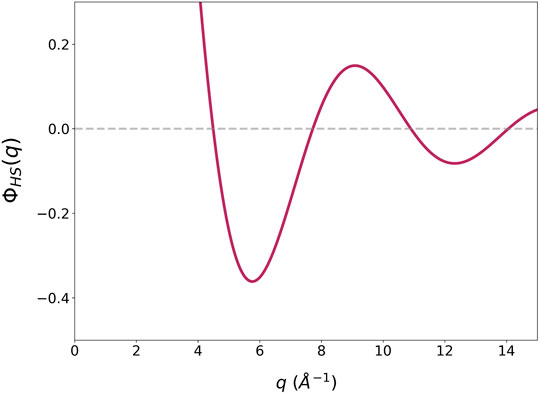
FIGURE 7. The Fourier transform of the pseudopotential of the hard-sphere potential, ϕ_HS(q), with the cut-off at 1 energy unit and D_HS = 1 Å.

Thus, the idea of the minimum of ϕ(q) producing the density wave and the MRO appears to work widely, independent of details of the interatomic potential, possibly including even the hard-sphere model. As will be described elsewhere the dynamics of the density wave, through the amplitudons and phasons, is directly related to atomic dynamics. Thus, the stiffness of the density wave controls the cooperative atomic dynamics, affecting many physical properties of liquid. To what extent the same argument applies to covalently bonded network glass needs to be examined.

Conclusion

To characterize the atomic structure of liquid and glass, it is customary to start with focusing on the local structural units made of several atoms, and to consider adding them up to form the global structure. This bottom-up approach is so prevalent that its wisdom has not even been questioned. However, glasses are not formed in such a manner. In the process of glass formation through the glass transition all atoms equally contribute to glass formation during cooling through cooperative processes. To capture this many-body aspect of global glass formation, we propose a new holistic concept, made of dual bottom-up and top-down approaches. In the top-down approach we consider an assembly of many atoms in a high-density gas state and apply interatomic potentials to all atoms at once. The interatomic potential in reciprocal space causes collective density wave instability, which tries to create the ideal glass state. The final structure is determined through the competition and compromise of frustration between these two, local and global, driving forces. The balance between the two driving forces can be quantified in terms of the coherence length of the MRO, ξ_s, and the ideality of the liquid structure (Ryu et al., 2020). This approach explains the distinct natures of short-range order and medium-range order, and strong temperature dependence of various properties of liquid.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

This work was conceived and authored by TE with assistance by CR. The data in this work were generated by CR. Both authors contributed to the article and approved the submitted version.

Funding

This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors TE.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alexander, S., and McTague, J. (1978). Should All Crystals Be Bcc? Landau Theory of Solidification and Crystal Nucleation. Phys. Rev. Lett. 41, 702–705. doi:10.1103/PhysRevLett.41.702

CrossRef Full Text | Google Scholar

Berthier, L., and Kob, W. (2012). Static Point-To-Set Correlations in Glass-Forming Liquids. Phys. Rev. E 85, 011102. doi:10.1103/PhysRevE.85.011102

PubMed Abstract | CrossRef Full Text | Google Scholar

Croxton, C. A. (1974). Liquid State Physics – A Statistical Mechanical Introduction. Cambridge: Cambridge University Press.

Google Scholar

Debenedetti, P. G., and Stillinger, F. H. (2001). Supercooled Liquids and the Glass Transition. Nature 410, 259–267. doi:10.1038/35065704

PubMed Abstract | CrossRef Full Text | Google Scholar

Egami, T. (2020). Local Density Correlations in Liquids. Front. Phys. 8, 50. doi:10.3389/fphy.2020.00050

CrossRef Full Text | Google Scholar

Egami, T., and Ryu, C. W. (2021). Medium-Range Atomic Correlation in Simple Liquids. II. Theory of Temperature Dependence. Phys. Rev. E 104, 064110. doi:10.1103/PhysRevE.104.064110

PubMed Abstract | CrossRef Full Text | Google Scholar

Egelstaff, P. A. (1967). An Introduction to the Liquid State. Oxford: Academic Press Oxford University Press.

Google Scholar

Hansen, J.-P., and McDonald, I. R. (1976). Theory of Simple Liquids. London: Academic Press.

Google Scholar

Lange, E., Caballero, J. B., Puertas, A. M., and Fuchs, M. (2009). Comparison of Structure and Transport Properties of Concentrated Hard and Soft Sphere Fluids. J. Chem. Phys. 130, 174903. doi:10.1063/1.3124182

PubMed Abstract | CrossRef Full Text | Google Scholar

Levine, D., and Steinhardt, P. J. (1984). Quasicrystals: A New Class of Ordered Structures. Phys. Rev. Lett. 53, 2477–2480. doi:10.1103/PhysRevLett.53.2477

CrossRef Full Text | Google Scholar

March, N. H., and Tosi, M. P. (2002). Introduction to Liquid State Physics. Singapore: World Scientific.

Google Scholar

Miracle, D. B. (2004). A Structural Model for Metallic Glasses. Nat. Mater. 3, 697–702. doi:10.1038/nmat1219

PubMed Abstract | CrossRef Full Text | Google Scholar

Nelson, D. R. (1983). Order, Frustration, and Defects in Liquids and Glasses. Phys. Rev. B 28, 5515–5535. doi:10.1103/PhysRevB.28.5515

CrossRef Full Text | Google Scholar

Ornstein, L. S., and Zernike, F. (1914). Accidental Deviations of Density and Opalescence at the Critical Point of a Single Substance. Roy. Neth. Acad. Arts Sci. (KNAW) 17, 793–806.

Google Scholar

Parisi, G., and Zamponi, F. (2010). Mean-Field Theory of Hard Sphere Glasses and Jamming. Rev. Mod. Phys. 82, 789–845. doi:10.1103/RevModPhys.82.789

CrossRef Full Text | Google Scholar

Phillips, J. C., and Kleinman, L. (1959). New Method for Calculating Wave Functions in Crystals and Molecules. Phys. Rev. 116, 287–294. doi:10.1103/physrev.116.287

CrossRef Full Text | Google Scholar

Rissone, P., Corwin, E. I., and Parisi, G. (2021). Long-Range Anomalous Decay of the Correlation in Jammed Packings. Phys. Rev. Lett. 127, 038001. doi:10.1103/PhysRevLett.127.038001

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, J. F., TurciRoth, F. R., Roth, R., and Royall, C. P. (2019). Morphometric Approach to Many-Body Correlations in Hard Spheres. Phys. Rev. Lett. 122, 068004. doi:10.1103/PhysRevLett.122.068004

PubMed Abstract | CrossRef Full Text | Google Scholar

Rowley, L. A., Nicholson, D., and Parsonage, N. G. (1975). Monte Carlo Grand Canonical Ensemble Calculation in a Gas-Liquid Transition Region for 12-6 Argon. J. Comput. Phys. 17, 401–414. doi:10.1016/0021-9991(75)90042-X

CrossRef Full Text | Google Scholar

Ryu, C. W., Dmowski, W., and Egami, T. (2020). Ideality of Liquid Structure: A Case Study for Metallic Alloy Liquids. Phys. Rev. E 101, 030601. doi:10.1103/PhysRevE.101.030601

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryu, C. W., Dmowski, W., Kelton, K. F., Lee, G. W., Park, E. S., Morris, J. R., et al. (2019). Curie-Weiss Behavior of Liquid Structure and Ideal Glass State. Sci. Rep. 9, 18579. doi:10.1038/s41598-019-54758-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryu, C. W., and Egami, T. (2021). Medium-Range Atomic Correlation in Simple Liquids. I. Distinction from Short-Range Order. Phys. Rev. E 104, 064109. doi:10.1103/PhysRevE.104.064109

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadoc, J. F. (1981). Use of Regular Polytopes for the Mathematical Description of the Order in Amorphous Structures. J. Non-Crystalline Solids 44, 1–16. doi:10.1016/0022-3093(81)90128-9

CrossRef Full Text | Google Scholar

Sethna, J. P. (1983). Frustration and Curvature: Glasses and the Cholesteric Blue Phase. Phys. Rev. Lett. 51, 2198–2201. doi:10.1103/PhysRevLett.51.2198

CrossRef Full Text | Google Scholar

Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M., and Ma, E. (2006). Atomic Packing and Short-To-Medium-Range Order in Metallic Glasses. Nature 439, 419–425. doi:10.1038/nature04421

PubMed Abstract | CrossRef Full Text | Google Scholar

Tarjus, G., Kivelson, S. A., Nussinov, Z., and Viot, P. (2005). The Frustration-Based Approach of Supercooled Liquids and the Glass Transition: A Review and Critical Assessment. J. Phys. Condens. Matter 17, R1143–R1182. doi:10.1088/0953-8984/17/50/R01

CrossRef Full Text | Google Scholar

Warren, B. E. (1969). X-Ray Diffraction. Reading: Addison-Wesley.

Google Scholar

Wu, T.-Y., and Ohmura, T. (1962). Quantum Theory of Scattering. Englewood Cliffs: Prentice-Hall, Englewood Cliffs.

Google Scholar