Phase-Field Simulation of γ′-Co3 (Al, W) Evolution Kinetics with Antiphase Boundaries in Co-Based Monocrystal Superalloys

Antiphase boundaries (APBs) of L1₂ ordered γ′-Co₃ (Al, W) precipitates have an essential effect on the high-temperature strength of Co-based monocrystal superalloys. In this work, the antiphase boundaries and their effects on the evolution kinetics of γ′ phase are studied with the phase-field model. The formation of APBs between γ′ phases with different crystallographic variants induces a sharp increase in free energy; the width of APBs measured by the edge-to-edge distances of the γ′ phase is consistent with the experimental results of superalloys. Also, a coupling behavior of Ostwald ripening and APB’s migration in the coarsening of the γ′ phase is revealed. In addition, the volume fraction of the γ′ phase with four antiphase domains is lower than that of the single-domain γ′ phase, and the time exponent of the particles’ number density of the γ′ phase at the steady coarsening stage changes from –0.99 of single domain to –0.8 of APBs. The results show that the high-energy APBs can reduce the coarsening rate of γ′ phases, which are significant in the microstructure and composition designing of the ordered precipitates with APBs in Co-based superalloys.

Introduction

The ordered L1₂-γʹ phase precipitation-strengthened Co-based superalloys have attracted many interests due to their excellent properties at high temperature, such as good resistance to corrosion, oxidation, and fracture (Sato et al., 2006; Yan et al., 2014). Thus, instead of the Ni-based superalloys, the Co-based superalloy containing γʹ-Co₃ (Al_xW_1-x) precipitates will be served as the next-generation high-temperature materials (Suzuki et al., 2008). The superior performance of Co-based superalloys at elevated temperatures is originated from the γʹ phase, which has a strong obstacle to the slip of dislocation (Nathal et al., 1987). The stability of the γ+γʹ microstructure is dependent on their retarding effect of coarsening, so the kinetic evolution of the γʹ phase in Co-based superalloys is significant on the mechanical properties. Extensive studies found that cobalt-based superalloys with a high γʹ volume fraction and slow coarsening rate are typically expected (Boothmorrison et al., 2009; Gupta et al., 2020; Liu et al., 2020).

As is known, γʹ-Co₃ (Al, W) precipitates with a L1₂ ordered f.c.c (face-centered cubic) structure have a special microstructure called the antiphase domains (APDs). The microstructure is introduced to the superalloys in the representation of the region of four equivalent ordered states, obtained by the movement of the crystal lattice from its initial position to [0, 0, 0], [1/2, 1/2, 0], [1/2, 0, 1/2], and [0, 1/2, 1/2], respectively (Li et al., 1998). If these four types of APDs impinge on each other during growth and coarsening, a structural L1₂ planar defect called antiphase domain boundary (APB) will be generated. However, the interaction between those “out-of-phase” particles (OPPs) is crucial to produce the high-energy APBs. In contrast, the contact among the particles which happen to be “in phase” (IPPs) with respect to each other is quite different. By definition, the IPPs generate a single perfect ordered domain rather than the high-energy APBs (Wang et al., 1995). Therefore, the coalescence events almost occurred in IPPs rather than in OPPs.

There are several studies relating to the APBs and their effects on the evolution kinetics of the γ′ phase in Ni-based alloys. Yang et al. (2017) studied the effects of the APDs and the elastic energy on the morphological evolution and coarsening behavior of γ′ precipitates in Ni-based alloys using the phase-field method. It was found that the presence of the APDs reduces the coarsening of γ′ precipitates. The studies of Wang et al. (1998); Chen et al., 2004) show that when the APB energy is greater than twice the γ/γʹ coherent interfacial energy, no APBs can exist between γʹ precipitates, except when the alloys are subjected to high-temperature annealing or severe plastic deformation (Yang et al., 2021).

Although some studies have been carried out on the coarsening kinetics of the γ′ phase in cobalt-based superalloys (Sauza et al., 2016; Azzam et al., 2018; Shi et al., 2020; Wang et al., 2020), the effect of APBs on the evolution kinetics of the γ′ phase from nucleation to growth is not disclosed, especially for an elastically strain system like Co-Al-W alloy. This work is focused on the formation of APBs, and the relationship between the APBs and coarsening behavior of γ′ phases in Co-10Al-10W at% alloy aged at 1173 K. The Kim–Kim–Suzuki (KKS) model (Kim et al., 1999) is introduced to the phase-field model in this work. Coupling with the KKS model, the extra potential at interfaces will be removed to guarantee the smooth interfacial diffusion between γ/γʹ phases. The advantage of the KKS model is that it distinguishes the different crystallographic variants of the γʹ phase and therefore can account for effects associated with antiphase boundaries. In sum, it is conventional to reveal the effect of the APBs on the free energy as well as the coarsening rate from the perspectives of energy and kinetics.

Materials and Methods

Phase-Field Model

The nucleation and growth of γ′ precipitates in Co–Al–W alloys is driven by the minimum of the total free energy, so the phase-field model for describing the evolution of ordered precipitates can be constructed by two equations (Wu et al., 2004): one is the composition fields characterized by the Cahn–Hilliard equation (Cahn et al., 1958) and the other is order parameter field ${\eta }_i\left(\mathit{r},t\right)$ characterized by the Ginzburg–Landau equation (Allen et al., 1979).

$\frac{\partial x_i\left(\mathbf{r},t\right)}{\partial t}=V_{\text{m}}^2\nabla \left[M_i\nabla \left(\frac{\delta F}{\delta x_i\left(\mathbf{r}, t\right)}\right)\right]+{\xi }_c\left(\mathbf{r},t\right),i=\mathrm{Al}, \mathrm{W}(1)$

$\frac{\partial {\eta }_p\left(\mathbf{r},t\right)}{\partial t}=-L\left(\frac{\delta F}{\text{δ}{\eta }_p\left(\mathbf{r},t\right)}\right)+{\xi }_p\left(\mathbf{r},t\right),p=\mathrm{1,2,3}(2)$

where $M_i\left(i=\text{Al},\text{W}\right)$ are the chemical mobilities of Al and W, L is the interfacial mobility for the structural transformation (Chang et al., 2015), which is chosen to be 6 × 10^–7 m³ J⁻¹ s⁻¹. ${\xi }_c\left(\mathit{r},t\right)$ and ${\xi }_p\left(\mathit{r},t\right)$ are the random noise terms that are used to activate the thermal fluctuation for the nucleation. According to the study of Gaubert et al. (2010), the mobilities can be expressed as follows:

$M_i=D_i/\left(V_m\frac{{\partial }^2{f}^{\text{γ}}}{\partial x_i^2}\right),(3)$

$\mathit{ }{D}_i=D_0\text{exp}\left(-\mathrm{\Delta }U/kT\right),(4)$

where $D_0=1.45\times {10}^4{\text{m}}^2{\text{s}}^{-1}$ and $\mathrm{\Delta }U=2.8 eV$, V_m is the molar volume, and k is the Boltzmann constant.

The total free energy includes the chemical free energy, the gradient energy arising from the compositional and structural inhomogeneity, and the coherent elastic strain energy (Ji et al., 2016).

$F={\displaystyle \underset{V}{\int }\left[\begin{array}{c}{f}_{\text{ch}}\left(x_{\text{Al}}, x_{\text{W}}, \left\{{\eta }_p\right\},T\right)+\frac{1}{2}{\displaystyle \sum _{i=\text{Al},\text{W}}{k}_i{\left(\nabla x_i\right)}^2}\\ + \frac{1}{2}{k}_{\eta }{\displaystyle \sum _{p=1}^3{\left(\nabla {\eta }_p\right)}^2}+f_{\text{el}}\end{array}\right]dV},(5)$

where k_i and k_η are the gradient energy coefficients (Meher et al., 2013), and $f_{\text{ch}}\left(x_{\text{Al}}, x_{\text{W}}, \left\{{\eta }_p\right\},T\right)$ and $f_{el}$ are the chemical free energy density and elastic energy density, respectively.

The chemical free energy density coupling with the KKS model is related with the molar Gibbs free energy of γ matrix $f^{\text{γ}}$ and γ′ precipitate $f^{{\text{γ}}^{\text{′}}}$ by

$\begin{array}{l}{f}_{\text{ch}}\left(x_{\text{Al}}, x_{\text{W}}, \left\{{\eta }_p\right\},T\right)=V_{\text{m}}^{-1}{\displaystyle \sum _{p=1}^{3}h\left({\eta }_p\right)f^{\text{γ′}}\left(x_{\text{Al}}^{\text{γ′}},x_{\text{W}}^{\text{γ′}},T\right)}\\ +V_{\text{m}}^{-1}\left(1-{\displaystyle \sum _{p=1}^{3}h\left({\eta }_p\right)}\right)f^{\text{γ}}\left(x_{\text{Al}}^{\text{γ}},x_{\text{W}}^{\text{γ}},T\right)+g\left(\left\{{\eta }_p\right\}\right),\end{array}(6)$

where $h\left({\eta }_p\right)={\eta }_p^3(6{\eta }_p^2-15{\eta }_p+10)$ is an interpolation function coupling the matrix phase to the precipitated phase. $g\left(\left\{{\eta }_p\right\}\right)$ is a Landau-type double-well function getting rid of the coexistence of four antiphase domains with different variants at the same grid space,

$\text{g}\left(\left\{{\eta }_p\right\}\right)=\omega {\displaystyle \sum _{p=1}^3{\eta }_p^2\left(1-{\eta }_p^2\right)}+\theta {\displaystyle \sum _{p\ne q}{\eta }_p^2{\eta }_q^2},(7)$

where $\theta$ = 8.0 is selected so that Eq. 7 satisfies the energy minimum theorem at $\left({\eta }_1,{\eta }_2,{\eta }_3\right)=\left(\mathrm{0,0,0}\right){\eta }_{\text{max}}$, $\left({\eta }_1,{\eta }_2,{\eta }_3\right)=\left(\pm 1,\mp 1,\mp 1\right){\eta }_{\text{max}}$, $\left({\eta }_1,{\eta }_2,{\eta }_3\right)=\left(\mp 1,\pm 1,\mp 1\right){\eta }_{\text{max}}$, and $\left({\eta }_1,{\eta }_2,{\eta }_3\right)=\left(\mp 1,\mp 1,\pm 1\right){\eta }_{\text{max}}$, which represent four different variants of the γʹ phase, respectively. ω is a parameter in description of the height of the double-well function $g\left(\left\{{\eta }_p\right\}\right)$. In this model, we approximate $f^{\phi }(x_{Al}^{\phi },x_{\text{W}}^{\phi },T)(\phi =\gamma , \gamma \text{′})$ by the Taylor series expansion at equilibrium compositions up to the second order,

$\begin{array}{l}{f}^{\varphi }\left(x_{\text{Al}}^{\varphi },x_{\text{W}}^{\varphi },T\right)=A^{\varphi }+B_{\text{Al}}^{\varphi }\left(x_{\text{Al}}^{\varphi }-x_{\text{Al}}^{\varphi ,\text{eq}}\right)+B_{\text{W}}^{\varphi }\left(x_{\text{W}}^{\varphi }-x_{\text{W}}^{\varphi ,\text{eq}}\right)\\ +\frac{1}{2}{C}_{\text{AlAl}}^{\varphi }{\left(x_{\text{Al}}^{\varphi }-x_{\text{Al}}^{\varphi ,\text{eq}}\right)}^2+\frac{1}{2}{C}_{\text{WW}}^{\varphi }{\left(x_{\text{W}}^{\varphi }-x_{\text{W}}^{\varphi ,\text{eq}}\right)}^2\\ +C_{\text{AlW}}^{\varphi }\left(x_{\text{Al}}^{\varphi }-x_{\text{Al}}^{\varphi ,\text{eq}}\right)\left(x_{\text{W}}^{\varphi }-x_{\text{W}}^{\varphi ,\text{eq}}\right) ,\end{array}(8)$

where $x_W^{\phi ,eq}$ and $x_{Al}^{\phi ,eq}$ are the equilibrium composition of W and Al in phase $\phi$ at the given temperature, respectively. $A^{\varphi }$, $B_{Al}^{\varphi }$, $B_{\text{W}}^{\varphi }$, $C_{AlAl}^{\varphi }$, $C_{WW}^{\varphi }$, and $C_{AlW}^{\varphi }$ are Taylor expansion coefficients which can be calculated as follows:

$A^{\varphi }=f^{\varphi }\left(x_{\text{Al}}^{\varphi ,\text{eq}},x_{\text{W}}^{\varphi ,\text{eq}},T\right),(\mathrm{9a})$

$B_i^{\varphi }={\frac{\partial f^{\varphi }}{\partial x^{\varphi }}|}_{x_i^{\varphi }=x_i^{\varphi ,\text{eq}}}\left(i=\text{Al},\text{W}\right),(\mathrm{9b})$

$C_{i,j}^{\varphi }={\frac{{\partial }^2{f}^{\varphi }}{\partial x_i^{\varphi }\partial x_j^{\varphi }}|}_{x_i^{\varphi }=x_i^{\varphi ,\text{eq}},x_j^{\varphi }=x_j^{\varphi ,\text{eq}}}\left(i,j=\text{Al},\text{W}\right).(\mathrm{9c})$

To determine the values of the concentrations $x_i^{\text{γ′}}$ and $x_i^{\text{γ}}$ from the actual Al and W concentration $x_i$, the KKS model imposes the local equilibrium condition:

$\frac{\partial f^{\text{γ′}}}{\partial x_i^{\text{γ′}}}=\frac{\partial f^{\text{γ}}}{\partial x_i^{\text{γ}}},\left(i=\text{Al},\text{W}\right).(10)$

Therefore, the equilibrium composition in the total system can be achieved when the solution of concentration fields in γ and γ′ phases obeys the following equations:

$x_i=\left(1-{\displaystyle \sum _{p=1}^{3}h\left({\eta }_p\right)}\right)x_i^{\text{γ}}+{\displaystyle \sum _{p=1}^{3}h\left({\eta }_p\right)x_i^{\text{γ′}}},\left(i=\text{Al},\text{W}\right).(11)$

The elastic energy density caused by the coherent misfit between the γ matrix and γ′ phase is given by the following equation:

$f_{el}=\frac{1}{2}{C}_{ijkl}{\epsilon }_{ij}^{el}{\epsilon }_{kl}^{el}=\frac{1}{2}{C}_{ijkl}\left({\overline{\epsilon }}_{ij}+\delta {\epsilon }_{ij}-{\epsilon }_{ij}^0\left(r\right)\right)\left({\overline{\epsilon }}_{kl}+\delta {\epsilon }_{kl}-{\epsilon }_{kl}^0\left(r\right)\right),(12)$

where C_ijkl is the tensor of the elastic constant (Li et al., 1998), ${\overline{\epsilon }}_{ij}$ and $\delta {\epsilon }_{ij}$ are the homogeneous strain and heterogeneous strain, respectively. ${\epsilon }_{ij}^0$ is the eigenstrain and defined as (Wen et al., 2010) ${\epsilon }_{ij}^0={\displaystyle \sum _p\mathrm{\Delta }{x}_p\left(r\right){\epsilon }_{ij}^0\left(p\right)}$, where p represents the elements Al and W, $\mathrm{\Delta }{x}_p\left(r\right)$ is the difference between the solute atomic composition at random and initial time, and the stress-free strain ${\epsilon }_{ij}^0\left(p\right)$ can be expressed as ${\epsilon }_{ij}^0\left(p\right)={\delta }_{ij}\frac{\partial a\left(x_{\text{Al}},x_{\text{W}}\right)}{a_0\partial x_p}$, where ${\delta }_{ij}$ is the Kronecker delta function. The average lattice parameter $a_0$ can be approximated by Vegard’s law with the lattice parameter $a(x_{\text{Al}},x_{\text{W}})$.

To solve Eqs 1, 2 numerically, the dimensionless form of the equations is given as follows:

$\frac{\partial x_i\left({\mathbf{r}}^{\ast },t^{\ast }\right)}{\partial t^{\ast }}={\nabla }^{\ast }\left\{M_i^{\text{*}}{\nabla }^{\text{*}}\left[\frac{\partial f_{\text{ch}}^{\ast }}{\partial x_i\left({\mathbf{r}}^{\ast },t^{\ast }\right)}-k_i^{\ast }{\nabla }^{\ast 2}{x}_i\left({\mathbf{r}}^{\ast },t^{\ast }\right)+\frac{\partial f_{el}^{\ast }}{\partial x_i\left({\mathbf{r}}^{\ast },t^{\ast }\right)}\right]\right\}+{\xi }_c^{\ast }\left({\mathbf{r}}^{\ast },t^{\ast }\right),i=\text{Al},\text{W,}(\mathrm{13a})$

$\frac{\partial {\eta }_p\left({\mathbf{r}}^{\ast },t^{\ast }\right)}{d{t}^{\ast }}=-\left[\frac{\delta f_{\text{ch}}^{\ast }}{\delta {\eta }_p\left({\mathbf{r}}^{\ast },t^{\ast }\right)}-k_{\eta }^{\ast }{\nabla }^{\ast 2}{\eta }_p\left({\mathbf{r}}^{\ast },t^{\ast }\right)\right]+{\xi }_p^{\ast }\left({\mathbf{r}}^{\ast },t^{\ast }\right),p=\mathrm{1,2,3.}(\mathrm{13b})$

The non-dimensional parameters are given as follows:

${\mathbf{r}}^{\ast }=\frac{\mathbf{r}}{l},t^{\ast }=L\text{Δ}ft,{\nabla }^{\ast }=\frac{\partial }{\partial {\mathbf{r}}^{\ast }}=\frac{\partial }{\partial \left(\frac{\mathbf{r}}{l}\right)}=\nabla l,M_i^{\ast }=\frac{V_m^2{M}_i}{L{l}^2},$

$f_{\text{ch}}^{\ast }=\frac{f_{\text{ch}}}{\text{Δ}f},k_i^{\ast }=\frac{k_i}{\text{Δ}f{l}^2},k_{\eta }^{\ast }=\frac{k_{\eta }}{\text{Δ}f{l}^2} ,(14)$

where $\text{Δ}f$ is the maximum free energy density used to obtain the non-dimensional parameter and is chosen to be $\text{Δ}f$ = 6 × 10⁷ J/m³.

The simulation is operated in the cell with size 256Δx^∗ ×256Δy^∗, and the time step is 0.01. Eqs. 13a, 13b are solved by using the semi-implicit Fourier spectral method (Chen et al., 1998). The parameters used in the simulation are given as follows: the gradient energy coefficients related to composition and order parameter k_Co = k_Al = k_W = 9.5 × 10^–11 J/m, k_η = 1.15 × 10^–7 J/m. The elastic constants of γ′ precipitate and γ matrix are implemented as $C_{11}^{\text{γ}}=230 \text{GPa}$, $C_{12}^{\text{γ}}=170 \text{GPa}$, $C_{44}^{\text{γ}}=90 \text{GPa}$, $C_{11}^{{\text{γ}}^{\text{'}}}=253 \text{GPa}$, $C_{12}^{{\text{γ}}^{\text{'}}}=147 \text{GPa}$, $C_{44}^{{\text{γ}}^{\text{'}}}=117 \text{GPa}$ (Xu et al., 2013), and the grid length l = 2 × 10^–9 m. In addition, the γ′ phase with the single-ordered domain represents three same order parameters in the model like η₁ = η₂ = η₃ = η, while the condition of four APDs is quite different. The sides of the square-shaped mesh micrographs are along the [10] and [01] directions of the system.

Results and Discussion

The formation of APBs and their impacts on the evolution kinetics of γʹ phases are studied in Co–10Al–10W at% superalloys at 1173 K aging for 1 h. According to the three order parameter fields, the emergence of the APBs can be described by the four types of APDs. The four APDs of the γʹ phase are distinguished from the perspective of order parameters, which are η_max (1, 1, 1), η_max (1, −1,−1), η_max (−1, −1,1), and η_max (−1,1,−1) (η_max = η_1max = η_2max = η_3max) (Wang et al., 2007). In these four APDs, the IPPs and OPPs are considered as two types of particles. In addition, we also take the distinction of γʹ phases with a single domain and four kinds of APDs on the process of growth and coarsening.

The order parameter fields are shown pictorially in Figure 1A–C, where the dark areas represent the γ matrix, and other color areas represent the γʹ phases with different orientations. Thus, particles with the same color are defined as IPPs, while OPPs represent particles with different colors.

FIGURE 1

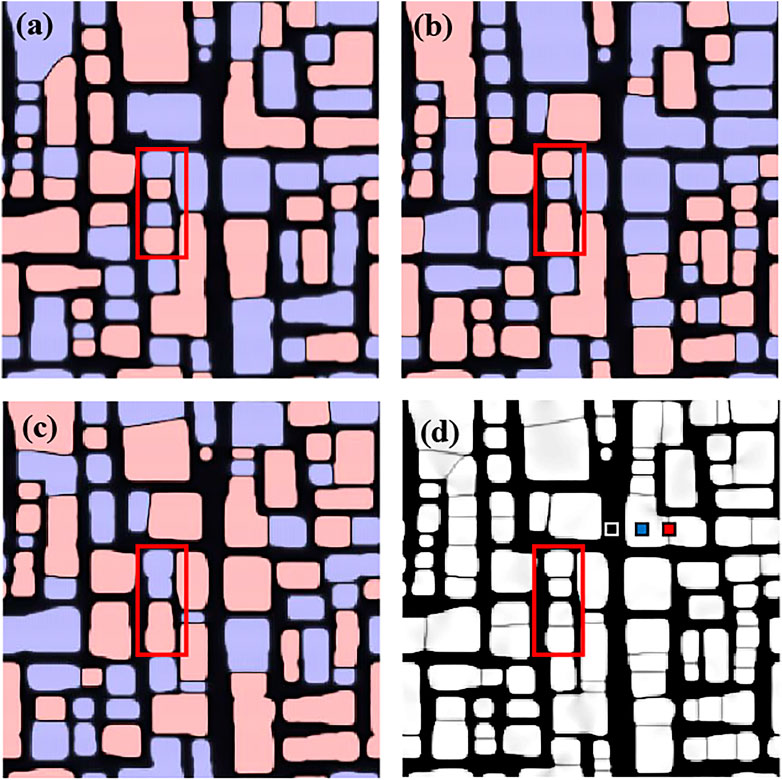
FIGURE 1. Order parameter fields: (A) η₁, (B) η₂, (C) η₃, and morphology (D) of Co–10Al–10W (at%) alloy aged for t = 1 h at 1173 K.

Figure 1D shows the mesoscopic microstructure of Co–10Al–10W at% alloy aged for 1 h at 1173 K, in which the white areas represent the γʹ phases with equilibrium composition field of W.

In Figure 1A–D, each γʹ phase has reached the equal value 1 or –1 of order parameters at 1 h. As indicated in the red block, four APDs with different order parameters η_max collide with the neighbor one to form the APBs. Previous studies have shown that there are mainly two types of APBs in superalloys, namely, [010] APB and [111] APB (Saal et al., 2016). Of course, the energies of these two types of APBs are different due to their degree of ordering, which has been demonstrated by the density-functional theory (DFT) calculations (Karnthaler et al., 1996).

The presence of APBs plays an essential role in the morphology evolution of the γʹ phase. Therefore, the formation of APBs and their effects on the morphology evolution of the γʹ phase are studied. As is shown in Figure 2A, the variations of free energy are illustrated from the γ matrix to the γʹ phase, the data of each curve are obtained from the position signed with three points of corresponding colors in Figure 1D. As the aging goes on, the free energy in the γʹ phase decreases to the minimum to ensure it is in a steady state. On the contrary, the energy in the γ matrix keeps at a relatively high level in order to satisfy the law of conservation of energy (Lifshitz et al., 1969). In particular, it is indicated in the red circle that free energy in the γ matrix, the γʹ phase, and the APBs all have a decline at the beginning stage. However, a sharp increase in regions of APBs occurs to overcome the energy barrier for the formation of APBs. During the stage of APB formation, the γ′ phases with different APDs keep growing and eventually impinging to form an APB.

FIGURE 2

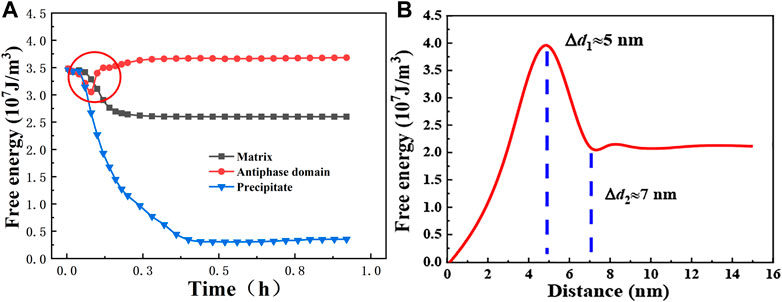
FIGURE 2. Free energy variations in regions of APBs: (A) with aging time t from γ matrix to γʹ phase and (B) with edge-to-edge distance of two γ′ phases.

Further investigation has been carried out to clarify the relationship of free energy change and the particle’s edge-to-edge distance Δd, as shown in Figure 2B, the free energy between two neighboring γ′ phases rises with the increasing of the Δd. When Δd₁ = 5nm, the energy reaches the maximum, which is in good agreement with the width of APBs in experimental results of superalloys (Hemker et al., 1993; Mebed et al., 2003). This supports the fact that the free energy in the APBs reaches its peak shortly after the formation of the APBs. In addition, when the Δd >7 nm, almost no energy fluctuations are produced due to the weak interaction of γʹ phases. In this state, the position is not the interface regions of γʹ phases, while it becomes the matrix phase.

The previous study found that the emergence of the high-energy APBs inevitably has a crucial impact on the coarsening of the γ′ precipitates. Therefore, the problem is studied from different perspectives. Figure 3 shows the variations of the γ′ area fraction with aging time t for the single domain and four APDs, which indicates the effect of APBs on slowing down the nucleation and growth of the γʹ phases. In particular, when t < 0.15 h, the slope of the γ′ area fraction is k^APB = 5.77 and k^single = 9.28, so the volume fraction of the single domain increases faster than that of the four APDs in the early stage of aging, and reaches a steady state when its volume fraction is around 3% higher than that of the four APDs. Then, the difference of volume fractions becomes small at 1.5%, which is shown in the inserted picture. Above all, during the whole aging time, APBs make the certain influence on the γ′ area fraction because of the decline of the coarsening rate and the variation of the coarsening mode.

FIGURE 3

FIGURE 3. Variations of the γ′ area fraction with aging time t for single domain and four domains.

As discussed before, the effect of APBs on the kinetics evolution of the γ′ phase from nucleation to growth is not investigated. Usually, the Ostwald ripening and coalescence coarsening are two types of coarsening mechanisms in experimental TEM or SEM morphology (Mebed et al., 2003), while the evolution of APBs is not detected clearly in the experimental morphology. Therefore, the effects of the APBs on the growth and coarsening of the ordered γʹ phase need a further study.

In this work, the particles’ number density in unit volume is defined as $N_V=\frac{N_A}{2r}$, where N_A is the particles’ number of the unit area and <r> is the average size of the γ′ phase (Shi et al., 2020). As shown in Figure 4A, B, the variations of N_V of the γʹ phase for four APDs and single domain are exhibited with aging time at 1173 K. At the stage of coarsening, the N_V declines with the decrease in particles’ number, the time exponent of N_V for APB is n₃^APB = −0.80 ± 0.03 and for single domain is n₃^single = −0.99 ± 0.02. The time exponents approach to –1 of Kuehmann–Voorhees (KV) theory (Kuehmann et al., 1996) in ternary alloy. At the nucleation and growth stage, the time exponents N_V are n₁^APB = 1.23 ± 0.03 and n₁^single = 1.52 ± 0.07, n₂^APB = 0.49 ± 0.05, and n₂^single = 0.28 ± 0.01.

FIGURE 4

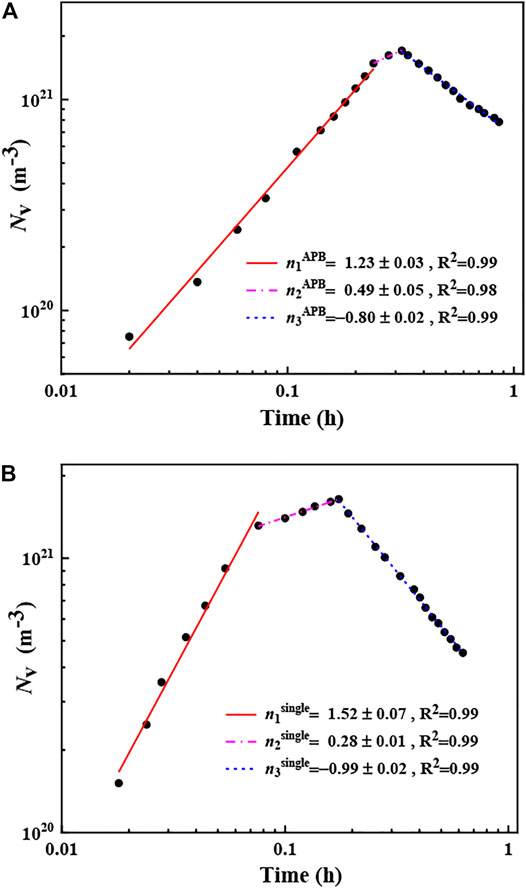
FIGURE 4. Evolution of the particles number density of the γ′ phase with time in Co–10Al–10W at% alloy aged at 1173 K: (A) four APDs and (B) single domain.

However, the time for nucleation and early growth stage is 0.37 h in possession of APBs, which is much longer than that of 0.19 h with a single domain. Therefore, the existence of APBs in four APDs significantly elongated the period of nucleation and growth. Furthermore, compared with the single-domain γ′ phase, the time exponent of N_V becomes small at the coarsening stage for the γ′ phase with four APDs, which reveals that the coalescence is inhibited due to the presence of APBs. In addition, the coarsening mode of the γ′ phase with APBs is Ostwald ripening, while for single domains, there is also the coalescence coarsening. So the decline of the coarsening rate in the presence of APBs is caused by the interface structure change of OPPs, whose duration of forming a single γʹ phase is noticeably longer than that of coalescence (Chen et al., 2021). It is indicated that more participation of Ostwald ripening occurs in the late stage of coarsening when APBs exist.

As mentioned before, the Ostwald ripening is considered as the dominant form of coarsening with the existence of APBs. Figure 5 shows the movement of APBs during the process of Ostwald ripening between two neighboring OPPs. The purple and pink ones represent the two γʹ precipitates with different orientations, delegated by η_eq = –1, η_eq = 1, respectively, and the black one delegates the γ matrix with η_eq = 0. The distribution of order parameter fields with aging time shows that the APB keeps moving toward the small particle until absorption by the larger one; this process is similar to the Ostwald ripening where small particles dissolve and large particles grow up. However, this is not a simple process of coalescence or Ostwald ripening, but a coupling behavior of Ostwald ripening and APBs mobility due to the extremely narrow distance between the two γʹ phases with different order parameters. It is hard to capture this interesting phenomenon in the experimental morphology, so the phase-field simulation with crystal structure information will play a predictive role in the further study.

FIGURE 5

FIGURE 5. Evolution of OPPs and order parameter η₁ through the APB at x* = 87–123, y* = 210 at 1173 K.

Conclusion

In this work, the antiphase boundaries and their effects on the evolution kinetics of the γ′ phase were studied with the KKS model to reveal the feature of free energy variation during the formation of APBs, as well as the reason for the sharp increase in free energy. From the new perspective of free energy, the relationship between the particle edge-to-edge distance and the APB formation, and the width of APBs are revealed in this simulation. In addition, the presence of antiphase domains can slow down the rate of growth and coarsening of the γ′ phase. Finally, a novelty phenomenon is explained in the late stage of coarsening of the OPP-typed γʹ phase with APBs, where the Ostwald ripening is the nature of APB migration with the interface structure reconstruction between two γʹ phases.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YJ performed the simulations, analysis, and wrote the first draft of the manuscript. YL supervised the research and proposed the concept and the modeling, rewriting the manuscript, and the data and results checking. SS, PS, HW, and HL offer useful suggestions on picture processing and manuscript writing.

Funding

This work was supported by the National Natural Science Foundation of China (No. 51571122) and the Fundamental Research Funds for the Central Universities (No. 30921013107).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank Professor YL for fruitful discussions and manuscript revision during manuscript writing. In addition, the authors thank SS, HW, and other colleagues for their useful suggestions on picture processing.

References

Allen, S. M., and Cahn, J. W. (1979). A Microscopic Theory for Antiphase Boundary Motion and its Application to Antiphase Domain Coarsening. Acta Metallurgica 27, 1085–1095. doi:10.1016/0001-6160(79)90196-2

CrossRef Full Text | Google Scholar

Azzam, A., Philippe, T., Hauet, A., Danoix, F., Locq, D., Caron, P., et al. (2018). Kinetics Pathway of Precipitation in Model Co-Al-W Superalloy. Acta Materialia 145, 377–387. doi:10.1016/j.actamat.2017.12.032

CrossRef Full Text | Google Scholar

Boothmorrison, C., Noebe, R., and Seidman, D. (2009). Effects of Tantalum on the Temporal Evolution of a Model Ni-Al-Cr Superalloy during Phase Decomposition. Acta Materialia 57, 909–920. doi:10.1016/j.actamat.2008.10.029

CrossRef Full Text | Google Scholar

Cahn, J. W., Hilliard, J. E., and Chem, J. (1958). Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 28, 258–267. doi:10.1063/1.1744102

CrossRef Full Text | Google Scholar

Chang, H., Xu, G., Lu, X.-G., Zhou, L., Ishida, K., and Cui, Y. (2015). Experimental and Phenomenological Investigations of Diffusion in Co-Al-W Alloys. Scripta Materialia 106, 13–16. doi:10.1016/j.scriptamat.2015.03.021

CrossRef Full Text | Google Scholar

Chen, C. Y., and Stobbs, W. M. (2004). Interfacial Segregation and Influence of Antiphase Boundaries on Rafting in a γ/γ′ alloy. Metall. Mat Trans. A. 35, 733–740. doi:10.1007/s11661-004-0001-3

CrossRef Full Text | Google Scholar

Chen, J., Guo, M., Yang, M., Su, H., Liu, L., and Zhang, J. (2021). Phase-field Simulation of γʹ Coarsening Behavior in Cobalt-Based Superalloy. Comput. Mater. Sci. 191, 110358. doi:10.1016/j.commatsci.2021.110358

CrossRef Full Text | Google Scholar

Chen, L. Q., and Shen, J. (1998). Applications of Semi-implicit Fourier-Spectral Method to Phase Field Equations. Comput. Phys. Commun. 108, 147–158. doi:10.1016/S0010-4655(97)00115-X

CrossRef Full Text | Google Scholar

Gaubert, A., Le Bouar, Y., and Finel, A. (2010). Coupling Phase Field and Viscoplasticity to Study Rafting in Ni-Based Superalloys. Philos. Mag. 90, 375–404. doi:10.1080/14786430902877802

CrossRef Full Text | Google Scholar

Gupta, S., and Bronkhorst, C. A. (2021). Crystal Plasticity Model for Single crystal Ni-Based Superalloys: Capturing Orientation and Temperature Dependence of Flow Stress. Int. J. Plasticity 137, 102896. doi:10.1016/j.ijplas.2020.102896

CrossRef Full Text | Google Scholar

Hemker, K. J., and Mills, M. J. (1993). Measurements of Antiphase Boundary and Complex Stacking Fault Energies in Binary and B-Doped Ni₃Al Using TEM. Philosophical Mag. A 68, 305–324. doi:10.1080/01418619308221207

CrossRef Full Text | Google Scholar

Ji, Y., Lou, Y., Qu, M., Rowatt, J. D., Zhang, F., Simpson, T. W., et al. (2016). Predicting Coherency Loss of γ′′ Precipitates in IN718 Superalloy. Metall. Mat Trans. A. 47, 3235–3247. doi:10.1007/s11661-016-3480-0

CrossRef Full Text | Google Scholar

Karnthaler, H. P., Mühlbacher, E. T., and Rentenberger, C. (1996). The Influence of the Fault Energies on the Anomalous Mechanical Behaviour of Ni₃Al Alloys. Acta Materialia 44, 547–560. doi:10.1016/1359-6454(95)00191-3

CrossRef Full Text | Google Scholar

Kim, S. G., Kim, W. T., and Suzuki, T. (1999). Phase-field Model for Binary Alloys. Phys. Rev. E 60, 7186–7197. doi:10.1103/PhysRevE.60.7186

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuehmann, C. J., and Voorhees, P. W. (1996). Ostwald Ripening in Ternary Alloys. Metall. Mater. Trans. A. 27, 937–943. doi:10.1007/BF02649761

CrossRef Full Text | Google Scholar

Li, D. Y., and Chen, L. Q. (1998). Shape Evolution and Splitting of Coherent Particles under Applied Stresses. Acta Materialia 47, 247–257. doi:10.1016/S1359-6454(98)00323-1

CrossRef Full Text | Google Scholar

Lifshitz, E. M. (1969). Lev Davidovich Landau (1908-1968). Sov. Phys. Usp. 12, 135–145. doi:10.1070/PU1969v012n01ABEH003922

CrossRef Full Text | Google Scholar

Liu, X., Kong, H., Lu, Y., Huang, J., and Wang, C. (2020). Phase-field Simulation on Microstructure Evolution of D0₁₉ Phase in γ/γ′ Structure of Co-Al-W Superalloys. Prog. Nat. Sci. Mater. Int. 30, 382–392. doi:10.1016/j.pnsc.2020.05.004

CrossRef Full Text | Google Scholar

Mebed, A. M., and Johnson, W. C. (2003). Computational and Experimental Study of the Effect of the Composition on the Morphology of the Ordered Domains and APBs Structures. Mater. Sci. Eng. A 352, 76–84. doi:10.1016/S0921-5093(02)00906-1

CrossRef Full Text | Google Scholar

Meher, S., Nag, S., Tiley, J., Goel, A., and Banerjee, R. (2013). Coarsening Kinetics of γ′ Precipitates in Cobalt-Base Alloys. Acta Materialia 61, 4266–4276. doi:10.1016/j.actamat.2013.03.052

CrossRef Full Text | Google Scholar

Nathal, M. V. (1987). Effect of Initial Gamma Prime Size on the Elevated Temperature Creep Properties of Single crystal Nickel Base Superalloys. Metall. Trans. A. 18, 1961–1970. doi:10.1007/BF02647026

CrossRef Full Text | Google Scholar

Saal, J. E., and Wolverton, C. (2016). Energetics of Antiphase Boundaries in γ′ Co₃(Al,W)-based Superalloys. Acta Materialia 103, 57–62. doi:10.1016/j.actamat.2015.10.007

CrossRef Full Text | Google Scholar

Sato, J., Omori, T., Oikawa, K., Ohnuma, I., Kainuma, R., and Ishida, K. (2006). Cobalt-base High-Temperature Alloys. Science 312, 90–91. doi:10.1126/science.1121738

PubMed Abstract | CrossRef Full Text | Google Scholar

Sauza, D. J., Bocchini, P. J., Dunand, D. C., and Seidman, D. N. (2016). Influence of Ruthenium on Microstructural Evolution in a Model Co-Al-W Superalloy. Acta Materialia 117, 135–145. doi:10.1016/j.actamat.2016.07.014

CrossRef Full Text | Google Scholar

Shi, S., Yan, Z., Li, Y., Muhammad, S., Wang, D., Chen, S., et al. (2020). Phase-field Simulation of Early-Stage Kinetics Evolution of γ′ Phase in Medium Supersaturation Co-Al-W alloy. J. Mater. Sci. Technol. 53, 1–12. doi:10.1016/j.jmst.2020.02.038

CrossRef Full Text | Google Scholar

Suzuki, A., and Pollock, T. M. (2008). High-temperature Strength and Deformation of γ/γ′ Two-phase Co-Al-W-base Alloys. Acta Materialia 56, 1288–1297. doi:10.1016/j.actamat.2007.11.014

CrossRef Full Text | Google Scholar

Wang, D., Li, Y., Shi, S., Tong, X., and Yan, Z. (2020). Phase-field Simulation of γ′ Precipitates Rafting and Creep Property of Co-base Superalloys. Mater. Des. 196, 109077. doi:10.1016/j.matdes.2020.109077

CrossRef Full Text | Google Scholar

Wang, J. C., Osawa, M., Yokokawa, T., Harada, H., and Enomoto, M. (2007). Modeling the Microstructural Evolution of Ni-Base Superalloys by Phase Field Method Combined with CALPHAD and CVM. Comput. Mater. Sci. 39, 871–879. doi:10.1016/j.commatsci.2006.10.014

CrossRef Full Text | Google Scholar

Wang, Y., Banerjee, D., Su, C. C., and Khachaturyan, A. G. (1998). Field Kinetic Model and Computer Simulation of Precipitation of L1₂ Ordered Intermetallics from F.C.C. Solid Solution. Acta Materialia 46, 2983–3001. doi:10.1016/S1359-6454(98)00015-9

CrossRef Full Text | Google Scholar

Wang, Y., and Khachaturyan, A. (1995). Microstructural Evolution during the Precipitation of Ordered Intermetallics in Multiparticle Coherent Systems. Philos. Mag. A 72, 1161–1171. doi:10.1080/01418619508236248

CrossRef Full Text | Google Scholar

Wen, Y. H., Lill, J. V., Chen, S. L., and Simmons, J. P. (2010). A Ternary Phase-Field Model Incorporating Commercial CALPHAD Software and its Application to Precipitation in Superalloys. Acta Materialia 58, 875–885. doi:10.1016/j.actamat.2009.10.002

CrossRef Full Text | Google Scholar

Wu, K., Chang, Y. A., and Wang, Y. (2004). Simulating Interdiffusion Microstructures in Ni-Al-Cr Diffusion Couples: a Phase Field Approach Coupled with CALPHAD Database. Scripta Materialia 50, 1145–1150. doi:10.1016/j.scriptamat.2004.01.025

CrossRef Full Text | Google Scholar

Xu, W. W., Han, J. J., Wang, Y., Wang, C. P., Liu, X. J., and Liu, Z.-K. (2013). First-principles Investigation of Electronic, Mechanical and Thermodynamic Properties of L1₂ Ordered Co₃(M,W) (M=Al, Ge, Ga) Phases. Acta Materialia 61, 5437–5448. doi:10.1016/j.actamat.2013.05.032

CrossRef Full Text | Google Scholar

Yan, H.-Y., Vorontsov, V. A., and Dye, D. (2014). Effect of Alloying on the Oxidation Behaviour of Co-Al-W Superalloys. Corrosion. Sci. 83, 382–395. doi:10.1016/j.corsci.2014.03.002

CrossRef Full Text | Google Scholar

Yang, M., Wei, H., Zhang, J., Zhao, Y., Jin, T., Liu, L., et al. (2017). Phase-field Study on Effects of Antiphase Domain and Elastic Energy on Evolution of γ′ Precipitates in Nickel-Based Superalloys. Comput. Mater. Sci. 129, 211–219. doi:10.1016/j.commatsci.2016.11.036

CrossRef Full Text | Google Scholar

Yang, M., Zhang, J., Gui, W., Hu, S., Li, Z., Guo, M., et al. (2021). Coupling Phase Field with Creep Damage to Study γʹ Evolution and Creep Deformation of Single crystal Superalloys. J. Mater. Sci. Technol. 71, 129–137. doi:10.1016/j.jmst.2020.07.036

CrossRef Full Text | Google Scholar