pH-Responsive Hydrogel Bilayer With Reversible, Bidirectional Bending Behavior

Smart hydrogels are promising materials for shape-shifting structures regarding their large reversible deformation in response to external stimuli in the absence of mechanical loading. Actuators composed of responsive hydrogels have gained significant attention due to their low power consumption, bio-compatibility, fast response, and accessibility. Among these structures, bidirectional hydrogel-based actuators are more fascinating, especially when they have similar reversible bending in both directions. This paper introduces a new design concept of a hydrogel bilayer made of a poly (HEMA-co-DMAEMA) layer and a poly (HEMA-co-AA) hydrogel layer that swells at low and high pH, respectively. This structure is capable of bending in diverse directions while the pH of the aqueous bath alters. The main characteristic of this structure is having reversible bidirectional bending, which has similar behaviors in both directions, unlike previous hydrogel-elastomer bilayers. Then, we develop an analytical method to solve the swelling-induced bidirectional bending of a pH-sensitive hydrogel bilayer. On the other hand, the finite bending of bilayer structure is studied by the finite element method in several cases to demonstrate the validity and accuracy of the proposed analytical solution. Lastly, the impacts of material composition and geometrical factors are investigated to be used for bilayer actuator design and application.

1 Introduction

A wide range of shape transformations of soft multifunctional structures observed in nature (Koller, 1990; Reyssat and Mahadevan, 2009; Stahlberg, 2009; Evangelista et al., 2011) has motivated researchers to design shape-shifting structures which are able to reconfigure under the environmental stimulus (Shojaeifard et al., 2022a; Shojaeifard et al., 2022b). Diverse types of materials have been utilized to construct shape transforming behaviour, including shape memory polymers (Meng and Li, 2013; Mao et al., 2016a), shape memory alloys (Lin et al., 2011; Liu et al., 2018), polymeric gels (Osada and Gong, 1998; Liu et al., 2018; Shojaeifard et al., 2022a), which received particular attention in various applications such as microfluidics (Jamal et al., 2011), soft robotics (Kim et al., 2013), actuators (Le et al., 2019), biomedical devices (Deligkaris et al., 2010).

Smart hydrogels as a group of stimuli-responsive and programmable materials owing to their large reversible deformation, swelling and deswelling, and their capability in changing shape, size, permeability, mechanical characteristics in response to environmental stimuli such as temperature (Shojaeifard and Baghani, 2020; Shojaeifard et al., 2021), pH (Shojaeifard et al., 2019; Niroumandi et al., 2021a), light (Shojaeifard and Baghani, 2019), electric and magnetic fields (Pourjavadi et al., 2021). The hydrogel actuation has been vastly used in microfluidic devices for controlling the fluid flow as hydrogel-based valves (Beebe et al., 2000; Yu et al., 2001; Shojaeifard et al., 2020a; Niroumandi et al., 2021b; Niroumandi et al., 2021c). In these hydrogel-based structures, the homogeneous expansion and shrinkage only alter material volume which is employed to control or block the microfluidic channels. However, complex designs of hydrogel composite are requisite for shape transforming induced by inhomogeneous deformations, including twisting, bending, and buckling (Jeong et al., 2011; Kim et al., 2012). Accordingly, various designs have been developed to generate dynamic surface instabilities (Curatolo et al., 2017; Curatolo et al., 2021) and also reversible programmable shape-shifting structures by integrating multi-layered systems composed of smart soft materials which behave differently in response to environmental stimuli. For example, Morales et al. (Morales et al., 2014) fabricated a walker structure made of two opposite electro-active hydrogels. The cationic and anionic legs bend in opposite directions which led the structure to have a unidirectional motion on a flat substrate. Also, Mao et al. (Mao et al., 2016b) introduced reversibly-actuating architectures composed of hydrogels and shape memory polymers that are sensitive to temperature. Controlling the temperature and the aqueous bath surrounding the structure, they illustrated diverse reversible bending and twisting Shape-Changing.

Using bending structures composed of hydrogels is a conventional approach to design valves, actuators, and sensors that are significantly applicable in biological and medical applications (Kwon et al., 2010; Kwon et al., 2011). The bending of single layer beams is captured utilizing functionally graded layered (Shojaeifard and Baghani, 2019; Shojaeifard et al., 2019; Shojaeifard et al., 2020a) or by applying inhomogeneous external fields (Kwon et al., 2010; Ionov, 2013); while multi-layer structure bends due to the variety in swelling ratio of each layer (Abdolahi et al., 2016; Arbabi et al., 2017). Liu et al. (Liu et al., 2018) designed a hydrogel-elastomer bilayer system that bends in just one direction regarding the humidity sensitivity of the hydrogel strip. They investigated the mechanical behaviour of this structure to design actuators. Zhang et al. (Zhang et al., 2012) fabricated a bilayer structure made of two acrylamide-based gels strips that have various swelling ratios. Accordingly, since each hydrogel layer swells differently in response to temperature change, unidirectional pure bending can be observed. Due to the importance of the bending of multi-layered structures in diverse applications, recently, analytical solutions were proposed to inspect the bending behavior of hydrogel-elastomer bilayer (Abdolahi et al., 2016; Arbabi et al., 2017). In these works, the bilayer is composed of an elastomer strip and also hydrogel strips which was sensitive to temperature (Abdolahi et al., 2016) and pH (Arbabi et al., 2017) which enables the structure to bend in one direction when the temperature or pH, respectively, varies. They verified these analytical solutions with the finite element analysis and investigated the effects of different material and geometrical properties on structural bending. However, structures with bidirectional bending could have more complicated applications in valves, sensors, and actuators which required new designs. Recently, some experimental studies conducted some efforts to achieve bidirectional bending. He et al. (He et al., 2019) designed a dual-responsive polyNIPAM/GO hydrogels bilayer to capture the bidirectional reversible bending. The bilayer strips were dual thermo- and near-infrared (NIR)-responsive properties which have distinct network structures and swelling behaviour. Accordingly, controlling the bidirectional bending in this study, they demonstrated different actuator design using bidirectional bending. Li et al. (Li et al., 2017) prepared pNIPAm-pDADMAC semi-IPN hydrogels/PDMS bilayers which were responsive to pH and temperature. By carefully inspecting the properties of the hydrogel layer, they could use the swelling and deswelling of hydrogel layer in response to pH and temperature variation to illustrate the bidirectional bending in the structure. It is notable that the pure bending in this structure stems from the volume change in hydrogel layer while the PDMS layer does not swell in response to alteration of external fields. He et al. (Hu et al., 1995) integrated a positive temperature sensitive hydrogel (PAAM) layer with a negative temperature sensitive (PNIPAAm) hydrogel layer to obtain bidirectional bending to be used in gripper actuators, and self-folding structures.

As mentioned above, in the literature, most bidirectional reversible bendings are studied considering bilayers that are responsive to more than one external field or applied complex external fields in different directions. Additionally, although pH-sensitive hydrogels have vast applications in biology, drug delivery, medical devices, as well as sensors and actuators, there is a gap to study the bidirectional reversible bending of a structure composed of pH-sensitive hydrogels. In the pH-sensitive hydrogels, some of the acidic groups attached to the main chain gradually ionized in response to the pH variation of the aqueous environment. Several studies (De et al., 2002; Kim et al., 2003; Marcombe et al., 2010; Niroumandi et al., 2021a) investigated the theory behind the concentrations of the ions within the hydrogel body and their effects on water absorption. Particularly, Marcombe et al. (Marcombe et al., 2010) presented a theory to describe the pH-sensitive hydrogel behavior. Similar to the large deformation theory defined for soft materials (Valiollahi et al., 2019a; Valiollahi et al., 2019b; Sheikhi et al., 2019; Shojaeifard et al., 2020b), in this constitutive model, a free energy density was proposed to capture four different phenomena in the swelling of pH-sensitive hydrogels. Thus, the total free energy density is decomposed into four energy parts: network stretching, mixing of solvent with mobile ions and network, and also the acidic dissociating groups. Regarding the conformity of this model results with experimental data, this constitutive model has been used for various applications in recent studies (Arbabi et al., 2017; Shojaeifard et al., 2019; Niroumandi et al., 2021a; Shojaeifard et al., 2022c).

In this paper, regarding the wide applications of bidirectional reversible bending in designing actuators, sensors, and valves, we propose a new design concept of a bilayer composed of a poly (HEMA-co-DMAEMA) and a poly (HEMA-co-AA) hydrogel layers. The poly (HEMA-co-DMAEMA) hydrogel swells considerably at low pH and shrinks when the hydrogel is exposed to a high pH solution. On the contrary, the poly (HEMA-co-AA) hydrogels absorb a huge amount of water and swell at high pH and also expel solvent and deswell at low pH. In this regard, we could experience bending in bilayer structure in one direction at high pH and bending in the other direction at low pH. One of the important characteristics of this structure is that we could easily experience similar bending in both directions which is hardly achieved by previous designs containing hydrogel/elastomer bilayers (Abdolahi et al., 2016; Arbabi et al., 2017) or bilayers with similar hydrogel types with diverse swelling ratios (Zhang et al., 2012) or bilayers which capture bidirectional bending due to different external stimuli (Li et al., 2017; He et al., 2019). Accordingly, based on the theory presented by Marcombe et al. (Marcombe et al., 2010), we proposed an analytical solution to describe the swelling bidirectional reversible bending of bilayer composed of two types of pH-sensitive hydrogels. In this study, based on finite deformation theory, the total deformation gradient tensor is defined to map the initial state, Cartesian coordinate, to the final polar coordinate. To evaluate the obtained results from the analytical solution, we conducted finite element analysis for the same problem. Comparing the results of both approaches, it is depicted that the results of analytical solution conforms excellently to the ones of finite element method. Finally, we investigate diverse material and geometrical properties of the hydrogel bilayer to obtain the proper shape shifting and swelling behavior for each particular application.

This article is organized as follows: firstly, in section 2, a constitutive model is presented to predict the mechanical behavior and swelling of pH-sensitive hydrogels. In one of the subsections, the finite deformation theory and the swelling-induced bending of the bilayer structure are introduced. In the last part of this section, the formulations are recast into two coupled second-order nonlinear equations are solved using diverse boundary conditions.

In section 3, the proposed analytical solution is utilized to compute the deformation, stress, bending angle, and curvature and these results are verified with finite element analysis. Several case studies are inspected to find the impacts of the external pH field and also material properties on the swelling of hydrogels and also bidirectional bending of the whole smart structure. Finally, in the last section, we present a summary and draw conclusions.

2 Finite Bending Deformation of pH-Responsive Hydrogel Bilayers

In this study, the swelling induced finite bidirectional reversible bending of a bilayer composed of two pH-sensitive hydrogel layers under plane strain conditions is studied. As depicted in Figure 1, the hydrogel-based bilayer is made of the bottom poly (HEMA-co-DMAEMA) hydrogel layer denoted by index n = 1 and the top poly (HEMA-co-AA) hydrogel layer denoted by index n = 2. From now on, we use superscription “n” to determine each specific parameter related to which layer. As illustrated in Figure 1, the bilayer strips have rectangular shapes and are attached through the intermediate edge at $y=H_1$. At the initial state, the bilayer is in a stress-free state and the Cartesian coordinate is defined to describe the problem at the reference state. Altering the pH value, the bilayer bends regarding different swelling ratios of each layer at that particular pH. For instance, increasing pH value causes the upper poly (HEMA-co-AA) layer to swell significantly, however, the bottom layer hinders the whole structure to swell in the longitudinal direction and brings about the bilayer to bend.

FIGURE 1

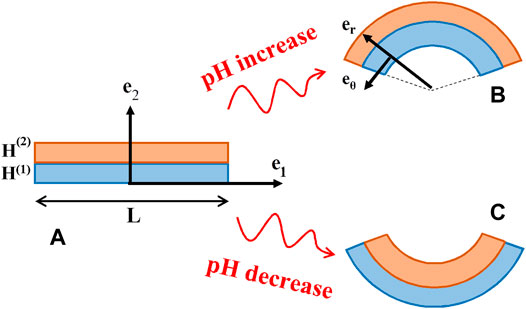
FIGURE 1. The schematics of the bilayer composed of poly (HEMA-co-AA) and poly (HEMA-co-DMAEMA) hydrogel at (A) the reference state, and the deformed state created by (B) an increase and (C) decrease in pH.

2.1 Kinematics

Defining Cartesian coordinate for the reference configuration, the position vector at the initial state is defined as:

$\mathbf{X}=X_1{\mathbf{e}}_1+X_2{\mathbf{e}}_2+X_3{\mathbf{e}}_3\mathbf{w}\mathbf{h}\mathbf{e}\mathbf{r}\mathbf{e}\{\begin{array}{l}{X}_1Î\left[-L/2,L/2\right];\\ X_2Î\left[0,H^{\left(1\right)}\right]\mathbf{\cup }\left[H^{\left(1\right)},H^{\left(2\right)}\right];\\ X_3Î[-\mathbf{\infty },\mathbf{\infty }];\end{array}(1)$

where e¹ and e⁻¹ are defined the in-plane axes at the reference state; while $e_3$ is assumed the out-plane axis. In this equation, $H^{\left(1\right)}\text{and}{H}^{\left(2\right)}$ are the thickness of layers (1) and (2), respectively. Thus, the total thickness of the bilayer at the initial state is computed as $H=H^{\left(1\right)}+H^{\left(2\right)}$. Regarding the shape-shifting of the bilayer structure from a flat strip to a semi-annular shape after bending, the deformed configuration is defined in polar coordinates as follows:

$\mathbf{x}=r\left(R\right){\mathbf{e}}_R+\theta {\mathbf{e}}_{\theta }+z{e}_z\mathbf{w}\mathbf{h}\mathbf{e}\mathbf{r}\mathbf{e}\{\begin{array}{l}{r}^{\left(1\right)}Î\left[r_1,r_2\right]\mathbf{\cup }{r}^{\left(2\right)}Î\left[r_2,r_3\right];\\ \theta Î\left[-\overline{\theta },\overline{\theta }\right];\\ zÎ[-\mathbf{\infty },\mathbf{\infty }];\end{array}(2)$

In which $\overline{\theta }$ is considered as bending semi-angle. Additionally, $r_1\text{and}{r}_3$ are used to describe the inner and outer radii of the whole bilayer at the deformed state; while $r_2$ is the interfacial radius. Due to the restriction in out-plane direction, the stretch along this direction is ${\lambda }_z=1$. Furthermore, all of the variables do not have variations in the tangential direction. Additionally, the tangential component of the position vector, $\theta$, is a linear function of $X_1$. Therefore, the deformation gradient tensor corresponding to the pH-sensitive hydrogel layers is determined as:

${\mathbf{F}}^{\left(i\right)}\left(X_2\right)=\frac{\mathbf{d}{r}^{\left(i\right)}\left(X_2\right)}{\mathbf{d}{X}_2}{\mathrm{e}}_R\otimes {\mathrm{e}}_1+r^{\left(i\right)}\frac{2\overline{\theta }}{L}{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_2+{\mathbf{e}}_z\otimes {\mathbf{e}}_3(3)$

where i can be one and two for two layers. Accordingly, the principal stretches in each layer can be computed as follow:

${\lambda }_r^{\left(n\right)}=\frac{\mathbf{d}{r}^{\left(2\right)}\left(X_2\right)}{\mathbf{d}{X}_2},{\lambda }_{\theta }^{\left(n\right)}=r^{\left(2\right)}\frac{2\overline{\theta }}{L},{\lambda }_z^{\left(n\right)}=1(4)$

2.2 Free Energy Density Function for pH-Sensitive Hydrogel

As discussed before, in this section, a well-known constitutive model proposed by Marcombe et al. (Marcombe et al., 2010) is utilized to predict the mechanical behavior and swelling of pH-sensitive hydrogel. In this model, the free energy density is additively formed of four energy parts as below:

$\begin{array}{l}W\mathbf{F},C_{+},C_{H^{+}},C_{-}=\left\{\frac{1}{2}G\left[I-3-2Log\left(J\right)\right]\right\}+\left\{\frac{KT}{v}\left[\left(J-1\right)\log \left(1-\frac{1}{J}\right)-\frac{\chi }{J}\right]\right\}\\ \left\{KT\left\{C_{H^{+}}\left[\log \left(\frac{C_{H^{+}}}{J{c}_{H^{+}}^{ref}}\right)-1\right]+C_{+}\left[\log \left(\frac{C_{+}}{J{c}_{+}^{ref}}\right)-1\right]+C_{-}\left[\log \left(\frac{C_{-}}{J{c}_{-}^{ref}}\right)-1\right]\right\}\right\}\\ \left\{KT\left[C_{A^{-}}\log \left(\frac{C_{A^{-}}}{C_{A^{-}}+C_{AH}}\right)+C_{AH}\log \left(\frac{C_{AH}}{C_{A^{-}}+C_{AH}}\right)\right]+\gamma C_{A^{-}}\right\}\end{array}(5)$

in which $C_{•}$ is the nominal concentration of each ion, including, the counter- and co-ions, and also hydrogen ions which are defined as $C_{+},C_{-},C_{H^{+}}$, respectively. $c_{•}^{ref}$ represents the concentration of mobile ions at the reference state, including co- and counter-ions, and hydrogen ions. The first term, $W_{net}$, is the network stretching free energy. The second and third ones are defined as the part of the total free energy which is the result of mixing the solvent with polymer network and mobile ions, respectively. Additionally, the final term, $W_{dis}$, is the portion of free energy corresponding to the dissociation of the acidic groups dissociating which is a function of concentrations of associated acidic groups, $AH$, fixed charges, $A$, and also the rise of enthalpy energy during the dissociation process of each acidic group, $\gamma$.

In this equation, the elastic modulus of each layer $G^{\left(n\right)}$ is a function of polymer chains’ density $N^{\left(n\right)}\left(X_2\right)$ and temperature $T$ as $G^{\left(n\right)}=N^{\left(n\right)}\left(X_2\right)KT$. $K$ is the Boltzmann’s constant which is equal to $k=1.38\times {10}^{-23}J/K$. Additionally, considering the right Cauchy-Green tensor as $C=F^{T}F$, the first invariant of this tensor is $I$. All of the energy parts are described as a function of the ratio of the hydrogel volume in the current state to the initial state, which is obtained by the determinant of the deformation gradient tensor, $J$. Moreover, parameters $v$ and $\chi$ , respectively, represent the volume of each solvent molecule and the mixing parameter which is calculated through the experimental test.

Moreover, Prevailing the electro-neutrality in the body of pH-sensitive hydrogel and the surrounded solution as well as considering the consistency of the number of acidic groups are led to:

$\begin{array}{l}{C}_{H^{-}}+C_{+}=C_{A^{-}}+C_{-}\\ C_{A^{-}}+C_{AH}=\frac{f}{V}\end{array}(6)$

In this equation, the ratio of the number of the acidic groups which are attached to the network to the number of monomers is shown by parameter $f$.

2.3 Stress Distribution

Regarding the large deformation theory, considering the Marcombe et al. (Marcombe et al., 2010) free energy density, the Cauchy stress can be computed using the following relation:

${\sigma }_i=\left(\frac{{\lambda }_i}{j}\right)\left(\frac{\partial W}{\partial {\lambda }_i}\right)(7)$

Therefore, substituting the total free energy density into Equation 7, the Cauchy stress components for pH-sensitive hydrogel are determined as:

${\sigma }_i=KT\left[\left(N\left(X_2\right)J\right)\left({\lambda }_i^2-1\right)+\frac{1}{v}\left[\log \left(1-\frac{1}{J}\right)+\frac{1}{J}+\frac{\chi }{J^2}\right]-{\displaystyle \sum _{\alpha }\left(c_{\alpha }-c_{\alpha }^{ref}\right)}\right](8)$

where $c_{\alpha }$ in this equation represents the nominal concentration of ion $\alpha$ in the deformed state. The determinant of the deformation gradient tensor relates the concentration of each ion in the current state and the initial state.

$c_{\alpha }=\frac{C_{\alpha }}{J}(9)$

To simplify the obtained equations for stress components, we rewrite the equations in order to be a function of just two ions’ concentrations, $C_{H^{+}}$ and $C_{+}$. In this regard, the Donnan equations, as given below, are employed to satisfy the ionic equilibrium condition.

$\frac{c_{+}}{c_{+}^{ref}}=\frac{c_{H+}}{c_{H+}^{ref}},(10)$

$\frac{c_{-}}{c_{-}^{ref}}={\left(\frac{c_{H+}}{c_{H+}^{ref}}\right)}^{-1}(11)$

using Equations 6, 10, and 11, the chemical dissociation equilibrium is recast as follows:

$\frac{c_{H+}\left(c_{H+}+c_{+}-c_{-}\right)}{\left(f/v\right){\left(\det \mathbf{F}\right)}^{-1}-\left(c_{H+}+c_{+}-c_{-}\right)}=N_A{K}_a(12)$

in which $N_A$ and $K_a$ denote the Avogadro number and acidic dissociation constant, respectively. Rewriting Equation (12) based on Equations 10, 11, all of the ions’ concentrations at the current state can be substituted by a function of hydrogen concentration. Thus, this equation is given by:

${\zeta }_1{c}_{H+}^3+{\zeta }_2{c}_{H+}^2+{\zeta }_3{c}_{H+}+{\zeta }_4=0(13)$

where

$\begin{array}{l}{\zeta }_1=v^3\left(1+\frac{c_{+}^{ref}}{c_{H+}^{ref}}\right)\\ {\zeta }_2=v^5{\zeta }_1{N}_A{K}_a{c}_{H+}^{ref}{c}_{-}^{ref}\\ {\zeta }_3=-v^3{c}_{H+}^{ref}{c}_{-}^{ref}-\frac{v^2{N}_A{K}_{a}f}{J}\\ {\zeta }_4=-v^3{N}_A{K}_a{c}_{H+}^{ref}{c}_{-}^{ref}\end{array}(14)$

Solving this cubic equation, the hydrogen concentration at the current state can be found. Additionally, by substituting principal stretches and ions concentration into Equation 8, the radial and tangential stress components for each hydrogel layer are determined as:

$\frac{{\sigma }_r^{\left(n\right)}\nu }{KT}=\frac{1}{4{\lambda }_0^6{\overline{\theta }}^2{\left(r^{\left(n\right)}\right)}^2{\left({r^{\prime }}^{\left(n\right)}\right)}^2}\left[-4{\left({\lambda }_0^{\left(n\right)}\right)}^6{\overline{\theta }}^2{\left(r^{\left(n\right)}\right)}^2{\left({r^{\prime }}^{\left(n\right)}\right)}^2\ln \left(1-\frac{L}{2{\lambda }_0^3\overline{\theta }{r}^{\left(n\right)}{r^{\prime }}^{\left(n\right)}}\right)+\chi L^2+-2N{v}^{\left(n\right)}{\left({\lambda }_0^{\left(n\right)}\right)}^3{r^{\prime }}^{\left(n\right)}L\overline{\theta }{r}^{\left(n\right)}+2L{\left({\lambda }_0^{\left(n\right)}\right)}^3{r^{\prime }}^{\left(n\right)}\overline{\theta }{r}^{\left(n\right)}+2LN{v}^{\left(n\right)}{\left({r^{\prime }}^{\left(n\right)}\right)}^3{r}^{\left(n\right)}{\left({\lambda }_0^{\left(n\right)}\right)}^5\overline{\theta }\right]-v{\mathrm{\Pi }}_{ion}(15)$

$\frac{{\sigma }_{\theta }^{\left(n\right)}\nu }{KT}=\frac{1}{4{\lambda }_0^6{\overline{\theta }}^2{\left(r^{\left(n\right)}\right)}^2{\left({r^{\prime }}^{\left(n\right)}\right)}^{2}L}\left[4{\left({\lambda }_0^{\left(n\right)}\right)}^6{\left({r^{\prime }}^{\left(n\right)}\right)}^{2}L{\overline{\theta }}^2{\left(r^{\left(n\right)}\right)}^2\ln \left(1-L/2{\lambda }_0^3{r^{\prime }}^{\left(n\right)}\overline{\theta }{r}^{\left(n\right)}\right)+\chi L^3+8N{v}^{\left(n\right)}{r^{\prime }}^{\left(n\right)}{\left(r^{\left(n\right)}\right)}^3{\left({\lambda }_0^{\left(n\right)}\right)}^5{\overline{\theta }}^3-2L^{2}N{v}^{\left(n\right)}{r}^{\left(n\right)}{r^{\prime }}^{\left(n\right)}{\left({\lambda }_0^{\left(n\right)}\right)}^3\overline{\theta }+2L^2{\left({\lambda }_0^{\left(n\right)}\right)}^3\overline{\theta }{r}^{\left(n\right)}{r^{\prime }}^{\left(n\right)}\right]-v{\mathrm{\Pi }}_{ion}(16)$

in which

${\mathrm{\Pi }}_{ion}=c_{H+}^{\left(n\right)}+\frac{c_{+}^{ref,\left(n\right)}{c}_{H+}^{ref,\left(n\right)}}{c_{H+}^{\left(n\right)}}+\frac{c_{H+}^{\left(n\right)}{c}_{-}^{ref,\left(n\right)}}{c_{H+}^{ref,\left(n\right)}}-c_{H+}^{ref,\left(n\right)}-c_{-}^{ref,\left(n\right)}-c_{+}^{ref,\left(n\right)}(17)$

In this equation, for the sake of simplicity, the derivative of the current radius for layer (n) with respect to $X_2$ is named ${r^{\prime }}^{\left(n\right)}$. Accordingly, Equations 15, 16 describe the radial and tangential components of stress for both layers. It is notable that the initial stretch, current radius, derivative of current radius, cross-linked density, and the height of each layer are different which results in unequal stress values for the layers. Additionally, the length and the semi-angle are similar in both layers. Superscript (n) distinguishes that the parameter belongs to which layer. Considering the symmetry, the equilibrium equation for each layer which is determined as follows should be utilized to find the current radius and semi-angle at the current state. Finding these variables, we can calculate all of the parameters since they are written as a function of just these variables.

$\frac{\partial {\sigma }_r^{\left(n\right)}/\partial X_2}{\partial r^{\left(n\right)}/\partial X_2}=\frac{{\sigma }_r^{\left(n\right)}-{\sigma }_{\theta }^{\left(n\right)}}{r^{\left(n\right)}}(18)$

Substituting the stress components in equilibrium equations, we obtain two nonlinear equations for the hydrogel layers.

${{\rm E}}_1^{\left(n\right)}{r^{″}}^{\left(n\right)}+{{\rm E}}_2^{\left(n\right)}{\left({r^{\prime }}^{\left(n\right)}\right)}^5+{{\rm E}}_3^{\left(n\right)}{\left({r^{\prime }}^{\left(n\right)}\right)}^4+{{\rm E}}_4^{\left(n\right)}{\left({r^{\prime }}^{\left(n\right)}\right)}^3+{{\rm E}}_5^{\left(n\right)}{\left({r^{\prime }}^{\left(n\right)}\right)}^2=0(19)$

The coefficients of this nonlinear equation for each layer are given as follows:

$\begin{array}{l}{E}_1^{\left(n\right)}=c_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}\left[N{v}^{\left(n\right)}\left(2L^2{\left({r^{\prime }}^{\left(n\right)}\right)}^4{\left(r^{\left(n\right)}\right)}^2{\left({\lambda }_0^{\left(n\right)}\right)}^6{\overline{\theta }}^2+2L^2{\left({r^{\prime }}^{\left(n\right)}\right)}^2{\left(r^{\left(n\right)}\right)}^2{\left({\lambda }_0^{\left(n\right)}\right)}^6{\overline{\theta }}^2-L^3{\left({r^{\prime }}^{\left(n\right)}\right)}^3{r}^{\left(n\right)}{\left({\lambda }_0^{\left(n\right)}\right)}^5\overline{\theta }\right)+{r^{\prime }}^{\left(n\right)}{L}^3{r}^{\left(n\right)}{\left({\lambda }_0^{\left(n\right)}\right)}^3\overline{\theta }\left(1-N{v}^{\left(n\right)}-2\chi \right)+L^4\chi \right]\\ E_2^{\left(n\right)}=\left(8L{\left(r^{\left(n\right)}\right)}^2{\left({\lambda }_0^{\left(n\right)}\right)}^9{\overline{\theta }}^3\right)\left[\begin{array}{l}{c}_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}\ln \left(1-L/2{\left({\lambda }_0^{\left(n\right)}\right)}^3{r^{\prime }}^{\left(n\right)}\overline{\theta }{r}^{\left(n\right)}\right)+c_{H+}^{ref\left(n\right)}{c}_{-}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}-c_{+}^{ref,\left(n\right)}{\left(c_{H+}^{\left(n\right)}\right)}^2-c_{H+}^{ref,\left(n\right)}{\left(c_{H+}^{\left(n\right)}\right)}^2+{\left(c_{H+}^{ref,\left(n\right)}\right)}^2{c}_{H+}^{\left(n\right)}\\ -{\left(c_{H+}^{ref,\left(n\right)}\right)}^2{c}_{-}^{ref,\left(n\right)}+c_{H+}^{ref,\left(n\right)}{c}_{+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}+L{\left({\lambda }_0^{\left(n\right)}\right)}^{-1}{\overline{\theta }}^{-1}{c}_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}\left(N{v}^{\left(n\right)}\right)/4\end{array}\right]\\ E_3^{\left(n\right)}=4L^2{r}^{\left(n\right)}{\left({\lambda }_0^{\left(n\right)}\right)}^6{\overline{\theta }}^2\left[\begin{array}{l}{c}_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}\mathit{ln}\left(1-L/2{\left({\lambda }_0^{\left(n\right)}\right)}^3{r^{\prime }}^{\left(n\right)}\overline{\theta }{r}^{\left(n\right)}\right)+c_{H+}^{ref,\left(n\right)}{\left(c_{H+}^{\left(n\right)}\right)}^2+-c_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}{c}_{+}^{ref,\left(n\right)}+0.5N{v}^{\left(n\right)}{c}_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}+c_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}+\\ {\left(c_{H+}^{\left(n\right)}\right)}^2{c}_{+}^{ref,\left(n\right)}-{\left(c_{H+}^{ref,\left(n\right)}\right)}^2{c}_{H+}^{\left(n\right)}+{\left(c_{H+}^{ref,\left(n\right)}\right)}^2{c}_{-}^{\left(n\right)}-c_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}{c}_{-}^{ref,\left(n\right)}+2c_{H+}^{ref\left(n\right)}{c}_{H+}^{\left(n\right)}N{v}^{\left(n\right)}{\left(r^{\left(n\right)}{\lambda }_0^{\left(n\right)}\overline{\theta }\right)}^2-c_{H+}^{ref\left(n\right)}{c}_{H+}^{\left(n\right)}L\left(N{v}^{\left(n\right)}\right)/\left(4{\lambda }_0^{\left(n\right)}\overline{\theta }\right)\end{array}\right]\\ E_4^{\left(n\right)}=c_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}\left[-4LN{v}^{\left(n\right)}{\left(r^{\left(n\right)}\right)}^2{\left({\lambda }_0^{\left(n\right)}\right)}^5{\overline{\theta }}^3+L^3{\left({\lambda }_0^{\left(n\right)}\right)}^3\overline{\theta }\left(N{v}^{\left(n\right)}-1\right)-2L^2{\left(r^{\left(n\right)}\right)}^2{\left({\lambda }_0^{\left(n\right)}\right)}^6{\overline{\theta }}^2\left(N{v}^{\left(n\right)}\right)\prime \right]\\ E_5^{\left(n\right)}=+L^3{r}^{\left(n\right)}{\left({\lambda }_0^{\left(n\right)}\right)}^3\overline{\theta }{c}_{H+}^{ref,\left(n\right)}{c}_{H+}^{\left(n\right)}\left(N{v}^{\left(n\right)}\right)\end{array}(20)$

In order to solve these two nonlinear second-order equations, we firstly substitute the hydrogen concentration as a function of semi-angle, current radius, and its derivative to these equations. Then, we required several boundary conditions to solve the two coupled nonlinear equations. Moreover, the convexity of the energy considered in this paper results in the unique solution for the problem.

The first two boundary conditions are that the upper surface of layer 2) and also the bottom surface of the hydrogel layer 1) are traction-free as given in Equation 21, 22. Additionally, at the intermediate surface between two layers, we have two other boundary conditions. The first one is that the current radius at the intermediate surface should be equal in both layers which is stated in Equation 23. Secondly, the radial stress of the two hydrogel layers should be equal at the intermediate surface, Equation 24. Moreover, the bilayer’s shape-shifting is due to the internal force and moments generated by the variation in pH. However, there is no external force or moment applied to the structure. Accordingly, the force and moment generated by the hoop stress component in each cross-section of the hydrogel bilayer are required to be zero, as given in Equations 25, 26.

${\sigma }_r^{\left(1\right)}=0at{X}_2=0(21)$

${\sigma }_r^{\left(2\right)}=0at{X}_2=H_1+H_2(22)$

$r^{\left(1\right)}\left(X_2\right)=r^{\left(2\right)}\left(X_2\right)at{X}_2=H_1(23)$

${\sigma }_r^{\left(1\right)}={\sigma }_r^{\left(2\right)}at{X}_2=H_1(24)$

${\displaystyle \underset{0}{\overset{H_1}{\int }}{\sigma }_{\theta }^{\left(1\right)}\frac{\mathbf{d}{r}^{\left(1\right)}\left(X_2\right)}{\mathbf{d}{X}_2}}\mathbf{d}{X}_2+{\displaystyle \underset{H_1}{\overset{H_2}{\int }}{\sigma }_{\theta }^{\left(2\right)}\frac{\mathbf{d}{r}^{\left(2\right)}\left(X_2\right)}{\mathbf{d}{X}_2}}\mathbf{d}{X}_2+=0(25)$

${\displaystyle \underset{0}{\overset{H_1}{\int }}{r}^{\left(1\right)}\left(X_2\right){\sigma }_{\theta }^{\left(1\right)}\frac{\mathbf{d}{r}^{\left(1\right)}\left(X_2\right)}{\mathbf{d}{X}_2}}\mathbf{d}{X}_2+{\displaystyle \underset{H_1}{\overset{H_2}{\int }}{r}^{\left(2\right)}\left(X_2\right){\sigma }_{\theta }^{\left(2\right)}\frac{\mathbf{d}{r}^{\left(2\right)}\left(X_2\right)}{\mathbf{d}{X}_2}}\mathbf{d}{X}_2=0(26)$

To solve the coupled nonlinear equation, using the above boundary condition, an iterative method has been implemented. In the first stage, the initial semi-angle is assumed by the initial guess. Then, since the net force and momentum should be vanished, employing an optimization technique (Byrd et al., 2000), the semi-angle in each iteration is determined by minimizing the residuals tolerance of the equations system. This iterative method continues till we reach a proper residual value. After that, the calculated semi-angle is utilized to determine $r\left(X_2\right)$, $r^{\prime }\left(X_2\right)$ which results in computing all of the other parameters.

3 Results and Discussion

In this section, in order to demonstrate the accuracy and performance of the presented analytical solution for bidirectional reversible bending of hydrogel bilayer, we investigate some case studies and compare the results with the finite element analysis.

Accordingly, here, we first explain how we analyzed this problem in the finite element package, Abaqus, and then we utilize this method to evaluate the presented analytical solution. In the first step, we need to implement the pH-sensitive hydrogel constitutive model in finite element software and next, use that to predict the mechanical behavior of this material under various loading conditions. Therefore, regarding the Abaqus user’s guide, to define the mechanical properties for soft materials with large deformation, we can implement the UHYPER subroutine using the free energy density defined for that particular material. According to the Abaqus user’s guide, in order to define a User subroutine UHYPER for hyperelastic material, we first should compute the strain energy density function, and its first, second, and third derivatives with respect to strain invariants. Thus, using the constitutive model introduced by Marcombe et al. (Marcombe et al., 2010), we calculated the total energy, and energy derivatives to implement the UHYPER subroutine for pH-sensitive hydrogel. Then, we added this subroutine to Abaqus instead of the material properties of hydrogels. Using the material parameters reported in Marcombe et al. (Marcombe et al., 2010), we verify our subroutine with the results presented by Marcombe et al. (Marcombe et al., 2010).

Then, two rectangular strips made of pH-sensitive hydrogels with a thickness of 0.005 m and length of 0.02 m are considered at the initial state under plane strain conditions. The upper layer of the bilayer is made of poly (HEMA-co-DMAEMA) and the lower layer is composed of poly (HEMA-co-AA). The material parameters used in this paper are extracted from Marcombe et al. (Marcombe et al., 2010) and are reported in Table 1. In order to analyze the same problem in FEM, two rectangular strips with a thickness of 0.005 m and length of 0.02 m are sketched in the “part section”. Due to the symmetry assumption, one-half of the hydrogel bilayer is modeled with proper boundary conditions. The 2D plane strain deformable parts are assumed with a 4-node bilinear plane strain quadratic element type mesh, which is called CPE4. Additionally, an extra length is considered in FE modeling and then eliminated to avoid the end effect. Furthermore, the material parameters are assigned in the “property section” or in the UHYPER subroutine.

TABLE 1

TABLE 1. The material parameters of poly (HEMA-co-DMAEMA) and poly (HEMA-co-AA) pH-sensitive hydrogel (Marcombe et al., 2010).

To elaborate the swelling of each hydrogel layer, we first consider two hydrogel cubes made of poly (HEMA-co-DMAEMA) and poly (HEMA-co-AA) pH-sensitive hydrogel and investigate the free-swelling of these hydrogel materials. For the poly (HEMA-co-DMAEMA) cube, the pH value alters from nine to two and the hydrogel cube swells freely and absorbs a considerable amount of water. While for the poly (HEMA-co-AA) cube, changing pH from two to nine brings about the hydrogel structure to undergo large deformation and swell. In the free-swelling loading, the principal stretches in all directions are equal as ${\lambda }_1^{\left(n\right)}={\lambda }_2^{\left(n\right)}={\lambda }_3^{\left(n\right)}=\lambda$. Regarding Equation 7 and the stress-free condition in this loading, the reference stretches of hydrogel structure can be computed by satisfying the equilibrium condition. As depicted in Figure 2A,B, the swelling ratio of poly (HEMA-co-AA) and poly (HEMA-co-DMAEMA) under free-swelling are presented for diverse cross-linked densities. It is illustrated that the swelling ratio for poly (HEMA-co-AA) and poly (HEMA-co-DMAEMA) in the pH range of two–nine are similar in magnitude and Symmetry at pH = 5.5. as demonstrated in this figure, changing pH could result in significant volume change in both hydrogel materials which enables us to use them in different smart valves, sensors, and actuators.

FIGURE 2

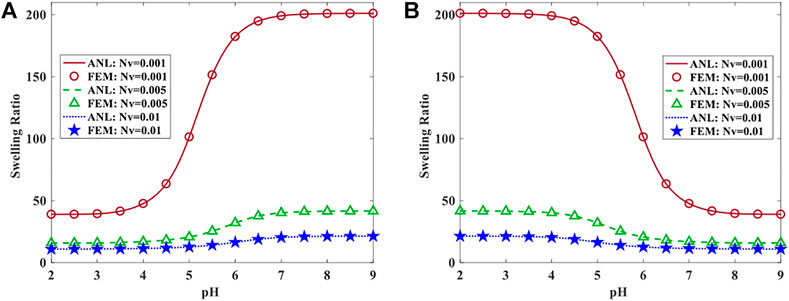
FIGURE 2. The swelling ratio of a free (A) poly (HEMA-co-AA) and (B) poly (HEMA-co-DMAEMA) hydrogel subjecting to pH change of the surrounded solution.

As shown in Figure 2, the cross-linked density of the hydrogels alters from 0.001 to 0.01 which is a conventional range for hydrogels as seen before (Shojaeifard and Baghani, 2019; Shojaeifard et al., 2019; Shojaeifard et al., 2020c). It is depicted that the higher the cross-linked density of the hydrogel structure is the smaller the swelling ratio we archives. This point implies the higher stiffness the hydrogel has in structures with higher cross-linked density. Additionally, it can be observed that these pH-sensitive hydrogels undergo dramatic volume changes in the range of 4.5–6.

In the next case study, the hydrogel bilayer at the initial state is located in a water solution with pH = 5.5. The lower strip is made of poly (HEMA-co-AA) and the upper layer is composed of poly (HEMA-co-DMAEMA). Applying pH variation in the external solution results in the structure bending. To illustrate the bidirectional reversible bending of this hydrogel-based bilayer, we changed the pH of the aqueous solution in the following order:

$\begin{array}{l}Step1:pH=5.5\to pH=9\\ Step2:pH=9\to pH=5.5\\ Step3:pH=5.5\to pH=2\\ Step4:pH=2\to pH=5.5\end{array}(27)$

As shown in Figure 3, increasing pH from 5.5 to nine causes the bilayer structure to bend downward since the top poly (HEMA-co-AA) layer swells and the bottom poly (HEMA-co-DMAEMA) layer deswells. Next, decreasing pH from nine to 5.5 makes the hydrogel structure undergo reversible bending due to swelling of the lower strip and deswelling of the upper strip. To generate the opposite side bending, the smart bilayer is exposed to a pH drop from 5.5 to 2. Accordingly, the upper poly (HEMA-co-AA) layer shrinks regarding the pH reduction while the poly (HEMA-co-DMAEMA) one enlarges significantly and absorbs a great amount of water solution. To return the structure to its initial configuration, straight rectangular layers, the pH of the external solvent alters from 2 to 5.5. Therefore, the circular shaper bilayer at pH = 2 undergoes shape-shifting and becomes a flat bilayer at pH = 5.5. As depicted in Figure 3, changing pH from 5.5 to 9 generates downward bending; while pH variation from 5.5 to 9 creates upward bending. Therefore, this hydrogel-based bilayer can easily be controlled by altering the pH of the surrounded solvent. The shape-transforming observed in this smart structure is bidirectional reversible bending which can be employed in different applications regarding its swelling behavior in response to the external field.

FIGURE 3

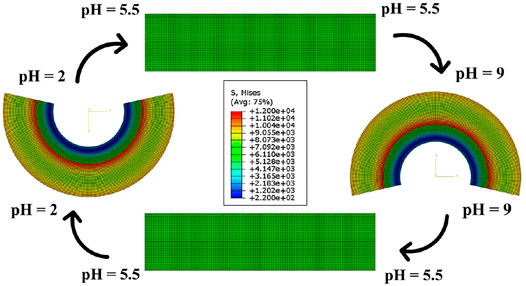
FIGURE 3. The bidirectional reversible bending of hydrogel bilayer composed of poly (HEMA-co-AA) and poly (HEMA-co-DMAEMA) under pH variation described in Equation 27.

Here, we want to focus more on the bidirectional bending of the hydrogel bilayer. Thus, to evaluate the proposed analytical solution, from now on, finite element analysis is conducted beside the analytical solution or the same problem and the results are compared. Accordingly, the first parameter we aim to study is the bending curvature which is defined as $\kappa =1/r_{in}$. In this equation, $r_{in}$ is the inner radius during that bending; for instance, for upward bending the surface at $X_2=0$ maps into the inner radius while in downward bending the surface at $X_2=H_1+H_2$ turns into the inner radius. Figure 4, depicts the bending semi-angle in both upward and downward bending considering analytical solution as well as finite element analysis. It is notable that the trend of bending curvature variation in response to pH variation is similar to bending angle. As shown in this figure, the bending semi-angle is presented versus pH variation for diverse cross-linked densities, including 0.001, 0.005, and 0.01. It is observed that whether the pH reduces or increases, the bending curvature and also the semi angle begin to grow. The bending curvature grows from zero to 40, 57, and 98 with a similar trend to the bending angle for 0.01, 0.005, and 0.001. It is obvious that in the vicinity of pH = 5.5, the bending curvature of the hydrogel bilayer varies significantly regarding the large volume change of poly (HEMA-co-AA) and poly (HEMA-co-DMAEMA) in this pH range. It is also apparent that since hydrogels with lower cross-linked density are softer than the ones with larger cross-linked density, hydrogel wih $N\nu =0.001$ has a larger swelling ratio than the one with $N\nu =0.01$ which results in approximately 2.5 times larger bending curvature and semi angle. Additionally, it is depicted that the results of the analytical solution and finite element study have an excellent agreement which illustrates the accuracy of the presented solution. Accordingly to be short, the smaller the cross-linked density of the hydrogel structure is, the larger swelling ratio the hydrogel has which brings about a larger bending angle and curvature.

FIGURE 4

FIGURE 4. The bending semi-angle of pH-sensitive hydrogel bilayer with $N\nu =0.001,0.005,$ and $0.01$ under pH variation.

In the next case study, we aim to investigate the deformation of the hydrogel bilayer with various cross-linked densities in response to a variety of pH variations. As illustrated in Figure 5A, the pH of the surrounded solution changes from the initial state pH = 5.5 to different values, including 6, 7, and 8.5 to explore its effects on the swelling of hydrogel bilayer and its bending. In Figure 5A case study, the cross-linked density is considered $N\nu =0.001$ and as depicted in this figure, raising the pH value from 5.5 causes the structure to bend more which results in a higher bending angle and lower inner radius. Since the current radius is independent of the bilayer aspect ratio, the in-plane direction $X_2$ is normalized with the height of the bilayer, $\text{H}$. Figure 5B also demonstrates the normalized current radius when the pH of the solution diminished from 5.5 to 5, 4, and 2.5. It is obvious that the current radius in two case studies, increasing and decreasing pH, varies symmetrical with respect to pH = 5.5. Accordingly, the hydrogel bilayer has symmetrical bi-directional bending which is not observed in previous studies in which the structure is sensitive to two diverse external stimuli or in the case that the bilayer is made of hydrogel and elastomer. As observed in Figure 5A,B the deformation of the bilayer is presented using the analytic solution and finite element method which illustrates great conformity. This accuracy between the results of the two approaches evaluates the proposed analytical solution.

FIGURE 5

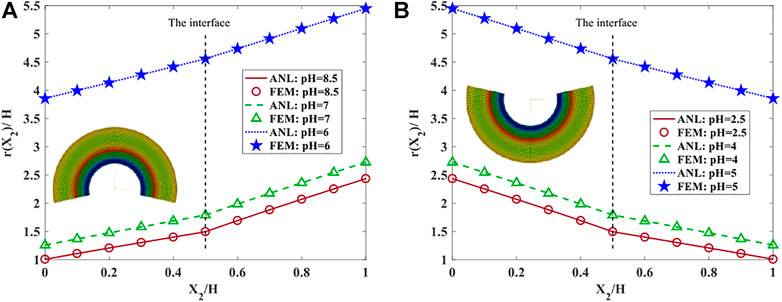
FIGURE 5. The comparison of deformation in hydrogel bilayer with $N\nu =0.001$ (A) at pH $6,7,\text{and}8.5$ as well as (B) pH $5,4,\text{and}2.5$ using both analytical solution and finite element analysis.

Here, the normalized radial and tangential stress distributions along the height of the bilayer are inspected for the above case studies in which solution pH increases and also decreases from the reference condition with pH = 5.5. Figures 6A, 7A presented the radial and hoop stress components in both pH-sensitive layers when solution pH varies from 5.5 to 6, 7, and 8.5. It is depicted that raising the pH generates stresses with higher magnitude in the bilayer structure. Additionally, Figures 6B,7B demonstrate the stress component under the decrease of solution pH which has symmetrical trends in comparison with results under pH increase. The symmetrical behavior in bidirectional bending of bilayer enables us to use this structure in diverse applications. It is also obvious that the stress distribution computed in both analytical and finite element methods agrees with each other and satisfies the boundary conditions presented in Equations 21, 22 and 24. The radial stress at the inner and outer surfaces vanishes and at the interface, both layers have equal radial stress at $X_2=H_1$. The swelling in response to the increase and decrease of pH results in raising the stress components in the bilayer.

FIGURE 6

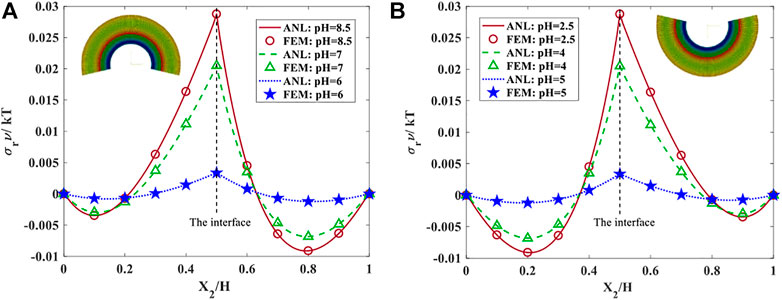
FIGURE 6. The radial stress distributions for both hydrogel layers with $N\nu =0.001$ when (A) pH increases from 5.5 to 6, 7, and 8.5 as well as (B) decrease of pH from 5.5 to 5, 4, 2.5.

FIGURE 7

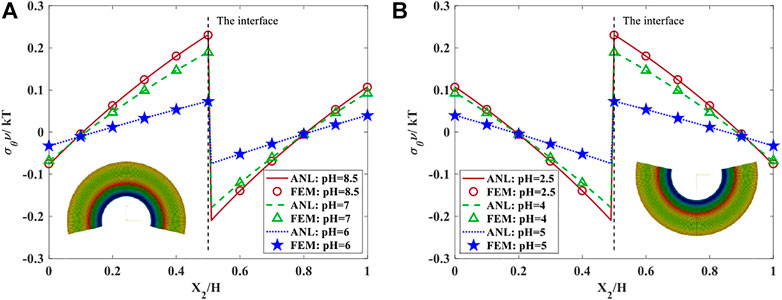
FIGURE 7. The hoop stress distributions for both hydrogel layers with $N\nu =0.001$ when (A) pH increases from 5.5 to 6, 7, and 8.5 as well as (B) decrease of pH from 5.5 to 5, 4, 2.5.

In this part, we aim to investigate the cross-linked density effects on deformation and stress components. As shown in Figure 8, the current radius of the bilayer is presented along with the bilayer’s height after changing pH from 5.5 to 9. As observed in this figure, the radius distribution in each layer has an approximately linear function. It is illustrated that the higher cross-linked density results in a stiffer structure which swells less in response to pH variation. Accordingly, this structure bends less and has a larger current radius. It is clear that the outer radius of the bottom layer is equal to the inner radius of the top layer which also satisfies the boundary condition presented in Equation 23. The agreement between the finite element method and analytical solution results in this case study also verifies the accurate performance of the proposed solution.

FIGURE 8

FIGURE 8. The comparison of normalized current radius in hydrogel bilayer with diverse cross-linked densities at pH = 8.

Figure 9A,B depict the radial and hoop stress distribution along with the normalized height of the bilayer after altering the pH of the solution from 5.5 to 9 to undergo the maximum bending. It is shown that the different stiffnesses are considered to inspect hydrogel bilayer behavior. It is obvious that the trends of the stress components are the same while the magnitudes are different. For instance, the stress components of the bilayer composed of hydrogel with $N\nu =0.01$ have an extreme magnitude in response to the others regarding its stiffness. It is clear that the radial stress components at the bottom and top surfaces of each layer satisfy the boundary conditions. Figure 9A illustrates tensile radial stress in the middle region of the bilayer in both layers. While Figure 9B depicts that in the middle of the bilayer, each layer experiences a different type of hoop stress in each layer: tensile and compressive.

FIGURE 9

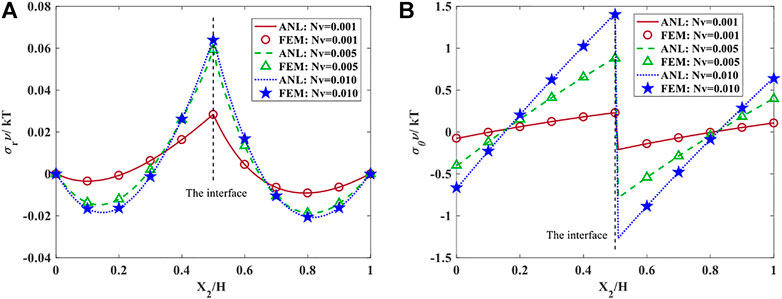
FIGURE 9. The normalized (A) radial and (B) hoop stress distributions in hydrogel bilayer with diverse cross-linked densities at pH = 8.

Moreover, the hoop stress is zero at approximately $X_2/H=0.1$ and 0.8 for pH values higher than 5.5. While the hoop stress vanishes at approximately $X_2/H=0.2$ and 0.9 for pH values lower than 5.5 for diverse cross-linked densities as depicted in Figures 7, 9. These points are considered as the neutral axes of the bilayer. The hydrogel bilayer that is assumed for this study, contains two neutral axes, each one located on a layer, and their locations are fixed for the materials with different cross-linked densities Nν′s. The number and location of the neutral axes might be influenced by the geometry or the difference between the stiffness of the layers.

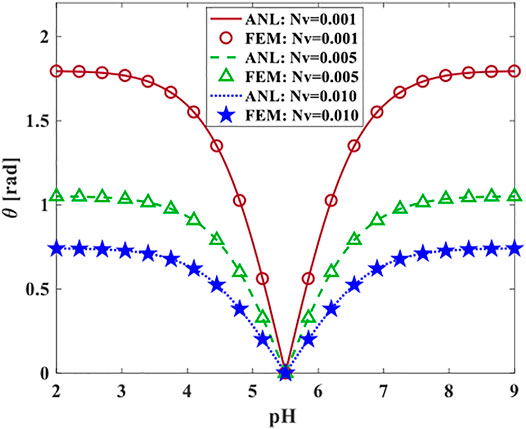
Here, we examined the effects of different parameters on bending semi-angle. As, shown in Figure 10, a hydrogel bilayer with diverse aspect ratios and cross-linked density $N\nu =0.005$ considered at the reference state pH = 5.5. The water solution pH changes from 5.5 to higher and lower values. The pH alteration results in hydrogel swelling and bending of the bilayer. Accordingly, the semi-angle bending of this bilayer is presented in Figure 10, for each case with various final pH and also different aspect ratios using both analytical solution and finite element analysis. It is demonstrated that for a higher aspect ratio $L/H$, the bending semi-angle is larger. For instance, for $L/H=8$ both upward and downward bending at pH = 9 and also pH = 2, respectively, have bending semi-angle 2.7 times larger than hydrogel bilayer with $L/H=4$. Additionally, during the pH increase process, the higher the pH value we reach, the higher hydrogel swelling and bending angle we take. However, during pH reduction, the lower the pH the solution has the larger semi-angle the hydrogel bilayer undertake. It is also depicted that the analytical solution and finite element method achieved similar bending angles which verifies the accuracy of the proposed analytical solution for bending of bilayer structure.

FIGURE 10

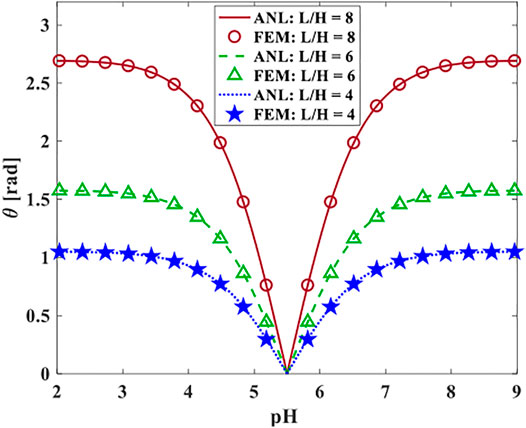
FIGURE 10. The bending semi-angle of hydrogel with $N\nu =0.005$ for diverse aspect ratios, including $L/H=4,6,\text{and}8$ in response to pH variation from pH = 5.5 at reference state to higher and lower values.

4 Conclusion and Summary

In this study, regarding the importance of bidirectional reversible bending of structures in diverse applications such as valves, actuators, and sensors, we introduce a new design concept of a hydrogel bilayer composed of poly (HEMA-co-DMAEMA) layer and a poly (HEMA-co-AA) which undergoes similar finite bending in both directions. Then, we developed an analytical approach to solve the swelling induced by reversible bidirectional bending of each layer in response to pH variation. The poly (HEMA-co-DMAEMA) and the poly (HEMA-co-AA) layers have diverse mechanical behavior when they are exposed to pH change. poly (HEMA-co-AA) swells drastically at higher pH while the structures made of poly (HEMA-co-DMAEMA) absorb water and swell considerably at lower pH. Using this opposite behavior which results in diverse swelling ratios in each layer at the same pH, the bidirectional bending of this bilayer is introduced while the bending in both directions is completely the same unlike previous methods presented to capture bidirectional bending.

The formulation of this problem recast into two coupled second-order nonlinear equations which are solved using boundary conditions on deformation, stress, force, and momentum. The proposed analytical method is verified with finite element analysis for diverse case studies and the conformity between the results of both approaches illustrates the accuracy and robustness of the presented analytical method. The deformation, bending curvature, bending angle, and stress components are examined to find the effects of material properties and also the external field on the bilayer mechanical behavior. It is shown that the softer hydrogels with smaller cross-linked density have a larger swelling ratio which results in a higher bending angle and bending curvature. While the stress magnitudes of the softer hydrogels are less than the ones with higher cross-linked density. Additionally, changing pH value from 5.5 to higher pH brings about considerable swelling and larger bending angles. For instance, it was shown that the final solution pH = 9 generates a stress magnitude 10 times larger than the one with final pH equals to 6.

To sum up, it was shown that different bending angles and curvatures could be captured by controlling material properties, external pH field, and geometry of the structure. Using this approach, the researchers can construct various controllable structures which required bidirectional reversible bending.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Authors contribution statement MS: Methodology, Coding, Writing—original draft. SN: Methodology, Writing—original draft. MB: Conceptualization, Supervision.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors MB.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdolahi, J., Baghani, M., Arbabi, N., and Mazaheri, H. (2016). Analytical and Numerical Analysis of Swelling-Induced Large Bending of Thermally-Activated Hydrogel Bilayers. Int. J. Solids Struct. 99, 1–11. doi:10.1016/j.ijsolstr.2016.08.017

CrossRef Full Text | Google Scholar

Arbabi, N., Baghani, M., Abdolahi, J., Mazaheri, H., and Mashhadi, M. M. (2017). Finite Bending of Bilayer pH-Responsive Hydrogels: A Novel Analytic Method and Finite Element Analysis. Compos. Part B Eng. 110, 116–123. doi:10.1016/j.compositesb.2016.11.006

CrossRef Full Text | Google Scholar

Beebe, D. J., Moore, J. S., Bauer, J. M., Yu, Q., Liu, R. H., Devadoss, C., et al. (2000). Functional Hydrogel Structures for Autonomous Flow Control inside Microfluidic Channels. Nature 404 (6778), 588–590. doi:10.1038/35007047

PubMed Abstract | CrossRef Full Text | Google Scholar

Byrd, R. H., Gilbert, J. C., and Nocedal, J. J. M. P. (2000). A Trust Region Method Based on Interior Point Techniques for Nonlinear Programming. Math. Program. 89 (1), 149–185. doi:10.1007/pl00011391

CrossRef Full Text | Google Scholar

Curatolo, M., Napoli, G., Nardinocchi, P., and Turzi, S. (2021). Dehydration-induced Mechanical Instabilities in Active Elastic Spherical Shells. Proc. R. Soc. A 477 (2254), 20210243. doi:10.1098/rspa.2021.0243

CrossRef Full Text | Google Scholar

Curatolo, M., Nardinocchi, P., Puntel, E., and Teresi, L. (2017). Transient Instabilities in the Swelling Dynamics of a Hydrogel Sphere. J. Appl. Phys. 122 (14), 145109. doi:10.1063/1.5007229

CrossRef Full Text | Google Scholar

De, S. K., Aluru, N. R., Johnson, B., Crone, W. C., Beebe, D. J., and Moore, J. (2002). Equilibrium Swelling and Kinetics of pH-Responsive Hydrogels: Models, Experiments, and Simulations. J. Microelectromechanical Syst. 11 (5), 544–555. doi:10.1109/jmems.2002.803281

CrossRef Full Text | Google Scholar

Deligkaris, K., Tadele, T. S., Olthuis, W., and van den Berg, A. (2010). Hydrogel-based Devices for Biomedical Applications. Sensors Actuators B Chem. 147 (2), 765–774. doi:10.1016/j.snb.2010.03.083

CrossRef Full Text | Google Scholar

Evangelista, D., Hotton, S., and Dumais, J. (2011). The Mechanics of Explosive Dispersal and Self-Burial in the Seeds of the Filaree, Erodium Cicutarium (Geraniaceae). J. Exp. Biol. 214 (4), 521–529. doi:10.1242/jeb.050567

PubMed Abstract | CrossRef Full Text | Google Scholar

He, X., Sun, Y., Wu, J., Wang, Y., Chen, F., Fan, P., et al. (2019). Dual-stimulus Bilayer Hydrogel Actuators with Rapid, Reversible, Bidirectional Bending Behaviors. J. Mater. Chem. C 7 (17), 4970–4980. doi:10.1039/c9tc00180h

CrossRef Full Text | Google Scholar

Hu, Z., Zhang, X., and Li, Y. (1995). Synthesis and Application of Modulated Polymer Gels. Science 269 (5223), 525–527. doi:10.1126/science.269.5223.525

PubMed Abstract | CrossRef Full Text | Google Scholar

Ionov, L. (2013). Biomimetic Hydrogel-Based Actuating Systems. Adv. Funct. Mat. 23 (36), 4555–4570. doi:10.1002/adfm.201203692

CrossRef Full Text | Google Scholar

Jamal, M., Zarafshar, A. M., and Gracias, D. H. (2011). Differentially Photo-Crosslinked Polymers Enable Self-Assembling Microfluidics. Nat. Commun. 2 (1), 527. doi:10.1038/ncomms1531

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeong, K.-U., Jang, J.-H., Kim, D.-Y., Nah, C., Lee, J. H., Lee, M.-H., et al. (2011). Three-dimensional Actuators Transformed from the Programmed Two-Dimensional Structures via Bending, Twisting and Folding Mechanisms. J. Mat. Chem. 21 (19), 6824–6830. doi:10.1039/c0jm03631e

CrossRef Full Text | Google Scholar

Kim, B., La Flamme, K., and Peppas, N. A. (2003). Dynamic Swelling Behavior of pH‐sensitive Anionic Hydrogels Used for Protein Delivery. J. Appl. Polym. Sci. 89 (6), 1606–1613. doi:10.1002/app.12337

CrossRef Full Text | Google Scholar

Kim, J., Hanna, J. A., Byun, M., Santangelo, C. D., and Hayward, R. C. (2012). Designing Responsive Buckled Surfaces by Halftone Gel Lithography. Science 335 (6073), 1201–1205. doi:10.1126/science.1215309

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Laschi, C., and Trimmer, B. (2013). Soft Robotics: a Bioinspired Evolution in Robotics. Trends Biotechnol. 31 (5), 287–294. doi:10.1016/j.tibtech.2013.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Koller, D. (1990). Light-driven Leaf Movements*. Plant Cell Environ. 13 (7), 615–632. doi:10.1111/j.1365-3040.1990.tb01079.x

CrossRef Full Text | Google Scholar

Kwon, G. H., Choi, Y. Y., Park, J. Y., Woo, D. H., Lee, K. B., Kim, J. H., et al. (2010). Electrically-driven Hydrogel Actuators in Microfluidic Channels: Fabrication, Characterization, and Biological Application. Lab. Chip 10 (12), 1604–1610. doi:10.1039/b926443d

PubMed Abstract | CrossRef Full Text | Google Scholar

Kwon, G. H., Jeong, G. S., Park, J. Y., Moon, J. H., and Lee, S.-H. (2011). A Low-Energy-Consumption Electroactive Valveless Hydrogel Micropump for Long-Term Biomedical Applications. Lab. Chip 11 (17), 2910–2915. doi:10.1039/c1lc20288j

PubMed Abstract | CrossRef Full Text | Google Scholar

Le, X., Lu, W., Zhang, J., and Chen, T. (2019). Recent Progress in Biomimetic Anisotropic Hydrogel Actuators. Adv. Sci. 6 (5), 1801584. doi:10.1002/advs.201801584

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Cai, X., Gao, Y., and Serpe, M. J. (2017). Reversible Bidirectional Bending of Hydrogel-Based Bilayer Actuators. J. Mater. Chem. B 5 (15), 2804–2812. doi:10.1039/c7tb00426e

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, H. T., Leisk, G. G., and Trimmer, B. (2011). GoQBot: a Caterpillar-Inspired Soft-Bodied Rolling Robot. Bioinspir Biomim. 6 (2), 026007. doi:10.1088/1748-3182/6/2/026007

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Boatti, E., Bertoldi, K., and Kramer-Bottiglio, R. (2018). Stimuli-induced Bi-directional Hydrogel Unimorph Actuators. Extreme Mech. Lett. 21, 35–43. doi:10.1016/j.eml.2018.03.001

CrossRef Full Text | Google Scholar

Mao, Y., Ding, Z., Yuan, C., Ai, S., Isakov, M., Wu, J., et al. (2016). 3D Printed Reversible Shape Changing Components with Stimuli Responsive Materials. Sci. Rep. 6 (1), 24761–24813. doi:10.1038/srep24761

PubMed Abstract | CrossRef Full Text | Google Scholar

Mao, Y., Ding, Z., Yuan, C., Ai, S., Isakov, M., Wu, J., et al. (2016). 3D Printed Reversible Shape Changing Components with Stimuli Responsive Materials. Sci. Rep. 6 (1), 24761. doi:10.1038/srep24761

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcombe, R., Cai, S., Hong, W., Zhao, X., Lapusta, Y., and Suo, Z. (2010). A Theory of Constrained Swelling of a pH-Sensitive Hydrogel. Soft Matter 6 (4), 784–793. doi:10.1039/b917211d

CrossRef Full Text | Google Scholar

Meng, H., and Li, G. (2013). A Review of Stimuli-Responsive Shape Memory Polymer Composites. polymer 54 (9), 2199–2221. doi:10.1016/j.polymer.2013.02.023

CrossRef Full Text | Google Scholar

Morales, D., Palleau, E., Dickey, M. D., and Velev, O. D. (2014). Electro-actuated Hydrogel Walkers with Dual Responsive Legs. Soft Matter 10 (9), 1337–1348. doi:10.1039/C3SM51921J

PubMed Abstract | CrossRef Full Text | Google Scholar

Niroumandi, S., Shojaeifard, M., and Baghani, M. (2021). Finite Deformation of Swollen pH-Sensitive Hydrogel Cylinder under Extension and Torsion and its Poynting Effect: Analytical Solution and Numerical Verification. Int. J. Appl. Mech. 13 (6), 2150071. doi:10.1142/s175882512150071x

CrossRef Full Text | Google Scholar

Niroumandi, S., Shojaeifard, M., and Baghani, M. (2021). On Single and Multiple pH-Sensitive Hydrogel Micro-valves: A 3D Transient Fully Coupled Fluid–Solid Interaction Study. Transp. Porous Media, 1–22. doi:10.1007/s11242-021-01625-y

CrossRef Full Text | Google Scholar

Niroumandi, S., Shojaeifard, M., and Baghani, M. (2021). PH-sensitive Hydrogel-Based Valves: A Transient Fully-Coupled Fluid-Solid Interaction Study. J. Intelligent Material Syst. Struct. 33 (1), 196–209. doi:10.1177/1045389x211011671

CrossRef Full Text | Google Scholar

Osada, Y., and Gong, J.-P. (1998). Soft and Wet Materials: Polymer Gels. Adv. Mat. 10 (11), 827–837. doi:10.1002/(sici)1521-4095(199808)10:11<827::aid-adma827>3.0.co;2-l

CrossRef Full Text | Google Scholar

Pourjavadi, A., Heydarpour, R., and Tehrani, Z. M. (2021). Multi-stimuli-responsive Hydrogels and Their Medical Applications. New J. Chem. 45 (35), 15705–15717. doi:10.1039/d1nj02260a

CrossRef Full Text | Google Scholar

Reyssat, E., and Mahadevan, L. (2009). Hygromorphs: from Pine Cones to Biomimetic Bilayers. J. R. Soc. Interface. 6 (39), 951–957. doi:10.1098/rsif.2009.0184

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheikhi, S., Shojaeifard, M., and Baghani, M. (2019). Finite Bending and Straightening of Hyperelastic Materials: Analytical Solution and FEM. Int. J. Appl. Mech. 11 (9), 1950084. doi:10.1142/s1758825119500844

CrossRef Full Text | Google Scholar

Shojaeifard, M., and Baghani, M. (2020). Finite Deformation Swelling of a Temperature-Sensitive Hydrogel Cylinder under Combined Extension-Torsion. Appl. Math. Mech.-Engl. Ed. 41 (3), 409–424. doi:10.1007/s10483-020-2585-6

CrossRef Full Text | Google Scholar

Shojaeifard, M., and Baghani, M. (2019). On the Finite Bending of Functionally Graded Light-Sensitive Hydrogels. Meccanica 54 (6), 841–854. doi:10.1007/s11012-019-01004-4

CrossRef Full Text | Google Scholar

Shojaeifard, M., Bayat, M. R., and Baghani, M. (2019). Swelling-induced Finite Bending of Functionally Graded pH-Responsive Hydrogels: a Semi-analytical Method. Appl. Math. Mech. 40 (5). doi:10.1007/s10483-019-2478-6

CrossRef Full Text | Google Scholar

Shojaeifard, M., Dolatabadi, R., Sheikhi, S., and Baghani, M. (2021). Coupled Thermo-Mechanical Swelling of a Thermo-Responsive Hydrogel Hollow Cylinder under Extension-Torsion: Analytical Solution and FEM. J. Intelligent Material Syst. Struct. 32 (2), 140–155. doi:10.1177/1045389x20951273

CrossRef Full Text | Google Scholar

Shojaeifard, M., Niroumandi, S., and Baghani, M. (2022). Programmable Self-Folding of Trilayer and Bilayer-Hinge Structures by Time-dependent Swelling of Tough Hydrogels. J. Intelligent Material Syst. Struct., 1045389X2210774. doi:10.1177/1045389x221077435

CrossRef Full Text | Google Scholar

Shojaeifard, M., Niroumandi, S., and Baghani, M. (2022). Programming Shape-Shifting of Flat Bilayers Composed of Tough Hydrogels under Transient Swelling. Acta Mech. 233 (1), 213–232. doi:10.1007/s00707-021-03117-y

CrossRef Full Text | Google Scholar

Shojaeifard, M., Niroumandi, S., and Baghani, M. (2022). Swelling of pH-Sensitive Hydrogel Pressure Vessel under Altered-pH Coupled with Inflation, Extension, and Torsion. Meccanica 1-21. doi:10.1007/s11012-022-01497-6

CrossRef Full Text | Google Scholar

Shojaeifard, M., Sheikhi, S., Baniassadi, M., and Baghani, M. (2020). On Finite Bending of Visco-Hyperelastic Materials: A Novel Analytical Solution and FEM. Acta Mech. 231 (8), 3435–3450. doi:10.1007/s00707-020-02733-4

CrossRef Full Text | Google Scholar

Shojaeifard, M., Tahmasiyan, S., and Baghani, M. (2020). Swelling Response of Functionally Graded Temperature-Sensitive Hydrogel Valves: Analytic Solution and Finite Element Method. J. Intelligent Material Syst. Struct. 31 (3), 457–474. doi:10.1177/1045389x19891544

CrossRef Full Text | Google Scholar

Shojaeifard, M., Wang, K., and Baghani, M. (2020). Large Deformation of Hyperelastic Thick-Walled Vessels under Combined Extension-Torsion-Pressure: Analytical Solution and FEM. Mech. Based Des. Struct. Mach., 1–18. doi:10.1080/15397734.2020.1826963

CrossRef Full Text | Google Scholar

Stahlberg, R. (2009). The Phytomimetic Potential of Three Types of Hydration Motors that Drive Nastic Plant Movements. Mech. Mater. 41 (10), 1162–1171. doi:10.1016/j.mechmat.2009.05.003

CrossRef Full Text | Google Scholar

Valiollahi, A., Shojaeifard, M., and Baghani, M. (2019). Closed Form Solutions for Large Deformation of Cylinders under Combined Extension-Torsion. Int. J. Mech. Sci. 157, 336–347. doi:10.1016/j.ijmecsci.2019.04.053

CrossRef Full Text | Google Scholar

Valiollahi, A., Shojaeifard, M., and Baghani, M. (2019). Implementing Stretch-Based Strain Energy Functions in Large Coupled Axial and Torsional Deformations of Functionally Graded Cylinder. Int. J. Appl. Mech. 11 (04), 1950039. doi:10.1142/s175882511950039x

CrossRef Full Text | Google Scholar

Yu, Q., Bauer, J. M., Moore, J. S., and Beebe, D. J. (2001). Responsive Biomimetic Hydrogel Valve for Microfluidics. Appl. Phys. Lett. 78 (17), 2589–2591. doi:10.1063/1.1367010

CrossRef Full Text | Google Scholar

Zhang, J., Wu, J., Sun, J., and Zhou, Q. (2012). Temperature-sensitive Bending of Bigel Strip Bonded by Macroscopic Molecular Recognition. Soft Matter 8 (21), 5750–5752. doi:10.1039/c2sm25511a

CrossRef Full Text | Google Scholar