- 1Materials Genome Institute, Shanghai University, Shanghai, China
- 2State Key Laboratory of Functional Materials for Informatics, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai, China
Materials genome methods have played an essential role in accelerating the discovery of high-performance novel materials, and include high-throughput calculation, database construction, and machine learning. Over the past decades, these approaches have been increasingly used in lithium battery materials, solar cells, transparent conductors, and thermoelectrics. Thermoelectrics are functional materials that can directly convert electricity into heat and vice versa, offering new ideas for conventional power generation and refrigeration. The application of high-throughput methods can achieve more efficient screening of new thermoelectric materials and accelerate experimental development. This review summarizes the recent progress in the application of materials genome methods for different thermoelectric materials, such as half-Heuslers, diamond-like structures, oxides, and other materials. Finally, current advances in machine learning for thermoelectrics are discussed. The progress of the theoretical design of thermoelectrics has driven the development of high-performance thermoelectrics.
Introduction
With the emergence of the global energy crisis and environmental problems, novel green and environmentally friendly materials for energy conversion have received much attention. Thermoelectric (TE) materials are a type of energy conversion material that can directly convert heat into electricity and vice versa for power generation and refrigeration (Goldsmid, 2010; Rowe, 2018). TE materials are employed in a variety of applications, such as household refrigerators and space probes. TE materials are even expected to be used in wearable devices (Petsagkourakis et al., 2018). Bi2Te3 is the only compound currently used commercially as a TE material (Chen et al., 2018; Mamur et al., 2018). Therefore, methods of improving the TE performance and finding more TE materials for use in practical applications is a critical challenge.
The performance of TE devices is determined by a dimensionless figure of merit, ZT=(S2σT)/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, S2σ is referred to as the power factor (PF), T is the absolute temperature, and κ is the thermal conductivity. Generally, a high PF or a low κ results in a high ZT value; nevertheless, the interdependency between S and σ creates a challenge in optimizing TE performance. For example, an increase in S leads to the decrease of σ, and vice versa. To improve TE performance, many methodologies have been introduced. These include band degeneracy (Pei et al., 2012; Fu et al., 2015b; Tan et al., 2016; Wang N. et al., 2021), defect engineering (Liu Y. et al., 2016; Zhu et al., 2016; Zhao et al., 2020; Zheng et al., 2021), and conductive networks in complex compounds (Yang et al., 2016; Xi et al., 2018). The identification of new, high-performance TE materials is important; however, the traditional “trial and error” research methodology is time-consuming and laborious. The Materials Genome Initiative (MGI), proposed in 2011, is an effective way to accelerate the design, development, and application of novel materials.
The announcement of the MGI played a crucial role in accelerating the discovery of TE materials, including computational tools, experimental tools, collaborative networks, and digital data (Dima et al., 2016). First-principles calculations based on density functional theory (DFT) (Kohn and Sham, 1965) are used to predict and optimize the TE performance of materials. The calculations can analyze the properties of the electronic structure, density of states, phonons (Togo and Tanaka, 2015), elasticity, and other parameters (Slack, 1973).
First-principles high-throughput (HTP) (Jain et al., 2015) methods have become a universal tool for the discovery of novel materials (Jain et al., 2011; Curtarolo et al., 2013; Calderon et al., 2015; Yan et al., 2015; Chen et al., 2016; Körbel et al., 2016). The Materials Project (MP, materialsproject.org) is an open-access database established in 2011. MP uses HTP screening to establish a data-rich ecosystem for the discovery of solar photovoltaics, piezoelectrics, TEs, and other materials (Jain et al., 2013). The MP data comprise known materials from the Inorganic Crystal Structures database (ICSD) (Belsky et al., 2002) and predicted materials generated by the web-based collaboration. MP now contains over 140,000 structures of inorganic compounds (de Jong et al., 2015), including new battery materials (Kim et al., 2011), piezoelectrics (Armiento et al., 2011), photovoltaics (Yu and Zunger, 2012), and TE materials (Wang S. et al., 2011). Automatic-FLOW (AFLOW, aflowlib.org) is a globally available database (Curtarolo et al., 2012; Calderon et al., 2015) including 3,500,000 material compounds with over 705,000,000 calculated properties that can support a post-processing tool for material analysis. The data in AFLOW were generated by the DFT software Vienna Ab Initio Simulation Package (VASP) (Kresse and Furthmuller, 1996; Kresse and Joubert, 1999) and Quantum Espresso (QE) (Giannozzi et al., 2017). Novel Materials Discovery (NOMAD, nomad-coe.eu) is a tool for creating, collecting, and storing computational materials science data. NOMAD contains over 50,000,000 total energy calculations (Draxl and Scheffler, 2019). MatCloud (matcloud.cnic.cn) is a Chinese HTP platform, which is a computational materials platform where users can perform online job setup, job submission, and monitoring via a web browser (Yang et al., 2018). The Materials Hub with three-dimensional structures (MatHub-3d, www.mathub3d.net, formerly MIP-3d) is a HTP platform developed by the MGI of Shanghai University, and focuses on energy, electronic structures, and electrical transport properties (Yao et al., 2021).
Based on the material databases, many screening studies have been performed on functional materials, such as metal-organic frameworks (Zornoza et al., 2013; Colon and Snurr, 2014), transparent conducting materials (Hautier et al., 2013; Brunin et al., 2019), Li-ion battery materials (Wang Y. et al., 2017), and other materials. The HTP research approach brings material development into the fourth paradigm. The combination of “experiment-calculation-data” opens new avenues for the development of novel high-performance TE materials. In this review, we highlight the recent application of materials genome methods to different materials, including half-Heuslers, diamond-like compounds, and perovskites, and discuss the recent progress in the application of machine learning (ML) to TEs.
Recent Progress in Thermoelectrics
The evolution of ZT values in different materials from 1954 to 2021 is shown in Figure 1, with two distinct major leaps visible. The first is the development of the classical semiconductor theory in the 1960s, which promoted the development of alloy semiconductor TE materials with a ZT value of approximately 1.0, such as Bi2Te3, PbTe, and SiGe (Goldsmid and Douglas, 1954; Dismukes et al., 1964). The second leap in development occurred because of new concepts and technologies, such as phonon glass electron crystals (PGECs) (Rowe, 2018), nanotechnology (Shakouri, 2011), and energy band engineering (Capasso, 1987). Some new TE materials with complex structures have been discovered and their thermal and electric properties are greatly improved; these materials include skutterudites (Rogl et al., 2015), diamond-like compounds (Xie et al., 2021), half-Heuslers (Fu et al., 2015a), Cu2Se (Olvera et al., 2017), SnSe (Chang et al., 2018), and other materials. HTP calculations and ML have injected “new blood” into the discovery of high-performance TE materials in recent years and may lead to a third leap forward.
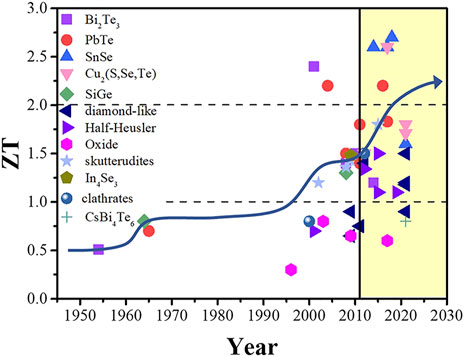
FIGURE 1. The evolution of ZT values in different TE materials (Goldsmid and Douglas, 1954; Dismukes et al., 1964; Ohtaki et al., 1996; Kuznetsov et al., 2000; Shen et al., 2001; Dyck et al., 2002; Shi et al., 2008; Wang et al., 2008; Liu et al., 2009a; Liu et al., 2009b; Li et al., 2009; Ohtaki et al., 2009; Pei et al., 2011; Yang et al., 2011; Saiga et al., 2012; Hu et al., 2014; Rogl et al., 2015; Fu et al., 2016; Olvera et al., 2017; Zhang et al., 2017; Beretta et al., 2019; Pang et al., 2019; Cao et al., 2021; Xie et al., 2021; Xiong et al., 2021; Zhang et al., 2021).
Half-Heuslers
Half-Heuslers (HH) have a valence electron count of 8 or 18, and are generally represented by the formula ABX, where A and B are usually transition metal elements and X is a leading group element. A typical HH compound is MgAgAs, with a face-centered cubic (FCC) crystal structure, as shown in Figure 2A (Larson et al., 1999; Uher et al., 1999; Fang et al., 2018). HH compounds have high mechanical strength, excellent electrical properties, and good thermal stability (Everhart and Newkirk, 2019); they are considered to be the most promising high-temperature TE material candidates studied in recent years (Fu et al., 2015b).
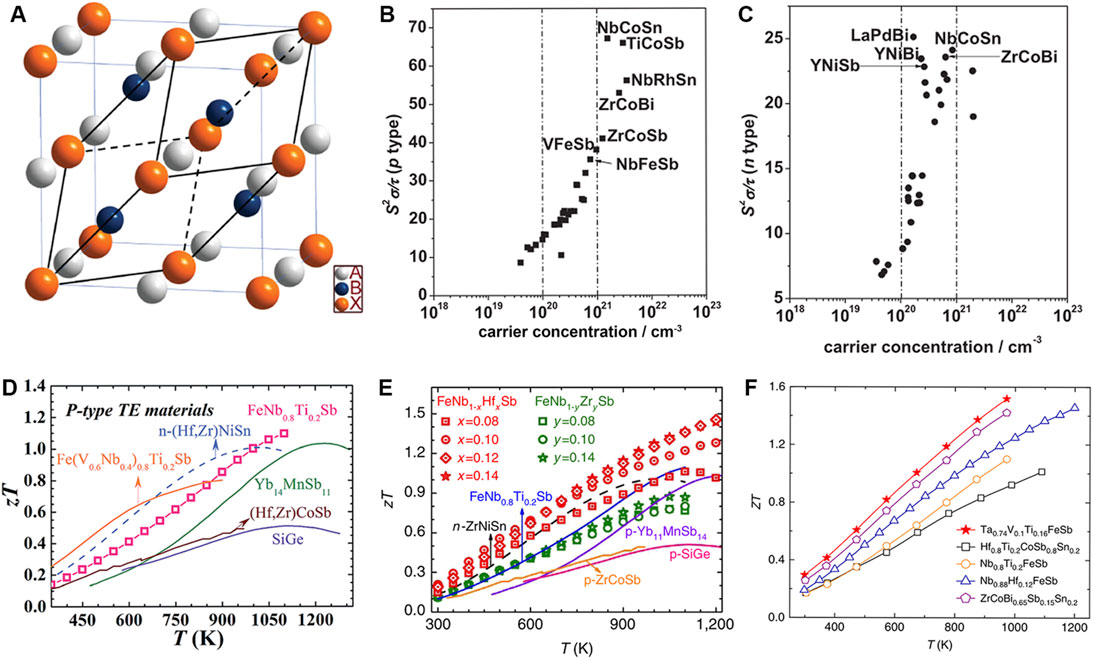
FIGURE 2. (A) Typical crystal structure of HH compounds of the type ABX (Yang et al., 2008); (B,C) The maximum power factor versus carrier concentration of the p-type and n-type HH compounds (Yang et al., 2008); (D) The ZT value of p-type FeNb0.8Ti0.2Sb compounds at different temperatures. (Fu et al., 2015b); (E) ZT comparison for Hf- or Zr-doped FeNbSb and other typical high-temperature TE materials (Fu et al., 2015a); (F) The time-dependent ZT value of TaFeSb-based Ta1-xTixFeSb (Zhu et al., 2019).
Starting from the available experimental data, Yang et al. (2008) used ab initio calculations and Boltzmann transport theory under the constant relaxation time approximation to screen more than 100 HH compounds taken from the ICSD and studied the electrical transport properties of 36 HH compounds. The p-type and n-type HH compounds with high power factors are shown in Figures 2B,C. The recommended potential HH compounds were Co-, Rh-, and Fe-based HH compounds for p-type prospective materials, and LaPdBi for n-type, with some subsequently confirmed experimentally (Yang et al., 2008). Up to the present day, the experimental ZT values of HH compounds are 1.0–1.5. For example, for the p-type NbFeSb-based HH compound, a maximum ZT of 1.1 at 1100 K was reported (Figure 2D), with the TE properties optimized by a band engineering approach via the tradeoff between the band effective mass and carrier mobility (Fu et al., 2015b). Heavy-band p-type FeNbSb with doped Hf reached a high ZT of 1.5 (Figure 2E) (Fu et al., 2015a). A p-type TaFeSb-based HH compound demonstrated a record high ZT of ∼1.52 at 973 K, which was identified by screening the family of V1-VIII-V2 HH compounds (with V1 = V, Nb, or Ta; VIII = Fe, Ru, or Os; and V2 = As, Sb, or Bi) (Figure 2F) (Zhu et al., 2019). Guo et al. (2019) screened 95 HH compounds using HTP and predicted six p-type and four n-type unreported promising HH compounds, with the finding that the cooperative effects of high band degeneracy, small deformation potential, light band, and large phonon velocity led to a big power factor.
HH compounds have high lattice thermal conductivity; forming solid solutions can effectively reduce the lattice thermal conductivity (He et al., 2014; Tavassoli et al., 2017; Yu et al., 2017; Dylla et al., 2020). As the formation of solid solutions affects the electronic structure, the electronic structure of HH compounds needs to be studied. Dylla et al. (2020) constructed an orbital phase diagram (Figure 3B) according to the atomic orbital composition of HH valence bands; this technique helps to track the changes in electronic structure through the solid solutions. They used HTP calculations and ML to compare the valence band maximum (VBM) of known HH compounds and discover new chemical guidelines for promoting the highly degenerate W-point to the VBM. The k-point of the VBM is different for different electronic structures, and the VBM may occur at the Γ-point (with a band degeneracy Nv of 1), L-point (Nv = 4), or W-point (Nv = 6), where Nv is the total band degeneracy (Yan et al., 2015).
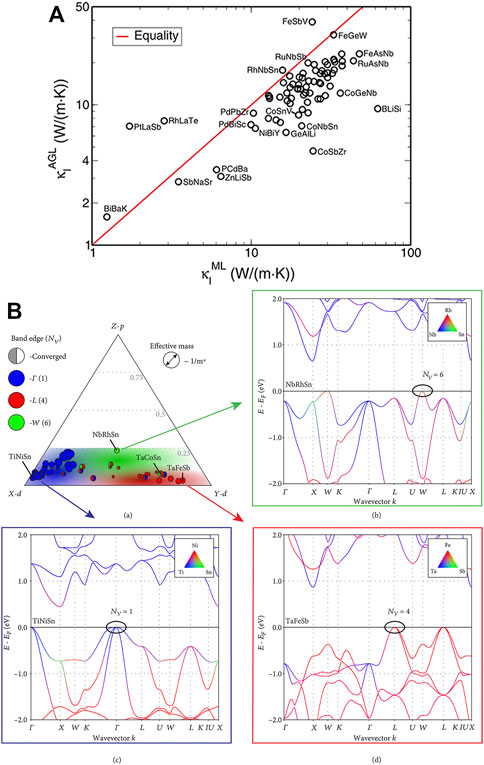
FIGURE 3. (A) Thermal conductivities of HH compounds using AGL at 300 K compared with machine learning algorithm predictions (Toher et al., 2014); (B) The orbital phase diagram of HH compounds (Dylla et al., 2020).
HTP calculations and ML techniques have been increasingly used for the development of HH compounds in recent years. The lattice thermal conductivity of HH compounds (Carrete et al., 2014) was screened from approximately 79,000 HH entries in the AFLOWLIB.org database (Curtarolo et al., 2012; Taylor et al., 2014). All possible compounds in the periodic table of elements, excluding radioactive elements, were considered for HH compounds. By enthalpy calculations, second-order force constant phonon dispersion calculations, and global thermodynamic stability analysis, 75 stable structures of HH compounds were obtained. Three computational methods were proposed to estimate the thermal conductivity of those 75 compounds. Eventually, they concluded that compounds were most likely to have low thermal conductivity if the average atomic radius of the atoms in structural positions A and B was large. Moreover, they proposed that PtLaSb, RhLaTe, and SbNaSr had low lattice thermal conductivity (less than 5 W/m K). After that, Toher et al. (2014) used the automatic Gibbs library (AGL) to analyze these 107 HH compounds (Figure 3A), and demonstrated that the AGL method was much cheaper computationally compared with the full ab initio approach.
Overall, the HTP method has yielded some success in both electrical and thermal transport performance, and a set of guidelines has been established for the screening and optimization of HH compounds. Starting from the experimental data, in combination with first-principles calculations and ML, HH compounds have achieved ZT values of 1.0–1.5.
Diamond-like Compounds
Diamond-like compounds are derived from tetrahedrally bonded diamonds. The anions in these compounds occupy an FCC sublattice, and the cations occupy the tetrahedral center. The cations and anions in the unit cell follow the simple valence-octet rule (Xi et al., 2018). Diamond-like compounds can be divided into two types according to the ratio of the number of anions and cations in the compound: a cation/anion ratio of <1 is referred to as a defect diamond-like compound (e.g., In2Te3, CdIn2Se4), and a cation/anion ratio = 1 is referred to as a normal diamond-like compound (e.g., ZnS, CuInTe2) (Li et al., 2020). Owing to the flexibility of the cation sublattice, the diamond-like compounds have many possible compositions, including unitary, binary, ternary, and quaternary components or even higher. Diamond-like compounds play an essential role in the field of photovoltaics and infrared detectors. In 2009, the discovery of quaternary Cu2MSnQ4 (M = Zn, Cd; Q = S, Se) as promising TE materials attracted intensive study; the ZT reached 0.65 at 700 K (Liu et al., 2009a). Ternary CuGaTe2 is a high-efficiency TE material with a high ZT of 1.4 at 950 K (Plirdpring et al., 2012), and the ZT value of CuInTe2 reached 1.18 at 850 K, and displayed good electrical properties and low thermal conductivity (Liu et al., 2012). The advantages of environmentally friendly constituent elements, relatively large Seebeck coefficient, and low thermal conductivity mean that the diamond-like structures are promising TE materials.
In an initial attempt at HTP, Zhang et al. (2014) used a series of ternary diamond-like compounds (Figure 4A) and proposed a pseudocubic approach to search for and design high-performance non-cubic TE materials. Zhang et al. tuned crystal structures to design pseudocubic or cubic-like structure blocks in non-cubic materials, to lead directly to cubic-like degenerate band-edge electronic states (Figure 4B) (Zhang et al., 2014). The diamond-like structure might show increased randomness of the locally irregular tetrahedra through a rationally designed mixing strategy while maintaining the cubic-like degenerate electronic states at the band edge. The ZT had peak values when the crystal field splitting energy, ΔCF, was close to zero (Figure 4C). The distortion parameter η (η = c/2a) was also proposed as a means to evaluate and quantify the TE performance. When η was close to 1, ΔCF was close to 0 (Figure 4D). The unity-η rule provided a systematic strategy for guiding the evaluation and optimization of TE diamond-like structures. The parameter η could be easily obtained from lattice parameters a and c; based on this theory, Liu R. et al. (2016) synthesized a series of Cu1-x-δAgxInTe2 structures, obtaining a high ZT of 1.24 from the Cu0.75Ag0.2InTe2 structure (Figure 4E).
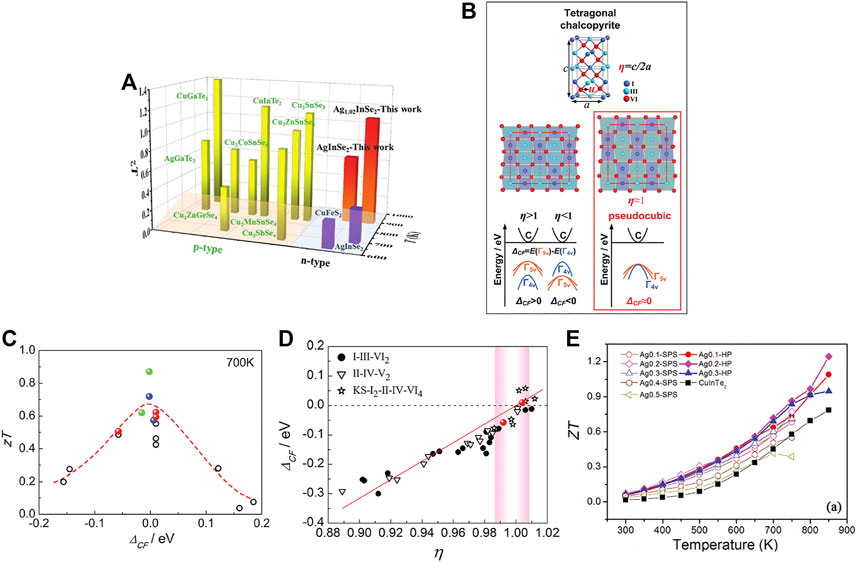
FIGURE 4. (A) The ZT values of the ternary diamond-like structure compounds (Zhang et al., 2014); (B) The pseudocubic structure in tetragonal chalcopyrite compounds (Zhang et al., 2014); (C) The relationship between crystal field splitting energy ΔCF and ZT (Zhang et al., 2014); (D) The relationship between crystal field splitting energy ΔCF and distortion parameter η (Zhang et al., 2014); (E) The ZT value of Cu1-x-δAgxInTe2, which consolidated by SPS (Spark Plasma Sintering) and HP (Hot Pressing) (Liu R. et al., 2016).
In TE materials, it is difficult to calculate the carrier relaxation time, and the accurate calculation of electron–phonon coupling is time-consuming, which is not suitable for HTP calculation (Noffsinger et al., 2010; Chen et al., 2012; Liu et al., 2017). Deformation potential method (Bardeen and Shockley, 1950) are usually used in HTP calculations. However, their accuracy has always been questioned. In 2018, Xi et al. (2018) screened chalcogenides with a diamond-like structure, space group 225, from the MatHub-3d database (Yao et al., 2021) through HTP calculations (Figure 5A). This work reported a new strategy for computing the electronic relaxation time τ, which was efficient enough for HTP calculation and more accurate than the more advanced electron–phonon coupling method. One type of novel compound with a defect-chalcopyrite structure, such as CdIn2Te4 and ZnIn2Te4, has been proposed a potentially good TE material, and Cd2Cu3In3Te8 has been experimentally synthesized and proved to have a high ZT, of above 1 (Figure 5B). Following the work of (Xi et al., 2018), Li et al. (2019) used the HTP method to screen the TE performance of ABX2 compounds with diamond-like structures (Figure 5C). ZnSnSb2, AgInS2, AgGaSe2, AgInSe2, and LiInTe2 were predicted to have high ZT values for both n-type and p-type. The aforementioned work achieves the full flow from material design of HTP screening to experimental validation, which is of great significance for the prediction of the novel high-performance TE materials.
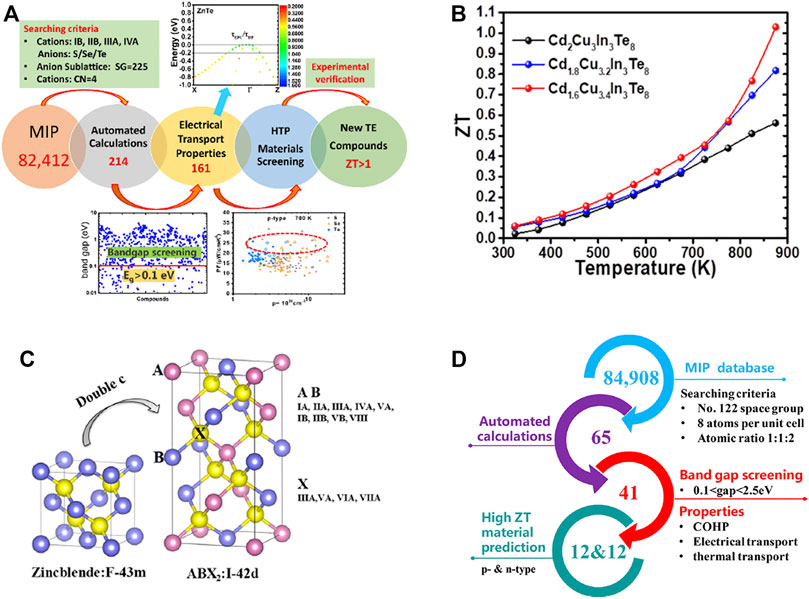
FIGURE 5. (A) The workflow of screening ABX compounds (Xi et al., 2018); (B) The ZT value of Cd2Cu3In3Te8 at different high temperatures (Xi et al., 2018); (C) The crystal structure of ABX2 compounds with diamond-like structures (Li et al., 2019); (D) The workflow for ABX2 screening, COHP is the Crystal Orbital Hamilton Population (Li et al., 2019).
Oxides
Since the discovery of p-type NaCo2O4 with high TE performance (Terasaki et al., 1997), many oxides, such as the binary oxide ZnO (Ong et al., 2011) and the perovskite-type oxides SrTiO3 (Muller et al., 2004), CaMnO3 (Wang et al., 2009), and LaCoO3 (Vulchev et al., 2012), have been investigated as TE materials. The high-temperature stability, environmentally friendly properties, and low cost make them suitable for various applications, such TE, photoelectric, catalysis, photocatalytic (Sawada and Nakajima, 2018; Nkwachukwu and Arotiba, 2021), and dielectric materials. Unlike the favored materials in the field of TE, such as SnSe (Wang et al., 2015; Zhao et al., 2016), PbTe (Pei et al., 2011; Xiao and Zhao, 2018), and Cu2Se (Nunna et al., 2017; Olvera et al., 2017), the ZT values of oxides were not very high (Wang H. C. et al., 2011; Wang J. et al., 2017).
With the help of the materials genome, Chen et al. (2016) analyzed the TE properties of over 48,000 compounds from the MP. The dataset in this work was primarily composed of oxygen-containing compounds, and the majority of the compounds performed better as n-type (Figure 6A). The ZT of p-type oxides reached 1; the ZT of n-type oxides was only approximately 0.3. There has been renewed interest in developing new n-type oxide TEs. Chen et al. also compared the power factors of oxides, tellurides, selenides, and sulfides (Figure 6B), which were estimated using a constant relaxation time approximation. The red lines represent the median computed power factor for different anions; the oxides exhibited the lowest power factors. Additionally, the higher band gaps of the oxides complicated doping. Combining high thermal conductivity with excellent TE performance is challenging for oxides (Chen et al., 2016). Additionally, Garrity (2016) employed HTP first-principles calculations to identify promising n-type transition metal oxides, nitrides, and sulfides from ICSD. At 700 K, the Seebeck coefficient and electronic conductivity of 551 oxides, 53 nitrides, and 25 sulfides were estimated using a constant relaxation time approximation. They discovered that a combination of symmetry-enforced degeneracies, low dimensionality, or accidental degeneracies could result in high power factors for these compounds.
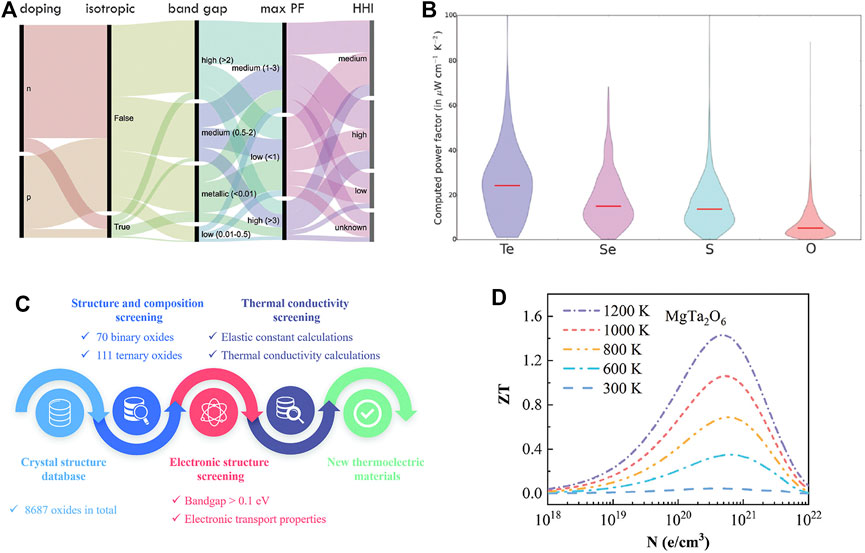
FIGURE 6. (A) Flow diagram representation of the dataset of over 48,000 compounds (Chen et al., 2016); (B) The power factors of oxides, tellurides, selenides, and sulfides (Chen et al., 2016); (C) The workflow for screening new high-temperature oxides TEs (Peng et al., 2021); (D) The ZT values of MgTa2O6 at different temperatures with the carrier concentration (Peng et al., 2021).
The poor TE performance of oxides has become the principal stumbling block to their widespread use. However, recent discoveries in the field have produced oxide TE materials. Peng et al. (2021) employed the ALKEMIE (Wang G. et al., 2021) platform HTP calculation (see Figure 6C) to screen new high-temperature TE oxides. They discovered a new novel oxide (Mg, Ca) Ta2O6 with promising TE properties. CaTa2O6 exhibited a band structure similar to SrTiO3, and MgTa2O6 had a higher Seebeck coefficient than SrTiO3 or CaTa2O6. The maximum ZT of MgTa2O6 was greater than 1 at 1000 K (Figure 6D), which was higher than SrTiO3. These compounds were promising TE candidates for high-temperature function. Although the current HT method prediction of oxide performance is less than desirable, the accuracy of the method prediction, which is still under investigation, has potential for improvement.
Machine Learning
ML usually obtains factors associated with the target properties by evaluating previous experiments or calculated data; these factors are often called features, fingerprints, or descriptors, and can usually be represented by physical models (Zunger, 2018; Recatala-Gomez et al., 2020). ML can be classified into supervised learning and unsupervised learning. Supervised learning learns a model that maps an input (labeled data) to an output based on an existing dataset. The main types of supervised include regression and classification. Unsupervised learning finds previously unknown patterns of given inputs, and no labels are given to the learning algorithm, leaving it on its own to find a model in its input (Wang et al., 2019). Material databases are usually much smaller and sometimes more diverse than in other fields, such as image processing and industrial manufacturing (de Jong et al., 2016; Zhang and Ling, 2018). Therefore, small databases may affect the prediction accuracy more than expected. Active learning can be used to process small databases. Iterative supervised learning is referred to as an active learning model based on Bayesian optimization. Bayesian optimization is shown to significantly reduce the computational cost of discovering the optimal structure compared to finding an optimal structure by building a regression model (supervised learning) to predict the material properties (Bassman et al., 2018).
In recent years, ML methods, known for their data analysis capabilities, have been successfully applied in TE materials research. Iwasaki et al. (2019) applied an interpretable ML for spin-driven TE materials with anomalous Nernst effects, and discovered a novel spin-driven TE material with large thermopower. Oliynyk et al. (2016) used a random forest algorithm (Tin Kam, 1998) to predict Heusler compounds vs. non-Heusler compounds. To support research, ML algorithmic software to determine the best descriptors has also been proposed. The proposed software includes OMP (orthogonal matching pursuit) (Tropp and Gilbert, 2007) and commercial software EUREQA (Schmidt and Lipson, 2009), LASSO (least absolute shrinkage and selection operator) (Tibshirani, 1996; Ghiringhelli et al., 2015; Ghiringhelli et al., 2017), and SISSO (Sure Independence Screening and Sparsifying Operator) (Ouyang et al., 2018).
Sheng et al. (2020) employed active learning to predict the p-type power factors of diamond-like materials based on the original 158 entries cited previous work (Xi et al., 2018; Li et al., 2019). Then they created a search space of diamond-like materials with 482 entries by exhausting all possible combinations of the cations and anions mentioned above, as shown in Figure 7A. 324 uncalculated materials were used to build a model by ML algorithms. According to the model, two Sigle-model strategies (Top and Random) and one several-model strategy (Query by Committee, including Support Vector Regression (Smola and Schölkopf, 2004), Gradient Boosting Regression (Friedman, 2001), Random Forest Regression (Breiman, 2001), Adaptive Boosting Regression (Freund and Schapire, 1997), and Kernel Ridge Regression (Robert, 2014) ML model) strategies were carried out, as shown in Figure 7A. Top strategy selected the 15 candidates with the highest predicted PFs. Random strategy just recommended 15 candidates at random. Query by Committee strategy selected 15 candidates with large ambiguity, then measured the ambiguity by the variance of the 5 ML models. The recommended 15 candidates in each strategy were verified by HTP autoflow based on TransOpt. The unsatisfactory extrapolation should be added to the DFT database, the convergence conditions are Pearson R is > 0.9 or the number of iterations reaches the set maximum 10. Finally, they found that Query by Committee has the highest extrapolation accuracy; Binary pnictides, vacancy, and small atom-containing chalcogenides were predicted to have large PFs, as shown in Figure 7B. The active learning architecture updates the ML model through external verification, and uses as few verification samples as possible to improve the extrapolation ability of the ML model to the greatest extent. The application of active learning architecture is not only limited to TE materials, but also can be used in other functional materials, which is of great significance to accelerate the discovery of high-performance materials.
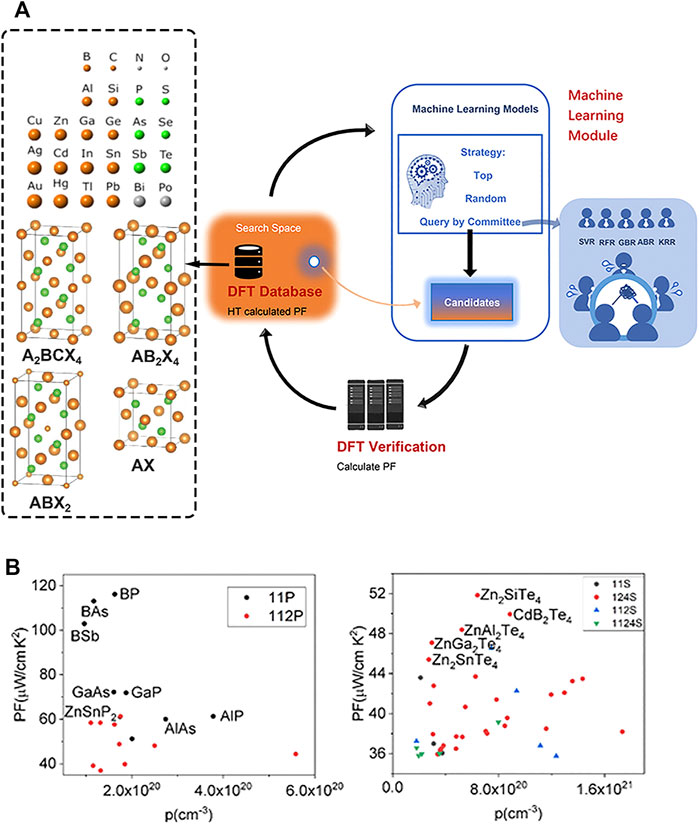
FIGURE 7. (A) The workflow of active learning loop; (B) The screened pnictides and chalcogenides with high PFs (Sheng et al., 2020).
The above description is based on the nature of the materials, which can be defined as digital data. However, ML image segmentation is more difficult than digital data. In the field of medical images, ML image segmentation has proven to be effective (Dolezal et al., 2021), but it has not been studied in the TE field. Interestingly, Sheng et al. (2021) first applied an active learning loop with a fully connected neural network aimed at fast and automated image segmentation. The researchers took promising ternary TE materials, using Cu-Sn-S as an example, and combined the HTP synthesis, HTP characterization, and HTP analysis, and post-processed 99 backscattered electron images of these compounds. Two ML image segmentation strategies were proposed. One strategy was to quickly and efficiently post-process the batch of Bayesian images based on supervised learning (Figure 8A), as active learning greatly reduced the workload of manual annotation, and Cu7Sn3S10 was identified to have good TE potential. The other strategy was unsupervised learning (Figure 8B), by which the unreported compound Cu1.6S was found to be a promising TE material.
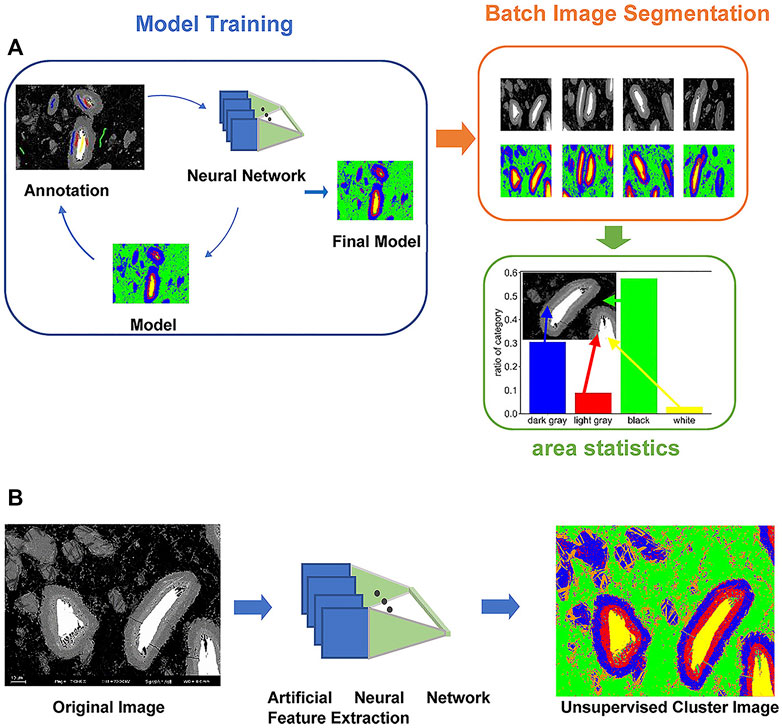
FIGURE 8. (A) Workflow of the supervised strategy; (B) Workflow of the unsupervised image segmentation strategy based on backscattered electron images of the nine-segment Cu-Sn-S bulk sample (Sheng et al., 2021).
Conclusion and Outlook
In this review, we have provided an overview of the current material genome approaches applied to TE materials. We have also summarized recent research into material genome approaches when applied to Half-Heuslers, diamond-like compounds, and oxides. Since the release of the Materials Genome Projects, emerging materials, such as Half-Heuslers and diamond-like compounds, have been extensively studied, with ZT values of 1.0–1.5 obtained. With the integration of ML and HTP calculations, the poor oxide TE materials also achieved high TE performance. Currently, the majority of electrical transport methods are based on the constant relaxation time approximation, and advancements in calculation methods could increase the reliability of the results. Active learning, which can be utilized for digital data and image segmentation, has had some successful cases in predicting TE material properties and discovering novel materials as the research develops.
With the growth of computer processing power, the speed of HTP calculation to obtain data on material properties has been accelerated, and the systematization, intelligence, and standardization of material databases have been comprehensively promoted. Data is the core resource for the development of materials science, and the combination between machine learning and databases has greatly improved the efficiency of screening new high-performance materials by discovering the relationship between the properties and performance of various materials. With the development of data sharing, it greatly reduces the repetitive resource investment and research and development. With the continuous breakthrough of technical means, the Material Genome Project is about to usher in the third breakthrough development, which is of great importance in the discovery of new materials. These material genome methods will be further improved in the future, with further achievements, discoveries, and optimization of functional materials expected.
Author Contributions
YC wrote the paper. YS and XL helped with writing and literature review. LLX and JY supervised the writing and gave technical advice. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by the National Key Research and Development Program of China (Nos. 2018YFB0703600), the Natural Science Foundation of China (Grant Nos. 52172216 and 92163212).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Armiento, R., Kozinsky, B., Fornari, M., and Ceder, G. (2011). Screening for High-Performance Piezoelectrics Using High-Throughput Density Functional Theory. Physical Review B 84(1). doi:10.1103/PhysRevB.84.014103
Bardeen, J., and Shockley, W. (1950). Deformation Potentials and Mobilities in Non-polar Crystals. Phys. Rev. 80 (1), 72–80. doi:10.1103/PhysRev.80.72
Bassman, L., Rajak, P., Kalia, R. K., Nakano, A., Sha, F., Sun, J., et al. (2018). Active Learning for Accelerated Design of Layered Materials. Npj Computational Materials 4(1). doi:10.1038/s41524-018-0129-0
Belsky, A., Hellenbrandt, M., Karen, V. L., and Luksch, P. (2002). New Developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in Support of Materials Research and Design. Acta Crystallogr. B 58 (Pt 3 Pt 1), 364–369. doi:10.1107/s0108768102006948
Beretta, D., Neophytou, N., Hodges, J. M., Kanatzidis, M. G., Narducci, D., Martin- Gonzalez, M., et al. (2019). Thermoelectrics: From History, a Window to the Future. Mater. Sci. Eng. R: Rep. 138. doi:10.1016/j.mser.2018.09.001
Brunin, G., Ricci, F., Ha, V.-A., Rignanese, G.-M., and Hautier, G. (2019). Transparent Conducting Materials Discovery Using High-Throughput Computing. npj Comput. Mater. 5 (1). doi:10.1038/s41524-019-0200-5
Calderon, C. E., Plata, J. J., Toher, C., Oses, C., Levy, O., Fornari, M., et al. (2015). The AFLOW Standard for High-Throughput Materials Science Calculations. Comput. Mater. Sci. 108, 233–238. doi:10.1016/j.commatsci.2015.07.019
Cao, W., Wang, Z., Miao, L., Shi, J., and Xiong, R. (2021). Thermoelectric Properties of Strained β-Cu2Se. ACS Appl. Mater. Inter. 13 (29), 34367–34373. doi:10.1021/acsami.1c08686
Capasso, F. (1987). Band-gap Engineering: from Physics and Materials to New Semiconductor Devices. Science 235 (4785), 172–176. doi:10.1126/science.235.4785.172
Carrete, J., Li, W., Mingo, N., Wang, S., and Curtarolo, S. (2014). Finding Unprecedentedly Low-Thermal-Conductivity Half-Heusler Semiconductors via High-Throughput Materials Modeling. Phys. Rev. X 4 (1). doi:10.1103/PhysRevX.4.011019
Chang, C., Wu, M., He, D., Pei, Y., Wu, C.-F., Wu, X., et al. (2018). 3D Charge and 2D Phonon Transports Leading to High Out-Of-Plane ZT in N-type SnSe Crystals. Science 360 (6390), 778–783. doi:10.1126/science.aaq1479
Chen, J., Wang, D., and Shuai, Z. (2012). First-Principles Predictions of Thermoelectric Figure of Merit for Organic Materials: Deformation Potential Approximation. J. Chem. Theor. Comput. 8 (9), 3338–3347. doi:10.1021/ct3004436
Chen, W., Pöhls, J.-H., Hautier, G., Broberg, D., Bajaj, S., Aydemir, U., et al. (2016). Understanding Thermoelectric Properties from High-Throughput Calculations: Trends, Insights, and Comparisons with experiment. J. Mater. Chem. C 4 (20), 4414–4426. doi:10.1039/c5tc04339e
Chen, Y., Hou, X., Ma, C., Dou, Y., and Wu, W. (2018). Review of Development Status of Bi2Te3-Based Semiconductor Thermoelectric Power Generation. Adv. Mater. Sci. Eng. 2018, 1–9. doi:10.1155/2018/1210562
Colón, Y. J., and Snurr, R. Q. (2014). High-throughput Computational Screening of Metal-Organic Frameworks. Chem. Soc. Rev. 43 (16), 5735–5749. doi:10.1039/c4cs00070f
Curtarolo, S., Hart, G. L. W., Nardelli, M. B., Mingo, N., Sanvito, S., and Levy, O. (2013). The High-Throughput Highway to Computational Materials Design. Nat. Mater 12 (3), 191–201. doi:10.1038/nmat3568
Curtarolo, S., Setyawan, W., Wang, S., Xue, J., Yang, K., Taylor, R. H., et al. (2012). AFLOWLIB.ORG: A Distributed Materials Properties Repository from High-Throughput Ab Initio Calculations. Comput. Mater. Sci. 58, 227–235. doi:10.1016/j.commatsci.2012.02.002
de Jong, M., Chen, W., Angsten, T., Jain, A., Notestine, R., Gamst, A., et al. (2015). Charting the Complete Elastic Properties of Inorganic Crystalline Compounds. Sci. Data 2, 150009. doi:10.1038/sdata.2015.9
de Jong, M., Chen, W., Notestine, R., Persson, K., Ceder, G., Jain, A., et al. (2016). A Statistical Learning Framework for Materials Science: Application to Elastic Moduli of K-Nary Inorganic Polycrystalline Compounds. Sci. Rep. 6, 34256. doi:10.1038/srep34256
Dima, A., Bhaskarla, S., Becker, C., Brady, M., Campbell, C., Dessauw, P., et al. (2016). Informatics Infrastructure for the Materials Genome Initiative. Jom 68 (8), 2053–2064. doi:10.1007/s11837-016-2000-4
Dismukes, J. P., Ekstrom, L., Steigmeier, E. F., Kudman, I., and Beers, D. S. (1964). Thermal and Electrical Properties of Heavily Doped Ge‐Si Alloys up to 1300°K. J. Appl. Phys. 35 (10), 2899–2907. doi:10.1063/1.1713126
Dolezal, J. M., Trzcinska, A., Liao, C.-Y., Kochanny, S., Blair, E., Agrawal, N., et al. (2021). Deep Learning Prediction of BRAF-RAS Gene Expression Signature Identifies Noninvasive Follicular Thyroid Neoplasms with Papillary-like Nuclear Features. Mod. Pathol. 34 (5), 862–874. doi:10.1038/s41379-020-00724-3
Draxl, C., and Scheffler, M. (2019). The NOMAD Laboratory: from Data Sharing to Artificial Intelligence. Journal Of Physics: Materials 2(3). doi:10.1088/2515-7639/ab13bb
Dyck, J. S., Chen, W., Uher, C., Chen, L., Tang, X., and Hirai, T. (2002). Thermoelectric Properties of Then-type Filled Skutterudite Ba0.3Co4Sb12 Doped with Ni. J. Appl. Phys. 91 (6), 3698–3705. doi:10.1063/1.1450036
Dylla, M. T., Dunn, A., Anand, S., Jain, A., and Snyder, G. J. (2020). Machine Learning Chemical Guidelines for Engineering Electronic Structures in Half-Heusler Thermoelectric Materials. Research (Wash D C) 2020, 6375171. doi:10.34133/2020/6375171
Everhart, W., and Newkirk, J. (2019). Mechanical Properties of Heusler Alloys. Heliyon 5 (5), e01578. doi:10.1016/j.heliyon.2019.e01578
Fang, T., Zhao, X., and Zhu, T. (2018). Band Structures and Transport Properties of High-Performance Half-Heusler Thermoelectric Materials by First Principles. Mater. (Basel) 11(5). doi:10.3390/ma11050847
Freund, Y., and Schapire, R. E. (1997). A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comp. Syst. Sci. 55 (1), 119–139. doi:10.1006/jcss.1997.1504
Friedman, J. H. (2001). Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 29 (5). doi:10.1214/aos/1013203451
Fu, C., Bai, S., Liu, Y., Tang, Y., Chen, L., Zhao, X., et al. (2015a). Realizing High Figure of merit in Heavy-Band P-type Half-Heusler Thermoelectric Materials. Nat. Commun. 6, 8144. doi:10.1038/ncomms9144
Fu, C., Wu, H., Liu, Y., He, J., Zhao, X., and Zhu, T. (2016). Enhancing the Figure of Merit of Heavy‐Band Thermoelectric Materials through Hierarchical Phonon Scattering. Adv. Sci. 3 (8), 1600035. doi:10.1002/advs.201600035
Fu, C., Zhu, T., Liu, Y., Xie, H., and Zhao, X. (2015b). Band Engineering of High Performance P-type FeNbSb Based Half-Heusler Thermoelectric Materials for Figure of merit zT > 1. Energy Environ. Sci. 8 (1), 216–220. doi:10.1039/c4ee03042g
Garrity, K. F. (2016). First Principles Search for N-type Oxide, Nitride, and Sulfide Thermoelectrics. Phys. Rev. B 94(4). doi:10.1103/PhysRevB.94.045122
Ghiringhelli, L. M., Vybiral, J., Ahmetcik, E., Ouyang, R., Levchenko, S. V., Draxl, C., et al. (2017). Learning Physical Descriptors for Materials Science by Compressed Sensing. New J. Phys. 19(2). doi:10.1088/1367-2630/aa57bf
Ghiringhelli, L. M., Vybiral, J., Levchenko, S. V., Draxl, C., and Scheffler, M. (2015). Big Data of Materials Science: Critical Role of the Descriptor. Phys. Rev. Lett. 114 (10), 105503. doi:10.1103/PhysRevLett.114.105503
Giannozzi, P., Andreussi, O., Brumme, T., Bunau, O., Buongiorno Nardelli, M., Calandra, M., et al. (2017). Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29 (46), 465901. doi:10.1088/1361-648X/aa8f79
Goldsmid, H. J., and Douglas, R. W. (1954). The Use of Semiconductors in Thermoelectric Refrigeration. Br. J. Appl. Phys. 5 (11), 386–390. doi:10.1088/0508-3443/5/11/303
Guo, S., Jia, T., and Zhang, Y. (2019). Electrical Property Dominated Promising Half-Heusler Thermoelectrics through High-Throughput Material Computations. J. Phys. Chem. C 123 (31), 18824–18833. doi:10.1021/acs.jpcc.9b04580
Hautier, G., Miglio, A., Ceder, G., Rignanese, G.-M., and Gonze, X. (2013). Identification and Design Principles of Low Hole Effective Mass P-type Transparent Conducting Oxides. Nat. Commun. 4(1). doi:10.1038/ncomms3292
He, R., Kim, H. S., Lan, Y., Wang, D., Chen, S., and Ren, Z. (2014). Investigating the Thermoelectric Properties of P-type Half-Heusler Hfx(ZrTi)1−xCoSb0.8Sn0.2 by Reducing Hf Concentration for Power Generation. RSC Adv. 4 (110), 64711–64716. doi:10.1039/c4ra14343d
Hu, L., Zhu, T., Liu, X., and Zhao, X. (2014). Point Defect Engineering of High-Performance Bismuth-Telluride-Based Thermoelectric Materials. Adv. Funct. Mater. 24 (33), 5211–5218. doi:10.1002/adfm.201400474
Iwasaki, Y., Sawada, R., Stanev, V., Ishida, M., Kirihara, A., Omori, Y., et al. (2019). Identification of Advanced Spin-Driven Thermoelectric Materials via Interpretable Machine Learning. Npj Computational Materials 5(1). doi:10.1038/s41524-019-0241-9
Jain, A., Hautier, G., Moore, C. J., Ping Ong, S., Fischer, C. C., Mueller, T., et al. (2011). A High-Throughput Infrastructure for Density Functional Theory Calculations. Comput. Mater. Sci. 50 (8), 2295–2310. doi:10.1016/j.commatsci.2011.02.023
Jain, A., Ong, S. P., Chen, W., Medasani, B., Qu, X., Kocher, M., et al. (2015). FireWorks: a Dynamic Workflow System Designed for High‐throughput Applications. Concurrency Computat.: Pract. Exper. 27 (17), 5037–5059. doi:10.1002/cpe.3505
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 1 (1). doi:10.1063/1.4812323
Kim, J. C., Moore, C. J., Kang, B., Hautier, G., Jain, A., and Ceder, G. (2011). Synthesis and Electrochemical Properties of Monoclinic LiMnBO3 as a Li Intercalation Material. J. Electrochem. Soc. 158(3). doi:10.1149/1.3536532
Kohn, W., and Sham, L. J. (1965). Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140 (4A), A1133–A1138. doi:10.1103/PhysRev.140.A1133
Körbel, S., Marques, M. A. L., and Botti, S. (2016). Stability and Electronic Properties of New Inorganic Perovskites from High-Throughput Ab Initio Calculations. J. Mater. Chem. C 4 (15), 3157–3167. doi:10.1039/c5tc04172d
Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169
Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/PhysRevB.59.1758
Kuznetsov, V. L., Kuznetsova, L. A., Kaliazin, A. E., and Rowe, D. M. (2000). Preparation and Thermoelectric Properties of A8IIB16IIIB30IV Clathrate Compounds. J. Appl. Phys. 87 (11), 7871–7875. doi:10.1063/1.373469
Larson, P., Mahanti, S. D., Sportouch, S., and Kanatzidis, M. G. (1999). Electronic Structure of Rare-Earth Nickel Pnictides: Narrow-gap Thermoelectric Materials. Phys. Rev. B 59 (24), 15660–15668. doi:10.1103/PhysRevB.59.15660
Li, H., Tang, X., Zhang, Q., and Uher, C. (2009). High Performance InxCeyCo4Sb12 Thermoelectric Materials with In Situ Forming Nanostructured InSb Phase. Appl. Phys. Lett. 94(10). doi:10.1063/1.3099804
Li, M.-Y., Ma, Z., Li, B., Wu, X.-T., Lin, H., and Zhu, Q.-L. (2020). HgCuPS4: An Exceptional Infrared Nonlinear Optical Material with Defect Diamond-like Structure. Chem. Mater. 32 (10), 4331–4339. doi:10.1021/acs.chemmater.0c01258
Li, R., Li, X., Xi, L., Yang, J., Singh, D. J., and Zhang, W. (2019). High-Throughput Screening for Advanced Thermoelectric Materials: Diamond-Like ABX2 Compounds. ACS Appl. Mater. Inter. 11 (28), 24859–24866. doi:10.1021/acsami.9b01196
Liu, M.-L., Chen, I.-W., Huang, F.-Q., and Chen, L.-D. (2009a). Improved Thermoelectric Properties of Cu-Doped Quaternary Chalcogenides of Cu2CdSnSe4. Adv. Mater. 21 (37), 3808–3812. doi:10.1002/adma.200900409
Liu, M.-L., Huang, F.-Q., Chen, L.-D., and Chen, I. W. (2009b). A Wide-Band-gap P-type Thermoelectric Material Based on Quaternary Chalcogenides of Cu2ZnSnQ4 (Q=S,Se). Appl. Phys. Lett. 94(20). doi:10.1063/1.3130718
Liu, R., Qin, Y., Cheng, N., Zhang, J., Shi, X., Grin, Y., et al. (2016a). Thermoelectric Performance of Cu1−x−δAgxInTe2 diamond-like Materials with a Pseudocubic crystal Structure. Inorg. Chem. Front. 3 (9), 1167–1177. doi:10.1039/c6qi00162a
Liu, R., Xi, L., Liu, H., Shi, X., Zhang, W., and Chen, L. (2012). Ternary Compound CuInTe2: a Promising Thermoelectric Material with diamond-like Structure. Chem. Commun. 48 (32), 3818–3820. doi:10.1039/c2cc30318c
Liu, T.-H., Zhou, J., Liao, B., Singh, D. J., and Chen, G. (2017). First-principles Mode-By-Mode Analysis for Electron-Phonon Scattering Channels and Mean Free Path Spectra in GaAs. Phys. Rev. B 95 (7). doi:10.1103/PhysRevB.95.075206
Liu, Y., Zhou, M., and He, J. (2016b). Towards Higher Thermoelectric Performance of Bi2Te3 via Defect Engineering. Scripta Materialia 111, 39–43. doi:10.1016/j.scriptamat.2015.06.031
Mamur, H., Bhuiyan, M. R. A., Korkmaz, F., and Nil, M. (2018). A Review on Bismuth telluride (Bi2Te3) Nanostructure for Thermoelectric Applications. Renew. Sust. Energ. Rev. 82, 4159–4169. doi:10.1016/j.rser.2017.10.112
Muller, D. A., Nakagawa, N., Ohtomo, A., Grazul, J. L., and Hwang, H. Y. (2004). Atomic-scale Imaging of Nanoengineered Oxygen Vacancy Profiles in SrTiO3. Nature 430 (7000), 657–661. doi:10.1038/nature02756
Nkwachukwu, O. V., and Arotiba, O. A. (2021). Perovskite Oxide-Based Materials for Photocatalytic and Photoelectrocatalytic Treatment of Water. Front. Chem. 9, 634630. doi:10.3389/fchem.2021.634630
Noffsinger, J., Giustino, F., Malone, B. D., Park, C.-H., Louie, S. G., and Cohen, M. L. (2010). EPW: A Program for Calculating the Electron-Phonon Coupling Using Maximally Localized Wannier Functions. Comp. Phys. Commun. 181 (12), 2140–2148. doi:10.1016/j.cpc.2010.08.027
Nunna, R., Qiu, P., Yin, M., Chen, H., Hanus, R., Song, Q., et al. (2017). Ultrahigh Thermoelectric Performance in Cu2Se-Based Hybrid Materials with Highly Dispersed Molecular CNTs. Energ. Environ. Sci. 10 (9), 1928–1935. doi:10.1039/c7ee01737e
Ohtaki, M., Araki, K., and Yamamoto, K. (2009). High Thermoelectric Performance of Dually Doped ZnO Ceramics. J. Elec Materi 38 (7), 1234–1238. doi:10.1007/s11664-009-0816-1
Ohtaki, M., Tsubota, T., Eguchi, K., and Arai, H. (1996). High‐temperature Thermoelectric Properties of (Zn1−xAlx)O. J. Appl. Phys. 79 (3), 1816–1818. doi:10.1063/1.360976
Oliynyk, A. O., Antono, E., Sparks, T. D., Ghadbeigi, L., Gaultois, M. W., Meredig, B., et al. (2016). High-Throughput Machine-Learning-Driven Synthesis of Full-Heusler Compounds. Chem. Mater. 28 (20), 7324–7331. doi:10.1021/acs.chemmater.6b02724
Olvera, A. A., Moroz, N. A., Sahoo, P., Ren, P., Bailey, T. P., Page, A. A., et al. (2017). Partial Indium Solubility Induces Chemical Stability and Colossal Thermoelectric Figure of merit in Cu2Se. Energ. Environ. Sci. 10 (7), 1668–1676. doi:10.1039/c7ee01193h
Ong, K. P., Singh, D. J., and Wu, P. (2011). Analysis of the Thermoelectric Properties of N-type ZnO. Phys. Rev. B 83 (11). doi:10.1103/PhysRevB.83.115110
Ouyang, R., Curtarolo, S., Ahmetcik, E., Scheffler, M., and Ghiringhelli, L. M. (2018). SISSO: A Compressed-Sensing Method for Identifying the Best Low-Dimensional Descriptor in an Immensity of Offered Candidates. Phys. Rev. Mater. 2 (8). doi:10.1103/PhysRevMaterials.2.083802
Pang, H.-J., Yu, H., Chen, L.-C., Fu, C.-G., Zhu, T.-J., and Chen, X.-J. (2019). Pressure Tuning of Thermoelectric Performance in FeNbSb. J. Alloys Comp. 805, 1224–1230. doi:10.1016/j.jallcom.2019.07.165
Pei, Y., LaLonde, A., Iwanaga, S., and Snyder, G. J. (2011). High Thermoelectric Figure of merit in Heavy Hole Dominated PbTe. Energy Environ. Sci. 4(6). doi:10.1039/c0ee00456a
Pei, Y., Wang, H., and Snyder, G. J. (2012). Band Engineering of Thermoelectric Materials. Adv. Mater. 24 (46), 6125–6135. doi:10.1002/adma.201202919
Peng, L., Miao, N., Wang, G., Zhou, J., Elliott, S. R., and Sun, Z. (2021). Novel Metal Oxides with Promising High-Temperature Thermoelectric Performance. J. Mater. Chem. C. doi:10.1039/d1tc02404c
Petsagkourakis, I., Tybrandt, K., Crispin, X., Ohkubo, I., Satoh, N., and Mori, T. (2018). Thermoelectric Materials and Applications for Energy Harvesting Power Generation. Sci. Tech. Adv. Mater. 19 (1), 836–862. doi:10.1080/14686996.2018.1530938
Plirdpring, T., Kurosaki, K., Kosuga, A., Day, T., Firdosy, S., Ravi, V., et al. (2012). Chalcopyrite CuGaTe(2): Chalcopyrite CuGaTe2: A High-Efficiency Bulk Thermoelectric Material. Adv. Mater. 24 (27), 3622–3626. doi:10.1002/adma.201200732
Recatala-Gomez, J., Suwardi, A., Nandhakumar, I., Abutaha, A., and Hippalgaonkar, K. (2020). Toward Accelerated Thermoelectric Materials and Process Discovery. ACS Appl. Energ. Mater. 3 (3), 2240–2257. doi:10.1021/acsaem.9b02222
Robert, C. (2014). Machine Learning, a Probabilistic Perspective. Chance 27 (2), 62–63. doi:10.1080/09332480.2014.914768
Rogl, G., Grytsiv, A., Yubuta, K., Puchegger, S., Bauer, E., Raju, C., et al. (2015). In-doped Multifilled N-type Skutterudites with ZT= 1.8. Acta Materialia 95, 201–211. doi:10.1016/j.actamat.2015.05.024
Saiga, Y., Du, B., Deng, S. K., Kajisa, K., and Takabatake, T. (2012). Thermoelectric Properties of Type-VIII Clathrate Ba8Ga16Sn30 Doped with Cu. J. Alloys Comp. 537, 303–307. doi:10.1016/j.jallcom.2012.05.049
Sawada, K., and Nakajima, T. (2018). High-throughput Screening of Perovskite Oxynitride and Oxide Materials for Visible-Light Photocatalysis. APL Mater. 6 (10). doi:10.1063/1.5041784
Schmidt, M., and Lipson, H. (2009). Distilling Free-form Natural Laws from Experimental Data. Science 324 (5923), 81–85. doi:10.1126/science.1165893
Shakouri, A. (2011). Recent Developments in Semiconductor Thermoelectric Physics and Materials. Annu. Rev. Mater. Res. 41 (1), 399–431. doi:10.1146/annurev-matsci-062910-100445
Shen, Q., Chen, L., Goto, T., Hirai, T., Yang, J., Meisner, G. P., et al. (2001). Effects of Partial Substitution of Ni by Pd on the Thermoelectric Properties of ZrNiSn-Based Half-Heusler Compounds. Appl. Phys. Lett. 79 (25), 4165–4167. doi:10.1063/1.1425459
Sheng, Y., Deng, T., Qiu, P., Shi, X., Xi, J., Han, Y., et al. (2021). Accelerating the Discovery of Cu-Sn-S Thermoelectric Compounds via High-Throughput Synthesis, Characterization, and Machine Learning-Assisted Image Analysis. Chem. Mater. 33 (17), 6918–6924. doi:10.1021/acs.chemmater.1c01856
Sheng, Y., Wu, Y., Yang, J., Lu, W., Villars, P., and Zhang, W. (2020). Active Learning for the Power Factor Prediction in diamond-like Thermoelectric Materials. npj Comput. Mater. 6 (1), 171. doi:10.1038/s41524-020-00439-8
Shi, X., Kong, H., Li, C. P., Uher, C., Yang, J., Salvador, J. R., et al. (2008). Low thermal Conductivity and High Thermoelectric Figure of merit in N-type BaxYbyCo4Sb12 Double-Filled Skutterudites. Appl. Phys. Lett. 92(18). doi:10.1063/1.2920210
Slack, G. A. (1973). Nonmetallic Crystals with High thermal Conductivity. J. Phys. Chem. Sol. 34 (2), 321–335. doi:10.1016/0022-3697(73)90092-9
Smola, A. J., and Schölkopf, B. (2004). A Tutorial on Support Vector Regression. Stat. Comput. 14 (3), 199–222. doi:10.1023/b:stco.0000035301.49549.88
Tan, G., Zhao, L.-D., and Kanatzidis, M. G. (2016). Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem. Rev. 116 (19), 12123–12149. doi:10.1021/acs.chemrev.6b00255
Tavassoli, A., Failamani, F., Grytsiv, A., Rogl, G., Heinrich, P., Müller, H., et al. (2017). On the Half-Heusler Compounds Nb1-x{Ti,Zr,Hf}xFeSb: Phase Relations, Thermoelectric Properties at Low and High Temperature, and Mechanical Properties. Acta Materialia 135, 263–276. doi:10.1016/j.actamat.2017.06.011
Taylor, R. H., Rose, F., Toher, C., Levy, O., Yang, K., Buongiorno Nardelli, M., et al. (2014). A RESTful API for Exchanging Materials Data in the AFLOWLIB.Org Consortium. Comput. Mater. Sci. 93, 178–192. doi:10.1016/j.commatsci.2014.05.014
Terasaki, I., Sasago, Y., and Uchinokura, K. (1997). Large Thermoelectric Power inNaCo2O4single Crystals. Phys. Rev. B 56 (20), R12685–R12687. doi:10.1103/PhysRevB.56.R12685
Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodological) 58 (1), 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x
Tin Kam Ho, H. (1998). The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Machine Intell. 20 (8), 832–844. doi:10.1109/34.709601
Togo, A., and Tanaka, I. (2015). First Principles Phonon Calculations in Materials Science. Scripta Materialia 108, 1–5. doi:10.1016/j.scriptamat.2015.07.021
Toher, C., Plata, J. J., Levy, O., de Jong, M., Asta, M., Nardelli, M. B., et al. (2014). High-throughput Computational Screening of thermal Conductivity, Debye Temperature, and Grüneisen Parameter Using a Quasiharmonic Debye Model. Physical Review B 90(17). doi:10.1103/PhysRevB.90.174107
Tropp, J. A., and Gilbert, A. C. (2007). Signal Recovery from Random Measurements via Orthogonal Matching Pursuit. IEEE Trans. Inform. Theor. 53 (12), 4655–4666. doi:10.1109/tit.2007.909108
Uher, C., Yang, J., Hu, S., Morelli, D. T., and Meisner, G. P. (1999). Transport Properties of Pure and dopedMNiSn (M=Zr, Hf). Phys. Rev. B 59 (13), 8615–8621. doi:10.1103/PhysRevB.59.8615
Vulchev, V., Vassilev, L., Harizanova, S., Khristov, M., Zhecheva, E., and Stoyanova, R. (2012). Improving of the Thermoelectric Efficiency of LaCoO3 by Double Substitution with Nickel and Iron. J. Phys. Chem. C 116 (25), 13507–13515. doi:10.1021/jp3021408
Wang, F. Q., Zhang, S., Yu, J., and Wang, Q. (2015). Thermoelectric Properties of Single-Layered SnSe Sheet. Nanoscale 7 (38), 15962–15970. doi:10.1039/c5nr03813h
Wang, G., Peng, L., Li, K., Zhu, L., Zhou, J., Miao, N., et al. (2021a). ALKEMIE: An Intelligent Computational Platform for Accelerating Materials Discovery and Design. Comput. Mater. Sci. 186. doi:10.1016/j.commatsci.2020.110064
Wang, H. C., Wang, C. L., Su, W. B., Liu, J., Sun, Y., Peng, H., et al. (2011a). Doping Effect of La and Dy on the Thermoelectric Properties of SrTiO3. J. Am. Ceram. Soc. 94 (3), 838–842. doi:10.1111/j.1551-2916.2010.04185.x
Wang, J., Zhang, B.-Y., Kang, H.-J., Li, Y., Yaer, X., Li, J.-F., et al. (2017a). Record High Thermoelectric Performance in Bulk SrTiO3 via Nano-Scale Modulation Doping. Nano Energy 35, 387–395. doi:10.1016/j.nanoen.2017.04.003
Wang, N., Li, M., Xiao, H., Gao, Z., Liu, Z., Zu, X., et al. (2021b). Band Degeneracy Enhanced Thermoelectric Performance in Layered Oxyselenides by First-Principles Calculations. npj Comput. Mater. 7 (1). doi:10.1038/s41524-020-00476-3
Wang, S., Wang, Z., Setyawan, W., Mingo, N., and Curtarolo, S. (2011b). Assessing the Thermoelectric Properties of Sintered Compounds via High-Throughput Ab-InitioCalculations. Phys. Rev. X 1 (2). doi:10.1103/PhysRevX.1.021012
Wang, T., Zhang, C., Snoussi, H., and Zhang, G. (2019). Machine Learning Approaches for Thermoelectric Materials Research. Advanced Functional Materials 30(5). doi:10.1002/adfm.201906041
Wang, X. W., Lee, H., Lan, Y. C., Zhu, G. H., Joshi, G., Wang, D. Z., et al. (2008). Enhanced Thermoelectric Figure of merit in Nanostructured N-type Silicon Germanium Bulk alloy. Appl. Phys. Lett. 93 (19). doi:10.1063/1.3027060
Wang, Y., Sui, Y., Fan, H., Wang, X., Su, Y., Su, W., et al. (2009). High Temperature Thermoelectric Response of Electron-Doped CaMnO3. Chem. Mater. 21 (19), 4653–4660. doi:10.1021/cm901766y
Wang, Y., Zhang, W., Chen, L., Shi, S., and Liu, J. (2017b). Quantitative Description on Structure-Property Relationships of Li-Ion Battery Materials for High-Throughput Computations. Sci. Tech. Adv. Mater. 18 (1), 134–146. doi:10.1080/14686996.2016.1277503
Xi, L., Pan, S., Li, X., Xu, Y., Ni, J., Sun, X., et al. (2018). Discovery of High-Performance Thermoelectric Chalcogenides through Reliable High-Throughput Material Screening. J. Am. Chem. Soc. 140 (34), 10785–10793. doi:10.1021/jacs.8b04704
Xiao, Y., and Zhao, L.-D. (2018). Charge and Phonon Transport in PbTe-Based Thermoelectric Materials. npj Quan. Mater. 3 (1). doi:10.1038/s41535-018-0127-y
Xie, H., Hao, S., Bailey, T. P., Cai, S., Zhang, Y., Slade, T. J., et al. (2021). Ultralow Thermal Conductivity in Diamondoid Structures and High Thermoelectric Performance in (Cu1-xAgx)(In1-yGay)Te2. J. Am. Chem. Soc. 143 (15), 5978–5989. doi:10.1021/jacs.1c01801
Xiong, Q., Xie, D., Wang, H., Wei, Y., Wang, G., Wang, G., et al. (2021). Colloidal Synthesis of diamond-like Compound Cu2SnTe3 and Thermoelectric Properties of (Cu0.96InTe2)1−x(Cu2SnTe3)x Solid Solutions. Chem. Eng. J. 422. doi:10.1016/j.cej.2021.129985
Yan, J., Gorai, P., Ortiz, B., Miller, S., Barnett, S. A., Mason, T., et al. (2015). Material Descriptors for Predicting Thermoelectric Performance. Energ. Environ. Sci. 8 (3), 983–994. doi:10.1039/c4ee03157a
Yang, C., Huang, F., Wu, L., and Xu, K. (2011). New Stannite-like P-type Thermoelectric Material Cu3SbSe4. J. Phys. D: Appl. Phys. 44 (29). doi:10.1088/0022-3727/44/29/295404
Yang, J., Li, H., Wu, T., Zhang, W., Chen, L., and Yang, J. (2008). Evaluation of Half-Heusler Compounds as Thermoelectric Materials Based on the Calculated Electrical Transport Properties. Adv. Funct. Mater. 18 (19), 2880–2888. doi:10.1002/adfm.200701369
Yang, J., Xi, L., Qiu, W., Wu, L., Shi, X., Chen, L., et al. (2016). On the Tuning of Electrical and thermal Transport in Thermoelectrics: an Integrated Theory-experiment Perspective. Npj Comput. Mater. 2 (1), 15015. doi:10.1038/npjcompumats.2015.15
Yang, X., Wang, Z., Zhao, X., Song, J., Yu, C., Zhou, J., et al. (2018). MatCloud, a High-Throughput Computational Materials Infrastructure: Present, Future Visions, and Challenges. Chin. Phys. B 27 (11). doi:10.1088/1674-1056/27/11/110301
Yao, M., Wang, Y., Li, X., Sheng, Y., Huo, H., Xi, L., et al. (2021). Materials Informatics Platform with Three Dimensional Structures, Workflow and Thermoelectric Applications. Sci. Data 8 (1), 236. doi:10.1038/s41597-021-01022-6
Yu, J., Fu, C., Liu, Y., Xia, K., Aydemir, U., Chasapis, T. C., et al. (2017). Unique Role of Refractory Ta Alloying in Enhancing the Figure of Merit of NbFeSb Thermoelectric Materials. Adv. Energ. Mater. 8 (1). doi:10.1002/aenm.201701313
Yu, L., and Zunger, A. (2012). Identification of Potential Photovoltaic Absorbers Based on First-Principles Spectroscopic Screening of Materials. Phys. Rev. Lett. 108 (6), 068701. doi:10.1103/PhysRevLett.108.068701
Zhang, J., Liu, R., Cheng, N., Zhang, Y., Yang, J., Uher, C., et al. (2014). High-performance Pseudocubic Thermoelectric Materials from Non-cubic Chalcopyrite Compounds. Adv. Mater. 26 (23), 3848–3853. doi:10.1002/adma.201400058
Zhang, J., Wu, D., He, D., Feng, D., Yin, M., Qin, X., et al. (2017). Extraordinary Thermoelectric Performance Realized in N-type PbTe through Multiphase Nanostructure Engineering. Adv. Mater. 29 (39). doi:10.1002/adma.201703148
Zhang, J., Zhang, C., Zhu, T., Yan, Y., Su, X., and Tang, X. (2021). Mechanical Properties and Thermal Stability of the High-Thermoelectric-Performance Cu2Se Compound. ACS Appl. Mater. Inter. 13 (38), 45736–45743. doi:10.1021/acsami.1c12533
Zhang, Y., and Ling, C. (2018). A Strategy to Apply Machine Learning to Small Datasets in Materials Science. npj Comput. Mater. 4 (1). doi:10.1038/s41524-018-0081-z
Zhao, C., Li, Z., Fan, T., Xiao, C., and Xie, Y. (2020). Defects Engineering with Multiple Dimensions in Thermoelectric Materials. Research (Wash D C) 2020, 9652749. doi:10.34133/2020/9652749
Zhao, L.-D., Chang, C., Tan, G., and Kanatzidis, M. G. (2016). SnSe: a Remarkable New Thermoelectric Material. Energ. Environ. Sci. 9 (10), 3044–3060. doi:10.1039/c6ee01755j
Zheng, Y., Slade, T. J., Hu, L., Tan, X. Y., Luo, Y., Luo, Z.-Z., et al. (2021). Defect Engineering in Thermoelectric Materials: what Have We Learned? Chem. Soc. Rev. 50 (16), 9022–9054. doi:10.1039/d1cs00347j
Zhu, H., Mao, J., Li, Y., Sun, J., Wang, Y., Zhu, Q., et al. (2019). Discovery of TaFeSb-Based Half-Heuslers with High Thermoelectric Performance. Nat. Commun. 10 (1), 270. doi:10.1038/s41467-018-08223-5
Zhu, T., Hu, L., Zhao, X., and He, J. (2016). New Insights into Intrinsic Point Defects in V 2 VI 3 Thermoelectric Materials. Adv. Sci. 3 (7), 1600004. doi:10.1002/advs.201600004
Zornoza, B., Tellez, C., Coronas, J., Gascon, J., and Kapteijn, F. (2013). Metal Organic Framework Based Mixed Matrix Membranes: An Increasingly Important Field of Research with a Large Application Potential. Microporous Mesoporous Mater. 166, 67–78. doi:10.1016/j.micromeso.2012.03.012
Keywords: materials genome, high-throughput calculations, machine learning, thermoelectrics, first-principles calculations
Citation: Cao Y, Sheng Y, Li X, Xi L and Yang J (2022) Application of Materials Genome Methods in Thermoelectrics. Front. Mater. 9:861817. doi: 10.3389/fmats.2022.861817
Received: 25 January 2022; Accepted: 14 February 2022;
Published: 25 February 2022.
Edited by:
Douglas Soares Galvao, State University of Campinas, BrazilCopyright © 2022 Cao, Sheng, Li, Xi and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lili Xi, bGlseXhpQHQuc2h1LmVkdS5jbg==
 Yan Cao
Yan Cao Ye Sheng1
Ye Sheng1 Jiong Yang
Jiong Yang