Effect of Grain Structure on the Failure Mechanism of Cu/Cu3Sn Investigated Via Molecular Dynamic Simulations

The grain structure has a great influence on the mechanical reliability of miniaturized interconnect circuits. Under the working conditions, Cu₃Sn will be the main intermetallic compound that forms during electromigration and the thermal ageing process, which can easily induce cracks between Cu₃Sn and the copper pad. This paper investigated the effect of the Cu grain structure on the Cu₃Sn/Cu interface reliability via molecular dynamic simulations. Single-crystal Cu, twin-crystal Cu, and polycrystalline Cu models were implemented to form the interface structure, and uniaxial tension simulations were performed at strain rates of 0.01, 0.1, and 0.5% ps⁻¹ to evaluate the interfacial strength and interface failure mechanism. Results show that the polycrystalline Cu models always exhibits a lower degree of stress and shows a great ductile character. The existence of twin grain boundaries makes Cu layer more stable, and their failure processes are dominated by stair-rod type dislocations with a Burgers vector of 1/6 [110] instead of Shockley dislocations with a Burgers vector of 1/6 [112], which induce their interface models fail in Cu₃Sn layer near the interface. The strain rate dependence mechanical character of both interface and grains would be the main reason of phenomenon for the difference failure character affected by grain structure and strain rate.

Introduction

The increasing demand of electronic products requires highly miniaturized integrated circuits (ICs). These ICs cause the chip integration density to grow sharply and lead to a higher current density in the solder joints, which will induce the phenomenon of electromigration (EM) and an enhanced formation of intermetallic compound (IMCs) in the solder joints. For the widely used Sn-Ag-Cu (SAC) series of solder, Cu atoms in Cu pads and Sn atoms in SAC solder joints may combine together to form layer-shaped IMCs (mainly Cu₃Sn and Cu₆Sn₅) during EM and the thermal ageing process. As miniaturized solder joints contain only several large bulk grains, the performance of the solder grains and IMCs has a great effect on the solder reliability, which has attracted great attention from the research community (Hau-Riege and Thompson, 2001). At the working temperature and current density, the dominant failure mode under EM is the mechanical-loading-induced crack initiation and extension, and experimental results have shown that the most common IMC is Cu₃Sn under such working conditions (Zhang et al., 2015). Cu₃Sn has great prospect in power electronic device applications due to its high melting temperature (Liu et al., 2020), and the solder joints with the interfacial structure of Cu/Cu₃Sn/Cu is thought to be a substitute due to the ability of servicing under high temperature (Yao et al., 2017). While for this kind of structure, cracks can easily form between Cu₃Sn and Cu (Tseng et al., 2010), or within Cu₃Sn (Yao et al., 2019), which affects the reliability of the solder joints. Thus, it is important to investigate the mechanical reliability of the Cu₃Sn/Cu interface.

Due to IC manufacturing, the Cu pad always contains heterogeneous bulk single grains or polycrystalline Cu (Hu et al., 2007), and the mechanical properties vary depending on the grain structure. It is possible to control the grain orientation and distribution in crystalline materials (Todaro et al., 2020) for the purpose of improving the reliability of packaging. Works about mechanical properties of Cu and Cu3Sn with different combination of grain structure and orientation have been reported by experimental research separately (Yang et al., 2017; Juang et al., 2021; Shen et al., 2022), both of them show the great difference between them. while the manner in which the grain structure could affect the reliability of the interface between the pad and the solder joints is an important research topic in advanced electronic packaging (Zhang et al., 2018). The development of the molecular dynamics (MD) theory has enabled the microscale simulation of phenomena regarding the influence of the degree of crystallinity on the interface reliability (Zhang and Asle Zaeem, 2018), and uniaxial tension simulations can be used to evaluate the mechanical properties of materials (Cheng et al., 2012; Mackenchery et al., 2016). In this work, the mechanical reliability of the Cu₃Sn/Cu interface is investigated through MD tension simulations.

The significant differences in the mechanical properties between single crystal and polycrystalline Cu (Liu et al., 2005; Qiu et al., 2017) affect the reliability of the Cu₃Sn/Cu interface considerably. On the other hand, nanotwinned Cu has many unique mechanical characteristics, which can have a dramatic effect on the solder reliability (Fu et al., 2018). Furthermore, the (111) grain orientation has been proved to be beneficial in improving EM (Cheng et al., 2018). Hence, models based on single-grain Cu, twin-crystal Cu with (111) twin grain interface, and polycrystalline Cu were implemented and compared. Additionally, three different strain rates were applied to the interface models to evaluate the interface strength and strain rate response under uniaxial tension. Finally, the failure mechanism of the Cu₃Sn/Cu interface structure was analyzed from an atomic perspective.

Simulation Details

The MD simulations were performed using a Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) (Plimpton, 1995). The modified embedded atom method (MEAM) interatomic potential was used to describe the interactions between the Cu and Sn atoms. The MEAM interatomic potential has obtained good results in many fields (Xu and Kim, 2019; Attarian and Xiao, 2022). The parameters of the MEAM potential and the lattice structure of Cu₃Sn and Cu can be found in Refs. (Baskes et al., 1994; Aguilar et al., 2000; Cheng et al., 2012). and are shown in Table 1.

TABLE 1

TABLE 1. Parameters of the MEAM potential used in the LAMMPS.

The crystal structure of Cu₃Sn was reported by Watanabe et al. (Watanabe et al., 1983) that it is a hexagonal close-packed Cu₃Ti-type transition-metal IMC. Villars and Calvet (Villars and Calvet, 1985) gave the complete description of the atomic positions within the crystal structure of Cu₃Sn. its structure could be treated as a supercell consisted by eight atoms with orthorhombic symmetry (space group Pmmn), which was proved to have a better measurement from crystallographic studies (Pang et al., 2008). In order to validate the accuracy of MEAM interatomic potentials used for the Cu₃Sn structure, the orthorhombic elastic constants of Cu₃Sn was calculated by applying a strain field to the simulation cell, as shown in Table 2. It can be seen our MD results are in good agreement with the ab initio calculations.

TABLE 2

TABLE 2. The isotropic elastic constants of Cu₃Sn polycrystalline IMC by this work, ab inito calculations, and with long period lattice structure (unit: GPa).

For the problems discussed in this domain, to better describe the different grain structures of Cu, single-crystal Cu, twin-crystal Cu, and polycrystalline Cu as the pad layer were investigated. Two types of twin copper models with one twin grain boundary (has two grains) and four twin grain boundaries (has five grains) were built with the (111) surface as the twin plane to study the effect of grain size. Furthermore, the polycrystalline Cu model contained 10 grains with random orientation. Both of these four types of Cu combine with single-crystal Cu₃Sn to form the interface structure for the axial tension simulations; the interface consisted of the (001) surface of Cu₃Sn combined with the (112) surface of single-crystal Cu and twin-crystal Cu. The total size of the interface structure built for the MD simulations was 110.58 × 90.6 × 180.72 Å with the same heights of Cu and Cu₃Sn, as shown in Figure 1.

FIGURE 1

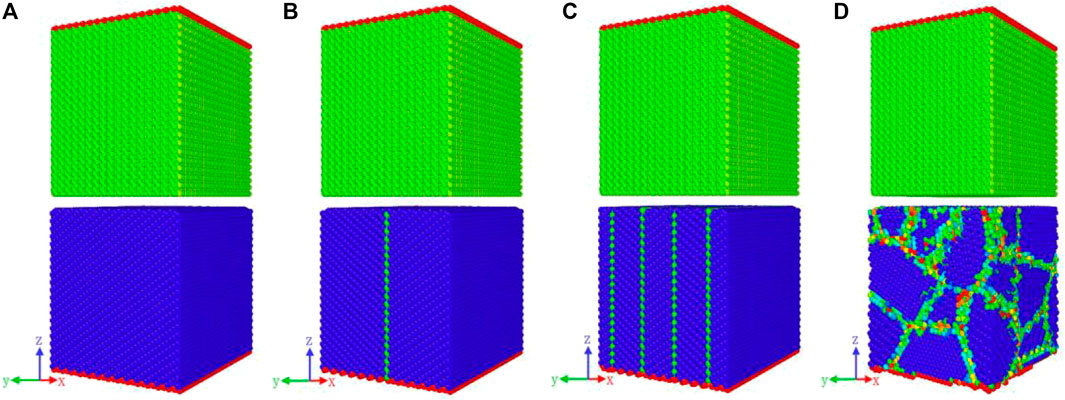
FIGURE 1. Molecular models of the interface between Cu₃Sn and Cu with different grain structures: (A) single-crystal Cu, (B) twin-crystal Cu with one twin grain boundary, (C) twin-crystal Cu with four twin grain boundaries, and (D) polycrystalline Cu.

For the axial tension simulations performed in this study, asymmetric boundary conditions were used in each direction. The Cu₃Sn and Cu layers were placed next to each other at a distance of 3 Å, and all structures were then equilibrated to obtain the balanced models, structures were preheated from 100 to 300 K for 50 ps under the condition of NVE (constant Number of atoms, Volume and Energy) with a berendsen thermostat. After that 34.6 Å for both edges along z-axial of models were set as rigid bodies; then, uniform velocities at strain rates of 0.01, 0.1, and 0.5% ps⁻¹ were applied to the rigid region of Cu₃Sn along the direction perpendicular to the interface. Virial stress was used to calculate the tensile stress at the atomic level according to (Spearot et al., 2004; Dandekar and Shin, 2011), which could be of great help to get the von Mises stress as introduced in (Rahmati et al., 2020). The expression of virial stress is defined as (Spearot et al., 2004):

${\mathit{\Pi }}_{\alpha \beta }^i=\frac{1}{{\mathit{\Omega }}^i}\left[\frac{1}{2}{\displaystyle \sum _{j\ne i}\left(\frac{1}{r^{ij}}\frac{\partial U}{\partial r}\right)r_{\alpha }^{ij}{r}_{\beta }^{ij}}-m^i{v}_{\alpha }^i{v}_{\beta }^i\right],(1)$

With

${\sigma }_{\alpha \beta }=\frac{1}{N^{\ast }}{\displaystyle \sum _i^{N^{\ast }}{\mathit{\Pi }}_{\alpha \beta }^i},(2)$

Where the first term within the square brackets in Eq. 1 accounts for the force between two atoms, as a function of the potential energy U, and the second term accounts for the kinetic contribution to the virial stress. In the above equations, $m^i$, $v_{\alpha }^i$ and $v_{\beta }^i$ are the mass and velocity of the ith atom in the α and β directions respectively; $r_{\alpha }^{ij}$ and $r_{\beta }^{ij}$ are α and β components of total distance $r^{ij}$ between atoms i and j. the atomic dipole force tensor ${\mathit{\Pi }}_{\alpha \beta }^i$ is averaged over volume that the atom occupies in a unit cell. Then the global stress tensor ${\sigma }_{\alpha \beta }$ is defined as the average over the number of atoms that in the region to be calculated. As the tension simulation was implemented in this paper, virial stress tensor of ${\sigma }_{33}$ was extracted for comparison which is along the loading direction.

Results and Discussion

After the simulations, virial stress versus displacement curves were extracted for the different cases, as shown in Figure 2. It can be directly seen that the polycrystalline Cu model show a great ductile character under all strain rates, and the maximum stress is considerably lower than that obtained for the other models. Furthermore, the maximum stress obtained for the single-crystal Cu models is slightly larger than that obtained for the twin-crystal Cu models at a strain rate of 0.5% ps⁻¹ (8,150 MPa for the single-crystal Cu models and 7,700 MPa for the twin-crystal Cu models). However, as the strain rate is reduced to 0.1 and 0.01% ps⁻¹, this difference decreases, and Figure 2 shows that the number of twin grain boundaries does not change significantly as the virial stress exhibits the same trend for all strain rates investigated in this work.

FIGURE 2

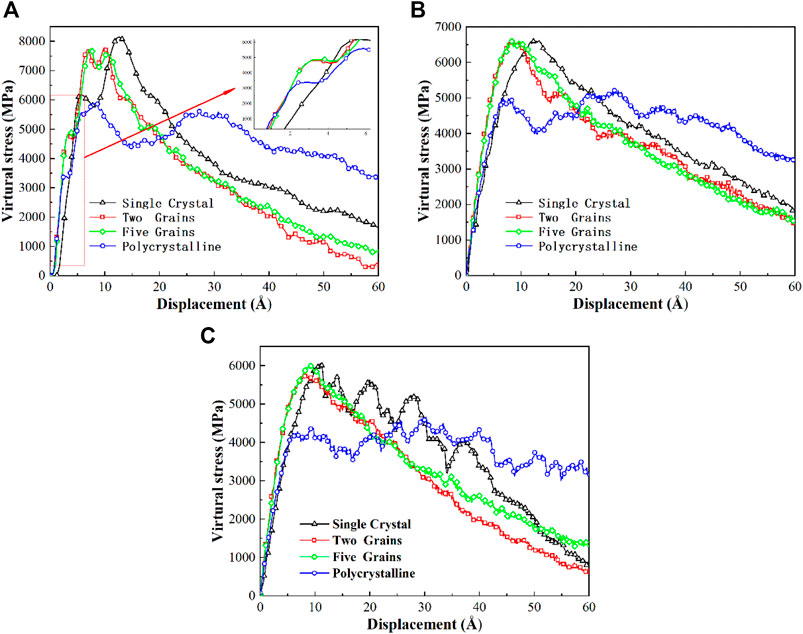
FIGURE 2. Virial stress–displacement curves of the different models at strain rates of (A) 0.5% ps⁻¹, (B) 0.1% ps⁻¹, and (C) 0.01% ps⁻¹.

On the other hand, it can be seen from Figure 2 that the displacement at which the stress reaches the highest peak for the single-crystal Cu model is always larger than that of the other models for all strain rates. Since the difference in the maximum stress obtained for the single-crystal Cu and twin-crystal Cu models is not large at a low strain rate, we investigated the elastic stage of these two cases. It can be seen that the single-crystal Cu and polycrystalline Cu models are characterized by stress curves that always have the same slope. The same is true for the twin-grain-boundary models. Furthermore, the slope of the stress curve obtained for the twin-grain-boundary models is higher than that obtained for the other two models. At a strain rate of 0.5% ps⁻¹, the stress curve of the polycrystalline Cu model follows that of the twin-crystal Cu model at first, while, after a small peak, it follows that of the single-crystal Cu model. To investigate the mechanism of this phenomenon, the work of adhesion and dislocation distribution were studied for both cases.

The work of adhesion is typically used to describe the adhesion strength of an interface. In this case, the work of adhesion (W_Cu/Cu3Sn) was obtained as the energy change when splitting the Cu/Cu₃Sn interface into the two Cu and Cu₃Sn surfaces. The value of W_Cu/Cu3Sn was calculated as follows (AlMotasem et al., 2016):

$W_{Cu/Cu3Sn}=\left(E_{Cu}+E_{Cu3Sn}-E_{tot}\right)/S_{\text{inter}},(3)$

where E_Cu and E_Cu3Sn correspond to the potential energies of Cu and Cu₃Sn in a system with a free surface, respectively. E_tot represents the total potential energy of the whole model, and S_inter is the surface-interactive area of the model. The work of adhesion calculated for both models is shown in Table 3.

TABLE 3

TABLE 3. Works of adhesion of the different models.

It can be seen that the work of adhesion between Cu and Cu₃Sn increases due to the existence of a twin crystal boundary, and more twin crystal boundaries in the same Cu region result in a higher work of adhesion. Considering the maximum stress illustrated in Figure 2, the single-crystal Cu model shows higher stresses than the other models, which appears in contradiction with our previous conclusions. However, it is noteworthy that the work of adhesion obtained for the polycrystalline Cu model is 2.89 J/m², which is twice larger than that of the other models, while the maximum stresses at different strain rates are substantially lower than those of the other models. This indicates that the existence of twin crystal boundaries or even ordinary grain boundaries has a great influence on the reliability of the Cu₃Sn/Cu interface. Thus, the work of adhesion alone cannot explain the reliability of interfaces that contain grain boundaries. Indeed, the mechanical strength of each layer changes considerably in the presence of grain boundaries as these cause a change in the defects in each layer during loading, which directly affects the stress evolution.

To investigate the mechanism of the phenomenon introduced above, the atomic position snapshot for all interface models was extracted at a displacement of 60 Å, where the structures are close to undergoing total failure. Additionally, to derive the defect evolution during the tensile process, the centro-symmetry parameter (CSP) introduced by Kelchner et al. (2011) was used to visualize the defects (dislocations, stacking faults, and nanotwins) during deformation. The CSP for a given atom is defined as follows:

$\text{CSP}={\displaystyle \sum _{i=1}^{N/2}{\left|{\mathrm{R}}_i-{\mathrm{R}}_{i+N/2}\right|}^2},(4)$

where N is the number of nearest neighbors (as Cu has the face-centered cubic (FCC) structure, N = 12) for the underlying lattice of atoms, and R_i and R_i+N/2 are the vectors corresponding to a specific pair of nearest neighbors opposite to the central atom. For a perfect lattice, the value of CSP is zero, whereas, for the regions characterized by defects or atoms close to the free surfaces, the CSP value is positive. A large CSP value indicates that the symmetry is broken. The OVITO software (Stukowski, 2009) was used for the CSP analysis and the dislocation extraction algorithm (DXA) (i.e., the dislocation analysis module in the software) was used to visualize the extracted dislocations and the corresponding Burgers vectors, which are indicated by lines in Figure 3.

FIGURE 3

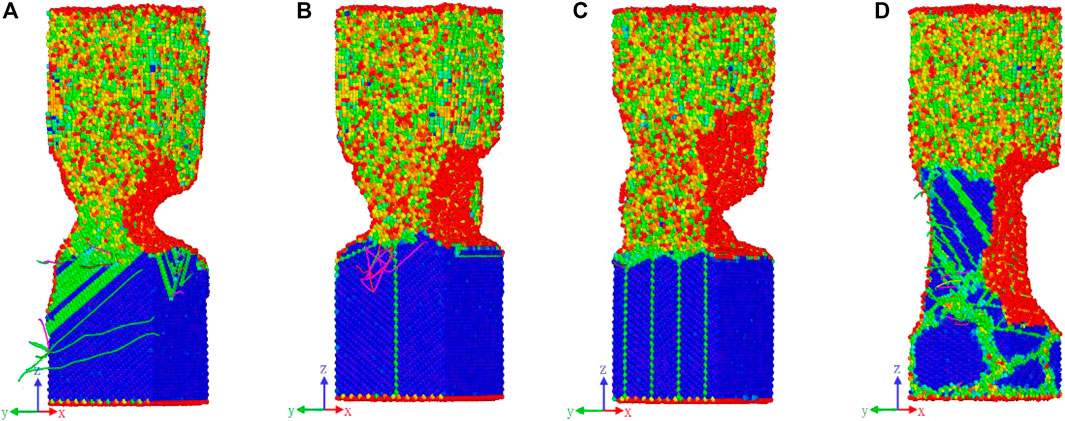
FIGURE 3. CSP and DXA results at a displacement of 60 Å under a strain rate of 0.01% ps⁻¹: (2A) single-crystal Cu, (B) twin-crystal Cu with one twin grain boundary, (C) twin-crystal Cu with four twin grain boundaries, and (D) polycrystalline Cu.

It is noticeable from Figure 3A that the degeneration position is located at the Cu layer that is close to the interface for the single-crystal Cu model, while the existence of twin grain boundaries causes the degeneration position to move toward the Cu₃Sn layer: for the model that contains only one twin boundary, the degeneration position is located at the interface, while when four twin boundaries are considered, the degeneration position is located inside the Cu₃Sn layer, as shown in Figures 3B,C. Regarding the polycrystalline Cu model, although this model exhibits the maximum work of adhesion, its mechanical strength is lower than that of the other models; thus, the failure of this model is predominantly caused by the collapse of polycrystalline Cu, as shown in Figure 3D. Furthermore, the snapshot shows the great ductile character of this model, which explains why its stress evolution curve has a lower maximum stress than the other models at all strain rates.

The model with one twin grain boundary has a lower work of adhesion than the model with four twin grain boundaries, which indicates that the adhesion between Cu and Cu₃Sn is weaker; the lower work of adhesion leads to the structure failure at the interface first. By contrast, the maximum stress of the single-crystal Cu model is slightly higher than that of the other models, as shown in Figure 2A; however, this model has the lowest work of adhesion, and its degeneration position is located in the Cu region, not at the interface. Since this phenomenon does not occur at strain rates of 0.1 and 0.01% ps⁻¹, it may be attributed to the fact that the rate dependence of mechanical properties that affects the atom distribution during deformation. Indeed, Figure 2A shows that the stress evolution curve of this model exhibits a peak before reaching the maximum stress, which indicates that several Cu atoms changed their position at this stage, thereby affecting the interface structure.

From the DXA results shown in Figure 3, it can be observed that a large number of Shockley dislocations with a Burgers vector of 1/6 [112] appeared in the single-crystal Cu model, and the existence of twin grain boundaries resulted in the main type of dislocation being the stair-rod dislocation with a Burgers vector of 1/6 [110]. Both dislocations types formed around the twin grain boundaries and near the interface; when considering four twin grain boundaries in the Cu layer, only a small number of dislocations could be found along the interface. As twin grain boundaries enhance the mechanical strength (Gao et al., 2012), once the mechanical strength exceeds the interface strength, a degeneration will occur at the interface. This is why a lower number of dislocations appeared in the twin-crystal Cu model, and the degeneration positions of each model are different.

On the other hand, the mechanical behavior of the Cu/Cu₃Sn interface depends considerably on the strain rate. Not only the stress evolution (shown in Figure 2) but also the degeneration position was significantly influenced by the strain rate, especially for the single-crystal Cu model. By comparing the degeneration positions of the single-crystal Cu model at strain rates of 0.01 and 0.1% ps⁻¹, as shown in Figure 4, it is clear that a lower strain rate leads the structure failure at the Cu layer near the interface, while a higher strain rate results in the structure failure inside the Cu₃Sn region. This indicates that Cu₃Sn is highly affected by the strain rate, and a higher strain rate causes the brittle failure of Cu₃Sn, while a lower strain rate results in the degeneration position being located at the interface for the twin-crystal Cu models and inside the Cu layer for the single-crystal Cu model.

FIGURE 4

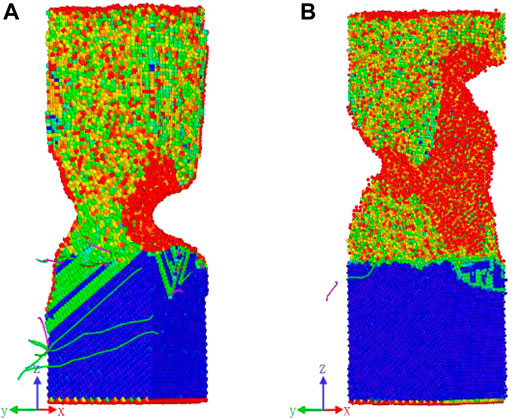
FIGURE 4. CSP and DXA results of the single-crystal Cu/Cu₃Sn interface at strain rates of (A) 0.01% ps⁻¹ and (B) 0.1% ps⁻¹.

Conclusion

The effect of the grain structure on the failure mechanism of the Cu₃Sn/Cu interface was investigated via MD simulations. Single-crystal Cu, twin-crystal Cu, and polycrystalline Cu models were built and compared. Axial tension simulations were performed at strain rates of 0.01, 0.1, and 0.5% ps⁻¹. The stress evolution and work of adhesion were then calculated and compared for each case to evaluate the mechanical reliability of the interface. Furthermore, both CSP and DXA were analyzed to investigate the interface failure mechanism from the perspective of defect evolution.

The stress versus displacement curves indicates that the ductile failure of polycrystalline Cu lead polycrystalline Cu model has a lower stress level and a great ductile character, which is induced by the sliding of grain boundaries. Additionally, the number of twin grain boundary has less influence on the interfacial character under the strain rates of 0.01 and 0.1% ps⁻¹. On the other hand, more twin crystal boundaries in the same Cu region would result in a higher work of adhesion, while with the existence of grain boundaries, only by comparing the work of adhesion cannot be used to evaluate the mechanical reliability of the interface. Investigation of the failure position and calculation of CSP and DXA could be of great help to gain a deeper understanding of this problem. By combining with the atom position, CSP and DXA results, it can be concluded that twin grain boundaries have the ability to enhance the mechanical strength of Cu layer, and when this mechanical strength exceeds the interfacial strength, degeneration will occur at the interface, this is why a lower number of dislocations appeared in the twin-crystal model. Results also show that the strain rate have great influence on mechanical character of Cu₃Sn. A high strain rate induces the brittle failure of Cu₃Sn, while a low strain rate causes the degeneration position to be located at the interface for the twin-crystal Cu models and inside the Cu layer for the single-crystal Cu model. In summary, our results provide information about the failure mechanism of the Cu₃Sn/Cu interface from MD simulation, which will be helpful for applications in the electronic packaging industry.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, JZ and YZ; methodology, YZ; software and calculating, JZ; writing—original draft preparation, JZ; writing—review and editing, ZJ.

Funding

This work was supported by the National Natural Science Foundation of China (No. 51605252).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aguilar, J. F., Ravelo, R., and Baskes, M. I. (2000). Morphology and Dynamics of 2D Sn-Cu Alloys on (100) and (111) Cu Surfaces. Model. Simul. Mater. Sci. Eng. 8 (3), 335–344. doi:10.1088/0965-0393/8/3/313

CrossRef Full Text | Google Scholar

AlMotasem, A. T., Bergström, J., Gåård, A., Krakhmalev, P., and Holleboom, L. J. (2016). Adhesion between Ferrite Iron-Iron/cementite Countersurfaces: A Molecular Dynamics Study. Tribology Int. 103, 113–120. doi:10.1016/j.triboint.2016.06.027

CrossRef Full Text | Google Scholar

An, R., Wang, C., Tian, Y., and Wu, H. (2008). Determination of the Elastic Properties of Cu3Sn through First-Principles Calculations. J. Elec Materi 37 (4), 477–482. doi:10.1007/s11664-007-0358-3

CrossRef Full Text | Google Scholar

Attarian, S., and Xiao, S. (2022). Development of a 2NN-MEAM Potential for Ti B System and Studies of the Temperature Dependence of the Nanohardness of TiB2. Comput. Mater. Sci. 201, 110875. doi:10.1016/j.commatsci.2021.110875

CrossRef Full Text | Google Scholar

Baskes, M. I., Angelo, J. E., and Bisson, C. L. (1994). Atomistic Calculations of Composite Interfaces. Model. Simul. Mater. Sci. Eng. 2 (3A), 505–518. doi:10.1088/0965-0393/2/3a/006

CrossRef Full Text | Google Scholar

Cheng, H.-C., Yu, C.-F., and Chen, W.-H. (2012). Strain- and Strain-rate-dependent Mechanical Properties and Behaviors of Cu3Sn Compound Using Molecular Dynamics Simulation. J. Mater. Sci. 47 (7), 3103–3114. doi:10.1007/s10853-011-6144-x

CrossRef Full Text | Google Scholar

Cheng, Y. L., Lee, C. Y., and Huang, Y. L. (2018). Copper Metal for Semiconductor Interconnects. Noble and Precious Metals–Properties. Nanoscale Effects and Applications. IntechOpen.

Google Scholar

Dandekar, C. R., and Shin, Y. C. (2011). Molecular Dynamics Based Cohesive Zone Law for Describing Al-SiC Interface Mechanics. Composites A: Appl. Sci. Manufacturing 42 (4), 355–363. doi:10.1016/j.compositesa.2010.12.005

CrossRef Full Text | Google Scholar

Fu, X., Chen, H., and Zhou, B. (2018). “Effect of Crystal Boundary Character and Crystal Orientation on Electromigration in Lead-free Solder Interconnects with Cyclic Twinning Structure,” in 2018 19th International Conference on Electronic Packaging Technology (ICEPT) (IEEE), 701–703.

CrossRef Full Text | Google Scholar

Gao, Y., Fu, Y., Sun, W., Sun, Y., Wang, H., Wang, F., et al. (2012). Investigation on the Mechanical Behavior of Fivefold Twinned Silver Nanowires. Comput. Mater. Sci. 55, 322–328. doi:10.1016/j.commatsci.2011.11.005

CrossRef Full Text | Google Scholar

Hau-Riege, C. S., and Thompson, C. V. (2001). Electromigration in Cu Interconnects with Very Different Grain Structures. Appl. Phys. Lett. 78 (22), 3451–3453. doi:10.1063/1.1355304

CrossRef Full Text | Google Scholar

Hu, C-K., Gignac, L., Baker, B., Liniger, E., and Yu, R. (2007). “Impact of Cu Microstructure on Electromigration Reliability,” in IEEE International Interconnect Technology Conference Proceedings, 93–95. doi:10.1109/iitc.2007.382357

CrossRef Full Text | Google Scholar

Juang, J.-Y., Lu, C.-L., Li, Y.-J., Hsu, P.-N., Tsou, N.-T., Tu, K. N., et al. (2021). A Solid State Process to Obtain High Mechanical Strength in Cu-To-Cu Joints by Surface Creep on (111)-oriented Nanotwins Cu. J. Mater. Res. Technology 14, 719–730. doi:10.1016/j.jmrt.2021.06.099

CrossRef Full Text | Google Scholar

Kelchner, C. L., Plimpton, S. J., and Hamilton, J. C. (2011). Dislocation Nucleation and Defect Structure during Surface Indentation. Phys. Rev. B. 58 (17), 11085–11088. doi:10.1103/PhysRevB.58.11085

CrossRef Full Text | Google Scholar

Liu, W., Zhu, K., Wang, C., Zheng, Z., An, R., Zhang, W., et al. (2020). Laser Induced Forward Transfer of Brittle Cu3Sn Thin Film. J. Manufacturing Process. 60, 48–53. doi:10.1016/j.jmapro.2020.10.003

CrossRef Full Text | Google Scholar

Liu, Y., Wang, B., Yoshino, M., Roy, S., Lu, H., and Komanduri, R. (2005). Combined Numerical Simulation and Nanoindentation for Determining Mechanical Properties of Single crystal Copper at Mesoscale. J. Mech. Phys. Sol. 53 (12), 2718–2741. doi:10.1016/j.jmps.2005.07.003

CrossRef Full Text | Google Scholar

Mackenchery, K., Valisetty, R. R., Namburu, R. R., Stukowski, A., Rajendran, A. M., and Dongare, A. M. (2016). Dislocation Evolution and Peak Spall Strengths in Single crystal and Nanocrystalline Cu. J. Appl. Phys. 119 (4), 044301. doi:10.1063/1.4939867

CrossRef Full Text | Google Scholar

Pang, X. Y., Wang, S. Q., and Zhang, L. (2008). First Principles Calculation of Elastic and Lattice Constants of Orthorhombic Cu3Sn crystal. J. Alloys Compounds 466 (1-2), 517–520. doi:10.1016/j.jallcom.2007.11.095

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117 (1), 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Qiu, R.-Z., Li, C.-C., and Fang, T.-H. (2017). Mechanical Properties and Crack Growth Behavior of Polycrystalline Copper Using Molecular Dynamics Simulation. Phys. Scr. 928, 085702. doi:10.1088/1402-4896/aa7c2c

CrossRef Full Text | Google Scholar

Rahmati, S., Zúñiga, A., Jodoin, B., and Veiga, R. G. A. (2020). Deformation of Copper Particles upon Impact: A Molecular Dynamics Study of Cold spray. Comput. Mater. Sci. 171, 109219. doi:10.1016/j.commatsci.2019.109219

CrossRef Full Text | Google Scholar

Shen, Y.-A., Chang, L., Chang, S.-Y., Chou, Y.-C., Tu, K. N., and Chen, C. (2022). Nanotwin Orientation on History-dependent Stress Decay in Cu Nanopillar under Constant Strain. Nanotechnology 33 (15), 155708. doi:10.1088/1361-6528/ac46d9

CrossRef Full Text | Google Scholar

Spearot, D. E., Jacob, K. I., and Mcdowell, D. L. (2004). Non-local Separation Constitutive Laws for Interfaces and Their Relation to Nanoscale Simulations. Mech. Mater. 36 (9), 825–847. doi:10.1016/j.mechmat.2003.08.002

CrossRef Full Text | Google Scholar

Stukowski, A. (2009). Visualization and Analysis of Atomistic Simulation Data with Ovito-The Open Visualization Tool. Model. Simul.mater.sci.eng 18 (6), 2154–2162. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

Todaro, C. J., Easton, M. A., Qiu, D., Zhang, D., Bermingham, M. J., Lui, E. W., et al. (2020). Grain Structure Control during Metal 3D Printing by High-Intensity Ultrasound. Nat. Commun. 11 (1), 142–149. doi:10.1038/s41467-019-13874-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Tseng, H. W., Lu, C. T., Hsiao, Y. H., Liao, P. L., Chuang, Y. C., Chung, T. Y., et al. (2010). Electromigration-induced Failures at Cu/Sn/Cu Flip-Chip Joint Interfaces. Microelectronics Reliability 50 (8), 1159–1162. doi:10.1016/j.microrel.2010.05.002

CrossRef Full Text | Google Scholar

Villars, P., and Calvet, L. D. (1985). Pearson’s Handbook of Crystallographic Data for Intermetallic Phases American Society of Metals: Cleveland, OH.

Google Scholar

Watanabe, Y., Fujinaga, Y., and Iwasaki, H. (1983). Lattice Modulation in the Long-Period Superstructure of Cu3Sn. Acta Crystallogr. Sect B 39 (3), 306–311. doi:10.1107/s0108768183002451

CrossRef Full Text | Google Scholar

Xu, W., and Kim, W. K. (2019). Molecular Dynamics Simulation of the Uniaxial Tensile Test of Silicon Nanowires Using the MEAM Potential. Mech. Mater. 137, 103140. doi:10.1016/j.mechmat.2019.103140

CrossRef Full Text | Google Scholar

Yang, Z., Zheng, L., Yue, Y., and Lu, Z. (2017). Effects of Twin Orientation and Spacing on the Mechanical Properties of Cu Nanowires. Sci. Rep. 7 (1), 10056–10059. doi:10.1038/s41598-017-10934-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, P., Li, X., Han, X., and Xu, L. (2019). Shear Strength and Fracture Mechanism for Full Cu-Sn IMCs Solder Joints with Different Cu3Sn Proportion and Joints with Conventional Interfacial Structure in Electronic Packaging. Soldering & Surface Mount Technology.

Google Scholar

Yao, P., Li, X., Liang, X., and Yu, B. (2017). Investigation of Soldering Process and Interfacial Microstructure Evolution for the Formation of Full Cu3Sn Joints in Electronic Packaging. Mater. Sci. Semiconductor Process. 58, 39–50. doi:10.1016/j.mssp.2016.11.019

CrossRef Full Text | Google Scholar

Zhang, J., Xu, Y., and Liang, L. (2015). “The Effect of Micro-structure Evolution in Electromigration on the Reliability of Solder Joints,” in 2015 16th International Conference on Electronic Packaging Technology (ICEPT). IEEE, 921–924.

CrossRef Full Text | Google Scholar

Zhang, N., and Asle Zaeem, M. (2018). Role of Grain Boundaries in Determining Strength and Plastic Deformation of Yttria-Stabilized Tetragonal Zirconia Bicrystals. J. Mater. Sci. 53 (8), 5706–5718. doi:10.1007/s10853-017-1595-3

CrossRef Full Text | Google Scholar

Zhang, X., Shi, C., Liu, E., Zhao, N., and He, C. (2018). Effect of Interface Structure on the Mechanical Properties of Graphene Nanosheets Reinforced Copper Matrix Composites. ACS Appl. Mater. Inter. 10 (43), 37586–37601. doi:10.1021/acsami.8b09799

PubMed Abstract | CrossRef Full Text | Google Scholar