Ergodic Structural Diversity Predicts Dynamics in Amorphous Materials

Identification of flexible local environments from a disordered medium has been a long-standing challenge. Here, we introduce a time-relevant structural Shannon entropy as a unique feature of the atomic-scale environment in glass, which is based on a metric of the time-invariant, or ergodic, and Voronoi structural diversity that an atom experiences during a sufficiently long-time thermal fluctuation. This new concept of time-relevant Shannon entropy simultaneously integrates the static topology and the vibrational feature such that it potentially probes all the possible configurational space in a sub-basin of the local potential energy landscape. This structural representation is not only capable of predicting the energy barrier of an elementary structural excitation but also demonstrates a robust correlation with the boson peak in metallic glasses, although the physical entity is defined from a purely structural aspect. The proposition, therefore, represents a successful demonstration of the physics-informed structure–property relationship in amorphous materials.

1 Introduction

The discipline that “structure determines property” is the cornerstone of the material science community. In conventional crystalline alloys, such a paradigm is a consensus and has achieved great success in virtue of well-defined structural imperfections in crystals, such as dislocation density and its feature described by a Burgers vector that are capable of predicting and interpreting plastic deformation, phase transformation, and other dynamic properties of crystalline materials. The Orowan equation predicting the rate of plastic deformation, which has incorporated geometrical features of lattice defects and the thermodynamics of defects, represents one of the most well-known and successful demonstrations of this paradigm in material science. In the more general amorphous materials in nature, however, the one-to-one structure-property relationship, especially at a micro-scale, has not yet been fully established up-to-date. This constitutes one of the most challenging open questions in modern material science. The difficulty lies in the fact that the structure of the disordered medium does not have either translational or rotational periodicity in terms of the atomic arrangement, causing the most intriguing unsolved problem—the lack of intuitive structural features that can be quantitatively associated with the thermal and/or mechanical responses (Cheng and Ma, 2011; Cubuk et al., 2017; Richard et al., 2020; Xu et al., 2021).

Over the past decades, relentless efforts have been devoted to seeking out suitable structural indicators and establishing the possible structure–property relationships in disordered materials from different perspectives. General structural descriptors invoked in the literature can be roughly categorized into two categories in which the first group is based on purely structural features while the second class refers to the physics-informed indicators. To be more explicit, the former contains free volume (Spaepen, 1977), local coordination number, Voronoi polyhedra (Sheng et al., 2006; Cao et al., 2009), local five-fold symmetry (Peng et al., 2011; Hu et al., 2015; Tian et al., 2017), inversion symmetry breaking (Milkus and Zaccone, 2016), and two-body excess entropy (Wallace, 1987; Yang et al., 2016; Piaggi and Parrinello, 2017). These indicators are clearly defined and easy to access. Still, almost all of them have their inherent limitations in deciphering all the dynamic properties since they only furnish the short-range structural information, which is insufficient to govern the thermodynamic or dynamic features that are embedded in both short- and possible medium-range structural fingerprints (Hu et al., 2018; Wei et al., 2019). In contrast, the physic-motivated descriptors, for example, soft spot (Manning and Liu, 2011; Ding et al., 2014), the Debye–Waller factor (Widmer-Cooper et al., 2004; Larini et al., 2008), local yielding stress (Patinet et al., 2016; Barbot et al., 2018), local thermal energy (Zylberg et al., 2017), flexibility volume (Ding et al., 2016), and the orientational order (Yang et al., 2019) show great capacity in predicting the properties of glasses. However, there is sometimes a threshold in obtaining these quantities, and it is user-friendly. Amongst these versatile descriptors, the flexibility volume and orientational order are advantageous due to their integration of proper static structural information. The remaining indicators can somehow indicate the state of glass but are not really descriptive of the particle packing.

It is of note that a third route has appeared recently. The emerging machine-learning strategies represent a great advancement in this direction (Cubuk et al., 2015; Schoenholz et al., 2016; Schoenholz et al., 2017; Wang and Jain, 2019; Tian et al., 2020; Zhang et al., 2021), which have yielded an unprecedented accuracy in predicting local structural features and other dynamics in glasses (Fan et al., 2020; Wang et al., 2020; Fan and Ma, 2021; Yang et al., 2021). Despite its advantage in dealing with big data, the machine-learning model usually works as a black box, causing some puzzles in interpreting the data-driven results from a physically relevant perspective. To this end, we propose a new purely structural indicator based on the conventional knowledge-driven strategy in this study. The time-invariant Voronoi structural diversity that an atom experiences during a sufficiently long-time thermal fluctuation is utilized to quantify the flexibility of local atomic environments in metallic glasses. This structural representation, in the form of Shannon information entropy (Shannon, 1948), extensively integrates information from the static positional topology and vibrational feature. It serves as a signature of long-time structural excitations and the short-time vibrational anomaly in metallic glasses.

2 Methods

2.1 Molecular Dynamics

Molecular dynamics (MD) simulations were performed with the LAMMPS code (Plimpton, 1995) for a well-studied Cu₅₀Zr₅₀ metallic glass. The glass sample containing 19,652 atoms was obtained by fast quenching the equilibrated liquid from 2000 to 0 K with a cooling rate of 10¹⁰ K/s. The interatomic interactions are described via a many-body Finnis–Sinclair–type embedded atom potential proposed by Mendelev et al. (2009). Period boundary conditions (PBCs) were used on the simulation box with 3D dimensions of $\sim 70,\times ,70,\times ,70$ ų. The temperature was controlled through the Nosé-Hoover thermostat (Nosé, 1984) while the external pressure in each direction is fully relaxed via the Parrinello–Rahman barostat (Parrinello and Rahman, 1981). The MD time step was set as 0.002 ps to numerically integrate Newton’s equation of motion.

2.2 Single-Particle Activation Energy

Before we extract the possible activation barriers in the complex 3N (N is the total number of atoms) dimensional potential energy landscape (PEL), the quenched glass sample was first fully relaxed to a local potential energy minimum via the conjugate gradient algorithm. Then, the widely adopted activation-relaxation technique nouveau (ARTn) (Barkema and Mousseau, 1996; Malek and Mousseau, 2000) was applied to sample possible local hopping pathways of the structural excitations from an initial energy sub-basin to a new neighboring minimum. The specific workflow of ARTn is described in the following sections. First, a small random perturbation was imposed on a central atom and its neighbors. In this study, the magnitude of the perturbation displacement was fixed as 0.1 Å, while the perturbation direction was chosen randomly. Second, the system was pulled toward the saddle point (with a high energy level) along the direction of the weakest Hessian matrix, following the Lanczos algorithm (Cancès et al., 2009). Finally, after convergence to the connected saddle state, the glass sample was eventually allowed to relax to a nearby sub-basin. In this connection, the activation energy for a specific structural excitation is defined as the energy difference between the saddle and the initial energy minimum states. ARTn searches were applied to all of the atoms, each one as the central triggered atom. After removing the failed tries, we used all 20 successful activation events for each atom. For statistical purposes, the average activation energy of the explored 20 events was then used as the single-particle activation energy for each atom.

2.3 Single-Particle Intensity of the Boson Peak

To quantify the local short-time thermodynamic property of metallic glass, we define the intensity of the boson peak at a single-particle level, which has been documented in Yang et al. (2022). First of all, the vibrational density of states (VDOS) of an inherent structure is obtained by direct diagonalizing its Hessian matrix. The single-particle VDOS for the ith atom is then defined as the sum contribution of ith atom over all vibrational modes. It is formulated as (Togo and Tanaka, 2015)

$g_i\left(\omega \right)=\frac{1}{3N}\sum _j{\delta \left(\omega -{\omega }_j\right)\left|{\mathbf{e}}_j^i\right|}^2,(1)$

where $g_i\left(\omega \right)$ denotes the single-particle VDOS for the ith atom. ω_j and e_j are the normal model frequency and the polarization vector of the jth vibrational mode, respectively. The phenomenon of the boson peak, that is, the excess vibrational modes over Debye squared law is then exhibited by the reduced VDOS (VDOS values divided by ω²). Thereafter, the peak value of the reduced VDOS for the ith atom, that is, $I_{\text{BP}}=\max \left[g_i\left(\omega \right)/{\omega }^2\right]$, is used to quantify the single-particle intensity of the boson peak.

3 Results

3.1 Time-Invariant Shannon Entropy

To establish the correlation between the local structure and dynamics of metallic glasses, a measure of the structural fluctuation that quantitatively predicts the long-time structural excitation and the short-time vibrational anomaly at a single-particle level is necessary. To settle this issue, we propose a time-relevant structural predictor, which is based on the diversity of the Voronoi motifs that an atom experiences during thermodynamic vibration and possible thermal activation.

First of all, the quenched glass sample is relaxed at 700 K (just below the glass transition temperature) for 1 ns; such time for thermal fluctuation is right below the α relaxation time (Yang et al., 2021), making sure that there is only a secondary β-relaxation process (Yu et al., 2014; Yu et al., 2017), and the structural transformations take place only between adjacent sub-basins (Fan et al., 2014; Fan et al., 2015). Then, the evolution of Voronoi polyhedra around each centered atom is recorded. Figure 1 shows the fluctuation history of possible short-range structures centered at two representative atoms. It is intuitively seen that the difference in atomic packing symmetry would lead to remarkably different thermal responses during relaxation at a thermal bath right below the glass transition temperature. Furthermore, it is evident that the local structural diversity is nonhomogeneous in metallic glasses since atoms are capable of retaining their initial short-range structure as shown in Figure 1A. Also, there are atoms experiencing completely distinct Voronoi motifs, causing an extremely high level of structural diversity, as evidenced by Figure 1B.

FIGURE 1

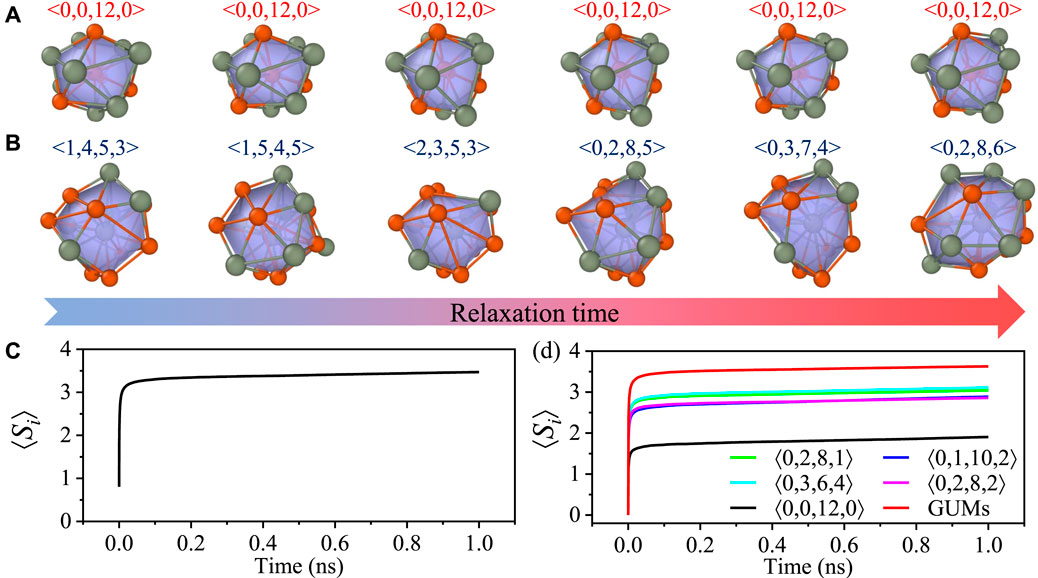
FIGURE 1. Definition of atomic-scale Shannon entropy S_i. (A,B) Representative evolution of Voronoi polyhedra with the lowest value of S_i in (A) and a relatively high degree of S_i in (B).(C) Ensemble average Shannon entropy as a function of relaxation time. (D) Evolution of S_i in five typical geometrically favored clusters (⟨0, 2, 8, 1⟩, ⟨0, 1, 10, 2⟩, ⟨0, 3, 6, 4⟩, ⟨0, 2, 8, 2⟩, and ⟨0, 0, 12, 0⟩) and GUMs.

Next, we perform statistics on the distribution of Voronoi polyhedra around each atom. Thus, the probability that each Voronoi motif appears in the fluctuation history of the ith atom is recorded and calculated as $P_i^j\left(t\right)$, where j denotes the jth existing Voronoi motif and t is the time for the thermal bath. By using the concept of Shannon information entropy (Shannon, 1948), the multiplicity of local structural variation is then quantified by the value of atomic Shannon entropy that is formulated as

$S_i=-\sum _j{P}_i^j\left(t\right)\ln \left(P_i^j\left(t\right)\right).(2)$

Because the distribution is, in principle, time-dependent, it is necessary to monitor the temporal evolution of S_i to understand its physical meaning and extract a time-invariant entity. The ensemble average time-relevant Shannon entropy is shown in Figure 1C as a function of time. The curve of S_i versus relaxation time has a tendency to level off. It indicates that atomic Shannon entropy displays a growth trend at very early stages, which is followed by the steady state for a longer time. The critical time appears at a timescale less than 0.1 ns. This is evidence for the saturation of the distribution of the local coordinated polyhedral motif. Thus, the long-time thermal fluctuation with an annealing time of 1 ns is sufficiently long for the local glass state to experience all the possible configurational space. In Figure 1D, the atomic Shannon entropy as a function of annealing time is further displayed for different atoms with distinct initial Voronoi motifs. It shows that all types of Voronoi clusters at the initial state become saturated with the statistical S_i at a relaxation time less than 0.1 ns. The full icosahedra (with the Voronoi index as ⟨0, 0, 12, 0⟩) has the lowest value of entropy, while the “geometrically unfavored motifs” (GUMs) exhibits the highest level of structural diversity. This is in line with the existing paradigm (Ma, 2015) that atomic packing with high symmetry such as full icosahedra (⟨0, 0, 12, 0⟩) constitutes the most inflexible local environments, while those GUMs contribute preferentially to the soft sites, acting as liquid-like regions (Ding et al., 2014). It should be noted that the critical time for the saturation of Shannon entropy is roughly estimated in the present work. The main scope of the critical time is to confirm the time-invariance of our proposed Shannon entropy. It is interesting to figure out the definition of such critical times. Consideration of the quantitative one-to-one correlation between the critical time and Shannon entropy or other dynamical properties is meaningful. However, it is beyond the scope of this article and will probably be discussed in future research studies.

3.2 Feature of Ergodic Shannon Entropy

Figure 2 displays the probability distribution of S_i for the Cu atoms (red line), Zr atoms (blue line), and all atoms (black line), respectively. It is intuitive that S_i is distributed over a very broad range, indicating a strong structural heterogeneity (Zhang et al., 2015) as commonly demonstrated by other structural predictors. This also resembles the frequently reported nonhomogeneous distribution of the short- or long-time dynamic properties in metallic glasses (Tanaka et al., 2010; Tong and Tanaka, 2018; Wang et al., 2018). Furthermore, it shows that the peak position of the Cu atoms shifts to the left when compared with that of Zr atoms. This is ascribed to the higher coordination number of Zr atoms than that of Cu atoms, resulting in a greater diversity in the local atomic packing of Zr atoms.

FIGURE 2

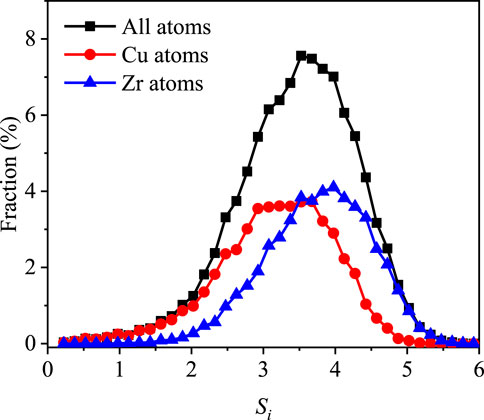
FIGURE 2. Distribution of atomic-scale Shannon entropy for all atoms (black line), Cu atoms (red line), and Zr atoms (blue line), respectively.

3.3 Structure–Property Relationship Based on Ergodic Shannon Entropy

Having characterized the level of structural diversity by S_i, we can now establish the long-sought structure-property relationship in metallic glasses. First of all, we focus on the correlation between ergodic Shannon entropy and the activation energy of local structure excitation, the latter of which is the energy barrier of the long-time transition from one local energy minimum to a neighboring one which is usually used as a universal indicator of the difficulty of structural excitations under external mechanical or thermal loadings. To address this issue, the particle-level activation energy ΔQ is calculated for each triggered atom. The statistical correlation between S_i and ΔQ is indeed seen in Figure 3 for Cu atoms (Figure 3A) and Zr atoms (Figure 3B), respectively. It shows a clear trend that decreasing values of ΔQ corresponds to growth in the magnitude of S_i. It further suggests that particles centered around motifs with a higher degree of structural diversity tend to have multiple basins with a lower activation barrier. To demonstrate this relation more explicitly, all Cu atoms (or Zr atoms) are sorted in terms of the value of S_i into groups, each containing 50 atoms. Then, the averaged ΔQ for each group is calculated. As shown in Figure 3C, an inverse scaling law between S_i and ΔQ is even more remarkable after such a numerical coarse-graining procedure. This intimate correlation applies to both Cu and Zr atoms. Furthermore, it is evident that Zr atoms are linked with deeper valleys in PEL, which correspond to higher activation barriers compared with Cu atoms. This is because Zr atoms are heavier than Cu atoms, causing the latter more easily to be activated under external stimuli.

FIGURE 3

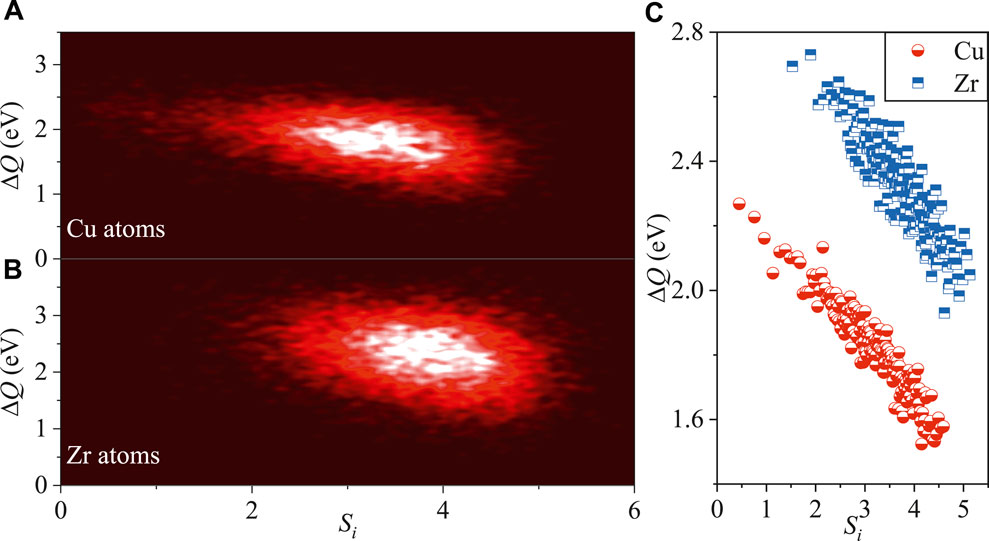
FIGURE 3. Correlation between atomic-scale Shannon entropy S_i and activation energy ΔQ of local structural excitation in Cu₅₀Zr₅₀ metallic glass. The color in each plot indicates the number density of atoms, with bright areas corresponding to high density. (A) for Cu atoms and (B) for Zr atoms. (C) shows the inverse proportionality between S_i and ΔQ. Each data point denotes the average for 0.25% of all atoms, sorted by the magnitude of S_i.

The next task at hand is to investigate how the structural diversity parameter S_i correlates with the short-time vibrational feature. For this purpose, the boson peak vibrational anomaly which is one of the most mysterious phenomena of metallic glasses and other disordered materials is utilized to benchmark the relation between S_i and thermodynamics. Here, the boson peak is the measure of excess vibrational density of states with respect to the Debye-squared law in 3D. It can be represented by the peak value of the reduced VDOS, that is, VDOS divided by ω². It has been extensively discussed that there is an intimate correlation between the activation energy and intensity of the boson peak. Thus, it is expected that there should be a strong correlation between S_i and I_BP. Figure 4 shows the semi-logarithmic plot of the single-particle boson peak intensity as a function of ergodic Shannon entropy for Cu (Figure 4A) and Zr atoms (Figure 4B), respectively. It shows that atoms with different values of S_i display different intensities of boson peaks. Mostly, atoms with a higher level of structural diversity will make more contributions to the boson peak. As shown in Figure 4C, this correlation is more apparent after numerical coarse graining with a proper bin size. Here, each bin contains 0.25% of all atoms that have been sorted based on the increasing value of S_i. It points out that atoms exhibiting a high value of ergodic Shannon entropy would indeed have an extraordinary vibrational anomaly, and large S_i does necessarily mean large intensity of boson peaks. This is indicative of the exponential susceptibility of the boson peak intensity to the diversity of structural environments and complexity of the PEL since S_i is proved linearly correlated with the PEL’s topology as evidenced by Figure 3.

FIGURE 4

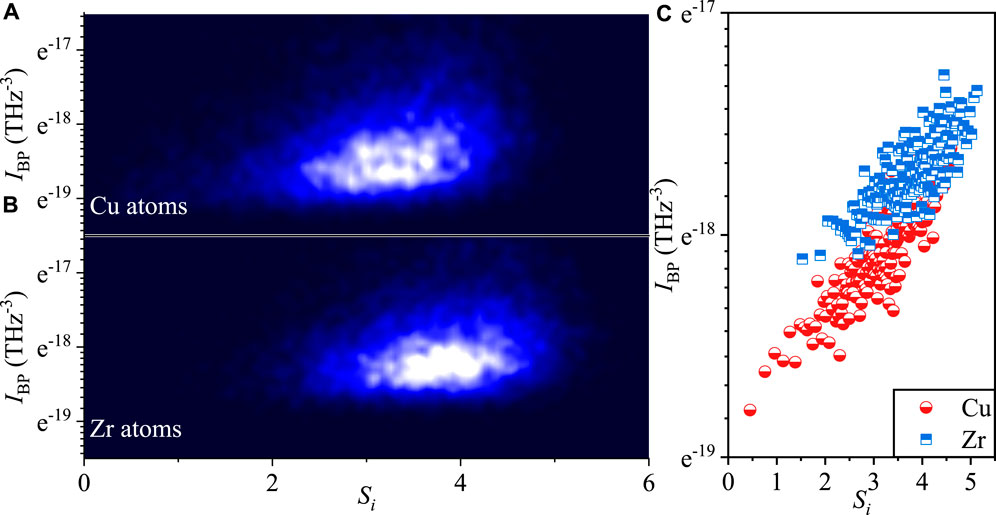
FIGURE 4. Correlation between atomic-scale Shannon entropy S_i and the single-particle boson peak I_BP in Cu₅₀Zr₅₀ metallic glass. The color in each plot indicates the number density of atoms, with bright areas corresponding to high density. (A) for Cu atoms and (B) for Zr atoms. (C) shows that S_i is exponentially proportional to I_BP. Each data point denotes the average for 0.25% of all atoms, sorted by the magnitude of S_i.

The strong correlation among S_i − ΔQ − I_BP can also be verified in terms of their spatial nature. The contour maps of S_i, ΔQ, and the I_BP field are shown in Figure 5. It is noticeable that all of these parameters are distributed in nonhomogeneous manners with atoms having high/low values of S_i (or ΔQ or I_BP) tend to aggregate spatially into clusters, which cover regions spanning nearly nanometers in diameter or $\sim 5$ Å in radius, which is corresponding to the second valley of the radial distribution function (RDF) of Cu₅₀Zr₅₀ MG. This is a direct piece of evidence that local structural diversity, local structural excitation, and vibrational anomalies share the same physical origin embedded in both short- and medium-range order of glass. This characteristic length scale is also commensurate with the critical size of soft regions that are responsible for triggering plastic shear transformations under thermal and/or mechanical stimuli. This is expected since the robust correlation between ΔQ and shear transformation has been well reported in the literature Kosiba et al. (2020), Han et al. (2020), and Wei et al. (2019). In this connection, local regions with a high level of S_i can be identified as potential glassy defects. Furthermore, it is evident in Figure 5 that high-S_i clusters are in striking overlap with the low-barrier and high-I_BP regions. It underpins the concept that ergodic Shannon entropy that conceives the information about the flexibility of the local structural packing can quantitatively correlate with both short-time and long-time dynamic features at a particle-level resolution.

FIGURE 5

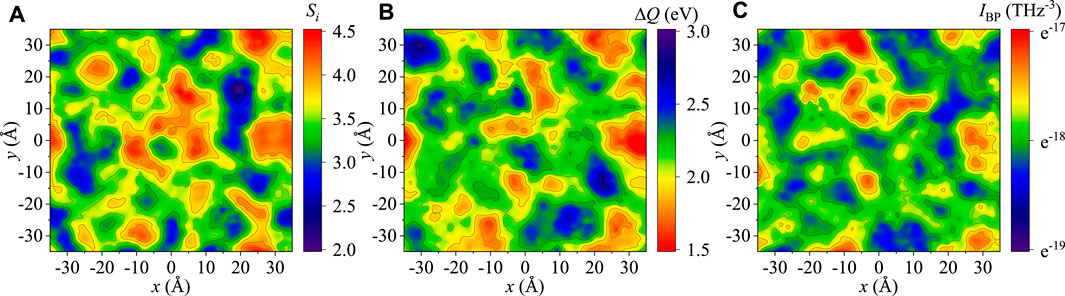
FIGURE 5. Heat maps showing the correspondence among (A) atomic-scale Shannon entropy S_i, (B) atomic-scale activation barriers, and (C) single-particle boson peaks, respectively. Each map has a thickness of 5 Å.

4 Discussion

In this section, we explain the underlying physics of the strong correction found in S_i − ΔQ − I_BP by tracing back the structural origin of ergodic Shannon entropy. Figure 6 shows the polyhedral makeups for the atoms with different values of S_i. The makeup for each atom is obtained by recording all Voronoi motifs that a specific atom has experienced during the relaxation process. In Figure 6, ergodic Shannon entropy is arranged in ascending order from left to right, with each solid bar containing 10% of all atoms. Remarkably, atoms with high levels of S_i preferentially experienced local environments stacking from GUMs, while those with low S_i values were mostly composed of geometrically favored clusters.

FIGURE 6

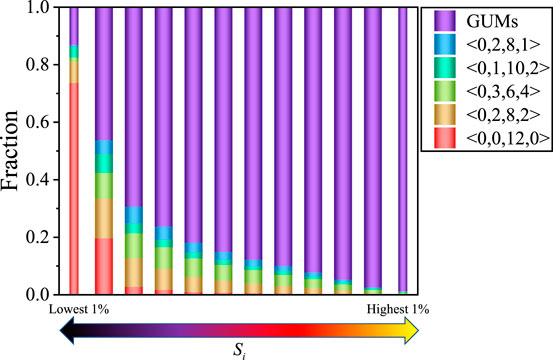
FIGURE 6. Structural diversity acts as the origin of atomic-scale Shannon entropy. The polyhedron makeups, averaged over all the snapshots during the relaxation process, of atoms with different values of S_i. The color bars, from left to right, are ordered by the value of S_i, with each bar containing 10% of all atoms. The two narrow bars on the left-most and right areas denote the results for atoms with the highest 1% and lowest 1% S_i, respectively.

It is even more striking when the statistics for atoms with extremely highest and lowest 1% S_i are presented for comparison (the two narrow bars in Figure 6). This observation is nontrivial since it is well reported that GUMs tend to contribute to the soft modes that are strongly in favor of low energy barriers for structural excitations, whereas the geometrically stable clusters barely participate in such soft modes and thus behave like hard regions that make up the mechanical rigidity of the glass sample Ding et al. (2014) and Fan et al. (2021). Therefore, it suggests that this ergodic Shannon entropy, as a numerical metric of the local structural diversity, hinting at the manifestation of the possibility that an atom will experience GUMs, or equally, the probability to participate in quasi-localized soft modes that are easy to lose mechanical stability.

5 Conclusion

In summary, we have identified a new physics-informed structural fingerprint based on an approximate expression for Shannon information entropy projected onto an individual atom. This atomic-scale Shannon entropy is time-invariant that extensively integrates both the static topology and the vibrational features. It presents a quantitative representation of the diversity of Voronoi polyhedra that an atom in a unique local atomic packing environment will explore during a substantial long-time relaxation process. On the basis of this innovative indictor, we partially establish the long-sought structure–property relation in the sense that S_i is shown to be an exceptional metric for both short-time vibrational anomalies and long-time structural excitations—both of which are critical and general dynamic properties in amorphous materials. Since ergodic Shannon entropy is clearly defined via the widely accepted Voronoi motifs in the community, the uncovered structure–property relation is interpretable and is also of interest in exploring nonhomogeneous dynamic features caused by the intricate local packing order in other disordered materials.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Z-YY and Y-JW designed the research. Z-YY performed the simulations. All the authors made contributions in analyzing and interpreting the data and writing the manuscript.

Funding

This work was financially supported by the National Natural Science Foundation of China (Grant No. 12072344) and the Youth Innovation Promotion Association of the Chinese Academy of Sciences (Grant No. 2017025).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barbot, A., Lerbinger, M., Hernandez-Garcia, A., García-García, R., Falk, M. L., Vandembroucq, D., et al. (2018). Local Yield Stress Statistics in Model Amorphous Solids. Phys. Rev. E 97, 033001. doi:10.1103/physreve.97.033001

PubMed Abstract | CrossRef Full Text | Google Scholar

Barkema, G. T., and Mousseau, N. (1996). Event-Based Relaxation of Continuous Disordered Systems. Phys. Rev. Lett. 77, 4358–4361. doi:10.1103/PhysRevLett.77.4358

PubMed Abstract | CrossRef Full Text | Google Scholar

Cancès, E., Legoll, F., Marinica, M.-C., Minoukadeh, K., and Willaime, F. (2009). Some Improvements of the Activation-Relaxation Technique Method for Finding Transition Pathways on Potential Energy Surfaces. J. Chem. Phys. 130, 114711. doi:10.1063/1.3088532

CrossRef Full Text | Google Scholar

Cao, A. J., Cheng, Y. Q., and Ma, E. (2009). Structural Processes that Initiate Shear Localization in Metallic Glass. Acta Materialia 57, 5146–5155. doi:10.1016/j.actamat.2009.07.016

CrossRef Full Text | Google Scholar

Cheng, Y. Q., and Ma, E. (2011). Atomic-level Structure and Structure-Property Relationship in Metallic Glasses. Prog. Mater. Sci. 56, 379–473. doi:10.1016/j.pmatsci.2010.12.002

CrossRef Full Text | Google Scholar

Cubuk, E. D., Ivancic, R. J. S., Schoenholz, S. S., Strickland, D. J., Basu, A., Davidson, Z. S., et al. (2017). Structure-property Relationships from Universal Signatures of Plasticity in Disordered Solids. Science 358, 1033–1037. doi:10.1126/science.aai8830

PubMed Abstract | CrossRef Full Text | Google Scholar

Cubuk, E. D., Schoenholz, S. S., Rieser, J. M., Malone, B. D., Rottler, J., Durian, D. J., et al. (2015). Identifying Structural Flow Defects in Disordered Solids Using Machine-Learning Methods. Phys. Rev. Lett. 114, 108001. doi:10.1103/PhysRevLett.114.108001

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, J., Cheng, Y.-Q., Sheng, H., Asta, M., Ritchie, R. O., and Ma, E. (2016). Universal Structural Parameter to Quantitatively Predict Metallic Glass Properties. Nat. Commun. 7, 13733. doi:10.1038/ncomms13733

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, J., Patinet, S., Falk, M. L., Cheng, Y., and Ma, E. (2014). Soft Spots and Their Structural Signature in a Metallic Glass. Proc. Natl. Acad. Sci. USA 111, 14052–14056. doi:10.1073/pnas.1412095111

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, H., Fan, Z., Liu, X., Lu, Z., and Ma, E. (2021). Atomic Vibration as an Indicator of the Propensity for Configurational Rearrangements in Metallic Glasses. Mater. Horiz. 8, 2359–2372. doi:10.1039/D1MH00491C

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Y., Iwashita, T., and Egami, T. (2015). Crossover from Localized to Cascade Relaxations in Metallic Glasses. Phys. Rev. Lett. 115, 045501. doi:10.1103/physrevlett.115.045501

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Y., Iwashita, T., and Egami, T. (2014). How Thermally Activated Deformation Starts in Metallic Glass. Nat. Commun. 5, 5083. doi:10.1038/ncomms6083

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Z., Ding, J., and Ma, E. (2020). Machine Learning Bridges Local Static Structure with Multiple Properties in Metallic Glasses. Mater. Today 40, 48–62. doi:10.1016/j.mattod.2020.05.021

CrossRef Full Text | Google Scholar

Fan, Z., and Ma, E. (2021). Predicting Orientation-dependent Plastic Susceptibility from Static Structure in Amorphous Solids via Deep Learning. Nat. Commun. 12, 1506. doi:10.1038/s41467-021-21806-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, D., Wei, D., Cao, P.-H., Wang, Y.-J., and Dai, L.-H. (2020). Statistical Complexity of Potential Energy Landscape as a Dynamic Signature of the Glass Transition. Phys. Rev. B 101, 064205. doi:10.1103/PhysRevB.101.064205

CrossRef Full Text | Google Scholar

Hu, Y.-C., Li, Y.-W., Yang, Y., Guan, P.-F., Bai, H.-Y., and Wang, W.-H. (2018). Configuration Correlation Governs Slow Dynamics of Supercooled Metallic Liquids. Proc. Natl. Acad. Sci. USA 115, 6375–6380. doi:10.1073/pnas.1802300115

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y. C., Li, F. X., Li, M. Z., Bai, H. Y., and Wang, W. H. (2015). Five-fold Symmetry as Indicator of Dynamic Arrest in Metallic Glass-Forming Liquids. Nat. Commun. 6, 9310. doi:10.1038/ncomms9310

CrossRef Full Text | Google Scholar

Kosiba, K., Scudino, S., Bednarcik, J., Bian, J., Liu, G., Kühn, U., et al. (2020). Guiding Shear Bands in Bulk Metallic Glasses Using Stress fields: A Perspective from the Activation of Flow Units. Phys. Rev. B 102, 134113. doi:10.1103/PhysRevB.102.134113

CrossRef Full Text | Google Scholar

Larini, L., Ottochian, A., De Michele, C., and Leporini, D. (2008). Universal Scaling between Structural Relaxation and Vibrational Dynamics in Glass-Forming Liquids and Polymers. Nat. Phys 4, 42–45. doi:10.1038/nphys788

CrossRef Full Text | Google Scholar

Ma, E. (2015). Tuning Order in Disorder. Nat. Mater 14, 547–552. doi:10.1038/nmat4300

PubMed Abstract | CrossRef Full Text | Google Scholar

Malek, R., and Mousseau, N. (2000). Dynamics of Lennard-Jones Clusters: A Characterization of the Activation-Relaxation Technique. Phys. Rev. E 62, 7723–7728. doi:10.1103/PhysRevE.62.7723

PubMed Abstract | CrossRef Full Text | Google Scholar

Manning, M. L., and Liu, A. J. (2011). Vibrational Modes Identify Soft Spots in a Sheared Disordered Packing. Phys. Rev. Lett. 107, 108302. doi:10.1103/physrevlett.107.108302

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendelev, M. I., Kramer, M. J., Ott, R. T., and Sordelet, D. J. (2009). Molecular Dynamics Simulation of Diffusion in Supercooled Cu-Zr Alloys. Philos. Mag. 89, 109–126. doi:10.1080/14786430802570648

CrossRef Full Text | Google Scholar

Milkus, R., and Zaccone, A. (2016). Local Inversion-Symmetry Breaking Controls the Boson Peak in Glasses and Crystals. Phys. Rev. B 93, 094204. doi:10.1103/PhysRevB.93.094204

CrossRef Full Text | Google Scholar

Nosé, S. (1984). A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 81, 511–519. doi:10.1063/1.447334

CrossRef Full Text | Google Scholar

Parrinello, M., and Rahman, A. (1981). Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 52, 7182–7190. doi:10.1063/1.328693

CrossRef Full Text | Google Scholar

Patinet, S., Vandembroucq, D., and Falk, M. L. (2016). Connecting Local Yield Stresses with Plastic Activity in Amorphous Solids. Phys. Rev. Lett. 117, 045501. doi:10.1103/physrevlett.117.045501

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, H. L., Li, M. Z., and Wang, W. H. (2011). Structural Signature of Plastic Deformation in Metallic Glasses. Phys. Rev. Lett. 106, 135503. doi:10.1103/physrevlett.106.135503

PubMed Abstract | CrossRef Full Text | Google Scholar

Piaggi, P. M., and Parrinello, M. (2017). Entropy Based Fingerprint for Local Crystalline Order. J. Chem. Phys. 147, 114112. doi:10.1063/1.4998408

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Richard, D., Ozawa, M., Patinet, S., Stanifer, E., Shang, B., Ridout, S. A., et al. (2020). Predicting Plasticity in Disordered Solids from Structural Indicators. Phys. Rev. Mater. 4, 113609. doi:10.1103/PhysRevMaterials.4.113609

CrossRef Full Text | Google Scholar

Schoenholz, S. S., Cubuk, E. D., Kaxiras, E., and Liu, A. J. (2017). Relationship between Local Structure and Relaxation in Out-Of-Equilibrium Glassy Systems. Proc. Natl. Acad. Sci. USA 114, 263–267. doi:10.1073/pnas.1610204114

CrossRef Full Text | Google Scholar

Schoenholz, S. S., Cubuk, E. D., Sussman, D. M., Kaxiras, E., and Liu, A. J. (2016). A Structural Approach to Relaxation in Glassy Liquids. Nat. Phys 12, 469–471. doi:10.1038/nphys3644

CrossRef Full Text | Google Scholar

Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell Syst. Tech. J. 27, 379–423. doi:10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M., and Ma, E. (2006). Atomic Packing and Short-To-Medium-Range Order in Metallic Glasses. Nature 439, 419–425. doi:10.1038/nature04421

PubMed Abstract | CrossRef Full Text | Google Scholar

Spaepen, F. (1977). A Microscopic Mechanism for Steady State Inhomogeneous Flow in Metallic Glasses. Acta Metallurgica 25, 407–415. doi:10.1016/0001-6160(77)90232-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanaka, H., Kawasaki, T., Shintani, H., and Watanabe, K. (2010). Critical-like Behaviour of Glass-Forming Liquids. Nat. Mater 9, 324–331. doi:10.1038/nmat2634

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, L., Fan, Y., Li, L., and Mousseau, N. (2020). Identifying Flow Defects in Amorphous Alloys Using Machine Learning Outlier Detection Methods. Scripta Materialia 186, 185–189. doi:10.1016/j.scriptamat.2020.05.038

CrossRef Full Text | Google Scholar

Tian, Z.-L., Wang, Y.-J., Chen, Y., and Dai, L.-H. (2017). Strain Gradient Drives Shear Banding in Metallic Glasses. Phys. Rev. B 96, 094103. doi:10.1103/PhysRevB.96.094103

CrossRef Full Text | Google Scholar

Togo, A., and Tanaka, I. (2015). First Principles Phonon Calculations in Materials Science. Scripta Materialia 108, 1–5. doi:10.1016/j.scriptamat.2015.07.021

CrossRef Full Text | Google Scholar

Tong, H., and Tanaka, H. (2018). Revealing Hidden Structural Order Controlling Both Fast and Slow Glassy Dynamics in Supercooled Liquids. Phys. Rev. X 8, 011041. doi:10.1103/PhysRevX.8.011041

CrossRef Full Text | Google Scholar

Wallace, D. C. (1987). On the Role of Density Fluctuations in the Entropy of a Fluid. J. Chem. Phys. 87, 2282–2284. doi:10.1063/1.453158

CrossRef Full Text | Google Scholar

Wang, N., Ding, J., Yan, F., Asta, M., Ritchie, R. O., and Li, L. (2018). Spatial Correlation of Elastic Heterogeneity Tunes the Deformation Behavior of Metallic Glasses. Npj Comput. Mater. 4, 19. doi:10.1038/s41524-018-0077-8

CrossRef Full Text | Google Scholar

Wang, Q., Ding, J., Zhang, L., Podryabinkin, E., Shapeev, A., and Ma, E. (2020). Predicting the Propensity for Thermally Activated β Events in Metallic Glasses via Interpretable Machine Learning Events in Metallic Glasses via Interpretable Machine Learning. Npj Comput. Mater. 6, 194. doi:10.1038/s41524-020-00467-4

CrossRef Full Text | Google Scholar

Wang, Q., and Jain, A. (2019). A Transferable Machine-Learning Framework Linking Interstice Distribution and Plastic Heterogeneity in Metallic Glasses. Nat. Commun. 10, 5537. doi:10.1038/s41467-019-13511-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, D., Yang, J., Jiang, M.-Q., Wei, B.-C., Wang, Y.-J., and Dai, L.-H. (2019). Revisiting the Structure-Property Relationship of Metallic Glasses: Common Spatial Correlation Revealed as a Hidden Rule. Phys. Rev. B 99, 014115. doi:10.1103/physrevb.99.014115

CrossRef Full Text | Google Scholar

Widmer-Cooper, A., Harrowell, P., and Fynewever, H. (2004). How Reproducible Are Dynamic Heterogeneities in a Supercooled Liquid? Phys. Rev. Lett. 93, 135701. doi:10.1103/physrevlett.93.135701

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, B., Falk, M. L., Patinet, S., and Guan, P. (2021). Atomic Nonaffinity as a Predictor of Plasticity in Amorphous Solids. Phys. Rev. Mater. 5, 025603. doi:10.1103/physrevmaterials.5.025603

CrossRef Full Text | Google Scholar

Yang, J., Wang, Y.-J., Ma, E., Zaccone, A., Dai, L. H., and Jiang, M. Q. (2019). Structural Parameter of Orientational Order to Predict the Boson Vibrational Anomaly in Glasses. Phys. Rev. Lett. 122, 015501. doi:10.1103/physrevlett.122.015501

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, X., Liu, R., Yang, M., Wang, W.-H., and Chen, K. (2016). Structures of Local Rearrangements in Soft Colloidal Glasses. Phys. Rev. Lett. 116, 238003. doi:10.1103/physrevlett.116.238003

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z.-Y., Wang, Y.-J., and Zaccone, A. (2022). Correlation between Vibrational Anomalies and Emergent Anharmonicity of the Local Potential Energy Landscape in Metallic Glasses. Phys. Rev. B 105, 014204. doi:10.1103/physrevb.105.014204

CrossRef Full Text | Google Scholar

Yang, Z.-Y., Wei, D., Zaccone, A., and Wang, Y.-J. (2021). Machine-learning Integrated Glassy Defect from an Intricate Configurational-Thermodynamic-Dynamic Space. Phys. Rev. B 104, 064108. doi:10.1103/PhysRevB.104.064108

CrossRef Full Text | Google Scholar

Yu, H. B., Richert, R., and Samwer, K. (2017). Structural Rearrangements Governing Johari-Goldstein Relaxations in Metallic Glasses. Sci. Adv. 3, e1701577. doi:10.1126/sciadv.1701577

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, H. B., Wang, W. H., Bai, H. Y., and Samwer, K. (2014). The β-relaxation in Metallic Glasses-Relaxation in Metallic Glasses. Natl. Sci. Rev. 1, 429–461. doi:10.1093/nsr/nwu018

CrossRef Full Text | Google Scholar

Zhang, J. C., Chen, C., Pei, Q. X., Wan, Q., Zhang, W. X., and Sha, Z. D. (2015). Ab Initio molecular Dynamics Study of the Local Atomic Structures in Monatomic Metallic Liquid and Glass. Mater. Des. 77, 1–5. doi:10.1016/j.matdes.2015.04.002

CrossRef Full Text | Google Scholar

Zhang, Y. X., Xing, G. C., Sha, Z. D., and Poh, L. H. (2021). A Two-step Fused Machine Learning Approach for the Prediction of Glass-Forming Ability of Metallic Glasses. J. Alloys Comp. 875, 160040. doi:10.1016/j.jallcom.2021.160040

CrossRef Full Text | Google Scholar

Zylberg, J., Lerner, E., Bar-Sinai, Y., Bouchbinder, E., and Langer, J. S. (2017). Local thermal Energy as a Structural Indicator in Glasses. Proc. Natl. Acad. Sci. USA 114, 7289–7294. doi:10.1073/pnas.1704403114

PubMed Abstract | CrossRef Full Text | Google Scholar