Multifunctional Coding Metasurface With Left and Right Circularly Polarized and Multiple Beams

In this paper, a multifunctional coding metasurface (MCMS) has been proposed to realize dual-circularly polarized beams and beam focusing with transmission and reflection. The phase of transmissive wave is controlled by rotating the elements, and the corresponding element, which consists of two quadrate voids etched on a single layer substrate, is designed for the metasurface with Pancharatnam-Berry (PB) phase. The phase distribution of the circularly polarized four-beam is determined according to the convolution theorem of patterns and the phase compensation principle. In order to validate the proposed metasurface, the multifunctional meta-device is fabricated and measured to illustrate the four-beam with left circular polarization in transmissive space and the right circularly polarized four-beam in reflective space by MCMS with x-polarized incidence. The experimental results heavily agree with the simulated data. The MCMS has potential applications in wireless communications due to its low profile, compact, and lightweight features.

Introduction

Circular polarization has been extensively applied in wireless satellite communications, optical displays, optical remote sensors, synthetic aperture radar imaging systems, contrast enhanced polarization micro-imaging, and biomolecular detection because of the incredible characteristics of chiral wave vector, uniform polarization distribution, lower glare effect, strong anti-interference ability, and low sensitivity between the receiver and transmitter (Lin et al., 2013; Cheng et al., 2021a; Li et al., 2021a; Li et al., 2021b; Fan et al., 2021; Han et al., 2021). In general, the left or right circularly polarized electromagnetic (EM) waves are obtained by the antennas in microwave band. For example, an active dual circularly polarized spherical phased-array antenna has been discussed based on the multiplexing of the resources among the antenna element (Kumar et al., 2013). Furthermore, a U-shaped slot antenna was designed to achieve the broadband dual circularly polarized radiation (Xu et al., 2017). Recently, a dual circularly polarized array antenna was presented based on the corporate feeding network in square waveguide technology (Garcia-Marin et al., 2021). Nevertheless, it is difficult for antennas to simultaneously achieve dual-circular polarization beam at the same frequency due to the cumbersome design process and the complicated micro-structure. Therefore, it is necessary to research a novel way to realize multiple beams with dual-circular polarization.

Metasurfaces, which can flexibly manipulate the amplitude, phase, polarization, and propagation direction of electromagnetic (EM) waves, are artificial electromagnetic materials arranged periodically or aperiodically by element micro-structure in two-dimension (Li et al., 2014; Li et al., 2016; Li et al., 2019; Li et al., 2020a). Thus, it is a new way to regulate the dual-circularly polarized electromagnetic wave by metasurface. Several metasurfaces have been proposed to control the polarization of transmissive EM waves. The dual-band polarization conversion from linearly polarized (LP) EM waves into left circularly polarized (LCP) EM waves in a low band and right circularly polarized (RCP) EM waves in a high band can be obtained by transmissive metasurface with arrow-shaped micro-structures. The different transmission modes are excited and the y-polarized waves are transmitted into LCP waves from 7.31 to 10.58 GHz and RCP waves in the range of 14.26–17.36 GHz, respectively (Han et al., 2020). Similarly, the two layers’ transmission metasurface was proposed to transform the x-polarized wave into RCP in the frequency range of 9.05–9.65 GHz and LCP in the range of 12.55–13.1 GHz (Liu et al., 2020). Nevertheless, these metasurfaces realized the dual-circularly polarized EM waves in frequency domain. The research of dual-circularly polarized EM waves in spatial domain has become essential due to the limited frequency resources.

Coding metasurface, which was illuminated by Cui’s group in 2014, provides an excellent scheme to manipulate the reflective EM waves based on interference (Cui et al., 2014). In general, the phase interference metasurface forms n bits coding elements by several structures with 2π/2ⁿ phase difference. Moreover, the active, reconfigurable, and multifunctional coding metasurfaces have been designed while the PIN diodes or micro-electromechanical systems are introduced in the unit cell of metasurfaces (Liu et al., 2016; Chen et al., 2017; Yuan et al., 2019; Zhao et al., 2019; Li et al., 2020b; Li et al., 2020c; Cheng et al., 2021b; Pan et al., 2021; Zhu et al., 2022). A transmissive metasurface which consists of periodic strip slits and rectangular C-slits etched on substrate integrated waveguide cavities has been designed in order to split a linearly polarized (LP) EM wave into two symmetrical CP beams. By introducing the gradient-oriented C-slit array on such metasurface-based cavities, the opposite equivalent phase gradients have been readily created for the RCP and LCP transmitting waves (Zhang and Yang, 2019). However, there are only transmissive beams in the half space. Different from the existing metasurfaces (Li et al., 2015; Zhang et al., 2016; Han et al., 2018; Ding et al., 2019; Chen et al., 2020; Li et al., 2021c; Tang et al., 2021; Zhao et al., 2021; Cheng et al., 2022), this paper proposed a multifunctional coding metasurface based on the convolution theorem of patterns and the phase compensation principle. The experimental and simulated results verified the multifunctional coding metasurface with four LCP beams in the transmissive space and four RCP beams in the reflective space as the x-polarized incidence.

Metasurface Design

A conceptual illustration of MCMS is presented in Figure 1A. The coding metasurface consists of 1024 elements, which can convert the x-polarized incident waves into four transmissive beams with LCP and four reflective beams with RCP, and an opposite role for the y-polarized wave. Figure 1B shows the perspective and front views of the unit cell with elements “0” and “1”. The metallic dumbbell with two quadrate voids etched on the front side of the substrate is the Rogers RT5880 (ε_r = 2.2 and tanδ = 0.0009) with a thickness of 3 mm. The bottom metallic patch is the same as that on the substrate. The transmission and reflection coefficients are manipulated by the metallic dumbbell with two quadrate voids. Their optimized parameters are chosen as L = 10 mm, t = 3 mm, l₁ = 1.02 mm, l₂ = 8.1 mm, l₃ = 3.9 mm, s₁ = 0.3 mm, s₂ = 2.3 mm, and s₃ = 2.1 mm Φ is the rotation angle in the geometric center of the metallic dumbbell with two quadrate voids. The elements “0” and “1” are the unit cell with the rotation angle of 0 and 90deg.

FIGURE 1

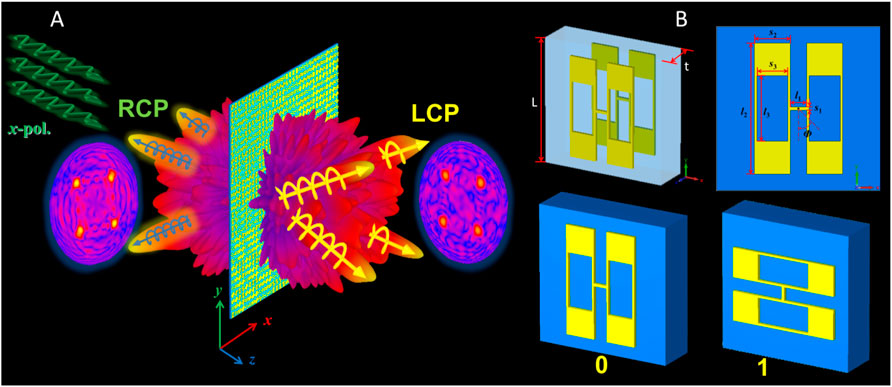
FIGURE 1. Conceptual illustration of the proposed multifunctional coding metasurface and the unit cell. (A) MCMS with multi-function of multi RCP beams in reflection and multi LCP beams in transmission. (B) The perspective and front views of the unit cell with elements “0” and “1”.

Results and Discussion

Design Theory of Unit Cell

The MCMS realize the function of transmissive and reflective polarization conversion. To elaborate the mechanism of the unit cell, a two-port network and the Jones matrices for transmission along the +z axis and reflection along the -z axis can be respectively given by (Lin et al., 2013) and (Fan et al., 2021)

$\left(\begin{array}{l}{E}_x^t\\ E_y^t\end{array}\right)={\overrightarrow{T}}_l\left(\begin{array}{c}{E}_x^i\\ E_y^i\end{array}\right)=\left(\begin{array}{cc}{t}_{xx}& t_{xy}\\ t_{yx}& t_{yy}\end{array}\right)\left(\begin{array}{c}{E}_x^i\\ E_y^i\end{array}\right)(1)$

$\left(\begin{array}{l}{E}_x^r\\ E_y^r\end{array}\right)={\overrightarrow{R}}_l\left(\begin{array}{c}{E}_x^i\\ E_y^i\end{array}\right)=\left(\begin{array}{cc}{r}_{xx}& r_{xy}\\ r_{yx}& r_{yy}\end{array}\right)\left(\begin{array}{c}{E}_x^i\\ E_y^i\end{array}\right)(2)$

Where Eⁱ_x, Eⁱ_y, E^r_x, E^r_y, E^t_x, and E^t_y represent the electric fields of incident, transmissive, and reflective waves with x- and y-polarization. ${\overrightarrow{T}}_l$ represents the Jones matrix transmitted by the linearly polarized waves along the +z axis. ${\overrightarrow{R}}_l$ is the Jones matrix reflected by the linearly polarized incidence along the -z axis. According to the generation condition of circularly polarized waves, the transformation matrices of reflection ${\overrightarrow{R}}_{cp}$ and transmission ${\overrightarrow{T}}_{cp}$ are calculated as follows:

${\overrightarrow{T}}_{cp}=\left(\begin{array}{cc}{t}_{++}& t_{+-}\\ t_{-+}& t_{--}\end{array}\right)=\frac{1}{2}\left(\begin{array}{cc}{t}_{xx}-t_{yy}-j\left(t_{xy}+t_{yx}\right)& t_{xx}+t_{yy}+j\left(t_{xy}-t_{yx}\right)\\ t_{xx}+t_{yy}-j\left(t_{xy}-t_{yx}\right)& t_{xx}-t_{yy}+j\left(t_{xy}+t_{yx}\right)\end{array}\right)(3)$

${\overrightarrow{R}}_{cp}=\left(\begin{array}{cc}{r}_{++}& r_{+-}\\ r_{-+}& r_{--}\end{array}\right)=\frac{1}{2}\left(\begin{array}{cc}{r}_{xx}-r_{yy}-j\left(r_{xy}+r_{yx}\right)& r_{xx}+r_{yy}+j\left(r_{xy}-r_{yx}\right)\\ r_{xx}+r_{yy}-j\left(r_{xy}-r_{yx}\right)& r_{xx}-r_{yy}+j\left(r_{xy}+r_{yx}\right)\end{array}\right)(4)$

Where r represents reflection coefficient of circular polarization for MCMS. + and - represent RCP wave and LCP wave propagating along + z axis respectively. So r₋₊ represents the reflection coefficient of LCP wave reflected as LCP wave, the meaning of r₊₊, r_+−, and r₋₋ will not be elaborated on too much. Moreover, t represents the transmission coefficient of circular polarization for MCMS. t₋₋ represents the transmission coefficient of LCP wave transmitted as LCP wave. According to the principle of PB phase, the transmissive circularly polarized wave can be achieved as |t_xx| = |t_yy| = 1 and phase difference Δφ_t = 180deg. It means that the metasurface can transmit the cross-circularly polarized waves and restrain the co-circularly polarized waves when |t₊₊| = |t₋₋| = 0 and |t₊₋| = |t₋₊| = 1. What is more, the realization conditions of co-circularly polarized reflection are |r_xx| = |r_yy| = 1 and phase difference Δφ_t = 180deg.

Simulated Results of Unit Cell and Elements

MCMS is simulated by the CST STUDIO 2020 with the infinite periodic boundary and the Flouquet ports and its numerical method is Finite Integration Theory (FIT). When the linearly polarized incidence occurs along + z axis, the simulated results of transmission and reflection coefficients are shown in Figure 2. It is obvious that the simulated amplitude results of reflection coefficient |r_xx| are approximately equal to that of |r_yy| from 9.35 to 9.65 GHz and the amplitude results of transmission coefficient |t_xx| and |t_yy| are more than 0.7 at the same frequency range from Figure 2A. Moreover, the reflective phase difference of 180deg can be obtained in the frequency range of 9.2–10.6 GHz and the transmissive phase difference of 180deg is realized from 8.5 to 11.2 GHz from Figure 2C. Therefore, the co-circularly polarized reflection and cross-circularly polarized transmission are achieved from 9.35 to 9.65 GHz.

FIGURE 2

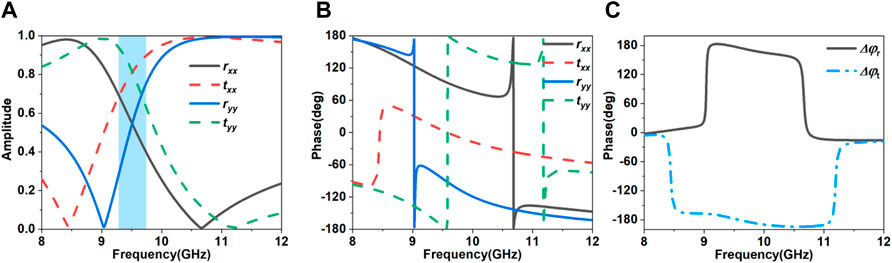
FIGURE 2. Reflection coefficient, transmission coefficient, and phase difference of unit cell for MCMS with x-and y-polarized incidences. (A) Simulated amplitude results of reflection and transmission coefficients with co-polarization. (B) Simulated phase results of reflection and transmission coefficients with co-polarization. (C) phase differences of reflection coefficient and transmission coefficient.

The reflection and transmission coefficients of elements “0” and “1” are illumined in Figures 3, 4 with LCP and RCP incidences. On one hand, the amplitude of refection coefficient with co-circular polarization is more than 0.5 from 9.35 to 10.65 GHz in Figure 3A. The phase difference of co-circular polarization between elements “0” and “1” is about 180deg in the same frequency range from Figure 3B. These results satisfy the reflection principle of PB phase. On the other hand, the amplitude of transmission coefficient with cross-circular polarization is more than 0.7 from 9 to 9.85 GHz and their phase difference is about 180deg between element “0” and element “1”. Consequently, the elements “0” and “1” of MCMS are an excellent choice to realize the LCP transmission and RCP reflection.

FIGURE 3

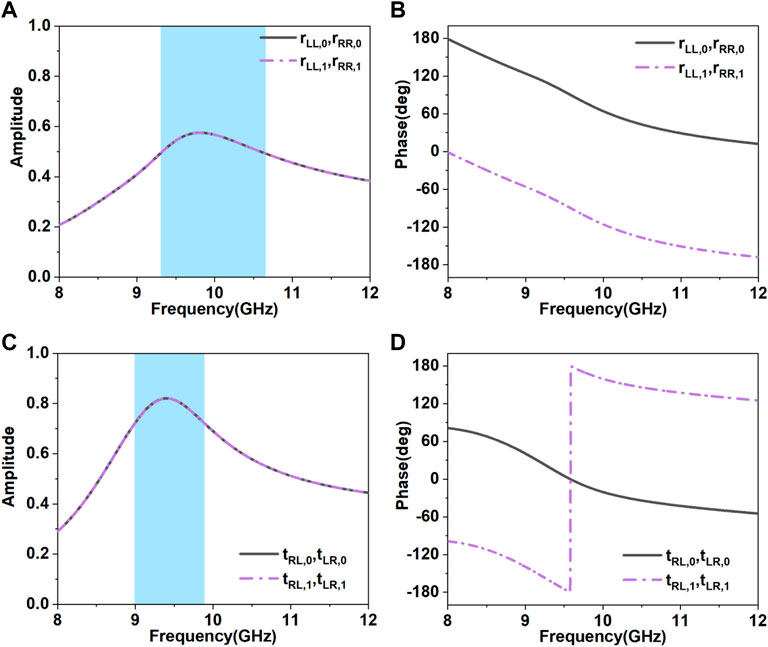
FIGURE 3. Reflection and transmission coefficients of elements “0” and “1” with LCP and RCP incidences. (A) Simulated amplitude results of reflection coefficient with co-circularly polarization. (B) Simulated phase results of reflection coefficient with co-circularly polarization. (C) Simulated amplitude results of transmission coefficient with cross-circularly polarization. (D) Simulated phase results of transmission coefficient with cross-circularly polarization.

FIGURE 4

FIGURE 4. Rotation angle distribution of 32 × 32 elements for MCMS based on the convolution theorem of patterns and the phase compensation principle. (A) Rotation angle distribution of 1024 elements with angle changing along x-axis based on elements “0” and “1”. (B) Rotation angle distribution of 1024 elements with changing along y-axis based on elements “0” and “1”. (C) Rotation angle distribution of phase compensation for 1024 elements. (D) Rotation angle distribution of 32 × 32 elements for the proposed MCMS.

Metasurface and its Performance

The multifunctional coding metasurface has been designed based on the convolution theorem of patterns. In the design, 1024 elements have been used. The rotation angle distributions of the 1024 elements are respectively demonstrated in Figures 3A,B with the angle changing along x- and y-axis based on elements “0” and “1”. The excited source of MCMS is a linearly polarized horn antenna with frequency band of 8–12 GHz. In order to eliminate the directly transmitted beam, the phase compensation method is used in the design for MCMS. When the horn antenna is at the position of (0, 0, z_f), the compensational phase of the element with (x_m, y_n) position can be generally calculated by

${\varphi }_{mn}=k_0\left(r_{mn}-z_f\right)=k_0\left(\sqrt{{\left(x_m\right)}^2+{\left(y_n\right)}^2}-z_f\right)=\frac{2\pi f_0}{c}\left(\sqrt{{\left(x_m\right)}^2+{\left(y_n\right)}^2}-z_f\right)(5)$

Where f₀ is the frequency and k₀ is the wave vector. c is the speed of light. Consequently, the rotation angle distribution of phase compensation can be determined for 1024 elements in Figure 3C, when the z_f = 240 mm is chosen. Finally, the rotation angle distribution of 32 × 32 elements for MCMS is illustrated in Figure 3D according to the convolution theorem. The array of MCMS is shown in Figure 1.

The simulated results of MCMS are illustrated in Figure 5. MCMS respectively realizes the four reflective beams in Figure 5A, and four transmissive beams in Figure 5B. It is clear that the four beams with RCP are obvious in the reflective space and their gain is much more than that in the transmissive space. On the contrary, we can see the four transmissive beams with gain of 17dBi and the chaotically reflective beam for MCMS with left circular polarization. It is necessary to note that the gain of four transmissive beams with LCP is more than that of four reflective beams for 3dB because the transmission coefficients of unit cell are more than the reflection coefficients. The position of the beam can be defined by deflection angle and azimuth angle (θ_s, φ_s). According to the generalized Snell’s law, the unidimensional deflection angle θ_u of the beams in x- or y-axis can be defined as follows

$\begin{array}{cc}{\theta }_{ui}=\arcsin \left(\lambda /Le\right),& i\in \left[x,y\right]\end{array}(6)$

Where λ is the wavelength and Le is the length of subarray. The deflection angle θ_s in space is calculated by

${\theta }_s=\mathrm{s}\mathrm{i}{\mathrm{n}}^{-1}{\left({\sin }^2{\theta }_{ux}+{\sin }^2{\theta }_{uy}\right)}^{0.5}(7)$

FIGURE 5

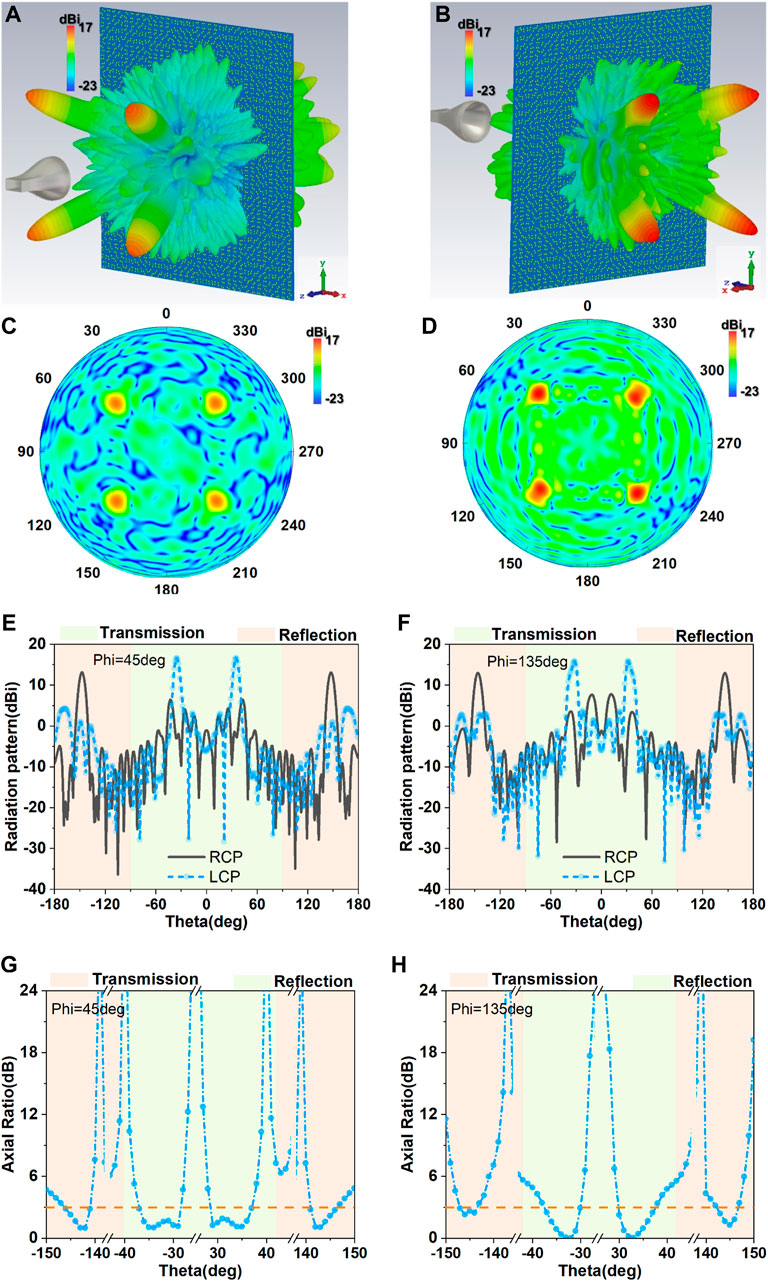
FIGURE 5. Four reflective beams of RCP and four transmissive beams of LCP in three-dimension and two-dimension for x-polarized incidence at 9.5 GHz. (A) Four reflective beams of RCP in three-dimension. (B) Four transmissive beams of LCP in three-dimension. (C) Reflective beam distribution with RCP. (D) Transmissive beam distribution with LCP. (E) Four reflective beams of RCP in two-dimension in the plane of 45deg. (F) Four transmissive two-dimension beams of LCP in the plane of 135deg. (G) Axial ratio results of transmissive and reflective beams in the plane of 45deg. (H) Axial ratio results of transmissive and reflective beams in the plane of 135deg.

Furthermore, the azimuth angle φ_s is calculated by

${\phi }_s=\mathrm{t}\mathrm{a}{n}^{-1}\left(\frac{\sin {\theta }_{uy}}{\sin {\theta }_{ux}}\right)(8)$

In the design, λ = 31.6 mm at 9.5 GHz. Le = 8 × 10 = 80 mm. So the deflection angle in x-axis can be chosen as θ_ux = 23.3deg and that in y-axis is θ_uy = 23.3deg. Moreover, the theoretical deflection angle and azimuth angle of transmissive beams for MCMS in space are 33.9, 45, 135, 225, and 315deg according to the formulas (6–8), respectively. (θ_s = 33.9deg. φ_s = 45, 135, 225, 315deg). The position of the transmissive beams are (33.9deg, 45deg), (33.9deg, 135deg), (33.9deg, 225deg), and (33.9deg, 315deg). The theoretical deflection angle and azimuth angle of reflective beams are 146.1, 45, 135, 225, and 315deg respectively. (θ_s = 146.1deg. φ_s = 45, 135, 225, 315deg). The position of the reflective beams are (146.1deg, 45deg), (146.1deg, 135deg), (−146.1deg, 225deg), and (−146.1deg, 315deg). The position of beams is verified in Figures 5C,D and the simulated results agree well with the theoretical data. Two dimensional radiation patterns in the plane of φ_s = 45 and 135deg are respectively demonstrated in Figures 5E,F. From simulated results, it is found that the excellent four beams of left circular polarization are obtained by MCMS in the transmissive space and the four beams of right circular polarization with gain of 13.8dBi are achieved in the reflective space. Meanwhile, the lower side-lobe level of -12.8dB is achieved for transmission as well as the side-lobe level of -8.1dB for reflection of MCMS. The simulated deflection angles of transmissive beams are 35 and 147deg. It is necessary to note that there are only negligible differences of 1.1 and 0.9deg between the simulation and the theory. From Figures 5G,H, we can see that the axial ratio is less than 3dB for the reflective and transmissive beams. Correspondingly, when it is the y-polarized incidence, the transmissive RCP waves and reflective LCP waves are obtained for the proposed metasurface. Consequently, the MCMS can realize the dual-circularly polarized beams and the beam focusing with transmission and reflection in the whole space.

Fabrication and Measurement

To validate the multifunction, a prototype of MCMS was fabricated by printed circuit board technology and measured by the free-space method in a microwave anechoic chamber in Figure 6A. The F4B substrate with permittivity of 2.2, loss tangent of 0.001, and thickness of 3 mm had been chosen for the MCMS prototype. A vector network analyzer (Agilent N5230C) and three standard-gain horn antennas with linear and dual-circular polarization were used for emitting and receiving EM waves. The focal-distance-to-diameter ratio is 0.75 between linear horn antenna and metasurface prototype and their distance is 240 mm. Experimental normalized radiation patterns with measured gain of 16.3dB are given in Figures 6B,C. The four beams with LCP in transmission space and the four beams with RCP in reflection space are demonstrated by measurement. As shown in Figures 6B,C, the side-lobe level of LCP beam is about −10dB and that of RCP beam is about −6.1dB. It can also be seen that the experimental deflection angle of transmissive and reflective beams is 35 and 145deg respectively. Furthermore, the transmission efficiency is defined as the transmissive field energy divided by the total radiated energy and then multiplied by radiation efficiency. The reflection efficiency is defined as the reflective field energy divided by the total radiated energy and then multiplied by radiation efficiency. The simulated and experimental results of radiation efficiency, transmission efficiency, and reflection efficiency are illustrated in Figures 6D,E for MCMS at 9.5 GHz respectively. The simulated and experimental radiation efficiencies are all more than 90% for the linearly polarized horn antenna with MCMS. It is obvious that the transmission efficiency of 0.62 is more than the reflection efficiency of 0.32 for MCMS prototype in measurement. The difference between simulation and measurement is attributed to the limited machining accuracy of the MCMS prototype and the experimental environment. The overall measurement verifies the performance of LCP transmissive beams and RCP reflective beams for MCMS with x-polarized incidence.

FIGURE 6

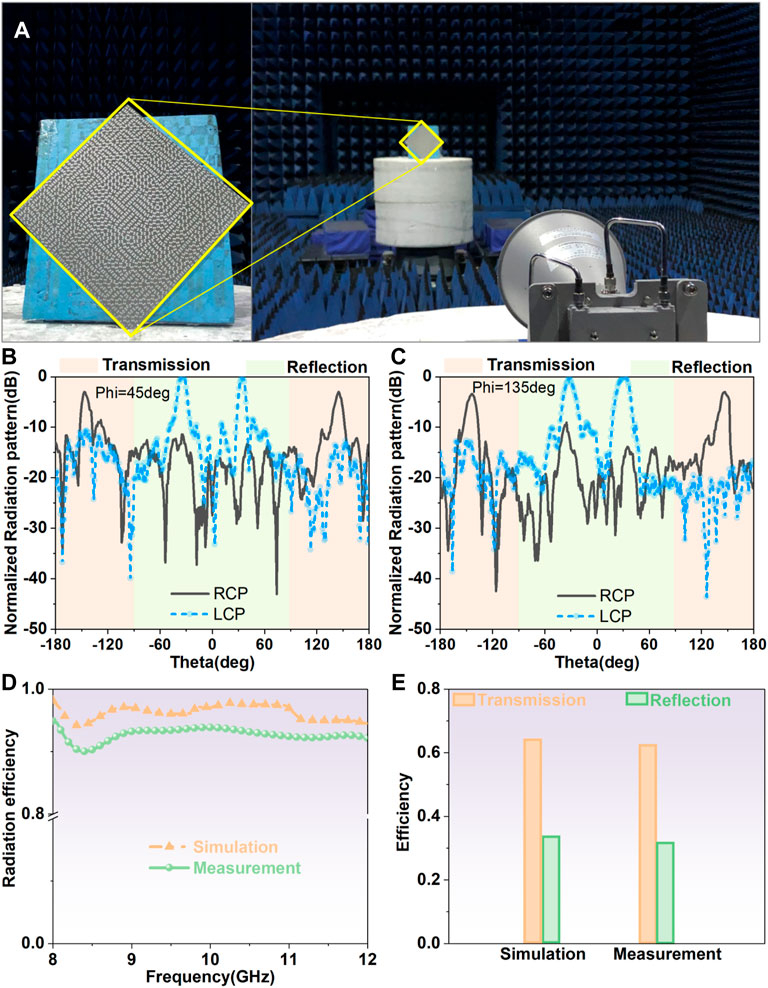
FIGURE 6. Measured environment and normalized radiation patterns of MCMS prototype in measurement. (A) Measured environment and the prototype of MCMS. (B) Normalized radiation patterns of MCMS prototype with phi = 45deg at 9.5 GHz. (C) Normalized radiation patterns of MCMS prototype with phi = 135deg at 9.5 GHz. (D) Simulated and experimental radiation efficiency. (E) Simulated and experimental results of transmission efficiency and reflection efficiency for MCMS at 9.5 GHz.

Conclusion

In summary, we designed, fabricated, and experimentally demonstrated a multifunctional coding metasurface with multi beams and dual-circular polarization. The metallic dumbbell with two quadrate voids etched on the single layer substrate were designed for the element of proposed metasurface. The phases of transmissive and reflective waves are controlled by rotating the metallic dumbbell. Based on the Pancharatnam-Berry phase, the convolution theorem of patterns, and the phase compensation principle, the four-beam with left circular polarization in the transmissive space and the right circularly polarized four-beam in the reflective space have been proven by the proposed MCMS with x-polarized incidence in simulation and measurement. The proposed MCMS are promising for many practical applications such as target detection systems, wireless communication, and microwave imaging.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

ZL contributed by analyzing the model. BH and GH contributed to data processing. XL, HY, and XC contributed to fabrication and measurement.

Funding

This work was supported by the China Postdoctoral Science Foundation (Grant Nos. 2021T140111, 2019M650098, and 2019M653960), the Postdoctoral Research Funding of Jiangsu Province (2019K219), the National Natural Science Foundation of China (Grant Nos.62171460 and 61801508), the Natural Science Basic Research Program of Shaanxi Province, China (Grant Nos. 2020JM-350, 20200108, and 20210110), the Young Innovation Team at Colleges of Shaanxi Province, China (Grant No.2020022), and the Postdoctoral Innovative Talents Support Program of China (Grant No. BX20180375).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, F., Cheng, Y., and Luo, H. (2020). Temperature Tunable Narrow-Band Terahertz Metasurface Absorber Based on InSb Micro-Cylinder Arrays for Enhanced Sensing Application. IEEE Access 8, 82981–82988. doi:10.1109/ACCESS.2020.2991331

CrossRef Full Text | Google Scholar

Chen, K., Feng, Y., Monticone, F., Zhao, J., Zhu, B., Jiang, T., et al. (2017). A Reconfigurable Active Huygens' Metalens. Adv. Mater. 29 (17), 1606422. doi:10.1002/adma.201606422

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, Y., Liu, J., Chen, F., Luo, H., and Li, X. (2021). Optically Switchable Broadband Metasurface Absorber Based on Square Ring Shaped Photoconductive Silicon for Terahertz Waves. Phys. Lett. A 402, 127345. doi:10.1016/j.physleta.2021.127345

CrossRef Full Text | Google Scholar

Cheng, Y., Zhu, X., Li, J., Chen, F., Luo, H., and Wu, L. (2021). Terahertz Broadband Tunable Reflective Cross-Polarization Convertor Based on Complementary Cross-Shaped Graphene Metasurface. Physica E: Low-dimensional Syst. Nanostructures 134, 114893. doi:10.1016/j.physe.2021.114893

CrossRef Full Text | Google Scholar

Cheng, Y., Yu, J., and Li, X. (2022). Tri-band High-Efficiency Circular Polarization Convertor Based on Double-Split-Ring Resonator Structures. Appl. Phys. B 128 (1), 1–8. doi:10.1007/s00340-021-07724-4

CrossRef Full Text | Google Scholar

Cui, T. J., Qi, M. Q., Wan, X., Zhao, J., and Cheng, Q. (2014). Coding Metamaterials, Digital Metamaterials and Programmable Metamaterials. Light Sci. Appl. 3, e218. doi:10.1038/lsa.2014.99

CrossRef Full Text | Google Scholar

Ding, G., Chen, K., Luo, X., Zhao, J., Jiang, T., and Feng, Y. (2019). Dual-helicity Decoupled Coding Metasurface for Independent Spin-To-Orbital Angular Momentum Conversion. Phys. Rev. Appl. 11 (4), 044043. doi:10.1103/physrevapplied.11.044043

CrossRef Full Text | Google Scholar

Fan, J., Cheng, Y., and He, B. (2021). High-efficiency Ultrathin Terahertz Geometric Metasurface for Full-Space Wavefront Manipulation at Two Frequencies. J. Phys. D: Appl. Phys. 54 (11), 115101. doi:10.1088/1361-6463/abcdd0

CrossRef Full Text | Google Scholar

Garcia-Marin, E., Sanchez-Olivares, P., Masa-Campos, J. L., Ruiz-Cruz, J. A., Herranz-Alpanseque, J., Garcia-Froilan, R., et al. (2021). Dual Circularly Polarized Array Antenna Based on Corporate Feeding Network in Square Waveguide Technology. IEEE Trans. Antennas Propagat. 69 (3), 1763–1768. doi:10.1109/TAP.2020.3019355

CrossRef Full Text | Google Scholar

Han, J., Cao, X., Gao, J., Wei, J., Zhao, Y., Li, S., et al. (2018). Broadband Radar Cross Section Reduction Using Dual-Circular Polarization Diffusion Metasurface. Antennas Wirel. Propag. Lett. 17 (6), 969–973. doi:10.1109/LAWP.2018.2827124

CrossRef Full Text | Google Scholar

Han, B., Li, S., Cao, X., Han, J., Jidi, L., and Li, Y. (2020). Dual-band Transmissive Metasurface with Linear to Dual-Circular Polarization Conversion Simultaneously. AIP Adv. 10 (12), 125025. doi:10.1063/5.0034762

CrossRef Full Text | Google Scholar

Han, B., Li, S., Li, Z., Huang, G., Tian, J., and Cao, X. (2021). Asymmetric Transmission for Dual-Circularly and Linearly Polarized Waves Based on a Chiral Metasurface. Opt. Express 29, 19643. doi:10.1364/OE.425787

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, C., Kumar, B. P., Kumar, V. S., and Srinivasan, V. V. (2013). Dual Circularly Polarized Spherical Phased-Array Antenna for Spacecraft Application. IEEE Trans. Antennas Propagat. 61 (2), 598–605. doi:10.1109/TAP.2012.2220328

CrossRef Full Text | Google Scholar

Li, S., Gao, J., Cao, X., Li, W., Zhang, Z., and Zhang, D. (2014). Wideband, Thin, and Polarization-Insensitive Perfect Absorber Based the Double Octagonal Rings Metamaterials and Lumped Resistances. J. Appl. Phys. 116 (4), 043710. doi:10.1063/1.4891716

CrossRef Full Text | Google Scholar

Li, S.-J., Gao, J., Cao, X.-Y., Zhang, Z., Liu, T., Zheng, Y.-J., et al. (2015). Hybrid Metamaterial Device with Wideband Absorption and Multiband Transmission Based on Spoof Surface Plasmon Polaritons and Perfect Absorber. Appl. Phys. Lett. 106 (18), 181103. doi:10.1063/1.4919789

CrossRef Full Text | Google Scholar

Li, S. J., Cao, X. Y., Xu, L. M., Han, J. F., Zhang, Z., Zhang, D., et al. (2016). Ultra-broadband Reflective Metamaterial with RCS Reduction Based on Polarization Convertor, Information Entropy Theory and Genetic Optimization Algorithm. Sci. Rep. 6, 37409. doi:10.1038/srep37409

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S. J., Cui, T. J., Li, Y. B., Zhang, C., Li, R. Q., Cao, X. Y., et al. (2019). Multifunctional and Multiband Fractal Metasurface Based on Inter-metamolecular Coupling Interaction. Adv. Theor. Simul. 2, 1900105. doi:10.1002/adts.20197003010.1002/adts.201900105

CrossRef Full Text | Google Scholar

Li, S. J., Li, Y. B., Li, H., Wang, Z. X., Zhang, C., Guo, Z. X., et al. (2020). A Thin Self-Feeding Janus Metasurface for Manipulating Incident Waves and Emitting Radiation Waves Simultaneously. Annalen der Physik 532 (5), 2000020. doi:10.1002/andp.202000020

CrossRef Full Text | Google Scholar

Li, S. J., Li, Y. B., Li, R. Q., Cheng, Q., and Cui, T. J. (2020). Digital-Coding-Feeding Metasurfaces for Differently Polarized Wave Emission, Orbit Angular Momentum Generation, and Scattering Manipulation. Adv. Photo Res. 1, 2000012. doi:10.1002/adpr.202000012

CrossRef Full Text | Google Scholar

Li, H., Li, Y. B., Shen, J. L., and Cui, T. J. (2020). Low-Profile Electromagnetic Holography by Using Coding Fabry-Perot Type Metasurface with In-Plane Feeding. Adv. Opt. Mater. 8 (9), 1902057. doi:10.1002/adom.201902057

CrossRef Full Text | Google Scholar

Li, Z. Y., Li, S. J., Han, B. W., Huang, G. S., Guo, Z. X., and Cao, X. Y. (2021). Quad-band Transmissive Metasurface with Linear to Dual-Circular Polarization Conversion Simultaneously. Adv. Theor. Simulations 4 (8), 2100117. doi:10.1002/adts.202100117

CrossRef Full Text | Google Scholar

Li, S. J., Li, Y. B., Zhang, L., Luo, Z. J., Han, B. W., Li, R. Q., et al. (2021). Programmable Controls to Scattering Properties of a Radiation Array. Laser Photon. Rev. 15 (2), 2000449. doi:10.1002/lpor.202000449

CrossRef Full Text | Google Scholar

Li, S. J., Han, B. W., Huang, G. S., Li, Z. Y., and Cao, X. Y. (2021). Two-bit Coding-Feeding Metasurface with Radiation and Scattering Manipulation. Chin. J. radio Sci. 36 (6), 925–931. doi:10.12265/j.cjors.2021111

CrossRef Full Text | Google Scholar

Lin, J., Mueller, J. P. B., Wang, Q., Yuan, G., Antoniou, N., Yuan, X.-C., et al. (2013). Polarization-controlled Tunable Directional Coupling of Surface Plasmon Polaritons. Science 340, 331–334. doi:10.1126/science.1233746

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, K., Wang, G., Cai, T., and Li, T. (2020). Dual-band Transmissive Circular Polarization Generator with High Angular Stability. Opt. Express 28 (10), 14995–15005. doi:10.1364/oe.393388

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Cui, T. J., Zhang, L., Xu, Q., Wang, Q., Wan, X., et al. (2016). Metasurfaces: Convolution Operations on Coding Metasurface to Reach Flexible and Continuous Controls of Terahertz Beams (Adv. Sci. 10/2016). Adv. Sci. 3, 1600156. doi:10.1002/advs.201670053

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, R., Liu, Z., Zhu, W., Du, S., Gu, C., and Li, J. (2021). Asymmetrical Chirality in 3D Bended Metasurface. Adv. Funct. Mater. 31 (31), 2100689. doi:10.1002/adfm.202100689

CrossRef Full Text | Google Scholar

Tang, X., Li, C., Gan, H., He, Y., Jing, X., Fang, B., et al. (2021). Enhancement of Transmission Efficiency on Pancharatnam−Berry Geometric Phase Encoding Metasurfaces. Annalen der Physik 533 (2), 2000494. doi:10.1002/andp.202000494

CrossRef Full Text | Google Scholar

Xu, R., Li, J.-Y., Yang, J.-J., Wei, K., and Qi, Y.-X. (2017). A Design of U-Shaped Slot Antenna with Broadband Dual Circularly Polarized Radiation. IEEE Trans. Antennas Propagat. 65 (6), 3217–3220. doi:10.1109/TAP.2017.2689069

CrossRef Full Text | Google Scholar

Yuan, Y., Zhang, K., Ding, X., Ratni, B., Burokur, S. N., and Wu, Q. (2019). Complementary Transmissive Ultra-thin Meta-Deflectors for Broadband Polarization-independent Refractions in the Microwave Region. Photon. Res. 7 (1), 80–88. doi:10.1364/PRJ.7.000080

CrossRef Full Text | Google Scholar

Zhang, A., and Yang, R. (2019). Anomalous Birefringence through Metasurface-Based Cavities with Linear-To-Circular Polarization Conversion. Phys. Rev. B 100 (24), 245421. doi:10.1103/PhysRevB.100.245421

CrossRef Full Text | Google Scholar

Zhang, Z., Cao, X., Gao, J., and Li., S. (2016). Broadband Metamaterial Reflectors for Polarization Manipulation Based on Cross/ring Resonators. Radioengineering 25 (3), 436–441. doi:10.13164/re.2016.0436

CrossRef Full Text | Google Scholar

Zhao, J., Yang, X., Dai, J. Y., Cheng, Q., Li, X., Qi, N. H., et al. (2019). Programmable Time-Domain Digital-Coding Metasurface for Non-linear Harmonic Manipulation and New Wireless Communication Systems. Natl. Sci. Rev. 6 (2), 231–238. doi:10.1093/nsr/nwy135/5184479

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, T., Jing, X., Tang, X., Bie, X., Luo, T., Gan, H., et al. (2021). Manipulation of Wave Scattering by Fourier Convolution Operations with Pancharatnam-Berry Coding Metasurface. Opt. Lasers Eng. 141 (2), 106556. doi:10.1016/j.optlaseng.2021.106556

CrossRef Full Text | Google Scholar

Zhu, X., Cheng, Y., Fan, J., Chen, F., Luo, H., and Wu, L. (2022). Switchable Efficiency Terahertz Anomalous Refraction and Focusing Based on Graphene Metasurface. Diamond Relat. Mater. 121, 108743. doi:10.1016/j.diamond.2021.108743

CrossRef Full Text | Google Scholar