Magnetically Reconfigurable Unidirectional Propagation of Electromagnetic Waves by Zero-Index–Based Heterostructured Metamaterials

Luo, Qilin; Zhao, Lingzhong; Zhou, Jialin; Zhang, Lin; Wen, Guangfeng; Ba, Qingtao; Wu, Huabing; Lin, Zhifang; Liu, Shiyang

doi:10.3389/fmats.2022.845344

ORIGINAL RESEARCH article

Front. Mater., 16 March 2022

Sec. Metamaterials

Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.845344

This article is part of the Research Topic Magneto-Optic Effect-Based Metamaterials and Photonic Crystals View all 5 articles

Magnetically Reconfigurable Unidirectional Propagation of Electromagnetic Waves by Zero-Index–Based Heterostructured Metamaterials

Qilin Luo^1,2

Lingzhong Zhao¹

Jialin Zhou¹

Lin Zhang¹

Guangfeng Wen¹

Qingtao Ba³

Huabing Wu⁴

Zhifang Lin^5,6

Shiyang Liu¹*

¹Key Laboratory of Optical Information Detecting and Display Technology, Zhejiang Normal University, Jinhua, China
²Xiangsihu College, Guangxi University for Nationalities, Nanning, China
³Department of Physics and Institute of Electromagnetics and Acoustics, Xiamen University, Xiamen, China
⁴School of Electronic Sciences and Engineering, Nanjing University, Nanjing, China
⁵State Key Laboratory of Surface Physics, Key Laboratory of Micro and Nano Photonic Structures and Department of Physics, Fudan University, Shanghai, China
⁶Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing, China

We present a zero-index–based heterostructured magnetic metamaterial (HSMM) composed of two arrays of ferrite rods with different radii and lattice separations, which exhibits unidirectional propagation of electromagnetic (EM) waves, and the unidirectionality is reconfigurable dependent on the bias magnetic field (BMF). By calculating the photonic band diagrams and the effective constitutive parameters, it is shown that, for the MMs with two groups of lattice separations and ferrite rod radii, the effective refractive index is switched either from effective zero index (EZI) to effective positive index (EPI) by decreasing the BMF for one MM or from EZI to effective negative index (ENI) for the other MM by increasing the BMF. As a result, two kinds of HSMMs can be constructed with the combination of either EZI and ENI or EZI and EPI, both of which can be used to implement the unidirectional transport of EM waves and exhibit reconfigurable unidirectionality by either decreasing or increasing the BMF, thus providing us with more degrees of freedom. The concept put forward in the present work can be possibly extended to the heterostructured metamaterials made of phase-change materials and realize reconfigurable EM properties in optical frequency by tuning the temperature.

1 Introduction

Unidirectional manipulation of the signal is a widely involved phenomenon from the traffic control in everyday life to the electronic diodes in modern electronic devices. The idea is also scientifically interesting due to the rich physics and the promising applications. As is certain, regarding electromagnetic (EM) waves, the unidirectionality originates from the symmetry breaking of either the photonic systems or the photons or both of them due to the mutual interaction. Hitherto, a variety of systems have been shown to be functionalized as the platforms to implement unidirectional rectification on different waves, especially with the aid of metamaterials, such as photonic systems for EM waves (Wang et al., 2008, 2009; Yu and Fan, 2009; Liu et al., 2011; Lin et al., 2011; Poo et al., 2011; Khanikaev et al., 2013; Fang and Fan, 2013; Lin et al., 2013; Pors et al., 2014; Fu et al., 2014; Shi et al., 2015; Morgado and Silveirinha, 2018; Guo et al., 2019; Thomaschewski et al., 2019; He et al., 2019; Yuan and Lu, 2019; Deng et al., 2020; Chen et al., 2020; Wang M. D et al., 2021), phononic systems for acoustic waves (Liang et al., 2010; Li et al., 2011; Cicek et al., 2012; Midya, 2014; Lu et al., 2016; Kan et al., 2018; Qian et al., 2020; Zhu et al., 2020; Gu et al., 2021; Liu et al., 2021; Zhang et al., 2021), elastic metamaterial systems for elastic waves (Mousavi et al., 2015; Yan et al., 2018), thermal systems for heat flux (Li et al., 2004; Zhang et al., 2020), optomechanical systems for the unidirectional response of optomechanical interactions (Coulais et al., 2017; Brandenbourger et al., 2019), and even the valley-dependent nanophotonic systems for quantum information processing (Barik et al., 2020; Chen Y et al., 2021). A great deal of proposals have been brought out to serve this purpose, among which the non-reciprocal systems with the time-reversal-symmetry breaking nature are typical paradigms, fulfilled either by introducing the bias magnetic field (BMF) in magneto-optical materials (Wang et al., 2008, 2009; Liu et al., 2011; Poo et al., 2011; Chen et al., 2020; Wang M. D et al., 2021) or by introducing the drift current in graphene-based systems (Morgado and Silveirinha, 2018; Zhang et al., 2020) or by employing the spatiotemporal materials (Yu and Fan, 2009; Fang and Fan, 2013; Sounas et al., 2013; Guo et al., 2019) or non-linear materials (Liang et al., 2010; Shi et al., 2015). Besides, the valley-based topological systems (Khanikaev et al., 2013; Lu et al., 2016; He et al., 2019; Zhang et al., 2021) and the parity–time symmetric systems (Lin et al., 2011; Midya, 2014; Kan et al., 2018; Yuan and Lu, 2019) have been adopted to unidirectionally engineer the transport of both EM waves (Lin et al., 2011; Khanikaev et al., 2013; He et al., 2019; Yuan and Lu, 2019) and acoustic waves (Midya, 2014; Lu et al., 2016; Kan et al., 2018; Zhang et al., 2021). It should be pointed out that based on the polarization sensitivity of the metasurfaces (Wang S et al., 2021), unidirectional manipulation on the light beam can be achieved such as unidirectional transmission by bianisotropic metasurfaces (Pfeiffer et al., 2014), unidirectional polarization encryption by layered plasmonic metasurfaces (Frese et al., 2019), and spin-selective terahertz unidirectional transmission by all-silicon metasurfaces (Li et al., 2021).

With regard to the wave functional systems with Lorentz reciprocity, the unidirectional wave control can be achieved by breaking the symmetry of either the geometric configurations (Cicek et al., 2012; Li et al., 2013; Fu et al., 2014; Han et al., 2016; Shen et al., 2016; Gu et al., 2021) or the mode profiles (Qian et al., 2020; Chen J. H et al., 2021; Liu et al., 2021) or both simultaneously (Li et al., 2011; Zhu et al., 2020). Among others, zero-index materials (ZIMs) have been used as a fundamental ingredient to implement the unidirectional transmission for both EM waves (Fu et al., 2014) and acoustic waves (Li et al., 2013; Shen et al., 2016). ZIMs can be roughly classified into an epsilon-near-zero (ENZ) material, mu-near-zero (MNZ) material, and epsilon-and-mu-near-zero (EMNZ) material (Liberal and Engheta, 2017) for EM waves and are further extended to the other circumstances such as acoustic waves (Dubois et al., 2017), elastic waves (Liu and Liu, 2015), thermal radiation (Li et al., 2019), and even the zero-index Weyl semimetals (Zangeneh-Nejad and Fleury, 2020). There have been many miraculous phenomena triggered by the ZIMs such as wave tunneling (Silveirinha and Engheta, 2006; Hajian et al., 2016; Liberal et al., 2020), cloaking effect (Nguyen et al., 2010; Chu et al., 2018), non-linear effect (Suchowski et al., 2013; Dass et al., 2020), wavefront engineering (Alù et al., 2007; Huang et al., 2011), two-qubit entanglement in the long range (Özgün et al., 2016), unidirectional single-photon generation (Xu et al., 2016), and three-dimensional (3D) perfect wave steering by the recently reported 3D ZIMs (Xu et al., 2021).

For most of the ZIMs, the effective indices cannot be changed once the structure is fixed, which makes the properties of the associated systems non-adjustable. To release this restriction, the ZIM concerned in this work is composed of an array of ferrite rods so that the effective index can be transformed from zero to negative or to positive controlled by the magnitude of BMF, thus termed magnetic metamaterials (MMs). As illustrated in the earlier research, the EM properties of MMs can be controlled by either the BMF or the ambient temperature (Liu et al., 2008a; Yu et al., 2014). Due to the non-reciprocal feature of magnetic surface plasmons inherently in the magneto-optical materials (Liu et al., 2008b), the MM-based systems exhibit strong unidirectional features such as unidirectional scattering (Liu et al., 2010), unidirectional reflection (Chui et al., 2010), unidirectional absorption (Yu et al., 2012), and the unidirectional Goos–Hänchen effects reinforced by the topological surface states (Chen et al., 2017; Wu et al., 2019). However, in the present work, the operating frequency is far from the magnetic surface plasmon resonance, and thus, the unidirectional propagation does not arise from the non-reciprocity, but solely from the controllable effective zero index (EZI) of MMs. The construction of ZIM-based heterostructured MMs (HSMMs) is to break the geometric symmetry of left-hand side (LHS) with respect to the right-hand side (RHS). As a consequence, the EM wave propagating in HSMMs experiences a transition from the “LHS passing” state to the “RHS passing” state with the reconfigurability associated with the transformation of HSMMs from one combination to another combination controlled by tuning the BMF. The EZI and its change to effective negative index (ENI) or to effective positive index (EPI) can be visualized by the effective-medium calculations and photonic band diagrams. The unidirectional propagation and its reconfigurability are further examined by simulating the electric field patterns. The results presented in this work add more flexibility in unidirectionally controlling EM waves and might find potential applications in microwave photonics.

2 ZIM-Based HSMMs

The ZIMs are constructed by MMs composed of an array of ferrite rods arranged periodically in the air as a triangular lattice with the rod axes along z axes. For the convenience of comparison, the HSMMs are constructed either by the building blocks of different effective indices realized by solely varying the rod radius or by the building blocks of different effective indices realized by varying both the rod radius and the lattice separation, which will be further specified later for the HSMMs with different functionalities. The ferrite materials possess the intrinsic magnetic response with the magnetic permeability a second-rank tensor under full magnetization along the rod axis (Pozar, 2005):

\hat{μ} = (\begin{matrix} μ_{r} & - i μ_{κ} & 0 \\ i μ_{κ} & μ_{r} & 0 \\ 0 & 0 & 1 \end{matrix}), (1)

where $μ_{r} = 1 + ω_{m} (ω_{0} + i α ω) / [{(ω_{0} + i α ω)}^{2} - ω^{2}]$ , $μ_{κ} = ω_{m} ω / [{(ω_{0} + i α ω)}^{2} - ω^{2}]$ with ω₀ = 2πf₀ = 2πγH₀ being the resonant frequency determined by the sum of the BMF applied along the z direction and the anisotropy field and ω_m = 2πf_m = 2πγM_s being the characteristic frequency determined by the saturation magnetization M_s, where the gyromagnetic ratio γ = 2.8 MHz/Oe. The relative permittivity is taken as ɛ_s = 25, the typical value for the saturation magnetization of single-crystal yttrium-iron-garnet (YIG) is M_s = 1750 Gauss, and the decay coefficient is α = 3 × 10^–4, which is ignored for the simplicity of analysis. In a two-dimensional system, the magnetic permeability only takes effect for the transverse magnetic (TM) mode with the electric field polarized along the rod axis (Wang et al., 2009; Poo et al., 2011).

To illustrate how the unidirectional propagation is implemented by the HSMMs, in Figure 1, the schematic diagram is presented to explain the principle, where the BMFs $H_{0}^{2}$ and $H_{0}^{1}$ are along the z axis. The building blocks involved in the construction of HSMMs include the effective ZIMs, the effective negative-index materials (NIMs), and the effective positive-index materials (PIMs). As shown in panel A, the HSMM is made up of the ZIM and NIM, and due to the momentum match requirement of ZIM, only the LHS incident EM wave can be transmitted, while the EM wave incident from the RHS is totally reflected, resulting in the unidirectional propagation as illustrated by the arrows. Then, by decreasing the BMF from $H_{0}^{1}$ to $H_{0}^{2}$ , the ZIM is turned into the PIM and the NIM is turned into the ZIM so that a different HSMM is obtained as shown in panel B, which allows for only the transmittance of the RHS incident EM wave, corresponding to the “RHS passing” state. Therefore, the reconfigurable unidirectional propagation is implementable by designing the HSMMs with its unidirectionality controlled by the BMF. The second kind of HSMM made up of the ZIM and PIM is shown in Figure 1C, which can be used to achieve a similar reconfigurable unidirectionality by increasing the BMF from $H_{0}^{2}$ in panel C to $H_{0}^{1}$ in panel D. The schematic diagram exhibits the feasibility of present design, and the corresponding performance will be further elaborated by the field simulations in the latter part.

FIGURE 1

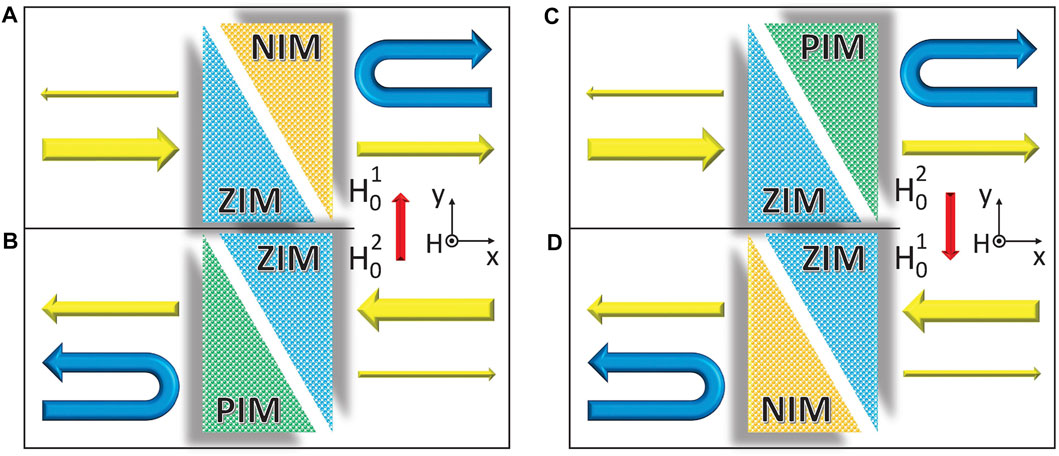
FIGURE 1. Schematic diagram illustrating the reconfigurable unidirectional propagation by HSMMs with ZIMs, NIMs, and PIMs as the building blocks. (A) For the HSMM made up of the ZIM and NIM, the LHS incidence corresponds to the “passing” state as marked by the yellow arrows, while the RHS incidence corresponds to the total reflection as marked by the blue arrows. (B) By decreasing the BMF from $H_{0}^{1}$ to $H_{0}^{2}$ , the HSMM is turned into that made up of the PIM and ZIM, thus leading to the “passing” state for the RHS incidence, while LHS incidence is forbidden, giving rise to the reconfigurable unidirectionality from the “LHS passing” state to the “RHS passing” state. For the second kind of HSMM shown in (C,D), the reconfigurability is functionalized by increasing the BMF from $H_{0}^{2}$ (C) to $H_{0}^{1}$ (D), resulting in the transformation from the “LHS passing” state to the “RHS passing” state. Although the reconfigurable unidirectionality in (A,B) is the same as that in (C,D), the beam steering effect is different.

3 EZI Controlled by BMF

To examine the zero-index features of the MMs, we first retrieve the effective constitutive parameters by using the coherent potential approximation–based effective-medium theory (Jin et al., 2009). For the convenience of analysis, two typical MMs with the same lattice separation a = 15 mm and yet different ferrite rod radii are considered to obtain the required effective indices so that they can be used as the appropriate building blocks. Two typical rod radii of r₁ = 3.64 mm and r₂ = 3.82 mm are chosen, and the corresponding effective constitutive parameters are calculated and presented in Figures 2B,D, respectively. At the operating frequency f = 2.5 GHz, it can be found that the effective permittivity is ɛ_eff = − 0.5 and the effective permeability is μ_eff = − 2.0 for r₁ = 3.64 mm, corresponding to the ENI of $n_{eff, 1} = \sqrt{ε_{eff, 1}} \cdot \sqrt{μ_{eff, 1}} = - 1$ as shown in panel B. With the increase of rod radius to r₂ = 3.82 mm, the effective parameters are changed to be ɛ_{eff, 2} = μ_{eff, 2} = 0.0, corresponding to the EZI of n_{eff, 2} = 0.0 as shown in panel D. To understand the results, the corresponding photonic band diagrams are also calculated with the use of the multiple scattering theory (Felbacq et al., 1994; Liu and Lin, 2006). As can be found in Figure 2C, there appears a clear correspondence between the EMNZ and the triple accidental degeneracy of photonic bands at the Brillouin zone center Γ, which is in agreement with the theoretical analysis in dielectric photonic crystals (Huang et al., 2011; Hajian et al., 2016). Differently, in the MM system, the ratio of wavelength to lattice separation is about 10 so that it can be considered an effective medium due to the intrinsic magnetic resonance and the high permittivity. In addition, the impedance is nearly matched to the air in the vicinity of EZI. Then, as shown in panel A, with the decrease of the rod radius from r₂ = 3.82 mm to r₁ = 3.64 mm, the photonic band diagram shifts upward from the well-known knowledge in photonic crystals (Joannopoulos et al., 1995). As a consequence, the effective constitutive parameters shift upward accordingly so that the effective index is changed from the EZI in panel D to the ENI in panel B.

FIGURE 2

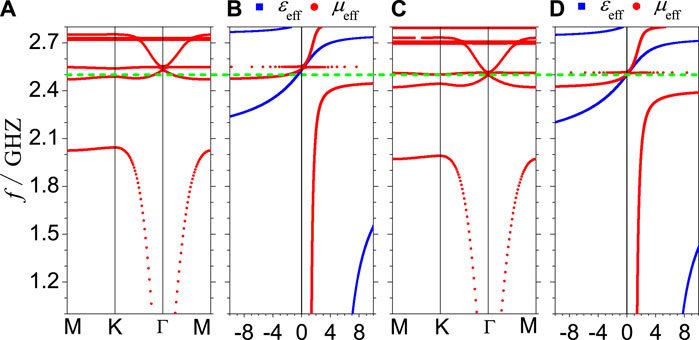
FIGURE 2. Photonic band diagrams (A,C) as well as the corresponding effective permittivities ɛ_eff and permeabilities μ_eff (B,D) for the triangular lattice of MMs with the same lattice separation a = 15 mm but different ferrite rod radii r = 3.64 mm (A,B) and 3.82 mm (C,D), respectively. The BMF is the same for two MMs with the magnitude H₀ = 500 Oe. The green dashed line marks the operating frequency f = 2.5 GHz, which is fixed unchanged for all the HSMMs.

Then, we turn to examine the dependence of the effective constitutive parameters on the filling ratio by plotting ɛ_eff and μ_eff as the functions of the rod radius at the operating frequency f = 2.5 GHz for the fixed lattice separation a = 15 mm. The result is shown in Figure 3A, where both ɛ_eff and μ_eff are nearly continuously tuned in a specified range of the rod radius. For the convenience of comparison, two typical rod radii r₁ = 3.64 mm and r₂ = 3.82 mm discussed in Figure 2 are denoted by green solid lines, and by further increasing the rod radius to r₃ = 4.2 mm, the effective index is turned from the ENI of n_{eff, 1} to the EZI of n_{eff, 2}, and then to the EPI of n_{eff, 3} = 1 with ɛ_{eff, 3} = 1.25 and μ_{eff, 3} = 0.8. With the above three MMs as the building blocks, two kinds of HSMMs are to be constructed with the combinations of either EZI and ENI or EZI and EPI. To realize the reconfigurable unidirectionality, a flexibly tunable effective index is required. Therefore, the effective parameters ɛ_eff and μ_eff are also plotted as the functions of a BMF H₀. Two delicately designed MMs with the lattice separation ${\tilde{a}}_{1} = 14.55$ mm, the rod radius ${\tilde{r}}_{1} = 3.78$ mm and the lattice separation ${\tilde{a}}_{2} = 12.25$ mm, the rod radius ${\tilde{r}}_{2} = 3.58$ mm are considered as shown in Figure 3B and Figure 3C, respectively. For both cases, the effective indices exhibit nearly continuous variation and two EZIs are obtained under the BMFs $H_{0}^{1} = 497$ Oe and $H_{0}^{2} = 480$ Oe, respectively, as marked by the green solid lines. Meanwhile, the ENI of ${\tilde{n}}_{eff, 1}$ with ${\tilde{ε}}_{eff, 1} = - 1.3$ and ${\tilde{μ}}_{eff, 1} = - 2.5$ and the EPI of ${\tilde{n}}_{eff, 2}$ with ${\tilde{ε}}_{eff, 2} = 0.9$ and ${\tilde{μ}}_{eff, 2} = 0.7$ are also obtained under $H_{0}^{1}$ and $H_{0}^{2}$ , respectively, as shown in panels C and B, respectively, so that two kinds of HSMMs with the combinations of either EZI and ENI or EZI and EPI can be constructed. However, different from the HSMMs constructed solely dependent on the radius difference, the HSMMs with these specified parameters can be transformed from the first kind to the second kind by decreasing or increasing the BMFs. It should be noted that, with the lattice separation kept unchanged, we can hardly obtain the matched zero index simultaneously at two different BMFs by solely tuning the rod radius, which leads to a larger reflection at the interface and thus degrading the efficiency. This is the reason why we optimize the rod radius and the lattice separation, which is also the core part in designing the photonic heterostructures.

FIGURE 3

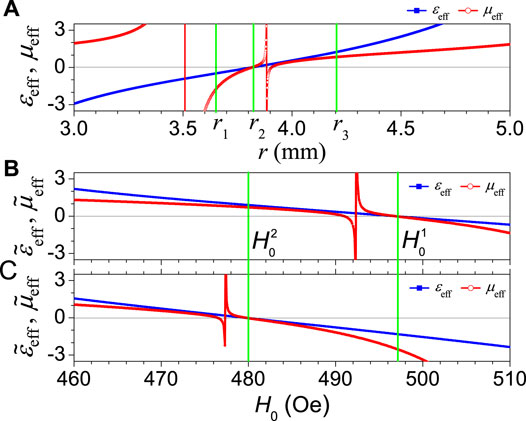
FIGURE 3. (A) The effective constitutive parameters ɛ_eff and μ_eff are plotted as the functions of the rod radius r for the MM with the lattice separation fixed as a = 15 mm. For another two MMs with the lattice separation ${\tilde{a}}_{1} = 14.55$ mm, the rod radius ${\tilde{r}}_{1} = 3.78$ mm (B) and the lattice separation ${\tilde{a}}_{2} = 12.25$ mm, the rod radius ${\tilde{r}}_{2} = 3.58$ mm (C), ${\tilde{ε}}_{eff}$ and ${\tilde{μ}}_{eff}$ are plotted as the functions of a BMF H₀. The BMF in panel A is H₀ = 500 Oe, and the operating frequency is f = 2.5 GHz, kept unchanged.

4 Reconfigurable Unidirectionality by HSMMs

To visualize the unidirectional propagation, the electric field patterns are simulated by the use of multiple scattering theory (Felbacq et al., 1994; Liu and Lin, 2006), which can guarantee the high precision as well as the high efficiency. The results are shown in Figure 4, where a TM polarized Gaussian beam incident from both the LHS and the RHS on the HSMMs is presented. For the HSMM made up of the EZI and ENI, the Gaussian beam incident from the LHS experiences nearly no phase change in the EZI as evidenced by the nearly uniform electric field. Then, the beam is bent upward and enters the ENI. Finally, at the right interface of HSMM, the Gaussian beam is negatively refracted with the refractive angle of 30° as shown in panel A, corresponding to the “passing” state with the transmittance of about 49%. The Gaussian beam incident from the RHS enters the ENI and strikes obliquely at the interface of EZI. Due to the momentum mismatch, the Gaussian beam is totally reflected as shown in Figure 4B, giving rise to the unidirectional propagation of the Gaussian beam. Then, for the HSMM made up of the EZI and EPI, the LHS incident Gaussian beam can be transmitted and bent upward with the transmittance of about 57.8% and the angle of 30° with respect to the x axis, as shown in Figure 4C. Although both panel A and panel C exhibit the “LHS passing” state, the Gaussian beam is bent downward and upward, respectively, corresponding to the different beam steering effect. Similarly, as shown in panel D, the total reflection is observed for the RHS incident Gaussian beam, thus leading to the unidirectional propagation. It should be noted that, in Figure 4D, the effective index of the right part of heterostructure is about 1, equal to the refractive index of the air, resulting in an evident reflection beam. Differently, in Figure 4B, the effective index of the right part of heterostructure is about −1 and the impedance is mismatched to the air as indicated in Figure 3C, resulting in the complicate reflection and refraction at the interfaces of heterostructure. Therefore, on the RHS of the heterostructure, the interference pattern is observed, corresponding no longer to the reflected beam as that in Figure 4D. As a further extension of the present research, the oblique incident Gaussian beam can also be considered. In the usual case, the beam will be totally reflected for both the LHS and RHS incidence due to the momentum mismatch at the interface. Nonetheless, from the Lorentz reciprocity, we can expect that, for the oblique incidence with the incident angle of 30°, the reconfigurable unidirectional propagation can possibly be implemented. However, the oblique incidence will result in the larger reflectance at the interface, thus reducing the efficiency.

FIGURE 4

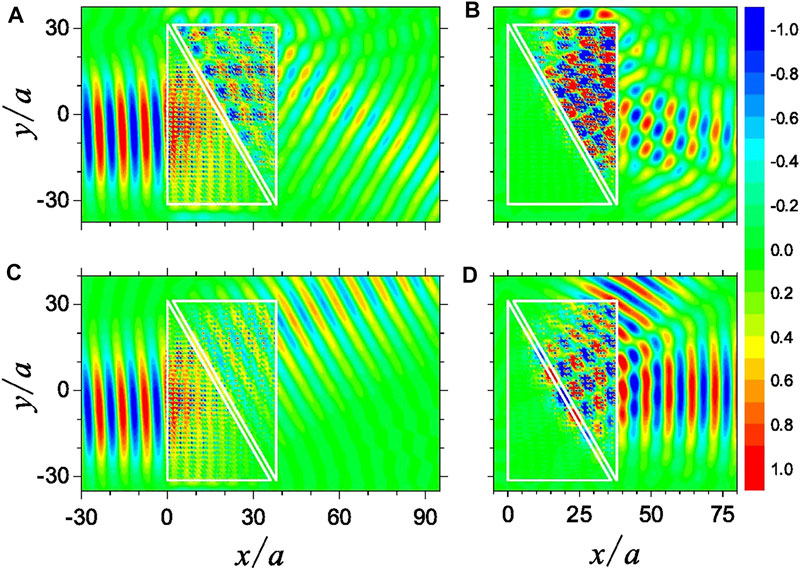
FIGURE 4. Electric field patterns illustrating the unidirectional propagation by the HSMM made up of the EZI and ENI with the LHS incident Gaussian beam exhibiting the “passing” state (A), but the RHS incident Gaussian beam exhibiting total reflection (B). For the HSMM made up of the EZI and EPI, the electric field patterns also exhibit the “passing” state for the LHS incidence (C) and the total reflection for the RHS incidence (D). The rod radii corresponding to the ENI of n_{eff, 1} =−1, the EZI of n_{eff, 2} = 0, and the EPI of n_{eff, 3} = 1 are r₁ = 3.64 mm, r₂ = 3.82 mm, and r₃ = 4.2 mm, respectively, as marked in Figure 3A. The BMF exerted upon two HSMMs is H₀ = 500 Oe, and the operating frequency is f = 2.5 GHz, kept unchanged.

Although the unidirectional transmittance of the Gaussian beam is observed for the HSMMs presented in Figure 4, no further tunability on the unidirectionality can be realized. To improve the controllability, we turn to the MMs shown in Figures 3B,C, where the effective indices can be flexibly tuned by the BMF. Under the BMF $H_{0}^{1} = 497$ Oe, the HSMM can be constructed with the combination of EZI and ENI, which can be used to generate the “LHS passing” state as shown in Figures 5A,B with the similar mechanism as that in Figures 4A,B. The different field profiles arise from the difference of the lattice separations as well as the different effective constitutive parameters. Then, by decreasing the BMF from $H_{0}^{1} = 497$ Oe to $H_{0}^{2} = 480$ Oe, the HSMM is transformed into the combination of EZI and EPI. As can be observed in Figures 5C,D, the “RHS passing” state is demonstrated, resulting in the reconfigurable unidirectionality. In this manner, the manipulation on the Gaussian beam is more flexible, adding additional degrees of freedom.

FIGURE 5

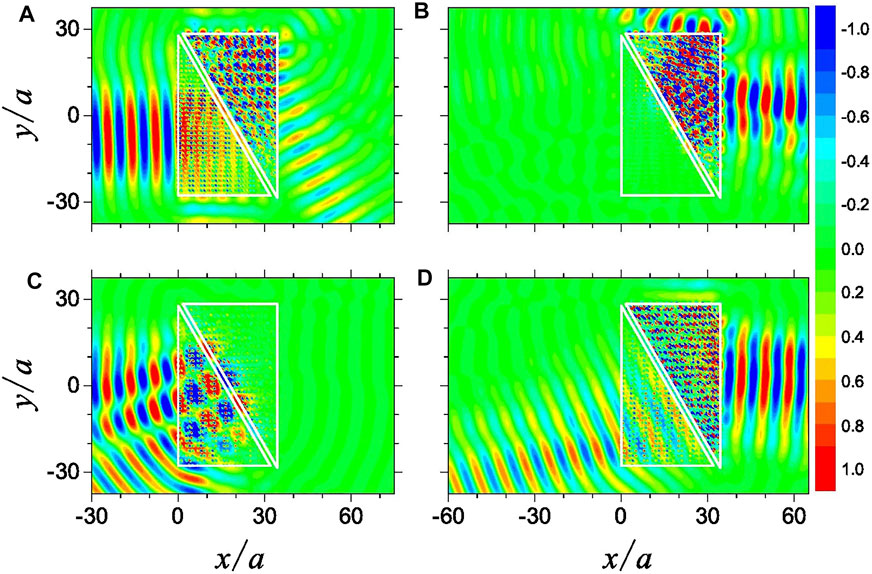
FIGURE 5. Electric field patterns illustrating the reconfigurable unidirectional propagation by the HSMM made up of the EZI and ENI with the LHS incidence exhibiting the “passing” state (A), but the RHS incidence exhibiting total reflection (B). By decreasing the bias magnetic field from $H_{0}^{1} = 497$ Oe to $H_{0}^{2} = 480$ Oe, the HSMM is transformed into that made up of the EZI and EPI and the “RHS passing” state can be observed from the field patterns in panels (C,D). For the left part of the HSMM, the lattice separation is ${\tilde{a}}_{1} = 14.55$ mm and the rod radius is ${\tilde{r}}_{1} = 3.78$ mm, and for the right part of the HSMM, the lattice separation is ${\tilde{a}}_{2} = 12.25$ mm and the rod radius is ${\tilde{r}}_{2} = 3.58$ mm. The operating frequency is f = 2.5 GHz, kept unchanged.

Actually, the construction of HSMM can be further tuned by interchanging the left part and the right part, which can lead to the reversing of the unidirectionality straightforwardly, namely, the transition between the “RHS passing” state and the “LHS passing” state. As an illustration of the idea, the interchanging of the left part and the right part in Figure 5C can lead to the construction of the second kind of HSMM with the combination of EZI and EPI. The electric field patterns are shown in Figures 6A,B, respectively, and compared to the results shown in Figures 5C,D, the unidirectionality is transformed from the “RHS passing” state to the “LHS passing” state. Compared to the field pattern in Figure 5A, the transmitted Gaussian beam is bent upward but not downward due to the change of effective index from negative to positive for the right part of HSMM. In addition, the total reflection for the RHS incidence in Figure 6B exhibits a deeper penetration into the left part compared to that in Figure 5B. The reason lies in that the absolute value of the refractive index of the left part in Figure 5B $(|{\tilde{n}}_{eff, 1}| = 1.8)$ is larger than that in Figure 6B $(|{\tilde{n}}_{eff, 2}| = 1)$ . As a result, the transmitted Gaussian beam is also bent much stronger in Figure 5A than that in Figure 6A. Then, by increasing the BMF from $H_{0}^{2} = 480$ Oe to $H_{0}^{1} = 497$ Oe, the HSMM is transformed into the combination of EZI and ENI. As a consequence, the unidirectionality is transformed from the “LHS passing” state to the “RHS passing” state as can be observed from the field patterns shown in Figures 6C,D.

FIGURE 6

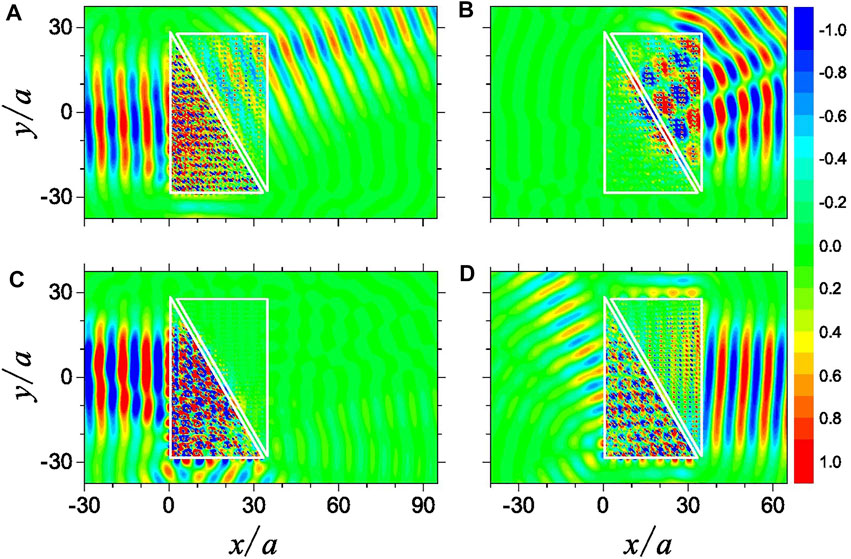
FIGURE 6. Electric field patterns illustrating the reconfigurable unidirectional propagation by the second kind of HSMM made up of the EZI and EPI with the LHS incidence exhibiting the “passing” state (A), but the RHS incidence exhibiting total reflection (B). By increasing the BMF from $H_{0}^{2} = 480$ Oe to $H_{0}^{1} = 497$ Oe, the HSMM is transformed into that made up of the EZI and ENI; thus, the “RHS passing” state can be observed from the field patterns in panels (C,D). For the left part of the HSMM, the lattice separation is ${\tilde{a}}_{2} = 12.25$ mm and the rod radius is ${\tilde{r}}_{2} = 3.58$ mm, and for the right part of the HSMM, the lattice separation is ${\tilde{a}}_{1} = 14.55$ mm and the rod radius is ${\tilde{r}}_{1} = 3.78$ mm. The operating frequency is f = 2.5 GHz, kept unchanged.

Finally, it should be pointed out that, in our proof-of-principle demonstration, the absorption of ferrite material is not considered. For the HSMMs in our research, the thickness is three times as large as the operating wavelength, resulting in the reduction of nearly 50 percent for the transmitted beam considering exactly the material loss. Moreover, more than 2,000 ferrite rods were involved in the HSMMs, making our results hardly realizable in experiments. Actually, by designing the HSMMs with a little bit complicate configuration, the thickness can be miniaturized to the size of about 1 wavelength and the number of ferrite rods is decreased to be less than 1,000, resulting in a relatively weaker absorption, thus making our design more feasible and applicable. The BMF controlling the unidirectionality of HSMMs can be furnished by electromagnets (Wang et al., 2009; Poo et al., 2011). To increase the tunability of HSMMs, the coated ferrite rod with the dielectric core of high permittivity can be considered and the effective-medium theory can be extended to retrieve the corresponding effective constitutive parameters. In the present work, the essential part in designing the HSMM is obtaining the EZI tunable by a BMF. To generalize the concept to the optical range, the tunable EZI should be obtained first, and as such, the phase-change material can serve as a good candidate. Interestingly, by combining magnetic and non-magnetic metamaterials, the photonic heterostructures constructed by two different EZIs are expected to be designed, which can possibly be used to realize unidirectional beam steering.

5 Conclusion

In summary, the MMs composed of the ferrite rods are designed and demonstrated to possess the EZI, ENI, and EPI by tuning either the rod radius or the magnitude of BMF. Based on the effective-medium theory and photonic band diagrams, the EZI is corroborated and shown to be associated with the accidental degeneracy. Two kinds of HSMMs are constructed with the combination of either EZI and ENI or EZI and EPI, both of which exhibit unidirectional wave propagation. In addition, for the HSMMs made up of building blocks with the effective index tunable by the BMF, the reconfigurable unidirectional propagation is achieved with the unidirectionality reversible by either decreasing or increasing the BMF depending on the construction of the first or second kind of HSMM. The results presented in this work add more degrees of freedom in wave manipulation and can be possibly extended to the optical frequency range by introducing phase-change materials.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (NNSFC) (grant No. 11574275) and Zhejiang Provincial Natural Science Foundation of China (LR16A040001). ZL was supported by the NNSFC (12074084), and QL was supported by the Basic Research Program of Science for Young Scholars in Universities of Guangxi Province.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alù, A., Silveirinha, M. G., Salandrino, A., and Engheta, N. (2007). Epsilon-Near-Zero Metamaterials and Electromagnetic Sources: Tailoring the Radiation Phase Pattern. Phys. Rev. B 75 (15), 155410. doi:10.1103/PhysRevB.75.155410