Band Structure Analysis of SH Wave Propagating in Nanoscale Layered Metamaterial Structures

This study is devoted to the analysis of the band structures of the anti-plane transverse wave (SH wave) in nanoscale layered metamaterial structures. Attention is restricted to normal incidence of waves. The localization factor is introduced to characterize the band structures. The general transfer matrix method based on the nonlocal elastic continuum theory is employed to calculate the localization factor. Based on the analysis of band structures, the influences of random disorder of the internal characteristic length and the external thickness of each sub-layer, the aperiodic arrangements, the location of different material components, the ratio of mass density, the ratio of the transverse wave velocity, the ratio of the internal characteristic length or the external thickness of each sub-layer on the band structures, the cut-off frequency, the peak points and the dense band zones are investigated and discussed in detail, which can provide some new thoughts for the designs and applications of the nanoscale wave devices.

1 Introduction

The metamaterials, phononic crystals (PCs) (Kushwaha et al., 1993), have been studied intensely over the past 2 decades due to their potential capability of controlling and tuning the propagation of acoustic/elastic waves. These metamaterials have band gap characteristics, that is, waves in the band gap frequency range are prohibited from passing through these structures. The unusual effect of PCs with band gaps has a wide range of potential important applications such as sound detectors, transducers, filters, waveguides, sensors, etc. Compared with two-dimensional (2D) and three-dimensional (3D) PCs, one dimensional (1D) layered PCs have simpler structure and can fully show the characteristics of wave propagation, thus, many experimental and theoretical researches on the band structures of 1D macroscale layered PCs are witnessed over the past decades (Nougaoui and Rouhani, 1987; Economou and Sigalas, 1994; Sigalas and Soukoulis, 1995; Luntiaov and Rogerson, 2010; Golub et al., 2012; Yu et al., 2012; Nguyen et al., 2016). The PCs are generally periodic. However, the random disorder (Chen and Wang, 2007; Yan et al., 2009; Yan et al., 2010) and quasi-periodic arrangement (Fernández-Alvarez and Velasco, 1998; Zárate et al., 1999; Barco and Ortuno, 2012; Chen et al., 2012; Yan and Zhang, 2012), may exhibit unique characteristics of a mixture of acoustic/elastic wave propagation and localization, which are of significant interest in both basic and applied sciences (Anderson, 1958). Although the macroscale quasi-periodic or aperiodic phononic crystals (APNCs) have been extensively investigated and reported in literature (Fernández-Alvarez and Velasco, 1998; Zárate et al., 1999; Barco and Ortuno, 2012; Chen et al., 2012; Yan and Zhang, 2012), (Aynaou et al., 2005; King and Cox, 2007; Sesion et al., 2007; Parsons and Andrews, 2009; Chen et al., 2010; Gazi and Bernhard, 2014), very little theoretical study on the band structures of nanoscale APNCs has been performed.

In recent years, owing to the wide potential applications in new thermo-elecrical, acousto-optical, nanoscale electro-mechanical devices and computer chips (Du et al., 2000; Hu et al., 2000; Kana et al., 2013), more and more researchers have conducted extensive research on nanoscale structures. As we all know, when the structure size is several namometers, the size effect must be considered. In this case, the constitutive relationships cannot be described accurately by the conventional elastic continuum theory (Ramprasad and Shi, 2005; Hepplestone and Srivastava, 2008). Therefore, many methods have been developed to study the mechanical behaviors of nanoscale materials and structures (Toupin, 1962; Mindlin, 1965; Eringen, 1972; Eringen, 1983; Nowinski, 1991; Gurtin et al., 1998; Aifantis, 1999; Yang et al., 2002; Eringen, 2006; Huang and Sun, 2007), in which the nonlocal elastic (NLE) continuum theory proposed by Eringen (Eringen, 1983; Eringen, 2006) can describe the long-range inter-atomic interactions and can account for the nanoscale size effect inside the structures. By utilizing the NLE continuum theory, Artan et al. (Artan and Altan, 2002) studied the effect of nonlocality on the dynamic behavior of laminated composites by means of dispersion of SV waves propagating in the direction parallel to layering. Heireche et al. (2008) studied the sound wave propagation in single-walled carbon nanotubes using NLE continuum theory, and revealed the significance of the small-scale effect on wave propagation in single-walled carbon nanotubes. Shaat (2017) presented the paradoxes in the existing solutions of the nonlocal field equation by introducing the high-order boundary conditions. Ke et al. (2012) investigated the nonlinear vibration of the piezoelectric nanobeams based on the NLE continuum theory and Timoshenko beam theory. And the influences of the nonlocal parameter, temperature change and external electric voltage on the size-dependent nonlinear vibration characteristics of the piezoelectric nanobeams are conducted. Nowinski (1984) studied the propagation of Love waves in an isotropic homogeneous elastic medium in the frame of the NLE continuum theory, and determined the nonlocal modulus by comparing the dispersion equation of the plane transverse waves with the corresponding equation given by the atomic lattice dynamics. Alibeigloo (2011) analyzed the vibration of a nano-plate based on the NLE continuum theory. In addition, the nonlocality also plays an important role in electronic and magnetic materials (Hashemi and Samaei, 2011; Adhikari et al., 2015; Chen et al., 2017a; Waksmanski and Pan, 2017; El-Nabulsi, 2018a; El-Nabulsi, 2018b). For example, Waksmanski and Pan (2017) presented an exact closed-form solution for the three-dimensional free vibrational response of a simply-supported and multilayered magneto-electro-elastic plate considering the nonlocal effect. Chen et al. (2017a) derived the analytical solutions for propagation of time-harmonic waves in three-dimensional magneto-electro-elastic multilayered plates with nonlocal effect, and investigated the influences of the nonlocal parameter on the dispersion curves. It should be noted that by developing the transfer matrix method based on the NLE continuum theory (Chen and Wang, 2011; Chen et al., 2013; Chen et al., 2016; Yan et al., 2018; Chen et al., 2019; Yan et al., 2020), a series of extensive studies on wave propagation in nanoscale periodic structures have been carried out. The results showed that a cut-off frequency was found, beyond which the waves are prohibited from passing through the structure. Besides, the dense band zones (DBZs) appeared in the band structures when the nanoscale size-effect is taken into account. However, the PCs in the above studies are all perfect periodic. For nearly periodic nanoscale layered PCs, Chen et al. (2017b) studied the size effect on the band structures of randomly disordered, quasi-periodic and defected nanoscale PCs. Therein, only the disorder of the external thickness of the first sub-layer is considered for simplicity. Besides, only Fibonacci sequence is studied. However, the influences of random disorder of the internal characteristic length and the external thickness of each sub-layer, the aperiodic arrangements, the location of different material components, the ratio of the mass density, the ratio of the transverse wave velocity, the ratio of the internal characteristic length or the external thickness of each sub-layer on the band structures, the cut-off frequency, the peak points and the DBZs have not been investigated, which requires a detailed study of these problems.

In this paper, we attempt to address these questions and the band structures of the SH wave in the nanoscale layered structures are studied in detail. The general transfer matrix method based on the NLE continuum theory is used to calculate the localization factor describing the band structures. A detailed parametric study is conducted to investigate the influences of random disorder of the internal characteristic length and the external thickness of each sub-layer, the aperiodic arrangements, the location of different components, the ratio of the mass density, the ratio of the transverse wave velocity, the ratio of the internal characteristic length or the external thickness of each sub-layer on the band structures, the cut-off frequency, the peak points and the DBZs.

The paper is structured as follows: Section 2 introduces the nonlocal elastic continuum theory. And the theoretical models and the general transfer matrix method are given in Section 3. Section 4 is devoted to the illustration and discussion of the results based on the calculations of the localization factor, where different influence factors are taken into account. Finally, some conclusions and future perspectives are presented in Section 5.

2 The Nonlocal Elastic Continuum Theory

In nonlocal elastic theory, owing to the long-range interaction between atoms or molecules in nanoscale materials and structures, the stresses at a point are related not only to the strains at the same point, but also to the strains at other points of the whole body. The nonlocal elastic continuum model proposed by Eringen (Eringen, 1983; Eringen, 2006) well explains that the physical phenomenon represented by one point in the continuum is affected by all other points in the whole domain, and the results are consistent with the experimental observations of lattice atomic dynamics and phonon scattering. For homogeneous, isotropic and elastic solids, the nonlocal and classical stress tensor has the following relationship, which includes an integral involving the whole region, i.e., (Eringen, 1983).

$\mathbf{\varsigma }\left(\mathbf{x}\right)={\displaystyle {\int }_V\alpha \left(\left|{\mathbf{x}}^{\prime }-\mathbf{x}\right|,a\right)}\mathbf{\sigma }\left({\mathbf{x}}^{\prime }\right)dV\left({\mathbf{x}}^{\prime }\right)(1)$

where $\mathbf{\varsigma }\left(\mathbf{x}\right)$ represents the nonlocal stress tensor at point $\mathrm{x}$, the kernel function $\alpha \left(\left|{\mathbf{x}}^{\prime }-\mathbf{x}\right|\right)$ is the nonlocal modulus, $\left|{\mathbf{x}}^{\text{'}}-\mathbf{x}\right|$ is the Euclidean distance, $a$ is the internal characteristic length, $\mathrm{\sigma }\left({\mathrm{x}}^{\text{'}}\right)$ is the classical stress tensor whose components can be defined by

${\sigma }_{ij}\left({\mathbf{x}}^{\prime }\right)=\lambda e_{rr}\left({\mathbf{x}}^{\prime }\right){\delta }_{ij}+2\mu e_{ij}\left({\mathbf{x}}^{\prime }\right)(2)$

with the strain components

$e_{ij}\left({\mathbf{x}}^{\prime }\right)=\frac{1}{2}\left(\frac{\partial u_i\left(\mathbf{x}\prime \right)}{\partial {x\prime }_j}+\frac{\partial u_j\left(\mathbf{x}\prime \right)}{\partial {x\prime }_i}\right)(3)$

where $\lambda$ and $\mu$ are classical Lamé constants, ${\delta }_{ij}$ is the Kronecker-delta, $u_i$ and $u_j$ are the displacement components, respectively.

The kernel function $\alpha \left(\left|{\mathbf{x}}^{\prime }-\mathbf{x}\right|,a\right)$ in Eq. 1 which depends on the internal characteristic length $a$ can be determined by matching the dispersion curves with those obtained from atomic lattice dynamics, first principle method and experiments. Because the structures considered in this paper are infinite along the $y$ direction, the kernel function along the $y$ direction is supposed to be a Delta function, and then

$\alpha \left(\left|{\mathbf{x}}^{\prime }-\mathbf{x}\right|\right)=\alpha \left(\left|x^{\prime }-x\right|\right)\delta \left(\left|y^{\prime }-y\right|\right)(4)$

where $\alpha \left(\left|x^{\text{'}}-x\right|\right)$ is the kernel function along the $x$ direction. Therefore, Eq. 1 can be written as the following component form

$\begin{array}{l}{\varsigma }_{mn}\left(\mathbf{x}\right)={\displaystyle {\int }_s\alpha \left(\left|{\mathbf{x}}^{\prime }-\mathbf{x}\right|\right)}{\sigma }_{mn}\left({\mathbf{x}}^{\prime }\right)ds\left({\mathbf{x}}^{\prime }\right)\\ ={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle {\int }_0^{l_k}\alpha \left(\left|x^{\prime }-x\right|\right)\delta \left(\left|y^{\prime }-y\right|\right)}}{\sigma }_{mn}\left(\mathbf{x}\right)\prime dxd\prime y\end{array}(5)$

It is well known that the kernel function $\alpha \left(\left|{\mathbf{x}}^{\text{'}}-\mathbf{x}\right|,a\right)$ has different forms (Eringen, 1983). Considering the time-harmonic elastic waves in this paper, it is more suitable to choose $\alpha \left(\left|{\mathbf{x}}^{\text{'}}-\mathbf{x}\right|,a\right)$ as (Eringen, 2006), i.e., exponential kernel function

$\alpha \left(\left|x^{\text{'}}-x\right|,a\right)=\frac{1}{2a}{e}^{-\frac{\left|x^{\text{'}}-x\right|}{a}}(6)$

In Eringen’s NLE theory, the integral form of Eq. 1 can be approximated in the following differential form (Eringen, 1983):

$\left(1-a^2{\nabla }^2\right){\varsigma }_{ij}={\sigma }_{ij}(7)$

where ${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ is the Laplace operator. The equations of wave motion without body forces are expressed as

${\varsigma }_{mn,m}=\rho {\ddot{u}}_n(8)$

with $\rho$ being the mass density. Here, the repeated indices denote the conventional summation rule. Substituting Eqs 2, 3, and 7 into Eq. 8, the wave motion equation based on the NLE theory can be written as the following differential ones

$\left(\lambda +\mu \right)u_{m,nm}+\mu u_{n,mm}=\left(1-a^2{\nabla }^2\right)\rho {\ddot{u}}_n(9)$

3 Theoretical Model and the General Transfer Matrix Method

The SH wave propagating normally in the nanoscale periodic structures are presented in Figure 1A. Figures 1B–D shows the schematic diagrams of the nanoscale layered PCs arranged as Thue-Morse sequence, Rudin-Shapiro sequence and Fibonacci sequence, respectively, and the random disorder, quasi-periodic and aperiodic structures considered in this paper can be obtained by the following theoretical model designs.

FIGURE 1

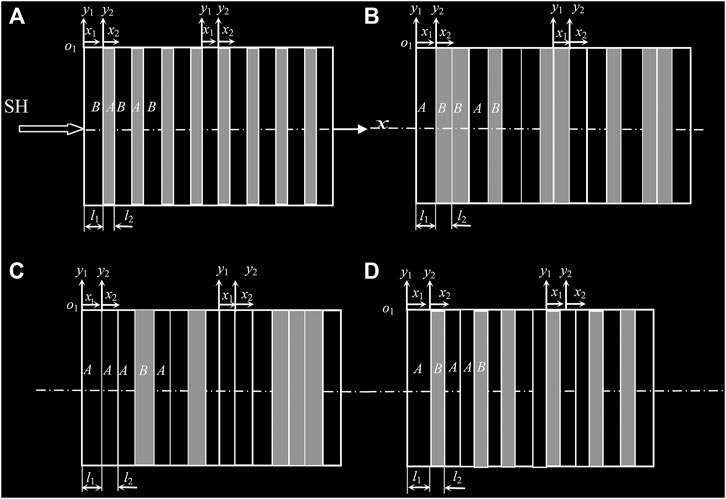
FIGURE 1. The schematic of the SH wave propagating normally in the nanoscale periodic layered structure (A), the layered PCs arranged as Thue-Morse sequence (B), Rudin-Shapiro sequence (C) and Fibonacci sequence (D).

3.1 Theoretical Model

3.1.1 Nanoscale Random Disordered Structure

Here, we consider the elastic SH waves propagating in normally distributed randomly disordered PCs. let $D$ denote the internal characteristic length ${\tau }_k(k=\mathrm{1,2})$ and the external thickness $l_k(k=\mathrm{1,2})$ of the each sub-layer, respectively. For the normally distributed randomly disordered PC, the characteristic length $D$ can be written as

$D=D_0+\delta V_1\sqrt{\left(-2\ln \left(S\right)/S\right)}(10)$

where $D_0$ is the mean of $D$ (corresponding to the perfect periodic distribution), and $\delta$ is the variance of the internal characteristic length or the external thickness representing the disorder degree of this system, $\delta =0$ corresponds to a perfect periodic system. $V_1=2t_1-1$, $V_2=2t_2-1$ in which $t_1,t_2\in \left[\mathrm{0,1}\right]$ are standard uniformly distributed random variables, $S=V_1^2+V_2^2$.

3.1.2 Nanoscale Quasi-Periodic Structure

Here, we consider the nanoscale quasi-periodic layered structures arranged in the Fibonacci sequence (Merlin et al., 1985) as shown in Figure 1D. The Fibonacci sequence can be obtained by repeating operations of the concurrent substitution rules: $A\to AB$ and $B\to A$ (Hu an et al., 1992). The $m\text{th}$ generation of the Fibonacci sequence is denoted as $F_m$ with $F_0=B$ and $F_1=A$. Then the Fibonacci sequence can be written as $F_{m+1}=F_m{F}_{m-1}$, for example, $F_2=AB,F_3=ABA,F_4=ABAAB,F_5=ABAABABA,\cdots$ where $A$ and $B$ are sub-layers made up of different materials.

3.1.3 Nanoscale Aperiodic Structures

Being a bridge of linking periodic models with quasi-periodic systems in a geometrical structure, Thue-Morse system (Bovier and Ghez, 1995) and Rudin-Shapiro systems illustrated in Figures 1B,C are thought to be more random than the quasi-periodic Fibonacci lattices.

The Thue-Morse sequence is based on the two letter alphabet $(A,B)$, and can be generated by the inflation rules, as follows: $A\to AB$, $B\to BA$. The lower-order Thue-Morse lattices are the strings $T_0=A,T_1=AB,T_2=ABBA,T_3=ABBABAAB$, etc.

The Rudin-Shapiro sequence is an infinite sequence and can be generated by a four state automaton as follows: $AA\to AAAB$, $AB\to AABA$, $BA\to BBAB$, $BB\to BBBA$, respectively. It should be noticed that for the two aperiodic systems mentioned above, the letters $A$ and $B$ denote two different material sub-layers.

3.2 General Transfer Matrix Method

In this section, we start from the periodic system, i.e., the normal propagation of the time-harmonic SH elastic waves in a nanoscale periodic multilayered phononic crystal is considered. This structure depicted in Figure 1A is composed of materials $A$ and $B$ layers, with the thicknesses $l_1$ and $l_2$, respectively, and $l=l_1+l_2$ is the thickness of one unit-cell. The local coordinates of the monolayers are also given in the figure. We assume that the layered composite consists of $\mathbb{N}$ unit-cells. Each unit-cell includes, unless otherwise stated, two sub-layers which are denoted by the subscript $k=\mathrm{1,2}$. For this problem, the displacement components in the $x$- and $y$-directions, i.e., $u_x$ and $u_y$ are zero, and the only non-zero displacement $u_k$ is along the $z$-direction, which is perpendicular to the $xy$-plane. Then Eq. 9 can be simplified into the following form for the $k\text{th}$ sub-layer

${\mu }_k\frac{{\partial }^2{u}_k}{\partial x_k^2}=\rho {\omega }^2\left(a^2\frac{{\partial }^2}{\partial x_k^2}-1\right)u_k\left(k=\mathrm{1,2}\right)(11)$

By introducing the dimensionless local coordinate ${\zeta }_k=x_k/l$, $0\le {\zeta }_k\le {\overline{l}}_k=l_k/l$, Eq. 11 can be rewritten into the following dimensionless form

$\frac{{\partial }^2{u}_k}{\partial {\zeta }_k^2}+\frac{{\varpi }_k^2}{1-{\varpi }_k^2{\tau }_k^2}{u}_k=0(12)$

where ${\varpi }_k=\omega l/c_k$ is the non-dimensional frequency with $c_k=\sqrt{{\mu }_k/{\rho }_k}$ being the velocity of the transverse elastic wave, and ${\tau }_k=a_k/l$ is the ratio of the internal characteristic length and the external thickness of the unit-cell.

Then, the general harmonic solution for the $k\text{th}$ sub-layer can be obtained, which has the following form:

$u_k\left({\zeta }_k\right)=\left(U_k{e}^{\text{i}{q}_k{\zeta }_k}+V_k{e}^{-\text{i}{q}_k{\zeta }_k}\right)e^{-\text{i}\omega t}(13)$

where $q_k=\sqrt{{\varpi }_k^2/\left(1-{\tau }_k^2{\varpi }_k^2\right)}$, $U_k$ and $V_k$ are the unknown coefficients to be determined. According to Eqs 13, 5, the nonlocal stresses can be obtained as

$\begin{array}{l}{\varsigma }_k\left({\zeta }_k\right)={\displaystyle {\int }_0^{{\overline{l}}_k}\frac{{\mu }_k}{2{\tau }_k}{e}^{-\left|{\zeta }_k-{\zeta }_k^{\prime }\right|/{\tau }_k}\frac{\partial u_k}{\partial {\zeta }_k^{\text{'}}}d{\zeta }_k^{\prime }}\\ =\frac{\text{i}{q}_k{\mu }_k}{2}\left(\frac{e^{\text{i}{q}_k{\zeta }_k}-e^{-{\zeta }_k/{\tau }_k}}{1+\text{i}{q}_k{\tau }_k}-\frac{e^{\text{i}{q}_k{\overline{l}}_k}{e}^{\left({\zeta }_k-{\overline{l}}_k\right)/{\tau }_k}-e^{\text{i}{q}_k{\zeta }_k}}{1-\text{i}{q}_k{\tau }_k}\right)U_k\\ -\frac{\text{i}{q}_k{\mu }_k}{2}\left(\frac{e^{-\text{i}{q}_k{\zeta }_k}-e^{-{\zeta }_k/{\tau }_k}}{1-\text{i}{q}_k{\tau }_k}-\frac{e^{-\text{i}{q}_k{\overline{l}}_k}{e}^{\left({\zeta }_k-{\overline{l}}_k\right)/{\tau }_k}-e^{-\text{i}{q}_k{\zeta }_k}}{1+\text{i}{q}_k{\tau }_k}\right)V_k\end{array}(14)$

Then, the state vector $\mathrm{W}={\left\{\overline{u},\overline{\varsigma }\right\}}^{\text{T}}$ with the bar denoting the dimensionless parameters is chosen in order to obtain the transfer matrix of the unit-cell. Based on the continuity conditions on the left (subscript $L$) and right (subscript $R$) sides of the interface of two adjacent sub-layers in the $\beta \text{th}$ unit cell, the state vectors can be defined as

$\begin{array}{l}{\mathrm{W}}_{kL}^{\left(\beta \right)}={\left\{{\overline{u}}_k,{\overline{\varsigma }}_k\right\}}_{{\zeta }_k=0}^{\mathrm{T}}={\mathrm{T}}_{kL}{\left\{U_k,V_k\right\}}^{\mathrm{T}}\\ {\mathrm{W}}_{kR}^{\left(\beta \right)}={\left\{{\overline{u}}_k,{\overline{\varsigma }}_k\right\}}_{{\zeta }_k={\overline{l}}_k}^{\mathrm{T}}={\mathrm{T}}_{kR}{\left\{U_k,V_k\right\}}^{\mathrm{T}}\end{array}(15)$

where the matrices ${\mathbf{T}}_{kL}$ and ${\mathbf{T}}_{kR}$ can be obtained from Eqs 13, 5, whose elements are given by

$\begin{array}{l}{\text{T}}_{kL}\left(\mathrm{1,1}\right)={\text{T}}_{kL}\left(\mathrm{1,2}\right)=1,{\text{T}}_{kL}\left(\mathrm{2,1}\right)=-\text{i}{\mu }_k{q}_k\frac{1-e^{-\text{i}{q}_k{l}_k}{e}^{-\raisebox{1ex}{$l_k$}\!\left/ \!\raisebox{-1ex}{${\tau }_k$}\right.}}{2\left(1+\text{i}{q}_k{\tau }_k\right)},{\text{T}}_{kL}\left(\mathrm{2,2}\right)=\text{i}{\mu }_k{q}_k\frac{1-e^{\text{i}{q}_k{l}_k}{e}^{-\raisebox{1ex}{$l_k$}\!\left/ \!\raisebox{-1ex}{${\tau }_k$}\right.}}{2\left(1-\text{i}{q}_k{\tau }_k\right)}\\ {\text{T}}_{kR}\left(\mathrm{1,1}\right)=e^{-\text{i}{q}_k{l}_k},{\text{T}}_{kR}\left(\mathrm{1,2}\right)=e^{\text{i}{q}_k{l}_k},{\text{T}}_{kR}\left(\mathrm{2,1}\right)=-\text{i}{\mu }_k{q}_k\frac{e^{-\text{i}{q}_k{l}_k}-e^{-\raisebox{1ex}{$l_k$}\!\left/ \!\raisebox{-1ex}{${\tau }_k$}\right.}}{2\left(1-\text{i}{q}_k{\tau }_k\right)},{\text{T}}_{kR}\left(\mathrm{2,2}\right)=\text{i}{\mu }_k{q}_k\frac{e^{\text{i}{q}_k{l}_k}-e^{-\raisebox{1ex}{$l_k$}\!\left/ \!\raisebox{-1ex}{${\tau }_k$}\right.}}{2\left(1+\text{i}{q}_k{\tau }_k\right)}\end{array}(16)$

Obviously, the two state vectors in Eq. 15 have the following relation by eliminating the common vector, i.e.,

${\mathbf{W}}_{kR}^{\left(\beta \right)}={\mathbf{T}}_{kR}{\mathbf{T}}_{kL}^{-1}{\mathbf{W}}_{kL}^{\left(\beta \right)}\triangleq {\mathbf{T}}_k{\mathbf{W}}_{kL}^{\left(\beta \right)}\left(k=\mathrm{1,2}\right)(17)$

where ${\mathbf{T}}_k={\mathbf{T}}_{kR}{\mathbf{T}}_{kL}^{-1}$ is the transfer matrix of the $k\text{th}$ sub-layer.

The displacements and nonlocal stresses are continuous at the interface of two adjacent sub-layers in the same unit-cell and between the $\beta \text{th}$ and the $(\beta -1)\text{th}$ unit-cells, that is,

${\mathbf{W}}_{2R}^{\left(\beta -1\right)}={\mathbf{W}}_{1L}^{\left(\beta \right)},{\mathbf{W}}_{1R}^{\left(\beta \right)}={\mathbf{W}}_{2L}^{\left(\beta \right)}(18)$

From Eqs 17, 18, the following relation can be obtained

${\mathbf{W}}_{2R}^{\left(\beta \right)}={\mathbf{T}}_2{\mathbf{W}}_{2L}^{\left(\beta \right)}={\mathbf{T}}_2{\mathbf{W}}_{1R}^{\left(\beta \right)}={\mathbf{T}}_2{\mathbf{T}}_1{\mathbf{W}}_{1L}^{\left(\beta \right)}={\mathbf{T}}_2{\mathbf{T}}_1{\mathbf{W}}_{2R}^{\left(\beta -1\right)}\triangleq {\mathbf{T}}_{\beta }{\mathbf{W}}_{2R}^{\left(\beta -1\right)}(19)$

which shows the relationship between the state vectors of the $\beta \text{th}$ and the $(\beta -1)\text{th}$ unit-cells, where ${\mathbf{T}}_{\beta }={\mathbf{T}}_2{\mathbf{T}}_1={\mathbf{T}}_{2R}{\mathbf{T}}_{2L}^{-1}{\mathbf{T}}_{1R}{\mathbf{T}}_{1L}^{-1}$ is the transfer matrix between the two consecutive unit-cells, i.e., the transfer matrix of the $\beta \text{th}$ unit-cell. For perfect periodic two-component PCs, ${\mathbf{T}}_{\beta }={\mathbf{T}}_2{\mathbf{T}}_1$ for all $\beta =\mathrm{1,2,3},\cdots ,\mathbb{N}$ are the same and denoted as $\mathbf{T}$. It should be noticed that the above derivation is applicable for not only the ordered periodic PNCs but also the disordered, quasi-periodic and aperiodic ones. However the transfer matrices of the “unit-cells” of the disordered, quasi-periodic and APNCs are different from those of the perfect periodic ones. For quasi-periodic or aperiodic structures, ${\mathbf{T}}_{\beta }={\mathbf{T}}_2{\mathbf{T}}_1$ are not all the same and the Bloch theory is not applicable, for example, Using the above method, for the aperiodic structure composed of $\mathbb{N}$ unit-cells, the total transfer matrix can be obtained, that is,

${\mathbf{T}}_{total}={\mathbf{T}}_{\mathbb{N}R}{\mathbf{T}}_{\mathbb{N}L}^{-1}{\mathbf{T}}_{\left(\mathbb{N}-1\right)R}{\mathbf{T}}_{\left(\mathbb{N}-1\right)L}^{-1}{\mathbf{T}}_{\left(\mathbb{N}-2\right)R}\cdots {\mathbf{T}}_{3L}^{-1}{\mathbf{T}}_{2R}{\mathbf{T}}_{2L}^{-1}{\mathbf{T}}_{1R}{\mathbf{T}}_{1L}^{-1}(20)$

The detailed mathematical derivation is not given here for the sake of brevity. Interested readers may refer to many publications for more details.

In this paper, we use the well-defined localization factor to characterize the band structures and localization phenomenon of 1D nanoscale layered PCs. The localization factor is defined as the minimum positive Lyapunov exponent which describes the average exponential rate of growth or attenuation of the wave amplitude (Gastanier and Pierre, 1997). And it can be calculated by using the Wolf’s method (Wolf et al., 1985) once the transfer matrix is obtained. If the dimension of the transfer matrices is $2ƛ\times 2ƛ$, then the smallest positive Lyapunov exponent ${\ell }_{ƛ}$ is the localization factor. The expression for the localization factor ${\ell }_{ƛ}$ of the system with $\mathbb{N}$ unit-cells is given as follows:

${\ell }_{ƛ}=\underset{\mathbb{N}\to \infty }{\mathbf{lim}}\frac{1}{\mathbb{N}}{\displaystyle \sum _{\beta =1}^{\mathbb{N}}\ln \Vert {\widehat{\mathbf{W}}}_{2R,ƛ}^{\left(\beta \right)}\Vert }(21)$

where the vector in Eq. 21 is given by

${\widehat{\mathbf{W}}}_{2R,ƛ}^{\left(\beta \right)}={\mathbf{W}}_{2R,ƛ}^{\left(\beta \right)}-\left({\mathbf{W}}_{2R,ƛ}^{\left(\beta \right)},{\mathit{v}}_{ƛ-1}^{\left(\beta \right)}\right){\mathit{v}}_{ƛ-1}^{\left(\beta \right)}-\cdots -\left({\mathbf{W}}_{2R,ƛ}^{\left(\beta \right)},{\mathit{v}}_1^{\left(\beta \right)}\right){\mathit{v}}_1^{\left(\beta \right)}(22)$

in which ${\mathit{v}}_{ƛ}^{\left(\beta \right)}=\frac{{\widehat{\mathbf{W}}}_{2R,ƛ}^{\left(\beta \right)}}{\Vert {\widehat{\mathbf{W}}}_{2R,ƛ}^{\left(\beta \right)}\Vert }$ are orthogonal unit vectors, $(\cdot ,\cdot )$ denotes the dot-product, $\Vert \cdot \Vert$ is the vector norm, and $\mathbb{N}$ represents the number of the unit-cells. The $ƛ\text{th}$ orthogonal unit state vector ${\widehat{\mathbf{W}}}_{2R,ƛ}^{\left(\beta \right)}$ is obtained through the iteration using the Gram–Schmidt orthonormalization procedures (Kissel, 1991). If the localization factor is equal to zero, the corresponding frequency intervals are known as pass-bands. Otherwise if the localization factor is positive, the frequency intervals are known as stop-bands or band-gaps. In this paper, only the normal incidence of SH wave is considered, thus, the dimension of the transfer matrix is $2\times 2$ and ${\ell }_1$ is the localization factor, which is denoted as $\ell$ in the following analysis.

4 Numerical Results and Discussions

In this section, the band structures and localization properties of the anti-plane elastic waves propagating normally in nanoscale layered structures are studied by the general transfer matrix method. Different factors affecting the band structures are considered. Numerical results are presented and discussed. During the calculations, we refer to Ref. (Yan et al., 2020) for the material constants and list the values in Table 1. For convenience, the frequency is normalized as ${\varpi }_1=\omega l/c_1$ with $c_1=\sqrt{{\mu }_1/{\rho }_1}$.

TABLE 1

TABLE 1. Material constants.

4.1 Nanoscale Random Disordered Layered PCs

Firstly, In order to check the correctness of the present method, the 1D nanoscale periodic layered structures arranged alternately by HfO2 ($A$) and ZrO2 ($B$), as shown in Figure 1A, are studied. The same material constants as the Ref. (Yan et al., 2020) are selected, and the results are shown in Figure 2A. We find that the present results (black solid lines) are in good agreement with the results (red solid lines) of Figure 2C in Ref. (Yan et al., 2020), which verifies the correctness and effectiveness of the current method. In the following, In order to reveal the influence of random disorder of the sub-layers on the band structures by considering the internal characteristic lengths and the external thicknesses, the localization factors in the cases of ${\tau }_1=0,l_1=l_2=0.5,{\tau }_2=0.18+\delta V_2\sqrt{(-2\ln \left(S\right)/S)}$ (i.e., disorder is considered only for the internal characteristic length of the second sub-layer $B$) and ${\tau }_1=0.18+\delta V_1\sqrt{(-2\ln \left(S\right)/S)},{\tau }_2=0.18+\delta V_2\sqrt{(-2\ln \left(S\right)/S)}$, $l_1=0.5+\delta V_1\sqrt{(-2\ln \left(S\right)/S)},l_2=0.5+\delta V_2\sqrt{(-2\ln \left(S\right)/S)}$ (i.e., disorder is considered for both internal characteristic lengths and external thickness of sub-layers $A$ and $B$), are calculated and the results are illustrated in Figures 2B,C. The disorder degree denoted by $\delta$ is assumed to be $\delta =\mathrm{0,0.02}$ and $0.04$, respectively. It can be seen that there is one peak point $a$ in Figure 2B and two peak points $b,c$ in Figure 2C whose positions are determined by the cut-off frequency of a specific material sub-layer. The second peak point $c$ in Figure 2C is a cut-off frequency beyond which the localization factor becomes stable and positive, which means that the elastic waves cannot propagate through the structure over the cut-off frequency. In addition, the dense band zones (DBZs) as defined in Ref (Yan et al., 2020) appears, where the localization factors are very big with multiple, dense, flat and narrow band-gaps in the frequency range $(7.28,7.35)$ in Figure 2B and $(5.47,5.56)$ in Figure 2C, meaning a very strong wave localization phenomenon. The disorder degree has little effect on the DBZ, the cut-off frequency and the localization factor whose frequencies are larger than the peak points $a$ and $c$. However, when the disorder caused by the sub-layer’s length or thickness is introduced to the periodic phononic crystals, the disorder degree still has some influences on the band structures in both pass-bands and band gaps, which are demonstrated by the enlarged sub-figure in Figures 2B,C. For example, in the pass-band $(6.519,6.704)$ for $\delta =0$ shown in the partly enlarged regions in Figure 2B, the localization factors become positive with the increase of $\delta$, indicating a wave localization phenomenon, and the localization degree increases with the increase of $\delta$ in the pass-bands while the localization degree decreases with the increase of $\delta$ in the band gaps. Next, the disorder of the internal characteristic length and the external thickness of the same sub-layer, the disorder of different sub-layers and the number of disorder are considered to show more detailed results in Figures 3A–C, respectively. The disorder degree is $\delta =0.08$. It can be seen from Figure 3A that the influences of the disorder caused by the internal characteristic lengths are a little bigger than those caused by the external thicknesses. In addition, in Figures 3B,C the localization factors change a lot and have a strong dependence on the disorder of different sub-layers and the number of disorder. Moreover, with the increase of the number of disorder, the degree of wave localization in the pass-bands increases, and the localization phenomenon becomes more and more obvious. From Figure 3, we can conclude that the disorder degree and the localization factor depend on different types of disorders of each sub-layer.

FIGURE 2

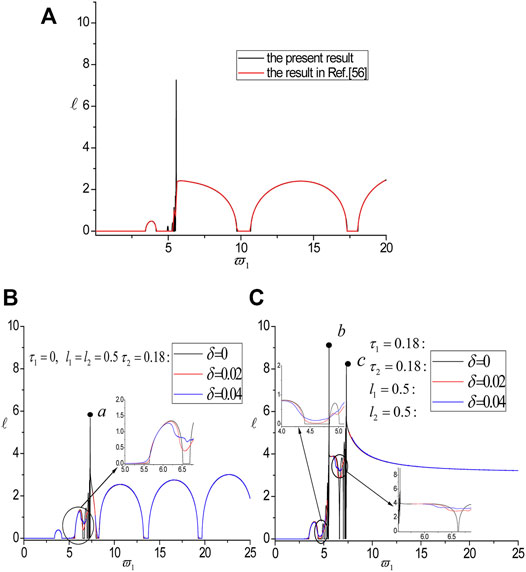
FIGURE 2. The results obtained by the current method are compared with the reference (A). The influences of δ on the localization factors and the disordered parameters are internal characteristic length τ₂ of the second sub-layer (B) and the internal characteristic length and the external thickness of sub-layers A and B (C), respectively.

FIGURE 3

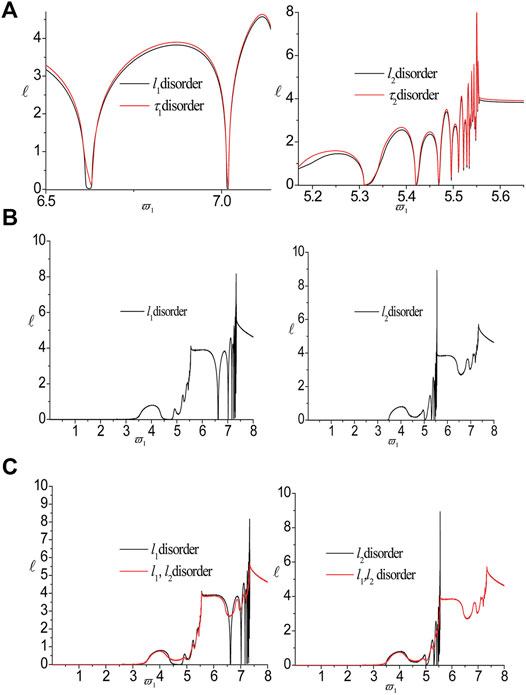
FIGURE 3. The influences of disorder on the localization factors for δ = 0.08. The internal characteristic lengths and the external thickness of the same sub-layer (A), the disorder of different sub-layers (B) and the number of disorder (C), respectively.

4.2 Nanoscale Aperiodic Layered PCs

Due to the lack of periodicity, a finite but sufficiently large number of unit-cell $n$ is very important to calculate the localization factor. After trial calculation, $n=1024$ is taken in the following computations. Next, the influences of the material combinations on the band structures are analyzed by considering changing the order of material components, only the single sub-layer material and two sub-layers are both changed, respectively. Specifically, the order of material components is selected as ${\text{HfO}}_2/{\text{ZrO}}_2$, ${\text{ZrO}}_2/{\text{HfO}}_2$ and ${\text{HfO}}_2/\text{Cu}$, $\text{Cu}/{\text{HfO}}_2$. Only the change of the second sub-layer material is taken as ${\text{HfO}}_2/\text{Cu}$, ${\text{HfO}}_2/{\text{ZrO}}_2$ and ${\text{HfO}}_2/\text{Al}$. The examples where the materials of two sub-layers are both changed are ${\text{ZrO}}_2/\text{Cu}$, ${\text{HfO}}_2/{\text{ZrO}}_2$ and $\text{Cu}/\text{Al}$. The band structures for the nanoscale Thue-Morse laminate with the change in order of material components are plotted in Figure 4. The ratio of internal characteristic length and the thickness of the unit-cell is ${\tau }_1={\tau }_2=0.18$. It can be seen that with the exchange of material components, the distance between the two peak points becomes narrower, and the two peak points and the first distinct band gap move to the low frequency zone. Furthermore, Compared with the two DBZs (5.42, 5.56) and (6.53, 7.34) for ${\text{HfO}}_2/{\text{ZrO}}_2$, the first and the second DBZs move left to (4.1, 4.21) and (4.98, 5.56) for ${\text{ZrO}}_2/{\text{HfO}}_2$, respectively. While the two DBZs for $\text{Cu}/{\text{HfO}}_2$ move left to (4.61, 4.72) and (5.3, 5.56) compared with the corresponding DBZs (5.31, 5.56) and (5.9, 6.54) for ${\text{HfO}}_2/\text{Cu}$. It is worth noted that compared with the first peak points for ${\text{HfO}}_2/{\text{ZrO}}_2$ and ${\text{HfO}}_2/\text{Cu}$, the second peak points, i.e., the cut-off frequencies, stay in the almost same position for ${\text{ZrO}}_2/{\text{HfO}}_2$ and $\text{Cu}/{\text{HfO}}_2$, that is to say, the cut-off frequencies for ${\text{ZrO}}_2/{\text{HfO}}_2$ and $\text{Cu}/{\text{HfO}}_2$ are almost $\varpi =5.56$ which are exactly the right edges of the corresponding DBZs, i.e., the cut-off frequency of the material ${\text{HfO}}_2$. In addition, when the frequency is higher than the cut-off frequency, the value of the localization factor will become stable at approximately 3.23 (as illustrated by the dashed lines in Figure 4).

FIGURE 4

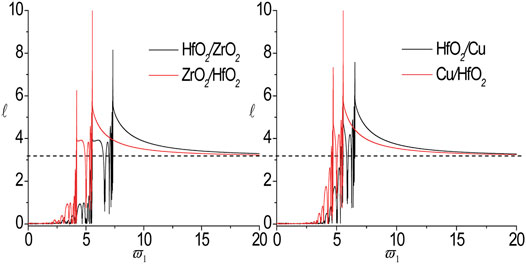
FIGURE 4. The influences of the mateiral component order on the lovalization factors of the Thue-Morse systems aperiodic systems.

In the following, we only change the material of the second sub-layer and the localization factors for the nanoscale aperiodic Thue-Morse sequences with different material combinations are presented in Figure 5. Here, the material combinations is taken as ${\text{HfO}}_2/\text{Cu}$, ${\text{HfO}}_2/{\text{ZrO}}_2$ and ${\text{HfO}}_2/\text{Al}$, respectively. It can be observed that the peak points, i.e., the DBZs with the frequency ranges of (5.3, 5.56), (6.48, 6.54), (7.03, 7.35) and (7, 7.32) correspond to materials ${\text{HfO}}_2$, $\text{Cu}$, ${\text{ZrO}}_2$ and $\text{Al}$, respectively. The band structures between the two DBZs have almost the same distributions, however, when the frequency is lower than the first peak point, the localization factors change a lot. More specifically, the first distinct band gap becomes wider and moves to the low frequency zone. Compared with Figures 5B,C shows the two DBZs are located at almost the same position, because the transverse wave velocities of the two materials ${\text{ZrO}}_2$ and $\text{Al}$, have almost similar values. In addition, the examples where the materials of two sub-layers are both changed are chosen as ${\text{ZrO}}_2/\text{Cu}$, ${\text{HfO}}_2/{\text{ZrO}}_2$ and $\text{Cu}/\text{Al}$, respectively. It can be seen from Figure 6 that the position of the peak point shown by the dashed line corresponds to materials $\text{Cu}$ and ${\text{HfO}}_2$ because the shear wave velocities of the two materials have the similar values. The larger the difference in transverse wave velocity, the farther the two DBZs are from each other.

FIGURE 5

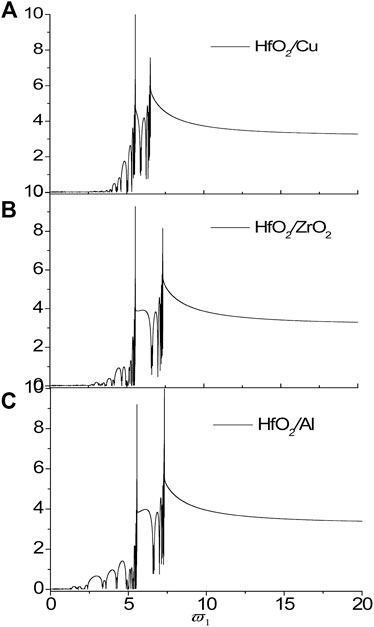
FIGURE 5. The localization factors of the SH wave propagating normally in the nanoscale aperiodic Thue-Morse sequences consisting of HfO₂/Cu (A), HfO₂/ZrO₂ (B) and HfO₂/Al (C) for τ₁ = τ₂ = 0.18.

FIGURE 6

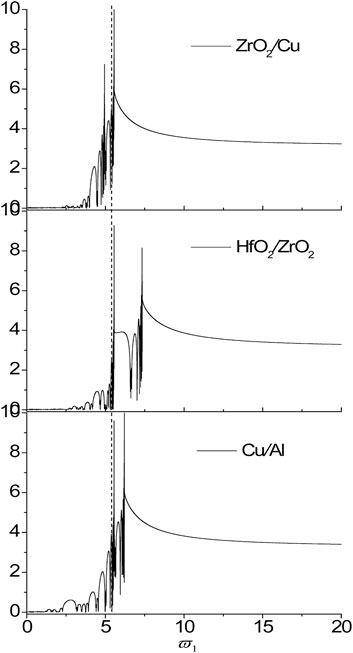
FIGURE 6. The localization factors of the SH wave propagating normally in the nanoscale aperiodic Thue-Morse sequences consisting of ZrO₂/Cu, HfO₂/ZrO₂ and Cu/Al for τ₁ = τ₂ = 0.18.

Next, the band structures of the systems with different aperiodic arrangements are calculated. As shown in Figures 1B–D, three different aperiodic arrangements are chosen, i.e., the Thue-Morse sequence, the Rudin-Shaprio sequence and the Fibonacci sequence, respectively. Figure 7 shows the influences of aperiodic arrangements on localization factors of the SH wave propagating normally in the nanoscale aperiodic systems consisting of ${\text{HfO}}_2/{\text{ZrO}}_2$ for ${\tau }_1={\tau }_2=0.18$. It can be seen that the tendencies of all curves are coincident for the three aperiodic systems, which implies the aperiodic arrangements have little effect on the peak points, the DBZs and the cut-off frequency. For example, the localization factors oscillate quickly with big values between the two peak points. The cut-off frequencies are all around about $\varpi =7.34$. However, the band structures before the first peak point becomes different for the three aperiodic arrangements. i.e., the main band gaps of the Fibonacci structure change a lot with the gradual disappearing and narrowing of the band gaps. Specifically, in the dot rectangle, compared with the Fibonacci structure, the localization factor is more like a defect state for the Thue-Morse and Rudin-Shapiro structures.

FIGURE 7

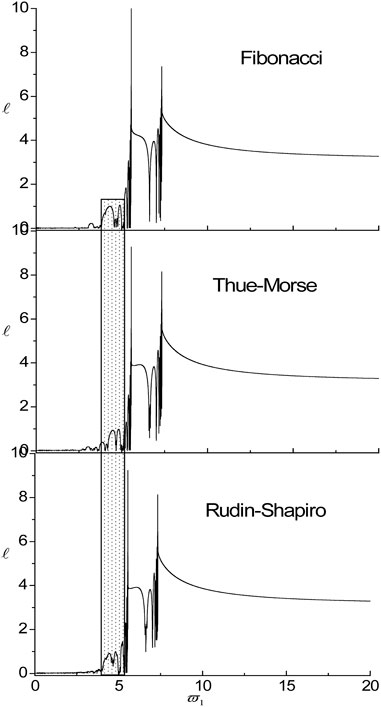
FIGURE 7. The influences of aperiodic arrangements on localization factors of the SH wave propagating normally in the nanoscale aperiodic systems consisting of HfO₂/ZrO₂ for τ₁ = τ₂ = 0.18.

Additionally, the influences of the ratio of the mass density ${\rho }_1/{\rho }_2$ and the ratio of the transverse wave velocity $c_1/c_2$ on the localization factors are examined. Here, the nanoscale $\text{Cu}/\text{Al}$ Fibonacci aperiodic laminate is selected as an example. It can be observed from Figure 8 that when the ratio of the mass density ${\rho }_1/{\rho }_2$ is not equal to $1$, the first distinct band gap emerges, while for ${\rho }_1/{\rho }_2=1$, it disappears (enlarged regions shown in Figure 8). The positions of the two DBZs, the two peak points, the cut-off frequency and the localization factors whose frequencies are larger than those of the first peak point have no changes. For example, after the first peak point, the tendencies of all curves are coincident, i.e., the localization factors oscillate quickly with big values after the first peak point, and then the second peak point appears. More detailed results are illustrated in Figure 9 for the localization factors varying with the normalized frequency and ${\rho }_1/{\rho }_2$. Compared with the results in Figure 8, the first distinct band gap disappears for ${\rho }_1/{\rho }_2=1$, when ${\rho }_1/{\rho }_2$ is less than 1 or ${\rho }_1/{\rho }_2$ is bigger than 1, the first distinct band gap appears and becomes wider with ${\rho }_1:{\rho }_2$ decreasing or increasing. Combining Figures 8, 9, we can conclude that the first distinct band gap will emerge for ${\rho }_1/{\rho }_2\ne 1$. and the ratio of the mass density has no influences on the peak points, the cut-off frequency, the DBZs and the localization factors whose frequencies are larger than those of the first peak point. From Figure 10, we can see that there is only one peak point when the ratio of transverse wave velocity is $c_1/c_2=1$, i.e., the cut-off frequency, and when the velocity ratio changes, the position of the peak point remains unchanged. However, when the ratio is not equal to $1$, there are two peak points. Among them, when the ratio of velocity is less than $1$, one peak point tends to the high-frequency region, and when the ratio is larger than $1$, a peak point tends to the low-frequency region. In addition, the low-frequency band gap is more likely to emerge with the increase of the ratio. This shows that the ratio of transverse wave velocity has significant effect on the cut-off frequency, the DBZ, the peak point and the low-frequency band gap. Furthermore, the localization factors varying with normalized frequency and $c_1/c_2$ are presented in Figure 11. There is only one peak point when the ratio of transverse wave velocity is $c_1/c_2=1$, i.e., the cut-off frequency of material Al, and when the velocity ratio changes, the position of the peak point remains unchanged since $c_2$ is a fixed value. On the contrary, the peak point other than the cut-off frequency moves the high-frequency region when $c_1/c_2$ is less than 1, and moves the low-frequency zone when $c_1/c_2$ is larger than 1. Combining Figures 10, 11, we can conclude that the position and the number of the peak point, i.e., the DBZ have strong dependence on $c_1/c_2$. There exists a wide pass-band when $c_1/c_2$ is less than 1, and the pass-band becomes wider with the decrease of $c_1/c_2$.

FIGURE 8

FIGURE 8. The influences of ratio of mass density on lacalization factors in the nanoscale Fibonacci systems consisting of Cu/Al for τ₁ = τ₂ = 0.18.

FIGURE 9

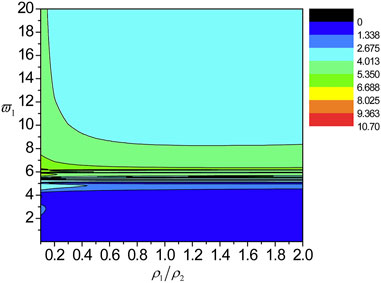
FIGURE 9. The localization factors varying with the normalized frequency and ${\rho }_1/{\rho }_2$for the SH wave propagating normally in the nanoscale Cu/Al Fibonacci laminate for τ₁ = τ₂ = 0.18.

FIGURE 10

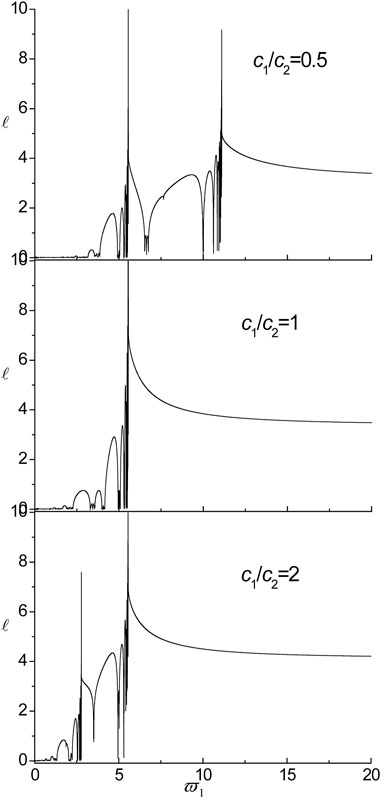
FIGURE 10. The influences of the ratio of transverse wave velocities on localization factors in the nanoscale Fibonacci systems consisting of Cu/Al for τ₁ = τ₂ = 0.18.

FIGURE 11

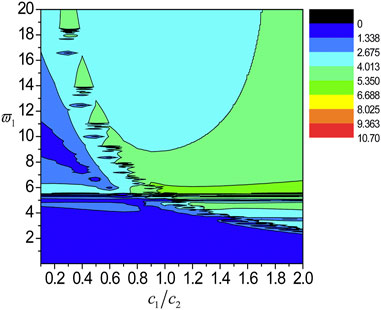
FIGURE 11. The localization factors varying with the normalized frequency and c₁/c₂ for the SH wave propagating normally in the nanoscale Cu/Al Fibonacci laminate for τ₁ = τ₂ = 0.18.

Finally, the influences of the structural parameter, i.e., the ratio of external characteristic thickness $l_1/l_2$ and the ratio of internal characteristic length ${\tau }_1/{\tau }_2$ on the localization factors are investigated. The localization factors for the nanoscale Fibonacci laminates with different values of $l_1/l_2$ are presented in Figure 12, From Figure 12, we can see that the pass-bands and band-gaps are affected by varying the ratio of external characteristic thickness, while the two peak points, the two DBZs and the cut-off frequency remain in the same position. Detailed results are shown in Figure 13, the position of the cut-off frequency remains unchanged, but the localization degree enhances with the increase of $l_1/l_2$. From Figure 14, we can see that the bigger the difference of internal characteristic length between the two materials, the farther the distance between the two peak points. The first distinct band gap disappears with the increase of ${\tau }_1/{\tau }_2$. More detailed numerical results are shown in Figure 15, It can be seen that the cut-off frequency does not appear when ${\tau }_1/{\tau }_2\le 0.2$, However, when $0.3\le {\tau }_1/{\tau }_2\le 1$, the cut-off frequency appears and decreases with the ${\tau }_1/{\tau }_2$ increasing. When ${\tau }_1/{\tau }_2>1$, the cut-off frequency remains unchanged and the first peak point tends to the low-frequency zone with the ${\tau }_1/{\tau }_2$ increasing. In addition, the localization degree of the cut-off frequency, the pass-bands and the band gaps varies with the ${\tau }_1/{\tau }_2$. And the localization degree whose frequencies are larger than the cut-off frequency decreases with ${\tau }_1/{\tau }_2$ increasing.

FIGURE 12

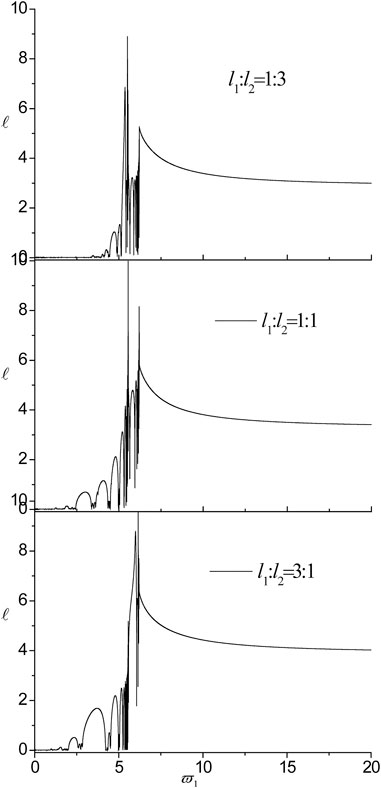
FIGURE 12. The influences of the ratio of external characteristic thickness on localization factors in the nanoscale Fibonacci systems consisting of Cu/Al for τ₁ = τ₂ = 0.18.

FIGURE 13

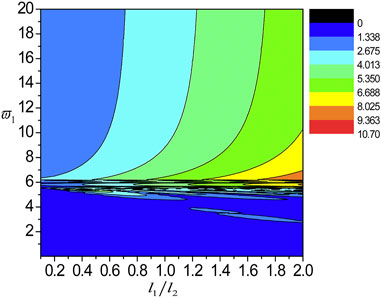
FIGURE 13. The localization factors varying with the normalized frequency and l₁/l₂ for the SH wave propagating normally in the nanoscale Cu/Al Fibonacci laminate for τ₁ = τ₂ = 0.18.

FIGURE 14

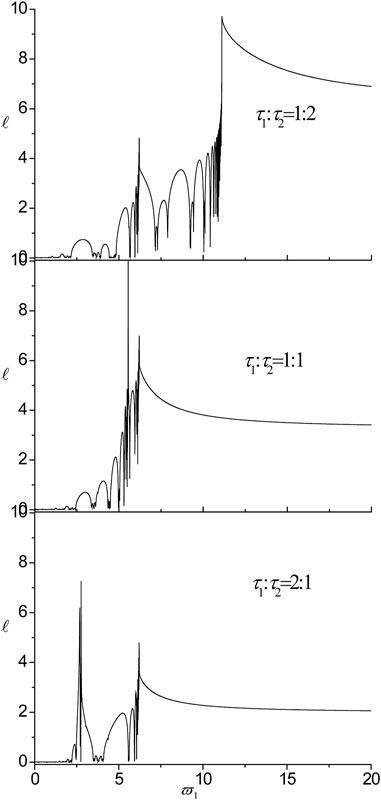
FIGURE 14. The influences of the ratio of the internal characteristic length on localization factors in the nanoscale Fibonacci systems consisting on Cu/Al for l₁ = l₂ = 0.5.

FIGURE 15

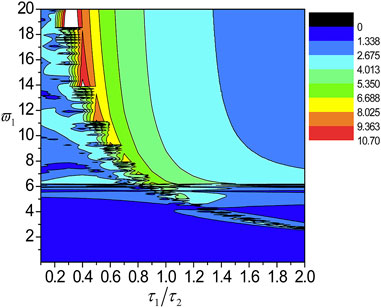
FIGURE 15. The localization factors varying with the normalized frequency and τ₁/τ₂ for the SH wave propagating normally in the nanoscale Cu/Al Fibonacci laminate for τ₁ = τ₂ = 0.18.

5 Conclusion

The results presented in this study are obtained by the numerical calculations of the wave localization properties in the nanoscale layered structures by using the general transfer matrix method based on the nonlocal elastic continuum theory. The key conclusions from this analysis can be summarized as follows:

1) No matter what kind of disorders, the disorder degree has little effect on the DBZ, the peak point, the cut-off frequency and the localization factor whose frequencies are larger than the cut-off frequency. However, the influences of the disorder caused by the internal characteristic lengths are a little bigger than those caused by the external thicknesses. The localization factors have a strong dependence on the disorder of different sub-layers and the number of disorder.

2) The first distinct band gap, the peak point, the cut-off frequency, the DBZ and the localization factor have strong dependence on the material combinations. With the exchange of material components, the distance between the two peak points becomes narrower, and the two peak points and the first distinct band gap move to the low frequency zone. The position of the peak point and the DBZ depends on the sub-layer materials under consideration.

3) The aperiodic arrangements have little effect on the peak points, the DBZs and the cut-off frequency. However, the band structures before the first peak point becomes different for the three aperiodic arrangements.

4) The first distinct band gap will emerge for ${\rho }_1/{\rho }_2\ne 1$. and the ratio of the mass density has no influences on the peak points, the cut-off frequency, the DBZs and the localization factors whose frequencies are larger than those of the first peak point.

5) There is only one peak point when the ratio of transverse wave velocity is $c_1/c_2=1$. However, when the ratio of velocity is less than $1$, one peak point tends to the high-frequency region, and when the ratio is larger than $1$, a peak point tends to the low-frequency region. In addition, the low-frequency band gap is more likely to emerge with the increase of the ratio. There exists a wide pass-band when $c_1/c_2$ is less than 1, and the pass-band becomes wider with the decrease of $c_1/c_2$.

6) The pass-bands and band gaps are affected by varying the ratio of external characteristic thickness, while the two peak points, the two DBZs and the cut-off frequency remain in the same position. In addition, the localization degree enhances with the increase of $l_1/l_2$.

7) When $0.3\le {\tau }_1/{\tau }_2\le 1$, the cut-off frequency appears and decreases with the ${\tau }_1/{\tau }_2$ increasing. When ${\tau }_1/{\tau }_2>1$, the cut-off frequency remains unchanged and the first peak point tends to the low-frequency zone with the ${\tau }_1/{\tau }_2$ increasing, And the localization degree whose frequencies are larger than the cut-off frequency decreases with ${\tau }_1/{\tau }_2$ increasing.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Funding

The authors greatly acknowledge the financial support from the National Natural Science Foundation of China (No. 11002026, 11372039), Beijing Natural Science Foundation (No. 3133039), and the Scientific Research Foundation for the Returned Overseas Chinese Scholars (No. 20121832001).

References

Adhikari, S., Gilchrist, D., Murmu, T., and McCarthy, M. A. (2015). Nonlocal normal Modes in Nanoscale Dynamical Systems. Mech. Syst. Signal Process. 60-61, 583–603. doi:10.1016/j.ymssp.2014.12.004

CrossRef Full Text | Google Scholar

Aifantis, E. C. (1999). Strain Gradient Interpretation of Size Effects. Int. J. Fract 95 (1-4), 299–314. doi:10.1007/978-94-011-4659-3_16

CrossRef Full Text | Google Scholar

Alibeigloo, A. (2011). Free Vibration Analysis of Nano-Plate Using Three-Dimensional Theory of Elasticity. Acta Mech. 222, 149–159. doi:10.1007/s00707-011-0518-7

CrossRef Full Text | Google Scholar

Anderson, P. W. (1958). Absence of Diffusion in Certain Random Lattices. Phys. Rev. 109, 1492–1505. doi:10.1103/physrev.109.1492

CrossRef Full Text | Google Scholar

Artan, R., and Altan, B. S. (2002). Propagation of SV Waves in a Periodically Layered media in Nonlocal Elasticity. Int. J. Sol. Structures 39, 5927–5944. doi:10.1016/s0020-7683(02)00476-6

CrossRef Full Text | Google Scholar

Aynaou, H., Boudouti, E. H. E., Djafari-Rouhani, B., Akjouj, A., Velasco, V. R., and Velasco, V.R (2005). Propagation and localization of acoustic waves in Fibonacci phononic circuits. J. Phys.: Condens. Matter 17, 4245–4262. doi:10.1088/0953-8984/17/27/002

CrossRef Full Text | Google Scholar

Barco, O, and Ortuno, M (2012). Localization length of nearly periodic layered metamaterials. Phys Rev A 86 (2), 023846. doi:10.1103/physreva.86.023846

CrossRef Full Text | Google Scholar

Bovier, A., and Ghez, J.-M. (1995). Remarks on the Spectral Properties of Tight-Binding and Kronig-Penney Models with Substitution Sequences. J. Phys. A: Math. Gen. 28, 2313–2324. doi:10.1088/0305-4470/28/8/022

CrossRef Full Text | Google Scholar

Chen, A.-L., Tian, L.-Z., and Wang, Y.-S. (2017). Band Structure Properties of Elastic Waves Propagating in the Nanoscaled Nearly Periodic Layered Phononic Crystals. Acta Mechanica Solida Sinica 30, 113–122. doi:10.1016/j.camss.2017.03.005

CrossRef Full Text | Google Scholar

Chen, A.-L., Wang, Y.-S., Ke, L.-L., Guo, Y.-F., and Wang, Z.-D. (2013). Wave Propagation in Nanoscaled Periodic Layered Structures. Jnl Comp. Theo Nano 10, 2427–2437. doi:10.1166/jctn.2013.3225

CrossRef Full Text | Google Scholar

Chen, A.-L., and Wang, Y.-S. (2011). Size-effect on Band Structures of Nanoscale Phononic Crystals. Physica E: Low-dimensional Syst. Nanostructures 44, 317–321. doi:10.1016/j.physe.2011.08.032

CrossRef Full Text | Google Scholar

Chen, A.-L., and Wang, Y.-S. (2007). Study on Band Gaps of Elastic Waves Propagating in One-Dimensional Disordered Phononic Crystals. Physica B: Condensed Matter 392, 369–378. doi:10.1016/j.physb.2006.12.004

CrossRef Full Text | Google Scholar

Chen, A.-L., Wang, Y.-S., and Zhang, C. (2012). Wave Propagation in One-Dimensional Solid-Fluid Quasi-Periodic and Aperiodic Phononic Crystals. Physica B: Condensed Matter 407, 324–329. doi:10.1016/j.physb.2011.10.041

CrossRef Full Text | Google Scholar

Chen, A.-L., Yan, D.-J., Wang, Y.-S., and Zhang, C. (2016). Anti-plane Transverse Waves Propagation in Nanoscale Periodic Layered Piezoelectric Structures. Ultrasonics 65, 154–164. doi:10.1016/j.ultras.2015.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, A.-L., Yan, D.-J., Wang, Y.-S., and Zhang, C. (2019). In-plane Elastic Wave Propagation in Nanoscale Periodic Piezoelectric/piezomagnetic Laminates. Int. J. Mech. Sci. 153-154, 416–429. doi:10.1016/j.ijmecsci.2019.02.017

CrossRef Full Text | Google Scholar

Chen, J.-J., Wang, Q., and Han, X. (2010). Lamb Wave Transmission through One-Dimensional Three-Component Fibonacci Composite Plates. Mod. Phys. Lett. B 24, 161–167. doi:10.1142/s0217984910022305

CrossRef Full Text | Google Scholar

Chen, J., Guo, J., and Pan, E. (2017). Wave Propagation in Magneto-Electro-Elastic Multilayered Plates with Nonlocal Effect. J. Sound Vibration 400, 550–563. doi:10.1016/j.jsv.2017.04.001

CrossRef Full Text | Google Scholar

Du, S. G., Shi, D. M., and Deng, H. (2000). Special effects and applications of nanostructured materials. Ziran Zazhi 22 (2), 101–106.

Google Scholar

Economou, E. N., and Sigalas, M. (1994). Stop bands for elastic waves in periodic composite materials. The Journal of the Acoustical Society of America 95, 1734–1740. doi:10.1121/1.408692

CrossRef Full Text | Google Scholar

El-Nabulsi, R. A. (2018). Nonlocal Approach to Energy Bands in Periodic Lattices and Emergence of Electron Mass Enhancement. J. Phys. Chem. Sol. 122, 167–173. doi:10.1016/j.jpcs.2018.06.028

CrossRef Full Text | Google Scholar

El-Nabulsi, R. A. (2018). On Nonlocal Complex Maxwell Equations and Wave Motion in Electrodynamics and Dielectric media. Opt. Quant Electron. 50, 170. doi:10.1007/s11082-018-1436-x

CrossRef Full Text | Google Scholar

Eringen, A. C. (2006). Nonlocal Continuum Mechanics Based on Distribution. Int. J. Eng. Sci. 44 (3-4), 141–147. doi:10.1016/j.ijengsci.2005.11.002

CrossRef Full Text | Google Scholar

Eringen, A. C. (1972). Nonlocal Polar Elastic Continua. Int. J. Eng. Sci. 10 (1), 1–16. doi:10.1016/0020-7225(72)90070-5

CrossRef Full Text | Google Scholar

Eringen, A. C. (1983). On Differential Equations of Nonlocal Elasticity and Solutions of Screw Dislocation and Surface Waves. J. Appl. Phys. 54 (9), 4703–4710. doi:10.1063/1.332803

CrossRef Full Text | Google Scholar

Fernández-Alvarez, L., and Velasco, V. R. (1998). Sagittal Elastic Waves in Fibonacci Superlattices. Phys. Rev. B 57, 14141–14147. doi:10.1103/physrevb.57.14141

CrossRef Full Text | Google Scholar

Gastanier, M. P., and Pierre, C. (1997). Predicting Localization via Lyapunov Exponents Statistics. J. Sound Vib 203, 151–157.

Google Scholar

Gazi, N. A., and Bernhard, G. (2014). Quasi-periodic Fibonacci and Periodic One-Dimensional Hypersonic Phononic Crystals of Porous Silicon: Experiment and Simulation. J. Appl. Phys. 116, 094903.

Google Scholar

Golub, M. V., Zhang, C., and Wang, Y.-S. (2012). SH-wave Propagation and Scattering in Periodically Layered Composites with a Damaged Layer. J. Sound Vibration 331, 1829–1843. doi:10.1016/j.jsv.2011.12.008

CrossRef Full Text | Google Scholar

Gurtin, M. E., Weissmüller, J., and Larché, F. (1998). A General Theory of Curved Deformable Interfaces in Solids at Equilibrium. Philosophical Mag. A 78 (5), 1093–1109. doi:10.1080/01418619808239977

CrossRef Full Text | Google Scholar

Hashemi, S. H., and Samaei, A. T. (2011). Buckling Analysis of Micro/nanoscale Plates via Nonlocal Elasticity Theory. Physica E: Low-dimensional Syst. Nanostructures 43, 1400–1404. doi:10.1016/j.physe.2011.03.012

CrossRef Full Text | Google Scholar

Heireche, H., Tounsi, A., Benzair, A., Maachou, M., and Adda Bedia, E. A. (2008). Sound Wave Propagation in Single-Walled Carbon Nanotubes Using Nonlocal Elasticity. Physica E: Low-dimensional Syst. Nanostructures 40, 2791–2799. doi:10.1016/j.physe.2007.12.021

CrossRef Full Text | Google Scholar

Hepplestone, S. P., and Srivastava, G. P. (2008). Hypersonic Modes in Nanophononic Semiconductors. Phys. Rev. Lett. 101 (10), 105502. doi:10.1103/physrevlett.101.105502

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu an, A., Jiang Shu-sheng, S. S., Peng Ru-Wen, R. W., Zhang Chun-sheng, C. S., and Feng Duan, D. (1992). Extended One-Dimensional Fibonacci Structures. Acta Phys. Sin. 41 (1), 62–68. doi:10.7498/aps.41.62

CrossRef Full Text | Google Scholar

Hu, H., Li, D.-J., Zhu, J.-L., and Xiong, J.-J. (2000). Size Effects on Excitons in Nano-Rings. J. Phys. Condens. Matter 12, 9145–9151. doi:10.1088/0953-8984/12/43/304

CrossRef Full Text | Google Scholar

Huang, G. L., and Sun, C. T. (2007). Continuum Modelling of Solids with Micro/nanostructures. Philosophical Mag. 87, 3689–3707. doi:10.1080/14786430701400137

CrossRef Full Text | Google Scholar

Kana, N., Khamlich, S., Kana Kana, J. B., and Maaza, M. (2013). Peculiar Surface Size-Effects in Nacl Nano-Crystals. Surf. Rev. Lett. 20, 1350001. doi:10.1142/s0218625x13500017

CrossRef Full Text | Google Scholar

Ke, L.-L., Wang, Y.-S., and Wang, Z.-D. (2012). Nonlinear Vibration of the Piezoelectric Nanobeams Based on the Nonlocal Theory. Compos. Structures 94, 2038–2047. doi:10.1016/j.compstruct.2012.01.023

CrossRef Full Text | Google Scholar

King, P. D. C., and Cox, T. J. (2007). Acoustic Band Gaps in Periodically and Quasiperiodically Modulated Waveguides. J. Appl. Phys. 102, 014902. doi:10.1063/1.2749483

CrossRef Full Text | Google Scholar

Kissel, G. J. (1991). Localization Factor for Multichannel Disordered Systems. Phys. Rev. A. 44, 1008–1014. doi:10.1103/physreva.44.1008

PubMed Abstract | CrossRef Full Text | Google Scholar

Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. (1993). Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 71, 2022–2025. doi:10.1103/physrevlett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Luntiaov, M., and Rogerson, G. A. (2010). Long Wave Motion in Layered Elastic media. Int. J. Eng. Sci. 48 (21), 1856–1871.

Google Scholar

Merlin, R., Bajema, K., Clarke, R., Juang, F.-Y., and Bhattacharya, P. K. (1985). Quasiperiodic GaAs-AlAs Heterostructures. Phys. Rev. Lett. 55, 1768–1770. doi:10.1103/physrevlett.55.1768

PubMed Abstract | CrossRef Full Text | Google Scholar

Mindlin, R. D. (1965). Second Gradient of Strain and Surface-Tension in Linear Elasticity. Int. J. Sol. Structures 1 (4), 417–438. doi:10.1016/0020-7683(65)90006-5

CrossRef Full Text | Google Scholar

Nguyen, T. T., Abdelmoula, R., Li, J., Roussigne, Y., and Stashkevich, A. (2016). Wave Propagating in Multilayers Composed of Piezo Electric and Piezo Magnetic Layers. Composites B: Eng. 93, 289–301. doi:10.1016/j.compositesb.2016.03.019

CrossRef Full Text | Google Scholar

Nougaoui, A., and Rouhani, B. D. (1987). Elastic Waves in Periodically Layered Infinite and Semi-infinite Anisotropic media. Surf. Sci. 185, 125–153. doi:10.1016/s0039-6028(87)80618-0

CrossRef Full Text | Google Scholar

Nowinski, J. L. (1984). On the Nonlocal Aspects of the Propagation of Love Waves. Int. J. Eng. Sci. 22, 383–392. doi:10.1016/0020-7225(84)90073-9

CrossRef Full Text | Google Scholar

Nowinski, J. L. (1991). On Wave Propagation in an Elastic Micropolar Medium with Nonlocal Cohesive Forces. J. Franklin Inst. 328 (4), 459–470. doi:10.1016/0016-0032(91)90020-4

CrossRef Full Text | Google Scholar

Parsons, L. C., and Andrews, G. T. (2009). Observation of Hypersonic Phononic crystal Effects in Porous Silicon Superlattices. Appl. Phys. Lett. 95, 241909. doi:10.1063/1.3275742

CrossRef Full Text | Google Scholar

Ramprasad, R., and Shi, N. (2005). Scalability of Phononic crystal Heterostructures. Appl. Phys. Lett. 87 (11), 111101. doi:10.1063/1.2043242

CrossRef Full Text | Google Scholar

Sesion, P. D., Albuquerque, E. L., Chesman, C., and Freire, V. N. (2007). Acoustic Phonon Transmission Spectra in Piezoelectric AlN/GaN Fibonacci Phononic Crystals. Eur. Phys. J. B 58, 379–387. doi:10.1140/epjb/e2007-00249-5

CrossRef Full Text | Google Scholar

Shaat, M. (2017). A General Nonlocal Theory and its Approximations for Slowly Varying Acoustic Waves. Int. J. Mech. Sci. 130, 52–63. doi:10.1016/j.ijmecsci.2017.05.038

CrossRef Full Text | Google Scholar

Sigalas, M. M., and Soukoulis, C. M. (1995). Elastic-wave Propagation through Disordered And/or Absorptive Layered Systems. Phys. Rev. B Condens Matter 51, 2780–2789. doi:10.1103/physrevb.51.2780

PubMed Abstract | CrossRef Full Text | Google Scholar

Toupin, R. A. (1962). Elastic Materials with Couple-Stresses. Arch. Rational Mech. Anal. 11 (1), 385–414. doi:10.1007/bf00253945

CrossRef Full Text | Google Scholar

Waksmanski, N., and Pan, E. (2017). An Analytical Three-Dimensional Solution for Free Vibration of a Magneto-Electro-Elastic Plate Considering the Nonlocal Effect. J. Intell. Mater. Syst. Structures 28 (11), 1501–1513. doi:10.1177/1045389x16672734

CrossRef Full Text | Google Scholar

Wolf, A., Swift, J. B., Swinney, H. L., and Vastano, J. A. (1985). Determining Lyapunov Exponents from a Time Series. Physica D: Nonlinear Phenomena 16, 285–317. doi:10.1016/0167-2789(85)90011-9

CrossRef Full Text | Google Scholar

Yan, D.-J., Chen, A.-L., Wang, Y.-S., Zhang, C., and Golub, M. (2018). In-plane Elastic Wave Propagation in Nanoscale Periodic Layered Piezoelectric Structures. Int. J. Mech. Sci. 142-143, 276–288. doi:10.1016/j.ijmecsci.2018.04.054

CrossRef Full Text | Google Scholar

Yan, D.-J., Chen, A.-L., Wang, Y.-S., and Zhang, C. (2020). Size-effect on the Band Structures of the Transverse Elastic Wave Propagating in Nanoscale Periodic Laminates. Int. J. Mech. Sci. 180, 105669. doi:10.1016/j.ijmecsci.2020.105669

CrossRef Full Text | Google Scholar

Yan, Z.-Z., and Zhang, C. (2012). Band Structures and Localization Properties of Aperiodic Layered Phononic Crystals. Physica B: Condensed Matter 407, 1014–1019. doi:10.1016/j.physb.2012.01.001

CrossRef Full Text | Google Scholar

Yan, Z.-Z., Zhang, C., and Wang, Y.-S. (2009). Analysis of Wave Propagation and Localization in Periodic/disordered Layered Composite Structures by a Mass-spring Model. Appl. Phys. Lett. 94, 161909–161913. doi:10.1063/1.3119206

CrossRef Full Text | Google Scholar

Yan, Z.-Z., Zhang, C., and Wang, Y.-S. (2010). Wave Propagation and Localization in Randomly Disordered Layered Composites with Local Resonances. Wave Motion 47, 409–420. doi:10.1016/j.wavemoti.2010.02.002

CrossRef Full Text | Google Scholar

Yang, F., Chong, A. C. M., Lam, D. C. C., and Tong, P. (2002). Couple Stress Based Strain Gradient Theory for Elasticity. Int. J. Sol. Structures 39 (10), 2731–2743. doi:10.1016/s0020-7683(02)00152-x

CrossRef Full Text | Google Scholar

Yu, D., Wen, J., Shen, H., Xiao, Y., and Wen, X. (2012). Propagation of Flexural Wave in Periodic Beam on Elastic Foundations. Phys. Lett. A 376, 626–630. doi:10.1016/j.physleta.2011.11.056

CrossRef Full Text | Google Scholar

Zárate, J. E., Fernández-Alvarez, L., and Velasco, V. R. (1999). Transverse Elastic Waves in Fibonacci Superlattices. Superlattices and Microstructures 25, 519–526. doi:10.1006/spmi.1998.0682

CrossRef Full Text | Google Scholar