Resistivity Signature of Graphene-Based Fiber-Reinforced Composite Subjected to Mechanical Loading

The paper reports on a piezoresistivity response of fiber-reinforced cement mortar with graphene nano-platelets. The use of a small quantity (0.25% by the weight of cement) of nano-sized conductive particles of graphene turned conventional portland cement-based composite into a semiconductive stress-sensing material. The resistivity was measured using a surface resistivity tester, well accepted by the concrete industry, which employs an alternative current through four electrodes. Tension and compression tests of standard specimens were used to establish the relationship between the resistivity and the applied strain. Finite element analyses were employed to predict the resistivity of the slab specimen under three-point bending. The tests results and simulation indicate that the electrical resistivity of the graphene-cement composite material can be used for structural health monitoring and damage detection.

Introduction

Concrete and other cement-based composites are widely used in physical infrastructure. The ability to deploy sensing into concrete can provide vital information on usage, loading, corrosion process and damage helping to avert catastrophic failures and loss of life (Sanchez and Sobolev, 2010; Aza et al., 2015; Tian et al., 2019). Sensing mechanisms in concrete in roadway and bridge structures must be low cost, durable, and distributed over large volumes. Piezo-resistivity can be a viable solution for concrete and cement-based composites to attain stress and damage sensing capabilities (Aza et al., 2015; Belli et al., 2018). The goal of this study is to examine a portland cement-based composite material that can detect the magnitude and distribution of applied loads as well as report on local damage.

Cement mortar consists of aggregate and hardened cement (solid), air (vapor) and pore solution (fluid). As summarized by Spragg et al. (2013), air is non-conductive with electrical resistivity up to $3\times {10}^{15}$ kΩ·cm and aggregates are non-conductive with a resistivity of up to 4,000 (sand) and 30,000 (limestone) kΩ·cm; however, the fluid in pores is usually conductive with a resistivity of 20 (tap water) down to 0.01 (concrete pore solution) kΩ·cm. Therefore, hardened cement mortar demonstrates conductivity due to the mobility of ionic solutions in pores and microcracks. The electrical conductivity or resistivity of concrete has been used to reflect durability, potential to corrosion, and service life estimates (Morris et al., 1996; Polder et al., 2000; Azarsa and Gupta, 2017; Cosoli et al., 2020). Specifically, bulk and surface resistivity has been used to analyze the permeability of concrete. In this case, concrete samples must be in saturated (to form a connected pore network) and surface dry condition (to avoid additional conductive paths outside concrete). When concrete is dry, partially missing the conductive pore fluid, the decrease of conductivity can be such significant that resistivity is beyond the measurement range of typical testing equipment.

Conductive nano materials such as carbon nanofibers (CnFs), carbon nanotubes (CnTs) and graphene nano-platelets (GnPs) have been added to nonconductive media to modify the electrical conductivity response (Gao et al., 2009; Konsta-Gdoutos and Aza 2014; Du and Dai Pang, 2015; D'Alessandro et al., 2016; Chen et al., 2017; Belli et al., 2018). Graphene is highly conductive with an electrical resistivity of $0.2\times {10}^{-6}$ kΩ·cm. The conductive nanoparticles may form a conductive point to point network in addition to the pore network in concrete when the conductive particles are properly dispersed in cement matrix and reach the percolation threshold. For example, Le et al. (2014) added 15% (by weight of cement) graphene in cement mortar such that the material essentially had a conductive matrix. The discussion in this paper is limited to composite cement materials with a relatively small amount of nano-sized conductive additives because smart material is expected to be deployed in the field as a construction material replacing a segment of concrete or a layer of concrete. The piezoresistivity of such smart materials has been demonstrated using simple compressive tests (Wen and Chung, 2001b; Yang et al., 2017). However, the connections have not been clearly defined between the piezoresistivity tests and practical applications of such self-sensing materials.

In this study, graphene nano-platelets at a dosage of 0.25% by weight of cement were incorporated into fiber-reinforced composite (FRC) to develop a smart material with sensing capability. It is envisioned that well-dispersed GnP particles may act complementary to pore fluid in concrete, leading to hybrid ionic fluid-conductive particle networks. Fibers are used in the proposed composite material to prevent the opening of major cracks such that the electrical resistivity changes within a measurable range (Hoheneder et al., 2015; Hoheneder et al., 2019). Applied stresses can change the connectivity of the hybrid conductive networks, making the concrete material sensitive to the applied loads. In addition, distresses such as cracks from mechanical loading and dry shrinkage may significantly change the connectivity of the conductive networks, making the developed material sensitive to service and environmental loads. Tension and compression tests of standard mortar specimens were conducted to establish the relationships between the resistivity and the applied strains. Finite element analyses were conducted to predict the resistivity of a slab specimen under three-point bending.

Literature Review

Smart Concrete and Applications

Conductive particles have been added to cement-based materials in various dosages. For examples, Wen and Chung (2001a) studied electric resistivity of carbon fiber-reinforced cement mortar with a focus on the effect of polarization while using direct current testing techniques. The amount of the carbon fibers varied from 0.5 to 1% by weight of cement. D'Alessandro et al. (2016) investigated electrical resistivity of treated carbon nanotube (0.5%) reinforced cement mortar using cyclic compressive loading. Gao et al. (2009) investigated the mechanical and electrical properties of concrete with carbon nanofibers up to 2% by weight of cement. Konsta-Gdoutos and Aza (2014) investigated the self-sensing of cementitious composites reinforced with carbon nanotubes (0.1%) and nanofibers (0.3%). Konsta-Gdoutos et al. (2017) later studied bulk electrical resistivity of nanomodified portland cement mortars with carbon nanotubes (0.1%) and nanofibers (0.5%).

Resistivity and Conductivity Measurements

The resistivity of semiconductive materials has been measured using two- or four-probe methods with direct current (DC) or alternative current (AC). For example, Hoheneder et al. (2015) used two-probe DC measurements on prism specimens; Saafi et al. (2013) used four-probe AC measurements on prism specimens; and Laflamme and Ubertini (2020) used two-probe AC measurements on cube specimens. Wen and Chung (2001a) revealed that DC-based measurements cause electric polarization, which leads to an increase of the measured electrical resistivity over time. The AC-based measurement can thus be used to reduce the impact of electric polarization. In addition to the polarization at the electrode-sample interfaces, cement composite material may develop polarization during AC-based resistivity measurements. Therefore, the resistivity of semiconductive materials can vary with AC frequencies.

Cement-based materials usually have large resistances; hence resistivity measurement using 2-probe schemes leads to insignificant difference from 4-probe schemes. However, the resistivity measurements can be affected by interfacial gaps between electrodes and concrete (McCarter et al., 2015) and electrode sizes. Newlands et al. (2008) used a simple low-frequency AC end-to-end resistivity test. The authors examined the sensitivity of electrode contact solutions and contact pressures at the electrode-concrete interface with the use of synthetic sponges. In this case, the conductive solution contained in the sponge was found to greatly affect the resistance readings of dry samples, and fully saturated samples were suggested. Therefore, it is critical to create a sound electrode-concrete interface for reliable measurements. It may be desirable to have embedded electrodes; however, embedded metal wire mesh may interfere with the deformation and damage propagation in samples during loading.

In addition, Elkey and Sellevold (1995) pointed out that the temperature and relative humidity (RH) at the time of resistance testing is important for the evaluation of concrete samples. Temperature increase leads to the increases in the ionic mobility while the increase in the relative humidity of samples may provide an additional conductive media in pore networks. The authors concluded that the observed resistivity dropped by about three percent for every one-degree (Celsius) rise in temperature or every one percent increase in the degree of saturation.

Piezoresistivity Study

The applied stresses in most existing tests were limited in the elastic range. Wen and Chung (2007) and Wen and Chung (2008) demonstrated that compressive stresses cause the decrease in the electrical resistivity of carbon fiber-reinforced cement composites, and the authors attributed the phenomenon to slight fiber push-in in compression. Meanwhile, uniaxial tension had been previously reported to cause the increase in resistivity due to slight fiber pull-out that accompanies crack opening. The compressive strains were observed to reach up to 140 $\mu \epsilon$. The beam specimens in reported by Hoheneder et al. (2015) and Saafi et al. (2013) were loaded till flexural fracture; however, the observed behavior may not be attributed to a material response because the materials in the specimens were subjected to a range of stresses depending upon their locations.

The cube specimens in the study by D'Alessandro et al. (2016) were subjected to repeated compressive strains up to 400 $\mu \epsilon$. The tests indicated that at small strains, the piezoresistivity of the carbon nanotube reinforced cement mortar had a repeatable response upon loading and unloading. However, the observed resistances had nonlinear increase with time, indicating that the resistivity measurement may have been affected by the environment or the resistivity measurement techniques. The cube specimens in the study by Meoni et al. (2018) were monotonically loaded beyond the measured peak strains. The tests showed the resistivity of the specimens decreased at a larger rate with an increase in the compressive strain in the post-peak region. Note that the four layers of embedded wire mesh electrodes may have affected the mechanical response of the specimens such that the observed behavior from a sample with 1.0% multiwall carbon nanotubes was different from the sample produced with 0.5% nanotubes. Laflamme and Ubertini (2020) also used cube specimens, but with only two embedded wire mesh electrodes to minimize their impact on the mechanical responses. In addition, an LCR meter was used with an AC input at 100 kHz. Linear relationship was observed between the applied compressive strain (up to 400 $\mu \epsilon$) and the measured decrease in the electrical resistance.

Materials and Methods

Materials

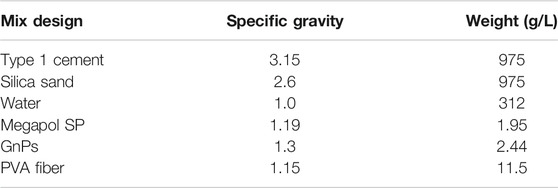
Table 1 reports on the mixture proportions of the fiber reinforced Portland cement-based composites with graphene nano-platelets (GnPs). The weight proportion of all components was calculated based on a water-cement ratio of 0.32, a sand-cement ratio of 1.0, a superplasticizer dosage of 0.2%, a GnP dosage of 0.25%, and a volume ratio of 1.0% for PVA fibers. The weight of the ingredients was thus calculated using a specific gravity of 3.15 for Type I Portland cement from Lafarge Holcim, 2.6 for the silica sand from Granusil, 1.19 for the Megapol MP 40-DF superplasticizer from Ruetgers Polymers with 39.8% solids, 1.3 for the graphene nano-platelets from XG Sciences with 13.2% solids, and 1.15 for the Kuralon K-II PVA fibers from Kuraray.

TABLE 1

TABLE 1. Mixture design of portland cement mortar with graphene nano-platelets.

The dispersion of the graphene nano-platelets was performed before the component was mixed into the mortar. The GnP samples were placed in deionized water (W) with superplasticizer (SP) using a weight ratio of GnP:SP:W = 1:0.1:10. Water and superplasticizer dosages in the mortar mix were adjusted accordingly to account for the quantities introduced with GnP suspension. The dispersion of GnP was achieved using a Fisher Scientific 2.5L ultrasonic bath (operating at 110 W at 40 kHz) and a Hielscher UIP1000hd ultrasonic horn system, which took 3 hours of cycled sonication: Two rounds for 45 min of sonication in bath followed by 15 min of sonication using horn. The temperature of the samples in the ultrasonic bath was maintained between 25 and 30°C by using ice and cold water. The same temperature was maintained in the ultrasonic horn unit by placing the sample bottle in a beaker filled with ice water. At the end of the procedure, the sample bottle was placed in the ultrasonic bath for 60 min to complete the dispersion. Dynamic light scattering tests were conducted upon the dispersion, and the results indicated that the dispersed GnPs had an average diameter of 20.9 μm with a standard deviation of 11.2 μm.

The cement-based composite was mixed according to ASTM 305 using a standard Hobart mixer. Portion (75%) of mixing water was first added to the bowl with silica sand and mixed at a low speed for 30 s. After mixing sand and water, the PVA fibers were added in two portions and mixed for 30 s at a low speed after each portion. Portland cement was also added to the mix in two portions and mixed for 30 s at a low speed. The remaining water was added to the mix along with premixed GnPs as described above and the composite was mixed at a low speed for 30 s and another 30 s at a medium speed. After mixing, standard cube and prism samples were cast along with a 300 × 300 × 19 mm slab. Some PVA fibers were not completely dispersed; therefore, manual dispersion was used to break up the fiber balls. The samples were cured in molds for 24 h in a standard curing room. After 24 h, the samples were demolded and cured in the curing room till the testing days.

Specimens and Test Setup

The impact of tensile loading on the electrical resistivity of GnP-FRC composites was studied using a standard prism specimen (Figure 1A). The prism had a dimension of 38 × 12.7 × 160 mm. Two concrete strain gages were attached to the wide faces to capture the tensile strains. The resistivity of the material within the gaged length was measured using two steel plate electrodes (12.7 mm square), clamped to a side face. Carbon grease was used between the plate electrodes and the specimen and pressure was applied using zip cable ties to ensure a proper electrode-specimen contact.

FIGURE 1

FIGURE 1. Configuration of tension test (A) test setup; (B) finite element models (the colored map showing the electrical potential field).

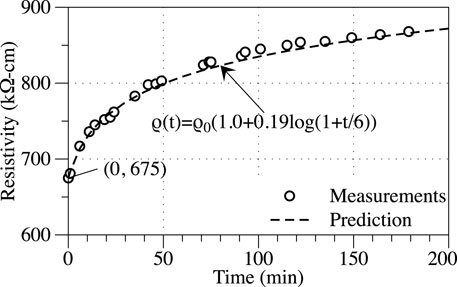
Trial tests had demonstrated that the resistance of oven-dried samples was beyond the measuring range of the surface resistivity tester (200 kΩ), indicating that GnPs alone at the relatively low dosage of 0.25% may not be sufficient to form conductive networks. Therefore, the resistivity measurement considered the moisture conditions of the sample: the sample taken out of the curing room was considered fully saturated; the condensation water on the surface was wiped and the sample was air dried to achieve a saturated surface dry condition. The resistivity of the sample was measured periodically over the next 3 h, and the measurements are reported in Figure 2. Initially, the resistivity of the prism specimen increased rapidly, and the rate of resistivity increase greatly reduced towards the end of the 3-h observation period. A logarithmic function, $\rho \left(t\right)={\rho }_0\left[1+K_c\log \left(1+t/6\right)\right]$, where ${\rho }_0$ is the initial resistivity, $t$ is time in minutes, and $K_c$ is a constant related to ambient conditions such as relative humidity (RH), temperature (T), and air movement. The function with a $K_c$-factor of 0.191 and the initial resistivity of 675 kΩ cm fits well the experimental data corresponding to typical room conditions (RH = 60%, T = 18.3°C, and common indoor air movement). Further study on the impact of ambient condition over a long period of time was beyond the scope of the study; nevertheless, the mechanical loading commenced after the stabilization of the resistivity readings.

FIGURE 2

FIGURE 2. Effect of ambient condition on resistivity of prism specimen.

The tensile test setup is presented in Figure 1. The end regions of the specimen (within 25 mm from the ends) were coated with a thin layer of epoxy to insulate the specimen from the metal testing frame. Tensile loading was applied using an Instron universal testing machine at a loading rate of 0.13 mm/min through standard wedge grips at the end regions. The epoxy coating may also strengthen the gripped regions such that fracture would likely occur outside the regions. The entire test was finished within 3 min such that the resistivity increase of the specimen due to moisture loss could be ignored. A donut load cell (Model THD-50K-Y from Transducer Techniques) was placed above the loading beam to measure the applied tensile forces. An IO Tech DaqBook 2000 data acquisition system was used to collect data from the LVDTs and the load cell with a sampling rate of 10 Hz. In addition to the collected data, video was recorded capturing the surface resistivity tester with the data acquisition screen, and the resistivity readings were recovered after the test from synchronized video playback.

The impact of compressive loading on the electrical resistivity of GnP-FRC composites was studied using a standard 50-mm cube specimen (Figure 3). Compressive loading was applied using an ELE compression machine at a loading rate of 1.4 kN/sec. Instead of embedded metal wire mesh electrodes, steel plate electrodes were used in this study. A thin layer of carbon grease was again used between the electrodes and the sample to minimize the impact of potential gaps on resistivity measurements. A 3-mm plastic sheet was used between the metal loading heads and the electrodes to insulate the specimen. Strain gages were installed in the vertical direction to record the compressive strain in the cube and the donut load cell from Transducer Technology was placed below the specimen to record the applied compressive load. Strain gages were also placed horizontally to provide data for the Poisson’s ratio. In addition to strain gages, two Type ZX-PA string pots from Unimeasure were used to monitor the shortening of the cube specimen.

FIGURE 3

FIGURE 3. Configuration of compression test (A) test setup; (B) finite element models (the colored map showing the electrical potential field).

The same procedure was followed for the cube specimen to achieve saturated surface dry condition after it was taken out of the curing room. However, the metal plate electrodes could not be pre-clamped to the cube specimen; therefore, the readings from the study of the ambient condition were significantly affected by the pressure applied to the assembly. Again, the mechanical loading commenced after the stabilization of resistivity readings, and the test was finished in about 5 min such that the resistivity change due to moisture loss could be ignored. The same data acquisition and manual resistivity logging procedure reported for the tensile test was used in the compressive test.

Resistivity Measurement

The electrical resistance of the samples was measured using a Resipod surface resistivity meter for concrete from Proceq®. The surface resistivity meter operates using the principle of Wenner probe (Wenner, 1916; Tanesi and Ardani, 2012): A current is applied to the two outer probes (current probes) and the potential difference is measured between the two inner probes (potential probes). The Resipod operates with a digitally generated 40 Hz alternating current (with a maximum potential drop of 38 V). A constant current ($I$) of 200 $\mu A$ is driven through concrete when the resistance is below 190 kΩ; otherwise, the current is automatically lowered to 50 $\mu A$. The Resipod is expected to operate on the surface of semi-infinite concrete; hence a geometry factor ($K_{sr}$) of $2\pi a$ is usually assumed, where $a$ is the probe spacing in cm ($a=5$ cm in this study). Therefore, the reported resistivity (${\rho }_r$) is the potential drop ($\Delta V$) divided by the AC current ($I$) and multiplied by $2\pi a$.

Plate electrodes were used in the tests of the cube and prism specimens. A resistor of 5 kilohm was used to separate the current probes and the potential probes. This resistor was selected to have a resistance comparable to the cube specimen of the GnP-FRC composite material. The cube specimen had two plate electrodes slightly larger than the cross section of the specimen (Figure 3), hence the resistivity of the material ($\rho$) was calculated from the reported resistivity (${\rho }_r$) by $\rho =\frac{{\rho }_r}{2\pi a}\frac{A}{L}$, where $A$ is the cross-sectional area and $L$ is the length of the cube specimen. Meanwhile, the prism specimen had two 12.7 × 12.7 mm plate electrodes on a side face (Figure 1B) with a center-on-center spacing of 8 cm, the length of the concrete strain gage. The current flow through the prism specimen is not uniform as that observed in the cube specimen (Figure 3B). Hence, a geometry correction factor was obtained from the finite element analyses as reported below. The analysis indicated that the resistivity readings should be reduced by a geometry factor ($K_g$) of 0.7313 to consider the impact of non-uniform current flow. The corrected resistivity (${\rho }_r$) is then modified by $\rho =\frac{{\rho }_r}{2\pi a}\frac{A}{L}$, where $A$ is the cross-sectional area of the prism specimen and $L$ is the distance between the plate electrodes (8 cm), to properly capture the resistivity of the material.

Finite Element Analysis

Multiple ways of conduction contribute to the electrical conductivity of GnP-FRC composite materials, similar to natural rocks (Telford et al., 1990), including electronical conduction (like metals), electrolytic conduction (through pore fluid), dielectric conduction (under an external varying electric field), and emission conduction (between adjacent GnP particles under a high electric field). The analysis in this paper considered only the electronical conduction, which is governed by the Ohm’s law: the electrical resistance ($R$) of a homogeneous cylindrical solid with a cross section area of $A$ and a length of $L$ between end faces is known as $R=\frac{V}{I}$, where $V$ is the potential difference applied at the ends and $I$ is the resulting current. The electrical resistivity of the solid with a uniform current is determined by $\rho =\frac{V}{I}\frac{A}{L}=\frac{V/L}{I/A}$, where $V/L$ is the electric field ($E$) and $I/A$ is the current density ($J$). In a general conductive solid, the electrical field vector is the gradient of the electrical potential, $E=-\nabla V$, and the current density is thus $J=-{\rho }^{-1}\nabla V$. Note that the inverse of the electric resistivity (${\rho }^{-1}$) is defined as the electric conductivity (σ). Electrical charges cannot accumulate in a conductive material (the total amount of electrical charge is conserved); therefore, $\nabla J=\nabla \left({\rho }^{-1}\nabla V\right)=0$. If the solid is homogeneous and isotropic, the equation reduces to ${\rho }^{-1}{\nabla }^{2}V=0$, which governs the electrical potential in the solid with current flux entering and exiting the enclosed surface of the solid. The solution of the governing partial differential equation requires proper boundary conditions.

In the case of using Wenner probe for measuring the resistivity of earth or similar semi-infinite mediums, the current fluxes entering the medium (through Probe 1 as illustrated below in Figure 7) may be views as point boundary conditions, and the electrical charges spread evenly through the medium (Hambley, 2018). The current density on the semi-spheric surface with a radius of $r$ is thus calculated as $J=\frac{I}{2\pi r^2}$. The electrical potential at the first potential probe (Probe 2) is $V_2=\rho \frac{I}{2\pi a^2}a=\rho \frac{I}{2\pi a}$, where $a$ is the probe spacing, and the potential at the second potential probe (Probe 3) is $V_3=\rho \frac{I}{2\pi {\left(2a\right)}^2}\left(2a\right)=\rho \frac{I}{2\pi \left(2a\right)}$. The potential difference between the two potential probes is thus $\Delta V=V_2-V_3= \rho \frac{I}{2\pi \left(2a\right)}$. The potential difference under an equal current flux exiting (Probe 4) the medium is also $\Delta V=V_2-V_3= \rho \frac{I}{2\pi \left(2a\right)}$. Using the principle of superposition for the assumed linear analysis, the potential difference is $\Delta V=\rho \frac{I}{2\pi a}$, and the electrical resistivity can thus be obtained by $\rho =\frac{\Delta V}{I}2\pi a$.

The ideal spheric dispersion of electrical charges is disturbed when the object is not semi-infinite, with a variety of insulating or conductive boundaries, or the current fluxes are from an electrode with a non-negligible geometry. In this case, the solution to the governing differential equation is usually in the form of infinite series (Valdes 1954). An open-source package FEATool Multiphysics by Precise Simulation was used in this study for finite element (FE) analyses. A variety of analyses were first conducted to study the impact of specimen geometry and electrode geometry. For example, the prism specimen was modeled as reported in Figure 1B. The contour of electrical potential field indicates that the 12.7 × 12.7 mm plate electrodes led to an increased potential difference between the electrodes such that the reported resistivity could be higher than the actual material property (the conductivity, ${\rho }^{-1}$, was a required material property in the analyses). In addition, an analysis of the cube specimen (Figure 3B) indicated that the electrical potential field was uniform over the cross section when the current boundary conditions were applied to the specimen using two slightly larger plate electrodes. Therefore, no geometric correction was needed in this case.

Results and Discussion

Effect of Tensile Strains

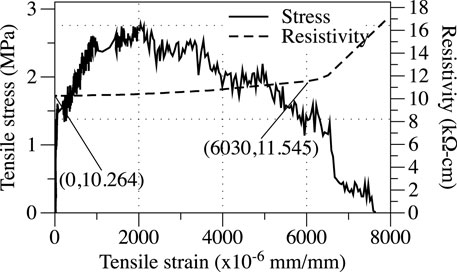
Figure 4 reports on the results of the tensile test. A transverse crack initiated at one side of the specimen within the gaged length at a stress of 1.5 MPa, which is smaller than the expected cracking stress. This may have been attributed to the slight offset and the resulting bending created by the mis-aligned grips and the different thickness in the epoxy coatings at the gripped ends. The strain gage readings indicated that the transverse crack extended to the whole cross section (Figure 6A) at a stress about 3.0 MPa and a strain of 2,000 $\mu \epsilon$. The load carrying capacity of the prism specimen was maintained till a strain of 6,000 $\mu \epsilon$ because of the crack bridging effect of PVA fibers.

FIGURE 4

FIGURE 4. Results of tension test.

The resistivity of the material ($\rho$) started at 10.264 kΩ cm when the tensile strain was zero, corresponding to a resistivity reading of 731 kΩ cm using $\rho =\frac{{\rho }_r{K}_g}{2\pi a}\frac{A}{L}$, where $K_g$ is the geometry factor, 0.7313 from the finite element analyses, $L$ is 8 cm, the gage length, $A$ is 4.84 cm², and $a$ is 5 cm. This resistivity reading was lower than that observed at the end of the moisture sensitivity study (868 kΩ cm) shown in Figure 2. This may have been attributed to the fact that the temperature of the testing lab was five degrees higher and the ambient relative humidity 10 percent higher than that of the office. The observed 15% resistivity drop is close to that predicted by Elkey and Sellevold (1995). The resistivity of the material increased approximately linearly to 11.545 kΩ cm when the tensile strain increased to 6,030 $\mu \epsilon$. A curve fitting indicates that the resistivity of the material in this study can be determined by

$\rho ={\rho }_0\left(1+K_s\epsilon \right),(1)$

where ${\rho }_0$ is the resistivity at zero loading, $\epsilon$ is the strain in mm/mm, and the $K_s$ is the strain factor, 20 kΩ cm/mm/mm from the linear regression analysis. Note that this relationship is applicable up to a strain of 6,030 $\mu \epsilon$, beyond which, the resistivity of the material quickly increased because of the crack opening as demonstrated by Figure 6A.

Effect of Compressive Strains

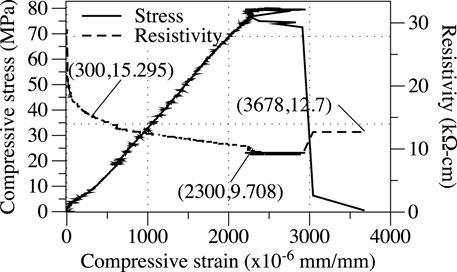
Figure 5 reports on the results of the compression test. The stress-strain behavior of the GnP-FRC composite material had a nearly linear ascending branch followed by a steep descending branch. Note that the strains in Figure 5 used the strains from strain gages before the first peak stress and those from the string pots after the peak. The peak stress (80 MPa) was reached at a strain of 2,300 $\mu \epsilon$, beyond which, the specimen started developing vertical splitting cracks as shown by the failure mode in Figure 6B. The average measured Poisson’s ratio was 0.31, corresponding to stresses from 1.20 to 10.5 MPa. This ratio seemed high compared with that of typical concrete.

FIGURE 5

FIGURE 5. Results of compression test.

FIGURE 6

FIGURE 6. Failure modes (A) prism specimen after tension test; (B) cube specimen after compression test.

The initial resistivity measurement was affected by the gap between the plate electrodes and the specimen as the initial resistivity was 28.7 kΩ cm (converted from a Resipod reading (${\rho }_r$) of 180.4 kΩ cm using $\rho =\frac{{\rho }_r}{2\pi a}\frac{A}{L}$, where $L$ is 5 cm, $A$ is 25 cm², and $a$ is 5 cm), as shown in Figure 7. The measured electrical resistivity decreased rapidly when the applied pressure closed the gap, and the resistivity-strain relationship appears nonlinear during this stage of loading. Upon further loading beyond a strain of 500 $\mu \epsilon$ and a stress of 20 MPa, the resistivity decreased linearly with an increase in compressive strains. Hence, it may be reasonable to use Eq. 1 to describe the resistivity-strain behavior, and a regression analysis indicated that the strain factor ($K_s$) was about −200.0 kΩ cm/mm/mm. Again, this linear relationship may be applicable up to a strain of 2,300 $\mu \epsilon$. Both the stress-strain response and the resistivity-strain behavior near the peak stress had fluctuation as the cube sample broke into several smaller columns, some of which failed by shear fracture, leading to the end of the test. These smaller columns in parallel did not cause much damage in the conductive networks; therefore, the electrical resistivity of the failed sample was 12.7 kΩ cm upon removal of the compressive loading. This resistivity may be viewed as the same as the initial material property without electrode-sample gaps. In addition, an extension of the regression equation using Eq. 1 indicates that the initial resistivity might have been 10.168 kΩ cm at the zero strain, close to the above initial material property.

FIGURE 7

FIGURE 7. Schematics of slab specimen with electrode grid.

Finite Element Analysis of a Slab Specimen

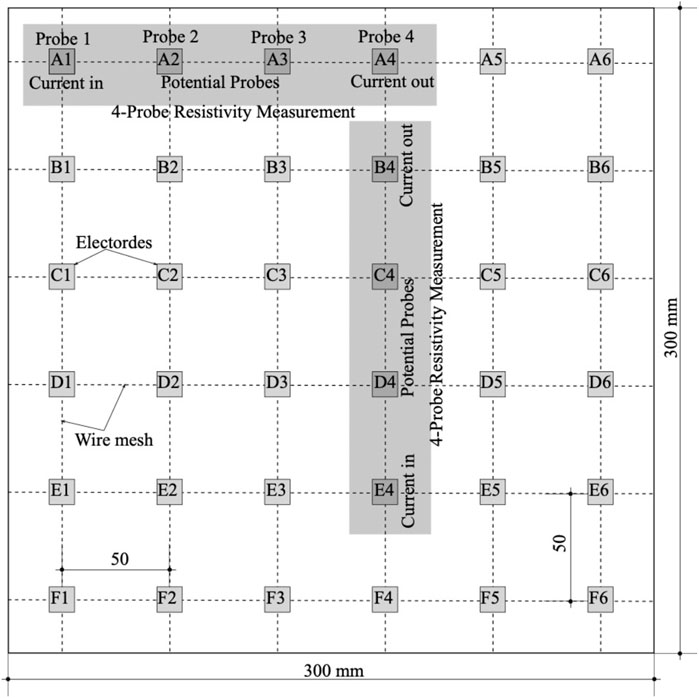
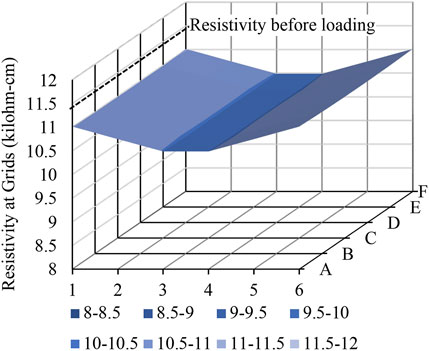
Beyond simple specimens, the scale-up of the GnP-FRC composite materials to serve realistic structural elements is expected to provide a better representation of stress sensing functions. For example, the 300 × 300 × 19 mm slab specimen had thirty-six 12.7 × 12.7 mm embedded plate electrodes as illustrated by Figure 7. The electrodes were located 12.7 mm from the top face and were positioned using a basalt fiber reinforced polymer wire mesh with a 50-mm grid. Following a resistivity measurement scheme using the Resipod, four electrodes (A1, A2, A3, and A4) can be used to capture the electrical resistivity between A2 and A3. Sufficient measurements can be made to create an electrical resistivity map to reflect the impact of complex loading on realistic structural elements. Tests of the slab specimen is beyond the scope of this study. Instead, finite element analyses were used to demonstrate the strain sensing capability of structural members made of GnP-FRC composite materials.

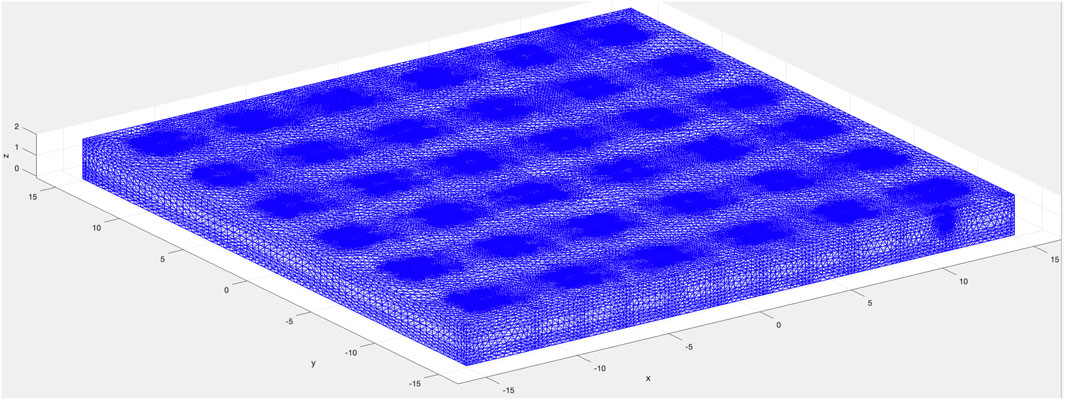
The finite element models were created for the slab shown in Figure 8 using the open-source package FEATool Multiphysics. It is envisioned that when the slab specimen is subjected to three-point bending, material at the top layers may have decreased electrical resistivity due to compressive strains while the bottom layers may have an increased resistivity due to tensile strains and cracking. FEATool Multiphysics does not have coupled modeling capabilities between mechanical stress analyses and electrical potential analyses. Therefore, the slab was divided into eleven segments along the span, and six layers across the slab thickness. The analysis was conducted for the moment, when maximum strains were 2,000 $\mu \epsilon$ in both tension and compression. The required conductivity constants (${\rho }^{-1}$) for the total of 66 segments were specified manually and the strain-dependent electrical resistivities were calculated using Eq. 1 with the observed $K_s$ factors, that is 20 kΩ/mm/mm in tension and −200 kΩ/mm/mm in compression.

FIGURE 8

FIGURE 8. Finite element model of scaled-up slab specimen.

The boundary conditions for the electrical potential analysis included two equal and opposite current flux on two current electrodes (e.g., Electrodes A1 and A4 in Figure 7) in terms of a current density; and the current (200 $\mu A$, similar to that used in the surface resistivity tester) was the specified current density multiplied by the area of the plate electrodes. The electrical potential field was obtained as the result of the finite element analyses; and the potential differences at the two inner electrodes (e.g., Electrodes A2 and A3 in Figure 7) were used to calculate the simulated resistivity measurements. The 36 plate electrodes enabled six groups of three resistivity measurements in either horizontal or vertical direction. In order to generate more intuitive surface plots, these simulated measurements in between grid nodes (e.g., A2-A3) were used to calculate the resistivities at the nodes. Specifically, ${\rho }_{A2}$ (the resistivity at Node A2) is assumed to be the same as that from A2-A3; ${\rho }_{A3}$ is the average value from A2-A3 and A3-A4; and ${\rho }_{A1}$ is obtained by a linear interpolation using ${\rho }_{A3}$ and ${\rho }_{A2}$. The final calculated resistivity at nodes was the average values from the horizontal measurements and the vertical measurements.

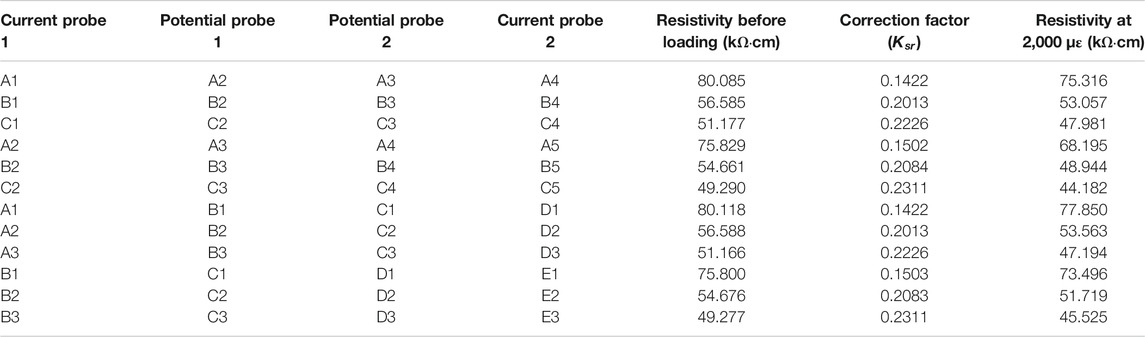
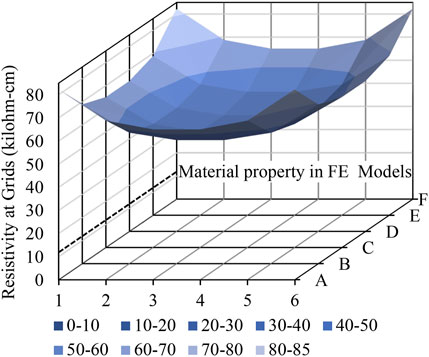
A group of analyses was first conducted for the slab specimen with an electrical resistivity (${\rho }_0$) of 11.39 kΩ cm (the conductivity, ${\rho }^{-1}$, was thus 0.0878 mS/cm). Due to symmetry, only partial simulated resistivity measurements were calculated as listed in Table 2 and reported in a surface plot in Figure 9. The simulated electrical resistivity measurements were higher than the assumed material property. Specifically, the analysis results from simulated Wenner probes close to edges (e.g., A2-A3) are higher than those in the middle (e.g., C2-C3). This is related to the edge effect (Valdes, 1954) and the thickness effect (Topsoe, 1968) in the resistivity measurements of semiconductive media. A group of correction factors was obtained by dividing the assumed electrical resistivity (${\rho }_0$) by the calculated resistivities as listed in Table 2. The same correction factors were used for the simulation before and after loading.

TABLE 2

TABLE 2. Simulated resistivity measurements of slab specimen.

FIGURE 9

FIGURE 9. Simulated electrical resistivity mapping of slab specimen without loading.

Figure 10 reports on the resistivity of the slab after a point load applied at the mid-span of a simply supported slab. With the correction factors in Table 2, the resistivity of the slab under the point load would in general decrease because the resistivity decreases of materials in compression are higher than the resistivity increases of materials in tension. In addition, the simulated electrical resistivity map reflected the moment diagram of the slab. Although the simulated behavior must be verified by experiments, the analysis indicated that GnP-FRC composite materials can have stress sensing capabilities. Meanwhile, it should be noted that the maximum simulated resistivity changes were less than 10 percent of the initial resistivity as listed in Table 2; therefore, the stress-related resistivity changes may not be clearly shown in physical tests as the resistivity measurements may be affected by many factors.

FIGURE 10

FIGURE 10. Simulated electrical resistivity mapping of slab specimen under three-point bending.

Conclusion

Graphene nano-platelets (GnPs) used at a relatively low dosage of 0.25% by the weight of portland cement was shown to be able to enhance the conductivity of the otherwise nearly nonconductive cement-based material. Electrical resistivity of the resulting GnP-FRC material was examined for its potential stress sensing properties. The resistivity was measured using a surface resistivity tester, well accepted by the concrete industry. The resistivity measurement employed the alternative current through a four-point Wenner probe. Tension and compression tests of standard mortar specimens were conducted to establish the relationships between the resistivity and the applied strains. It was observed from the reported tests that the resistivity of the GnP-FRC composite material increased with an increase in tensile strains and decreased at a faster pace with an increase in compressive strains. This may have been attributed to the fact that the observed tensile strain was mainly from a transverse crack while the compressive strains reflect the material deformation of the entire sample. A linear relationship was proposed based on the test results to describe the change of electrical resistivity (conductivity) of the material with compressive and tensile strains. The highly simplified linear relationships may be applicable to strains less than 2,300 $\mu \epsilon$ for the material used in this study. Finite element analyses were conducted to predict the resistivity response of a scaled-up slab specimen under three-point bending. The tests and simulations indicate that the electrical resistivity of the GnP-FRC composite material can be used for structural health monitoring.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HL: Experimental tests, literature review, and manuscript review AD: Smart concrete study, literature review, and manuscript review NS: Research guidance, manuscript review JZ: Research supervision, and manuscript draft KS: Research concept formulation, smart concrete, and manuscript revision.

Funding

The project was funded by UWM Research Growth Initiative (RGI) program. The opinions, findings, and recommendations or conclusions expressed in this paper are those of the authors only.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

UWM undergraduate student Jonathan Paul wrote the code for Arduino microcontroller for automatic resistivity measurements.

Abbreviations

a, Probe spacing in Wenner probe; A, cross-sectional area of sample; E, electrical field; I, electrical current; J, electrical current density; K_c, ambient condition factor; K_g, geometry correction factor; K_s, strain factor; K_sr, geometry correction factor for surface resistivity measurements; l, sample length or distance between electrodes; SP, weight of superplasticizer; t, time in minutes; V, potential drop between two inner probes or points; W, weight of water; ε, strain in material; ρ, resistivity; ρ_o, initial resistivity in moisture condition study; ρ_r, reported resistivity by surface resistivity tester.

References

Aza, C. A., Danoglidis, P. A., and Konsta-Gdoutos, M. S. (2015). “Self Sensing Capability of Multifunctional Cementitious Nanocomposites,” in Nanotechnology in Construction (Cham: Springer), 363–369. doi:10.1007/978-3-319-17088-6_47

CrossRef Full Text | Google Scholar

Azarsa, P., and Gupta, R. (2017). Electrical Resistivity of concrete for Durability Evaluation: a Review. Adv. Mater. Sci. Eng. 2017, 1. doi:10.1155/2017/8453095

CrossRef Full Text | Google Scholar

Belli, A., Mobili, A., Bellezze, T., Tittarelli, F., and Cachim, P. (2018). Evaluating the Self-Sensing Ability of Cement Mortars Manufactured with Graphene Nanoplatelets, virgin or Recycled Carbon Fibers through Piezoresistivity Tests. Sustainability 10 (11), 4013. doi:10.3390/su10114013

CrossRef Full Text | Google Scholar

Chen, M., Gao, P., Geng, F., Zhang, L., and Liu, H. (2017). Mechanical and Smart Properties of Carbon Fiber and Graphite Conductive concrete for Internal Damage Monitoring of Structure. Construction Building Mater. 142, 320–327. doi:10.1016/j.conbuildmat.2017.03.048

CrossRef Full Text | Google Scholar

Cosoli, G., Mobili, A., Tittarelli, F., Revel, G. M., and Chiariotti, P. (2020). Electrical Resistivity and Electrical Impedance Measurement in Mortar and concrete Elements: A Systematic Review. Appl. Sci. 10 (24), 9152. doi:10.3390/app10249152

CrossRef Full Text | Google Scholar

D'Alessandro, A., Rallini, M., Ubertini, F., Materazzi, A. L., and Kenny, J. M. (2016). Investigations on Scalable Fabrication Procedures for Self-Sensing Carbon Nanotube Cement-Matrix Composites for SHM Applications. Cement and Concrete Composites 65, 200–213. doi:10.1016/j.cemconcomp.2015.11.001

CrossRef Full Text | Google Scholar

Du, H., and Pang, S. D. (2015). “Mechanical Response and Strain Sensing of Cement Composites Added with Graphene Nanoplatelet under Tension,” in Nanotechnology in Construction (Cham: Springer), 377–382. doi:10.1007/978-3-319-17088-6_49

CrossRef Full Text | Google Scholar

Elkey, W., and Sellevold, E. (1995). Electrical Resistivity of Concrete. Publication No. 80. Oslo, Norway: Norwegian Road Research Laboratory.

Google Scholar

Gao, D., Sturm, M., and Mo, Y. L. (2009). Electrical Resistance of Carbon-Nanofiber concrete. Smart Mater. Struct. 18 (9), 095039. doi:10.1088/0964-1726/18/9/095039

CrossRef Full Text | Google Scholar

Hambley, A. R. (2018). Electrical Engineering: Principles and Applications. London, UK: Pearson.

Google Scholar

Hoheneder, J., Flores-Vivian, I., Lin, Z., Zilberman, P., and Sobolev, K. (2015). The Performance of Stress-Sensing Smart Fiber Reinforced Composites in Moist and Sodium Chloride Environments. Composites B: Eng. 73, 89–95. doi:10.1016/j.compositesb.2014.12.028

CrossRef Full Text | Google Scholar

Hoheneder, J., Flores-Vivian, I., and Sobolev, K. (2019). Performance of Fiber-Reinforced Carbon Nanotubes-Nanofibers Composites, 335. Farmington Hills, MI: ACI, 27–36.

Google Scholar

Konsta-Gdoutos, M. S., and Aza, C. A. (2014). Self Sensing Carbon Nanotube (CNT) and Nanofiber (CNF) Cementitious Composites for Real Time Damage Assessment in Smart Structures. Cement and Concrete Composites 53, 162–169. doi:10.1016/j.cemconcomp.2014.07.003

CrossRef Full Text | Google Scholar

Konsta-Gdoutos, M. S., Batis, G., Danoglidis, P. A., Zacharopoulou, A. K., Zacharopoulou, E. K., Falara, M. G., et al. (2017). Effect of CNT and CNF Loading and Count on the Corrosion Resistance, Conductivity and Mechanical Properties of Nanomodified OPC Mortars. Construction Building Mater. 147, 48–57. doi:10.1016/j.conbuildmat.2017.04.112

CrossRef Full Text | Google Scholar

Laflamme, S., and Ubertini, F. (2020). “Use of Styrene Ethylene Butylene Styrene for Accelerated Percolation in Composite Cement-Based Sensors Filled with Carbon Black,” in Nanotechnology in Cement-Based Construction ( Dubai, U.A.E.: Jenny Stanford Publishing), 49–66. doi:10.1201/9780429328497-4

CrossRef Full Text | Google Scholar

Le, J.-L., Du, H., and Pang, S. D. (2014). Use of 2D Graphene Nanoplatelets (GNP) in Cement Composites for Structural Health Evaluation. Composites Part B: Eng. 67, 555–563. doi:10.1016/j.compositesb.2014.08.005

CrossRef Full Text | Google Scholar

McCarter, W. J., Taha, H. M., Suryanto, B., and Starrs, G. (2015). Two-point concrete Resistivity Measurements: Interfacial Phenomena at the Electrode-concrete Contact Zone. Meas. Sci. Technol. 26 (8), 085007. doi:10.1088/0957-0233/26/8/085007

CrossRef Full Text | Google Scholar

Meoni, A., D’Alessandro, A., Downey, A., García-Macías, E., Rallini, M., Materazzi, A., et al. (2018). An Experimental Study on Static and Dynamic Strain Sensitivity of Embeddable Smart concrete Sensors Doped with Carbon Nanotubes for SHM of Large Structures. Sensors 18 (3), 831. doi:10.3390/s18030831

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, W., Moreno, E. I., and Sagüés, A. A. (1996). Practical Evaluation of Resistivity of concrete in Test Cylinders Using a Wenner Array Probe. Cement concrete Res. 26 (12), 1779–1787. doi:10.1016/s0008-8846(96)00175-5

CrossRef Full Text | Google Scholar

Newlands, M. D., Jones, M. R., Kandasami, S., and Harrison, T. A. (2008). Sensitivity of Electrode Contact Solutions and Contact Pressure in Assessing Electrical Resistivity of concrete. Mater. Struct. 41 (4), 621–632. doi:10.1617/s11527-007-9257-6

CrossRef Full Text | Google Scholar

Polder, R., Andrade, C., Elsener, B., Vennesland, Ø., Gulikers, J., Weidert, R., et al. (2000). Test Methods for on Site Measurement of Resistivity of concrete. Mat. Struct. 33 (10), 603–611. doi:10.1007/bf02480599

CrossRef Full Text | Google Scholar

Saafi, M., Andrew, K., Tang, P. L., McGhon, D., Taylor, S., Rahman, M., et al. (2013). Multifunctional Properties of Carbon Nanotube/fly Ash Geopolymeric Nanocomposites. Construction Building Mater. 49, 46–55. doi:10.1016/j.conbuildmat.2013.08.007

CrossRef Full Text | Google Scholar

Sanchez, F., and Sobolev, K. (2010). Nanotechnology in concrete - A Review. Construction building Mater. 24 (11), 2060–2071. doi:10.1016/j.conbuildmat.2010.03.014

CrossRef Full Text | Google Scholar

Spragg, R., Villani, C., Snyder, K., Bentz, D., Bullard, J. W., and Weiss, J. (2013). Factors that Influence Electrical Resistivity Measurements in Cementitious Systems. Transportation Res. Rec. 2342 (1), 90–98. doi:10.3141/2342-11

CrossRef Full Text | Google Scholar

Tanesi, J., and Ardani, A. (2012). Surface Resistivity Test Evaluation as an Indicator of the Chloride Permeability of concrete (No. FHWA-HRT-13-024). United States: Federal Highway Administration.

Google Scholar

Telford, W. M., Geldart, L. P., and Sheriff, R. E. (1990). “Applied Geophysics,” in Resistivity Measurements on Germanium for Transistors. Proceedings of the IRE. Editors L. B. Valdes (Cambridge, UK: Cambridge university press.) 42 (2), 420–427.

Google Scholar

Tian, Z., Li, Y., Zheng, J., and Wang, S. (2019). A State-Of-The-Art on Self-Sensing concrete: Materials, Fabrication and Properties. Composites Part B: Eng. 177, 107437. doi:10.1016/j.compositesb.2019.107437

CrossRef Full Text | Google Scholar

Topsoe, H. (1968). Geometric Factors in Four point Resistivity Measurement. Bulletin 472 (13), 63.

Google Scholar

Valdes, L. (1954). Resistivity Measurements on Germanium for Transistors. Proc. IRE 42 (2), 420–427. doi:10.1109/jrproc.1954.274680

CrossRef Full Text | Google Scholar

Wen, S., and Chung, D. D. L. (2008). Effect of Moisture on Piezoresistivity of Carbon Fiber-Reinforced Cement Paste. ACI Mater. J. 105 (3), 274–280.

Google Scholar

Wen, S., and Chung, D. D. L. (2001a). Electric Polarization in Carbon Fiber-Reinforced Cement. Cement Concrete Res. 31 (1), 141–147. doi:10.1016/s0008-8846(00)00382-3

CrossRef Full Text | Google Scholar

Wen, S., and Chung, D. D. L. (2007). Electrical-resistance-based Damage Self-Sensing in Carbon Fiber Reinforced Cement. Carbon 45 (4), 710–716. doi:10.1016/j.carbon.2006.11.029

CrossRef Full Text | Google Scholar

Wen, S., and Chung, D. D. L. (2001b). Uniaxial Compression in Carbon Fiber-Reinforced Cement, Sensed by Electrical Resistivity Measurement in Longitudinal and Transverse Directions. Cement concrete Res. 31 (2), 297–301. doi:10.1016/s0008-8846(00)00438-5

CrossRef Full Text | Google Scholar

Wenner, F. (1916). A Method of Measuring Earth Resistivity (No. 258). Washington, DC: US Government Printing Office.

Google Scholar

Yang, H., Cui, H., Tang, W., Li, Z., Han, N., and Xing, F. (2017). A Critical Review on Research Progress of Graphene/cement Based Composites. Composites A: Appl. Sci. Manufacturing 102, 273–296. doi:10.1016/j.compositesa.2017.07.019

CrossRef Full Text | Google Scholar