Experimental Study on Residual Compressive Strength of Recycled Aggregate Concrete Under Fatigue Loading

Using recycled aggregate for producing concrete is an effective way to realize the resource utilization of construction and demolition waste. Understanding the variation law of the residual compressive strength of recycled aggregate concrete (RAC) under fatigue loading is significant for its practical application under repeated loads. Thus, this paper conducted uniaxial compression fatigue and static-load tests on recycled aggregate concrete with the different replacement ratios of recycled coarse aggregate, analyzed the probability distributions of the fatigue life and residual compressive strength of RAC and natural aggregate concrete (NAC), and revealed the attenuation law of their residual compressive strength. In addition, it studied and compared the evolution of fatigue damage to NAC and RAC by defining a damage variable based on residual compressive strength. The results show that the fatigue life of the RAC and NAC matches the two-parameter Weibull distribution, and their residual compressive strength follows the normal distribution. The attenuation law of the residual compressive strength of the RAC is similar to that of the NAC. In the initial stages of the fatigue loading, the attenuation is small, and the attenuation rate of the residual compressive strength of the RAC and NAC is low. In contrast, it gradually accelerates in the later stages; a sudden and significant decrease in the concrete strength is noticed in the final stage near failure. Compared with the NAC, the damage to the RAC develops faster in the initial stages of fatigue loading and slower in the later stages.

1 Introduction

Continuous industrial development, infrastructure construction, and housing construction activities have led to the excessive consumption of natural resources. In this context, about 40 billion tons of aggregate is consumed per year globally (Tam et al., 2018), and a large amount of construction and demolition waste (CDW) is produced (Guo et al., 2018). The massive stacking and landfilling of CDW exert tremendous pressure on the environment and ecology; therefore, it is necessary to recycle CDW. The waste concrete which accounts for the most significant proportion of CDW can be crushed and graded into recycled concrete aggregate. The preparation of recycled aggregate concrete (RAC) by replacing part or all of natural aggregate with recycled concrete aggregate can realize the recycling of CDW and reduce the shortage of natural sandstone for concrete. It is an essential path for the sustainable development of the construction industry (Akhtar and Sarmah, 2018; Feng et al., 2021.)

Recycled coarse aggregate (RCA) usually consists of the original aggregate, the mortar, and the interfacial transition zone (ITZ) between the mortar and the original aggregate (Evangelista and de Brito, 2007; Butler et al., 2011) Therefore, in addition to the new ITZ, there are old ITZs in the concrete prepared from RCA (Xiao et al., 2013b; Lee, and Choi, 2013). The existence of multiple ITZs is the primary reason for the difference in the mechanical properties of RAC and natural aggregate concrete (NAC) (Xiao et al., 2013b; Xiao et al., 2012; Tang et al., 2021).

Fatigue is an important mechanical property of concrete (Viswanath et al., 2021). Understanding the fatigue performance of recycled aggregate concrete is of great significance for its application in practical engineering under repeated loading. Xiao et al. (2013a) reported that the compression fatigue performance of RAC with a 100% replacement ratio of recycled coarse aggregate did not significantly differ from that of the natural aggregate concrete. Its fatigue deformation also conformed to the three-stage deformation law. Moreover, in two studies, Thomas et al. (2014a) and Thomas et al. (2014b) stated that using RAC reduced the fatigue cycle resistance of concrete. In addition, Arora and Singh (2016) and Xiao et al. (2013a) found that the bending fatigue life and fatigue limit of RAC were lower than those of NAC. Furthermore, Arora and Singh (2016) and You et al. (2021) proposed that the two-parameter Weibull distribution could approximately describe the fatigue life of RAC.

Fatigue can be regarded as a process in which fatigue damage occurs to the material under a cyclic load, leading to the continuous degradation of material performance. After fatigue loading, the static-load strength decays with the accumulation of fatigue damage, and fatigue failure occurs when its residual strength is reduced to the upper fatigue stress limit (Zhang and Keru, 1997). Therefore, the changing law of the residual strength of the material directly reflects its fatigue performance (Schaff and Davidson, 1997). The existing works on the fatigue performance of RAC (Sainz-Aja et al., 2020; Saini and Singh, 2020; Thomas et al., 2014; Xiao et al., 2013; Thomas et al., 2014; Arora and Singh, 2016; You et al., 2021) have paid more attention to the development of fatigue life, fatigue strength, and fatigue deformation, and there are few reports on the strength degradation of recycled aggregate concrete under fatigue loading.

Moreover, fatigue damage is essentially a random dynamic process, and there is high discreteness in fatigue properties such as fatigue life and residual fatigue strength of concrete (You et al., 2021; Zhang et al., 2004). Saucedo et al. (2013) studied the fatigue life, fatigue residual strength, and other fatigue properties of RAC cubic specimens at a maximum stress level of 0.75. However, the statistical properties of the fatigue life and residual strength of concrete have not been considered when describing its fatigue life and residual strength results (Schaff and Davidson, 1997; Peng et al., 2018; Enrique and Alfonso, 2001; Goel et al., 2012; Lio, 2009), and the probability theory and reliability theory have not been used for analysis to reduce the impact of this discreteness on the test results. Applying the probability and reliability theories to the analysis of concrete fatigue performance can quantitatively consider the random, uncertain factors of material fatigue damage. The reliability is also proposed to measure the reliability of fatigue performance, such as the fatigue life of materials. At present, the test methods for the fatigue performance of concrete are divided according to the loading mode of cyclic fatigue, including compression fatigue, tension fatigue, bending fatigue, and tension–compression fatigue. The compression fatigue performance of concrete is usually the most studied and concerned, and the uniaxial compression fatigue is the simplest and most representative.

Therefore, this work conducted fatigue and static-load tests on recycled aggregate concrete with different replacement ratios of recycled coarse aggregate, namely 0, 50, and 100%. Then, it analyzed the probability distribution of the fatigue life and residual compressive strength of the RAC and NAC. The degradation curves of the fatigue residual compressive strength of the RAC and NAC were obtained with certain reliability by combining the reliability theory with the residual strength degradation model. The degradation law of the residual strength of the RAC and NAC was also examined. In addition, the evolution law of fatigue damage to the natural and recycled aggregate concrete was studied and compared through a damage variable defined based on the residual compressive strength so as to provide a research basis for the application of RAC in structures under repeated loading.

2 Experimental Procedures

2.1 Specimen Preparation

The RCA used in the experiments was produced from the waste concrete of a pavement, processed by crushing and shaping. The RCA and NCA had a continuous particle size distribution with a diameter ranging from 5.0 to 20.0 mm. Table 1 presents their main physical and mechanical properties, and Figure 1 illustrates the RCA, the NCA, and their size distribution. The concrete comprised P.O 42.5 ordinary Portland cementand fly ash grade II as the auxiliary cementitious material, river sand with a fineness modulus of 2.19 and an apparent density of 2592 kg/m³ as the fine natural aggregate, polycarboxylic acid as the superplasticizer, and ordinary tap water.

TABLE 1

TABLE 1. The physical and mechanical properties of the NAC and RAC.

FIGURE 1

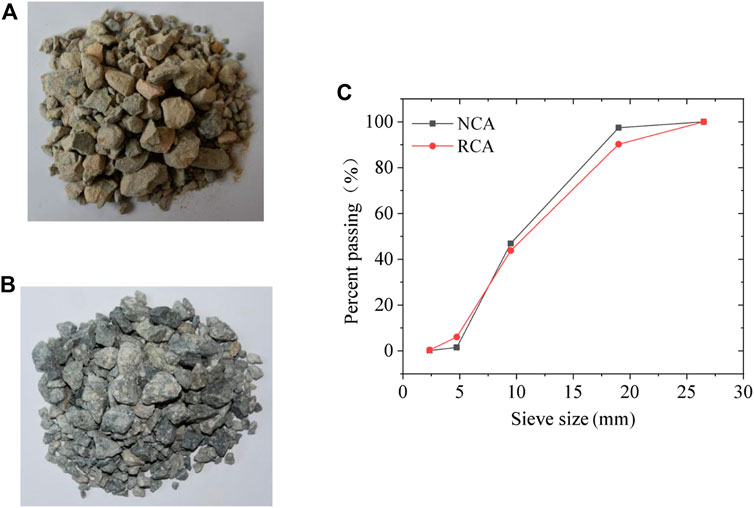
FIGURE 1. (A) The recycled coarse aggregate, (B) the natural coarse aggregate, and (C) their size distribution.

Table 1 demonstrates that, due to the loose and porous old cement mortar attached, the recycled coarse aggregate has lower apparent density, higher water absorption, and a higher crushing value than the natural coarse aggregate. It should also be noted that the mud content of the recycled coarse aggregate, i.e., the particles with a particle size of smaller than 75 µm, is significantly higher than that of the natural coarse aggregate because a large amount of powder is produced in the production process of recycled coarse aggregate. Figure 1 shows that a large amount of powder is attached to the surface of the RCA compared with the clean natural coarse aggregate.

Table 2 lists the mix proportions of the natural and recycled aggregate concrete, where NAC represents the natural aggregate concrete, and RAC50 and RAC100 indicate the recycled aggregate concrete with a replacement ratio of recycled coarse aggregate equal to 50 and 100 wt% respectively. The addition of additional water is not considered in the mix proportion of the RAC with different replacement ratios of the RCA. Superplasticizer was used to adjust the workability performance of the concrete specimens to have a similar slump. The mixing method is to add cementitious materials, sand and coarse aggregate into the mixing pot for dry mixing for 120 s, then add 90% of water by mass and stir for 90 s, and finally add the remaining water (10% by mass and with superplasticizer) and stir for 90 s.

TABLE 2

TABLE 2. The mix proportions of the NAC and RAC (kg·m⁻³).

Prismatic specimens with the dimensions 100 mm × 100 mm × 300 mm were employed for uniaxial compression static-load and fatigue tests. The specimens were demolded 24 h after pouring and molding concrete, cured in a standard curing room for 28 days, and then placed in an indoor dry environment for 90 days to eliminate the impact of the curing period on their fatigue performance.

2.2 Testing Method

The residual compressive strength of concrete under fatigue loading is obtained by loading the specimen to the set fatigue times and then further loading to failure according to the static-load test method. Therefore, the fatigue life of the concrete and its probability distribution must be known before the residual compressive strength test. The natural and recycled aggregate concrete are divided into four groups, with five specimens in each group. The initial strength, fatigue life, and residual compressive strength of the specimens are measured in the order of grouping. The specific groups of the specimens are as follows:

(1) A uniaxial compression static-load test is carried out on group 1 to determine the initial compressive strength of the concrete (σ₀) and calculate the probability distribution and average value of its compressive strength.

(2) A uniaxial compression fatigue test is conducted on groups 2–4 at the maximum stress level (S_max) of 0.8 and the minimum stress level (S_min) of 0.1; group 2 is fatigued to failure to measure the fatigue life of concrete (N_f) and calculate its probability distribution under different failure probabilities.

(3) Groups 3 and 4 are first fatigued to 30% and 60% of the fatigue life (reliability (p) of 0.5), and then they are unloaded to zero; after that, the compression static-load tests are performed to determine the corresponding residual compressive strength of the specimens, namely σ₁ and σ₂.

The uniaxial compression static-load tests on the prismatic specimens use the displacement-controlled loading mode at a loading rate of 0.2 mm/min. The fatigue test is conducted using a 1000 kN high-performance dynamic fatigue testing system produced by MTS Company, United States. The loading mode of the load control is also adopted, and a sinusoidal, reciprocating, cyclic load of equal amplitude is applied; the loading frequency is set at 4 Hz. Figure 2 illustrates the fatigue loading device, the fatigue loading scheme, and the stress–strain curves of the specimens during the fatigue cycling.

FIGURE 2

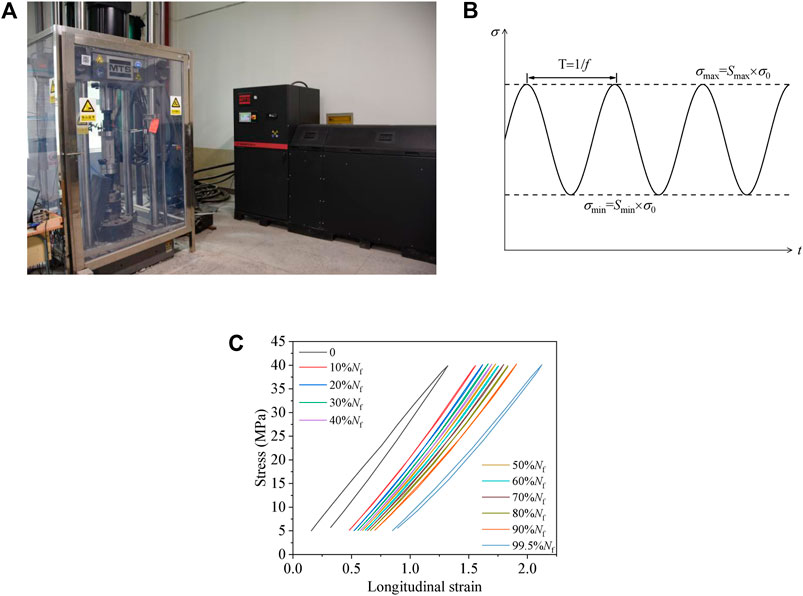
FIGURE 2. (A) The MTS fatigue testing machine, (B) the fatigue loading scheme, and (C) the stress–strain curves of the RAC during the fatigue cycling (N_f = 3135).

3 Results and Discussion

3.1 Fatigue Life and Distribution

Table 3 presents the test results of the fatigue life of the NAC and RAC specimens. The existing works have usually employed the Weibull distribution to study the fatigue life of concrete (Oh, 1991; Singh and Kaushik, 2000; Wu and Jin, 2019). This paper attempts to verify the application of the Weibull distribution to the compressive fatigue of RAC.

TABLE 3

TABLE 3. The fatigue life of the NAC and RAC.

The two-parameter Weibull cumulative distribution can be expressed by:

${\mathit{P}}_{\mathit{f}}=\mathbf{1}-\mathbf{ex}{\mathbf{p}}^{-{\left(\frac{{\mathit{N}}_{\mathit{f}}}{{\mathit{N}}_{\mathit{a}}}\right)}^{\mathit{b}}}(1)$

where N_f is the fatigue life, N_a represents the characteristic fatigue life parameter, b indicates the shape parameter of the Weibull distribution, and P_f is the failure probability.

Taking the natural logarithm of Eq. 1 twice yields the following equation:

$\mathbf{ln}\left[\mathbf{ln}\left(\frac{\mathbf{1}}{\mathbf{1}-{\mathit{P}}_{\mathit{f}}}\right)\right]=\mathit{b}\mathbf{ln}{\mathit{N}}_{\mathit{p}}-\mathit{b}\mathbf{ln}{\mathit{N}}_{\mathit{a}}(2)$

By setting $Y=\text{ln}\left[\text{ln}\left(\frac{1}{1-P_f}\right)\right]$, $X=\text{ln}{N}_f$, and $a=b\text{ln}{N}_a$, one can express Eq. 2 in:

$\mathit{Y}=\mathit{bX}-\mathit{a}(3)$

Eq. 3 can be used to verify whether a group of test data on the fatigue life of concrete conforms to the two-parameter Weibull distribution. If there is an excellent linear relationship between Y and X through graphical regression analysis, the assumption that the fatigue life of the concrete conforms to the Weibull distribution is tenable.

According to the fatigue life given in Table 3, the corresponding survival rate, i.e., reliability (p), can be calculated by:

$\mathit{p}=1-{\mathit{P}}_{\mathit{f}}=\frac{\mathit{i}}{\mathit{m}+1}\left(\mathit{i}=\mathbf{1},\mathbf{2},\mathrm{......},\mathit{m}\right)(4)$

where i is the serial number of the fatigue life in ascending order from small to large at the same stress level, and m represents the sample size of the fatigue test at a given stress level.

Then, linear regression was performed on the fatigue life of concrete in Table 3 according to Eq. 3; Table 4 presents the Weibull distribution parameters and regression analysis results of the NAC and RAC. The correlation coefficient (R₂) is higher than 0.9, and the linear relationship between X and Y is significant, indicating that the compression fatigue life of the natural and recycled aggregate concrete follows the two-parameter Weibull distribution.

TABLE 4

TABLE 4. The Weibull distribution parameters and regression analysis results of the NAC and RAC.

According to Eq. 2, the fatigue life of the concrete can be expressed by:

${\mathit{N}}_{\mathit{f}}={\mathit{N}}_{\mathit{a}}{\left[\mathbf{ln}\left(\frac{\mathbf{1}}{\mathit{p}}\right)\right]}^{\mathbf{1}/\mathit{b}}(5)$

According to Eq. 5, the corresponding fatigue life of concrete can be calculated under the condition of a given survival rate. Table 5 lists the compressive fatigue life of the NAC and RAC with a survival rate of 50%. At the same stress level, the fatigue life of the recycled aggregate concrete is lower than that of the natural aggregate concrete; in addition, the higher the replacement ratio of the recycled coarse aggregate is, the lower the fatigue life of the RAC becomes. When the stress level (S) equals 0.8, and the reliability is 50%, the fatigue life of RAC50 and RAC100 declines by 70.4% and 95.1% respectively compared with the NAC primarily. This is primarily because, for high-cycle fatigue, material failure is dominant due to the debonding of the between the matrix and aggregate. The slow progressive development of bond cracks at the interface between the mortar and coarse aggregate leads to the fatigue failure of concrete (Hsu, 1981; Zheng, et al., 2007). Recycled aggregate concrete has three types of ITZs (You et al., 2021), namely aggregate–new mortar interfacial transition zone (ITZ₁), aggregate–old mortar interfacial transition zone (ITZ₂), and old mortar–new mortar interfacial transition zone (ITZ₃). Multiple and weak ITZs lead to more bond cracks in RAC than in NAC, and the debonding of the interface between the matrix and aggregate is more likely in RAC than in NAC. Thus, the fatigue life of the recycled aggregate concrete specimens is lower than that of the natural aggregate concrete specimens.

TABLE 5

TABLE 5. The fatigue life of the NAC and RAC (p = 0.5).

3.2 Residual Compressive Strength

3.2.1 Residual Compressive Strength and Distribution

Table 6 lists the initial and residual compressive strength of the NAC and RAC specimens. Existing research shows that the compressive strength of the concrete follows the normal distribution (Schaff and Davidson, 1997). Therefore, this paper uses the normal distribution to analyze the initial and residual compressive strength of the NAC and RAC.

TABLE 6

TABLE 6. The initial and residual compressive strength of the NAC and RAC.

The probability density function of the normal distribution is defined as:

$\mathit{f}\mathbf{(}\mathit{x}\mathbf{)}=\frac{1}{\sqrt{\mathbf{2}\mathit{\pi \sigma }}}\mathbf{exp}\left[-\frac{{\left(\mathit{x}-\mathit{\mu }\right)}^{\mathbf{2}}}{\mathbf{2}{\mathit{\sigma }}^2}\right](6)$

where μ and σ, as the normal distribution parameters, represent the mean value and the variance respectively. If a random variable (x) obeys the above equation, it is called a normal distribution and recorded as x∼N (μ,σ); Eq. 7 also expresses the corresponding cumulative distribution function:

$\mathit{F}\left(\mathit{x}\right)=\mathit{P}\left(\mathit{X}\le \mathit{x}\right)=\mathit{\Phi }\left(\frac{\mathit{x}-\mathit{\mu }}{\mathit{\sigma }}\right)(7)$

The function value corresponding to the cumulative distribution function is the cumulative failure probability (P_n), and the corresponding survival rate or reliability (p_n) is defined as:

$\mathit{p}=1-{\mathit{P}}_{\mathit{n}}=\frac{\mathit{j}}{\mathit{K}+1}\left(\mathit{j}=\mathrm{1,2},\mathrm{......},\mathit{K}\right)(8)$

where j is the sequence number of random variables in ascending order from small to large, and K indicates the sample size.

Simultaneously taking the inverse function on both sides of Eq. 7 yields the relationship between the strength value and the survival rate as follows:

${\mathit{x}}_{\mathit{p}}=\mathit{\mu }+{\mathit{\Phi }}^{-1}\left(1-{\mathit{p}}_{\mathit{n}}\right)\mathit{\sigma }(9)$

Setting $Y=x_p$, $X={\Phi }^{-1}(1-p_n)$, $c=\mu$, and $d=\sigma$ can simplify Eq. 9 to the following first-order linear equation:

$\mathit{Y}=\mathit{c}+\mathit{dX}(10)$

Eq. 10 can be used to verify whether a group of test data on the concrete strength conforms to the normal distribution. If there is an excellent linear relationship between Y and X through graphical regression analysis, the assumption of conforming to the normal distribution is tenable. The normal distribution parameters μ and σ can also be determined through regressions.

Taking the initial or residual compressive strength of the NAC and RAC as random variables, linear regression is carried out on the test data in Table 6 according to Eq. 10. Table 7 tabulates the normal distribution parameters and correlation coefficients. Table 7 demonstrates that the linear relationship between X and Y with an R² greater than 0.9 is significant, implying that the initial and fatigue residual compressive strengths of the natural and recycled aggregate concrete follow the normal distribution.

TABLE 7

TABLE 7. The normal distribution parameters and the regression analysis results of the initial and residual compressive strength of the NAC and RAC.

3.2.2 Model Theory of Residual Compressive Strength Attenuation

According to the viewpoint of irreversible damage in thermodynamics, researchers believe that the residual strength model must satisfy the thermodynamic conditions of a strict monotonic decreasing function (Meng and Song, 2008). Therefore, the boundary conditions of the residual strength model are proposed as follows:

$\{\begin{array}{c}{\mathit{\sigma }}_{\mathit{r}}={\mathit{\sigma }}_{\mathit{max}}\\ {\mathit{\sigma }}_{\mathit{r}}\left({\mathit{N}}_{\mathit{f}}\right)={\mathit{\sigma }}_{\mathit{max}}\\ \frac{\mathit{d}{\mathit{\sigma }}_{\mathit{r}}\left(\mathit{n}\right)}{\mathit{dn}}\le 0\\ \frac{{\mathit{d}}^2{\mathit{\sigma }}_{\mathit{r}}\left(\mathit{n}\right)}{\mathit{d}{\mathit{n}}^2}\le 0\end{array}(11)$

where σ_r is the residual strength of the material, σ₀ indicates the static-load strength of the material, σ_max denotes the maximum stress under fatigue loading, n represents the number of the fatigue loading cycles, and N_f is the fatigue life of the material.

Many researchers have proposed various models for the residual strength attenuation of materials based on this assumption, and this work selects the model established by Schaff and Davidson (1997):

${\mathit{\sigma }}_{\mathit{r}}={\mathit{\sigma }}_0-\left({\mathit{\sigma }}_0-{\mathit{\sigma }}_{\mathit{max}}\right){\left(\frac{\mathit{N}}{{\mathit{N}}_{\mathit{f}}}\right)}^{\mathit{v}}(12)$

where N/N_f represents the cycle ratio of fatigue loading, and v is the parameter of the equation and is related to the material.

A nonlinear model can better fulfill the boundary conditions of the residual strength attenuation and can reflect the rapid growth of damage to the concrete and the rapid decline in the residual strength of the concrete when it is close to fatigue failure.

3.2.3 Degradation of Residual Compressive Strength

According to the parameters of the initial and residual compressive strength of NAC and RAC in Table 7, the correlation of the failure probability with the initial or residual compressive strength of the concrete, i.e., the P_n–$\sigma$₀ or P_n–$\sigma$_r relationship, can be obtained. Take specimen RAC100 as an example:

The initial static load compressive strength of the specimen is given by:

$\mathit{P}\left({\mathit{\sigma }}_0\le \mathit{r}\right)=\mathit{\Phi }\left(\frac{\mathit{r}-50.26}{3.5145}\right)(13)$

The residual compressive strength of the specimen at a fatigue loading cycle ratio of 30% is given by:

$\mathit{P}\left({\mathit{\sigma }}_{\mathit{r}}\le \mathit{r}\right)=\mathit{\Phi }\left(\frac{\mathit{r}-49.10}{2.4592}\right)(14)$

The residual compressive strength at a fatigue loading cycle ratio of 60% is calculated by:

$\mathit{P}\left({\mathit{\sigma }}_{\mathit{r}}\le \mathit{r}\right)=\mathit{\Phi }\left(\frac{\mathit{r}-47.53}{4.0749}\right)(15)$

where σ₀ is the initial static-load compressive strength of the concrete, σ_r indicates the residual compressive strength of the concrete, and Φ represents the standard normal distribution.

Substituting different P_n values into the above expression can determine σ₀ and σ_r under different failure probabilities. Figure 3 delineates the fatigue residual compressive strength attenuation curves of the NAC and RAC at a reliability of 50%, and Table 8 lists the curve parameters. In Figure 3, the values in brackets represent the decrease in the residual compressive strength of the specimen compared with its initial compressive strength. Figure 3 and Table 8 demonstrate that the model of J. R. Schaff can better describe the degradation of the fatigue residual compressive strength of the NAC and RAC. The attenuation of the residual compressive strength of the RAC is similar to that of the NAC: the residual compressive strength of the specimens gradually declines with an increase in the fatigue loading cycles. The residual compressive strength of the NAC and RAC decreases by about 6.5%–11.5% and 21.8%–27.2% at a cycle ratio of 0.3 and 0.6 respectively. In the final stages, i.e., 0.6 ≤ N/N_f ≤ 1.0, the residual compressive strength of the NAC and RAC decreases by about 70%–80%. Therefore, the attenuation rate of the residual compressive strength of the specimens varies during the whole fatigue loading; the degradation of the residual compressive strength of concrete is slow in the early stages of the fatigue loading and gradually accelerates in the later stages. When the specimen is close to failure, the concrete strength suddenly decreases significantly. Compared with the NAC, the attenuation rate of the RAC is higher in the early stage but lower in the later stages; however, the attenuation rate of the residual compressive strength of concrete is relatively uniform throughout the whole process. Near the failure stage, the sudden reduction in the compressive strength of the NAC is more significant than that of the RAC.

FIGURE 3

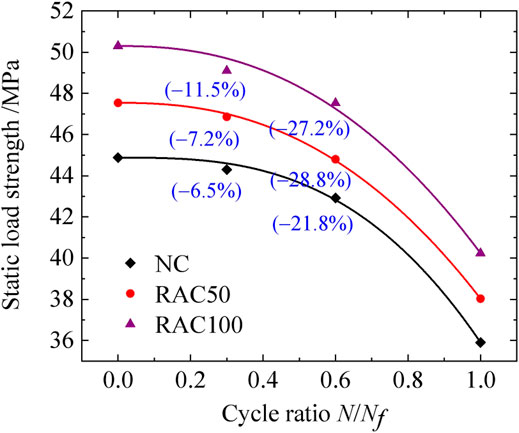
FIGURE 3. The degradation of the residual fatigue compressive strength of the NAC and RAC (p = 50%).

TABLE 8

TABLE 8. The model parameters for the residual compressive strength of the NAC and RAC.

Table 7 and Figure 3 demonstrate that the compressive strength of the RAC is higher than that of the NAC; nevertheless, the difference is no more than 5.5 MPa, possibly because the water absorption and micro powder content of the RAC are higher than those of the NAC, and the RCA can absorb more water from the slurry. Without considering the additional water consumption, the actual water-to-binder ratio of the RAC slurry is higher than that of the NAC slurry. Therefore, although the ITZ of the RAC is weaker than that of the NAC, the strength of the hardened RAC is higher than that of the hardened NAC.

3.3 Fatigue Damage

Fatigue damage is defined as the deterioration of the mechanical properties of materials under cyclic loading. It is a cumulative process and tends to a specific critical value. Strength is one of the most fundamental mechanical properties of concrete, and the internal fatigue damage of concrete is defined as the degradation of its strength. Therefore, the damage variable of concrete is defined using its residual compressive strength to describe the fatigue damage to RAC:

$\mathit{D}=\frac{{\mathit{\sigma }}_0-{\mathit{\sigma }}_{\mathit{r}}}{{\mathit{\sigma }}_0-{\mathit{\sigma }}_{\mathit{max}}}(16)$

Substitute Eq. 12 into Eq. 16 defines the formula for the damage variable of concrete as:

$\mathit{D}={\left(\frac{\mathit{N}}{{\mathit{N}}_{\mathit{f}}}\right)}^{\mathit{v}}(17)$

Differentiating Eq. 17 expresses the evolution rate of fatigue damage to the concrete in:

$\frac{\mathit{dD}}{\mathit{d}\left(\mathit{N}/{\mathit{N}}_{\mathit{f}}\right)}=\mathit{v}{\left(\frac{\mathit{N}}{{\mathit{N}}_{\mathit{f}}}\right)}^{\mathit{v}-1}(18)$

By utilizing Eq. 17 and Eq. 18, combined with the corresponding model parameter v and reliability of 50%, Figure 4 and Figure 5 respectively draw the evolution curves and evolution rate curves of fatigue damage to the NAC and RAC. Figure 3 and Figure 4 show that the fatigue damage to the NAC and RAC gradually extends with an increase in the cyclic loading period, that is, the cycle ratio. The evolution rate of fatigue damage to the specimens grows slowly in the early stages and gradually accelerates later. In the initial stages of fatigue loading, i.e., the fatigue life of about 10%–20%, the damage to the concrete is slight and develops slowly. In the middle stages, i.e., the fatigue life of about 70%–80%, the rate of damage development gradually accelerates, and in the final stage (the fatigue life of about 100%), the damage increases rapidly until failure. Furthermore, compared with the NAC, damage to the RAC develops faster in the initial stages of fatigue loading and slower in the later stages because fatigue is more sensitive to the initial defects in the concrete, and fatigue damage begins to grow at cracks and pores. The multiple ITZs of the RAC contain a large number of microcracks and pores that increase the initial defects in concrete, resulting in the rapid development of damage to the RAC in the initial stages of the fatigue loading.

FIGURE 4

FIGURE 4. The evolution of fatigue damage to the NAC and RAC.

FIGURE 5

FIGURE 5. The evolution rate of fatigue damage to the NAC and RAC.

4 Conclusion

From the results, the following conclusions can be drawn:

Like the NAC, the compressive fatigue life of the RAC obeys the two-parameter Weibull distribution. At a stress level of 0.8, the fatigue life of the RAC is lower than that of the NAC; moreover, the higher the replacement ratio of the recycled coarse aggregate is, the lower the fatigue life of the RAC becomes. When the reliability is 50%, the fatigue life of specimens RAC50 and RAC100 declines by 70.4% and 95.1% respectively compared with the NAC.

The static-load compressive strength and fatigue residual compressive strength of the NAC and RAC follow the normal distribution. The degradation of the residual compressive strength of the RAC is similar to that of the NAC; their residual compressive strength decreases gradually as the number of loading cycles increases. During the fatigue loading, the attenuation rate of the residual compressive strength of the concrete specimens varies. Indeed, the degradation of the residual compressive strength of the concrete is slow in the early stages of the fatigue loading but gradually accelerates in the later stages; the residual compressive strength of the concrete suddenly declines significantly in the final stage of the fatigue loading near failure. The attenuation rate of the fatigue residual compressive strength of the RAC is higher in the early stages and slower in the later stages compared to the NAC. The attenuation rate of the residual compressive strength is relatively uniform during the whole fatigue loading process. Near the failure stage, the sudden reduction in the residual compressive strength of the NAC is more significant than that of the RAC.

The fatigue damage to the NAC and RAC increases gradually as the cycle ratio rises. Further, the rate of damage development is low in the early stage of the fatigue loading and gradually accelerates in the later stages. Compared with the NAC, the damage to the recycled aggregate concrete develops faster in the initial stages of fatigue loading and slower in the later stages primarily because the multiple ITZs of the RAC contain many microcracks and pores that give rise to more initial defects. Thus, the RAC is more prone to damage in the early stage than the NAC.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52078139, 51578153, U1605242), Fujian Natural Science Foundation (Grant No. 2019H6025, 2020J01938), Scientific Research Talent Cultivation Project of Fujian Jiangxia University (Grant Nos. JXZ2021012, JXZ2020011), College Student Innovation and Entrepreneurship Training Program of Fujian Province (Grant Nos. S202113763070, S202113763069).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akhtar, A., and Sarmah, A. K. (2018). Construction and Demolition Waste Generation and Properties of Recycled Aggregate concrete: a Global Perspective. J. Clean. Prod. 186, 262–281. doi:10.1016/j.jclepro.2018.03.085

CrossRef Full Text | Google Scholar

Arora, S., and Singh, S. P. (2016). Analysis of Flexural Fatigue Failure of concrete Made with 100% Coarse Recycled concrete Aggregates. Constr Build Mater. 102, 782–791. doi:10.1016/j.conbuildmat.2015.10.098

CrossRef Full Text | Google Scholar

Butler, L., West, J. S., and Tighe, S. L. (2011). The Effect of Recycled concrete Aggregate Properties on the Bond Strength between RCA concrete and Steel Reinforcement. Cement Concrete Res. 41 (10), 1037–1049. doi:10.1016/j.cemconres.2011.06.004

CrossRef Full Text | Google Scholar

Enrique, C., and Alfonso, F. (2001). A General Regression Model for Lifetime Evaluation and Prediction. Int. J. Fract 107, 117–137. doi:10.1023/A:1007624803955

CrossRef Full Text | Google Scholar

Evangelista, L., and de Brito, J. (2007). Mechanical Behaviour of concrete Made with fine Recycled concrete Aggregates. Cement and Concrete Composites 29, 397–401. doi:10.1016/j.cemconcomp.2006.12.004

CrossRef Full Text | Google Scholar

Feng, J., Yin, G., Tuo, H., Wen, C., Liu, Z., Liang, J., et al. (2021). Uniaxial Compressive Behavior of Hook-End Steel and Macro-Polypropylene Hybrid Fibers Reinforced Recycled Aggregate concrete. Construction Building Mater. 304, 124559. doi:10.1016/j.conbuildmat.2021.124559

CrossRef Full Text | Google Scholar

Goel, S., Singh, S. P., and Singh, P. (2012). Fatigue Analysis of plain and Fiber-Reinforced Self-Consolidating concrete. Mj 109 (5), 573–582. doi:10.14359/51684089

CrossRef Full Text | Google Scholar

Guo, H., Shi, C., Guan, X., Zhu, J., Ding, Y., Ling, T.-C., et al. (2018). Durability of Recycled Aggregate concrete - A Review. Cement and Concrete Composites 89, 251–259. doi:10.1016/j.cemconcomp.2018.03.008

CrossRef Full Text | Google Scholar

Hsu, T. (1981). Fatigue of plain concrete. J. Am. Concr Inst. 78 (4), 292–305. doi:10.1016/0022-3115(81)90580-8

CrossRef Full Text | Google Scholar

Lee, G. C., and Choi, H. B. (2013). Study on Interfacial Transition Zone Properties of Recycled Aggregate by Micro-hardness Test. Construction Building Mater. 40, 455–460. doi:10.1016/j.conbuildmat.2012.09.114

CrossRef Full Text | Google Scholar

Lio, Y. L., Tsai, T.-R., and Wu, S.-J. (2009). Acceptance Sampling Plans from Truncated Life Tests Based on the Birnbaum-Saunders Distribution for Percentiles. Commun. Stat. - Simulation Comput. 39 (1), 119–136. doi:10.1080/03610910903350508

CrossRef Full Text | Google Scholar

Meng, X., and Song, Y. (2008). Experimental and Theoretical Research on Residual Strength of plain concrete under Compressive Fatigue Loading. J. Harbin Inst. Tech. 15 (01), 113–117. (In Chinese).

Google Scholar

Oh, B. H. (1991). Fatigue Life Distributions of concrete for Various Stress Levels. Mj 88 (2), 122–128. doi:10.14359/1870

CrossRef Full Text | Google Scholar

Peng, Q., Wang, L., and Lu, Q. (2018). Influence of Recycled Coarse Aggregate Replacement Percentage on Fatigue Performance of Recycled Aggregate concrete. Construction Building Mater. 169, 347–353. doi:10.1016/j.conbuildmat.2018.02.196

CrossRef Full Text | Google Scholar

Saini, B. S., and Singh, S. P. (2020). Flexural Fatigue Strength Prediction of Self Compacting concrete Made with Recycled concrete Aggregates and Blended Cements. Construction Building Mater. 264, 120233. doi:10.1016/j.conbuildmat.2020.120233

CrossRef Full Text | Google Scholar

Sainz-Aja, J., Thomas, C., Carrascal, I., Polanco, J. A., and de Brito, J. (2020). Fast Fatigue Method for Self-Compacting Recycled Aggregate concrete Characterization. J. Clean. Prod. 277, 123263. doi:10.1016/j.jclepro.2020.123263

CrossRef Full Text | Google Scholar

Saucedo, L., Yu, R. C., Medeiros, A., Zhang, X., and Ruiz, G. (2013). A Probabilistic Fatigue Model Based on the Initial Distribution to Consider Frequency Effect in plain and Fiber Reinforced concrete. Int. J. Fatigue 48, 308–318. doi:10.1016/j.ijfatigue.2012.11.013

CrossRef Full Text | Google Scholar

Schaff, J. R., and Davidson, B. D. (1997). Life Prediction Methodology for Composite Structures. Part I-Constant Amplitude and Two-Stress Level Fatigue. J. Compos. Mater. 31 (2), 128–157. doi:10.1177/002199839703100202

CrossRef Full Text | Google Scholar

Singh, S. P., and Kaushik, S. K. (2000). Flexural Fatigue Life Distributions and Failure Probability of Steel Fibrous concrete. Mj 97 (6), 658–667. doi:10.14359/9979

CrossRef Full Text | Google Scholar

Tam, V. W. Y., Soomro, M., and Evangelista, A. C. J. (2018). A Review of Recycled Aggregate in concrete Applications (2000-2017). Construction Building Mater. 172, 272–292. doi:10.1016/j.conbuildmat.2018.03.240

CrossRef Full Text | Google Scholar

Tang, Y., Chen, H., and Xiao, J. (2022). Size Effects on the Characteristics of Fracture Process Zone of plain concrete under Three-point Bending. Construction Building Mater. 315, 125725. doi:10.1016/j.conbuildmat.2021.125725

CrossRef Full Text | Google Scholar

Thomas, C., Setién, J., Polanco, J. A., Lombillo, I., and Cimentada, A. (2014a). Fatigue Limit of Recycled Aggregate concrete. Construction Building Mater. 52 (2), 146–154. doi:10.1016/j.conbuildmat.2013.11.032

CrossRef Full Text | Google Scholar

Thomas, C., Sosa, I., Setién, J., Polanco, J. A., and Cimentada, A. I. (2014b). Evaluation of the Fatigue Behavior of Recycled Aggregate concrete. J. Clean. Prod. 65, 397–405. doi:10.1016/j.jclepro.2013.09.036

CrossRef Full Text | Google Scholar

Viswanath, S., Lafave, J. M., and Kuchma, D. A. (2021). Concrete Compressive Strain Behavior and Magnitudes under Uniaxial Fatigue Loading. Construction Building Mater. 296 (4), 123718. doi:10.1016/j.conbuildmat.2021.123718

CrossRef Full Text | Google Scholar

Wu, B., and Jin, H. (2019). Compressive Fatigue Behavior of Compound concrete Containing Demolished concrete Lumps. Construction Building Mater. 210, 140–156. doi:10.1016/j.conbuildmat.2019.03.188

CrossRef Full Text | Google Scholar

Xiao, J., Li, H., and Yang, Z. (2013a). Fatigue Behavior of Recycled Aggregate concrete under Compression and Bending Cyclic Loadings. Construction Building Mater. 38, 681–688. doi:10.1016/j.conbuildmat.2012.09.024

CrossRef Full Text | Google Scholar

Xiao, J., Li, W., Sun, Z., Lange, D. A., and Shah, S. P. (2013b). Properties of Interfacial Transition Zones in Recycled Aggregate concrete Tested by Nanoindentation. Cement and Concrete Composites 37 (3), 276–292. doi:10.1016/j.cemconcomp.2013.01.006

CrossRef Full Text | Google Scholar

Xiao, J., Liu, Q., and Wu, Y. C. (2012). Numerical and Experimental Studies on Fracture Process of Recycled concrete. Fatigue Fracture Eng. Mater. Structures 35 (8), 801–808. doi:10.1111/j.1460-2695.2012.01673.x

CrossRef Full Text | Google Scholar

You, F., Luo, S., Zheng, J., and Lin, K. (2021). Analysis of Compressive Fatigue Failure of Recycled Aggregate concrete. Materials 14 (16), 4620. doi:10.3390/ma14164620

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, B., and Wu, K. (1997). Residual Fatigue Strength and Stiffness of Ordinary concrete under Bending. Cement Concrete Res. 27 (1), 115–126. doi:10.1016/S0008-8846(96)00183-4

CrossRef Full Text | Google Scholar

Zhang, L., Wang, S., and Zhao, Z. (2004). Analysis of Reliability Confidence Limits of Fatigue Damage Strength of concrete. Eng. Mech. 21 (4), 139–143. (In Chinese).

Google Scholar

Zheng, K., Sun, W., and Zhao, Q. (2007). Fatigue Equation Based on Properties of concrete Matrix and Interfacial Transition Zone. J. Chin. Ceram. Soc. 35 (2), 236–241. (In Chinese).

Google Scholar