- 1Key Laboratory of Low Dimensional Materials and Application Technology of Ministry of Education, School of Materials Science and Engineering, Xiangtan University, Xiangtan, China
- 2Department of Aerospace and Mechanical Engineering, Saint Louis University, Saint Louis, MO, United States
Twins, as a special structure, have been observed in a small number of experiments on ferroelectrics. A good understanding of the morphologies of twins is very important for twin engineering applications in ferroelectric materials. In this work, the morphologies of twins in tetragonal ferroelectrics are investigated using the compatibility analysis of the transformation strains and spontaneous polarization and the energetic analysis. The tetragonal BaTiO3 single crystal is chosen as an example for the material system. The results show that the lamellar twin structures with
1 Introduction
Due to their piezoelectric, dielectric, pyroelectric, ferroelectric, and electrocaloric properties, ferroelectric materials have shown great potential in sensors, actuators, capacitors, memories, solid-state refrigeration, and micro-electromechanical systems (Garcia and Bibes, 2012; Hwang et al., 2014; Martin and Rappe, 2016; Li et al., 2018a; Stadlober et al., 2019; Isaeva and Topolov, 2021; Manan et al., 2021; Shan et al., 2021; Asapu et al., 2022; Dan et al., 2022). The region with the same polarization is known as the ferroelectric domain, which corresponds to a ferroelectric variant. Different ferroelectric domains correspond to different ferroelectric variants with different transformation strains and spontaneous polarizations (Liu and Li, 2009). To form stable domain configurations, these variants must satisfy the compatibility conditions on transformation strains and spontaneous polarizations, leading to minimum energy. In tetragonal ferroelectrics, 90° and 180° domains have been observed (Le et al., 2013). In rhombohedral ferroelectrics, 71°, 109°, and 180° domains have been observed (Chen et al., 2007; Anthoniappen et al., 2017; Wan et al., 2021). In addition, the charged domain walls, across which the strain compatibility condition is satisfied, but the polarization compatibility condition is not satisfied, have been reported in the theoretical and experimental aspects (Liu et al., 2007; Liu and Li, 2009; Li et al., 2016). Therefore, the formation of domain structure is the basis for understanding the functional properties of ferroelectric materials. It is also the technological application of underpinned ferroelectric materials, making domain engineering being an effective way to enhance the performance of ferroelectrics (Shelke et al., 2011; Li et al., 2017; Geng et al., 2020; Qiu et al., 2020; Chen et al., 2022; Lei and Liu, 2022; Liu et al., 2022; Xu et al., 2022).
Domain engineering for ferroelectric materials has been extensively studied from both experimental and theoretical perspectives (Shelke et al., 2011; Li et al., 2017; Geng et al., 2020; Qiu et al., 2020; Chen et al., 2022; Lei and Liu, 2022; Liu et al., 2022; Xu et al., 2022). It is well known that twin structures are often observed in metals and alloys (Li et al., 2018b; Song et al., 2020; Li et al., 2023). Based on the formation of twins, twin engineering is widely used to enhance the mechanical properties of materials (Cheng et al., 2018; Li et al., 2022; Chen et al., 2023), thermal properties (Gao et al., 2021), electrical properties (Lei et al., 2018). Although domain engineering in ferroelectrics has received extensive attention, twins in ferroelectrics have rarely been reported. It is noticed that the 90° ferroelectric domain in some literature is called “twin”, but it is not a twin structure whose lattice should be symmetrical about the twin planes.
Twin structures have been experimentally observed in BaTiO3 powders (Eibl et al., 1987; Qin et al., 2010). For example, Qin et al. synthesized twinned BaTiO3 powders using BaCl2 and TiO2 at low temperatures, and their twin plane is
2 Theoretical frameworks
2.1 Tetragonal twin variants
In experiments, (111) twins have been observed in BaTiO3 powders and films at room temperature (Eibl et al., 1987; Qin et al., 2010; Cao et al., 2015; Cao et al., 2017). It is well known that BaTiO3 is tetragonal at room temperature. Guided by the experimental results (Eibl et al., 1987; Qin et al., 2010; Cao et al., 2015), the schematic of a tetragonal twin structure is plotted in Figure 1A, where the tetragonal unit cells TW1 and TW2 are symmetric about the twin plane. Each tetragonal unit cell has six possible polarization directions, corresponding to the six ferroelectric variants. Thus, there are a total of 12 ferroelectric variants in tetragonal twinned ferroelectrics. In their respective cubic crystallographic axes, such as TW1 in its local coordinate system
where
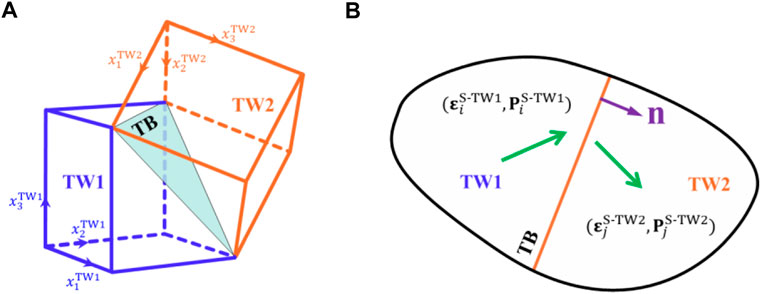
FIGURE 1. (A) Schematic of the tetragonal ferroelectric twin structure, where twin boundary (TB) represents the twin plane, TW1 and TW2 respectively denote the symmetric unit cells about the twin boundary.
2.2 Compatibility condition
In ferroelectrics, the stable interface between various ferroelectric variants is a consequence of energy minimization, across which the transformation strains and spontaneous polarizations of the variants satisfy the compatibility conditions (Shu and Bhattacharya, 2001; Li and Liu, 2004; Liu and Li, 2009; O'Reilly et al., 2022). For twin structures, the variants quantified by
where
2.3 Energetic of morphology
While the compatibility analysis is capable of identifying the orientation of twin structures, it cannot identify the grain shapes of the twins, as well as the charged interface, which is energetically metastable due to polarizations incompatibility (Liu et al., 2007; Liu and Li, 2009). These deficiencies can be overcome by energy analysis using the equivalent inclusion method, which has been successfully applied to analyze the morphologies of ferroelectric domain patterns (Liu et al., 2007) and the precipitates in thermoelectric compounds (Liu et al., 2014).
For a ferroelectric crystal possessing a transformation strain
where
The two types of constitutive Eqs. 4–7 can be rewritten as the following matrix forms:
where
with the superscript
In order to analyze the stable morphologies of stable twin structures in tetragonal ferroelectrics, the equivalent inclusion method is adopted (Dunn and Taya, 1993; Liu et al., 2007; Liu and Li, 2009). The twin structure is treated as a matrix region D and an inhomogeneous inclusion Ω, where the matrix is composed of TW1 with electromechanical moduli denoted by
The electromechanical fields can be obtained by Eshleby’s classical solution (Liu et al., 2007; Liu and Li, 2009).
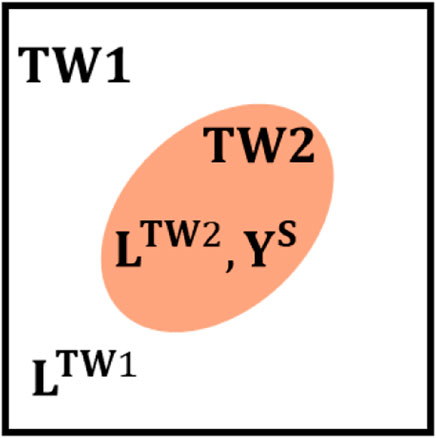
FIGURE 2. Schematic of the inhomogeneous inclusion, where TW1 and TW2 represent the unit cells in the twin structure.
Consider a uniform external field
which can be computed by Eshelby’s equivalent inclusion method (Liu et al., 2007; Liu and Li, 2009), such as:
where the inhomogeneous inclusion TW2 is replaced by an equivalent inclusion, which has the same electromechanical moduli
where
with
In the above expressions, I is the unit four-rank tensor,
S is the piezoelectric Eshelby’s tensors, which is a function of the electromechanical modulus
from which the electromechanical field in the twin structure can be determined.
The potential energy of the twin structure system can then be expressed by:
where the first term represents the elastic and electric energies, and the second term represents the work done by external loading. In the absence of the inhomogeneous inclusion TW2, the effective transformation strain and spontaneous polarization
Thus, due to the existence of the inhomogeneous inclusion TW2, which infers the formation of a twin structure, the resulting energy variation is
where the Hill’s condition is adopted for simplification (Dunn and Taya, 1993; Li and Dunn, 1999). In this work, we consider the scenario of no external field, and the energy variation is further reduced to:
Eq. 18 allows us to analyze the energy variation due to the emergence of twin structures, including its orientation and shape of the inhomogeneous inclusion TW2. The equilibrium morphologies of the twins can be identified by minimizing the energy variation with respect to the orientation and shape of the inhomogeneous inclusion TW2. For the inhomogeneous inclusion TW2, its shape can be assumed to be ellipsoidal, and the orientation can be described using Euler angles in the global coordinate system.
3 Results and discussions
In order to determine the morphologies of twins in tetragonal ferroelectrics, we employ the above theory to implement the compatibility analysis and energetic analysis of twin structures. We choose BaTiO3 as the material system, whose electromechanical moduli associated with the single domain with the polarization along

TABLE 1. The electromechanical moduli M of single-domain with polarization along [001] in its cubic crystallographic axes (FE: 10–12 m2/N; d: 10–12 C/N;
3.1 Compatibility analysis
Guided by the experimental results (Eibl et al., 1987; Qin et al., 2010; Cao et al., 2015), the tetragonal twin structure is schematically illustrated in Figure 1A. There are six variants with polarizations along the cubic crystallographic axes of TW1 unit cell. More explicitly, the polarizations are
In the
resulting in:
For the twin structure composed of TW1
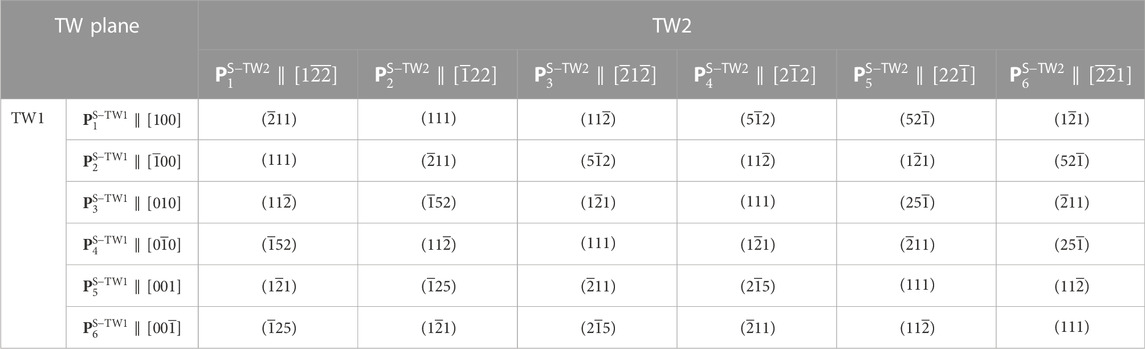
TABLE 2. The possible twin planes formed between various tetragonal variants identified by compatibility analysis. Note that all the polarization directions and twin plane normal are indicated in the local coordinate system
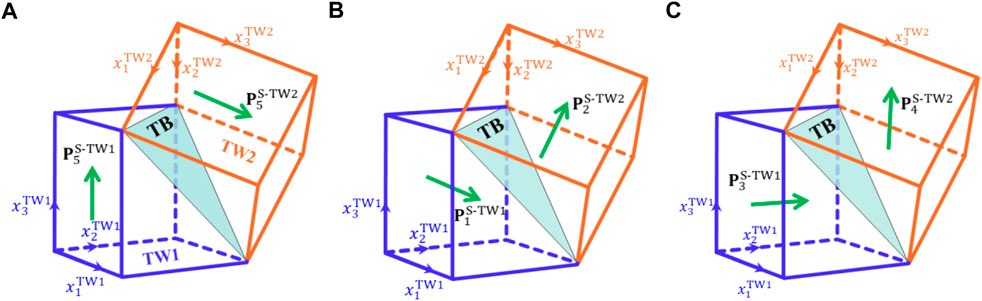
FIGURE 3. Schematics of the possible (111)-twins in tetragonal ferroelectrics; (A) Tetragonal ferroelectric variants
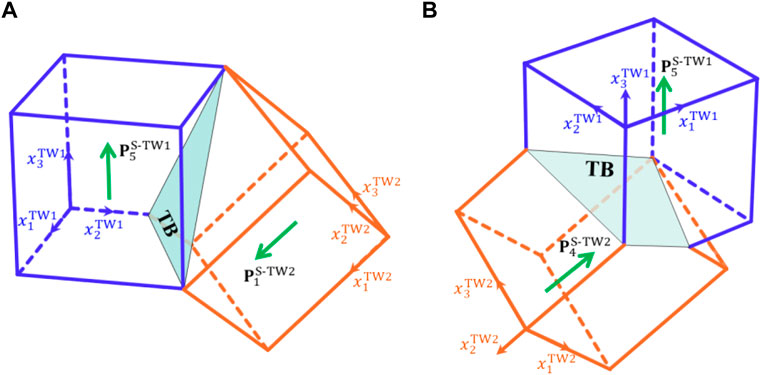
FIGURE 4. Schematics of the possible
3.2 Energetic analysis
Via the compatibility analysis, it is found that twin structures can be formed between different ferroelectric variants, and the twin planes are mainly
3.2.1 Twinned structure with variants
To be specific, the inhomogeneous inclusion TW2 is assumed to be spheroidal. For the twinned structure with variants
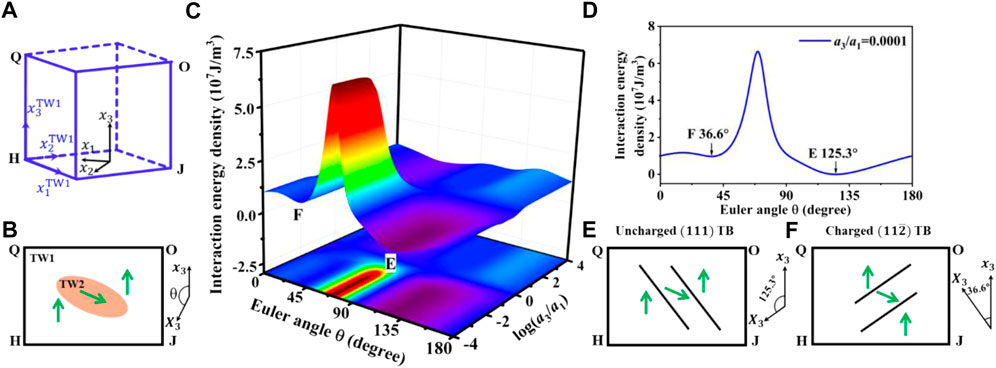
FIGURE 5. Energetic analysis of twinned structure with variants
The shape aspect ratio of the inhomogeneous inclusion TW2 can be defined by
3.2.2 Twinned structure with variants
For the twinned structure with
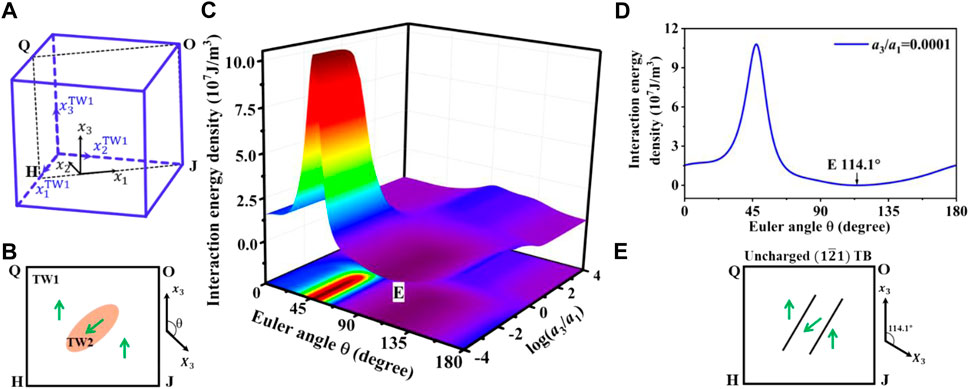
FIGURE 6. Energetic analysis of twinned structure with variants
3.2.3 Twinned structure with variants
For the twinned structure with
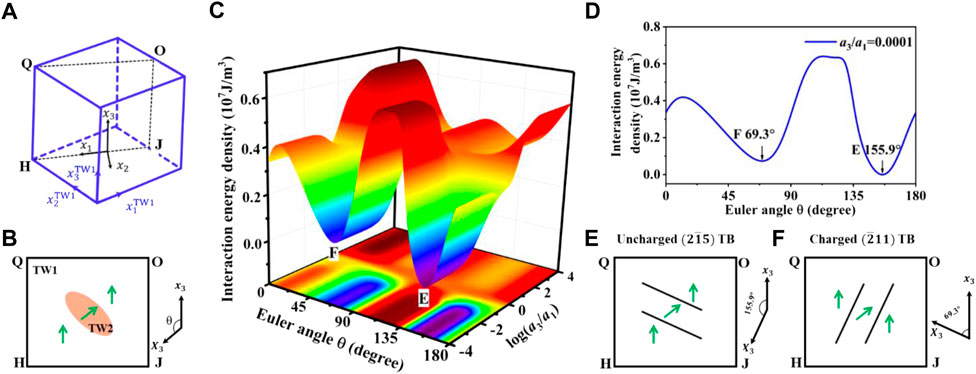
FIGURE 7. Energetic analysis of twinned structure with variants
3.3 Comparison between compatibility analysis and energetic analysis
For different combinations of variants, including the pairs
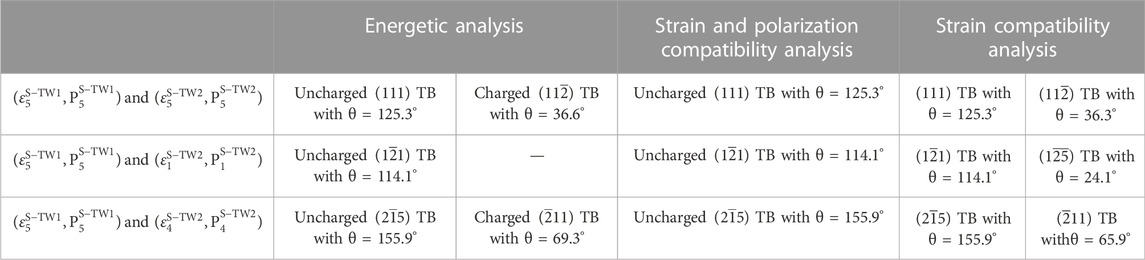
TABLE 3. Comparison of prediction results between compatibility analysis and energetic analysis. Note that the twin planes are specified in the
4 Conclusion
We have investigated the morphologies of twins in tetragonal BaTiO3 single crystals by using the compatibility analysis of the transformation strains and spontaneous polarizations and the energetic analysis. It is found that the lamellar twin structures with
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, upon reasonable request.
Author contributions
NH and CL have contributed equally to this work. All authors contributed to conceptualization, theoretical calculations, analysis and writing the original draft. CL and YL revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Natural Science Foundation of China (11572276 and 12172318), the Hunan Provincial Natural Science Foundation of China (2021JJ10006), and the science and technology innovation Program of Hunan Province (2022RC3069). He also acknowledges support from Hunan Provincial Innovation Foundation for Postgraduate (CX20200628). Lei acknowledges the startup fund supported jointly by the Dean of Parks College and the Provost of Saint Louis University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Anthoniappen, J., Chang, W. S., Soh, A. K., Tu, C. S., Vashan, P., and Lim, F. S. (2017). Electric field induced nanoscale polarization switching and piezoresponse in Sm and Mn co-doped BiFeO3 multiferroic ceramics by using piezoresponse force microscopy. Acta Mater. 132, 174–181. doi:10.1016/j.actamat.2017.04.034
Asapu, S., Pagaduan, J. N., Zhuo, Y., Moon, T., Midya, R., Gao, D., et al. (2022). Large remnant polarization and great reliability characteristics in W/HZO/W ferroelectric capacitors. Front. Mater. 9, 969188. doi:10.3389/fmats.2022.969188
Cao, S. G., Li, Y. S., Wu, H. H., Wang, J., Huang, B. L., and Zhang, T. Y. (2017). Stress-induced cubic-to-hexagonal phase transformation in perovskite nanothin films. Nano Lett. 17 (8), 5148–5155. doi:10.1021/acs.nanolett.7b02570
Cao, S. G., Wu, H. H., Ren, H., Chen, L. Q., Wang, J., Li, J. Y., et al. (2015). A novel mechanism to reduce coercive field of ferroelectric materials via {111} twin engineering. Acta Mater. 97, 404–412. doi:10.1016/j.actamat.2015.07.009
Chen, C., Liu, H., Lai, Q., Mao, X., Fu, J., Fu, Z., et al. (2022). Large-scale domain engineering in two-dimensional ferroelectric CuInP2S6 via giant flexoelectric effect. Nano Lett. 22 (8), 3275–3282. doi:10.1021/acs.nanolett.2c00130
Chen, L., Li, F., Gao, B. T., Zhou, C., Wu, J., Deng, S. Q., et al. (2023). Excellent energy storage and mechanical performance in hetero-structure BaTiO3-based relaxors. Chem. Eng. J. 452, 139222. doi:10.1016/j.cej.2022.139222
Chen, Y. B., Katz, M. B., Pan, X. Q., Das, R. R., Kim, D. M., Baek, S. H., et al. (2007). Ferroelectric domain structures of epitaxial (001) BiFeO3 thin films. Appl. Phys. Lett. 90 (7), 072907. doi:10.1063/1.2472092
Cheng, S.-Y., Ho, N.-J., and Lu, H.-Y. (2006). Crystallographic relationships of the {111} growth twins in tetragonal barium titanate determined by electron-backscatter diffraction. J. Am. Ceram. Soc. 89 (11), 3470–3474. doi:10.1111/j.1551-2916.2006.01231.x
Cheng, Z., Zhou, H. F., Lu, Q. H., Gao, H. J., and Lu, L. (2018). Extra strengthening and work hardening in gradient nanotwinned metals. Science 362 (6414), eaau1925. doi:10.1126/science.aau1925
Dan, H. Y., Li, H. Y., and Yang, Y. (2022). Flexible ferroelectric materials-based triboelectric nanogenerators for mechanical energy harvesting. Front. Mater. 9, 939173. doi:10.3389/fmats.2022.939173
Dunn, M. L., and Taya, M. (1993). An analysis of piezoelectric composite materials containing ellipsoidal inhomogeneities. Proc. R. Soc. Lond. A 443 (1918), 265–287. doi:10.1098/rspa.1993.0145
Eibl, O., Pongratz, P., Skalicky, P., and Schmelz, H. (1987). Formation of (111) twins in BaTiO3 ceramics. J. Am. Ceram. Soc. 70 (8), C-195–C-197. doi:10.1111/j.1151-2916.1987.tb05724.x
Gao, Y. F., Ning, W. B., Zhang, X. L., Liu, Y. Z., Zhou, Y. G., and Tang, D. W. (2021). The effective regulation of nanotwinning on the multichannel thermal transport in hybrid organic–inorganic halide perovskite. Nano Energy 82, 105747. doi:10.1016/j.nanoen.2021.105747
Garcia, V., and Bibes, M. (2012). Inside story of ferroelectric memories. Nature 483 (7389), 279–280. doi:10.1038/483279a
Geng, W. R., Guo, X. W., Zhu, Y. L., Wang, Y. J., Tang, Y. L., Han, M. J., et al. (2020). Oxygen octahedral coupling mediated ferroelectric-antiferroelectric phase transition based on domain wall engineering. Acta Mater. 198, 145–152. doi:10.1016/j.actamat.2020.08.007
Hwang, G. T., Park, H., Lee, J. H., Oh, S., Park, K. I., Byun, M., et al. (2014). Self-powered cardiac pacemaker enabled by flexible single crystalline PMN-PT piezoelectric energy harvester. Adv. Mater. 26 (28), 4880–4887. doi:10.1002/adma.201400562
Isaeva, A. N., and Topolov, V. Y. (2021). Lead-free 0–3-type composites: From piezoelectric sensitivity to modified figures of merit. J. Adv. Dielect. 11 (02), 2150010. doi:10.1142/S2010135X21500107
Le, D.-T., Kwon, S.-J., Yeom, N.-R., Lee, Y.-J., Jeong, Y.-H., Chun, M.-P., et al. (2013). Effects of the domain size on local d33 in tetragonal (Na0.53K0.45Li0.02)(Nb0.8Ta0.2)O3 ceramics. J. Am. Ceram. Soc. 96 (1), 174–178. doi:10.1111/j.1551-2916.2012.05445.x
Lei, C. H., and Liu, Y. Y. (2022). Correlations between local electrocaloric effect and domains in ferroelectric crystals. Appl. Phys. Lett. 121 (10), 102902. doi:10.1063/5.0094473
Lei, S. H., Fan, H. Q., Fang, J. W., Ren, X. H., Ma, L. T., and Tian, H. L. (2018). Unusual devisable high-performance perovskite materials obtained by engineering in twins, domains, and antiphase boundaries. Inorg. Chem. Front. 5 (3), 568–576. doi:10.1039/C7QI00711F
Li, F., Zhang, S. J., Xu, Z., and Chen, L.-Q. (2017). The contributions of polar nanoregions to the dielectric and piezoelectric responses in domain-engineered relaxor-PbTiO3 crystals. Adv. Funct. Mater. 27 (18), 1700310. doi:10.1002/adfm.201700310
Li, J. L., Li, F., Xu, Z., and Zhang, S. J. (2018a). Multilayer lead-free ceramic capacitors with ultrahigh energy density and efficiency. Adv. Mater. 30 (32), 1802155. doi:10.1002/adma.201802155
Li, J. Y., and Dunn, M. L. (1999). Analysis of microstructural fields in heterogeneous piezoelectric solids. Int. J. Eng. Sci. 37 (6), 665–685. doi:10.1016/S0020-7225(98)00091-3
Li, J. Y., and Liu, D. (2004). On ferroelectric crystals with engineered domain configurations. J. Mech. Phys. Solids 52 (8), 1719–1742. doi:10.1016/j.jmps.2004.02.011
Li, L. H., Liu, W. H., Qi, F. G., Wu, D., and Zhang, Z. Q. (2022). Effects of deformation twins on microstructure evolution, mechanical properties and corrosion behaviors in magnesium alloys - a review. J. Magnes. Alloy. 10 (9), 2334–2353. doi:10.1016/j.jma.2022.09.003
Li, L. L., Zhang, Z. J., Zhang, P., and Zhang, Z. F. (2023). A review on the fatigue cracking of twin boundaries: Crystallographic orientation and stacking fault energy. Prog. Mater. Sci. 131, 101011. doi:10.1016/j.pmatsci.2022.101011
Li, L. Z., Britson, J., Jokisaari, J. R., Zhang, Y., Adamo, C., Melville, A., et al. (2016). Giant resistive switching via control of ferroelectric charged domain walls. Adv. Mater. 28 (31), 6574–6580. doi:10.1002/adma.201600160
Li, Q., Xue, S. C., Wang, J., Shao, S., Kwong, A. H., Giwa, A., et al. (2018b). High-strength nanotwinned al alloys with 9R phase. Adv. Mat. 30 (11), 1704629. doi:10.1002/adma.201704629
Liu, Y., Yang, B., Lan, S., Pan, H., Nan, C.-W., and Lin, Y.-H. (2022). Perspectives on domain engineering for dielectric energy storage thin films. Appl. Phys. Lett. 120 (15), 150501. doi:10.1063/5.0090739
Liu, Y. Y., Chen, L. Q., and Li, J. Y. (2014). Precipitate morphologies of pseudobinary Sb2Te3–PbTe thermoelectric compounds. Acta Mater. 65, 308–315. doi:10.1016/j.actamat.2013.10.072
Liu, Y. Y., and Li, J. Y. (2009). Energetic analysis of ferroelectric domain patterns by equivalent inclusion method. J. Mater. Sci. 44 (19), 5214–5224. doi:10.1007/s10853-009-3536-2
Liu, Y. Y., Liu, J. J., Xie, S. H., and Li, J. Y. (2007). Energetics of charged domain walls in ferroelectric crystals. Appl. Phys. Lett. 91 (17), 172910. doi:10.1063/1.2803765
Manan, A., Rehman, M. U., Ullah, A., Ahmad, A. S., Iqbal, Y., Qazi, I., et al. (2021). High energy storage density with ultra-high efficiency and fast charging–discharging capability of sodium bismuth niobate lead-free ceramics. J. Adv. Dielect. 11 (04), 2150018. doi:10.1142/S2010135X21500181
Martin, L. W., and Rappe, A. M. (2016). Thin-film ferroelectric materials and their applications. Nat. Rev. Mater. 2 (2), 16087. doi:10.1038/natrevmats.2016.87
O'Reilly, T., Holsgrove, K., Gholinia, A., Woodruff, D., Bell, A., Huber, J., et al. (2022). Exploring domain continuity across BaTiO3 grain boundaries: Theory meets experiment. Acta Mater. 235, 118096. doi:10.1016/j.actamat.2022.118096
Oppolzer, H., and Schmelz, H. (1983). Investigation of twin lamellae in BaTiO3 ceramics. J. Am. Ceram. Soc. 66 (6), 444–446. doi:10.1111/j.1151-2916.1983.tb10078.x
Qin, S. B., Liu, D., Zheng, F. F., Zuo, Z. Y., Liu, H., and Xu, X. G. (2010). (111) Twinned BaTiO3 microcrystallites. CrystEngComm 12 (10), 3003–3007. doi:10.1039/B925863A
Qiu, C., Wang, B., Zhang, N., Zhang, S., Liu, J., Walker, D., et al. (2020). Transparent ferroelectric crystals with ultrahigh piezoelectricity. Nature 577 (7790), 350–354. doi:10.1038/s41586-019-1891-y
Shan, D. L., Lei, C. H., Cai, Y. C., Pan, K., and Liu, Y. Y. (2021). Mechanical control of electrocaloric response in epitaxial ferroelectric thin films. Int. J. Solids Struct. 216, 59–67. doi:10.1016/j.ijsolstr.2021.01.020
Shelke, V., Mazumdar, D., Srinivasan, G., Kumar, A., Jesse, S., Kalinin, S., et al. (2011). Reduced coercive field in BiFeO3 thin films through domain engineering. Adv. Mater. 23 (5), 669–672. doi:10.1002/adma.201000807
Shu, Y. C., and Bhattacharya, K. (2001). Domain patterns and macroscopic behaviour of ferroelectric materials. Philos. Mag. B 81 (12), 2021–2054. doi:10.1080/13642810108208556
Sluka, T., Tagantsev, A. K., Damjanovic, D., Gureev, M., and Setter, N. (2012). Enhanced electromechanical response of ferroelectrics due to charged domain walls. Nat. Commun. 3 (1), 748. doi:10.1038/ncomms1751
Song, M., Zhou, G., Lu, N., Lee, J., Nakouzi, E., Wang, H., et al. (2020). Oriented attachment induces fivefold twins by forming and decomposing high-energy grain boundaries. Science 367 (6473), 40–45. doi:10.1126/science.aax6511
Stadlober, B., Zirkl, M., and Irimia-Vladu, M. (2019). Route towards sustainable smart sensors: Ferroelectric polyvinylidene fluoride-based materials and their integration in flexible electronics. Chem. Soc. Rev. 48 (6), 1787–1825. doi:10.1039/C8CS00928G
Wan, H., Luo, C. T., Liu, C., Chang, W. Y., Yamashita, Y., and Jiang, X. N. (2021). Alternating current poling on sliver-mode rhombohedral Pb(Mg1/3Nb2/3)O3-PbTiO3 single crystals. Acta Mater. 208, 116759. doi:10.1016/j.actamat.2021.116759
Wang, B. (1992). Three-dimensional analysis of an ellipsoidal inclusion in a piezoelectric material. Int. J. Solids Struct. 29 (3), 293–308. doi:10.1016/0020-7683(92)90201-4
Wu, H. J., Ning, S. C., Waqar, M., Liu, H. J., Zhang, Y., Wu, H.-H., et al. (2021). Alkali-deficiency driven charged out-of-phase boundaries for giant electromechanical response. Nat. Commun. 12 (1), 2841. doi:10.1038/s41467-021-23107-x
Wu, Y.-C., Lee, C.-C., Lu, H.-Y., McCauley, D. E., and Chu, M. S. H. (2006). The {111} growth twins in tetragonal barium titanate. J. Am. Ceram. Soc. 89 (5), 1679–1686. doi:10.1111/j.1551-2916.2006.00948.x
Xu, X. Y., Wang, T. X., Chen, P. C., Zhou, C., Ma, J. N., Wei, D. Z., et al. (2022). Femtosecond laser writing of lithium niobate ferroelectric nanodomains. Nature 609 (7927), 496–501. doi:10.1038/s41586-022-05042-z
Keywords: ferroelectric, twin, compatibility analysis, energetic analysis, ferroelectric variant
Citation: He N, Li C, Lei C and Liu Y (2022) The morphologies of twins in tetragonal ferroelectrics. Front. Mater. 9:1100964. doi: 10.3389/fmats.2022.1100964
Received: 17 November 2022; Accepted: 25 November 2022;
Published: 22 December 2022.
Edited by:
Qingzhen Yang, Xi’an Jiaotong University, ChinaReviewed by:
Hong-Hui Wu, University of Science and Technology Beijing, ChinaJiaming Zhu, Shandong University, China
Copyright © 2022 He, Li, Lei and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chihou Lei, Y2hpaG91LmxlaUBzbHUuZWR1; Yunya Liu, eXlsaXVAeHR1LmVkdS5jbg==
†These authors have contributed equally to this work
 Ningbo He
Ningbo He Cuiping Li1†
Cuiping Li1† Chihou Lei
Chihou Lei Yunya Liu
Yunya Liu