Performance analysis of the functionally graded flexoelectric-piezoelectric energy harvesting

In the present paper, the output performances of the functionally graded flexoelectric-piezoelectric (FGFP) energy harvesting subjected to an external harmonic excitation, considering the effect of piezoelectric polarization direction, are addressed. Based on the Euler-Bernoulli beam model and generalized Hamiltonian principle, the dynamic governing equations and the corresponding boundary conditions of the functionally graded flexoelectric-piezoelectric energy harvesting are obtained. The natural frequency equation and the closed-form analytical expressions of electromechanical responses are further deduced. The numerical results show that the output performance of the functionally graded flexoelectric-piezoelectric energy harvesting is dependent on the piezoelectric polarization direction, gradient index and structure size. At the nanoscale, the flexoelectric effect dominates the output performances; however, at the microscale, the gradient piezoelectric effect dominates the output performances. At transition scales, from nano to micro, the output performances are very small sometimes, where, in some case, the gradient piezoelectric effect and flexoelectric effect cancel each other. The present study reveals the importance of the piezoelectric polarization direction and gradient index on the output performance of the functionally graded flexoelectric-piezoelectric energy harvesting from nano to micro scales.

Introduction

With the rapid development of nanotechnology, a large number of small electronic devices such as sensors, actuators and wireless transmitters have been integrated into every corner of the world for health monitoring, environmental protection, remote controls and wireless transmission (Hudak and Amatucci, 2008). These devices require only a small amount of electricity, and there is waste energy in the environment where micro-nano devices work. Converting ambient energy into electricity to power micro-nano devices is considered a promising approach, which has the advantages of small size, long life, no pollution and high energy density (Zi and Wang, 2017). In addition, some important system-level and circuit-level works about micro-scale energy harvesting have been reported (Chao et al., 2007; Lu et al., 2011). Piezoelectric and flexoelectric effects are ubiquitous in a wide variety of materials (Ma and Cross, 2001). Piezoelectric effect is described as the asymmetric shift of charges or ions of piezoelectric materials when subjected to mechanical strain (Sezer and Koç, 2021), which only exists in non-centrosymmetric dielectric materials. The flexoelectric effect is defined as the coupling between strain gradients and electrical polarization (Fu and Cross, 2007; Deng, 2017), which exists in all dielectrics and exhibits strong size-dependent properties at the nanoscale (Yan et al., 2013). Therefore, it is necessary to consider the flexoelectric effect in analyzing the electromechanical coupling of dielectrics at the nanoscale. Even in some micro-electromechanical systems or almost all nano-electromechanical systems, flexoelectric materials can replace piezoelectric materials (Zhang et al., 2014).

Recently, a series of studies have been conducted on the electromechanical coupling of nanobeams or nanoplates with flexoelectric effect. Cross (2006) firstly measured the flexoelectric coefficients of ferroelectric, incipient ferroelectric and relaxor ferroelectric perovskites by quasi-static and low frequency dynamic techniques. Majdoub et al. (2008) firstly discussed the electromechanical coupling responses of the nano-beams with strain gradient using molecular dynamics and linear piezoelectric theory. Their results showed that the piezoelectric and flexoelectric effects exhibit a non-linear interaction in piezoelectric materials. Shen and Hu (2010) established a theoretical framework including the electrostatic force, flexoelectricity, and surface effects through the variational principle of dielectrics. Based on the extended linear piezoelectric theory and Timoshenko beam model, Yan and Jiang (2013a), Yan and Jiang (2013b) found that the flexoelectric effect has a significant influence on the static bending and free vibration of simply supported piezoelectric nanobeams, and the flexoelectric effect is also sensitive to the mechanical boundary conditions and the direction of the applied electric field. Liang et al. (2014) investigated the influence of surface effect and flexoelectricity on the buckling and vibration of piezoelectric nanowires based on a continuum framework and the Euler-Bernoulli beam hypothesis. They detected that the effective Young’s modulus and bending rigidity are enhanced by flexoelectricity. Zhang et al. (2014) analyzed the influence of flexoelectric effect on the vibration behavior of piezoelectric nanoplate. Deng et al. (2014) discussed the flexoelectric energy harvester in the nanoscale based on the internal energy density. They solved the electromechanical frequency responses using the assumed-modes method. Wang and Wang (2016) developed an analytical model incorporating flexoelectric effect for nanoscale unimorph piezoelectric energy harvesters. In their analysis, when the thickness of the piezoelectric layer is small, the flexoelectric effect has a great influence on the voltage output and power output. Zhou et al. (2017) investigated the electromechanical coupling response of piezoelectric nanobeams with different electrical boundary conditions, in which the results showed that flexoelectricity effect has significant influence on stiffness and induced electric potential of the nanobeam. Moura and Erturk (2017) applied the distributed-parameter method to discuss the flexoelectric energy harvesters in elastic dielectrics. Zhao et al. (2019) studied the non-linear bending and free vibration of Timoshenko piezoelectric nanobeam incorporating flexoelectricity and surface effect. Their results indicated that strain gradient elastic effect, flexoelectricity, surface effect and applied electric voltage have significant influences on the non-linear mechanical behaviors of nanobeam. Su et al. (2019a) simulated the flexoelectric energy harvesting under the harmonic mechanical excitation. In the work, the closed-form voltage output, power density, and mechanical vibration response were obtained, which exhibit significant scale effects at the nanoscale. The above studies mainly focus on monolayer nanostructures, in which the piezoelectric effect can be ignored (Zhou et al., 2017). However, the micro-nano systems, constructing the bilayer or multilayer structures, always exhibit both piezoelectricity and flexoelectricity. Erturk and Imman (2008) derived the distributed parameter electromechanical model to analyze the unimorph piezoelectric energy harvester based on a uniform composite the Euler-Bernoulli beam. Li et al. (2014a) proposed a size-dependent model of a three-layer microbeam including a flexoelectric dielectric layer. Both the static bending and free vibration problems of cantilever and simply supported microbeams were studied. Abdollahi and Arias (2015) numerically analyzed the interplay between piezoelectricity and flexoelectricity in flexural sensors and actuators. They found that flexoelectricity could reduce or enhance the effective piezoelectric effect and electromechanical coupling, which is dependent on the structure design. Qi et al. (2016) established the bending model of an electro-elastic bilayer nanobeam. Their results demonstrated that both the strain gradient elastic effect and the flexoelectric effect significantly affect the deflection of the nanobeam. Su et al. (2019b) examined the electromechanical response of bilayer piezoelectric sensors due to flexoelectricity and strain gradient elasticity. The flexoelectric effect can significantly enhance the electrical performance of bilayer piezoelectric sensors at the nanoscale. Interestingly, the piezoelectric polarization direction of the piezoelectric layer also affects the electromechanical response of the system. Rojas et al. (2021) studied the output of piezoelectric only, flexoelectric only, and combined electromechanical configurations over various scales. Their results revealed that the combined system outperforms either piezoelectric only or flexoelectric only configuration from nano to micro scales. Fu and Zhang (2022) established a size-dependent bilayer piezoelectric microbeam model considering the strain gradient effect based on the modified piezoelectric theory. Fu and Zhou (2021) suggested a size-dependent model of the laminated microbeam partially covered by the flexoelectric layer, which solved the static bending problem of the beam under uniform load and voltage. All the above studies are static or dynamic electromechanical coupling analysis of mono-layer or multi-layer nanostructures. However, there are some studies on improving the effective flexoelectric effect through structural design or uneven distribution of materials. The introduction of functionally graded materials (FGMs) to improve material properties is a very useful and sensible approach (Ma and Lee, 2012; Ke et al., 2014). Combining flexoelectricity and simple functional grading, Mbarki et al. (2014) quantitatively demonstrated the possibility of achieving apparent piezoelectric materials with large and temperature-stable electromechanical coupling above the Curie temperature. Rafiee et al. (2014) addressed the non-linear analysis of energy harvesting, which is composed of FG piezoelectric carbon nanotube reinforced composite plates, under combined thermal and mechanical loadings. The results showed that temperature variation and material distribution have a great effect on the amplitude of vibration and the average harvested power. Li and Pan (2015) numerically solved the static bending and free vibration problems of FG piezoelectric microplates based on the modified couple-stress theories. Kumar et al. (2018) demonstrated the induced flexoelectricity in dielectric FGMs due to non-uniform Youngs’s modulus along the thickness. Their results showed that the optimum gradient index of FGMs can greatly enhance the output voltage. Chu et al. (2018), Chu et al. (2019) discussed the flexoelectric effect in FG composite piezoelectric nanobeams and FG flexoelectric nanocylinders. The results revealed that the static bending, free vibration behavior and electromechanical properties can be significantly influenced by the given FG configuration with graded material parameters. Furthermore, based on the non-local simplified strain gradient elasticity theory, Chu et al. (2020) analyzed the thermally induced non-linear dynamic behaviors of FG flexoelectric nanobeams, in which the thermally induced bending amplitude and non-linear frequency were discussed. Nan et al. (2020) studied the static bending and free vibration problem of porous FG piezoelectric nanobeams and indicated the gradient index, porosity distribution, external electrical voltage, flexoelectric effect and boundary conditions have significant effects on the static deformation and natural frequency of the nanobeams. Recently, Chen et al. (2021) analyzed the mechanical and electrical properties of FG flexoelectric sensors under different electrical boundary conditions. The results showed that the flexoelectric effect, piezoelectric effect, and gradient distribution have considerable influences on the electromechanical performance of the FG flexoelectric sensors. Moreover, the non-uniform piezoelectricity and piezoelectric polarization direction will play a leading role in the induced electric potential at a large scale. The flexoelectric effect will dominate the induced electric potential at the nano scale. However, it is important to clearly explain the interaction between the piezoelectricity and flexoelectricity in the FGFP energy harvesting. To the best of our knowledge, the effects of piezoelectric polarization direction, flexoelectric-piezoelectric distribution and gradient index on the FGFP energy harvesting have not been studied clearly. The closed-form analytical solutions for the FGFP energy harvesting have not been reported, which will be easy to understand and apply in practice.

The main goal of the present paper is to investigate the influence of piezoelectric effect, flexoelectric effect and gradient index on the FGFP energy harvesting at various scales. A FGFP energy harvesting with a tip mass has been analyzed using the coupled distributed-parameter model. Applying FGMs in the form of exponential distribution, based on electric Gibbs free energy and generalized Hamilton’s variational principle, the natural frequency equation under different electrical conditions and the closed-form analytical expressions of output performances under base excitations are derived. The effects of the piezoelectric polarization direction and gradient index on the performance of FGFP energy harvesting are discussed in detail.

Governing equation and boundary conditions of the FGFP energy harvesting

Figure 1 shows the schematic of the FGFP energy harvesting considered in the present study with length $L$, width $B$, thickness $h$, and a tip mass $M_{\mathrm{t}}$ of side length $d$. The cantilever beam is made from a mixture of two isotropic linear elastic constituents BaTiO₃ and PVDF. The top and bottom surfaces of the beam are completely covered with electrode layers, in which the thickness and stiffness of the electrode layers are negligible relative to the cantilever beam. The top and bottom surface electrodes are connected by an external resistance $R$, ignoring the resistance of the beam itself. The Cartesian coordinate system $o{x}_1{x}_2$ is set on the mid-plane of the beam $\left(x_3=0\right)$. It is assumed that the piezoelectric polarization direction of the FGFP energy harvesting is parallel to the $x_3$ direction. The end of the beam is fixed on a base that can move along the $x_3$ direction, where the base displacement is $w_{\mathrm{b}}\left(t\right)$. The cantilever beam is excited by the moving of the base to produce a corresponding vibration response. Free charges are generated on the top and bottom surface electrodes to form an output electric potential due to the electromechanical coupling effect.

FIGURE 1

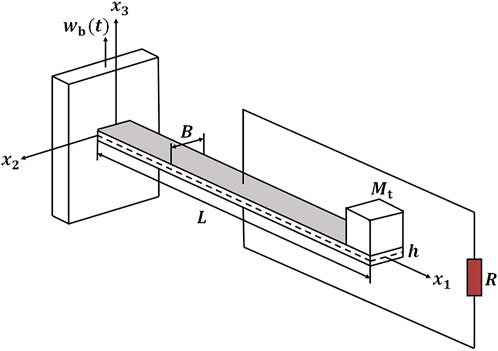
FIGURE 1. A schematic configuration of the FGFP energy harvesting with a tip mass under the base excitation.

It is assumed that the top surface $\left(x_3=\frac{h}{2}\right)$ of the beam is BaTiO₃-rich while the bottom surface $\left(x_3=-\frac{h}{2}\right)$ is PVDF-rich. The variation of material properties along the thickness of the beam is defined as an exponential gradient distribution as:

$\begin{array}{l}N\left(x_3\right)=N_0\exp \left[\alpha \left(\frac{2x_3+h}{2h}\right)\right]\end{array}(1)$

where the $N\left(x_3\right)$ is the effective material properties along the $x_3$ direction. $N_0$ denotes the material parameter value of the bottom material PVDF. $\alpha$ is the gradient index of material properties, which is used to describe the property gradation profiles of the beam, i.e., $\alpha =0$ corresponds to an isotropic homogeneous beam. The effective elastic modulus $c\left(x_3\right)$, effective dielectric coefficient $a\left(x_3\right)$, effective piezoelectric coefficient $e\left(x_3\right)$, effective flexoelectric coefficient $\mu \left(x_3\right)$ and effective density $\rho \left(x_3\right)$ of the beam are given as follows (Chen et al., 2021):

$\begin{array}{l}\left\{\begin{array}{l}c\left(x_3\right)=c_{1111}{e}^{{\alpha }_1\left(\frac{2x_3+h}{2h}\right)}\\ a\left(x_3\right)=a_{33}{e}^{{\alpha }_2\left(\frac{2x_3+h}{2h}\right)}\\ \begin{array}{l}e\left(x_3\right)=e_{311}{e}^{{\alpha }_3\left(\frac{2x_3+h}{2h}\right)}\\ \begin{array}{l}\mu \left(x_3\right)={\mu }_{3113}{e}^{{\alpha }_4\left(\frac{2x_3+h}{2h}\right)}\\ \rho \left(x_3\right)={\rho }_0{e}^{{\alpha }_5\left(\frac{2x_3+h}{2h}\right)}\end{array}\end{array}\end{array}\right.\end{array}(2)$

For the slender beam, combined with the small deformation assumption for Euler-Bernoulli beams, it can be assumed that the mechanical displacement vector $\mathit{u}$ of the FGFP energy harvesting can be written as:

$\begin{array}{l}\mathit{u}=\left\{-\left(x_3-l\right)\frac{\partial w}{\partial x_1},0,w\right\}\end{array}(3)$

where $w$ is the deflection of the cantilever beam. The symmetry breaking of the FGFP energy harvesting makes the position of the physical neutral layer not coincide with the geometric mid-plane, where $l$ denotes the deviation between the physical neutral layer and the geometric mid-plane. It can be determined using the formula (Zhang and Zhou, 2008; Chu et al., 2018; Chen et al., 2021):

$\begin{array}{l}l=\frac{{\int }_{A}c\left(x_3\right)x_3\mathrm{d}A}{{\int }_{A}c\left(x_3\right)\mathrm{d}A}\end{array}(4)$

where $A$ is the cross section of the FGFP energy harvesting. The non-trivial strains ${\epsilon }_{11}$ and strain gradients of the FGFP energy harvesting are obtained as follows:

$\begin{array}{l}{\epsilon }_{11}=-\left(x_3-l\right)\frac{{\partial }^{2}w}{\partial x_1^2},{\epsilon }_{\mathrm{11,1}}=-\left(x_3-l\right)\frac{{\partial }^{3}w}{\partial x_1^3},{\epsilon }_{\mathrm{11,3}}=-\frac{{\partial }^{2}w}{\partial x_1^2}\end{array}(5)$

For the slender beam structure, the strain gradient in the axial direction ${\epsilon }_{\mathrm{11,1}}$ is smaller than that in the transverse direction ${\epsilon }_{\mathrm{11,3}}$, so it can be ignored. Similarly, it is reasonable to consider only the electric field $E_3$ along the $x_3$ direction and ignore the electric field $E_1$ along the $x_1$ direction (Wang and Feng, 2010; Li et al., 2014b).

Under the assumption of infinitely small deformation, the constitutive equation of the FGFP energy harvesting can be derived as (Zhou et al., 2017; Chen et al., 2021):

$\begin{array}{l}\begin{array}{l}{\sigma }_{11}=c\left(x_3\right){\epsilon }_{11}-e\left(x_3\right)E_3\\ {\sigma }_{113}=-\mu \left(x_3\right)E_3\\ D_3=a\left(x_3\right)E_3+e\left(x_3\right){\epsilon }_{11}+\mu \left(x_3\right){\epsilon }_{\mathrm{11,3}}\end{array}\end{array}(6)$

where ${\sigma }_{11}$ is the non-zero stress, ${\sigma }_{113}$ is the higher order stress, which is caused by the electric field due to the flexoelectric effect, and $D_3$ is the electric displacement.

For simplicity, the dielectric coefficient, piezoelectric coefficient and flexoelectric coefficient of the FGFP energy harvesting have the same gradient distribution, which means ${\alpha }_2={\alpha }_3={\alpha }_4=\alpha$. The relationship between electric field and electric potential $\Phi$ is expressed as $E_3=-\frac{\partial \Phi }{\partial x_3}$. There is no free charge inside the FGFP energy harvesting, then the electric displacement should satisfy Gauss’s law: $D_{\mathrm{3,3}}=0$. Combining Eq. 6, we obtain:

$\begin{array}{l}\frac{{\partial }^2\Phi }{\partial x_3^2}=-\frac{\alpha }{h}\frac{\partial \Phi }{\partial x_3}-x_3\frac{\alpha }{h}\frac{e_{311}}{a_{33}}\frac{{\partial }^{2}w}{\partial x_1^2}-\left[\left(1-\frac{\alpha l}{h}\right)\frac{e_{311}}{a_{33}}+\frac{\alpha }{h}\frac{{\mu }_{3113}}{a_{33}}\right]\frac{{\partial }^{2}w}{\partial x_1^2}\end{array}(7)$

Considering the surface electrical boundary conditions $\Phi \left(x_1,x_3=\frac{h}{2},t\right)={\psi }_1\left(x_1,t\right)$ and $\Phi \left(x_1,x_3=-\frac{h}{2},t\right)={\psi }_2\left(x_1,t\right)$. The electric potential $\Phi$ and electric field $E_3$ inside the FGFP energy harvesting can be evaluated as:

$\begin{array}{l}\left\{\begin{array}{l}\Phi \left(x_1,x_3,t\right)=-r\left(x_3\right)\psi \left(x_1,t\right)+\left(nhr\left(x_3\right)+m{x}_3^2+n{x}_3\right)\frac{{\partial }^{2}w}{\partial x_1^2}+C\left(x_1,t\right)\\ E_3\left(x_1,x_3,t\right)=-\frac{\alpha }{h}\psi \left(x_1,t\right)r\left(x_3\right)+\left(\alpha nr\left(x_3\right)-2m{x}_3-n\right)\frac{{\partial }^{2}w}{\partial x_1^2}\end{array}\right.\end{array}(8)$

where $\psi \left(x_1,t\right)={\psi }_1\left(x_1,t\right)-{\psi }_2\left(x_1,t\right)$ is the electric potential difference between the top and bottom electrodes, which is the voltage generated by the electromechanical coupling effect. And $C\left(x_1,t\right)$ is an unknown function related to $x_1$ and $t$. $r\left(x_3\right)$, $m$, and $n$ are functions introduced to simplify the expression of the equation, which is:

$\begin{array}{l}n=\frac{l{e}_{311}-{\mu }_{3113}}{a_{33}},m=-\frac{e_{311}}{2a_{33}},r\left(x_3\right)=\frac{e^{-\frac{\alpha x_3}{h}}}{e^{\frac{\alpha }{2}}-e^{-\frac{\alpha }{2}}}\end{array}(9)$

Substituting Eq. 8 into Eq. 6, the stress, higher order stress, and electric displacement of the FGFP energy harvesting can be written as:

$\begin{array}{l}\left\{\begin{array}{l}{\sigma }_{11}=c\left(x_3\right){\epsilon }_{11}+\frac{\alpha e\left(x_3\right)\psi }{h}r\left(x_3\right)-e\left(x_3\right)\left(\alpha nr\left(x_3\right)-2m{x}_3-n\right)\frac{{\partial }^{2}w}{\partial x_1^2}\\ {\sigma }_{113}=\mu \left(x_3\right)\frac{\alpha r\left(x_3\right)\psi }{h}-\mu \left(x_3\right)\left(\alpha nr\left(x_3\right)-2m{x}_3-n\right)\frac{{\partial }^{2}w}{\partial x_1^2}\\ D_3=-a\left(x_3\right)\frac{\alpha r\left(x_3\right)\psi }{h}+a\left(x_3\right)\left(\alpha nr\left(x_3\right)-2m{x}_3-n\right)\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}_1^2}+e\left(x_3\right){\epsilon }_{11}+\mu \left(x_3\right){\epsilon }_{\mathrm{11,3}}\end{array}\right.\end{array}(10)$

For a dielectric material with flexoelectricity and piezoelectricity, a linearized extension of piezoelectric theory has been used. Considering the coupling relationship between the strain gradient and the electric field strength, the electric Gibbs free energy density function $U$ can be written as (Hu and Shen, 2009; Zhou et al., 2017):

$\begin{array}{l}U=\frac{1}{2}{\sigma }_{ij}{\epsilon }_{ij}+\frac{1}{2}{\sigma }_{ijk}{\epsilon }_{ij,k}+\frac{1}{2}{D}_i{E}_i\end{array}(11)$

Combining Eqs. 5, 8 and 10, The electric Gibbs free energy density function can be expanded as:

$\begin{array}{l}U=\frac{1}{2}k\left(x_3\right){\left(\frac{{\partial }^{2}w}{\partial x_1^2}\right)}^2-i\left(x_3\right)\frac{\psi }{h}\frac{{\partial }^{2}w}{\partial x_1^2}-{\alpha }^{2}a\left(x_3\right)r^2\left(x_3\right)\frac{{\psi }^2}{2h^2}\end{array}(12)$

where $k\left(x_3\right)$ and $i\left(x_3\right)$ are functions of $x_3$ introduced to simplify the equation, and the expressions are:

$\begin{array}{ll}\hfill k\left(x_3\right)& =\left[c\left(x_3\right)-4me\left(x_3\right)-4m^{2}a\left(x_3\right)\right]x_3^2-\left[(2lc\left(x_3\right)-4mle\left(x_3\right)+2ne\left(x_3\right)\right.\hfill \\ \hfill & +\left.4mna\left(x_3\right)+4m\mu \left(x_3\right)-2\alpha ne\left(x_3\right)r\left(x_3\right)-4\alpha mna\left(x_3\right)r\left(x_3\right)\right]x_3\hfill \\ \hfill & +c\left(x_3\right)l^2-2\alpha nle\left(x_3\right)r\left(x_3\right)+2nle\left(x_3\right)+2\alpha n\mu \left(x_3\right)r\left(x_3\right)-2n\mu \left(x_3\right)\hfill \\ \hfill & -{\alpha }^2{n}^{2}a\left(x_3\right)r^2\left(x_3\right)-n^{2}a\left(x_3\right)+2\alpha n^{2}a\left(x_3\right)r\left(x_3\right)\hfill \end{array}$

$\begin{array}{l}i\left(x_3\right)=\alpha r\left(x_3\right)\left[e\left(x_3\right)\left(x_3-l\right)+\mu \left(x_3\right)-a\left(x_3\right)\left(\alpha nr\left(x_3\right)-2m{x}_3-n\right)\right]\end{array}(13)$

The generalized Hamiltonian principle of the FGFP energy harvesting can be expressed as follows (Liang et al., 2015; Su et al., 2019a):

$\begin{array}{l}\delta {\int }_0^T\left(K-G+W\right)dt=0\end{array}(14)$

where $\delta$ is the variational operator, $K$, $G$ and $W$ are the total kinetic energy, total electrical Gibbs free energy, and external work, respectively. Assuming no external body forces and electric field for the FGFP energy harvesting showing in Figure 1, Eq. 14 can be written as:

$\begin{array}{l}\left\{\begin{array}{l}K=\underset{v}{{\displaystyle \int }}\frac{1}{2}\rho {\left|{\dot{w}}^m\right|}^2\mathrm{d}v+{\left.\left(\frac{1}{2}{M}_{\mathrm{t}}{\left|\frac{\partial w}{\partial t}+\frac{\partial w_{\mathrm{b}}}{\partial t}\right|}^2+\frac{1}{2}{I}_t{\left|\frac{\partial {\dot{w}}^m}{\partial x_1}\right|}^2\right)\right|}_{x_1=L}\\ G=\underset{v}{{\displaystyle \int }}U\mathrm{d}v\\ W=\underset{S}{\oint }\varpi \psi \mathrm{d}S\end{array}\right.\end{array}(15)$

where $w^m\left(x_1,t\right)=w_{\mathrm{b}}\left(t\right)+w\left(x_1,t\right)$ is the absolute displacement of the FGFP energy harvesting in the $x_3$ direction, and $w\left(x_1,t\right)$ is the deflection of the cantilever beam (relative to the base). $I_{\mathrm{t}}$ is the moment of inertia of the tip mass, and for a cube it can be expressed as $I_{\mathrm{t}}=\frac{1}{6}{M}_{\mathrm{t}}{d}^2+M_{\mathrm{t}}{\left(\frac{d+h}{2}\right)}^2$. $\varpi$ is the surface charge density on the surface electrodes, $v=L\times B\times h$ is the volume of the beam, and $S$ is the area of the top and bottom surfaces of the beam.

Using Eqs. 12, 15, the variational expression of total electric Gibbs free energy of the FGFP energy harvesting can be written as (Su et al., 2019a):

$\begin{array}{ll}\hfill \delta {\int }_0^T& \mathrm{d}t\underset{v}{{\displaystyle \int }}U\mathrm{d}v={\int }_0^T{\int }_0^L\left[\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{4}w}{\partial x_1^4}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{{\partial }^2\psi }{\partial x_1^2}\right)\delta w-B\left(\frac{C_{\mathrm{p}\mathrm{f}}}{2}\frac{{\partial }^{2}w}{\partial x_1^2}+\frac{Q}{h^2}\psi \right)\delta \psi \right]\mathrm{d}{x}_1\mathrm{d}t\hfill \\ \hfill & +{\left.{\int }_0^T\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{2}w}{\partial x_1^2}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\psi \right)\delta \left(\frac{\partial w}{\partial x_1}\right)\right|}_{x_1=L}dt-{\left.{\int }_0^T\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{3}w}{\partial x_1^3}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{\partial \psi }{\partial x_1}\right)\delta w\right|}_{x_1=L}dt\hfill \end{array}(16)$

where three parameters have been introduced. $Y_{\mathrm{e}\mathrm{p}}$ is the effective bending rigidity of the FGFP energy harvesting, which is related to the gradient index, dielectric coefficient, elastic modulus, piezoelectric coefficient, and flexoelectric coefficient of materials. $C_{\mathrm{p}\mathrm{f}}$ is defined as the flexo-piezoelectric coupling coefficient relating to the gradient index, piezoelectric and flexoelectric coefficients, which determines the electromechanical coupling performance of the FGFP energy harvesting. Parameter $Q$ is a function of $x_3$ introduced to simplify the equation. Their expressions are:

$\begin{array}{l}{Y}_{\mathrm{e}\mathrm{p}}=B\underset{-\frac{h}{2}}{\overset{\frac{h}{2}}{{\displaystyle \int }}}k\left(x_3\right)\mathrm{d}{x}_3,C_{\mathrm{p}\mathrm{f}}=\frac{2}{h}\underset{-\frac{h}{2}}{\overset{\frac{h}{2}}{{\displaystyle \int }}}i\left(x_3\right)\mathrm{d}{x}_3,Q={\alpha }^2\underset{-\frac{h}{2}}{\overset{\frac{h}{2}}{{\displaystyle \int }}}a\left(x_3\right)r^2\left(x_3\right)\mathrm{d}{x}_3\end{array}(17)$

Further substituting Eqs. 15, 16 into Eq. 14, the generalized Hamiltonian variational equation of the FGFP energy harvesting can be derived:

$\begin{array}{ll}\hfill {\int }_0^T& \left[\underset{v}{{\displaystyle \int }}\rho \left(\ddot{w}+{\ddot{w}}_{\mathrm{b}}\right)\delta w\mathrm{d}v+M_{\mathrm{t}}{\ddot{w}}_{\mathrm{b}}\delta \left(x_1-L\right)\delta w\right]\mathrm{d}t+{\int }_0^T\mathrm{d}t{\int }_0^L\left[\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{4}w}{\partial x_1^4}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{{\partial }^2\psi }{\partial x_1^2}\right)\delta w-B\left(\frac{C_{\mathrm{p}\mathrm{f}}}{2}\frac{{\partial }^{2}w}{\partial x_1^2}+\frac{Q}{h}\psi \right)\delta \psi \right]\mathrm{d}{x}_1+\hfill \\ \hfill & {\int }_0^T\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{2}w}{\partial x_1^2}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\psi +I_{\mathrm{t}}\frac{{\partial }^{3}w}{\partial x_1\partial t^2}\right){\left.\delta \left(\frac{\partial w}{\partial x_1}\right)\right|}_{x_1=L}\mathrm{d}t-{\int }_0^T\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{3}w}{\partial x_1^3}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{\partial \psi }{\partial x_1}-M_{\mathrm{t}}\frac{{\partial }^{2}w}{\partial t^2}\right){\left.\delta w\right|}_{x_1=L}\mathrm{d}t-{\int }_0^T\underset{S}{{\displaystyle \int }}\varpi \delta \psi dSdt=0\hfill \end{array}(18)$

where $\delta \left(x_1\right)$ is the Dirac delta function. Since $\delta w$ in Eq. 18 can be chosen arbitrarily, the undamped electromechanical coupling dynamic governing equation of the FGFP energy harvesting can be written as:

$\begin{array}{l}{Y}_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{4}w}{\partial x_1^4}+\left[M+M_{\mathrm{t}}\delta \left(x_1-L\right)\right]\frac{{\partial }^2{w}_{\mathrm{b}}}{\partial t^2}+M\frac{{\partial }^{2}w}{\partial t^2}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{{\partial }^2\psi }{\partial x_1^2}=0\end{array}(19)$

where $M=\rho Bh$ is the mass per unit length of the beam. However, damping in real structures is an important and complex issue. Two damping effects are considered in this paper: viscous air damping (external damping) and strain-rate damping (internal damping) (Erturk and Inman, 2011; Deng et al., 2014). With the damping effects, the electromechanical dynamic Equation 19 can be represented by Eq. 20:

$\begin{array}{l}{Y}_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{4}w}{\partial x_1^4}+\left[M+M_{\mathrm{t}}\delta \left(x_1-L\right)\right]\frac{{\partial }^2{w}_{\mathrm{b}}}{\partial t^2}+M\frac{{\partial }^{2}w}{\partial t^2}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{{\partial }^2\psi }{\partial x_1^2}+c_{\mathrm{s}}\frac{{\partial }^{5}w}{\partial x_1^4\partial t}+c_{\mathrm{a}}\frac{\partial w}{\partial t}=0\end{array}(20)$

where $c_{\mathrm{a}}$ is the viscous air damping coefficient and $c_{\mathrm{s}}$ is the strain-rate damping coefficient. Both of them satisfy the proportional damping criterion and they are mathematically convenient for the modal analysis (Erturk and Inman, 2011).

Similarly, $\delta \psi$ in Eq. 18 can also be chosen arbitrarily, so the FGFP energy harvesting also have the following relationship:

$\begin{array}{l}{\int }_0^L\left(\varpi +\frac{C_{\mathrm{p}\mathrm{f}}}{2}\frac{{\partial }^{2}w}{\partial x_1^2}+\frac{Q\psi }{h^2}\right)\mathrm{d}{x}_1=0\end{array}(21)$

When the external load resistor $R$ is connected to the top and bottom surface electrodes of the FGFP energy harvesting, the electric current must be equal to the change of the average output positive charge per unit time, i.e., $\frac{\psi }{R}=-\frac{1}{h}\underset{v}{{\displaystyle \int }}\dot{\varpi }\mathrm{d}v$. Using Eq. 21 and combining Gauss’s law (Erturk and Inman, 2011; Deng et al., 2014; Su et al., 2019a), the circuit equation can be obtained as:

$\begin{array}{l}{\int }_0^L\frac{BQ}{h^2}\dot{\psi }\mathrm{d}{x}_1+\frac{\psi }{R}=-{\int }_0^L\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{{\partial }^{3}w}{\partial x_1^2\partial t}\mathrm{d}{x}_1\end{array}(22)$

where $\dot{\psi }$ represents the first derivative of $\psi$ with respect to time. In the same way, the electromechanical coupling boundary conditions of FGFP energy harvesting can be obtained:

$\begin{array}{l}\left\{\begin{array}{l}\begin{array}{l}w\left(0\right)=0\\ {\left.\frac{\partial w}{\partial x_1}\right|}_{x_1=0}=0\end{array}\\ {\left.\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{2}w}{\partial x_1^2}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\psi +I_{\mathrm{t}}\frac{{\partial }^{3}w}{\partial x_1\partial t^2}\right)\right|}_{x_1=L}=0\\ {\left.\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{3}w}{\partial x_1^3}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{\partial \psi }{\partial x_1}-M_{\mathrm{t}}\frac{{\partial }^{2}w}{\partial t^2}\right)\right|}_{x_1=L}=0\end{array}\right.\end{array}(23)$

Free vibration responses of the FGFP energy harvesting

Natural frequency of the FGFP energy harvesting under the electrical open circuit condition

In this section, the free vibration of the FGFP energy harvesting under the electrical open circuit condition is investigated. The top and bottom surfaces of the cantilever beam are equipotential bodies because they are covered with electrodes. Hence, the electric potential difference $\psi \left(x_1,t\right)$ independent of $x_1$ is a function of time $t$ only. The base excitation $w_{\mathrm{b}}\left(t\right)$ is zero during the free vibration, so the Eq. 20 could be simplified as:

$\begin{array}{l}{Y}_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{4}w}{\partial x_1^4}+M\frac{{\partial }^{2}w}{\partial t^2}=0\end{array}(24)$

Correspondingly, Eq. 23 could be rewritten as:

$\begin{array}{l}\left\{\begin{array}{l}\begin{array}{l}w\left(0\right)=0\\ {\left.\frac{\partial w}{\partial x_1}\right|}_{x_1=0}=0\end{array}\\ {\left.\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{2}w}{\partial x_1^2}-\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\psi +I_{\mathrm{t}}\frac{{\partial }^{3}w}{\partial x_1\partial t^2}\right)\right|}_{x_1=L}=0\\ {\left.\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{3}w}{\partial x_1^3}-M_{\mathrm{t}}\frac{{\partial }^{2}w}{\partial t^2}\right)\right|}_{x_1=L}=0\end{array}\right.\end{array}(25)$

when the FGFP energy harvesting is bending, the surface charge will be redistributed on the electrodes. However, the total charge should remain zero, then Eq. 21 could be simplified to:

$\begin{array}{l}{\int }_0^L\left(\frac{C_{\mathrm{p}\mathrm{f}}}{2}\frac{{\partial }^{2}w}{\partial x_1^2}+\frac{Q}{h^2}\psi \right)d{x}_1=0\end{array}(26)$

And substituting Eq. 26 into the third equation of Eq. 25, the complete mechanical boundary condition can be obtained:

$\begin{array}{l}{\left.\left(Y_{\mathrm{e}\mathrm{p}}\frac{{\partial }^{2}w}{\partial x_1^2}+\frac{{C_{\mathrm{p}\mathrm{f}}}^{2}B{h}^2}{4QL}\frac{\partial w}{\partial x_1}+I_{\mathrm{t}}\frac{{\partial }^{3}w}{\partial x_1\partial t^2}\right)\right|}_{x_1=L}=0\end{array}(27)$

The separated variable method is employed to solve the natural frequency of the FGFP energy harvesting. Considering the form of Eq. 24, its solution can be set as:

$\begin{array}{l}w\left(x_1,t\right)=\varnothing \left(x_1\right)\eta \left(t\right)\end{array}(28)$

$\begin{array}{l}\left\{\begin{array}{l}\varnothing \left(x_1\right)=C_1\mathit{cos}\frac{\beta }{L}{x}_1+C_2\mathit{sin}\frac{\beta }{L}{x}_1+C_3\mathit{cos}h\frac{\beta }{L}{x}_1+C_4\mathit{sin}h\frac{\beta }{L}{x}_1\\ \eta \left(t\right)=C_5{e}^{j\lambda t}\end{array}\right.\end{array}(29)$

where $\varnothing \left(x_1\right)$ is the modal vibration pattern, $\eta \left(t\right)$ is the generalized coordinate, $C_1,C_2,C_3,C_4$ and $C_5$ are parameters independent of $x_1$ and $t$, $\beta$ is the eigenvalue of the structural vibration, $\lambda$ is the circular frequency of the natural vibration of the FGFP energy harvesting, and $j$ is the imaginary root. Substituting Eqs. 28, 29 into Eqs. 24, 25, the following governing equations and boundary conditions can be obtained:

$\begin{array}{l}\frac{{\mathrm{d}}^4\varnothing \left(x_1\right)}{\mathrm{d}{x}_1^4}-{\lambda }^2\frac{M}{Y_{\mathrm{e}\mathrm{p}}}\varnothing \left(x_1\right)=0\end{array}(30)$

$\begin{array}{l}\left\{\begin{array}{l}\begin{array}{l}\varnothing \left(0\right)=0\\ {\left.\frac{\mathrm{d}\varnothing \left(x_1\right)}{\mathrm{d}{x}_1}\right|}_{x_1=0}=0\end{array}\\ {\left.\left[Y_{\mathrm{e}\mathrm{p}}\frac{{\mathrm{d}}^2\varnothing \left(x_1\right)}{\mathrm{d}{x}_1^2}+\left(\frac{{C_{\mathrm{p}\mathrm{f}}}^{2}B{h}^2}{4QL}-I_{\mathrm{t}}{\lambda }^2\right)\frac{\mathrm{d}\varnothing \left(x_1\right)}{\mathrm{d}{x}_1}\right]\right|}_{x_1=L}=0\\ {\left.Y_{\mathrm{e}\mathrm{p}}\frac{{\mathrm{d}}^3\varnothing \left(x_1\right)}{\mathrm{d}{x}_1^3}\right|}_{x_1=L}+{\lambda }^2{M}_{\mathrm{t}}\varnothing \left(L\right)=0\end{array}\right.\end{array}(31)$

From the Eq. 30, ${\lambda }_o=\lambda ={\beta }^2\sqrt{\frac{Y_{\mathrm{e}\mathrm{p}}}{M{L}^4}}$ can be obtained, which is the circular frequency of the natural vibration of the FGFP energy harvesting under the electrical open circuit condition. After substituting Eq. 29 into Eq. 31, we can get:

$\begin{array}{l}\left\{\begin{array}{l}{C}_1{A}_1+C_2{A}_2=0\\ C_1{A}_3+C_2{A}_4=0\end{array}\right.\end{array}(32)$

where $A_1,A_2,A_3$ and $A_4$ are:

$\begin{array}{l}\left\{\begin{array}{l}\begin{array}{l}{A}_1=\left[\left(\frac{{C_{\mathrm{p}\mathrm{f}}}^{2}B{h}^2}{4QL}-I_{\mathrm{t}}{\lambda }^2\right)\left(\mathit{sin}\beta +\mathit{sin}h\beta \right)+Y_{\mathrm{e}\mathrm{p}}\left(\frac{\beta }{L}\right)\left(\mathit{cos}\beta +\mathit{cos}h\beta \right)\right]\\ A_2=\left[\left(\frac{{C_{\mathrm{p}\mathrm{f}}}^{2}B{h}^2}{4QL}-I_{\mathrm{t}}{\lambda }^2\right)\left(\mathit{cos}h\beta -\mathit{cos}\beta \right)+Y_{\mathrm{e}\mathrm{p}}\left(\frac{\beta }{L}\right)\left(\mathit{sin}\beta +\mathit{sin}h\beta \right)\right]\end{array}\\ A_3=\left[Y_{\mathrm{e}\mathrm{p}}{\left(\frac{\beta }{L}\right)}^3\left(\mathit{sin}\beta -\mathit{sin}h\beta \right)+{\lambda }^2{M}_{\mathrm{t}}\left(\mathit{cos}\beta -\mathit{cos}h\beta \right)\right]\\ A_4=-\left[Y_{\mathrm{e}\mathrm{p}}{\left(\frac{\beta }{L}\right)}^3\left(\mathit{cos}\beta +\mathit{cos}h\beta \right)+{\lambda }^2{M}_{\mathrm{t}}\left(-\mathit{sin}\beta +\mathit{sin}h\beta \right)\right]\end{array}\right.\end{array}(33)$

To ensure that Eq. 32 has the non-zero solution, the corresponding coefficient determinant of Eq. 32 should be equal to zero. The characteristic equation of the natural frequency of the FGFP energy harvesting in the open circuit condition is:

$\begin{array}{l}{Y}_{\mathrm{e}\mathrm{p}}\left(\frac{{C_{\mathrm{p}\mathrm{f}}}^{2}B{h}^2}{4QL}-I_{\mathrm{t}}{\lambda }^2\right){\left(\frac{\beta }{L}\right)}^3\left(\sin h\beta \cos \beta +\cos h\beta \sin \beta \right)+\\ {\left(Y_{\mathrm{e}\mathrm{p}}\right)}^2{\left(\frac{\beta }{L}\right)}^4\left(1+\cos \beta \cos h\beta \right)+{\lambda }^2{M}_{\mathrm{t}}\left(\frac{{C_{\mathrm{p}\mathrm{f}}}^{2}B{h}^2}{4QL}-I_{\mathrm{t}}{\lambda }^2\right)\\ \left(\cos \beta \cos h\beta -1\right)+\begin{array}{l}{\lambda }^2{M}_{\mathrm{t}}{Y}_{\mathrm{e}\mathrm{p}}\left(\frac{\beta }{L}\right)\left(\sin h\beta \cos \beta -\sin \beta \cos h\beta \right)=0\end{array}\end{array}(34)$

Equation 34 is a transcendental equation about the eigenvalue $\beta$, which can be solved numerically.

Natural frequency of the FGFP energy harvesting under the electrical short circuit condition

For the electrical short circuit condition, the top and bottom surface electrodes of the beam are connected by wires, and the induced potential between the top and bottom surface electrodes is zero. Hence, the governing equation and boundary constraints of free vibration are simplified as:

$\begin{array}{l}\frac{{\mathrm{d}}^4\varnothing \left(x_1\right)}{\mathrm{d}{x}_1^4}-{\lambda }^2\frac{M}{Y_{\mathrm{e}\mathrm{p}}}\varnothing \left(x_1\right)=0\end{array}(35)$

$\begin{array}{l}\left\{\begin{array}{l}\begin{array}{l}\varnothing \left(0\right)=0\\ {\left.\frac{\mathrm{d}\varnothing \left(x_1\right)}{\mathrm{d}{x}_1}\right|}_{x_1=0}=0\end{array}\\ {\left.\left[Y_{\mathrm{e}\mathrm{p}}\frac{{\mathrm{d}}^2\varnothing \left(x_1\right)}{\mathrm{d}{x}_1^2}-{\lambda }^2{I}_{\mathrm{t}}\frac{\mathrm{d}\varnothing \left(x_1\right)}{\mathrm{d}{x}_1}\right]\right|}_{x_1=L}=0\\ {\left.Y_{\mathrm{e}\mathrm{p}}\frac{{\mathrm{d}}^3\varnothing \left(x_1\right)}{\mathrm{d}{x}_1^3}\right|}_{x_1=L}+{\lambda }^2{M}_{\mathrm{t}}\varnothing \left(L\right)=0\end{array}\right.\end{array}(36)$

Similarly, the circular frequency of system vibration in the electrical short circuit condition is ${\lambda }_s=\lambda ={\beta }^2\sqrt{\frac{Y_{\mathrm{e}\mathrm{p}}}{M{L}^4}}$. The characteristic equation of the natural frequency in this case is:

$1+\cos \beta \cosh \beta +\beta \frac{M_{\mathrm{t}}}{mL}\left(\cos \beta \sinh \beta -\sin \beta \cosh \beta \right)-\begin{array}{l}\frac{{\beta }^3{I}_t}{M{L}^3}\left(\cosh \beta \sin \beta +\sinh \beta \cos \beta \right)+\frac{{\beta }^4{M}_t{I}_t}{M^2{L}^4}\left(1-\cos \beta \cosh \beta \right)=0\end{array}(37)$

Electromechanical coupling responses of the FGFP energy harvesting

The vibration response of the FGFP energy harvesting can be written as a linear combination of series of vibration modes:

$\begin{array}{l}w\left(x_1,t\right)={\displaystyle \sum }_{r=1}^{\infty }{w}_r\left(x_1,t\right)={\displaystyle \sum }_{r=1}^{\infty }{\varnothing }_r\left(x_1\right){\eta }_r\left(t\right)\end{array}(38)$

where ${\varnothing }_r\left(x_1\right)$ is the mass normalized eigenfunction of the rth vibrational mode, which should satisfy the electrical short-circuit condition. ${\eta }_r\left(t\right)$ is the modal mechanical response coefficient in the modal coordinate. The eigenfunction ${\varnothing }_r\left(x_1\right)$ could be obtained from Eqs. 35, 36 as follows:

$\begin{array}{l}{\varnothing }_r\left(x_1\right)=X_r\left[\left(\cos \frac{{\beta }_r}{L}{x}_1-\cos h\frac{{\beta }_r}{L}{x}_1\right)+{\mathcal{l}}_r\left(\sin \frac{{\beta }_r}{L}{x}_1-\sin h\frac{{\beta }_r}{L}{x}_1\right)\right]=X_r{\overline{\varnothing }}_r\left(x_1\right)\end{array}(39)$

where ${\mathcal{l}}_r=-\frac{A_3}{A_4}$, ${\beta }_r$ is the rth root of the transcendental characteristic Eq. 37, and $X_r$ is the modal amplitude constant, which could be solved by normalizing the eigenfunction using the following orthogonality condition:

${\int }_0^L{\varnothing }_s\left(x_1\right)M{\varnothing }_r\left(x_1\right)\mathrm{d}{x}_1+{\left.\left[{\varnothing }_s\left(x_1\right)M_{\mathrm{t}}{\varnothing }_r\left(x_1\right)\right]\right|}_{x_1=L}{\left.+\left[\frac{\mathrm{d}{\varnothing }_s\left(x_1\right)}{\mathrm{d}{x}_1}{I}_{\mathrm{t}}\frac{\mathrm{d}{\varnothing }_r\left(x_1\right)}{\mathrm{d}{x}_1}\right]\right|}_{x_1=L}={\delta }_{rs}$

$\begin{array}{l}{\int }_0^L\frac{{\mathrm{d}}^2{\varnothing }_s\left(x_1\right)}{\mathrm{d}{x}_1^2}{Y}_{\mathrm{e}\mathrm{p}}\frac{{\mathrm{d}}^2{\varnothing }_r\left(x_1\right)}{\mathrm{d}{x}_1^2}d{x}_1={\lambda }_r^2{\delta }_{rs}\end{array}(40)$

where ${\delta }_{rs}$ is the Kronecker delta, the modal amplitude constant $X_r$ can be expressed as:

$\begin{array}{l}{X}_r={\left\{{\int }_0^L{\overline{\varnothing }}_r^2\left(x_1\right)M\mathrm{d}{x}_1+\left[{\overline{\varnothing }}_r^2\left(L\right)M_{\mathrm{t}}+{\left.I_{\mathrm{t}}{\left(\frac{\mathrm{d}\overline{{\varnothing }_r}\left(x_1\right)}{\mathrm{d}{x}_1}\right)}^2\right|}_{x_1=L}\right]\right\}}^{-\frac{1}{2}}\end{array}(41)$

It should be noted that the output electric potential difference $\psi \left(x_1,t\right)$ of the FGFP energy harvesting is independent of $x_1$, so the spatial derivative of $\psi$ would vanish in Eq. 20. Erturk and Inman (2011) remained it in the dynamic equation by setting $\psi =\psi \left(x_1,t\right)=V\left(t\right)\left[\left(H\left(x_1\right)-H\left(x_1-L\right)\right.\right]$, where $V\left(t\right)$ is the output voltage of the FGFP energy harvesting, and $H\left(x_1\right)$ is the Heaviside function. The electromechanical coupling dynamic governing equations of the FGFP energy harvesting in modal coordinates can be expressed as:

$\frac{{\mathrm{d}}^2{\eta }_r\left(t\right)}{\mathrm{d}{t}^2}+{\lambda }_r^2{\eta }_r\left(t\right)+2{\xi }_r{\lambda }_r\frac{\mathrm{d}{\eta }_r\left(t\right)}{\mathrm{d}t}-{\int }_0^L\frac{C_{\mathrm{p}\mathrm{f}}B}{2}V\left(t\right){\varnothing }_r\left(x_1\right)\left[\frac{\mathrm{d}\delta \left(x_1\right)}{\mathrm{d}{x}_1}-\frac{\mathrm{d}\delta \left(x_1-L\right)}{\mathrm{d}{x}_1}\right]\mathrm{d}{x}_1=y_r,$

$\begin{array}{l}\frac{BQL}{h^2}\frac{\mathrm{d}V\left(t\right)}{\mathrm{d}t}+\frac{V\left(t\right)}{R}=-{\displaystyle \sum }_{r=1}^{\infty }{O}_r\frac{\mathrm{d}{\eta }_r\left(t\right)}{\mathrm{d}t}\end{array}(42)$

where $y_r=-\left[M\underset{0}{\overset{L}{{\displaystyle \int }}}{\varnothing }_r\left(x_1\right)\mathrm{d}{x}_1+M_{\mathrm{t}}{\varnothing }_r\left(L\right)\right]\frac{{\mathrm{d}}^2{w}_{\mathrm{b}}\left(t\right)}{\mathrm{d}{t}^2}$, $O_r={\left.\frac{C_{\mathrm{p}\mathrm{f}}B}{2}\frac{\mathrm{d}{\varnothing }_r\left(x_1\right)}{\mathrm{d}{x}_1}\right|}_{x_1=L}$. ${\xi }_r$ is the modal damping ratio of the rth including the air viscous damping coefficient $c_{\mathrm{a}}$ and the strain rate damping coefficient $c_{\mathrm{s}}$ (Erturk and Inman, 2011; Tang and Wang, 2017; Su et al., 2019a).

It is assumed that the fixed end of the energy harvesting is excited by a translational displacement in the transverse direction. The external excitation is a harmonic form with a circular frequency $\omega$, i.e., $w_{\mathrm{b}}\left(t\right)=W_0{e}^{j\omega t}$, where $W_0$ is the amplitude of the base vibration. According to the small deformation and linear system assumption, the output voltage response and the modal mechanical response of the FGFP energy harvesting can be set as $V\left(t\right)=V_0{e}^{j\omega t}$ and ${\eta }_r\left(t\right)=H_0{e}^{j\omega t}$, where $V_0$ and $H_0$ are both generally complex numbers. Hence, Eq. 42 can be written as:

$\begin{array}{l}\left\{\begin{array}{l}\left[\left({\lambda }_r^2-{\omega }^2\right)+2{\xi }_r{\lambda }_{r}j\omega \right]H_0-V_0{O}_r=Y_r\\ \left(\frac{BQL}{h^2}j\omega +\frac{1}{R}\right)V_0+j\omega {\displaystyle \sum }_{r=1}^{\infty }{O}_r{H}_0=0\end{array}\right.\end{array}(43)$

where $Y_r=W_0{\omega }^2\left[M\underset{0}{\overset{L}{{\displaystyle \int }}}{\varnothing }_r\left(x_1\right)\mathrm{d}{x}_1+M_t{\varnothing }_r\left(L\right)\right]$ is the amplitude of the modal mechanical force function. Solving Eq. 43, The analytical modal expressions of voltage $V\left(t\right)$ can be represented as follows:

$\begin{array}{l}V\left(t\right)=\frac{-j\omega {\sum }_{r=1}^{\infty }\frac{O_r{Y}_r}{\left({\lambda }_r^2-{\omega }^2\right)+2j\omega {\xi }_r{\lambda }_r}}{\left(\frac{1}{R}+\frac{BQL}{h^2}j\omega \right)+{\sum }_{r=1}^{\infty }\frac{j\omega O_r^2}{\left({\lambda }_r^2-{\omega }^2\right)+2j\omega {\xi }_r{\lambda }_r}}{e}^{j\omega t}\end{array}(44)$

Numerical results and discussion

Effect of the piezoelectric polarization direction on electromechanical coupling coefficient

To assess the effect of the piezoelectric polarization direction on performance of the FGFP energy harvesting, we simply change the piezoelectric coefficient to positive or negative, which expresses the opposite polarization direction. The piezoelectric coefficient of the FGFP energy harvesting Ⅰ is set to a negative value, and the corresponding top and bottom parameters are $e_{\mathrm{B}{\rm I}}=-4.4C/m^2$, $e_{\mathrm{P}{\rm I}}=-0.44C/m^2$. The piezoelectric coefficient of the FGFP energy harvesting Ⅱ is set to a positive value, and the corresponding top and bottom parameters are $e_{\mathrm{B}\Pi }=4.4C/m^2$, $e_{\mathrm{P}\Pi }=0.44C/m^2$, respectively (Zhou et al., 2017; Su et al., 2019a). Here, $\mathrm{B}$ and $\mathrm{P}$ in the subscript represent BaTiO₃ and PVDF materials, respectively. The other parameters of BaTiO₃ are the same as follows (Hong et al., 2010; Hahn et al., 2021): flexoelectric coefficient ${\mu }_{\mathrm{B}}={10}^{-6}C/m^2$, dielectric coefficient $a_{\mathrm{B}}=12.48nC/V\cdot m$, elastic modulus $c_{\mathrm{B}}=131GPa$, and density ${\rho }_{\mathrm{B}}=6.017\times {10}^{3}kg/m^3$. The other material parameters of PVDF are set as (Poddar and Ducharme, 2013; Lu et al., 2016): flexoelectric coefficient ${\mu }_{\mathrm{P}}={10}^{-7}C/m^2$, dielectric coefficient $a_P=1.248nC/V\cdot m$, elastic modulus $c_{\mathrm{P}}=3.7GPa$, and density ${\rho }_{\mathrm{P}}=1.78\times {10}^{3}kg/m^3$. Based on the above parameter values, the gradient index can be obtained by Eq. 2: ${\alpha }_1=3.567,{\alpha }_2={\alpha }_3={\alpha }_4=2.302,{\alpha }_5=1.218$. When the gradient index is infinitely close to zero, the functionally graded beam will become a uniform PVDF beam. Over the entire frequency range, when the thickness of the beam is changed, the length/width/thickness aspect ratio is set to be 100:10:1. The side length of the tip mass is taken as $d=B$, and the mass $M_{\mathrm{t}}$ is taken as $M\times L\times 0.2$. The damping ratios are given by ${\xi }_1={\xi }_2=0.0285$, and the two damping coefficients ($c_s$ and $c_a$) can be obtained (Erturk and Inman, 2011). All the simulation results are given inform of Frequency Response Functions (FRFs) for convenience, which are normalized by the base excitation acceleration ${\ddot{w}}_{\mathrm{b}}={\omega }^2{W}_0{e}^{j\omega t}$. Meanwhile, the excitation acceleration has been normalized according to the gravitational acceleration: $\mathrm{g}=9.81m/s^2$.

The normalized bending stiffness of the FGFP energy harvesting is defined as $Y_{\mathrm{e}\mathrm{p}}/EI$, where $EI$ is the bending stiffness of the FG dielectric beam ($e=0,\mu =0$). The variation of the normalized bending rigidity with thickness is shown in Figure 2A. The normalized bending stiffness of the FG energy harvesting with piezoelectric effect only is about 1.014, and does not change with the thickness, which indicates that the gradient piezoelectric effect has limited improvement on the bending stiffness of the dielectric beam. The normalized bending stiffness of the FG energy harvesting with flexoelectric effect only and the FGFP energy harvesting Ⅱ (piezoelectric coefficient is positive) decrease with increasing thickness, and tends to 1 and 1.014 respectively at large scale, which indicates that the flexoelectric effect have significant size dependence and there exists a strong coupling effect between flexoelectricity and gradient piezoelectricity. The normalized bending stiffness of the FGFP energy harvesting Ⅰ (piezoelectric coefficient is negative) firstly decreases then increases with decreasing thickness, which approaches 1 as the thickness is about 0.68 $\mu m$. The normalized bending stiffness of FGFP energy harvesting Ⅱ is always the largest, which can be regarded as the result of the superposition of the gradient piezoelectric effect and flexoelectric effect. Hence, the FGFP energy harvesting Ⅱ has the strongest resistance to bending deformation and the corresponding natural frequency is also the highest. The flexo-piezoelectric coupling coefficient $C_{\mathrm{p}\mathrm{f}}$ is a very important coupling parameter in the FGFP energy harvesting, which reflects the interplay between piezoelectric and flexoelectric effects and determines the output electromechanical performance of the FGFP energy harvesting. $C_{\mathrm{p}\mathrm{f}}$ also reflects the coupling relationship between the mechanical energy and electric energy of the FGFP energy harvesting. The variation of $C_{\mathrm{p}\mathrm{f}}$ with the thickness for two types of the FGFP energy harvesting is given in Figure 2B. $C_{\mathrm{p}\mathrm{f}}$ of the FGFP energy harvesting Ⅰ is always positive and gradually increases with increasing thickness. This indicates that the piezoelectric effect is always enhance the electromechanical coupling of the FGFP energy harvesting. However, $C_{\mathrm{p}\mathrm{f}}$ of the FGFP energy harvesting Ⅱ gradually decreases with increasing thickness and is equal to 0 when the thickness is 1.3 $\mu m$. This implies that the piezoelectric effect would weaken the electromechanical coupling of the FGFP energy harvesting in a certain range.

FIGURE 2

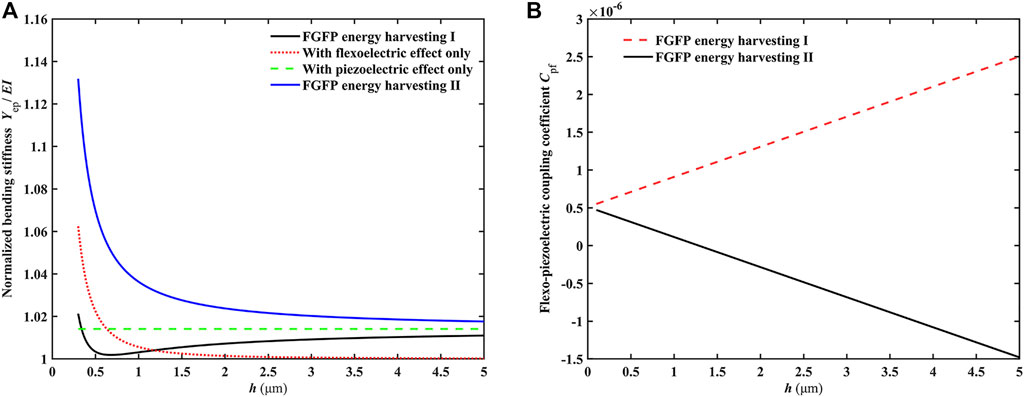
FIGURE 2. (A) Variation of $Y_{\mathrm{e}\mathrm{p}}/EI$ as a function of the beam thickness for two types of the FGFP energy harvesting; (B) Variation of $C_{\mathrm{p}\mathrm{f}}$ as a function of the beam thickness for two types of the FGFP energy harvesting.

Free vibration analysis of the FGFP energy harvesting

The natural frequency of the FGFP energy harvesting is a very important physical performance. The variation of natural frequencies ($f=\lambda /2\pi$) of two types of FGFP energy harvesting with the beam thickness under the electrical open circuit ($f_{\mathrm{o}}$) and electrical short circuit ($f_{\mathrm{s}}$) conditions are shown in Figure 3. The natural frequencies of the FGFP energy harvesting Ⅰ and Ⅱ both increase with decreasing thickness. The natural frequencies of the FGFP energy harvesting Ⅱ are greater than that of the FGFP energy harvesting Ⅰ regardless of the electrical open circuit or short circuit condition, because the difference of piezoelectric coefficients causes the effective bending rigidity $Y_{\mathrm{e}\mathrm{p}}$ of the FGFP energy harvesting Ⅱ to be greater than that of the FGFP energy harvesting Ⅰ (Chen et al., 2021). For both types of the FGFP energy harvesting, the natural frequency with the open circuit condition is higher than that of the short circuit condition, because under the open circuit condition, the induced potential generated by the electromechanical coupling resistances to bending deformation and enhances the apparent bending stiffness of the beam.

FIGURE 3

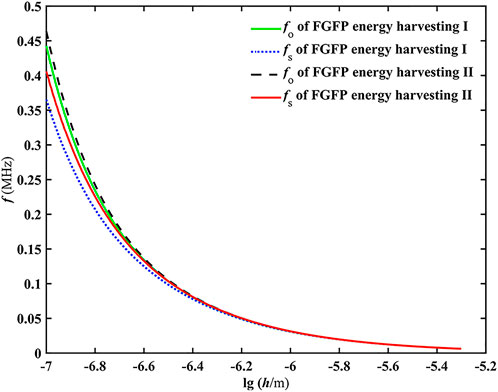
FIGURE 3. Variation of natural frequencies of the FGFP energy harvesting as a function of the beam thickness under different electrical conditions.

The natural frequency shift of beams is an important parameter for judging electromechanical coupling performance of the FGFP energy harvesting (Su et al., 2019a). Here, the effective natural frequency shift of the FGFP energy harvesting is defined as: $F=f_{\mathrm{o}}/f_{\mathrm{s}}$. Figure 4. Plots the curves of the effective natural frequency shift $F$ as a function of the beam thickness. The results show that $F$ increases with decreasing thickness, and when the thickness decreases to a certain critical value, $F$ tends to a saturation value. $F$ tends to 1 as the thickness becomes large, which means the electromechanical effect is very weak and the influence of the induced electric potential on the bending deformation is very small at the largescale. At transition scales, from nano to micro, $F$ is greatly affected by the beam thickness. $F$ of the FGFP energy harvesting Ⅰ is higher than that of the FGFP energy harvesting Ⅱ with the same beam thickness because, for the FGFP energy harvesting Ⅰ, the induced electric potential is higher owing to the enhancement of flexoelectric and piezoelectric effects and $f_{\mathrm{s}}$ is smaller due to the effective bending rigidity $Y_{\mathrm{e}\mathrm{p}}$.

FIGURE 4

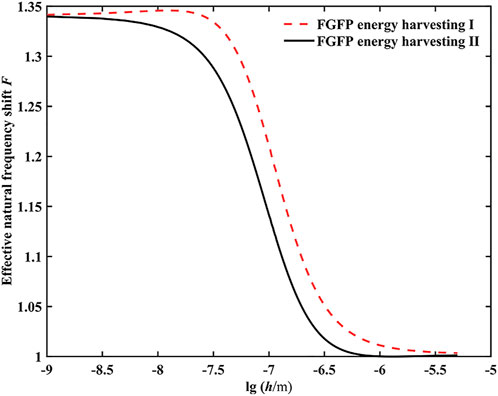
FIGURE 4. Variation of the effective natural frequency shift of two types of FGFP energy harvesting as a function of the beam thickness.

Output performance analysis of the FGFP energy harvesting

The power density response is an important parameter for evaluating the performance of the FGFP energy harvesting (Deng et al., 2014; Su et al., 2019a), which can be expressed in the following form:

$\begin{array}{l}\frac{P_d\left(t\right)}{{\left(-{\omega }^2{W}_0{e}^{j\omega t}\right)}^2}={\left[\frac{{\sum }_{r=1}^{\infty }\frac{-j\omega O_r{Z}_r}{\left({\lambda }_r^2-{\omega }^2\right)+2j\omega {\xi }_r{\lambda }_r}}{\left(\frac{1}{R}+\frac{BQL}{h^2}j\omega \right)+{\sum }_{r=1}^{\infty }\frac{j\omega O_r^2}{\left({\lambda }_r^2-{\omega }^2\right)+2j\omega {\xi }_r{\lambda }_r}}\right]}^2\times \frac{1}{R}\times \frac{1}{v}\end{array}(45)$

where $Z_r=-M\underset{0}{\overset{L}{{\displaystyle \int }}}{\varnothing }_r\left(x_1\right)\mathrm{d}x-M_t{\varnothing }_r\left(L\right)$. Figure 5 depicts the power density of two types of FGFP energy harvesting with the beam thickness $h=3\mu m$ under different excitation frequencies. When the load resistance R increases from 0.1 to 10 MΩ (as an electrical open circuit condition), the resonance frequencies of the two types of FGFP energy harvesting are almost the same values under all load resistances, 10,370 and 10,408 Hz, respectively. The resonance frequencies of the FGFP energy harvesting are not sensitive to external load resistances at the large scale ($h=3\mu m$). Both types of FGFP energy harvesting have maximum output power density when the load resistance is about 1.5 MΩ, which is the optimal load resistance. However, the maximum output power density of the FGFP energy harvesting Ⅰ is obviously higher than that of the FGFP energy harvesting Ⅱ, which indicates the electromechanical coupling effect of the FGFP energy harvesting Ⅰ is higher.

FIGURE 5

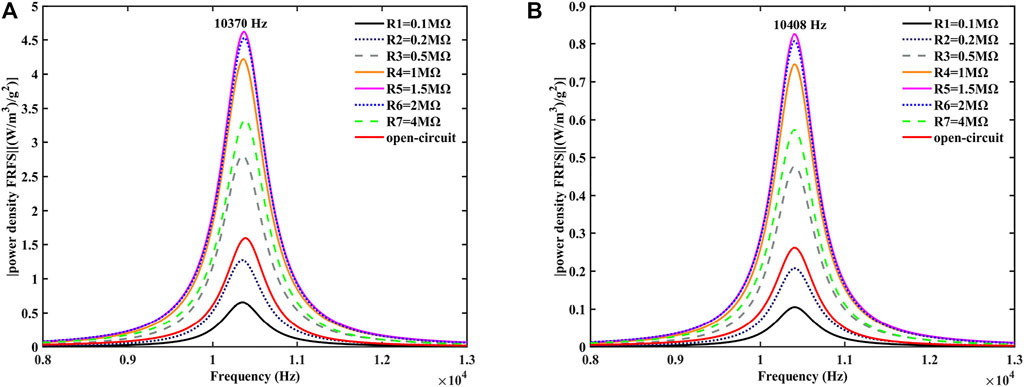
FIGURE 5. Variation of the power density FRFs of the FGFP energy harvesting with $h=3\mu m$: (A) FGFP energy harvesting I; (B) FGFP energy harvesting II.

The plotted curves in Figure 6 show the power density response for a smaller scale beam ($h=0.3\mu m$). For different load resistances, the power density response curves of the two types of the FGFP energy harvesting have an intersection phenomenon. At the small scale, effective flexoelectric effect (flexoelectricity and gradient piezoelectricity) can significantly affect the electromechanical coupling of the system. So that when the load resistance increases from 0.1 to 10 MΩ, the resonance frequency of the beam Ⅰ is shifted from 104,156 to 119,990 Hz, and the resonance frequency of the beam Ⅱ is shifted from 109,665 to 111,640 Hz. Comparing the results of Figure 5A and Figure 6A, it should be noted that the maximum power density for the beam with thickness 0.3 $\mu m$ is smaller than that for the beam with thickness 3 $\mu m$ in the FGFP energy harvesting Ⅰ. However, for the single layer uniformly flexoelectric energy harvesting, the power output increases with decreasing thickness (Deng et al., 2014; Su et al., 2019a). In the present case, the gradient piezoelectricity has a significant effective flexoelectric effect at the larger scale for the FGFP energy harvesting. Figure 2B also shows that the absolute value of electromechanical coupling coefficient $C_{\mathrm{p}\mathrm{f}}$ increases with increasing thickness at the large scale.

FIGURE 6

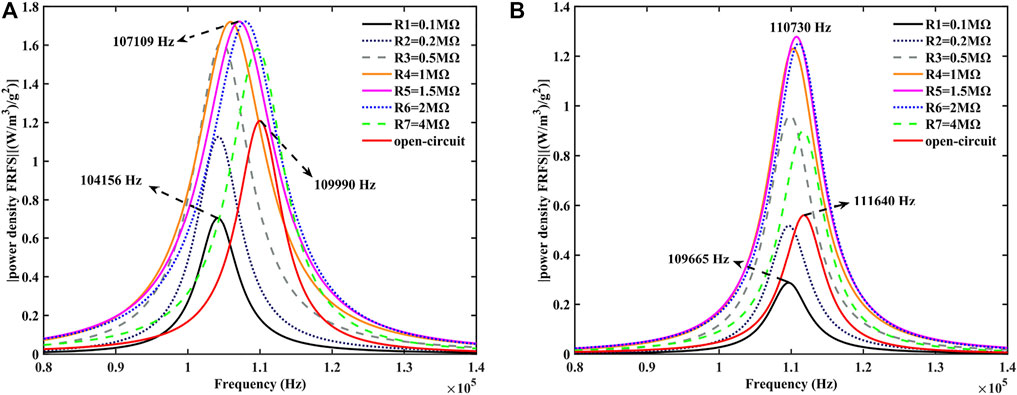
FIGURE 6. Variation of the power density FRFS of the FGFP energy harvesting with $h=0.3\mu m$: (A) FGFP energy harvesting I; (B) FGFP energy harvesting II.

Figure 7 presents the variation of maximum power density FRFs with the beam thickness for the different FGFP energy harvesting. The power density of the FGFP energy harvesting with only flexoelectric effect increases and then decreases with decreasing thickness. This is because when the thickness decreases to a certain value, the induced electric potential due to the flexoelectric effect will significantly act on the FGFP energy harvesting itself, resulting in a reduction on the mechanical deformation of the system, thereby reducing the mechanical vibration response of the FGFP energy harvesting. It achieves a maximum power density at about 0.4 $\mu m$. The power density of the FGFP energy harvesting with only piezoelectric effect linearly increases with increasing thickness, which intersects the curve of only flexoelectric effect. This means that the flexoelectric effect dominates the performance of the system at the small scale; however, at the large scale, the gradient piezoelectric effect becomes appreciable. Since the piezoelectric and flexoelectric effects of the FGFP energy harvesting Ⅰ produce output electric potentials with the same direction, the gradient piezoelectric effect would enhance the maximum power density response, in which the corresponding $C_{\mathrm{p}\mathrm{f}}$ is always positive. Due to the change of piezoelectric polarization direction, the induced electric potential generated by the gradient piezoelectric effect has the opposite direction with that generated by the flexoelectric effect. Hence, the maximum power density response of FGFP energy harvesting Ⅱ can be regarded as the result of the cancellation of the gradient piezoelectric effect and flexoelectric effect. The maximum power density response of FGFP energy harvesting Ⅱ is in phase with the external excitation when the beam thickness is less than 1.3 $\mu m$, and is in reverse phase with the external excitation when the beam thickness is greater than 1.3 $\mu m$. The corresponding $C_{\mathrm{p}\mathrm{f}}$ also satisfies the same law, which indicates that the positive and negative values of $C_{\mathrm{p}\mathrm{f}}$ can represent the induced electric potential direction of the FGFP energy harvesting. Clearly, the piezoelectric polarization direction of the FGFP energy harvesting is crucial to obtain optimal power output at the desired scale.

FIGURE 7

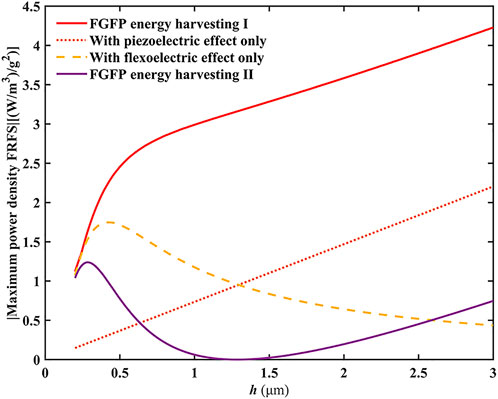
FIGURE 7. Variation of the maximum power density FRFs of two types of FGFP energy harvesting as a function of the beam thickness.

Influence of the gradient index on electromechanical coupling output of the FPFG energy harvesting

In this section, we will investigate the influence of the gradient index on the electromechanical coupling performance of the two types of FGFP energy harvesting. Keeping the bottom material (PVDF) of two types of FGFP energy harvesting invariable, we only change the parameters of the top material (BaTiO₃). The top material parameter remains unchanged ($\gamma =1$), indicating the gradient index remains unchanged (${\alpha }_1=3.567,{\alpha }_2={\alpha }_3={\alpha }_4=2.302,{\alpha }_5=1.218$); the top material parameters are twice the original material parameters ($\gamma =2$), indicating that the gradient index increases (${\alpha }_1=4.260,{\alpha }_2={\alpha }_3={\alpha }_4=3,{\alpha }_5=1.911$); the top material parameters are half of the original material parameters ($\gamma =0.5$), indicating the gradient index decreases (${\alpha }_1=2.874,{\alpha }_2={\alpha }_3={\alpha }_4=1.609,{\alpha }_5=0.525$).

Figure 8 depicts the variation of the maximum power density FRFs with the beam thickness of two types of FGFP energy harvesting with different gradient indexes. It can be seen that the gradient index does not change the trend of the curves. The maximum power density response of the FGFP energy harvesting Ⅰ increases with increasing gradient index. The large gradient index will therefore produce more significant material gradient changes along the beam thickness. The intense flexoelectric effect and gradient piezoelectric effect will enhance the electromechanical coupling output of system at the large scale for the FGFP energy harvesting Ⅰ. For the FGFP energy harvesting Ⅱ shown in Figure 8B, the output of system generated by flexoelectric effect and gradient piezoelectric effect will cancel each other. Hence, the power density response will become very small or even zero at a certain beam thickness. At the small scale, the maximum power density response will reach a peak value at a certain thickness, which increases with increasing gradient index. At the large scale, the maximum power density response increases with increasing thickness. However, for about $0.56\mu m<h<1.14\mu m$, the maximum power density response decreases with increasing gradient index. Hence, near the transition range from nano to micro scale, considering the FGFP energy harvesting Ⅱ is inapplicable, which should be adopted at the smaller or larger scale. Therefore, selection of materials, structure scale and external load resistance is essential to obtain the optimal harvestable power for the FGFP energy harvesting.

FIGURE 8

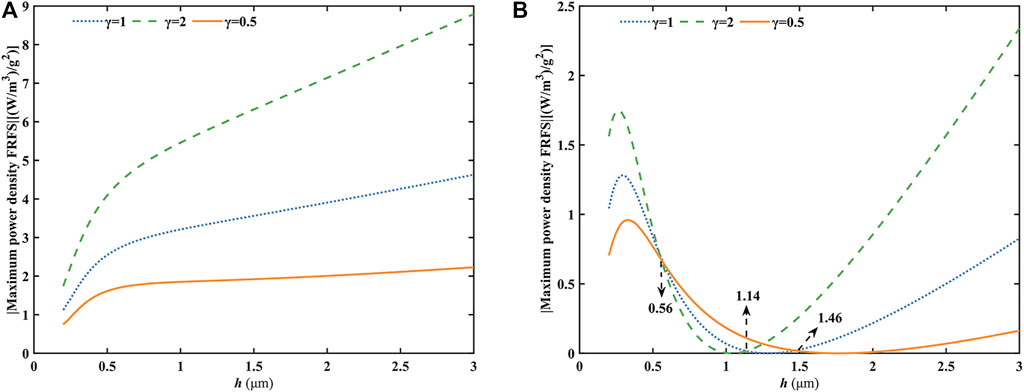
FIGURE 8. Variation of the maximum power density FRFs as a function of the beam thickness with different gradient indexes: (A) FGFP energy harvesting I; (B) FGFP energy harvesting II.

Conclusion

In this paper, the FGFP energy harvesting is studied based on the Euler-Bernoulli beam model. Utilizing the electric Gibbs free energy and the generalized Hamiltonian principle, the dynamic governing equations and boundary conditions are established. Further, the natural frequency equation is derived and the mode-superposition method is used to obtain the closed-form analytical expressions of the electromechanical responses of the FGFP energy harvesting in the modal space. The simulation results show that the change of piezoelectric polarization direction will significantly change the normalized bending stiffness and the flexo-piezoelectric coupling coefficient of the FGFP energy harvesting. Further, the piezoelectric polarization direction, gradient index, structure size and external load resistance have significant influences on the output performance of the FGFP energy harvesting. The change of piezoelectric polarization direction will lead to enhance or reduce the performance of the FGFP energy harvesting. The flexoelectric effect and gradient piezoelectric effect will dominate the output performance at the nanoscale and microscale, respectively. The present study reveals the importance of the piezoelectric polarization direction and gradient index on the output performance of the FGFP energy harvesting from nano to micro scales. This result also provides theoretical guidance for the selection of materials, gradient index, structure scale, and external load resistance to design new FGFP energy harvesting.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZK: Conceptualization, Mathematical modeling, Simulation test, Writing-Original Draft and Editing; ZZ: Conceptualization, Investigation, Funding acquisition, Supervision, Writing-Review and Editing.

Funding

This work was supported by Scientific and Technological Innovation Platform of Fujian Province (2006L2003).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdollahi, A., and Arias, I. (2015). Constructive and destructive interplay between piezoelectricity and flexoelectricity in flexural sensors and actuators. J. Appl. Mech. 82 (12), 121003. doi:10.1115/1.4031333

CrossRef Full Text | Google Scholar

Chao, L., Tsui, C. Y., and Ki, W. H. (2007). “A batteryless vibration-based energy harvesting system for ultra low power ubiquitous applications,” in IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 27-30 May 2007 (IEEE), 1349–1352.

Google Scholar

Chen, Y., Zhang, M., Su, Y., and Zhou, Z. (2021). Coupling analysis of flexoelectric effect on functionally graded piezoelectric cantilever nanobeams. Micromachines 12 (6), 595. doi:10.3390/mi12060595

PubMed Abstract | CrossRef Full Text | Google Scholar

Chu, L., Dui, G., and Ju, C. (2018). Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compos. Struct. 186, 39–49. doi:10.1016/j.compstruct.2017.10.083

CrossRef Full Text | Google Scholar

Chu, L., Dui, G., and Zheng, Y. (2020). Thermally induced nonlinear dynamic analysis of temperature-dependent functionally graded flexoelectric nanobeams based on nonlocal simplified strain gradient elasticity theory. Eur. J. Mech. - A/Solids 82, 103999. doi:10.1016/j.euromechsol.2020.103999

CrossRef Full Text | Google Scholar

Chu, L., Li, Y., and Dui, G. (2019). Size-dependent electromechanical coupling in functionally graded flexoelectric nanocylinders. Acta Mech. 230 (9), 3071–3086. doi:10.1007/s00707-019-02442-7

CrossRef Full Text | Google Scholar

Cross, L. E. (2006). Flexoelectric effects: Charge separation in insulating solids subjected to elastic strain gradients. J. Mat. Sci. 41 (1), 53–63. doi:10.1007/s10853-005-5916-6

CrossRef Full Text | Google Scholar

Deng, Q., Kammoun, M., Erturk, A., and Sharma, P. (2014). Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 51 (18), 3218–3225. doi:10.1016/j.ijsolstr.2014.05.018

CrossRef Full Text | Google Scholar

Deng, Q. (2017). Size-dependent flexoelectric response of a truncated cone and the consequent ramifications for the experimental measurement of flexoelectric properties. J. Appl. Mech. 84 (10), 4037552. doi:10.1115/1.4037552

CrossRef Full Text | Google Scholar

Erturk, A., and Inman, D. J. (2008). A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. J. Vib. Acoustics-Transactions Asme 130 (4), 041002. doi:10.1115/1.2890402

CrossRef Full Text | Google Scholar

Erturk, A., and Inman, D. J. (2011). Piezoelectric energy harvesting. Hoboken, NJ, USA: Wiley.

Google Scholar

Fu, G., and Zhou, S. (2021). On the size dependency of a dielectric partially covered laminated microbeam. Thin-Walled Struct. 161, 107489. doi:10.1016/j.tws.2021.107489

CrossRef Full Text | Google Scholar

Fu, J. Y., and Cross, L. E. (2007). On the flexoelectric effects in solid dielectrics: Theories and applications. Ferroelectrics 354 (1), 238–245. doi:10.1080/00150190701455005

CrossRef Full Text | Google Scholar

Fu, J., and Zhang, Z. (2022). Modeling of the bilayer piezoelectric microbeam based on the strain gradient effect. J. Appl. Phys. 131 (13), 134302. doi:10.1063/5.0084020

CrossRef Full Text | Google Scholar

Hahn, M., Trolier-McKinstry, S., and Meyer, R. J. (2021). Flexoelectric barium strontium titanate (BST) hydrophones. J. Appl. Phys. 129 (6), 064504. doi:10.1063/5.0038756

CrossRef Full Text | Google Scholar

Hong, J., Catalan, G., Scott, J. F., and Artacho, E. (2010). The flexoelectricity of barium and strontium titanates from first principles. J. Phys. Condens. Matter 22 (11), 112201. doi:10.1088/0953-8984/22/11/112201

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S., and Shen, S. (2009). Electric field gradient theory with surface effect for nano-dielectrics. Cmc-Computers Mater. Continua 13 (1), 63–87. doi:10.3970/CMC.2009.013.063

CrossRef Full Text | Google Scholar

Hudak, N. S., and Amatucci, G. G. (2008). Small-scale energy harvesting through thermoelectric, vibration, and radiofrequency power conversion. J. Appl. Phys. 103 (10), 101301. doi:10.1063/1.2918987

CrossRef Full Text | Google Scholar

Ke, L. L., Yang, J., Kitipornchai, S., and Wang, Y. S. (2014). Axisymmetric postbuckling analysis of size-dependent functionally graded annular microplates using the physical neutral plane. Int. J. Eng. Sci. 81, 66–81. doi:10.1016/j.ijengsci.2014.04.005

CrossRef Full Text | Google Scholar

Kumar, A., Kiran, R., Kumar, R., Chandra Jain, S., and Vaish, R. (2018). Flexoelectric effect in functionally graded materials: A numerical study. Eur. Phys. J. Plus 133 (4), 141–149. doi:10.1140/epjp/i2018-11976-1

CrossRef Full Text | Google Scholar

Li, A., Zhou, S., Zhou, S., and Wang, B. (2014a). Size-dependent analysis of a three-layer microbeam including electromechanical coupling. Compos. Struct. 116, 120–127. doi:10.1016/j.compstruct.2014.05.009

CrossRef Full Text | Google Scholar

Li, A., Zhou, S., Zhou, S., and Wang, B. (2014b). A size-dependent bilayered microbeam model based on strain gradient elasticity theory. Compos. Struct. 108, 259–266. doi:10.1016/j.compstruct.2013.09.020

CrossRef Full Text | Google Scholar

Li, Y. S., and Pan, E. (2015). Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple-stress theory. Int. J. Eng. Sci. 97, 40–59. doi:10.1016/j.ijengsci.2015.08.009

CrossRef Full Text | Google Scholar

Liang, X., Hu, S., and Shen, S. (2014). Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mat. Struct. 23 (3), 035020. doi:10.1088/0964-1726/23/3/035020

CrossRef Full Text | Google Scholar

Liang, X., Hu, S., and Shen, S. (2015). Size-dependent buckling and vibration behaviors of piezoelectric nanostructures due to flexoelectricity. Smart Mat. Struct. 24 (10), 105012. doi:10.1088/0964-1726/24/10/105012

CrossRef Full Text | Google Scholar

Lu, C., Raghunathan, V., and Roy, K. (2011). Efficient design of micro-scale energy harvesting systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 1 (3), 254–266. doi:10.1109/jetcas.2011.2162161

CrossRef Full Text | Google Scholar

Lu, J., Lv, J., Liang, X., Xu, M., and Shen, S. (2016). Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J. Appl. Phys. 119 (9), 094104. doi:10.1063/1.4943069

CrossRef Full Text | Google Scholar

Ma, L. S., and Lee, D. W. (2012). Exact solutions for nonlinear static responses of a shear deformable FGM beam under an in-plane thermal loading. Eur. J. Mech. - A/Solids 31 (1), 13–20. doi:10.1016/j.euromechsol.2011.06.016

CrossRef Full Text | Google Scholar

Ma, W., and Cross, L. E. (2001). Large flexoelectric polarization in ceramic lead magnesium niobate. Appl. Phys. Lett. 79 (26), 4420–4422. doi:10.1063/1.1426690

CrossRef Full Text | Google Scholar

Majdoub, M. S., Sharma, P., and Cagin, T. (2008). Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 77 (12), 125424. doi:10.1103/PhysRevB.77.125424

CrossRef Full Text | Google Scholar

Mbarki, R., Baccam, N., Dayal, K., and Sharma, P. (2014). Piezoelectricity above the Curie temperature? Combining flexoelectricity and functional grading to enable high-temperature electromechanical coupling. Appl. Phys. Lett. 104 (12), 122904. doi:10.1063/1.4869478

CrossRef Full Text | Google Scholar

Moura, A. G., and Erturk, A. (2017). Electroelastodynamics of flexoelectric energy conversion and harvesting in elastic dielectrics. J. Appl. Phys. 121 (6), 064110. doi:10.1063/1.4976069

CrossRef Full Text | Google Scholar

Nan, Z., Xie, Z., Shijie, Z., and Dejin, C. (2020). Size-dependent static bending and free vibration analysis of porous functionally graded piezoelectric nanobeams. Smart Mat. Struct. 29 (4), 045025. doi:10.1088/1361-665X/ab73e4

CrossRef Full Text | Google Scholar

Poddar, S., and Ducharme, S. (2013). Measurement of the flexoelectric response in ferroelectric and relaxor polymer thin films. Appl. Phys. Lett. 103 (20), 202901. doi:10.1063/1.4829622

CrossRef Full Text | Google Scholar

Qi, L., Zhou, S., and Li, A. (2016). Size-dependent bending of an electro-elastic bilayer nanobeam due to flexoelectricity and strain gradient elastic effect. Compos. Struct. 135, 167–175. doi:10.1016/j.compstruct.2015.09.020

CrossRef Full Text | Google Scholar

Rafiee, M., He, X. Q., and Liew, K. M. (2014). Nonlinear analysis of piezoelectric nanocomposite energy harvesting plates. Smart Mat. Struct. 23 (6), 065001. doi:10.1088/0964-1726/23/6/065001

CrossRef Full Text | Google Scholar

Rojas, E. F., Faroughi, S., Abdelkefi, A., and Park, Y. H. (2021). Investigations on the performance of piezoelectric-flexoelectric energy harvesters. Appl. Energy 288, 116611. doi:10.1016/j.apenergy.2021.116611

CrossRef Full Text | Google Scholar

Sezer, N., and Koç, M. (2021). A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 80, 105567. doi:10.1016/j.nanoen.2020.105567

CrossRef Full Text | Google Scholar

Shen, S., and Hu, S. (2010). A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 58 (5), 665–677. doi:10.1016/j.jmps.2010.03.001

CrossRef Full Text | Google Scholar

Su, Y., Lin, X., Huang, R., and Zhou, Z. (2019a). Analytical electromechanical modeling of nanoscale flexoelectric energy harvesting. Appl. Sci. 9 (11), 2273. doi:10.3390/app9112273

CrossRef Full Text | Google Scholar

Su, Y. X., Zhou, Z. D., and Yang, F. P. (2019b). Electromechanical analysis of bilayer piezoelectric sensors due to flexoelectricity and strain gradient elasticity. AIP Adv. 9 (1), 015207. doi:10.1063/1.5081072

CrossRef Full Text | Google Scholar

Tang, L., and Wang, J. (2017). Size effect of tip mass on performance of cantilevered piezoelectric energy harvester with a dynamic magnifier. Acta Mech. 228 (11), 3997–4015. doi:10.1007/s00707-017-1910-8

CrossRef Full Text | Google Scholar

Wang, G. F., and Feng, X. Q. (2010). Effect of surface stresses on the vibration and buckling of piezoelectric nanowires. EPL A Lett. J. Explor. Front. Phys. 91, 56007. doi:10.1209/0295-5075/91/56007

CrossRef Full Text | Google Scholar

Wang, K. F., and Wang, B. L. (2016). An analytical model for nanoscale unimorph piezoelectric energy harvesters with flexoelectric effect. Compos. Struct. 153, 253–261. doi:10.1016/j.compstruct.2016.05.104

CrossRef Full Text | Google Scholar

Yan, X., Huang, W., Ryung Kwon, S., Yang, S., Jiang, X., and Yuan, F. G. (2013). A sensor for the direct measurement of curvature based on flexoelectricity. Smart Mat. Struct. 22 (8), 085016. doi:10.1088/0964-1726/22/8/085016

CrossRef Full Text | Google Scholar

Yan, Z., and Jiang, L. (2013a). Size-dependent bending and vibration behaviour of piezoelectric nanobeams due to flexoelectricity. J. Phys. D. Appl. Phys. 46 (35), 355502. doi:10.1088/0022-3727/46/35/355502

CrossRef Full Text | Google Scholar

Yan, Z., and Jiang, L. Y. (2013b). Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J. Appl. Phys. 113 (19), 194102. doi:10.1063/1.4804949

CrossRef Full Text | Google Scholar

Zhang, D. G., and Zhou, Y. H. (2008). A theoretical analysis of FGM thin plates based on physical neutral surface. Comput. Mater. Sci. 44 (2), 716–720. doi:10.1016/j.commatsci.2008.05.016

CrossRef Full Text | Google Scholar

Zhang, Z., Yan, Z., and Jiang, L. (2014). Flexoelectric effect on the electroelastic responses and vibrational behaviors of a piezoelectric nanoplate. J. Appl. Phys. 116 (1), 014307. doi:10.1063/1.4886315

CrossRef Full Text | Google Scholar

Zhao, X., Zheng, S., and Li, Z. (2019). Size-dependent nonlinear bending and vibration of flexoelectric nanobeam based on strain gradient theory. Smart Mat. Struct. 28 (7), 075027. doi:10.1088/1361-665X/ab1cfc

CrossRef Full Text | Google Scholar

Zhou, Z. D., Yang, C. P., Su, Y. X., Huang, R., and Lin, X. L. (2017). Electromechanical coupling in piezoelectric nanobeams due to the flexoelectric effect. Smart Mat. Struct. 26 (9), 095025. doi:10.1088/1361-665X/aa7936

CrossRef Full Text | Google Scholar

Zi, Y., and Wang, Z. L. (2017). Nanogenerators: An emerging technology towards nanoenergy. Apl. Mater. 5 (7), 074103. doi:10.1063/1.4977208

CrossRef Full Text | Google Scholar