Significance of non-uniform heat source/sink and cattaneo-christov model on hybrid nanofluid flow in a Darcy-forchheimer porous medium between two parallel rotating disks

The suspension of nanoparticles in fluid influences several properties of the resulting fluid. Many production and manufacturing applications need knowledge of the heat transference mechanism in nanofluids. The current paper concerns the influence of non-uniform heat source/sink on (MoS₂-Go/water flow) hybrid nanofluid flow and (Go/water flow) nanofluid flow in a Darcy-Forchheimer porous medium between two parallel and infinite spinning disks in the occurrence of radiation. The Cattaneo-Christov model is utilized to analyze heat and mass transmission. The Cattaneo-Christov model introduces the time lag factors in the process of heat and mass transmission, known as the thermal relaxation parameter and solutal relaxation parameter, respectively. The governing equations are numerically solved employing the “bvp4c function in MATLAB.” The effect of the primary relevant parameters on the velocity, temperature, nanoparticle concentration, and is graphically depicted. Finally, a table is drawn to show the relationships of various critical factors on the Nusselt number, and Sherwood number. Results reveal that an increase in the thermal relaxation parameter reduces the heat transmission rate at both the upper and lower plate. Furthermore, an increase in the nanoparticle’s volume fraction causes enhancement in thermal conduction, which increases the heat transmission rate at the upper disk. The results of this study will be helpful to many transportation processes, architectural design systems, enhanced oil recovery systems, medical fields that utilize nanofluids, and so on.

1 Introduction

To address today’s escalating energy demands, the variety of industries has risen exponentially. Optimizing heating performance is an essential alternative for improving cooling and heating efficiency in nuclear and chemical reactors, electronic equipment, and so on. To extract the most out of these applications, scientists and researchers are very much concerned about boosting heating efficiency. Turkyilmazoglu (2022a) studied the influence of a horizontal uniform magnetic field in the flow instigated by a rotating disk. In another study, Turkyilmazoglu (2022b) investigated the influence of heat source/sink in the convective flow of fluids due to a vertical flat surface/cone immersed in porous media. Ali et al. (2019a) utilized the Bingham and Carreau models to investigate the complex rheology of slime. Asghar et al. (2020a) utilized the couple stress fluid model to study the movement of microorganisms in two-dimensional channel. Ali et al. (2019b) investigated the optimum speed of microorgamisms through Carreau fluid models with under magnetic and porous effects. Javid et al. (2019) studied and gave the numerical solution of magnetically induced flow of fluid confined inside two curled peristaltic walls. Asghar et al. (2020b) studied the non-Newtonian fluid flow confined within a complex wavy walls of a 2-dimensional channel using Taylor’s swimming sheet model. Asghar et al. (2022a) studied the non-Newtonian Couple stress fluid in 2-dimensional inclined channel with magnetic and electrical field. Some other remarkable studies on applications of fluid models on bio-medical fields can be refered from Refs. (Asghar et al., 2020c; Asghar et al., 2022d; Asghar et al., 2022b; Asghar et al., 2022c; Asghar et al., 2023; Wu et al., 2020; Shah et al., 2022). Two decades-long, exploration of nanofluids (Choi, 1995) has confirmed that they have superior heat transmission potential. The varied characteristics of nanoparticles (NPs) may be adjusted by modifying their size (diameter), substance (metallic oxides, non-metallic, metallic, etc.), and nanoparticle dispersion in the working fluid. Keeping in mind the properties, Rahman et al. (2022) studied the influence of suction and magnetic field on several water-based nanofluids over a decelerating rotating disk. They studied the different water-based nanofluids (NFs) with copper oxide, copper, alumina, silver, and titania. The primary issue with single nanoparticle NFs is that they have either better rheological characteristics or superior thermal networks. Mono nanoparticles lack all of the desirable characteristics needed for some applications. The features of nanofluids may be improved by adjusting the nanoparticle volume fraction; however, this has a limitation as the difficulty arises in the trade-off due rise in viscosity. This is a constraint, which may be overcome by combining more than one variety of NPs in the working fluid. Later, the researcher’s developed hybrid nanofluids (HNFs) that optimize the exclusive features of many varieties of nanoparticles.

Many studies have used hybrid nanofluid combinations of metallic and non-metal oxide nanoparticles to maximize thermal performance and nanoparticle stability. The development of nanoclusters increases the relative viscosity of HNFs, and HNFs have superior thermal conductivity than solitary nanoparticle nanofluids and base fluids (Ranga Babu et al., 2017). Ranga Babu et al. (2017) also marked out that metal nanoparticles make a nanolayer atop metallic oxide nanoparticles, and it produces a thermal interfacial layer between weak boundaries of the working fluid and hybrid NPs, resulting in significant thermal conductivity augmentation. Devi and Devi (2016) studied the significance of Newtonian heating in HNF flow over a three-dimensional stretched surface. They analyzed the comparative behavior of Cu–Al₂O₃/water and Cu/water. They concluded that HNF has a higher heat transmission rate (HTR) compared to NF. Waqas et al. (2021) also explained and gave the solution to a HNF flow problem over a rotating disk with non-linear radiation. They studied the model with water as a base fluid and SWCNT− TiO₂ and MWCNT− CoFe₂O₄ NPs. Khan et al. (2020c) expounded on the HNF flow over a thick moving surface instigated by mixed convection. They modeled the flow with water as a main fluid and SiO₂ and MoS₂ NPs. Masood et al. (2021) discussed the significance of a HNF flow over a stretched surface near a stagnation point. They studied the problem with heat generation/absorption and water as a working fluid with polystyrene and titanium oxide NPs. Alrabaiah et al. (2022) inspected the HNF flow inside a conical slit of a cone and a disk. They modeled the flow with water and magnesium oxide, and silver NPs. Yaseen et al. (2022c) expounded on the significance of the magnetic field on HNF flow and NF flow between two parallel plates. They studied the flow problem with MoS₂–SiO₂/H₂O–C₂H₆O₂ for HNF flow and MoS₂/H₂O for NF flow. Qureshi et al. (2021) investigated the HNF flow between two moving co-axial orthogonal disks. They considered the flow problem with water as a main fluid and titania and copper NPs and studied the significance of the magnetic field. Rashid et al. (2021) inspected the HNF flow over a cylinder in motion. They considered the flow problem with water as a main fluid and Titania and silver NPs. Khan et al. (2022) explicated the significance of suction in a HNF flow between two parallel plates. They considered the flow problem with water as a base fluid and carbon nanotubes and Fe₃O₄ NPs.

Technological advancements have considerably enhanced human interaction with fundamental tasks such as heating and cooling food and materials, transportation, and manufacturing. The heat altercation process in equipment or applications intended to suit social requirements is a key aspect typically seen in the aforementioned activities. This has been a significant issue for manufacturers over the decades, particularly recently, in improving the thermal control of various maneuvers in the electronic sector, power systems, thermal sector, and medicinal bids. For a long period, the Fourier law (Fourier, 1822) was used to analyze the heat transmission attributes. Years later, Cattaneo (Cattaneo, 1948) altered the Fourier law by including a parameter related to the time lag in the traditional Fourier law, which states that the heat transfer mechanism permits heat to be carried at a restricted pace through the transmission of heat waves. Later, Christov (Christov, 2009) used thermal relaxation time and the upper convective derivative of Oldroyd to overcome the limitation of the Cattaneo rule and arrive at a material invariant formulation. The developments by Cattaneo (Cattaneo, 1948) and Christov (Christov, 2009) have led the way for researchers to study the HTR with a time lag factor and it is called the Cattaneo-Christov heat flux model (CCM). Very recently, Turkyilmazoglu (2021) provided an analytical explanation of the application of CCM in cooling and its role in enhancing the HTR from surfaces. In recent times; Khan et al. (2020b) explicated the consequence of the thermal stratification and CCM in the water-based NF flow over a surface having an exponential stretching rate. They analyzed the behavior of NF with three diverse NPs, namely, copper, Titania, and alumina; Yaseen et al. (2022a) studied the difference in HTR of MoS₂/Kerosene oil and MoS₂-SiO₂/Kerosene oil flow between two spinning disks with CCM. They concluded that at the lower disk, the HTR of the hybrid nanofluid transcends the HTR of the nanofluid. (Ashraf and Ghehsareh (2021) explored the significance of CCM in the flow of Casson fluid past a heated surface; Kumar et al. (2021) studied the flow of water-based NF with carbon nanotubes (multi and single-walled) between two spinning disks in a porous medium with CCM. Bai et al. (2022) derived the analytical solution of an Oldroyd-B nanofluid flow problem through a vibrating tensile plate with CCM. Naz et al. (2022) also discussed the analytical solution of a Carreau nanoliquid flow problem over a rotating and stretchable disk with CCM. Some more interesting research on CCM can be found in Refs. (Irfan et al., 2018; Garia et al., 2021; Khan et al., 2021; Madhukesh et al., 2021).

According to the preceding discussion, it can be inferred that only a few studies are published to study the significance of HNF between two spinning disks. Authors have developed a model to analyze the HNF flow (MoS₂-Go/water flow) and NF flow (Go/water flow) between two parallel and infinite spinning disks. Furthermore, as a novelty, the significance of non-uniform heat source/sink, CCM, thermal radiation, magnetic field, and Darcy-Forchheimer porous medium are also studied. This research paper also aims to analyze the HTR and mass transmission rate (MTR) of HNF flow (MoS₂-Go/water flow) and NF flow (Go/water flow) at both disks. The numerical solution is sought via the bvp4c solver in MATLAB. As per the author’s information, such a comparative analysis of the HNF flow (MoS₂-Go/water) and NF flow (Go/water) between two parallel and infinite spinning disks has never been reported before and the results are new and novel.

2 Flow model and governing equations

2.1 Assumptions of the problem

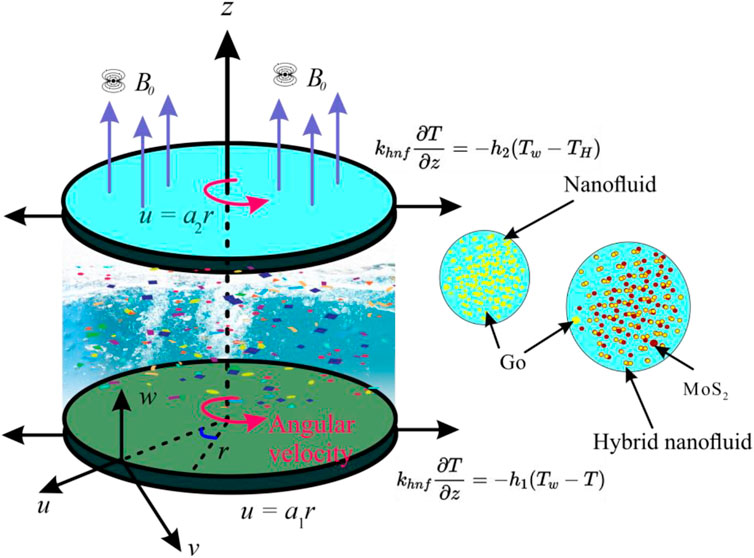
Consider the three-dimensional incompressible, steady, and axisymmetric flow of the HNF (MoS₂-Go/water) and NF (Go/water) between the two spinning infinite disks placed along parallel lines (see Figure 1). The notation $\left(r,\Theta ,z\right)$ has been used for the cylindrical coordinate system (see Figure 1). The flow is exposed to a magnetic field B_o in the z-direction. As a novelty, to develop the model, the Darcy-Forchheimer law is used for porous medium. In addition, the non-uniform heat source/sink, Cattaneo-Christov double diffusion model, and thermal radiation is used to investigate HTR and MTR. Moreover, the last term in the energy equation (Eq. 5) denotes the non-uniform heat source/sink term $\left(q^{‴}\right)$ and it is explained later. The lower disk and upper disk are placed at $z=0$ and $z=H$ (see Eq. 7). In the boundary conditions, a₁ and a₂ denote the shrinkage rates of the lower and upper disks in the radial direction, respectively. Furthermore, b₁ and b₂ are taken as the angular velocities of the lower and upper disks, respectively. The outer surfaces of the disks are assumed to be convectively heated by hot liquids having temperatures T_w (lower disk) and T_H (upper disk), with h₁ (lower disk) and h₂ (upper disk) as their heat transfer coefficients. In addition, C_w and C_H denote the NPs concentration at the lower and upper disks, respectively.

FIGURE 1

FIGURE 1. Physical Model.

Based on the aforesaid points, the flow equations are (see Bhattacharyya et al., 2020; Mabood et al., 2021; Yaseen et al., 2022a):

Continuity equation:

$\frac{\partial u}{\partial r}+\frac{\partial w}{\partial z}+\frac{u}{r}=0(1)$

Momentum equations:

${\rho }_{hnf}\left(u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{v^2}{r}\right)=-\frac{\partial p}{\partial r}+{\mu }_{hnf}\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{{\partial }^{2}u}{\partial z^2}+\frac{1}{r}\frac{\partial u}{\partial r}-\frac{u}{r^2}\right)-{\sigma }_{hnf}{B_0}^{2}u-\frac{{\mu }_{hnf}}{k_{fn}}u-\frac{{\rho }_{hnf}F}{\sqrt{k_{fn}}}{u}^2(2)$

${\rho }_{hnf}\left(u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{uv}{r}\right)={\mu }_{hnf}\left(\frac{{\partial }^{2}v}{\partial r^2}+\frac{{\partial }^{2}v}{\partial z^2}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^2}\right)-{\sigma }_{hnf}{B_0}^{2}v-\frac{{\mu }_{hnf}}{k_{fn}}v-\frac{{\rho }_{hnf}F}{\sqrt{k_{fn}}}{v}^2(3)$

${\rho }_{hnf}\left(w\frac{\partial w}{\partial z}+u\frac{\partial w}{\partial r}\right)=-\frac{\partial p}{\partial z}+{\mu }_{hnf}\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{{\partial }^{2}w}{\partial z^2}\right)(4)$

Energy equation:

$u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}+{\gamma }_t\left(\begin{array}{l}\frac{\partial T}{\partial r}\left(w\frac{\partial u}{\partial z}+u\frac{\partial u}{\partial r}\right)+\frac{\partial T}{\partial z}\left(w\frac{\partial w}{\partial z}+u\frac{\partial w}{\partial r}\right)\\ +2uw\frac{{\partial }^{2}T}{\partial z\partial r}+u^2\frac{{\partial }^{2}T}{\partial r^2}+w^2\frac{{\partial }^{2}T}{\partial z^2}\end{array}\right)=\frac{1}{{\left(\rho C_p\right)}_{hnf}}\left(k_{hnf}+\frac{16{\sigma }^{*}{T}_H^3}{3k^{*}}\right)\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{{\partial }^{2}T}{\partial z^2}+\frac{1}{r}\frac{\partial T}{\partial r}\right)+\frac{q^{‴}}{{\left(\rho C_p\right)}_{hnf}}(5)$

Concertation equation:

$u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}+{\gamma }_c\left(\begin{array}{l}\frac{\partial C}{\partial r}\left(w\frac{\partial u}{\partial z}+u\frac{\partial u}{\partial r}\right)+\frac{\partial C}{\partial z}\left(w\frac{\partial w}{\partial z}+u\frac{\partial w}{\partial r}\right)\\ +2uw\frac{{\partial }^{2}C}{\partial z\partial r}+u^2\frac{{\partial }^{2}C}{\partial r^2}+w^2\frac{{\partial }^{2}C}{\partial z^2}\end{array}\right)=D\left[\frac{1}{r}\frac{\partial C}{\partial r}+\frac{{\partial }^{2}C}{\partial r^2}+\frac{{\partial }^{2}C}{\partial z^2}\right](6)$

with Boundary conditions (BCs):

$\left.\begin{array}{l}u=a_{1}r,v=b_{1}r,w=0,k_{hnf}\frac{\partial T}{\partial z}=-h_1\left(T_w-T\right),C=C_w\mathrm{a}\mathrm{t}z=0\\ u=a_{2}r,v=b_{2}r,w=0,k_{hnf}\frac{\partial T}{\partial z}=-h_2\left(T-T_H\right),C=C_H\mathrm{a}\mathrm{t}z=H\end{array}\right\}(7)$

where “$\left(u,v,w\right)$ are the velocity components along with $\left(r,\Theta ,z\right)$ directions,” respectively, “C is nanoparticles concentration,” “T is temperature,” “p is pressure,” “k^* is the mean absorption coefficient,” “σ^* is the Stefan-Boltzmann constant,” “F is the Forchheimer coefficient and k_fh is the porous medium permeability,” respectively, “D is diffusion coefficient,” “${\gamma }_t$ is the thermal relaxation time,” and “${\gamma }_c$ is the solutal relaxation time.” Furthermore, “k is thermal conductivity, $\mu$ is dynamic viscosity, $C_p$ is heat capacity, $\rho$ is density, $\sigma$ is electrical conductivity.” Moreover, subscript hnf is for hybrid nanofluid, nf is for nanofluid, and f, bf is for fluid. In addition, the last term in the energy Eq. 5 i.e., $q^{‴}$ denotes the significance of “non-uniform heat source/sink” and it is demarcated as follows (Yaseen et al., 2022b):

$q^{‴}=\frac{k_{hnf}{u}_w\left(T_w-T_H\right)}{r{v}_{hnf}}\left\{A^{*}\frac{df}{\partial \xi }+B^{*}\theta \right\}(8)$

where $u_w=b_{1}r$ and the heat source/sink corresponding to space coefficients and corresponding to temperature dependence are signified by constants $A^{*}$ and $B^{*}$, respectively. As a result, the heat source phenomena is characterized by $A^{*}>0$ and $B^{*}>0$, whereas the heat sink phenomena is characterized by $A^{*}<0$ and $B^{*}<0$.

2.2 Properties of hybrid nanofluid and nanofluid

This study describes the analysis of HNF and NF. The thermal characteristics of HNF and NF are influenced by the base fluid (water) and NPs; as well as by the volume fraction of MoS₂ and Go NPs, as shown in Table 1 (Khan et al., 2020d). The Shape of MoS₂ and Go NPs is taken as spherical. In this paper, the volume fraction of Go NPs and MoS₂ NPs is denoted by ${\varphi }_1$ and ${\varphi }_2$, respectively. Furthermore, s₁ is used for Go NPs, and s₂ is used for MoS₂ NPs. The MoS₂ belongs to the transition metal class and Go belongs to the oxide class. The combination of MoS₂ and Go NPs is taken because metal nanoparticles make a nanolayer atop oxide nanoparticles, and it produces a thermal interfacial layer between weak boundaries of the working fluid and hybrid NPs, resulting in thermal conductivity augmentation.

TABLE 1

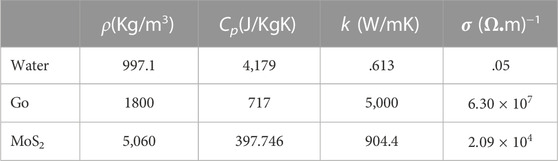
TABLE 1. Thermo-physical properties of water, MoS₂ and Go nanoparticles (Khan et al., 2020d).

2.2.1 Thermophysical correlations of Go/water nanofluid

The thermophysical correlations of the NF model used are as follows (Rawat and Kumar, 2020):

$\frac{{\mu }_{nf}}{{\mu }_f}=\frac{1}{{\left(1-{\phi }_1\right)}^{2.5}},{\rho }_{nf}=\left(1-{\phi }_1\right){\rho }_f+{\phi }_1{\rho }_{s1},\frac{k_{nf}}{k_f}=\left[\frac{k_{s1}+2k_f-2{\phi }_1\left(k_f-k_{s1}\right)}{k_{s1}+2k_f+{\phi }_1\left(k_f-k_{s1}\right)}\right](9)$

$\frac{{\sigma }_{nf}}{{\sigma }_f}=1+\frac{3\left(\sigma -1\right){\phi }_1}{2+\sigma -\left(\sigma -1\right){\phi }_1}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\sigma ={\sigma }_{s1}/{\sigma }_f,{\left(\rho C_p\right)}_{nf}=\left(1-{\phi }_1\right){\left(\rho C_p\right)}_f+{\phi }_1{\left(\rho C_p\right)}_{s1}(10)$

2.2.2 Thermophysical correlations of MoS2-Go/water hybrid nanofluid

The thermophysical correlations of the HNF model used are as follows (Khan et al., 2020c):

${\rho }_{hnf}=\left(1-{\phi }_2\right)\left[\left(1-{\phi }_1\right){\rho }_f+{\phi }_1{\rho }_{s1}\right]+{\phi }_2{\rho }_{s2},\frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\phi }_1\right)}^{2.5}{\left(1-{\phi }_2\right)}^{2.5}}(11)$

$\frac{k_{hnf}}{k_{bf}}=\left[\frac{k_{s2}+2k_{bf}-2{\phi }_2\left(k_{bf}-k_{s2}\right)}{k_{s2}+2k_{bf}+{\phi }_2\left(k_{bf}-k_{s2}\right)}\right]\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\frac{k_{bf}}{k_f}=\left[\frac{k_{s1}+2k_f-2{\phi }_1\left(k_f-k_{s1}\right)}{k_{s1}+2k_f+{\phi }_1\left(k_f-k_{s1}\right)}\right](12)$

$\frac{{\sigma }_{hnf}}{{\sigma }_{bf}}=\left[\frac{{\sigma }_{s2}+2{\sigma }_{bf}-2{\phi }_2\left({\sigma }_{bf}-{\sigma }_{s2}\right)}{{\sigma }_{s2}+2{\sigma }_{bf}+{\phi }_2\left({\sigma }_{bf}-{\sigma }_{s2}\right)}\right]\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\frac{{\sigma }_{bf}}{{\sigma }_f}=\left[\frac{{\sigma }_{s1}+2{\sigma }_f-2{\phi }_1\left({\sigma }_f-{\sigma }_{s1}\right)}{{\sigma }_{s1}+2{\sigma }_f+{\phi }_1\left({\sigma }_f-{\sigma }_{s1}\right)}\right](13)$

${\left(\rho C_p\right)}_{hnf}=\left(1-{\phi }_2\right)\left[\left(1-{\phi }_1\right){\left(\rho C_p\right)}_f+{\phi }_1{\left(\rho C_p\right)}_{s1}\right]+{\phi }_2{\left(\rho C_p\right)}_{s2}(14)$

2.3 Similarity transformations

The transformations listed below are utilized to transform the governing equations (Yaseen et al., 2022a):

$u=r{b}_1{f}^{\prime }\left(\eta \right),v=r{b}_{1}g\left(\eta \right),w=-2H{b}_{1}f\left(\eta \right),P=b_1{\rho }_{hnf}{v}_{hnf}\left[P\left(\eta \right)+\frac{r^2\epsilon }{2H^2}\right],\xi =\frac{z}{H},\theta =\frac{T-T_H}{T_w-T_H},\varphi =\frac{C-C_H}{C_w-C_H}(15)$

Eq. 1 is satisfied, and Eqs 2, 3, 4, 5, 6, 7 reduce to

$Re\frac{{\omega }_2}{{\omega }_1}\left(f{\prime }^2-2f{f}^{″}-g^2+\frac{{\omega }_3}{{\omega }_2}M{f}^{\prime }+F^{*}f{\prime }^2\right)+Re\lambda f^{\prime }=-\epsilon +f^{‴}(16)$

$g^{″}-Re\lambda g=Re\frac{{\omega }_2}{{\omega }_1}\left(\frac{{\omega }_3}{{\omega }_2}gM+g{F}^{*}-2\left(g^{\prime }f-f\prime g\right)\right)(17)$

$P^{\prime }+4\frac{{\omega }_2}{{\omega }_1}Reff\prime +2f^{″}=0(18)$

$\left({\omega }_5+R_d-{\omega }_4\mathrm{P}\mathrm{r}\mathrm{R}\mathrm{e}{\tau }_E{f}^2\right){\theta }^{″}+\frac{\mathrm{R}\mathrm{e}{\omega }_5{\omega }_2}{{\omega }_1}\left\{A^{*}{f}^{\prime }+B^{*}\theta \right\}+{\omega }_4\mathrm{P}\mathrm{r}\mathrm{R}\mathrm{e}\left(2f{\theta }^{\prime }-{\tau }_E\left(f{f}^{\prime }\theta \prime \right)\right)=0(19)$

${\varphi }^{″}=Re{\tau }_{c}Sc\left(f{f}^{\prime }\varphi \prime +f^2{\varphi }^{″}\right)-2\mathrm{R}\mathrm{e}Scf{\varphi }^{\prime }(20)$

The BCs are obtained as follows:

$\left.\begin{array}{l}f\left(\eta \right)=0,f^{\prime }\left(\eta \right)=k_1,g\left(\eta \right)=1,\theta \prime \left(\eta \right)=-\frac{{\gamma }_1}{{\omega }_5}\left(1-\theta \left(\eta \right)\right),P\left(\eta \right)=0,\varphi \left(\eta \right)=1\mathrm{a}\mathrm{t}\eta =0\\ f\left(\eta \right)=0,f^{\prime }\left(\eta \right)=k_2,g\left(\eta \right)=\Omega ,\theta \prime \left(\eta \right)=-\frac{{\gamma }_2}{{\omega }_5}\theta \left(\eta \right),\varphi \left(\eta \right)=0\mathrm{a}\mathrm{t}\eta =1\end{array}\right\}(21)$

In the aforementioned equations, “$Re\left(=\frac{b_1{H}^2}{v_f}\right)$ represents Reynold number, $F^{*}\left(=\frac{Fr}{\sqrt{k_{fn}}}\right)$ represents the inertial coefficient, $\mathit{Pr}\left(=\frac{v_f}{{\alpha }_f}\right)$ is the Prandtl number, $\lambda \left(=\frac{v_f}{b_1{k}_{fn}}\right)$ is the porosity parameter, $M\left(=\frac{{\sigma }_f{B_0}^2}{{\rho }_f{b}_1}\right)$ represents the magnetic field parameter, $A^{*}$ and $B^{*}$ represents heat source/sink parameters, $R_d\left(=\frac{16{\sigma }^{*}{T}_H^3}{3k_f{k}^{*}}\right)$ represents thermal radiation parameter, ${\tau }_E\left(=4{\gamma }_t{b}_1\right)$ represents the thermal relaxation parameter, ${\tau }_C\left(=4{\gamma }_c{b}_1\right)$ represents the solutal relaxation parameter, $k_1\left(=\frac{a_1}{b_1}\right)$ and $k_2\left(=\frac{a_2}{b_1}\right)$ represent shrinking parameters, $\Omega \left(=\frac{b_2}{b_1}\right)$ is the rotation parameter, ${\gamma }_1\left(=\frac{H{h}_1}{k_f}\right)$ and ${\gamma }_2\left(=\frac{H{h}_2}{k_f}\right)$ are Biot numbers, $Sc\left(=\frac{v_f}{D}\right)$ represents Schmidt number and ${\omega }_1=\frac{{\mu }_f}{{\mu }_{hnf}},{\omega }_2=\frac{{\rho }_{hnf}}{{\rho }_f},{\omega }_3=\frac{{\sigma }_{hnf}}{{\sigma }_f},{\omega }_4=\frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f},{\omega }_5=\frac{k_{hnf}}{k_f}$ are constants”.

Eq. 16 is then differentiated w.r.t $\eta$ for the elimination of $\epsilon$ (pressure variable), and we get:

${\omega }_1\left(f^{iv}-\lambda \mathrm{R}\mathrm{e}{f}^{″}\right)+{\omega }_2\mathrm{R}\mathrm{e}\left(2f{f}^{‴}+2g{g}^{\prime }-M\frac{{\omega }_3}{{\omega }_2}f″-2f\prime f″F^{*}\right)=0(22)$

Eqs 16–21 define the $\epsilon$ (pressure variable) as follows:

$\epsilon =f^{‴}\left(0\right)-\mathrm{R}\mathrm{e}\frac{{\omega }_2}{{\omega }_1}\left(f^{\prime }{\left(0\right)}^2-2f^{″}\left(0\right)f\left(0\right)-g{\left(0\right)}^2+F^{*}f\prime {\left(0\right)}^2+\frac{{\omega }_3}{{\omega }_2}Mf\prime \left(0\right)\right)-\lambda \mathrm{R}\mathrm{e}{f}^{\prime }\left(0\right)(23)$

To solve Eqn. (18) for P, use integration from 0 to $\eta$ and obtain the following form:

$P=-2\left\{\left(f^{\prime }-f\prime \left(0\right)\right)+\frac{{\omega }_2}{{\omega }_1}\mathrm{R}\mathrm{e}{\left(f\right)}^2\right\}=0(24)$

3 Engineering parameters

3.1 Nusselt numbers

The Nusselt numbers at the lower disk $\left(N{u_r}_0\right)$ and upper disk $\left(N{u_r}_1\right)$ are (Mabood et al., 2021) and (Yaseen et al., 2022a):

$N{u}_{r0}=-\left({\omega }_4+R_d\right){\theta }^{\prime }\left(0\right)\mathrm{a}\mathrm{n}\mathrm{d}N{u}_{r1}=-\left({\omega }_4+R_d\right){\theta }^{\prime }\left(1\right)(\mathrm{24a})$

3.2 Sherwood numbers

The Sherwood numbers at the lower disk $\left(S{h}_{r0}\right)$ and upper disk $\left(S{h}_{r1}\right)$ are defined as (Khan et al., 2020a):

$S{h}_{r0}=-{\varphi }^{\prime }\left(0\right)\mathrm{a}\mathrm{n}\mathrm{d}S{h}_{r1}=-{\varphi }^{\prime }\left(1\right)(25)$

4 Methodology of numerical approach

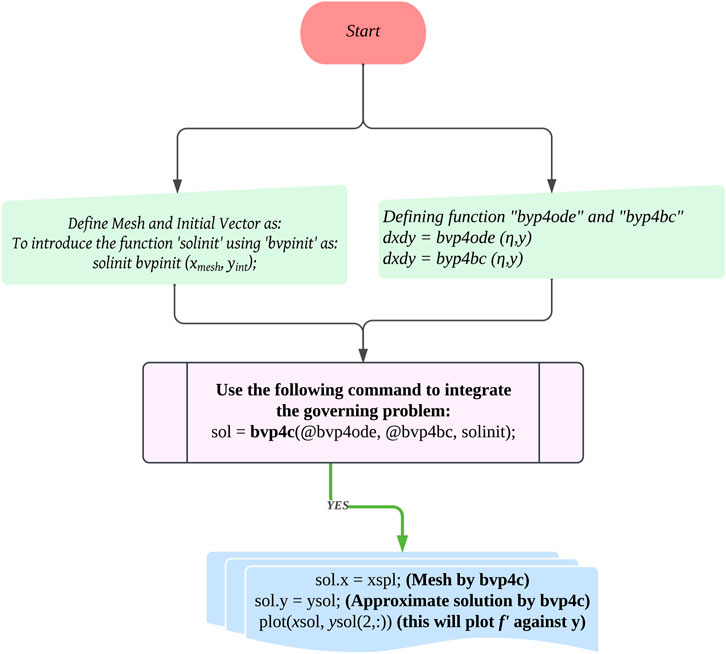
This section focuses on the methodology used for deducing solutions as well as code validation. The equations are at first modeled as PDEs and later, converted into ODEs via similarity variables. The numerical solution of the Eqs 16, 17, 18, 19, 20 along with BCs (21) is deduced with the “bvp4c function” (a built-in package in MATLAB), the more specific details of the bvp4c function can be referred from the Shampine et al. (2003). The “bvp4c function” uses a finite difference scheme together with a precision of fourth order with the help of the “3-stage Lobatto IIIA formula”. To deduce the solution of the model, the ODEs obtained after similarity transformation are reduced into first-order ODEs by the following substitution:

$“y_1=f,y_2=f^{\prime },y_3=f^{″},y_4=f^{‴},y_5=g,y_6=g^{\prime },y_7=\theta ,y_8={\theta }^{\prime },y_9=\varphi ,y_{10}={\varphi }^{\prime }”(26)$

Utilizing the new variables, the Eqs 16, 17, 18, 19, 20 are reduced to first-order ODEs and the following MATLAB syntax is used:

$\left(\begin{array}{l}y{y}_1\\ y{y}_2\\ y{y}_3\\ y{y}_4\end{array}\right)=\left(\begin{array}{l}Re\frac{{\omega }_2}{{\omega }_1}\left(-2y_1{y}_4-2y_5{y}_6+\frac{{\omega }_3}{{\omega }_2}M{y}_3+2F^{*}{y}_2{y}_3\right)+\lambda \mathrm{R}\mathrm{e}{y}_3;\\ Re\frac{{\omega }_2}{{\omega }_1}\left(-2y_1{y}_4-2y_5{y}_6+\frac{{\omega }_3}{{\omega }_2}M{y}_3+2F^{*}{y}_2{y}_3\right);\\ -\frac{Re\frac{{\omega }_5{\omega }_2}{{\omega }_1}\left(A_1{y}_2+B_1{y}_7\right)+{\omega }_{4}PrRe\left(2y_1{y}_8-{\tau }_E{y}_1{y}_2{y}_8\right)}{{\omega }_4+R_d-{\omega }_3{\tau }_{E}PrRe{y}_1^2};\\ \frac{Re{\tau }_{c}Sc\times y_1{y}_2{y}_{10}-2\mathrm{R}\mathrm{e}Sc{y}_1{y}_{10}}{1-Re{\tau }_{c}Sc{y}_1^2};\end{array}\right)(27)$

The above system Eq. 27 is subjected to the following BCs at the lower disk $\left(\eta =0\right)$ and upper disk $\left(\eta =1\right)$:

$\left.\begin{array}{l}{y}_1=0,y_2=k_1,y_5=1,y_8=-\frac{{\gamma }_1}{{\omega }_5}\left(1-y_7\right),y_9=1\mathrm{a}\mathrm{t}\eta =0\\ y_1=0,y_2=k_2,y_5=\mathrm{\Omega },y_8=-\frac{{\gamma }_2}{{\omega }_5}{y}_7,y_9=0\mathrm{a}\mathrm{t}\eta =1\end{array}\right\}(28)$

From new variables in Eq. 26 and BCs Eq. 28, it is seen that the following conditions at the $\left(\eta =0\right)$ and $\left(\eta =1\right)$ are missing:

$y_3\left(0\right),y_3\left(1\right),y_4\left(0\right),y_4\left(1\right),y_6\left(0\right),y_6\left(1\right),y_7\left(0\right),y_7\left(1\right),y_{10}\left(0\right),\mathrm{a}\mathrm{n}\mathrm{d}{y}_{10}\left(1\right)(29)$

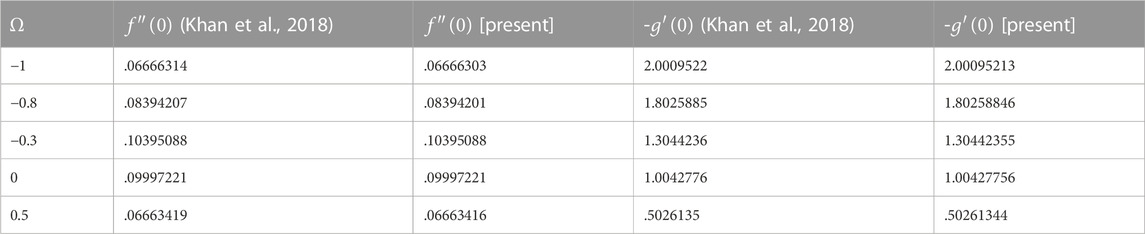
Furthermore, the values of missing conditions are guessed to initiate the process of finding the solution and other parameters present in the Eqs 27, 28 are set to find the desired solution. The process of iteration is repeated and the solution is accepted only when the conditions in Eq. 28 are satisfied. The process of finding the solution is shown via a flow chart in Figure 2. To validate the model and the code used to find the numerical solution, an assessment in Table 2 is outlined with the published computations of (Khan et al., 2018) study as a limiting case to validate the numerical code utilized to solve the current model. The comparative results are quite consistent, ensuring that the current conclusions are valid.

FIGURE 2

FIGURE 2. Flow-chart.

TABLE 2

TABLE 2. The comparison of the values $f^{\prime }\prime \left(0\right)$ and $g^{\prime }\left(0\right)$ for the various value of $\Omega$ and the rest parameters are, $\mathit{Pr}=6.2$, ${\varphi }_1={\varphi }_2=M=F^{*}=\lambda =\tau =k_1=k_2={\gamma }_1={\gamma }_2=0$.

5 Results and discussion

This section focuses on the numerical outcomes and graphical and tabular results are interpreted physically. Authors have used the following general values in the numerical computations: $\mathit{Pr}=6.2$, $M=1$, $Re=2.2$, $Sc=300$, $F^{*}=3$, $\lambda =1.5$, $R_d=.2$, ${\tau }_E=1$, ${\tau }_C=10$, $A^{*}=3$, $B^{*}=3$, $\mathrm{\Omega }=0.01$, ${\gamma }_1=.05$, ${\gamma }_2=0.1$, $-k_1=-k_2=.02$, and ${\phi }_1={\phi }_2=.03$. The analysis is performed for the porosity parameter $\left(1.5\le \lambda \le 9.5\right)$, magnetic field parameter $\left(1\le M\le 11\right)$, nanoparticles volume fraction $\left(.03\le \phi \le .21\right)$, thermal radiation parameter $\left(.2\le R_d\le 1\right)$, thermal relaxation parameter $\left(.2\le {\tau }_E\le 161\right)$, heat source/sink parameters $\left(-1\le A^{*}\le 3,-2\le B^{*}\le 4\right)$, solutal relaxation parameter $\left(10\le {\tau }_c\le 100\right)$, and Schmidt number $\left(100\le Sc\le 500\right)$. The influence of the primary relevant factors on the velocity, temperature, and nanoparticle concentration is graphically depicted. Finally, a Table is drawn to show the relationships of various critical factors on the Nusselt and Sherwood number. The results are shown for both HNF (MoS₂-Go/water flow) and NF (Go/water flow) and in the figures, solid lines are drawn for HNF and dot lines are drawn for NF.

5.1 Velocity distribution

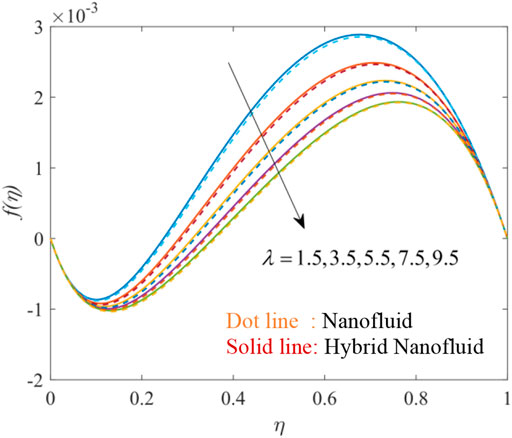
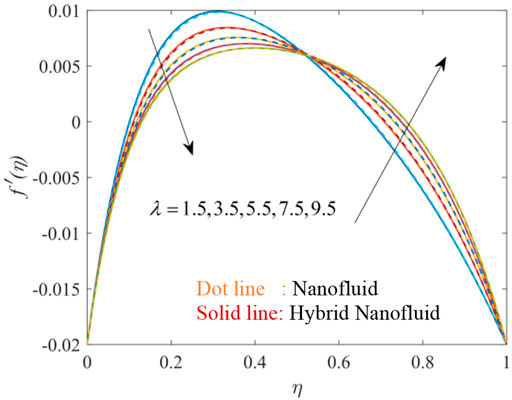
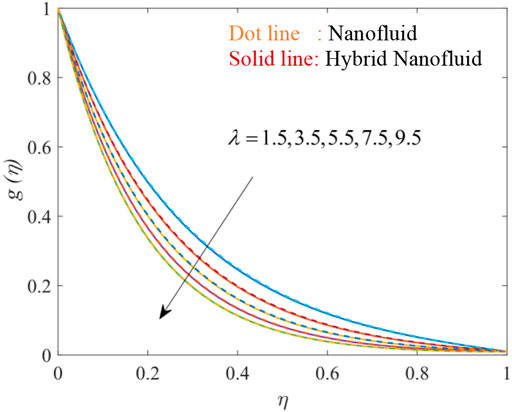
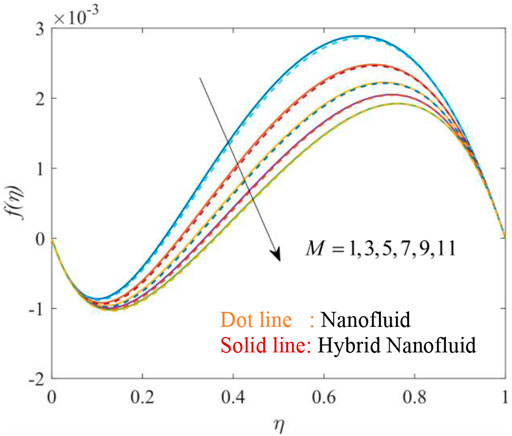
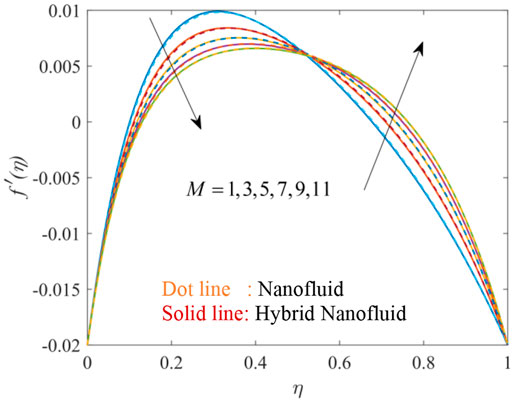
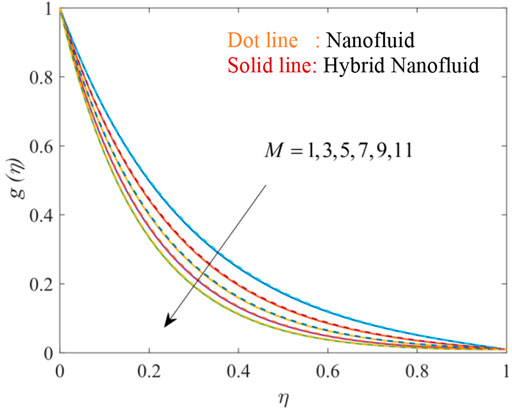
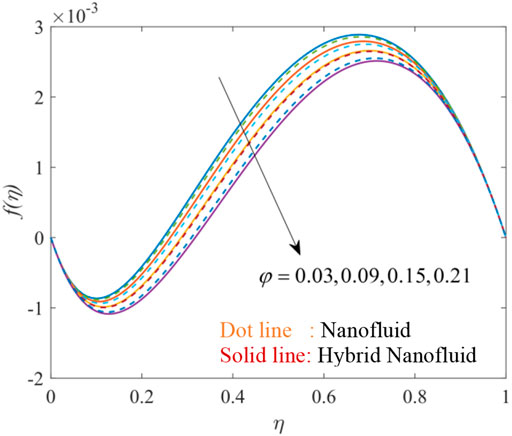
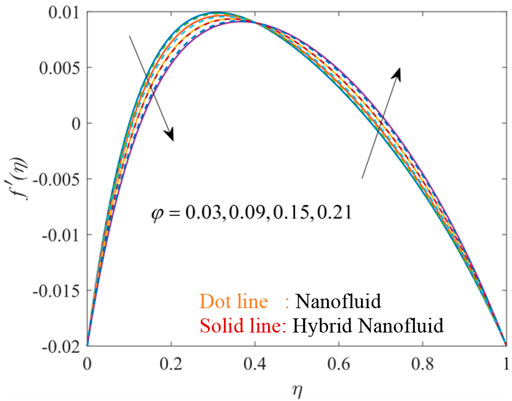
Figures 3, 4, 5, 6, 7, 8, 9, 10, 11 show the fluctuation of dimensionless velocity against the similarity variable while altering distinct flow-regulating parameters one at a time while leaving others unchanged. Figures 3, 4, 5 depict the influence of porosity parameter λ on axial velocity distribution $f\left(\eta \right)$, radial velocity distribution $f^{\prime }\left(\eta \right)$, and tangential velocity distribution $g\left(\eta \right)$, respectively. Within the core areas of the boundary layer region (BLR), there is a noticeable decrease in the axial velocity distribution $f\left(\eta \right)$ and tangential velocity distribution $g\left(\eta \right)$ with growing values of λ. The radial velocity shows transitioning nature in BLR and the transition point lies near $\eta \sim 0.5$. $f^{\prime }\left(\eta \right)$ rises near the lower disk and behavior changes near the upper disk w.r.t to growing values of λ. Physically, the porosity parameter is linked to the friction force. Resistance increases with a rise in the porosity parameter, and therefore the velocity falls. Figures 6, 7, 8 elucidate the effectiveness of magnetic parameter M on $f\left(\eta \right)$, $f^{\prime }\left(\eta \right)$ and $g\left(\eta \right)$. The increasing magnitude of parameter M is responsible for the decrease in velocity $f\left(\eta \right)$ and $g\left(\eta \right)$. The radial velocity $f^{\prime }\left(\eta \right)$ shows transitioning nature in BLR w.r.t parameter M. The decrease in the velocity $f\left(\eta \right)$ and $g\left(\eta \right)$ is related to the generation of Lorentz force. The presence of magnetic force generates the Lorentz force opposite to the flow direction, hence it opposes the motion, and hence velocity decreases.

FIGURE 3

FIGURE 3. Effect of porosity parameter $\lambda$ on $f\left(\eta \right)$.

FIGURE 4

FIGURE 4. Effect of porosity parameter $\lambda$ on $f^{\prime }\left(\eta \right)$.

FIGURE 5

FIGURE 5. Effect of porosity parameter $\lambda$ on $g\left(\eta \right)$.

FIGURE 6

FIGURE 6. Effect of Magnetic field parameter M on $f\left(\eta \right)$.

FIGURE 7

FIGURE 7. Effect of Magnetic field parameter M on $f^{\prime }\left(\eta \right)$.

FIGURE 8

FIGURE 8. Effect of Magnetic field parameter M on $g\left(\eta \right)$.

FIGURE 9

FIGURE 9. Effect of nanoparticles volume fraction $\phi$ on $f\left(\eta \right)$.

FIGURE 10

FIGURE 10. Effect of nanoparticles volume fraction $\phi$ on $f^{\prime }\left(\eta \right)$.

FIGURE 11

FIGURE 11. Effect of nanoparticles volume fraction $\phi$ on $g\left(\eta \right)$.

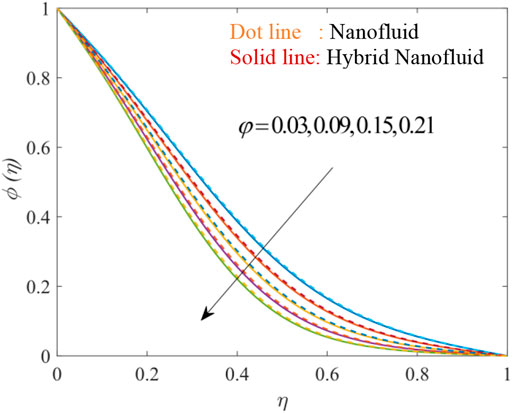
Figures 9, 10, 11 elucidate the effectiveness of volume fraction on velocity distribution. On increasing the volume fraction of each nanoparticle Go $\left({\phi }_1\right)$, and MoS₂ $\left({\phi }_2\right)$ in equal quantity $\left(\phi \right)$, the axial velocity $f\left(\eta \right)$ decreases and tangential velocity $g\left(\eta \right)$ increases, whereas radial velocity $f^{\prime }\left(\eta \right)$ shows transitioning nature in BLR, i.e., it first decreases and then increases. The increasing nanoparticles volume fraction in the base fluid causes the hindrance for the motion in the axial direction, hence the velocity $f\left(\eta \right)$ decreases. On contrary, the tangential velocity $g\left(\eta \right)$ increases, because the addition of nanoparticles causes the outward movement of fluid. In Figures 3, 4, 5, 6, 7, 8, 9, 10, 11, the authors have presented a comparison in velocity profiles of HNF (MoS₂-Go/water flow) and NF (Go/water flow). HNF is seen to have the higher axial velocity $f\left(\eta \right)$ and NF has the higher tangential velocity $g\left(\eta \right)$. Near the lower disk, HNF has a higher radial velocity, but as fluid approaches the upper disk, NF has a higher radial velocity.

5.2 Temperature distribution

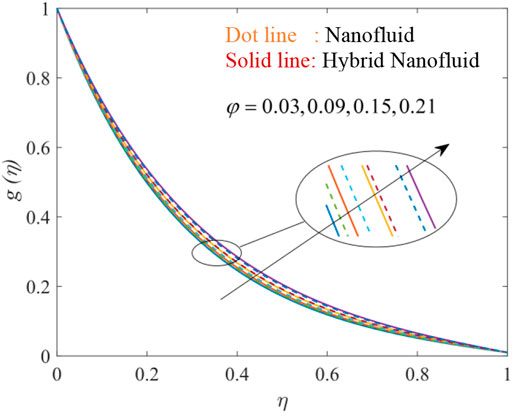
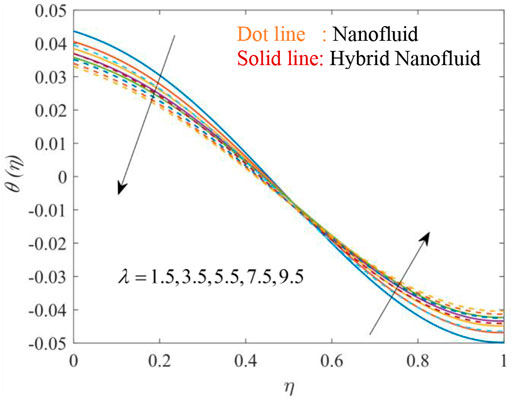
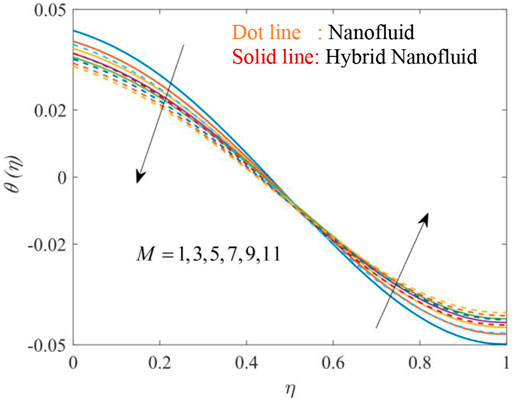
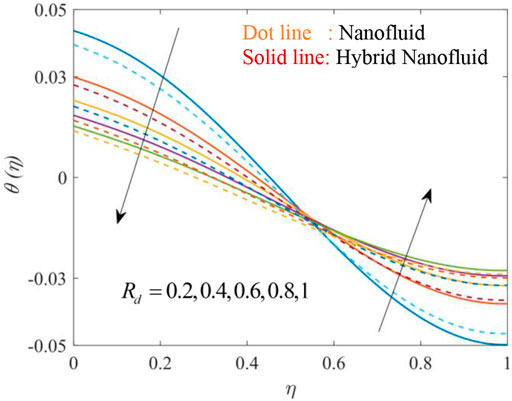
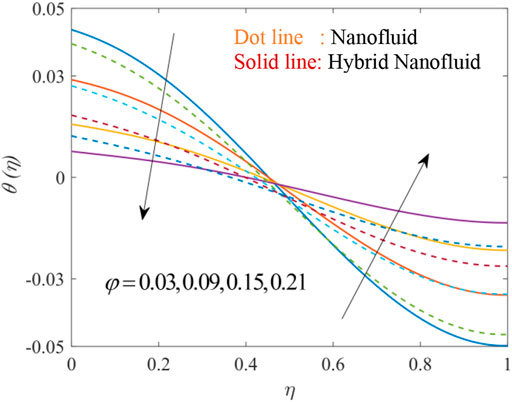
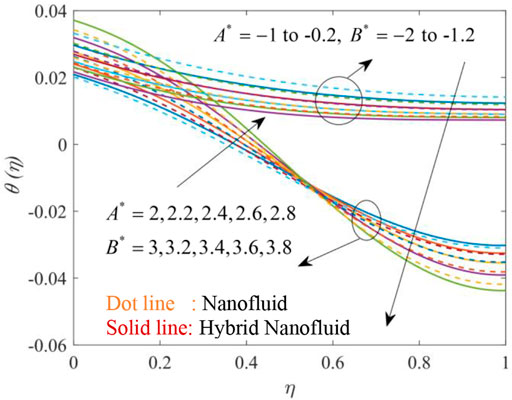
Figures 12, 13, 14, 15, 16, 17 show the fluctuation of dimensionless temperature $\theta \left(\eta \right)$ against the similarity variable while altering distinct flow-regulating parameters one at a time while leaving others unchanged. Figures 12, 13, 14 depict the influence of porosity parameter λ, magnetic parameter M, and radiation parameter R_d on the temperature profile. It is observed that with an increment in the aforesaid parameters, the temperature $\theta \left(\eta \right)$ shows transitioning nature in BLR. The temperature $\theta \left(\eta \right)$ falls near the lower disk and rises near the upper disk. The effect of resistance forces due to the porosity parameter and the effect of generated Lorentz force due to the magnetic field is significant near the upper disk, which opposes the motion of the flow and increases friction. As a result, the temperature rises near the upper disk with increasing porosity parameter λ and magnetic parameter M. Figure depicts that augmenting parameter R_d causes the temperature to decrease first, then after a transition point, it increases. This means that near the upper disk, the heat carried by radiation supplies energy to the particles, increasing their kinetic energy and velocity, and causing an increase in the temperature.

FIGURE 12

FIGURE 12. Effect of porosity parameter $\lambda$ on $\theta \left(\eta \right)$.

FIGURE 13

FIGURE 13. Effect of Magnetic field parameter M on $\theta \left(\eta \right)$.

FIGURE 14

FIGURE 14. Effect of thermal radiation parameter R_d on $\theta \left(\eta \right)$.

FIGURE 15

FIGURE 15. Effect of thermal relaxation parameter ${\tau }_E$ on $\theta \left(\eta \right)$.

FIGURE 16

FIGURE 16. Effect of nanoparticles volume fraction $\phi$ on $\theta \left(\eta \right)$.

FIGURE 17

FIGURE 17. Effect of heat source/sink parameter A^* and B^* on $\theta \left(\eta \right)$.

Figure 15 depicts that an increase in the thermal relaxation parameter ${\tau }_E$ lead the temperature $\theta \left(\eta \right)$ to rise near the lower disk but for the same, the temperature falls near the upper disk. The non-zero thermal relaxation parameter ${\tau }_E$ denotes time lag during heat transfer. For the zero value of ${\tau }_E$, the heat transfer is governed by Fourier’s law. The results depict that near the lower disk the more time lag in heat transfer implies higher temperature but the same condition near the upper disk relates to the lower temperature. Figure 16 elucidates the effectiveness of volume fraction on temperature $\theta \left(\eta \right)$. On increasing the volume fraction of each nanoparticle Go $\left({\phi }_1\right)$, and MoS₂ $\left({\phi }_2\right)$ in equal quantity $\left(\phi \right)$, the temperature falls near the lower disk and surges near the upper one. The rise in the temperature near the upper disk can be attributed to the enhancement in the thermal conduction of the HNF or NF due to an increase in the nanoparticles in the base fluid. Figure 17 depicts that for the case of heat source $\left(A^{*}>0,B^{*}>0\right)$, the temperature $\theta \left(\eta \right)$ shows transitioning nature in BLR. Temperature first increases then decreases for increasing $A^{*}$ and $B^{*}\left(A^{*}>0,B^{*}>0\right)$. Whereas, for the case of the heat sink $\left(A^{*}<0,B^{*}<0\right)$, the temperature increases for increasing magnitude of heat sink parameters. In Figures 12, 13, 14, 15, 16, 17, the authors have presented a comparison of temperature profiles of HNF (MoS₂-Go/water flow) and NF (Go/water flow). Near the lower disk, HNF has a higher thermal profile $\theta \left(\eta \right)$, but as fluid approaches the upper disk, NF has a higher thermal profile $\theta \left(\eta \right)$.

5.3 Nanoparticle concentration distribution

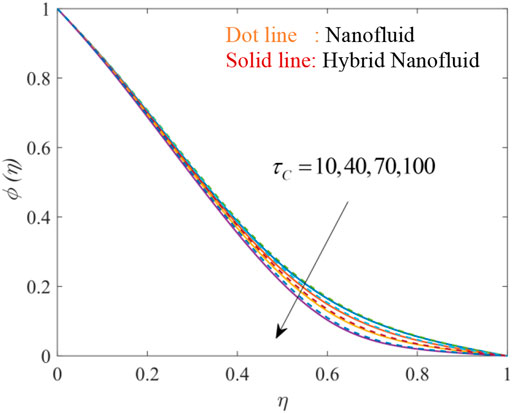
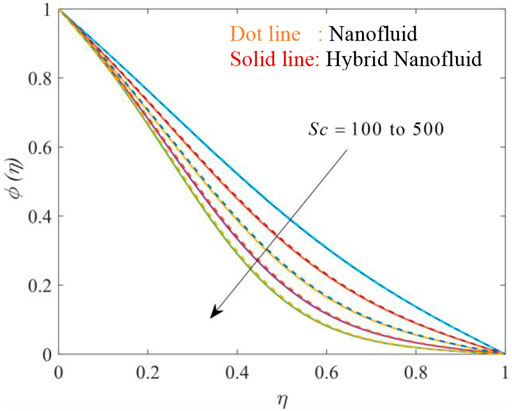
Figures 18, 19, 20 show the fluctuation of dimensionless concentration of nanoparticles against the similarity variable while altering distinct flow regulating parameters one at a time while leaving others unchanged. Figures 18, 19 depict the influence of the solutal relaxation parameter ${\tau }_C$ and Schmidt number Sc on the concentration $\varphi \left(\eta \right)$. Figure 18 depicts that increasing values of the solutal relaxation parameter ${\tau }_C$ leads concentration to fall. The non-zero values of the solutal relaxation parameter ${\tau }_C$ denote the presence of time lag during mass transfer. The increasing time lag during mass transfer has an adverse effect on concentration. The increasing time lag during mass transfer leads to a fall in the concentration profile. Figure 19 depicts that increasing values of Sc cause concentration to fall. The concentration decreases as Sc increases. The Schmidt number is an important parameter to consider as it physically connects the depths of the hydrodynamic layer and the mass transfer boundary layer. The momentum diffusion of particles in fluid increases as the strength of the Schmidt number increases in fluid flow. As a result, concentration falls. Figure 20 depicts that on increasing the volume fraction of each nanoparticle Go $\left({\phi }_1\right)$, and MoS₂ $\left({\phi }_2\right)$ in equal quantity $\left(\phi \right)$, the concentration falls. The reason for this behavior can be attributed to the fact the mixing of more nanoparticles causes the HNF or NF to be more viscous and flow is resisted, hence the concentration of NPs falls. In Figures 18, 19, 20, the authors have presented a comparison in concentration profiles of HNF (MoS₂-Go/water flow) and NF (Go/water flow). It is seen that NF has a higher concentration profile $\varphi \left(\eta \right)$ as compared to HNF.

FIGURE 18

FIGURE 18. Effect of solutal relaxation parameter ${\tau }_C$ on $\varphi \left(\eta \right)$.

FIGURE 19

FIGURE 19. Effect of Schmidt number Sc on $\varphi \left(\eta \right)$.

FIGURE 20

FIGURE 20. Effect of nanoparticles volume fraction $\varphi$ on $\phi \left(\eta \right)$.

5.4 Streamlines and engineering parameters

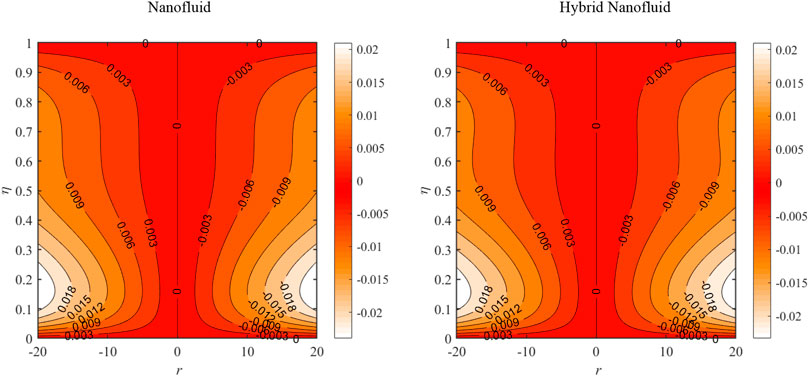
Figure 21 visualizes the streamlines pattern of HNF (MoS₂-Go/water flow) and NF (Go/water flow). The streamlines represent the movement of the suspended particles in the stream and which are driven by it. The direction of velocity at each point in the streamline is given by the tangent at that location. The denser streamlines indicate that the fluid velocity is greater than when it is open out. The HNF is seen to have slightly less dense streamlines in the present case which means more nanoparticles cause fluid to be more viscous and flow is resisted.

FIGURE 21

FIGURE 21. Streamlines for Nanofluid and Hybrid nanofluid.

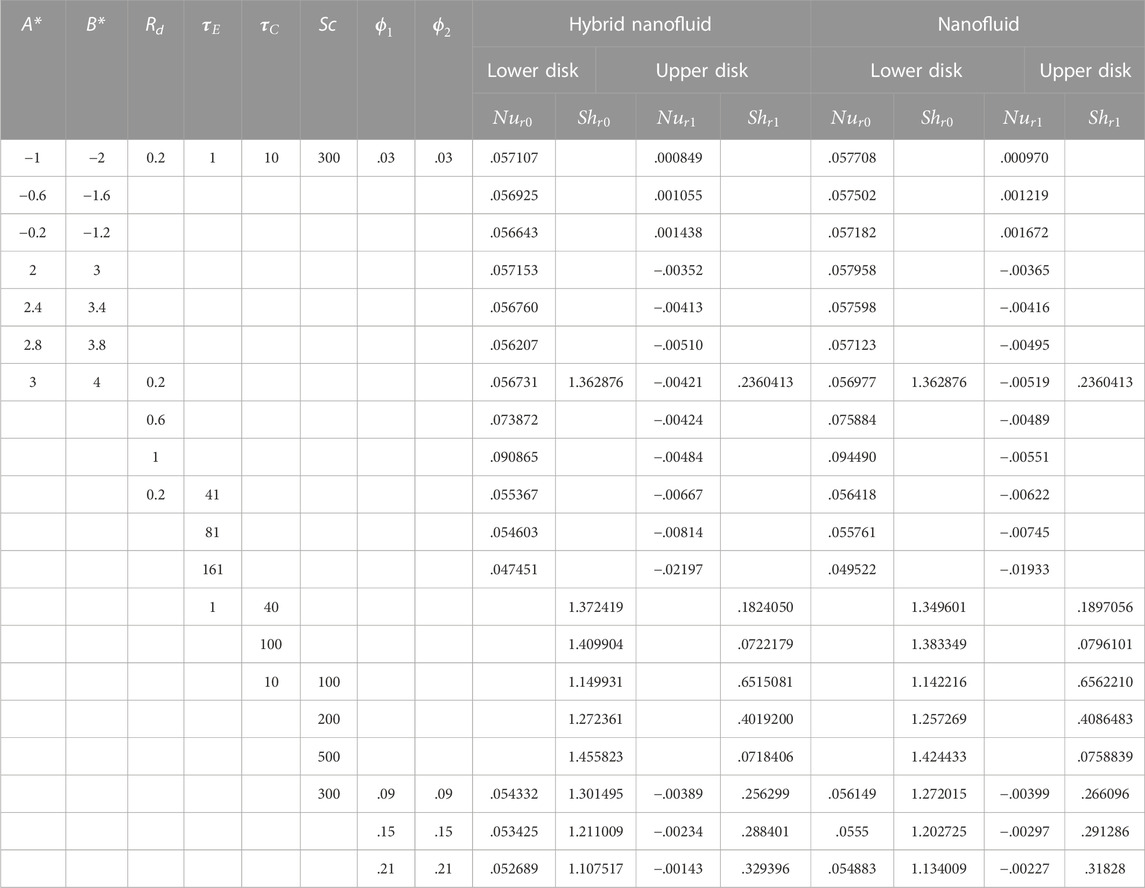
Table 3 elucidates the effectiveness of pertinent parameters on the Nusselt and Sherwood number. Nusselt number corresponds to the heat transmission rate (HTR) and the Sherwood number corresponds to the mass transmission rate (MTR) in the BLR at both disks. At the higher magnitude of the heat sink parameter, the HTR rises for HNF and NF at the lower disk but contrary behavior is seen at the upper disk. Whereas, the HTR decreases for HNF and NF at both the upper and lower disk. At the higher values of radiation parameter R_d, HTR increases at the lower disk and decreases at the upper disk. An increase in the volume fraction of each nanoparticle Go $\left({\phi }_1\right)$, and MoS₂ $\left({\phi }_2\right)$ in equal quantity $\left(\phi \right)$ enhances the thermal conductivity of the THNF due to an increase in the nanoparticles in the base fluid. The rising thermal conductivity enhances the MTR and HTR at the upper disk. It is also observed that at the higher values of the thermal relaxation parameter ${\tau }_E$, HTR reduces at both disks. The non-zero values of the thermal relaxation parameter ${\tau }_E$ denote the time lag during heat transfer. Thus on augmenting ${\tau }_E$, HTR at both disks reduces. Moreover, on increasing the magnitude of the Schmidt number Sc and solutal relaxation parameter ${\tau }_c$, the MTR reduces at upper disks, whereas, on increasing the magnitude of the same parameters, the MTR rises at the lower disk.

TABLE 3

TABLE 3. Numerical values of the heat transfer coefficient and Sherwood number when $\mathit{Pr}=6.2$.

6 Conclusion

The current problem concerns the influence of a non-uniform heat source/sink in the flow of a HNF (MoS₂-Go/water flow) and NF (Go/water flow) between two parallel and infinite spinning disks with the Cattaneo-Christov model in a porous medium in the presence of the magnetic field, and radiation. The numerical solution is deduced by employing the “bvp4c” function in MATLAB. Some vital conclusions are listed below.

• Radial velocity shows decreasing behavior near the lower disk and increasing behavior near the upper disk for increasing values of porosity parameter, magnetic parameter, and nanoparticles volume fraction.

• The heat transmission and mass transmission rate is higher at the lower disk.

• A higher magnitude of the heat sink parameter causes the rate of heat transmission to rise at the lower disk.

• The increase in nanoparticle volume fraction causes an enhancement in the rate of heat transmission at the upper disk and the time lag during heat transfer is negatively correlated with the heat transmission rate at both disks.

• The combination of heat sink parameter and thermal relxation parameter can be used to modulate the heat trnamission rate at the surface.

6.1 Future scope of research

The present study discuss the flow of nanofluid and hybrid nanofluid without the nanoparticle aggregation effect. The study can de extended with proper modeling of fluid flow by utilization of validated thermophysical correlations for nanoparticle aggregation effect.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SR and MY: Conceptualization, methodology, software, formal analysis, writing–original draft. MK and SE: Writing–original draft, data curation, investigation, visualization, validation. UK: Conceptualization, writing–original draft, writing–review and editing, supervision, resources. AA: Validation, investigation, writing–review and editing, formal analysis. AG: Writing–review and editing, data curation, validation, resources. Also, co-authors are thankful to NA for his very less contribution in the introduction part of the original paper. After, revision we have remove his name because of his permission due to his contribution was negligible. Further, he is not able to give us feedback and assisted us in the revised manuscript.

Funding

This work was partially funded by the research center of the Future University in Egypt 2022. Also, this study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, N., Asghar, Z., Sajid, M., and Anwar Bég, O. (2019b). Biological interactions between Carreau fluid and microswimmers in a complex wavy canal with MHD effects. Journal of the Brazilian Society of Mechanical Sciences and Engineering. 41, 446–513. doi:10.1007/S40430-019-1953-Y

CrossRef Full Text | Google Scholar

Ali, N., Asghar, Z., Sajid, M., and Abbas, F. (2019a). A hybrid numerical study of bacteria gliding on a shear rate-dependent slime. Physica A: Statistical Mechanics and its Applications. 535, 122435. doi:10.1016/J.PHYSA.2019.122435

CrossRef Full Text | Google Scholar

Alrabaiah, H., Bilal, M., Khan, M. A., Muhammad, T., and Legas, E. Y. (2022). Parametric estimation of gyrotactic microorganism hybrid nanofluid flow between the conical gap of spinning disk-cone apparatus. Scientific Reports. 12, 59–14. doi:10.1038/s41598-021-03077-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Asghar, Z., Ali, N., Javid, K., Waqas, M., Dogonchi, A. S., and Khan, W. A. (2020a). Bio-inspired propulsion of micro-swimmers within a passive cervix filled with couple stress mucus. The Computer Methods and Programs in Biomedicine. 189, 105313. doi:10.1016/j.cmpb.2020.105313

PubMed Abstract | CrossRef Full Text | Google Scholar

Asghar, Z., Ali, N., Waqas, M., and Javed, M. A. (2020b). An implicit finite difference analysis of magnetic swimmers propelling through non-Newtonian liquid in a complex wavy channel. Computers and Mathematics with Applications. 79, 2189–2202. doi:10.1016/J.CAMWA.2019.10.025

CrossRef Full Text | Google Scholar

Asghar, Z., Ali, N., Waqas, M., Nazeer, M., and Khan, W. A. (2020c). Locomotion of an efficient biomechanical sperm through viscoelastic medium. Biomechanics and Modeling in Mechanobiology. 19, 2271–2284. doi:10.1007/S10237-020-01338-Z

PubMed Abstract | CrossRef Full Text | Google Scholar

Asghar, Z., Saeed Khan, M. W., Gondal, M. A., and Ghaffari, A. (2022a). Channel flow of non-Newtonian fluid due to peristalsis under external electric and magnetic field. Proceedings of the Institution of Mechanical Engineers, Part E. 236, 2670–2678. doi:10.1177/09544089221097693

CrossRef Full Text | Google Scholar

Asghar, Z., Shah, R. A., and Ali, N. (2022b). A computational approach to model gliding motion of an organism on a sticky slime layer over a solid substrate. Biomechanics and Modeling in Mechanobiology. 21, 1441–1455. doi:10.1007/S10237-022-01600-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Asghar, Z., Shah, R. A., Pasha, A. A., Rahman, M. M., and Khan, M. W. S. (2022c). Controlling kinetics of self-propelled rod-like swimmers near multi sinusoidal substrate. Computers in Biology and Medicine. 151, 106250. doi:10.1016/J.COMPBIOMED.2022.106250

PubMed Abstract | CrossRef Full Text | Google Scholar

Asghar, Z., Shatanawi, W., Shah, R. A., and Gondal, M. A. (2023). Impact of viscoelastic ooze slime on complex wavy gliders near a solid boundary. Chinese Journal of Physics. 81, 26–36. doi:10.1016/J.CJPH.2022.10.013

CrossRef Full Text | Google Scholar

Asghar, Z., Waqas, M., Asif Gondal, M., and Azeem Khan, W. (2022d). Electro-osmotically driven generalized Newtonian blood flow in a divergent micro-channel. Alexandria Engineering Journal. 61, 4519–4528. doi:10.1016/J.AEJ.2021.10.012

CrossRef Full Text | Google Scholar

Bai, Y., Tang, Q., and Zhang, Y. (2022). Unsteady MHD oblique stagnation slip flow of Oldroyd-B nanofluids by coupling Cattaneo-Christov double diffusion and Buongiorno model. Chinese Journal of Physics. 79, 451–470. doi:10.1016/J.CJPH.2022.09.013

CrossRef Full Text | Google Scholar

Bhattacharyya, A., Seth, G. S., Kumar, R., and Chamkha, A. J. (2020). Simulation of Cattaneo–Christov heat flux on the flow of single and multi-walled carbon nanotubes between two stretchable coaxial rotating disks. Journal of Thermal Analysis and Calorimetry. 139, 1655–1670. doi:10.1007/s10973-019-08644-4

CrossRef Full Text | Google Scholar

Bilal Ashraf, M., and Roohani Ghehsareh, H. (2021). Model of Casson fluid with Cattaneo–Chirstov heat flux and Hall effect. Indian Journal of Physics. 95, 1469–1477. doi:10.1007/s12648-020-01819-y

CrossRef Full Text | Google Scholar

Cattaneo, C. (1948). Sulla Conduzione del Calore. Atti del Seminario Matematico e Fisico dell'Universita di Modena 3, 83–101. doi:10.1007/978-3-642-11051-1_5

CrossRef Full Text | Google Scholar

Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles. FED-American Society of Mechanical Engineers. Fluids Engineering Division Newsletter. 231, 99–105.

Google Scholar

Christov, C. I. (2009). On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mechanics Research Communications. 36, 481–486. doi:10.1016/j.mechrescom.2008.11.003

CrossRef Full Text | Google Scholar

Devi, S. S. U. P. A. S. U., and Devi, S. S. U. P. A. S. U. (2016). Numerical investigation of three-dimensional hybrid Cu-Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Canadian Journal of Physics. 94, 490–496. doi:10.1139/CJP-2015-0799

CrossRef Full Text | Google Scholar

Fourier, J. B. (1822). Théorie analytique de la chaleur. Wuhan, China; Scientific Research Publishing.

Google Scholar

Garia, R., Rawat, S. K., Kumar, M., and Yaseen, M. (2021). Hybrid nanofluid flow over two different geometries with cattaneo–christov heat flux model and heat generation: A model with correlation coefficient and probable error. Chinese Journal of Physics. 74, 421–439. doi:10.1016/j.cjph.2021.10.030

CrossRef Full Text | Google Scholar

Irfan, M., Khan, M., and Khan, W. A. (2018). Interaction between chemical species and generalized Fourier’s law on 3D flow of Carreau fluid with variable thermal conductivity and heat sink/source: A numerical approach. Results in Physics. 10, 107–117. doi:10.1016/j.rinp.2018.04.036

CrossRef Full Text | Google Scholar

Javid, K., Ali, N., and Asghar, Z. (2019). Rheological and magnetic effects on a fluid flow in a curved channel with different peristaltic wave profiles. Journal of the Brazilian Society of Mechanical Sciences and Engineering. 41, 483–514. doi:10.1007/S40430-019-1993-3

CrossRef Full Text | Google Scholar

Khan, M. I., Qayyum, S., Chu, Y. M., Khan, N. B., Kadry, S., Mackolil, J., et al. (2021). Transportation of Marangoni convection and irregular heat source in entropy optimized dissipative flow. International Communications in Heat and Mass Transfer. 120, 105031–105110. doi:10.1016/j.icheatmasstransfer.2020.105031

CrossRef Full Text | Google Scholar

Khan, M. I., Qayyum, S., Hayat, T., and Alsaedi, A. (2018). Entropy generation minimization and statistical declaration with probable error for skin friction coefficient and Nusselt number. Chinese Journal of Physics. 56, 1525–1546. doi:10.1016/j.cjph.2018.06.023

CrossRef Full Text | Google Scholar

Khan, M. S., Mei, S., ShabnamAli Shah, N., Chung, J. D., Khan, A., et al. (2022). Steady squeezing flow of magnetohydrodynamics hybrid nanofluid flow comprising carbon nanotube-ferrous oxide/water with suction/injection effect. Nanomaterials 12, 660. doi:10.3390/nano12040660

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, N. S., Shah, Q., Bhaumik, A., Kumam, P., Thounthong, P., and Amiri, I. (2020a). Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Scientific Reports. 10, 4448–4526. doi:10.1038/s41598-020-61172-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, U., Ahmad, S., Hayyat, A., Khan, I., Sooppy Nisar, K., and Baleanu, D. (2020b). On the cattaneo-christov heat flux model and OHAM analysis for three different types of nanofluids. Applied Sciences. 10, 886. doi:10.3390/app10030886

CrossRef Full Text | Google Scholar

Khan, U., Shafiq, A., Zaib, A., and Baleanu, D. (2020c). Hybrid nanofluid on mixed convective radiative flow from an irregular variably thick moving surface with convex and concave effects. Case Studies in Thermal Engineering. 21, 100660. doi:10.1016/j.csite.2020.100660

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Sheikholeslami, M., Wakif, A., and Baleanu, D. (2020d). Mixed convective radiative flow through a slender revolution bodies containing molybdenum-disulfide graphene oxide along with generalized hybrid nanoparticles in porous media. Crystal (Basel) 10, 771–818. doi:10.3390/cryst10090771

CrossRef Full Text | Google Scholar

Kumar, B., Seth, G. S., Singh, M. K., and Chamkha, A. J. (2021). Carbon nanotubes (CNTs)-based flow between two spinning discs with porous medium, Cattaneo–Christov (non-Fourier) model and convective thermal condition. Journal of Thermal Analysis and Calorimetry. 146, 241–252. doi:10.1007/s10973-020-09952-w

CrossRef Full Text | Google Scholar

Mabood, F., Berrehal, H., Yusuf, T. A., and Khan, W. A. (2021). Carbon nanotubes-water between stretchable rotating disks with convective boundary conditions: Darcy-forchheimer scheme. International Journal of Ambient Energy. 43, 3981–3994. doi:10.1080/01430750.2021.1874527

CrossRef Full Text | Google Scholar

Madhukesh, J. K., Naveen Kumar, R., Punith Gowda, R. J., Prasannakumara, B. C., Ramesh, G. K., Ijaz Khan, M., et al. (2021). Numerical simulation of aa7072-aa7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: A non-fourier heat flux model approach. Journal of Molecular Liquids. 335, 116103. doi:10.1016/j.molliq.2021.116103

CrossRef Full Text | Google Scholar

Masood, S., Farooq, M., and Anjum, A. (2021). Influence of heat generation/absorption and stagnation point on polystyrene-TiO 2/H 2 O hybrid nanofluid flow. Scientific Reports. 11, 22381. doi:10.1038/s41598-021-01747-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Naz, R., Raza, R., Zafran, Y., and Javed, M. (2022). Scrutiny of Carreau nanoliquid over rotating disk with radiation impacts and the Cattaneo–Christov flux theory. Waves Random Complex Media, 1–16. doi:10.1080/17455030.2022.2128231

CrossRef Full Text | Google Scholar

Qureshi, M. Z. A., Bilal, S., Malik, M. Y., Raza, Q., Sherif, E. S. M., and Li, Y. M. (2021). Dispersion of metallic/ceramic matrix nanocomposite material through porous surfaces in magnetized hybrid nanofluids flow with shape and size effects. Scientific Reports. 11, 12271–12319. doi:10.1038/s41598-021-91152-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahman, M., Sharif, F., Turkyilmazoglu, M., and Siddiqui, M. S. (2022). Unsteady three-dimensional magnetohydrodynamics flow of nanofluids over a decelerated rotating disk with uniform suction. Pramana 96, 170–179. doi:10.1007/S12043-022-02404-0

CrossRef Full Text | Google Scholar

Ranga Babu, J. A., Kumar, K. K., and Srinivasa Rao, S. (2017). State-of-art review on hybrid nanofluids. Pergamon.

Google Scholar

Rashid, U., Liang, H., Ahmad, H., Abbas, M., Iqbal, A., and Hamed, Y. S. (2021). Study of (Ag and TiO2)/water nanoparticles shape effect on heat transfer and hybrid nanofluid flow toward stretching shrinking horizontal cylinder. Results in Physics. 21, 103812. doi:10.1016/j.rinp.2020.103812

CrossRef Full Text | Google Scholar

Rawat, S. K., and Kumar, M. (2020). Cattaneo–christov heat flux model in flow of copper water nanofluid through a stretching/shrinking sheet on stagnation point in presence of heat generation/absorption and activation energy. International Journal of Applied and Computational Mathematics. 6, 112. doi:10.1007/s40819-020-00865-8

CrossRef Full Text | Google Scholar

Shah, R. A., Asghar, Z., and Ali, N. (2022). Mathematical modeling related to bacterial gliding mechanism at low Reynolds number with Ellis Slime. The European Physical Journal Plus. 137, 600–612. doi:10.1140/EPJP/S13360-022-02796-3

CrossRef Full Text | Google Scholar

Shampine, L. F., Gladwell, I., and Thompson, S. (2003). Solving ODEs with MATLAB. Cambridge, United States: Cambridge University Press.

Google Scholar

Turkyilmazoglu, M. (2022a). Flow and heat over a rotating disk subject to a uniform horizontal magnetic field. Zeitschrift fur Naturforschung - Section A Journal of Physical Sciences. 77, 329–337. doi:10.1515/zna-2021-0350

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2021). Heat transfer enhancement feature of the non-fourier cattaneo-christov heat flux model. Journal of Heat Transfer. 143, 094501. doi:10.1115/1.4051671

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2022b). Multiple exact solutions of free convection flows in saturated porous media with variable heat flux. Journal of Porous Media. 25, 53–63. doi:10.1615/JPORMEDIA.2022041870

CrossRef Full Text | Google Scholar

Waqas, H., Farooq, U., Naseem, R., Hussain, S., and Alghamdi, M. (2021). Impact of MHD radiative flow of hybrid nanofluid over a rotating disk. Case Studies in Thermal Engineering. 26, 101015. doi:10.1016/j.csite.2021.101015

CrossRef Full Text | Google Scholar

Wu, A., Abbas, S. Z., Asghar, Z., Sun, H., Waqas, M., and Khan, W. A. (2020). A shear-rate-dependent flow generated via magnetically controlled metachronal motion of artificial cilia. Biomechanics and Modeling in Mechanobiology. 19, 1713–1724. doi:10.1007/S10237-020-01301-Y

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaseen, M., Rawat, S. K., and Kumar, M. (2022a). Cattaneo–Christov heat flux model in Darcy–Forchheimer radiative flow of MoS2–SiO2/kerosene oil between two parallel rotating disks. Journal of Thermal Analysis and Calorimetry. 147, 10865–10887. doi:10.1007/s10973-022-11248-0

CrossRef Full Text | Google Scholar

Yaseen, M., Rawat, S. K., and Kumar, M. (2022b). Hybrid nanofluid (MoS2–SiO2/water) flow with viscous dissipation and Ohmic heating on an irregular variably thick convex/concave-shaped sheet in a porous medium. Heat transfer. 51, 789–817. doi:10.1002/htj.22330

CrossRef Full Text | Google Scholar

Yaseen, M., Rawat, S. K., Shafiq, A., Kumar, M., and Nonlaopon, K. (2022c). Analysis of heat transfer of mono and hybrid nanofluid flow between two parallel plates in a Darcy porous medium with thermal radiation and heat generation/absorption. Symmetry 14, 1943. doi:10.3390/sym14091943

CrossRef Full Text | Google Scholar

Nomenclature

Alphabetical Symbols

A*, B* Heat source/sink parameter

a₁ shrinkage rate of the lower disk

a₂ shrinkage rate of the upper disk

b₁ angular velocity of the lower disk

b₂ angular velocity of the upper disk

B_o Magnetic field strength

C Nanoparticles concentration

C_w Nanoparticles concentration at lower disk

C_H Nanoparticles concentration at the upper disk

C_p Heat capacity

D Diffusion coefficient

F Forchheimer coefficient

F* inertial coefficient

$\mathit{f}$ Axial velocity

${\mathit{f}}^{\prime }$ Radial velocity

h₁ heat transfer coefficient of hot liquid at lower plate

h₂ heat transfer coefficients of hot liquid at the upper plate

H Distance between disks

g Tangential velocity

k Thermal conductivity

${\mathit{k}}^{*}$ Mean absorption coefficient

k_fh Permeability of the porous medium

k₁, k₂ Shrinking parameters

M Magnetic field parameter

$\mathit{N}{\mathit{u}}_{\mathit{r}\mathit{o}},\mathit{N}{\mathit{u}}_{\mathit{r}\mathbf{1}}$ Nusselt numbers

p Pressure

Pr Prandtl number

$\left({\mathit{q}}^{‴}\right)$ Non-uniform heat source/sink term

R_d Radiation parameter

Re Reynolds number

$\mathit{S}{\mathit{h}}_{\mathit{r}\mathit{o}},\mathit{S}{\mathit{h}}_{\mathit{r}\mathbf{1}}$ Sherwood numbers

Sc Schmidt number

T Temperature

T_w Temperature of hot liquid at lower disk

T_H Temperature of hot liquid at lower disk

$\left(\mathit{u},\mathit{v},\mathit{w}\right)$ Components of velocity

$\left(\mathit{r},\mathit{\theta },\mathit{z}\right)$ cylindrical coordinate system

Greek Symbols

$\mathbf{\Omega }$ Rotation parameter

$\mathit{\lambda }$ Porosity parameter

${\mathit{\gamma }}_{\mathit{t}}$ Thermal relaxation time

${\mathit{\gamma }}_{\mathit{c}}$ Solutal relaxation time

${\mathit{\gamma }}_{\mathbf{1}},{\mathit{\gamma }}_{\mathbf{2}}$ Biot numbers

${\mathit{\tau }}_{\mathit{E}}$ thermal relaxation parameter

${\mathit{\tau }}_{\mathit{c}}$ solutal relaxation parameter

$\mathit{\varphi }$ Dimensionless concentration

${\mathit{\phi }}_{\mathbf{1}}$ Volume fraction of Go nanoparticles

${\mathit{\phi }}_{\mathbf{2}}$ Volume fraction of MoS₂ nanoparticles

Ɵ Dimensionless temperature

$\mathit{\mu }$ Dynamic viscosity

$\mathit{\epsilon }$ Pressure variable

$\mathit{\rho }$ Density

${\mathit{\sigma }}^{*}$ Stefan–Boltzmann constant

$\mathit{\sigma }$ Electrical conductivity

$\mathit{\xi }$ Similarity variable

${\mathit{\omega }}_{\mathit{i}}\left(\mathit{i}=\mathbf{1}-\mathbf{5}\right)$ Constant

Subscripts

bf, f Base fluid

nf Nanofluid

hnf Hybrid nanofluid

Superscripts

$\prime$ Derivative w. r. to $\eta$

Abbreviations

NPs Nanoparticles

NFs Nanofluids

HNFs Hybrid Nanofluids

HTR Heat transmission rate

CCM Cattaneo-Christov model

MTR Mass transmission rate

BLR Boundary layer region

MoS₂ Molybdenum disulfide

Go Graphene oxide