- College of Civil Engineering and Architecture, Henan University, Kaifeng, China
Thin-shell dome structures are conventionally built with concrete. However, the building process is time-consuming and of high labor cost. Composite Structural Insulation Panels (CSIPs) have recently been regarded to be suitable for large-span civil structures, in terms of its light weight, easy processing, and mass production. Hence, this paper explores the feasibility of CSIPs domes applied in large-span dome structures. Compared with the performance of thin-shell concrete domes, the stiffness, strength, and stability of CSIPs domes are studied by means of refined finite element analysis. Results demonstrate CSIPs dome possesses good dynamic performance, bears larger nonlinear loads, and even copes with stress loads under earthquakes. Moreover, the stiffness should be handled in the onsite applications to fulfil the safety requirements.
Introduction
Dome structure is one of the most important structural forms in the history of architectural development, which not only meets the demand for large-span architecture, but also enhances the aesthetics of architecture (Mu et al., 2017). And dome structures are often used in public buildings such as stadiums, conference halls, convention centers, botanical gardens, and industrial buildings. Initially dome structures were built by stone, wood, concrete and other materials. Until 1811, the dome structure with steel was developed (Cui et al., 2001). From the 1920s onwards, thin-shell concrete domes were favored by most architects for their reasonable and effective form of force (Popov, 1991). However, thin-shell concrete domes were very time-consuming and slow in construction, and gradually were replaced by new dome structures such as ordinary steel, high-strength steel, aluminum alloy, and cable dome structures. Thus, it can be found that the innovation of building materials has promoted the development of dome structures.
In addition, due to the wide application of dome structure in practical engineering, scholars have conducted extensive research on the performance of dome structures. In terms of the relationship between dome structures and architectural function, Fan (2001) proposed that dome structures could not only meet the need of architectural function for large space, but also be an important factor of art expression. In terms of the rationality of dome structure, Qian et al. (1996) investigated the mechanics and working mechanism of domes and proposed that the most reasonable dome structure should be the thin-shell structure. Yang (2010) mentioned that span was an important factor affecting thin-shell domes. In the analysis of dome structures with different materials, Noh (2005) stated that although the thin-shell concrete structure was a structure with excellent load-bearing performance, the high sensitivity of the shell to initial defects would lead to buckling damage. Zou (2019) stated that the cast-in-place concrete dome structure formwork and its support system were relatively complex, difficult to construct and costly. Dong and Yuan (2008) concluded that it was necessary to improve cable dome construction system in terms of new systems and materials. In terms of research methods, Lan et al. (2017) proved ANSYS software simulations could be used to analyse the performance of thin-shell dome. In summary, the thin-shell dome structure can meet the demand of buildings for large-span space and architectural aesthetics, but the structural rationality, economic factors and construction of different material domes will restrict the development and application of dome structure.
Currently, the Composite Structural Insulation Panels (CSIPs) using E-glass/polypropylene (PP) laminate as the panel and expanded polystyrene (EPS) foam as the core material, as shown in Figure 1A, are receiving more and more attentions. Firstly, due to the high strength-to-weight ratio, excellent impact resistance and high durability, CSIPs panels can take up the bending and axial stresses and prevent buckling or twisting. Secondly, with the application of core materials and its high R-value, CSIPs have better thermal resistance and resistance to shear stress. Thirdly, the fabrication process of CSIPs, as shown in Figure 1B, is more efficient and time-saving, and a large number of high-quality CSIPs can be produced in a short period of time. Finally, the CSIPs panels can be spliced by polyvinyl chloride (PVC) connectors to ensure overall performance. Based on the factors affecting the dome structure, CSIPs are the ideal alternative materials for thin-shell concrete dome structures. However, only a few scholars, including Mousa and Uddin (2010), Uddin and Du (2014), Du et al. (2019), and Yang et al. (2017), have conducted research on the mechanical properties and improvement of CSIPs, and no scholars conducted research on the application of CSIPs in dome structures. Therefore, on the basis of existing research, CSIPs domes are studied by comparing with thin-shell concrete domes through numerical simulations in this paper.
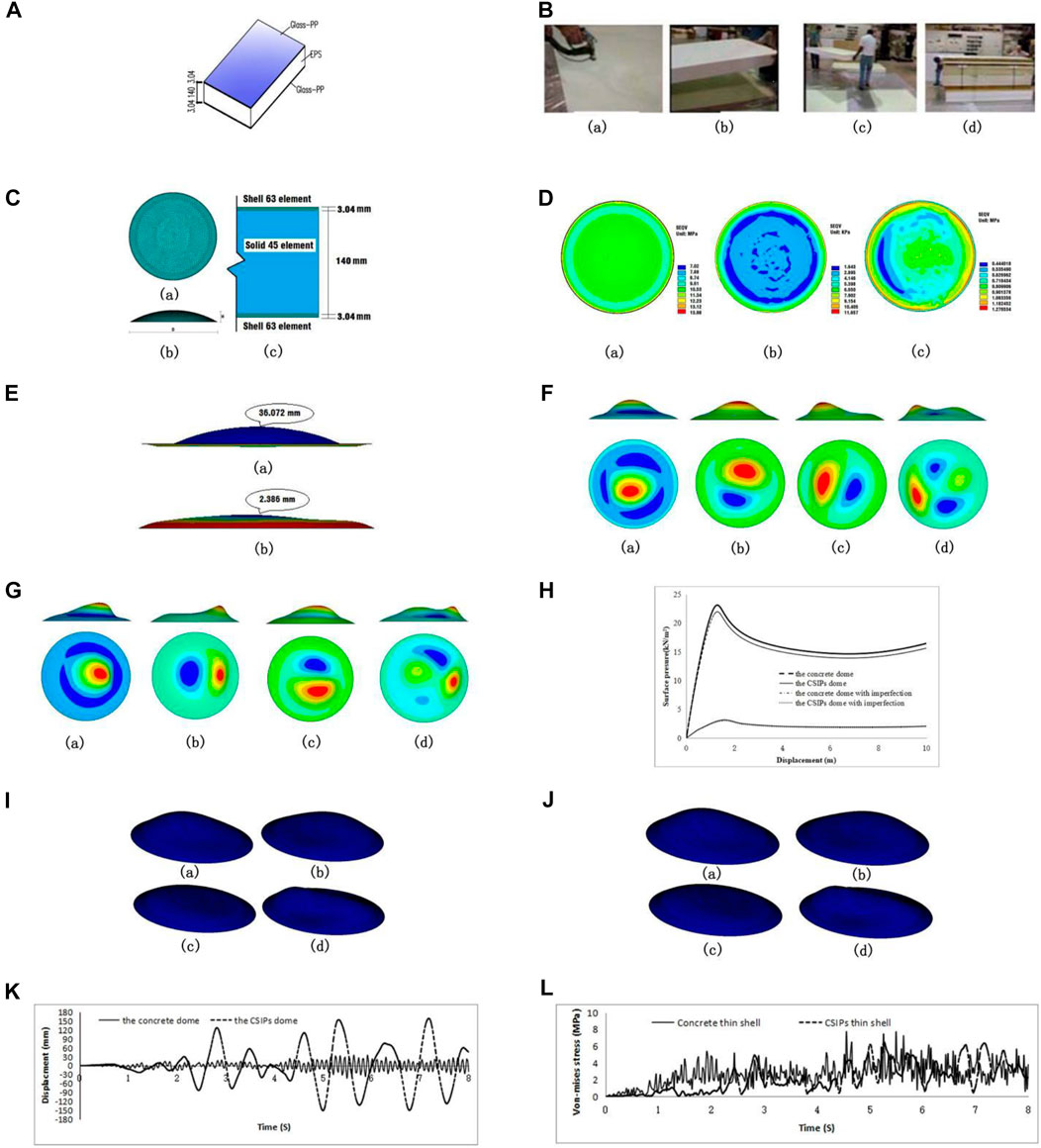
FIGURE 1. (A) Schematic diagram of CSIPs (unit: mm); (B) Manufacturing of CSIPs: (a) spraying hot-melt adhesive bonding agent; (b) placing the foam core on the lower panel sheet; (3) making a piece of completed CSIP; (d) storing the fabricated CSIPs panels; (C) Structural parameters of the finite element model of CSIPs dome: (a) plan; (b) elevation; (c) cross-section; (D) Von-Mises stress: (a) GFRP of CSIPs dome; (b) EPS of CSIPs dome (c) thin-shell concrete dome; (E) Vertical displacements: (a) vertical displacement of CSIPs dome; (b) vertical displacement of thin-shell concrete dome; (F) Top 4 buckling mode shapes of CSIPs dome: (a) first order; (b) second order; (c) third order; (d) fourth order; (G) Top 4 buckling mode shapes of thin-shell concrete dome: (a) first order; (b) second order; (c) third order; (d) fourth order; (H) Vertical displacement versus load curve at the center point; (I) Mode shapes and frequencies of CSIPs dome: (a) first order, f = 1. 1,033; (b) second order, f = 1.1064; (c) third order, f = 1.1307. (d) fourth order, f = 1.5323; (J) Mode shape and frequencies of thin-shell concrete dome: (a) first order, f = 12.065; (b) second order, f = 12,141; (c) third order, f = 12.680; (d) fourth order, f = 16.503; (K) Time-displacement curve of center point under EL-Centro seismic wave; (L) Time-stress curve of element with Maximum Von-mises stress under EL-Centro seismic wave.
Research methodology
Refinement of finite element analysis
The thin-shell dome structure, including CSIPs domes and thin-shell concrete domes, is an elastic system, which reduces the destructive effect of external load on the structure by deformation. However, the thin-shell dome structure will be feasible for buildings only when the structural stability is guaranteed. The structure stability usually includes the geometric stability of the structure, the displacement of the structure and the elastic stability of the structure (Qian and Yang, 2003). The main analysis method of current dome structure is to divide the whole structure into many very small unit elements when the dome structure can be assumed to be a homogeneous continuum structure. Then the strength, stiffness and stability of dome structure can be studied from static analysis, eigenvalue buckling analysis and modal analysis with finite element analysis software (Shen and Chen, 1999). The above-mentioned studies are carried out under ideal conditions, but in actual engineering dome structure often has large deflections and imperfect initial defects, so the performance of the dome structure should be studied by geometric nonlinear analysis to maintain structural stability (Lin and Shen, 1996). In addition, as dome structure is a space structure with obvious performance of deformation, studies show that both horizontal and vertical seismic forces would have a large effect on domes (Cao and Zhang, 1998). Therefore, the dynamic stability of domes under multidimensional seismic forces should be analyzed. Furthermore, the Time-history analysis under earthquakes has the advantage of analyzing the sequence of plastic hinges, and the weakness of the structure, so it is usually used to analyze the dynamic stability of dome structures (Deng and Zhu, 2002).
In this paper, ANSYS 14.0 software is used to analyze performance of CSIPs dome and thin-shell concrete dome. The research program is divided into three processes: selection of the basic dome research model, establishment of the finite element model, and comparative analysis of the strength, stiffness, and stability of the two research domes.
1) The selection of the basic dome research model. The model selection should be representative, which means the calculation should be reduced as much as possible under the condition of ensuring accuracy and the simulation should be able to fully reflect the distribution of the strain state of the dome structures.
2) Establish the finite element model. ANSYS14.0 was used to establish the basic dome research models with uniform loading. The calculation is chosen to stop after the dome reaches the ultimate load in order to save the calculation time. Finally, all the data obtained from the analysis are extracted for analysis.
3) Compare and analyze the performance of the domes with different material parameters. Analyze the performance of CSIPs domes and thin-shell concrete domes in terms of strength, stiffness and stability by comparing the analysis results in five aspects, including static analysis, eigenvalue buckling analysis, geometrical non-linear analysis, modal analysis, and Time-history analysis under earthquakes.
Finite element analysis research model
The research models shown in Figure 1C are geometrically identical CSIPs dome and thin-shell concrete dome. 3.04 mm thickness faceplates were selected for the E-glass/polypropylene laminate and the properties of the laminate and expanded polystyrene (EPS) foam cores are shown in Table 1 (A and B), respectively. Table 1 (C) lists the material properties of thin-shell concrete. The structural parameters of both domes are the same: the span is 60 m, the thickness is 146.08 mm, the vector-to-span ratio is 0.134.
It is assumed that both domes are fixed on supports and there is no relative slip between the faceplates and core materials in CSIPs dome model. The appropriate amount of shell elements could help to improve the efficiency and to ensure the analysis accuracy in ANSYS (Lan et al., 2017). In CSIPs dome model, 26,820 elements are analyzed, compared to 16,260 elements of the thin-shell concrete model we used. In this analysis, the faceplates of the CSIPs dome were simulated using Shell63 elements of the ANSYS while the standard Solid45 elements were used for the EPS foam core and concrete.
Results and discussion
Comparative study of static analysis
Static analysis refers to the static load response of the structure, which responds to the stiffness and load-bearing capacity of the structure. Static analysis is fundamental in structural research. In this paper, in addition to considering the self-weight of the structure, a uniform load of 1 KN/m2 was used for the external forces of the dome. Figure 1D demonstrates that the Von-Mises stress on the adjacent area of the faceplates in CSIPs dome has a maximum value of 13.98 MPa, while the maximum Von-Mises stress on the expanded polystyrene (EPS) foam core is only 11.66 KPa. The Von-Mises stress on the thin-shell concrete dome has a maximum value of 1.28 MPa. This indicates that the faces plates have high compression strength which can bear majority of the external load.
Moreover, the maximum vertical displacement of the CSIPs dome is 36.072 mm, which is much larger than that of thin-shell concrete dome of 2.386 mm (Figure 1E). This indicates that the E-glass/polypropylene laminate and the expanded polystyrene (EPS) foam core, which have a smaller modulus of elasticity, caused the structural stiffness of CSIPs dome to be lower than that of thin-shell concrete dome. Nevertheless, the maximum displacement of the CSIPs dome is about 1/1,663 of the span, which still meets the range allowed by the code. Further analysis shows that, if only gravity is considered, the displacements of CSIPs dome and thin-shell concrete dome are 1.928 mm and 1.889 mm which are close to each other. It indicates that the vertical stiffness of both domes is close when only self-weight is considered.
From the results of the static analysis, the CSIPs dome has the same performance of bearing the external load with thin-shell concrete dome. However, the stiffness of CSIPs dome is much less than that of thin-shell concrete dome. Therefore, for large-span dome structures using CSIPs, it is particularly important to consider the stiffness and to make the structural displacement within the scope of normative permission.
Comparative study of eigenvalue buckling analysis
The eigenvalue buckling analysis can be used to predict the theoretical strength (bifurcation point) of an ideal linear elastic structure. Figures 1F,G, show the first four buckling modes. They present the same buckling modes performance of CSIPs dome and thin-shell concrete dome. The first order buckling mode shapes of both domes are depressed downward in the central region of the dome. The shapes of the second and third order buckling modes are both half-shell up-convex and half-shell down-concave states.
The results of the eigenvalue buckling analysis show that the CSIPs dome has a similar buckling mode shape to the thin-shell concrete dome. It further shows that CSIPs material is suitable for replacing thin-shell concrete material to construct large-span domes and will not lead to significant changes in the stability of domes.
Comparative study of geometrical non-linear analysis
Practical situations such as large deflections and initial defect imperfections can be integrated by non-linear analysis. In ANSYS 14.0, the geometry updated after eigenvalue buckling analysis is usually used to consider imperfections. In terms of geometric defects, the most dangerous geometrically defective structures are configured with first order buckling mode shapes; and 1/1,000 of the span is the maximum deformation value that can be accepted for geometric defects.
Figure 1H presents the results of the geometric non-linear analysis of CSIPs dome and thin-shell concrete dome. From the results, it can be seen that CSIPs dome is subjected to fewer external loads than that of thin-shell concrete dome. The non-linear limit load on CSIPs dome is a uniform surface pressure with a pressure value of 3.17 KN/m2, while the non-linear limit load on thin-shell concrete dome has a value of 23.1 KN/m2. This is caused by the weak expanded polystyrene (EPS) foam core, which does not provide sufficient shear resistance. Further, it can be found that the initial geometric defect reduced the limit load of CSIPs dome from 3.17 KN/m2 to 3.04 KN/m2 with a percentage reduction of 4.1%, respectively, and reduced the limit load of thin-shell concrete dome from 23.1 KN/m2 to 21.9 KN/m2 with a percentage reduction of 5.2%. It indicates that the initial geometric defects have a relatively small effect on both domes to withstand external loads.
Comparative study of modal analysis
The modal analysis could determine the vibration characteristics of a structure. Figures 1I,J show the top 4 modal shapes and frequencies of CSIPs dome and thin-shell concrete dome, respectively.
Figures 1I,J show that the fourth order mode shapes of the CSIPs dome and thin-shell concrete dome are similar. The first order and second order modal shapes are both characterized by one half of the shell is convex upwards, and the other half is concave downwards. The third order and fourth order modal shapes are symmetric vertical vibrations with a two-wave shape. This indicates that the dynamic performance of CSIPs dome is stable and reliable. In addition, the frequencies of CSIPs dome are much smaller than those of thin-shell concrete dome. The fundamental frequencies of both domes are 1.1033 and 12.065, respectively, which are mainly caused by the low material elastic modulus and relatively low stiffness of the CSIPs domes.
Comparative study of time-history analysis under earthquakes
In this study, Firstly, the damping values and seismic load directions are brought into the system, and secondly, use the following equations to calculate the α and β coefficients of Rayleigh damping.
In which ζ represents the constant damping ratio, ζ of CSIPs and thin-shell concrete respectively equal 0.02 and 0.05 (Zhang et al., 2021), α represents the mass matrix multiplier, β represents the stiffness matrix multiplier, and ω represents the structural frequency got from the modalities analysis. Thirdly, vertical acceleration seismic waves with a peak value of 0.2 g were applied to each structural model and linear elastic material models were considered simultaneously.
Figure 1K shows that the maximum dynamic displacement of CSIPs dome is 151.0 mm and the thin-shell concrete dome is 42.3 mm. The deviations between the two values are large, with the former being about 3.6 times larger than the latter. This is due to the lower modulus of elasticity of the CSIPs material. Further, it can be found that the maximum Von-mises stress of the CSIPs dome is smaller than that of the thin-shell concrete dome. The values are 6.45 MPa and 7.72 MPa, respectively (Figure 1L). The former is a little lower than the latter. Finally, the above values indicate that CSIPs domes have better dynamic performance and can better cope with the stress loads under earthquakes.
Conclusion
This paper explores the feasibility of CSIPs domes applied in large-span dome structures. Compared with the performance of thin-shell concrete domes, the stiffness, strength, and stability of CSIPs domes are studied by means of refined finite element analysis. The following conclusion were obtained.
1) Through static analysis, it can be seen that, under the uniform load, the Von-Mises maximum stress value of CSIPs dome is slightly larger than that of thin-shell concrete dome. However, the displacement of CSIPs dome is larger than that of thin-shell concrete dome. This is caused mainly because the CSIPs dome has an advantage of lighter weight. Therefore, for large-span dome structures using CSIPs, it is particularly important to consider the stiffness and to make the structural displacement within the scope of normative permission.
2) The results of eigenvalue buckling analysis show that the buckling mode shapes of CSIPs dome and thin-shell concrete dome are the same, and the modal analysis results show that the first fourth order mode shapes of CSIPs dome and thin-shell concrete dome are also similar. It indicates that CSIPs material can replace the traditional thin-shell concrete material to build the dome and the stability and dynamic of the dome structures will not be significantly changed.
3) The nonlinear analysis of the geometry shows that the initial geometric defects have a relatively small effect on the surface pressure of CSIPs dome and thin-shell concrete dome. The surface pressure of CSIPs dome is much less than that of thin-shell concrete dome. This is due to the fact that the CSIPs core is weak and does not provide sufficient shear resistance. Hence, we can conclude that the overall performance of CSIPs dome is better than that of thin-shell concrete dome.
4) The results of the Time-history analysis under earthquake show that the displacement of CSIPs dome under seismic forces is 3.6 times more than that of thin-shell concrete dome. But the maximum Von-mises stress of CSIPs dome is less than that of thin-shell concrete dome. The reason of the results is that the weight of CSIPs dome is less than that of thin-shell concrete dome. Therefore it is safe to conclude that the CSIPs dome has better dynamic stability under seismic forces.
Furthermore, in this paper, only the selected single model is analyzed in details in the aspect of finite element analysis. Due to the limits of the research level and simulation calculation conditions, the following problems remain to be studied:
1) This study is based on only a single dome model for preliminary analysis between different materials, different spans, rise-span ratio, shell thickness and boundary conditions were not compared.
2) The research is a preliminary analysis under the premise of static stability. Various defects generated during the construction process often have a greater impact on the stability of domes. The influence of various defects in the actual construction on domes needs further analysis.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
CL conceived the idea and wrote the manuscript. LZ reviewed the manuscript. CL and LZ were involved the manuscript discussion and correction.
Funding
This research was supported by the National Science Foundation in China (NSFC) as a part of the research project (U1704141) and the project was supported by the Foundation of Zhejiang Provincial Key Laboratory of Space Structures (202106).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cao, Z., and Zhang, Y. G. (1998). Seismic response analysis of single-layer spherical mesh shell. Build. Struct. 8, 40–43. doi:10.19701/j.jzjg.1998.08.011
Cui, X. Q., Guo, Y. L., and Zhu, Z. Y. (2001). Dome structural system. Spat. Struct. 7 (1), 3–10. doi:10.13849/j.issn.1006-6578.2001.01.001
Deng, J., and Zhu, Y. P. (2002). A review of research methods on seismic performance of mesh and shell structures. Constr. Budg. 1, 37–38. doi:10.13993/j.cnki.jzyys.2002.01.012
Dong, S. L., and Yuan, X. F. (2008). Advances in research on cable domes. J. Zhejiang Univ. Eng. Sci. 42 (1), 1–7. doi:10.3785/j.issn.1008-973X.2008.01.001
Du, W. F., Liu, Q., Zhou, Z. Y., and Uddin, N. (2019). Experimental investigation of innovative composite folded thin cylindrical concrete shell structures. Thin-Walled Struct. 137 (1), 224–230. doi:10.1016/j.tws.2019.01.014
Fan, Z. H. (2001). Artistic form of expression of structure in architecture. J. Beijing Inst. Civ. Eng. Archit. 17 (1), 59–64. doi:10.3969/j.issn.1004-6011.2001.01.011
Lan, Y. Q., Xue, S. D., Li, X. Y., and Geng, L. (2017). Analysis on static behavior of levy rigid bracing domes. Spatital Struct. 23 (2), 22–29. doi:10.13849/j.issn.1006-6578.2017.02.022
Lin, Y. J., and Shen, S. Z. (1996). Stability of K6 single layer reticulated shells. J. Harbin Univ. C. E. Archit. 30 (2), 39–44.
Mousa, M., and Uddin, N. (2010). Debonding of composites structural insulated sandwich panels. J. Reinf. Plast. Compos. 29, 3380–3391. doi:10.1177/0731684410380990
Mu, Z. G., Yang, Y. Q., Ge, P., and Zhang, X. Y. (2017). “Analysis on the economic impact factors of the long-span spatial structure type selection,” in Proceedings of the 26th National Conference on Structural Engineering, Changsha, China, February 2, 2017, 75–82.
Noh, H. C. (2005). Ultimate strength of large scale reinforced concrete thin shell structures. Thin-Walled Struct. 43 (9), 1418–1443. doi:10.1016/j.tws.2005.04.004
Popov, E. P. (1991). Progress in analysis and design of RC shells. Eng. Struct. 13 (2), 128–143. doi:10.1016/0141-0296(91)90047-g
Qian, R. J., Shen, Z. Y., Xia, S. H., and Hong, X. Q. (1996). Structure concepts and mechanisms of tensegrity system. Spat. Struct. 2 (3), 2–7. doi:10.13849/j.issn.1006-6578.1996.03.001
Qian, R. J., and Yang, L. P. (2003). Analysis, design and construction of tensioned structures. Nanjing: Southeast University Press, 160.
Shen, S. Z., and Chen, X. (1999). Stability of the mesh shell structure. Peking: Science Press, 88–92.
Uddin, N., and Du, W. F. (2014). New thin shells made of composite structural insulated panels. J. Reinf. Plastics Compos. 33 (21), 1954–1965. doi:10.1177/0731684414549492
Yang, L. L. (2010). Structural response changes of thin-shell domes of different spans under seismic effects. Mass Technology 11, 19.
Yang, X., Du, W. F., Liu, C. Y., and Sun, Y. (2017). Mechanical properties and experimental researches of new CSIPs sandwich panels. J. Henan Univ. Sci. 47 (3), 358–365. doi:10.15991/j.cnki.411100.2017.03.014
Zhang, F., Du, W. F., and Zhang, H. (2021). A novel bionic-based substructure division method for topology optimization. Structures 29 (4), 937–946. doi:10.1016/j.istruc.2020.11.061
Keywords: composite structural insulation panels, large-span domes, numerical simulation, simulation analysis, application
Citation: Liang C and Zhu L (2022) A case study on dome structure of composite structural insulation panels with ANSYS simulations. Front. Mater. 9:1072600. doi: 10.3389/fmats.2022.1072600
Received: 17 October 2022; Accepted: 18 November 2022;
Published: 30 November 2022.
Edited by:
Huan Qi, Zhejiang University of Technology, ChinaCopyright © 2022 Liang and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liming Zhu, bGltaW5nemh1MTk4MEB0b20uY29t
 Chunhang Liang
Chunhang Liang Liming Zhu
Liming Zhu