
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 21 November 2022
Sec. Structural Materials
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.1061297
This article is part of the Research Topic Advanced Steel and Composite Structures in Civil Engineering Volume II View all 6 articles
In this research work, different combinations of normal strength concrete (NSC), ultra-high-performance concrete (UHPC), and steel fiber-reinforced UHPC (SFR-UHPC) concrete with re-bars of conventional steel and of carbon fiber-reinforced polymer (C-FRP) are used in a two-way square slab of size 1000mm x 1000mm x 75mm subjected to 2500 mm free-fall impact loading. Experimental arrangement consisting of 105 kg dropping weight with the circular flat impacting face of 40 mm diameter used for carrying out impact test is modeled using a high-fidelity physics-based finite element computer code, ABAQUS/Explicit-v.6.15. After validating the experimental results of the NSC slab with steel bars, analyses are extended by replacing NSC and steel bars with UHPC/SFR-UHPC and C-FRP bars, respectively, under the same dropping weight. Only the remote face (tension face) of the slabs is provided with the re-bars. Widely employed and available with the ABAQUS, the Concrete Damage Plasticity model with strain-rate effects has been entrusted for simulating the concrete plastic response. Re-bars of steel are idealized with the Johnson-Cook plasticity damage model. C-FRP re-bars are defined with the classical plasticity model following the elastic-plastic constitutive laws. The impact responses of the slabs consisting of NSC/UHPC/SFR-UHPC concrete with re-bars of steel, and C-FRP combinations considered are discussed and compared. Slabs made of UHPC/SFR-UHPC concrete with the C-FRP re-bars are found to offer a promising combination of materials to withstand low-velocity impact load with little damage and extraordinary impact performance.
Impulsive loadings on reinforced concrete structures are found to be commonly acting from projectile generated by tornados, blasts, accidental explosions, earthquakes, sea waves, and crashing of aircraft/helicopters (Yılmaz et al., 2018). Such loadings have a high magnitude and act over a small duration thereby causing a high strain rate in the materials. Impact loads particularly generated from rolling boulders by landslips, wind, or ground vibrations produced by heavy machines/earthquakes act on certain elements of a structure (Yılmaz et al., 2018). In comparison to quasi-static gravity/lateral loads, these loads are more detrimental to cause severe structural damage by developing strain rate in the materials along with the inertia effect. Current design standards do not have the provisions for impact loading on structures (Yılmaz et al., 2018). Rather the effect of impulsive loading is considered with richer specifications of the material’s strength. However, specifications for minimum impact load are not available. It is because of a lack of comprehensive understanding of structural response under impact loading. With the advent of UHPC, SFR-UHPC, and very high strength reinforcing bars made of C-FRP, these materials should be used to excel the impact response and damage resistance of the structural elements and control the disproportionate or catastrophic failures of the structure (Ruano et al., 2015; Hu et al., 2021).
RC slabs are thin plates and their thickness is governed by the limit state of serviceability-deflection criterion (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). More often they are singly reinforced with much less reinforcement than their limiting percentage of steel irrespective of their use in interior or exterior portions of the building structures (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c).
Response of the structural elements such as RC slabs under impact loading depends upon a number of parameters like geometry, boundary conditions, the strength of concrete and reinforcing material, percentage and orientation of the reinforcements, and nature of impact loading (low, moderate, and high-velocity) (Abbas et al., 2004; Zineddin and Krauthammer, 2007; Chen and May, 2009; Fareed, 2018; Anas et al., 2022a). The RC slabs being thin structural elements are susceptible to flexure and two-way shearing modes of failure and get damaged through phenomena of perforation/penetration and scabbing under projectile as well as drop-weight impacts (Abbas et al., 2004; Zineddin and Krauthammer, 2007; Chen and May, 2009; Fareed, 2018; Anas et al., 2022a). The most frequent impact situations in civil engineering are low-velocity, high-mass loads with speeds up to 10 m/sec. Transportation structures exposed to vehicle crashes, massive drop weights, airport runway platforms during aircraft landing, and offshore structures exposed to ice and/or ship impact were some examples of typical low-velocity impact scenarios. Also connected to low-velocity impact is impulsive loading brought on by natural disasters like earthquakes, landslides, and tornadoes.
To comprehensively understand the load-carrying phenomenon and response of RC slabs, a large number of experiments is required to be performed on slabs under impact loading which needs well organized strong laboratory setup equipped with sensors/transducers, gauges, data logger, and highly skilled technical support other than the requirement of the materials involving huge financial support (Abbas et al., 2004; Zineddin and Krauthammer, 2007; Chen and May, 2009; Fareed, 2018; Anas et al., 2022a). However, the finite-element method based numerical approach having conducted a few experiments only is being popularly followed by researchers (Chen and May, 2009; Anas et al., 2022a).
Striking of the rolling boulders from the top of the hills due to high-velocity wind, heavy rainfall, shelling from across the border, and seismic movement of the ground, on to the slabs of the nearby structures is quite common (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). Such incidents are more frequent in hilly terrain regions in close proximity to the rivers or water bodies having poor geological conditions/media (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c).
Concrete floors of a building quite often suffer from damage caused by the impact of falling rigid objects, explosion-induced flying debris, and vehicle accidents (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). Collapsing load of a floor under gravity may develop a large transient dynamic load on the lower slab. Also, the failure of a slab due to an explosion on it may cause a high-velocity impact on the lower slab.
A good number of studies have been done by the researchers in past years to examine the low- and high-velocity impact performance of RC slabs (Kojima, 1991; Kishi et al., 1997; Abbas et al., 2004; Zineddin and Krauthammer, 2007; Chen and May, 2009; Saatci and Vecchio, 2009; Kishi et al., 2011; Elavenil and Knight, 2012; Mokhatar and Abdullah, 2012; Erdem, 2014; Kuhn and Curbach, 2015; Sudarsana et al., 2015; Othman and Marzouk, 2016; Erdem and Gücüyen, 2017; Shaheen et al., 2017; Fareed, 2018; Sadraie et al., 2019; Erdem, 2021; Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). Apart from this, parametric studies considering thickness of slab (Anas et al., 2022b), strength of concrete (Sudarsana et al., 2015), percentage of steel (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019), shear reinforcement (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019), reinforcement orientation (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019), impact velocity (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019), drop-mass (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019), drop-height (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019), impactor geometry (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019), and opening in the slab (Othman and Marzouk, 2016; Shaheen et al., 2017; Sadraie et al., 2019). Miyamoto et al. (1991a); Miyamoto et al. (1991b), in an experimental study, found that shear mechanisms dominate the response of RC slabs under impact loading and the failure load is greatly associated with the rate of loading. A failure envelope was also developed based on the load-deflection response of RC slabs under impact. It was also observed that increasing the rate of loading caused a failure mode change from flexure-shear to two-way shearing. When compared to the elements’ equivalent quasi-static reaction, Saito et al. (1995) similarly observed an increase in the failure load of various RC structural components exposed to high-velocity impact. The deformation and damage mode changed as well. Delhomme et al. (2007) performed drop-weight experiments on RC slabs and discovered that bending failure occurs during the very first stage of impact, when the impactor makes contact with the slab. This results in an increase in slab stiffness that is equivalent to the impact noted by Hughes and Beeby (1982) and Cotsovos and Pavlovi (2008); Cotsovos (2010). In order to better understand the impact response of RC slabs, several approaches such as single-degree-of-freedom system, energy conservation models, and artificial neural networks have been utilized by a number of researchers (Zhao et al., 2010; Stochino and Carta, 2014; Pham and Hao, 2016; Pham and Hao, 2018). However, the load-carrying mechanism of the slab under impact is not yet well understood.
Fiber-reinforced concrete is increasingly being utilized in construction for its enormous strength, hardness, good energy absorption capacity, cracking resistance, durability, excellent ductility and it also imparts high stiffness to the structure. The use of fibers greatly enhances the tensile, fatigue, flexural, and shear strengths of the concrete (Gao et al., 1997; Zollo, 1997; Song and Hwang, 2004). Furthermore, the addition of fibers to concrete lessens brittleness and changes the mode of damage (Gao et al., 1997; Zollo, 1997; Song and Hwang, 2004).
Grdh and Laine (1999), in a FEM-based study using LS-DYNA, simulated the projectile impact effect on an FRC slab subjected to free-fall load with an impact velocity of 1500 m/s. Subsequently, Huang et al. (2005) performed a computational analysis in LS-DYNA code to study the bullet penetration effect on the RC slab, 610 mm × 610 mm x 178 mm. The crater sizes on the impacting and remote faces of the slab as well as residual velocities were computed, and the effect of steel bar mesh on the concrete slab perforation was investigated. Tham (2006) in AUTODYN code estimated the penetration depth and stress response of concrete slab subjected to impact loading. Rao et al. (2010), in an experimental study, investigated the effect of fiber volume (8%, 10%, and 12%) and reinforcement on the impact resistance of 600 mm × 600 mm x 50 mm two-way SIFCON slab, and compared its performance with FRC, RC, and PCC slabs under the identical impact load. It was reported that the SIFCON slab with conventional steel bar mesh showed higher energy absorption capacity than the other slabs, and the energy absorption capacity significantly increases with the increase of fiber volume. Song et al. (2004) found that steel FRC concrete outperformed non-fibrous concrete in static impact resistance tests. Ramakrishna and Sundararajan (2005) exposed cement mortar slabs to impact loading after reinforcing them with four different types of natural fibers: (1) coir, (2) sisal, (3) jute, and (4) Hibiscus cannabinus. The results demonstrate that adding fibers enhances impact resistance by 4–15 times that of the plain slab without fibers, and coir fiber outperforms the other four fibers. Teng et al.( 2004) established a finite element analysis based methodology for evaluating the impact response of RC slabs. Dancygier et al. (2007) investigated the behavior of high-strength concrete plates to non-deforming bullet impact. Lee et al. (2003) used the Impact-Echo technique to determine the concrete velocity–strength relation.
Numerous studies (Yon et al., 1992; Malvar and Ross, 1998; Lambert and Allen Ross, 2000; Grote et al., 2001; Li and Meng, 2003; Weerheijm and Van Doormaal, 2007; Kumar et al., 2022; Srivastava et al., 2022) have found that the pace of loading improves concrete’s tensile and compressive strengths. Cotsovos and Pavlovi (2008) provide an in-depth analysis of experimental studies pertaining to the enhancement of concrete strength with loading rate. The effect of strain rate on the strengths and modulus of concrete can be estimated as per fib Model Codes 1990 and 2010 (International Federation for Structural Concrete, 20102010). It is important to take into account how steel is affected by loading rate (Safaei, 2020; Shi-ju et al., 2020; Yi et al., 2020; Chen et al., 2021; Li et al., 2021; Safaei, 2021; Safaei and Nuhu, 2022). The research that is currently available (Campbell, 1953; Mainstone, 1975) shown that steel’s yield strength increases with the rate of loading. The model by Malvar and Crawford (1998) offers empirical relationships that show that steel’s yield strength increases with loading rate.
Resilience is the latent requirement of the structure against possible extreme loadings for safety and longevity against damage (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). Therefore, it necessitates to assess the response of the structure under such loadings to improve structure design philosophy (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). Understanding of the structure behavior subjected to impact loading is still in its infancy, nonetheless, development in this area is spurred by a wide range of engineering applications such as vehicular collisions with structures, aircraft crash loading on structures, the impact of projectiles, and impact of falling boulder/rock, etc.
The research work presented herein is divided into five main sections: section one discusses the background, review of the latest literature, and research significance; section two will discuss the description of the problem, the novelty of the work, and the methodology used; section three discusses on finite element modeling and validation of the RC slab subjected to low-velocity impact load; the fourth section deals with the discussion of the computational results in terms of peak displacement, principal stresses, peak acceleration, and damage profiles; and the last section highlights the major outcomes and practical application of the study.
A 105 kg steel weight was dropped onto the centroid of a reinforced concrete slab, 1,000 mm × 1,000 mm x 75 mm, at a height of 2,500 mm by Sadraie et al. (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c) as part of an experiment to determine how concrete would react in terms of damage. The experiment involved casting and testing 15 slabs, of which 2 were made of plain concrete, five had traditional steel reinforcement with different ratios, six had G-FRP bars mesh reinforcement, and 2 were 100 mm thick and had steel bar mesh only. Increases in the steel ratio or slab thickness, together with the performance of the G-FRP-reinforced slab above the steel-reinforced slab, were observed to increase the impact resistance of the slab.
Understanding the behaviour of RC components under impact load is particularly important for both the designing phases as well as any retrofitting opportunities later on in order to avoid disastrous implications of potential low-velocity impact occurrences. The current study emphasizes numerical investigation that focuses on the application of ultra-high-performance concretes (UHPC and SFR-UHPC) and high strength C-FRP tension reinforcement in slabs under free-fall impact loading.
Ultra-high-performance concrete (UHPC) is finding its application gradually increased for strengthening/retrofitting and construction of certain structural elements because of its superior characteristics with respect to strength, durability, toughness, cracking resistance, etc. Other reinforcing materials than conventional steel such as fiber-reinforced polymer are also not uncommon and need to be combined with UHPC to make CFRP-reinforced UHPC components like slabs to withstand low-velocity impact loads. Available Codes of Practice give no mention of such high-performance materials to design the slabs under impact loading. Investigations on the application of high-performance materials in the slabs to safely carry the impact load are of considerable interest.
Different approaches for investigating the response of RC slabs under impact loading conditions draw interest from many researchers (Anas et al., 2021a; Anas et al., 2022a). The most common numerical technique, Finite Element Method (FEM), is employed by many researchers to analyze structures under various types of dynamic loading conditions such as blast, impact, and wind. Therefore, the FEM investigations performed by researchers are presented herein.
ABAQUS/Explicit, a computer program, is used to carry out computational analysis utilising the FEM approach (ABAQUS, 2020). ABAQUS/Explicit is a finite element analysis product that is particularly well-suited to simulate brief transient dynamic events such as consumer electronics drop testing, automotive crashworthiness, and ballistic impact (Safaei, 2020; Shi-ju et al., 2020; Yi et al., 2020; Chen et al., 2021; Li et al., 2021; Safaei, 2021; Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c; Safaei and Nuhu, 2022). In order to mimic the impact experiments performed by Sadraie et al. [23], a three dimensional model consisting of an RC slab, a steel impactor, supporting beams, and columns is first created (Figure 1). The computed outcomes are then contrasted with the test findings that are already accessible. The verified slab model is also used in the parametric research.
Seven FE models of RC slabs with dimensions of 1,000 mm by 1,000 mm by 75 mm are used in the numerical analyses conducted herein, as shown in Table 1. The first model has a slab of strength 29.70 MPa reinforced with 8 mm diameter steel tension bar mesh of static yield strength 422 MPa at 100 mm c/c with 10 mm clear cover and percentage of steel 0.88%, Figures 2, 3A. This model is known as the control model, where each slab model is exposed to an identical impact load of 1035N at the center. The second and third slab models are having the reinforcement and its layout of the first model but with UHPC (99.50 MPa) and SFR-UHPC (149.50 MPa) concrete, respectively (Figure 3B,C). The next model is of NSC slab reinforced with the C-FRP re-bar mesh of 4.66 mm diameter of ultimate strength 1240 MPa at 100 mm c/c, Figure 3D. This model is made with an area of the C-FRP reinforcement equivalent to that of the steel provided in the first model. The fifth model is the prototype of the first model but with a difference in that the tension steel reinforcement is replaced by the C-FRP reinforcement of 8 mm diameter, Figure 3E. The last two slab models namely the sixth and seventh, have been obtained from the fifth model by replacing the NSC with UHPC and SFR-UHPC concrete, respectively (Figures 3F,G). A 1035N impact load is applied to the centroid of each slab model in the same way.
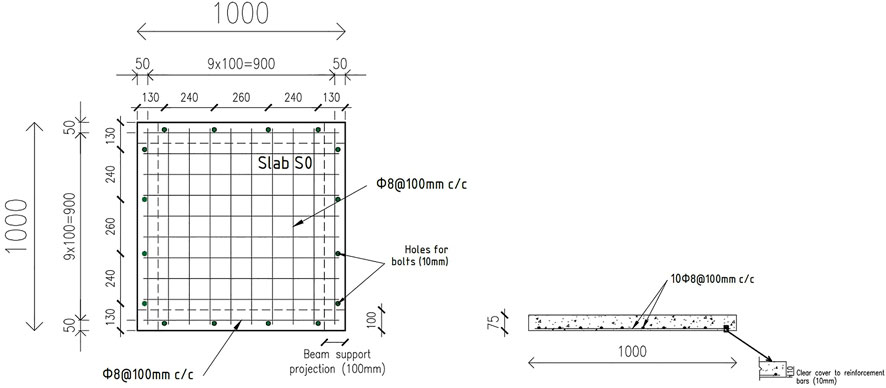
FIGURE 2. Details of reinforcement of the control model “S-NSC-Steel8”, adapted from (Sadraie et al., 2019; Anas et al., 2022a; Anas et al., 2022b).
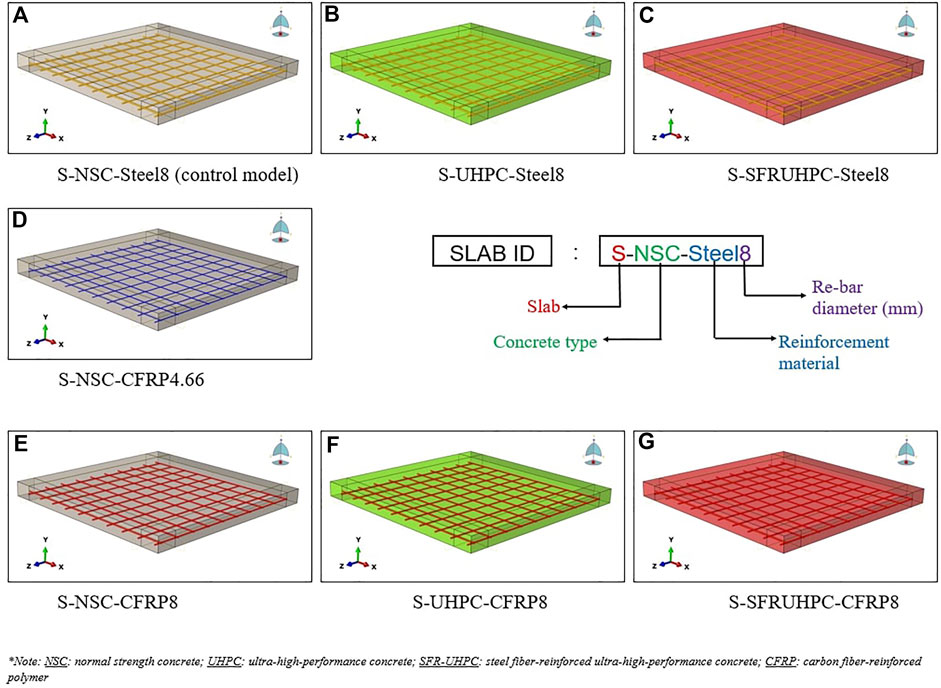
FIGURE 3. Slab models developed in ABAQUS explicit code. (A) S-NSC-Steel8 (control model). (B) S-UHPC-Steel8. (C) S-SFRUHPC-Steel8. (D) S-NSC-CFRP4.66. (E) S-NSC-CFRP8. (F) S-UHPC-CFRP8. (G) S-SFRUHPC-CFRP8.
The constructed finite element model utilized in this investigation is depicted schematically in 3-D rendered form in Figure 1. Except for the tension reinforcements, which are specified using 2-node beam elements (B31), the FE model is discretized using 8-node solid elements (C3D8R) of the explicit kind, more details of these elements are available in (ABAQUS, 2020). The slab is supported on a support system consisting of I-beams and columns, reported in (Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). The columns have their base fixed. Default interactions in the ABAQUS code have been used to define the contact between beams and columns and between the impactor and the slab. Hinges have been introduced between the common nodes of the slab and supporting beams through connecting bolts used by Sadraie et al. (2019) for stable boundary conditions of the slab. The boundary conditions that are taken into account and how they are described are the same as those in Refs [Anas and Alam, 2022a; Anas et al., 2022a; Shaheen et al., 2017]. Under free-fall conditions, the impactor is prevented from striking the slab by its sole translation in the vertical direction (-Y). Through a mesh sensitivity test, the proper element size for the slab has been determined. From Figure 4, the peak displacement increases with an increase in the finite element size. The slab with 10 mm size has a peak displacement of 27.31 mm (3% higher than experimental) while the 20 mm FE size shows a much higher displacement of 33.94 mm (25% higher than experimental). The 15 mm element size results in a peak displacement of 30.31 mm (11% higher than experimental). Thus, the 10 mm element size, with a difference of 3% in peak displacement, is deemed reasonable to predict the response of the slab in terms of peak displacement under the considered impact load. With reference to Figure 4, the mode of damage caused by punching shear, which includes the failure of the bond between embedded steel and surrounding concrete as well as the development of diagonal cracks and maximum displacement, closely matches and is in perfect agreement with the experimental findings of Sadraie et al., 2019) using 10 mm finite elements.
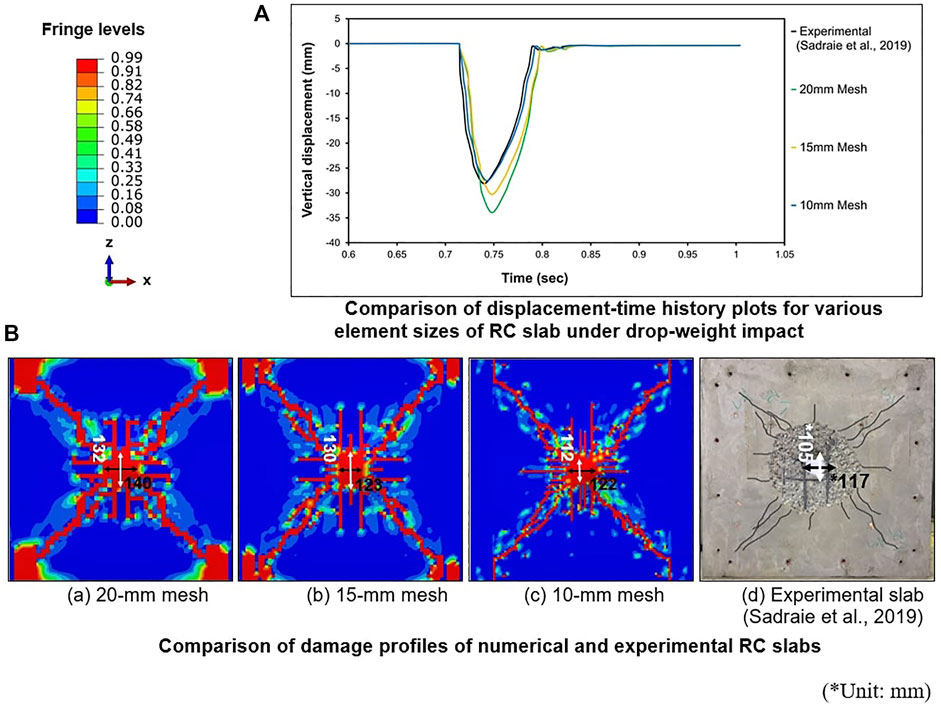
FIGURE 4. Comparison of computational results with Sadraie et al. (Sadraie et al., 2019) experimental observations for control slab model “S-NSC-Steel8”. (A) Comparison of displacement-time history plots for various element sizes of RC slab under drop-weight impact. (B) Comparison of damage profiles of numerical and experimental RC slabs.
Default constraint keycard in (ABAQUS, 2020) is selected to represent a flawless connection between the steel mesh and concrete. Applying drop-weight eliminates the possibility of any restitution since the slab top surface is deemed to be in close contact with the impacting instrument. Surface interaction keyword, which is used to specify the connection between the impacting device and the RC slab, is one of the default interactions that connects the geometric elements of the impacting test setup model. Defining the slab as the “slave surface” in ABAQUS and the hitting device as the “master surface”. References (Sadraie et al., 2019; ABAQUS, 2020; Anas et al., 2022a; Anas et al., 2022b) provide more details on the keycards used. In addition, while designing the contact surfaces, a little amount of friction with a coefficient of 0.02 is taken into account.
Time steps or increments are important for the outcomes since the problem is dynamic and nonlinear, reported in (Anas et al., 2022a; Anas et al., 2022b). The authors have utilised an explicit dynamic module of the software, which automatically determines the time step/increment, to reduce the amount of time the programmes need to execute. For this study, a step time that is a tiny bit longer (1.0 s) than the length of free fall (0.71 s) is taken into account.
Previous studies have demonstrated that the inertia effect, as opposed to the strain-rate effect, has a greater positive impact on a material’s strength properties (Kojima, 1991; Kishi et al., 1997; Abbas et al., 2004; Zineddin and Krauthammer, 2007; Chen and May, 2009; Saatci and Vecchio, 2009; Kishi et al., 2011; Elavenil and Knight, 2012; Mokhatar and Abdullah, 2012; Erdem, 2014; Kuhn and Curbach, 2015; Sudarsana et al., 2015; Othman and Marzouk, 2016; Erdem and Gücüyen, 2017; Shaheen et al., 2017; Fareed, 2018; Sadraie et al., 2019; Erdem, 2021; Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c). Further highlighting the effects of the inertia effect on the RC slab’s impact resistance are references (Anas et al., 2022a; Anas et al., 2022b). The software’s built-in explicit module is used to take the inertia effect into consideration.
Each of the geometric components, including concrete, reinforcing steel/CFRP, impactors, and supporting beams/columns, is given the sectional elastic and plastic characteristics required in the ABAQUS code. Similar to what was stated in (Zhao et al., 2019), C-FRP reinforcement bars have an ultimate strength of 1240MPa, an elastic modulus of 120GPa, and an ultimate strain of 1.07%. UHPC and SFR-UHPC concretes have static elastic moduli of 51 GPa and 63GPa, respectively (Anas et al., 2022d). Static tensile strengths for UHPC and SFR-UHPC concrete are 11.34 MPa and 19.50 MPa, respectively. In Refs. (Sadraie et al., 2019; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022d), the given attributes are further described. Numerous studies (Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022d; Ahmadi et al., 2021; Anas et al., 2020a; Anas et al., 2020b; Anas et al., 2020c; Anas and Ansari, 2021; Anas et al., 2021a; Anas et al., 2021b; Anas and Alam, 2021; Anas et al., 2021c; Anas et al., 2021d; Anas et al., 2021e; Anas et al., 2021f; Anas and Alam, 2022b; Anas and Alam, 2022c; Anas et al., 2022e; Anas et al., 2022f; Anas et al., 2022g; Anas et al., 2022h; Anas et al., 2021g; Shariq et al., 2022a; Tahzeeb et al., 2022a; Tahzeeb et al., 2022b; Tahzeeb et al., 2022c; Ul Ain et al., 2021; Ul Ain et al., 2022; Anas et al., 2022i; Anas et al., 2022j; Ahmadi et al., 2022; Shariq et al., 2022b; Shariq et al., 2022c; Shariq et al., 2022d; Anas et al., 2022k; Anas and Alam, 2022d; Anas et al., 2022m; Anas et al., 2022n; Shariq et al., 2022e; Anas et al., 2022o; Anas et al., 2022p; Shariq et al., 2022f; Anas and Alam, 2022e; Shariq et al., 2022g; Anas et al., 2022q; Shariq et al., 2022h; Anas et al., 2022r) employ the Concrete Damage Plasticity (CDP) model, which takes the strain-rate effect into account. A damage plasticity model can be used to describe the mechanical behavior of concrete. The program ABAQUS was adopted to build a damage plasticity model of concrete. This model required definition of the material's uni-axial constitutive relationships and the damage parameters. In order to define concrete plasticity properties and forecast damage to the slab under impact load, Model Code 2010 was used. The CDP model uses tension and compression damage parameters (dt and dc, respectively), to capture any degradation in strength and stiffness. dt and dc can take values from zero to one. Zero represents the undamaged material state where one represents totally damaged material with no stiffness left. There is a thorough explanation of the CDP in Ref. (Yılmaz et al., 2018; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022d; Ahmadi et al., 2021; Anas et al., 2020a; Anas et al., 2020b; Anas et al., 2020c; Anas and Ansari, 2021; Anas et al., 2021a; Anas et al., 2021b; Anas and Alam, 2021; Anas et al., 2021c; Anas et al., 2021d; Anas et al., 2021e; Anas et al., 2021f; Anas and Alam, 2022b; Anas and Alam, 2022c; Anas et al., 2022e; Anas et al., 2022f; Anas et al., 2022g; Anas et al., 2022h; Anas et al., 2021g; Shariq et al., 2022a; Tahzeeb et al., 2022a; Tahzeeb et al., 2022b; Tahzeeb et al., 2022c; Ul Ain et al., 2021; Ul Ain et al., 1007). The analysis makes use of previous research information on NSC, UHPC, and SFR-UHPC concrete found in References (Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022d). For the steel reinforcement, the Johnson-Cook model is employed as reported in (ABAQUS, 2020), but for the C-FRP reinforcement, the elastic-plastic constitutive law is applied. To simulate the load transfer between cracks through the rebar, the effects associated with the rebar-concrete interface were modeled approximately by introducing tension stiffening into the tensile stress-strain relationship of the concrete. The dynamic increase factors (DIFs) utilised in References (Anas et al., 2022a; Anas et al., 2022b) are in accordance with fib Model Code R2010 (International Federation for Structural Concrete, 20102010) and were used to take into account the strain rate influence on the strength of the materials employed in the study. It is important to note that the studies conducted in this study only take into account the first effect of free-fall and do not account for rebound consequences.
Control slab behavior under impact load: 1) the slab has very little movement and carries its own weight before the drop-weight force is applied., 2) the slab reacts as a temporary elastic tension membrane when the impacting object makes contact with the top surface, 3) When the concrete under and surrounding the affected region cracks severely, the reinforcing bars break, which causes the impactor to penetrate the concrete, followed by perforation, this causes the slab’s stiffness to degrade as the cracks spread before the reinforcement yields, 4) when the re-bars begin to give, diagonal fractures begin to form and spread from the edge of the affected region, 5) instantaneous movement of the slab accelerates the creation and fast propagation of yield lines, and 6) this loosened concrete is thrown out of the ground due to severe cracking beneath the impacting pressure, rupturing of the bars, and maximal displacement. A report on this slab’s impact resistance mechanism may be found in References (Abbas et al., 2004; Zineddin and Krauthammer, 2007; Anas and Alam, 2022a; Anas et al., 2022a; Anas et al., 2022b; Anas et al., 2022c).
Variation of Y-displacement with a time of the slabs is represented in Figure 5. The peak Y-displacements are given in Table 2. The displacement contours are shown in Figure 6. The peak displacement of the control slab S-1 is 27.31 mm at the impacted region.
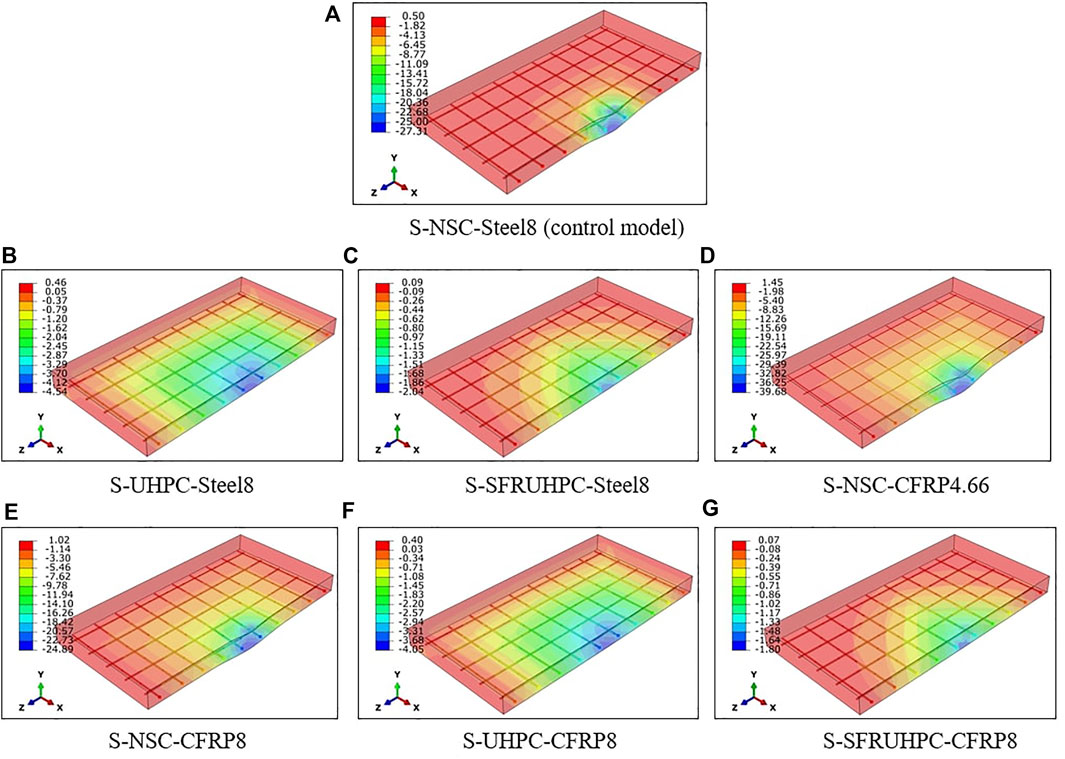
FIGURE 6. Y-displacement (mm) contour of the slabs. (A) S-NSC-Steel8 (control model). (B) S-UHPC-Steel8. (C) S-SFRUHPC-Steel8. (D) S-NSC-CFRP4.66. (E) S-NSC-CFRP8. (F) S-UHPC-CFRP8. (G) S-SFRUHPC-CFRP8.
From Table 2, it is found that the peak displacement value of slabs S-2 and S-3 made of UHPC and SFR-UHPC concrete, respectively, with embedded steel bars of 8 mm diameter is much lower than that of the control slab S-1 made of NSC with the steel bars. Slab S-2 made with UHPC exhibits 83% lesser displacement than slab S-1. The maximum displacement of slab S-3 is 93% lower than that of slab S-1. This increase in stiffness of the slabs is attributed to the enormous strength and modulus of the UHPC and SFR-UHPC concretes. Severe kind of localized damage in slab S-1 i.e., perforation, cracking, and steel yielding, is not encountered in slabs S-2 and S-3. The very high shear strength of UHPC/SFR-UHPC concrete controls localized shear failure and prevents penetration of the impactor into the slab. Accordingly, the normal stress in the re-bars of slabs S-2 and S-3 is much lesser than in the re-bars of slab S-1, Figure 7.
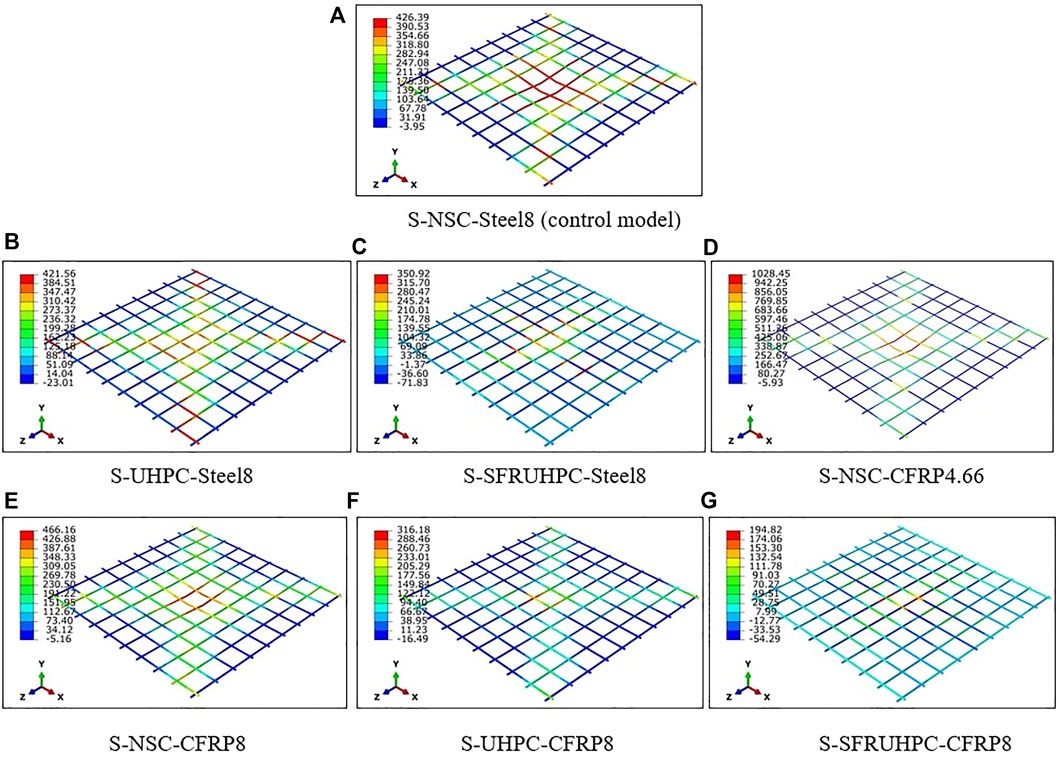
FIGURE 7. Principal stress (MPa) contour of the reinforcing bars (+ve values indicate tensile stress). (A) S-NSC-Steel8 (control model). (B) S-UHPC-Steel8. (C) S-SFRUHPC-Steel8. (D) S-NSC-CFRP4.66. (E) S-NSC-CFRP8. (F) S-UHPC-CFRP8. (G) S-SFRUHPC-CFRP8.
Computed normal stress profiles of the concrete of the slabs are shown in Figures 8, 9. Referring to Figure 10, it is observed that scabbing of concrete in UHPC and SFR-UHPC slabs i.e., S-2 and S-3, is on account of the flexural bond failure under the impacted area. Moreover, this failure occurs at much higher compressive stress of concrete (>>fc) in slabs S-2 and S-3 than in slab S-1, Figure 8. Replacing the steel bars of slab S-1 with an equivalent area of the C-FRP bars in slab S-4 increases the displacement, cracking, and DDE on account of decreased percentage of tension reinforcement. From Table 2, the respective maximum displacement values of slabs S-5 to S-7 i.e., with C-FRP bars of 8 mm diameter are found comparable to those of slabs S-1 to S-3 i.e., with 8 mm diameter steel bars. However, the slabs S-5 to S-7 exhibit much improved damage resistance as compared to slabs S-1 to S-3, Table 2.
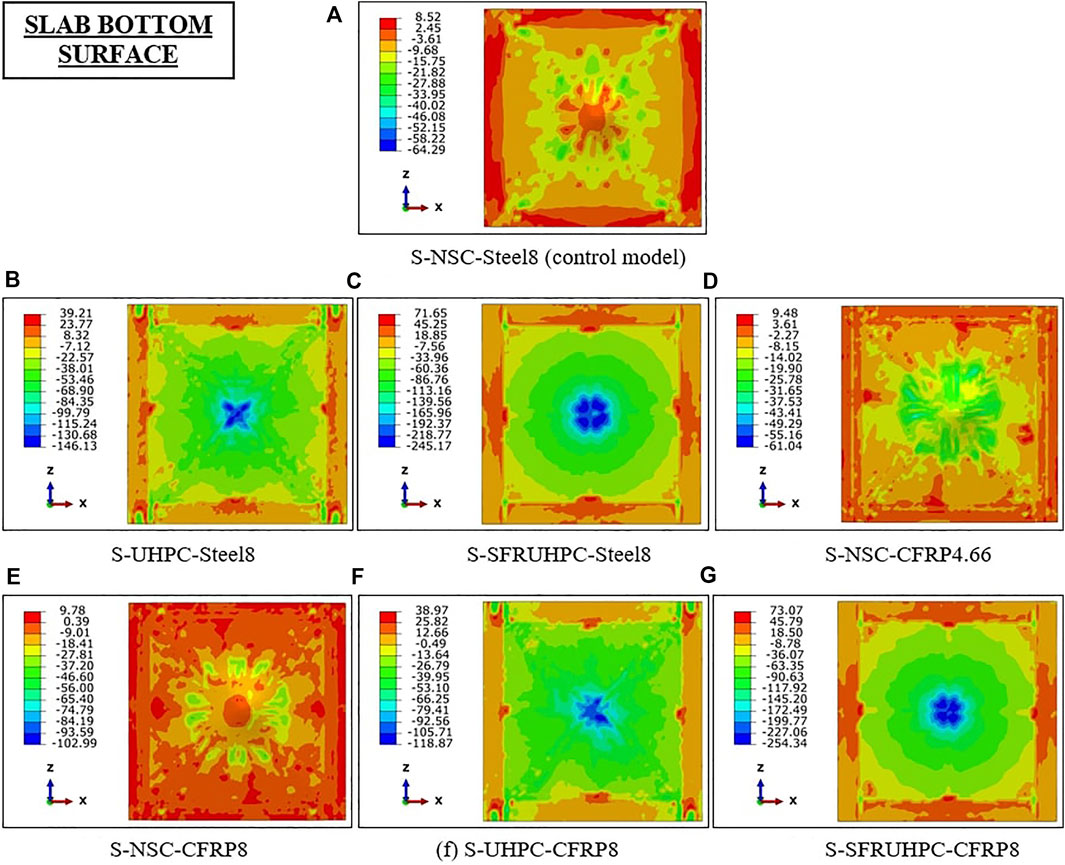
FIGURE 8. Principal stress (MPa) contour of the concrete of the slabs: Part I. (A) S-NSC-Steel8 (control model). (B) S-UHPC-Steel8. (C) S-SFRUHPC-Steel8. (D) S-NSC-CFRP4.66. (E) S-NSC-CFRP8. (F) S-UHPC-CFRP8. (G) S-SFRUHPC-CFRP8.
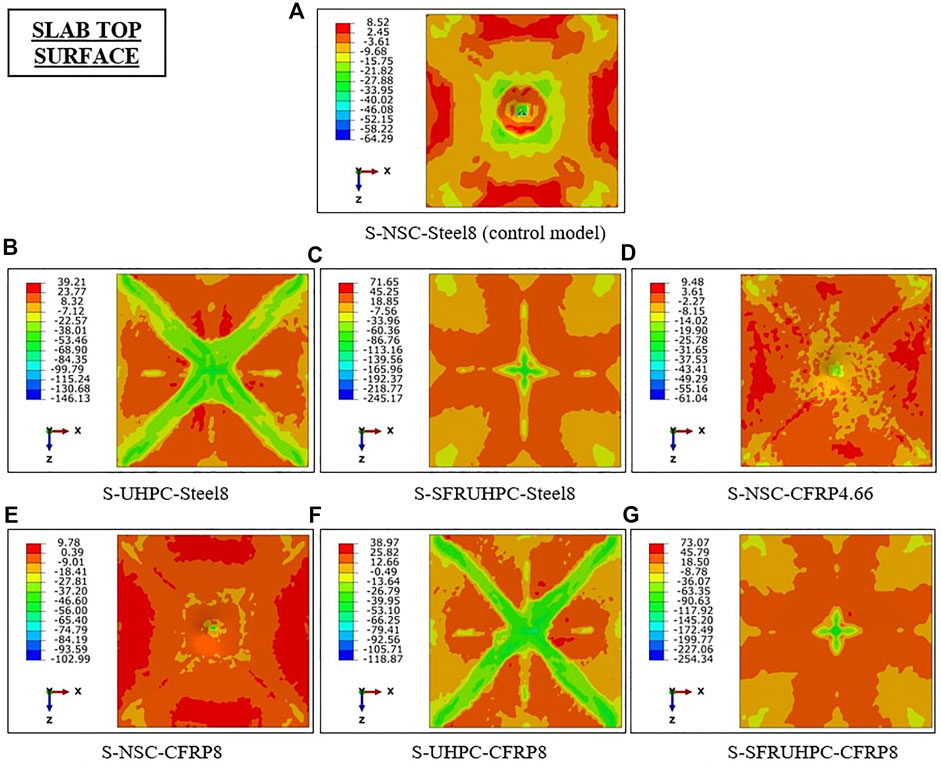
FIGURE 9. Principal stress (MPa) contour of the concrete of the slabs: Part II. (A) S-NSC-Steel8 (control model). (B) S-UHPC-Steel8. (C) S-SFRUHPC-Steel8. (D) S-NSC-CFRP4.66. (E) S-NSC-CFRP8. (F) S-UHPC-CFRP8. (G) S-SFRUHPC-CFRP8.
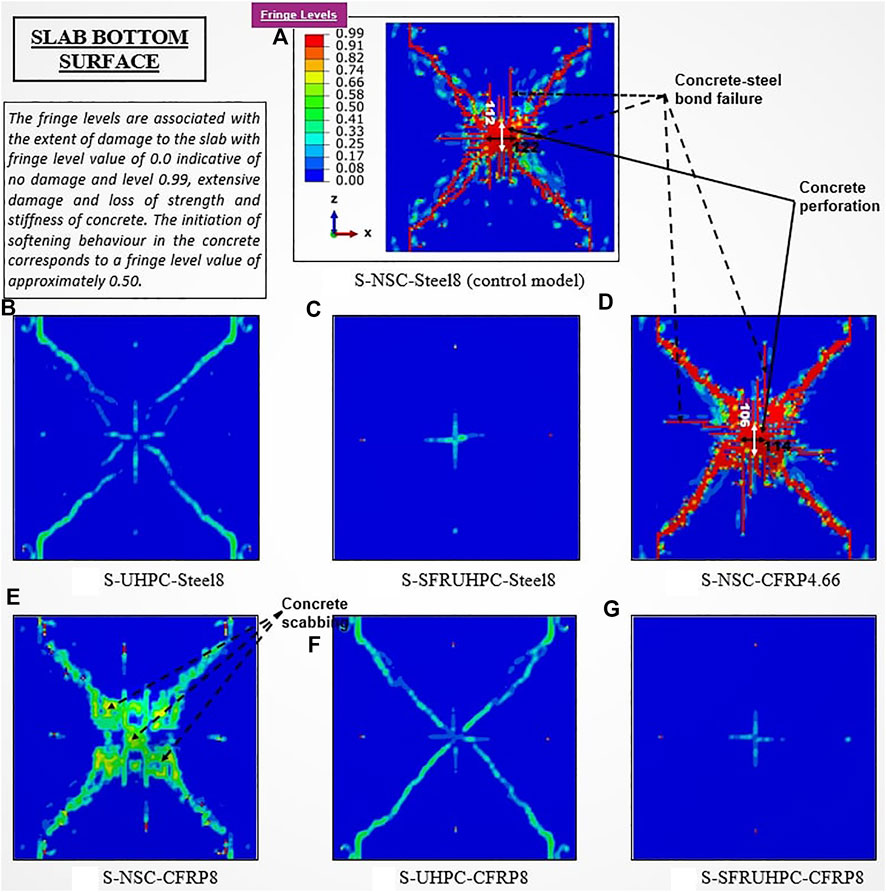
FIGURE 10. Damage profile of the slabs: Part I. (A) S-NSC-Steel8 (control model). (B) S-UHPC-Steel8. (C) S-SFRUHPC-Steel8. (D) S-NSC-CFRP4.66. (E) S-NSC-CFRP8. (F) S-UHPC-CFRP8. (G) S-SFRUHPC-CFRP8.
From above discussion, it is concluded that the strength of concrete plays a bigger in reducing the displacement of the slab than the strength of the reinforcement under the identical free-fall impacting load.
The peak acceleration of the slabs under the applied load is given in Table 2. From the comparison of data in Table 2, it is observed that maximum acceleration is directly related to the stiffness of the slabs. The maximum acceleration values of slabs made of UHPC and SFR-UHPC are greater than that of the NSC slab because increasing the concrete strength provides more stiffness/rigidity. The slabs S-2 and S-3 exhibit 34% and 45% greater maximum acceleration values, respectively, compared with the control slab S-1. On the other hand, the peak acceleration of the NSC slab S-3 with C-FRP bars of 4.66 mm diameter is 17% lower than that of the control model S-1 on account of decreased percentage of reinforcement. It is worth noting that the acceleration values of slabs S-5 to S-7 with C-FRP bars of 8 mm diameter are slightly lower than those of the slabs S-1 to S-3 with 8 mm steel bars attributed to the lower elastic modulus of the C-FRP bars than of the steel bars.
The damage profiles of the slabs are shown in Figure 10 and Figure 11. The damage dissipation energy (DDE) i.e., the amount of energy dissipated by damage, of the slabs under the applied impact is listed in Table 2. The control slab exhibits total damage (DDE) of 190.98J. Application of UHPC and SFR-UHPC in slabs S-2 and S-3 enhances the energy absorption capacity and significantly reduces the damage under the drop-weight load. From Table 2, it is observed that the DDE values for slabs S-2 and S-3 are 51% and 67% lower than that of control slab S-1. Replacement of the 8 mm steel bars by 4.66 mm C-FRP bars of the equivalent area in slab S-4 with NSC concrete increases the slab maximum displacement with widened diagonal cracks on the tension side. On the other hand, 8 mm diameter high tensile strength C-FRP bars in lieu of 8 mm steel bars in slabs S-5 to S-7 are much more effective to control the damage by limiting its severity to the level of little scabbing, Figure 10. However, the combination of UHPC and SFR-UHPC with C-FRP reinforcing bars in slabs S-6 and S-7, respectively, shows an extraordinary performance by enhancing the energy absorption capacity and cracking resistance of the slabs.
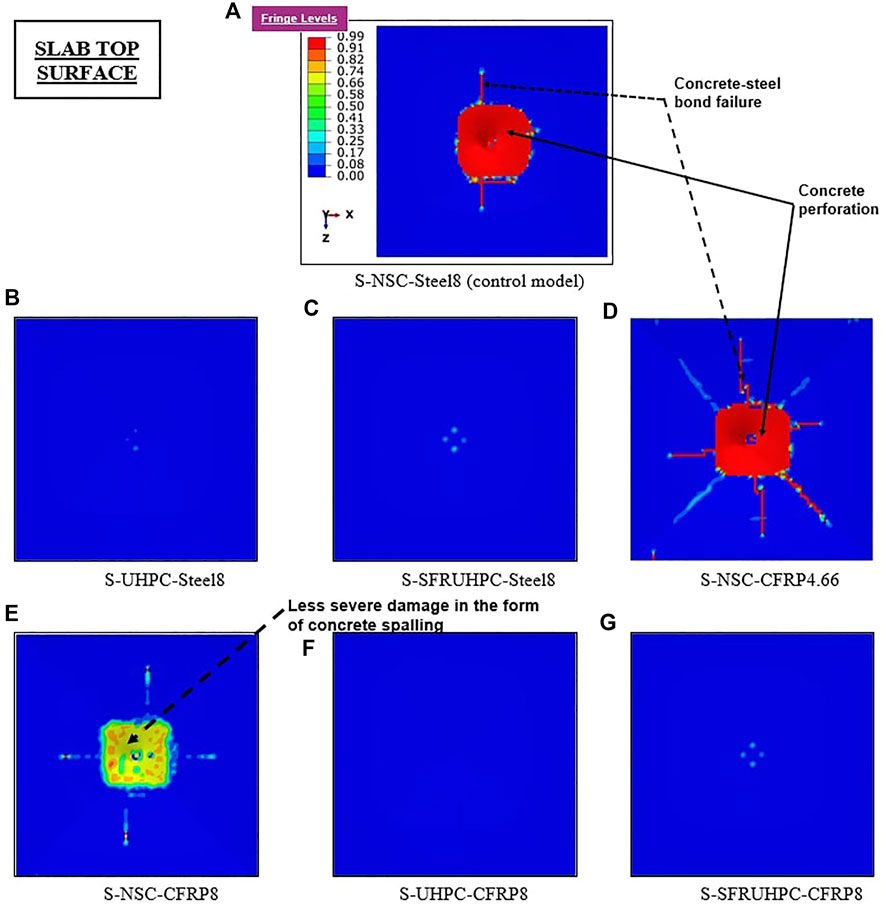
FIGURE 11. Damage profile of the slabs: Part II. (A) S-NSC-Steel8 (control model). (B) S-UHPC-Steel8. (C) S-SFRUHPC-Steel8. (D) S-NSC-CFRP4.66. (E) S-NSC-CFRP8. (F) S-UHPC-CFRP8. (G) S-SFRUHPC-CFRP8.
A research study using the ABAQUS code is performed to evaluate the performance of two-way NSC, UHPC, and SFR-UHPC concrete slabs with conventional tension reinforcements of (1) steel and (2) C-FRP under impact load of a falling weight. The striking event of the impactor generating an impacting weight of 105 kg through falling from rest at a height of 2500 mm with an impacting velocity of 7 m/s generating an impact force of 1035N on the slab top face at its mid-point has been simulated using FEM-based explicit solver of ABAQUS. The main conclusions are:
• Slabs made of UHPC and SFR-UHPC concrete with either conventional steel or C-FRP reinforcing bars of 8 mm diameter at 100 mm c/c, exhibited extraordinary performance in resisting applied falling-weight load nevertheless, the slabs with the C-FRP bars displayed slightly greater resistance than steel bars embedded slabs with regard to cracking and size of concrete scabbing.
• Slabs’ peak acceleration is influenced by their stiffness i.e., the slabs with higher stiffness displayed greater acceleration under the impacting load.
• The use of C-FRP re-bars in lieu of steel re-bars decreased the severity of diagonal cracks and scabbing size. More concrete was ejected from the bottom face of the slab with a lower reinforcement ratio (0.50%) and concrete strength (29.70 MPa), and vice versa. The steel re-bars yielded in the slab with NSC concrete only but not with UHPC/SFR-UHPC however, the C-FRP bars neither yielded with NSC nor with UHPC/SFR-UHPC under the drop-weight load.
• Replacement of the 8 mm steel bars by 4.66 mm C-FRP bars of the equivalent area in the slab with NSC concrete significantly reduced its performance under the impact on account of decreased steel ratio and led to an increase in maximum displacement, crack severity, scabbing size, and DDE.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
SA performed the numerical simulations and measurements. MA supervised this work. HI organized the database. HN and MS wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
The research is partially funded by the Ministry of Science and Higher Education of the Russian Federation under the strategic academic leadership program “Priority 2030” (Agreement 075-15-2021-1333 dated 09/30/2021).
The authors extend their thanks to the Ministry of Science and Higher Education of the Russian Federation for funding this work.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abaqus, (2020). ABAQUS 2020 Concrete Damage Plasticity model, explicit solver, three dimensional solid element library ABAQUS/Explicit finite element method based computer program. DS-SIMULIA User Assist. Guide
Abbas, H., Gupta, N. K., and Alam, M. (2004). Nonlinear response of concrete beams and plates under impact loading. Int. J. Impact Eng. 30, 1039–1053. doi:10.1016/j.ijimpeng.2004.06.011
Ahmadi, E., Alam, M., and Anas, S. M. (2021). “Blast performance of RCC slab and influence of its design parameters,” inResilient Infrastructure, Lect. Notes Civ. Eng. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 389–402. doi:10.1007/978-981-16-6978-1_31
Ahmadi, E., Alam, M., and Anas, S. M. (2022). Behaviour of C-FRP laminate strengthened masonry and unreinforced masonry compound walls under blast loading, Afghanistan scenario. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10049968
Anas, S. M., and Alam, M. (2021a). Comparison of existing empirical equations for blast peak positive overpressure from spherical free air and hemispherical surface bursts. Iran. J. Sci. Technol. Trans. Civ. Eng. 46, 965–984. doi:10.1007/s40996-021-00718-4
Anas, S. M., and Alam, M. (2022). Role of shear reinforcements on the punching shear resistance of two-way RC slab subjected to impact loading materials today: Proceedings. doi:10.1016/j.matpr.2022.08.510
Anas, S. M., and Alam, M. (2022). Performance of simply supported concrete beams reinforced with high-strength polymer re-bars under blast-induced impulsive loading. Int. J. Struct. Eng. 12 (1), 62–76. doi:10.1504/IJSTRUCTE.2022.119289
Anas, S. M., and Alam, M. (2022). Performance of brick-filled reinforced concrete composite wall strengthened with C-FRP laminate(s) under blast loading. Mater. Today Proc. 65, 1. doi:10.1016/j.matpr.2022.03.162
Anas, S. M., and Alam, M. (2022). Close-range blast response prediction of hollow circular concrete columns with varied hollowness ratio, arrangement of compression steel, and confining stirrups’ spacing. Iran. J. Sci. Technol. Trans. Civ. Eng. doi:10.1007/s40996-022-00951-5
Anas, S. M., and Alam, M. (2022). Dynamic behaviour of free-standing unreinforced masonry and composite walls under close-range blast loadings: A finite element investigation. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10051379
Anas, S. M., and Ansari, Md I. (2021). A study on existing masonry heritage building to explosive-induced blast loading and its response. Int. J. Struct. Eng. 11 (4), 387–412. doi:10.1504/IJSTRUCTE.2021.118065
Anas, S. M., Alam, M., and Umair, M. (2020). “Performance of one-way concrete slabs reinforced with conventional and polymer re-bars under air-blast loading,” in Recent advances in structural engineering. Lecture notes in civil engineering. Editors S. Chandrasekaran, S. Kumar, and S. Madhuri (Germany: Springer), 179–191. doi:10.1007/978-981-33-6389-2_18
Anas, S. M., Alam, M., and Umair, M. (2020). Performance of one-way composite reinforced concrete slabs under explosive-induced blast loading IOP conference series: Earth and environmental science, 1st International Conference on Energetics, Civil and Agricultural Engineering 2020, Tashkent, Uzbekistan, 14-16 October 2020. doi:10.1088/1755-1315/614/1/012094
Anas, S. M., Ansari, Md I., and Alam, M. (2020). Performance of masonry heritage building under air-blast pressure without and with ground shock. Aust. J. Struct. Eng. 21 (4), 329–344. doi:10.1080/13287982.2020.1842581
Anas, S. M., Alam, M., and Umair, M. (2021). Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: A state-of-the-art review. Structures 31, 428–461. doi:10.1016/j.istruc.2021.01.102
Anas, S. M., and Alam, M. (2021). “Air-blast response of free-standing: (1) unreinforced brick masonry wall, (2) cavity RC wall, (3) RC walls with (i) bricks, (ii) sand, in the cavity: A macro-modeling approach,” in Proceedings of SECON’21. SECON 2021. Lecture notes in civil engineering. Editors G. C. Marano, S. Ray Chaudhuri, G. Unni Kartha, P. E. Kavitha, R. Prasad, and R. J. Achison (Cham: Springer), 921–930. doi:10.1007/978-3-030-80312-4_78
Anas, S. M., Alam, M., and Umair, M. (2021). Performance of on-ground double-roof RCC shelter with energy absorption layers under close-in air-blast loading. Asian J. Civ. Eng. 22, 1525–1549. doi:10.1007/s42107-021-00395-8
Anas, S. M., Alam, M., and Umair, M. (2021). Air-blast and ground shockwave parameters, shallow underground blasting, on the ground and buried shallow underground blast-resistant shelters: A review. Int. J. Prot. Struct. 13 (1), 99–139. doi:10.1177/20414196211048910
Anas, S. M., Alam, M., and Umair, M. (2021). “Out-of-plane response of clay brick unreinforced and strengthened masonry walls under explosive-induced air-blast loading,” in Resilient infrastructure, lecture notes in civil engineering. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 477–491. doi:10.1007/978-981-16-6978-1_37
Anas, S. M., Alam, M., and Umair, M. (2021). “Influence of charge locations on close-in air-blast response of pre-tensioned concrete U-girder,” in Resilient infrastructure, lecture notes in civil engineering. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 513–527. doi:10.1007/978-981-16-6978-1_40
Anas, S. M., Alam, M., and Tahzeeb, R. (2022r). Impact response prediction of square RC slab of normal strength concrete strengthened with (1) laminates of (i) mild-steel and (ii) C-FRP, and (2) strips of C-FRP under falling-weight load. Mater. Today Proc. doi:10.1016/j.matpr.2022.07.324
Anas, S. M., Alam, M., and Umair, M. (2022m). Behaviour and damage assessment of monolithic and non-monolithic braced masonry walls subjected to blast loadings using a detailed micro-modelling approach. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10051512
Anas, S. M., Alam, M., and Umair, M. (2022n). Experimental studies on blast performance of unreinforced masonry walls of clay bricks and concrete blocks: A state-of-the-art review. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10049719
Anas, S. M., Alam, M., and Umair, M. (2022o). Performance prediction of braced unreinforced and strengthened clay brick masonry walls under close-range explosion through numerical modeling. Int. J. Comput. Mater. Sci. Surf. Eng. 11, 1. doi:10.1504/ijcmsse.2022.10051496
Anas, S. M., Alam, M., and Umair, M. (2022p). Role of UHPC in-lieu of ordinary cement-sand plaster on the performance enhancement of masonry wall under close-range blast loading: A finite element investigation. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10051229
Anas, S. M., Alam, M., Umair, M., and Kanaan, M. H. G. (2022q). Strengthening of unreinforced braced masonry wall with (1) CFRP laminate and (2) mild-steel strips: Innovative techniques, against close-range explosion. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10051230
Anas, S. M., Alam, M., and Umair, M. (2023). “Air-blast response of axially loaded clay brick masonry walls with and without reinforced concrete core,” in ASMA 2021, advances in structural mechanics and applications, STIN 19. Editors (Cham: Springer), 1–18. doi:10.1007/978-3-030-98335-2_4
Anas, S. M., Alam, M., and Alam, M. (2022a). “Performance prediction of axially loaded square reinforced concrete column with additional transverse reinforcements in the form of (1) master ties, (2) diamond ties, and (3) open ties under close-in blast,” in Proceedings of the 2nd international symposium on disaster resilience and sustainable development, lecture notes in civil engineering. Editors (Singapore: Springer), 294. doi:10.1007/978-981-19-6297-4_12
Anas, S. M., Alam, M., and Shariq, M. (2022b). Damage response of conventionally reinforced two-way spanning concrete slab under eccentric impacting drop weight loading. Def. Technol. doi:10.1016/j.dt.2022.04.011
Anas, S. M., Alam, M., and Alam, M. (2022c). Reinforced cement concrete (RCC) shelter and prediction of its blast loads capacity. Mater. Today Proc. doi:10.1016/j.matpr.2022.09.125
Anas, S. M., Alam, M., and Umair, M. (2022d). Effect of design strength parameters of conventional two-way singly reinforced concrete slab under concentric impact loading materials today: Proceedings. doi:10.1016/j.matpr.2022.02.441
Anas, S. M., Alam, M., Isleem, H. F., Najm, H. M., and Sabri, M. M. S. (2022e). Role of cross-diagonal reinforcements in lieu of seismic confining stirrups in the performance enhancement of square RC columns carrying axial load subjected to close-range explosive loading. Front. Mat. 9. doi:10.3389/fmats.2022.1002195
Anas, S. M., Alam, M., and Shariq, M. (2022f). Behavior of two-way RC slab with different reinforcement orientation layouts of tension steel under drop load impact materials today: Proceedings. doi:10.1016/j.matpr.2022.08.509
Anas, S. M., Alam, M., and Umair, M. (2022g). Performance based strengthening with concrete protective coatings on braced unreinforced masonry wall subjected to close-in explosion. Mater. Today Proc. 64, 161–172. doi:10.1016/j.matpr.2022.04.206
Anas, S. M., Shariq, M., and Alam, M. (2022h). Performance of axially loaded square RC columns with single/double confinement layer(s) and strengthened with C-frp wrapping under close-in blast. Mater. Today Proc. 58, 1128–1141. doi:10.1016/j.matpr.2022.01.275
Anas, S. M., Alam, M., and Umair, M. (2022i). Strengthening of braced unreinforced brick masonry wall with (i) C-frp wrapping, and (ii) steel angle-strip system under blast loading. Mater. Today Proc. 58, 1181–1198. doi:10.1016/j.matpr.2022.01.335
Anas, S. M., Shariq, M., Alam, M., and Umair, M. (2022j). Evaluation of critical damage location of contact blast on conventionally reinforced one-way square concrete slab applying CEL-FEM blast modeling technique. Int. J. Prot. Struct., 204141962210952. doi:10.1177/20414196221095251
Anas, S. M., Alam, M., and Umair, M. (2022k). Performance of (1) concrete-filled double-skin steel tube with and without core concrete, and (2) concrete-filled steel tubular axially loaded composite columns under close-in blast. Int. J. Prot. Struct., 204141962211041. doi:10.1177/20414196221104143
Campbell, J. D. (1953). The dynamic yielding of mild steel. Acta Metall. 1 (6), 706–710. doi:10.1016/0001-6160(53)90029-7
Chen, Y., and May, I. M. (2009). Reinforced concrete members under drop-weight impacts. Proc. Institution Civ. Eng. - Struct. Build. 162 (1), 45–56. doi:10.1680/stbu.2009.162.1.45
Chen, S. X., Sahmani, S., and Safaei, B. (2021). Size-dependent nonlinear bending behavior of porous FGM quasi-3D microplates with a central cutout based on nonlocal strain gradient isogeometric finite element modelling. Eng. Comput. 37, 1657–1678. doi:10.1007/s00366-021-01303-z
Cotsovos, D. M., and Pavlovi, C. M. N. (2008). Numerical investigation of concrete subjected to high rates of uniaxial tensile loading. Int. J. Impact Eng. 35 (5), 319–335. doi:10.1016/j.ijimpeng.2007.03.006
Cotsovos, D. M. (2010). A simplified approach for assessing the load-carrying capacity of reinforced concrete beams under concentrated load applied at high rates. Int. J. Impact Eng. 37 (8), 907–917. doi:10.1016/j.ijimpeng.2010.01.005
Dancygier, A. N., Yankelevsky, D. Z., and Jaegermann, C. (2007). Response of high performance concrete plates to impact of nondeforming projectiles. Int. J. Impact Eng. 34 (11), 1768–1779. doi:10.1016/j.ijimpeng.2006.09.094
Delhomme, F., Mommessin, M., Mougin, J., and Perrotin, P. (2007). Simulation of a block impacting a reinforced concrete slab with a finite element model and a mass-spring system. Eng. Struct. 29 (11), 2844–2852. doi:10.1016/j.engstruct.2007.01.017
Elavenil, S., and Knight, G. (2012). Impact response of plates under drop weight impact testing. Daffodil Int. uni. J. Sci. Technol. 7 (1), 1–11. doi:10.3329/diujst.v7i1.9580 Impact
Erdem, R. T., and Gücüyen, E. (2017). Linear analysis of reinforced concrete slabs under impact effect. Gradjevinar 69 (6), 479–487.
Erdem, R. T. (2014). Prediction of acceleration and impact force values of a reinforced concrete slab. Predict. Accel. impact force values a Reinf. Concr. slab Comput. Concr. 14 (5), 563–575. doi:10.12989/cac.2014.14.5.563
Erdem, R. T. (2021). Dynamic responses of reinforced concrete slabs under sudden impact loading. rdlc. 20 (2), 346–358. doi:10.7764/rdlc.20.2.346
Ernst (2010). International federation for structural concrete 2010 fib model Code for concrete structures 2010. Hoboken: Ernst & Sohn publishing house.
Fareed, S. (2018). Behavior of reinforced concrete slabs under accidental impacts. Streamlining Inf. Transf. between Constr. Struct. Eng. 44, 1–6.
Gao, J., Sun, W., and Morino, K. (1997). Mechanical properties of steel fiber-reinforced, high-strength, lightweight concrete. Cem. Concr. Compos. 19 (4), 307–313. doi:10.1016/s0958-9465(97)00023-1
grdh, L., and Laine, L. (1999). 3D fe-simulation of high-velocity fragment perforation of reinforced concrete slabs. Int. J. Impact Eng. 22, 911–922. doi:10.1016/S0734-743X(99)00008-1
Grote, D. L., Park, S. W., and Zhou, M. (2001). Dynamic behavior of concrete at high strain rates and pressures: I. Experimental characterization. Int. J. Impact Eng. 25 (9), 869–886. doi:10.1016/s0734-743x(01)00020-3
Hu, R., Fang, Z., Benmokrane, B., and Fang, W. (2021). Cyclic behaviour of UHPC columns with hybrid CFRP/Steel reinforcement bars. Eng. Struct. 238, 112245. doi:10.1016/j.engstruct.2021.112245
Huang, F., Wu, H., Jin, Q., and Zhang, Q. (2005). A numerical simulation on the perforation of reinforced concrete targets. Int. J. Impact Eng. 32, 173–187. doi:10.1016/j.ijimpeng.2005.05.009
Hughes, G., and Beeby, A. W. (1982). Investigation of the effect of impact loading on concrete beams. Struct. Eng. 60 (3), 45–52.
Kishi, N., Mastsuoka, K., Mikami, H., and Goto, Y. (1997). “Impact resistance of large scale RC slabs,” in Proceedings of the 2nd asia-pacific conference on shock & impact loads on structures. second ed. (Melbourne, Australia: CI-Premier Conference), 213–220.
Kishi, N., Kurihashi, Y., Ghadimi, K. S., and Mikami, H. (2011). Numerical simulation of impact response behavior of rectangular reinforced concrete slabs under falling-weight impact loading. Appl. Mech. Mat. 82, 266–271. doi:10.4028/www.scientific.net/amm.82.266
Kojima, I. (1991). An experimental study on local behavior of reinforced concrete slabs to missile impact. Nucl. Eng. Des. 130 (2), 121–132. doi:10.1016/0029-5493(91)90121-w
Kuhn, T. (2015). Curbach M 2015 behavior of RC-slabs under impact-loading EPJ web of conferences 94.
Kumar, V., Kumar, E. K., Dewangan, H. C., Sharma, N., Panda, S. K., and Mahmoud, S. R. (2022). Strain rate loading effects on fiber-reinforced polymeric composites with and without damage: A comprehensive review. Trans. Indian Inst. Mater., 1–10. doi:10.1007/s12666-022-02728-w
Lambert, D. E., and Allen Ross, C. (2000). Strain-rate effects on dynamic fracture and strength. Int. J. Impact Eng. 24 (10), 985–998. doi:10.1016/s0734-743x(00)00027-0
Lee, H-K., Yim, H., and Lee, K- M. (2003). Velocity–strength relationship of concrete by impact-echo method. ACI Mater J. 100 (1), 46–54.
Li, Q. M., and Meng, H. (2003). About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test. Int. J. Solids Struct. 40 (2), 343–360. doi:10.1016/s0020-7683(02)00526-7
Li, H., Li, Z., Safaei, B., Rong, W., Wang, W., Qin, Z., et al. (2021). Nonlinear vibration analysis of fiber metal laminated plates with multiple viscoelastic layers. Thin-Walled Struct. 168, 108297. doi:10.1016/j.tws.2021.108297
Mainstone, R. J. (1975). Properties of materials at high rates of straining or loading. Mat. Constr. 8 (2), 102–116. doi:10.1007/bf02476328
Malvar, L. J., and Crawford, J. E. (1998). “Dynamic increase factors for steel reinforcing bars,” in Twenty-eight Department of defense explosives safety board (DDESB) seminar (Orlando, Florida: ResearchGate).
Malvar, L. J., and Ross, C. A. (1998). Review of strain-rate effects for concrete in tension. ACI Mater J. 95 (6), 735–739.
Miyamoto, A., King, M. W., and Fujii, M. (1991). Analysis of failure modes for RC slabs under impulsive loads. ACI Struct. J. 88 (5), 538–545.
Miyamoto, A., King, M. W., and Fujii, M. (1991). Nonlinear dynamic analysis of RC slabs under impulsive loads. ACI Struct. J. 88 (4), 411–419.
Mokhatar, S., and Abdullah, R. (2012). Computational analysis of reinforced concrete slabs subjected to. Loads Int. J. Integr. Eng. 4 (2), 70–76. Impact
Othman, H., and Marzouk, H. (2016). An experimental investigation on the effect of steel reinforcement on impact response of reinforced concrete plates. Int. J. Impact Eng. 88, 12–21. doi:10.1016/j.ijimpeng.2015.08.015
Pham, T., and Hao, H. (2016). Prediction of the impact force on reinforced concrete beams from a drop weight. Adv. Struct. Eng. 19 (11), 1710–1722. doi:10.1177/1369433216649384
Pham, T. M., and Hao, H. (2018). Influence of global stiffness and equivalent model on prediction of impact response of RC beams. Int. J. Impact Eng. 113, 88–97. doi:10.1016/j.ijimpeng.2017.11.014
Ramakrishna, G., and Sundararajan, T. (2005). Impact strength of a few natural fibre reinforced cement mortar slabs: A comparative study. Cem. Concr. Compos. 27 (5), 547–553. doi:10.1016/j.cemconcomp.2004.09.006 Impact
Rao, S. H., Ghorpade, G. V., Ramana, V. N., and Ganeswar, K. (2010). Response of SIFCON two-way slabs under impact loading. Int. J. Impact Eng. 37, 452–458. doi:10.1016/j.ijimpeng.2009.06.003
Ruano, G., Isla, F., Sfer, D., and Luccioni, B. (2015). Numerical modeling of reinforced concrete beams repaired and strengthened with SFRC. Eng. Struct. 86, 168–181. doi:10.1016/j.engstruct.2014.12.030
Saatci, S., and Vecchio, F. (2009). Nonlinear finite element modeling of reinforced concrete structures under. Loads ACI Struct. J. 106 (5).
Sadraie, H., Khaloo, A., and Soltani, H. (2019). Dynamic performance of concrete slabs reinforced with steel and GFRP bars under impact loading. Eng. Struct. 191, 62–81. doi:10.1016/j.engstruct.2019.04.038
Safaei, B., and Nuhu, A. A. (2022). A comprehensive review on the vibration analyses of small-scaled plate-based structures by utilizing the nonclassical continuum elasticity theories. Thin-Walled Struct. 179, 109622. doi:10.1016/j.tws.2022.109622
Safaei, B. (2020). The effect of embedding a porous core on the free vibration behavior of laminated composite plates. Steel Compos. Struct. 35 (5), 659–670. doi:10.12989/scs.2020.35.5.659
Safaei, B. (2021). Frequency-dependent damped vibrations of multifunctional foam plates sandwiched and integrated by composite faces. Eur. Phys. J. Plus 136 (6), 646. doi:10.1140/epjp/s13360-021-01632-4
Saito, H., Imamura, A., Takeuchi, M., Okamoto, S., Kasai, Y., Tsubota, H., et al. (1995). Loading capacities and failure modes of various reinforced concrete slabs subjected to high speed loading. Nucl. Eng. Des. 156 (1-2), 277–286. doi:10.1016/0029-5493(94)00953-v
Shaheen, B. Y., Hekal, G., and Khalid, A. (2017). “Behavior of reinforced concrete slabs with openings under impact loads,” in Ninth conference of sustainable environmental development (Egypt: Menoufia University).
Shariq, M., Alam, M., Husain, A., and Anas, S. M. (2022). Jacketing with steel angle sections and wide battens of RC column and its influence on blast performance. Asian J. Civ. Eng. 23, 487–500. doi:10.1007/s42107-022-00437-9
Shariq, M., Saifi, F., Alam, M., and Anas, S. M. (2022). Effect of concrete strength on the dynamic behavior of axially loaded reinforced concrete column subjected to close-range explosive loading. Mater. Today Proc. doi:10.1016/j.matpr.2022.07.313
Shariq, M., Alam, M., Husain, A., and Islam, N. (2022). Response of strengthened unreinforced brick masonry wall with (1) mild steel wire mesh and (2) C-FRP wrapping, under close-in blast. Mater. Today Proc. 64, 643–654. doi:10.1016/j.matpr.2022.05.153
Shariq, M., Alam, M., and Husain, A. (2022). “Performance of RCC column retrofitted with C-frp wrappings and the wrappings with steel angle-batten jacketing under blast loading,” in Recent advances in civil engineering, lecture notes in civil engineering. Editors L. Nandagiri, M. C. Narasimhan, and S. Marathe (Singapore: Springer). doi:10.1007/978-981-19-1862-9_21
Shariq, M., Anas, S. M., and Alam, M. (2022). Blast resistance prediction of clay brick masonry wall strengthened with steel wire mesh, and C-frp laminate under explosion loading: A finite element analysis. Int. J. Reliab. Saf. 1, 1. doi:10.1504/IJRS.2022.10051370
Shariq, M., Alam, M., Anas, S. M., Islam, N., and Hussain, A. (2022). Performance enhancement of square reinforced concrete column carrying axial compression by (1) C-frp wrapping, and (2) steel angle system under air-blast loading. Int. J. Comput. Mater. Sci. Surf. Eng. 11, 1. doi:10.1504/ijcmsse.2022.10051781
Shariq, M., Alam, M., Anas, S. M., Hussain, A., and Islam, N. (2022). Influence of wire mesh, and CFRP strengthening on blast performance of brick masonry wall: A numerical study under close-range explosion. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10051479
Shariq, M., Alam, M., Anas, S. M., Hussain, A., and Islam, N. (2022). Blast response prediction of unreinforced masonry wall with varying mortar strength and axial load. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10051480
Shi-ju, M., Ming-yu, L., Yuan-cheng, G., and Safaei, B. (2020). Field test and research on shield cutting pile penetrating cement soil single pile composite foundation. Geomechanics Eng. 23 (6), 513–521. doi:10.12989/gae.2020.23.6.513
Song, P. S., and Hwang, S. (2004). Mechanical properties of high-strength steel fiber-reinforced concrete. Constr. Build. Mater. 18 (9), 669–673. doi:10.1016/j.conbuildmat.2004.04.027
Song, P. S., Hwang, S., and Sheu, B. C. (2004). Statistical evaluation for impact resistance of steel fibre-reinforced concretes. Mag. Concr. Res. 56 (8), 437–442. doi:10.1680/macr.2004.56.8.437
Srivastava, L., Krishnanand, L., Nath, N. K., Hirwani, C. K., and Panda, S. K. (2022). Effect of blast load on dynamic deflection responses of internally damaged carbon–epoxy laminated composite shallow shell panel using experimental properties. Trans. Indian Inst. Mater., 1–8. doi:10.1007/s12666-022-02698-z
Stochino, F., and Carta, G. (2014). SDOF models for reinforced concrete beams under impulsive loads accounting for strain rate effects. Nucl. Eng. Des. 276, 74–86. doi:10.1016/j.nucengdes.2014.05.022
Sudarsana, R., Sashidhar, C., Vaishali, G., and Venkata, R. (2015). Behavior of high performance concrete two way slabs in impact for fixed edge condition. Int. J. Emerg. Trends Eng. Dev. 2 (5).
Tahzeeb, R., Alam, M., and Mudassir, S. M. (2022). A comparative performance of columns: Reinforced concrete, composite, and composite with partial C-frp wrapping under contact blast. Mater. Today Proc. 62, 2191–2202. doi:10.1016/j.matpr.2022.03.367
Tahzeeb, R., Alam, M., and Mudassir, S. M. (2022). Performance of composite and tubular columns under close-in blast loading: A comparative numerical study. Mater. Today Proc. 65, 51–62. doi:10.1016/j.matpr.2022.04.587
Tahzeeb, R., Alam, M., and Mudassir, S. M. (2022). Effect of transverse circular and helical reinforcements on the performance of circular RC column under high explosive loading. Mater. Today Proc. 64, 315–324. doi:10.1016/j.matpr.2022.04.676
Teng, T-L., Chu, Y-A., Chang, F-A., and Chin, H- S. (2004). Simulation model of impact on reinforced concrete. Cem. Concr. Res. 34, 2067–2077. doi:10.1016/j.cemconres.2004.03.019
Tham, C. (2006). Numerical and empirical approach in predicting the penetration of a concrete target by an ogive-nosed projectile. Finite Elem. Anal. Des. 42, 1258–1268. doi:10.1016/j.finel.2006.06.011
Ul Ain, Q., Alam, M., and Anas, S. M. (2021). “Behavior of ordinary load-bearing masonry structure under distant large explosion, beirut scenario,” in Resilient infrastructure, lecture notes in civil engineering. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 239–253. doi:10.1007/978-981-16-6978-1_19
Ul Ain, Q., Alam, M., and Anas, S. M. (2022). “Response of two-way RCC slab with unconventionally placed reinforcements under contact blast loading,” in ASMA 2021, advances in structural mechanics and applications, STIN 19. Editors (Singapore: Springer), 1–18. doi:10.1007/978-3-031-04793-0_17
Weerheijm, J., and Van Doormaal, J. C. A. M. (2007). Tensile failure of concrete at high loading rates: New test data on strength and fracture energy from instrumented spalling tests. Int. J. Impact Eng. 34 (3), 609–626. doi:10.1016/j.ijimpeng.2006.01.005
Yi, H., Sahmani, S., and Safaei, B. (2020). On size-dependent large-amplitude free oscillations of FGPM nanoshells incorporating vibrational mode interactions. Arch. Civ. Mech. Eng. 20, 48. doi:10.1007/s43452-020-00047-9
Yılmaz, T., Kıraç, N., Ö, Anil, Erdem, R. T., and Sezer, C. (2018). Low-velocity impact behaviour of two way RC slab strengthening with CFRP strips. Constr. Build. Mater. 186, 1046–1063. doi:10.1016/j.conbuildmat.2018.08.027
Yon, J-H., Hawkins, N. M., and Kobayashi, A. S. (1992). Strain-rate sensitivity of concrete mechanical properties. ACI Mater J. 89 (2), 146–153.
Zhao, D. B., Yi, W. J., and Kunnath, S. K. (2010). Numerical simulation and shear resistance of reinforced concrete beams under impact. Eng. Struct. 166, 387–401. doi:10.1016/j.engstruct.2018.03.072
Zhao, J., Li, G., Wang, Z., and Zhao, X-L. (2019). Fatigue behavior of concrete beams reinforced with glass- and carbon-fiber reinforced polymer (GFRP/CFRP) bars after exposure to elevated temperatures. Compos. Struct. 229, 111427. doi:10.1016/j.compstruct.2019.111427
Zineddin, M., and Krauthammer, T. (2007). Dynamic response and behavior of reinforced concrete slabs under impact loading. Int. J. Impact Eng. 34, 1517–1534. doi:10.1016/j.ijimpeng.2006.10.012
Keywords: RC slabs, impact loading, strain-rates, UHPC, SFR-UHPC, CFRP, dynamic response, damage
Citation: Anas SM, Alam M, Isleem HF, Najm HM and Sabri MMS (2022) Ultra high performance concrete and C-FRP tension Re-bars: A unique combinations of materials for slabs subjected to low-velocity drop impact loading. Front. Mater. 9:1061297. doi: 10.3389/fmats.2022.1061297
Received: 04 October 2022; Accepted: 02 November 2022;
Published: 21 November 2022.
Edited by:
Zhicheng Yang, Zhongkai University of Agriculture and Engineering, ChinaReviewed by:
Subrata Kumar Panda, National Institute of Technology Rourkela, IndiaCopyright © 2022 Anas, Alam, Isleem, Najm and Sabri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: S. M. Anas, bW9oZGFuYXM0M0BnbWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.