Refined numerical study on the effect of grouting plumpness on bearing behavior of pipe roof

Pre-supported pipe roof grouting is difficult to be satisfied due to various influences, which may have an impact on its bearing characteristics. In order to determine the impact of grouting plumpness on the bearing behavior of pipe roof, based on the preliminary experimental research a refined numerical model that takes into account the bonding between the steel pipe and cement mortar was established in this paper. It was used to analyze the bending moment-deflection curve, variation laws of ultimate bearing capacity coefficient, and disengagement rate of pipe roof under different grouting plumpness. Meanwhile, the working conditions of reinforcement and casing in the pipe were conducted. The results show that compared with full grouting, the ultimate bearing capacity of the grouting pipe roof, pipe roof with reinforcement bundles and casing pipe decreases by 4.6%, 5.2%, and 4.8% respectively when grouting incompleteness is 2%, and decreases by 35.3%, 40.4%, and 37.1% respectively, when grouting incompleteness rises to 25%; The ultimate bearing capacity of the pipe roof can be greatly enhanced by adding reinforcement bundles and casing pipe, and the increases of this case is 7.7%–18.3%, 31.4%–51.6%, respectively; The disengagement rate of pipe roof and mortar under the same load increases with the increase of grouting incompleteness, which growing relatively slowly when the grouting incompleteness is less than 2%, and develops rapidly when it is 2%–30%, while growing little when it is more than 30%. Under the same grouting incompleteness, adding reinforcement bundles and casing pipe in the pipe roof can effectively reduce its debonding rate and the latter has a better effect, and the corresponding disengagement rate is 62.8%–97.9% and 29.1%–91.9% of the grouting pipe roof respectively.

1 Introduction

Tunnel construction inevitably encounters poorly self-stabilizing strata, and improper disposal will lead to instability of surrounding rock and tunnel collapse accidents. In order to reduce the disturbance of tunnel excavation to the surrounding rock, advance pre-supporting technology is often used in tunnel engineering to strengthen the stability of surrounding rock in weak strata. And the pipe roof pre-support is widely used as one of the most effective auxiliary methods to prevent collapse and sinking in tunnel and underground engineering due to the advantages of long pre-support distance, fast construction, high safety and short construction period (Singh et al., 1995; Wang, 2004; Gou et al., 2007; Li, 2008; Rao, 2008; Xia et al., 2008).

To this end, some scholars have conducted plenty of research on the layout scope, pipe diameter and construction technology of pipe roof (Musso, 1979; Miwa and Ogasawara, 2005; Su and Wang, 2021). The effect of different steel pipe diameters, lap lengths, and pipe roof lengths on the strength of pipe roofs was analyzed based on the Pasternak elastic foundation beam theory, and the results showed that there were optimal values for steel pipe diameters and lengths of pipe roof (Wang et al., 2010). The effect of tunnel boring distance on the force characteristics of the long and large pipe roof was carried out through field test and numerical simulation, and the results indicated that the force in all regions of the pipe roof increased with tunnel boring and fell into a regular slow after the first fast pattern (Geng et al., 2016). The mechanical response of the pipe roof during the whole excavation process was investigated based on numerical simulation and theoretical calculation, and the study suggested that the pipe roof had a circular micro-arch effect, the excavation length of large-span tunnel should be limited in 2 m, and the distance between pipe roofs within 30° near the tunnel vault should be 5–10 cm shorter compared with other parts (Li et al., 2022). A comparative study on the physical and mechanical properties of the secondary grouting was conducted after the steel pipe was disconnected from the concrete, and the results demonstrated that the crack width increased and the mechanical properties were sharply lost after disconnecting, but the mechanical properties of the steel pipe were basically restored when the second grouting was full (Ye, 2001; Ye et al., 2003; Ye et al., 2004). The influence of factors such as steel pipe diameter and concrete strength on the overall ultimate bearing capacity of concrete-filled steel tube was examined, the results revealed that the ultimate bearing capacity calculated by most codes was more conservative, and the design of concrete-filled steel tube had a large space for saving (Abed et al., 2012).

At present, the researches on the pipe roof pre-support still relatively lags behind the actual engineering, and the design still depends on experience and engineering analogy. The load determination and mechanical mode of the pre-support structure needs to be further studied. In addition, there is poorly attended to the incomplete grouting that often occurs in engineering, and it is not included in the design calculation. In the actual project, due to the influence of the construction process and site environment, the situation of incomplete grouting of pipe roof is often appeared, resulting in a significant reduction of its effect of pre-support and bearing behavior. Therefore, in this paper, the refined numerical simulations of grouting pipe roof, pipe roof with reinforcement bundles and pipe roof with casing pipe were carried out respectively under different grouting plumpness, and the results were then compared and verified with the model test results to obtain the influence of grouting incompleteness on the bearing behavior of the pipe roof.

2 Numerical modelling

2.1 Formulation of working conditions

Based on the previous stage of the experimental and preliminary numerical studies (Geng et al., 2019; Shi et al., 2019), the refined modeling calculations was further carried out by using ABAQUS finite element software in this study, and the influence of grouting incompleteness on the bearing behavior of the pipe roof was conducted under the three working conditions of grouting pipe roof, pipe roof with reinforcement bundles and pipe roof with casing pipe. The model of the grouting pipe roof is filled by cement mortar (shown in Figure 1A), and the model of pipe roof with reinforcement bundles is filled with cement mortar and 4 Φ 12 mm reinforcement bundles (shown in Figure 1B). The model of pipe roof with casing pipe is filled by cement mortar and Φ76 mm steel pipe (shown in Figure 1C).

FIGURE 1

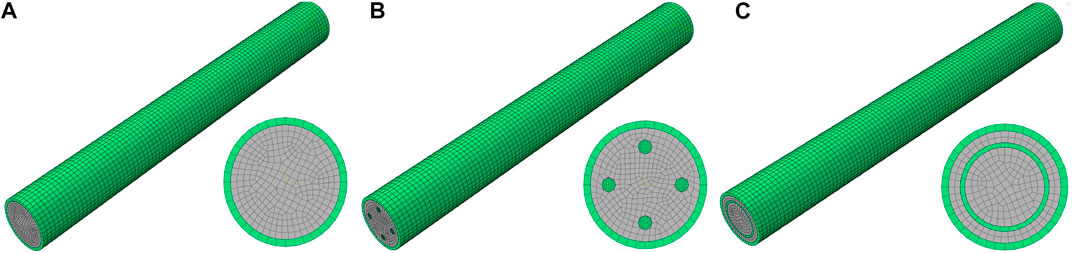
FIGURE 1. Model diagram of three types of pipe roof (A) Grouting pipe roof (B) Grouting pipe roof with reinforcement bundles; and (C) Grouting pipe roof with casing pipe.

The cross section of the three types of pipe roof mentioned above is shown in Figure 2 (illustrated for incomplete grouting). In order to better fit the test (Geng et al., 2019; Shi et al., 2019), the stress-strain curve of the steel pipe was modeled by a secondary plastic flow model (Zhuang, 2009) with an elastic modulus of 206 GPa, and the cement mortar was modeled by a viscoelastic model (Chang and Chen, 2007) with an elastic modulus of 36 GPa.

FIGURE 2

FIGURE 2. Model size and section diagram of three types of pipe roof.

2.2 Model parameters selection

The steel pipe, cement mortar, reinforcement and casing pipe were considered separately and all simulated as solid elements in the numerical analysis, and the mesh type is three-dimensional solid elements (C3D8R). The bonding action between the steel pipe and cement mortar was taken into account, including both normal and tangential behaviors. The former was simulated using hard contact, and separation after contact is allowed; the latter was simulated using a penalty function, and the friction coefficient was set to 0.6 (Liu et al., 2019). Parameter settings for the grouting incompleteness of pipe roof are shown in Table 1.

TABLE 1

TABLE 1. Parameter settings for numerical model.

2.3 Boundary conditions

The boundary conditions of the model are the same as described for researches related to concrete-filled steel tube (Mao, 2019; Zhang et al., 2020). Support constraints were applied at 50 mm from each end of the model, with one end constraining its displacement in the X, Y, and Z directions and the other end constraining its displacement in the Y and Z directions. Meanwhile, displacement loads were applied at the quartering points near the sides of the supports as shown in Figure 2.

3 Analysis of calculation results

Based on the establishment of the above refined numerical model, the numerical analysis of grouting pipe roof, pipe roof with reinforcement bundles and pipe roof with casing pipe under different grouting incompleteness was carried out, and the regular curves of bending moment-deflection, ultimate bearing capacity coefficient and disengagement rate were derived for the three types of pipe roof respectively.

3.1 Bending moment-deflection curves of pipe roof

3.1.1 Grouting pipe roof

The M-u_m (bending moment—mid-span deflection) curves of the grouting pipe roof under bending load are shown in Figure 3. The M-u_m curves of the grouting pipe roof at 10%–100% of grouting incompleteness are shown in Figure 3A. When the grouting incompleteness is 25%–100%, the M-u_m curve is roughly divided into elastic segment, elastic-plastic section and descending section, the reason for the decline section is that the flattening deformation of the steel pipe (the section develops from a circle to an ellipse) separates the pipe wall from the cement mortar (see Figure 10), resulting in a decrease in the ultimate bearing capacity of the pipe roof; When the grouting incompleteness is 10%–20%, the M-u_m curves has a strengthening section after the descending section, and the possible reason for this section is that the steel pipe is in contact with the upper surface of cement mortar after the flattening deformation when the grouting incompleteness is small, resulting in an improvement of the ultimate bearing capacity of the pipe roof instead. The M-u_m curves of the grouting pipe roof at 0%–5% of grouting incompleteness are shown in Figure 3B, and the curves can be divided into elastic section, elastic-plastic section and strengthening section. Compared with the case of 10%–100% of grouting incompleteness, the curves do not have an obvious descending section and the peak value is improved, indicating that the lower the grouting incompleteness, the higher the ultimate bearing capacity and the better the ductility of the pipe roof.

FIGURE 3

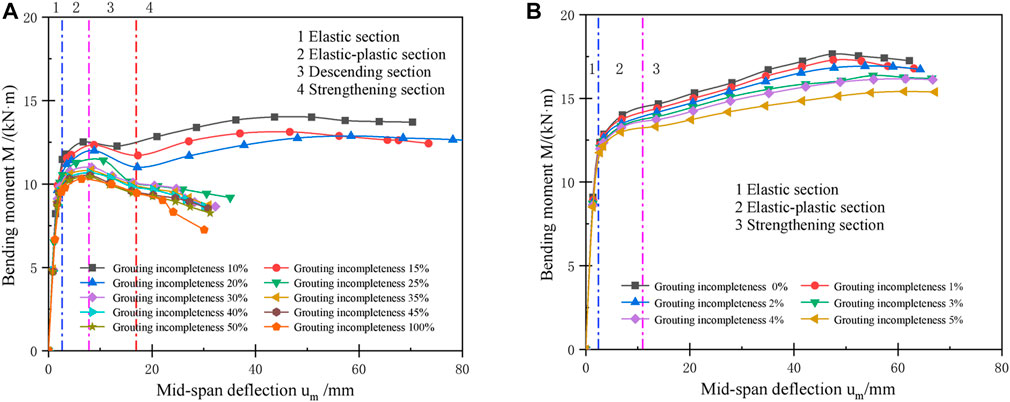
FIGURE 3. Bending moment—mid-span deflection curve of grouting pipe roof (A) Grouting incompleteness 10%–100%; and (B) Grouting incompleteness 0%–5%.

3.1.2 Pipe roof with reinforcement bundles

The M-u_m (bending moment—mid-span deflection) curves of the pipe roof with reinforcement bundles under bending load are shown in Figure 4. The M-u_m curves of this type of pipe roof as are shown in Figure 4A, and the curve pattern is similar to that of the grouting pipe roof. Compared with the grouting pipe roof, the ultimate bending moment of such pipe roof is improved and the slope of the descending section of the M-u_m curves is reduced under the same grouting incompleteness. The M-u_m curves of such pipe roof at 0%–5% of grouting incompleteness are shown in Figure 4B. Likewise, the curve pattern is similar and the ultimate bending moment is improved compared with the grouting pipe roof. This indicates that the addition of reinforcement bundles in the pipe roof can improve its ultimate bearing capacity and enhance its ductility.

FIGURE 4

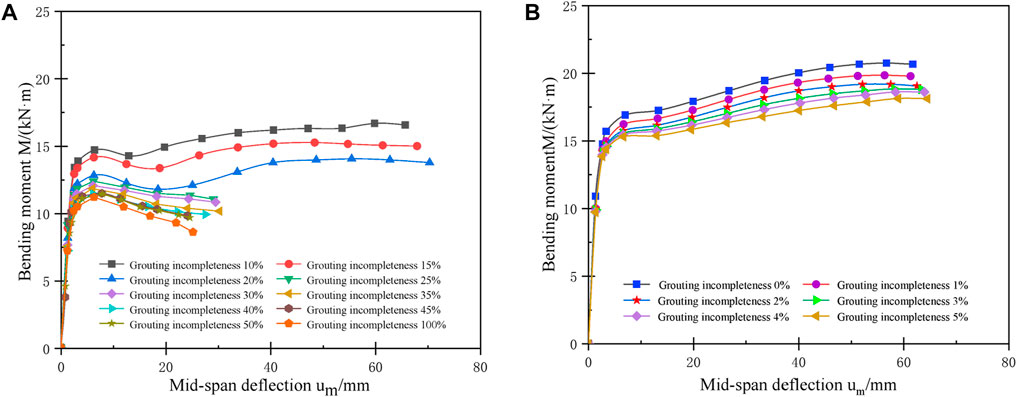
FIGURE 4. Bending moment—mid-span deflection curve of pipe roof with reinforcement bundles (A) Grouting incompleteness 10%–100%; and (B) Grouting incompleteness 0%–5%.

3.1.3 Pipe roof with casing pipe

The M-u_m (bending moment—mid-span deflection) curves of the pipe roof with casing pipe under bending load are shown in Figure 5. The M-u_m curves of the reinforcement bundles pipe roof at the grouting incompleteness of 10%–100% and 0%–5% are shown in Figures 5A,B respectively, and the curve pattern is similar to that of the grouting pipe roof and pipe roof with reinforcement bundles. Compared with the two types of pipe roof mentioned above, the ultimate bending moment of the pipe roof with casing pipe is improved, and the slope of the descending section of the M-u_m curve is slowed down. Moreover, the M-u_m curves of such pipe roof still have a strengthened section when the grouting incompleteness is 25%–50%. This may explain by the fact that the casing pipe has a better supporting effect on the steel pipe after the flattening deformation, which can significantly enhance the ultimate bearing capacity and ductility of the pipe roof.

FIGURE 5

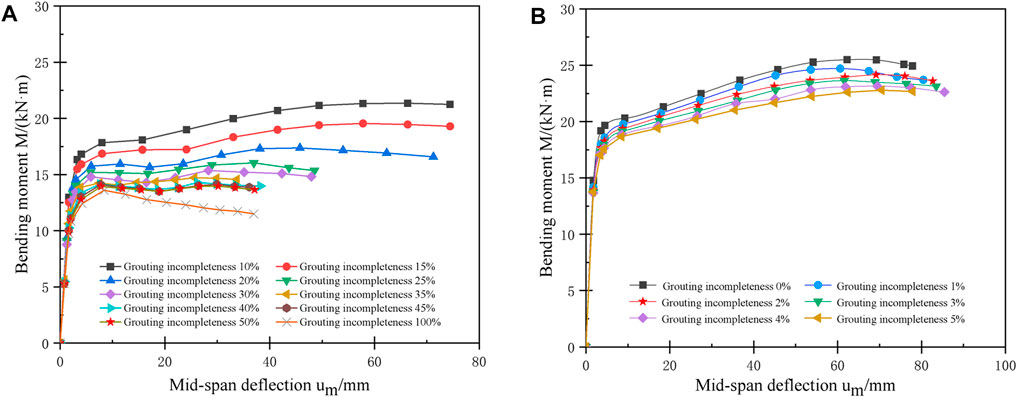
FIGURE 5. Bending moment—mid-span deflection curve of pipe roof with casing pipe (A) Grouting incompleteness 10%–100%; and (B) Grouting incompleteness 0%–5%.

3.1.4 Comprehensive analysis of bending moment-deflection curve

The bending moment—mid-span deflection curves of the three types of pipe roof under full grouting is shown in Figure 6. It can be seen that the M-u_m curve pattern of all the three is basically the same when grouting is full, but the value of the ultimate bending moment is different. The ultimate bending moment is increased by 3.02 kN·m and 7.76 kN·m for pipe roof with reinforcement bundles and pipe roof with casing pipe respectively, and the improvement rate is 17.6% and 44.4%, respectively. The steel used in the reinforcement bundles is 97.3% of the casing pipe, but the strengthening effect on the ultimate bearing capacity of the pipe roof is only 39.6% of the casing pipe. The results show that under the same amount of steel used, adding the casing pipe can better improve the ultimate bearing capacity of the pipe roof compared with adding the reinforcement bundles, and the improvement effect is more significant.

FIGURE 6

FIGURE 6. Bending moment—mid-span deflection curve of three types of pipe roof under full grouting.

3.2 Analysis of ultimate bearing capacity

3.2.1 Ultimate bearing capacity coefficient

In order to quantitatively analyze the influence of grouting incompleteness on the ultimate bending moment of the pipe roof, the ratio of the ultimate bending moment of the pipe roof when the grouting is not full and when the grouting is full is defined as MI, namely the ultimate bearing capacity coefficient of the pipe roof.

The MI-X (ultimate bearing capacity coefficient-grouting incompleteness) curve of the three types of pipe roof is shown in Figure 7. It can be seen that the ultimate bearing capacity coefficient of all the three decreases with the increase of grouting incompleteness, and the rate of decrease gradually slows down, and the ultimate bearing capacity of all the three reaches the peak. Specifically, when the grouting incompleteness is 2%, the ultimate bearing capacity of the three (grouting pipe roof, pipe roof with reinforcing bundle and pipe roof with casing pipe) is 95.4%, 94.8%, and 95.2% of that when grouting is full, respectively. When the grouting incompleteness rises to 25%, the ultimate bearing capacity of the three is only 64.7%, 59.6%, and 62.9% of that when grouting is full, respectively, while the ultimate bearing capacity of the three without grouting is only 58.4%, 54%, and 53.4% of that when grouting is full.

FIGURE 7

FIGURE 7. Ultimate bearing capacity coefficient-grouting incompleteness curve of pipe roof.

Due to the construction process and other reasons, it is difficult to achieve 100% grouting stone rate of pipe roof in actual projects, and the grouting is not full from time to time. According to the above analysis, when the grouting incompleteness is only 2%, the ultimate bearing capacity of the three types of pipe roof is reduced by 4.6%, 5.2%, and 4.8%, respectively compared with the full grouting, indicating that the ultimate bearing capacity of the pipe roof decreases slightly at this time; When the grouting incompleteness rises to 25%, the ultimate bearing capacity of the three types of pipe roof decreases by 35.3%, 40.4%, and 37.1% respectively, compared with the full grouting, suggesting that the ultimate bearing capacity of the pipe roof decreases significantly and is improved less than that without grouting.

3.2.2 Pipe roof ultimate bending moment analysis

The M-X (ultimate bending moment-grouting incompleteness) curve of the pipe roof is shown in Figure 8A, and the effect of adding reinforcement (reinforcement bundles, casing pipe) in the pipe roof on the ultimate bending moment at the same grouting incompleteness is shown in Figure 8B. It can be seen that adding reinforcement in the pipe roof has a certain elevation on its ultimate bending moment, and the elevation value differs with different types of reinforcement. The effect is best when the grouting is full and falls sharply when the grouting incompleteness is about 10%, and tends to level off when the grouting incompleteness rises to about 20%. Specifically, when the grouting incompleteness is 0%–10%, the elevated value of the ultimate bending moment is 2.35–3.02 kN m and 7.15–7.76 kN m for adding reinforcement bundles and casing pipe in the pipe roof respectively; When the grouting incompleteness is increased from 10% to 20%, the elevated value is reduced from 2.35 kN m and 7.15 kN m to 1.08 kN m and 4.43 kN m, respectively, with a decrease of 55.9% and 39%; when there is no grouting, the elevated value is 0.86 kN m and 3.25 kN m, respectively.

FIGURE 8

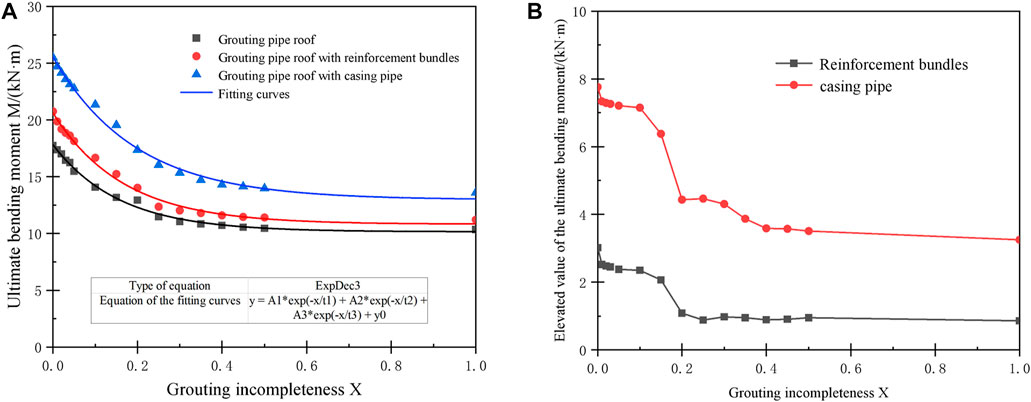
FIGURE 8. (A) Ultimate bending moment-grouting incompleteness curve of pipe roof (B) the influence of adding reinforcement in the pipe roof on the ultimate bending moment.

It is calculated that when the grouting incompleteness is 0%–100%, the elevated value of the ultimate bending moment of the pipe roof with reinforcement bundles and casing pipe is 0.86–3.02 kN m and 3.25–7.76 kN m respectively, and the corresponding increase rate is 7.7%–18.3% and 31.4%–51.6% respectively. The results suggest that when the grouting is not full, the enhancement effect of adding the casing pipe in the pipe roof on the ultimate bending moment is quite greater than that of adding reinforcement bundles.

3.3 Analysis of disengagement rate

The ratio of the circumferential disengagement length between the pipe wall and the cement mortar in the mid-span section of the pipe roof and the initial contact length under the same load is defined as the disengagement rate TI.

The TI-X (disengagement rate-grouting incompleteness) curve for the three types of pipe roof is shown in Figure 9. It can be seen that when the grouting incompleteness is 2%, the corresponding disengagement rate for all the three are around 2%; When the grouting incompleteness is 5%, the disengagement rate of the three (grouting pipe roof, pipe roof with reinforcing bundle and pipe roof with casing pipe) is 35.1%, 25.6%, and 16.9% respectively; When the grouting incompleteness is 30%, the disengagement rate of the three is 73.3%, 71.8%, and 58.7% respectively, and when the grouting incompleteness rises to 50%, the disengagement rate of the three increases to 78.3%, 76.4%, and 69.5%, respectively. This indicates that the disengagement rate of all the three grows with the increase of grouting incompleteness, which grows relatively slowly when the grouting incompleteness is less than 2%, develops rapidly when the grouting incompleteness is 2%–30%, and tends to level off when the grouting incompleteness is greater than 30%. Additionally, under the same grouting incompleteness, adding reinforcement bundles and casing pipe in the pipe roof can effectively reduce its disengagement rate and the latter has better effect, and the disengagement rate is 62.8%–97.9% and 29.1%–91.9% of the grouting pipe roof respectively.

FIGURE 9

FIGURE 9. Disengagement rate-grouting incompleteness curve of pipe roof.

Figure 10 shows the damage form of the pipe roof with reinforcement bundles when the grouting incompleteness is 20%. The overall deformation of the pipe shed is “V” shaped (shown in Figure 10A), and the flattening deformation of the steel pipe near the sections on both sides of the support (shown in Figure 10C, Figures 10E), the disengagement rate and disengagement distance between the steel pipe wall and the mortar on both sides are smaller than that of the mid-span section (shown in Figures 10D).

FIGURE 10

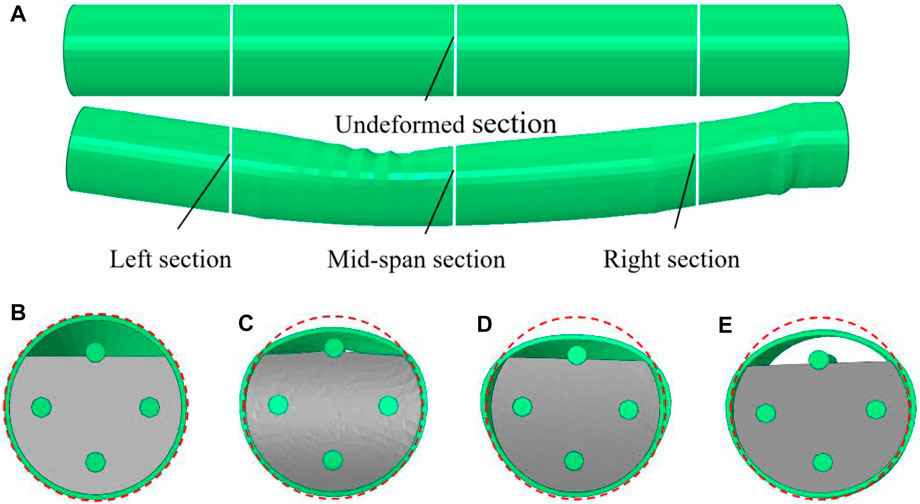
FIGURE 10. Damage form of the pipe roof with reinforcement bundles at 20% grouting incompleteness (A) Before and after deformation of the pipe roof (B) Undeformed section (C) Left section (D) Mid-span section; and (E) Right section.

3.4 Analysis of deflection curve

Figure 11 shows the distribution of deflection along the length of the component during the loading process for the three types of pipe roof when the grouting is full, respectively. The abscissa coordinates in the figure are the distance between the points of the component and the left end support, namely, the effective length L₀, and the ordinate coordinates are the deflection values u_m at different locations during the loading process of the component. The solid line is the u_m-L₀ curve obtained from numerical calculation, and the dashed line is the sine curve. The results show that the deflection curves of the three types of pipe roof are in good agreement with the sine curve.

FIGURE 11

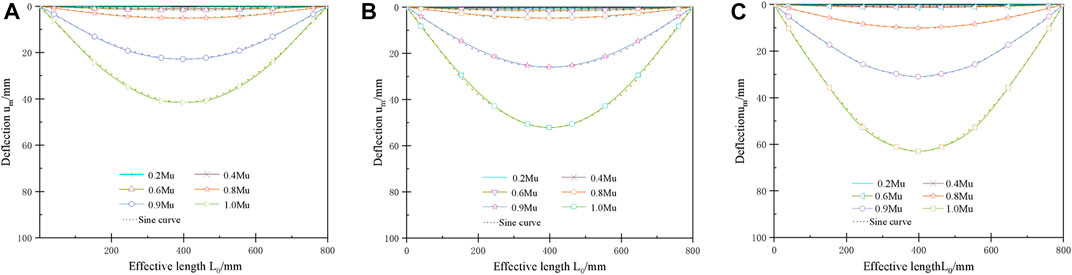
FIGURE 11. Deflection curves of three types of pipe roof (A) Grouting pipe roof (B) Grouting pipe roof with reinforcement bundles; and (C) pipe roof with casing pipe.

4 Comparative analysis

4.1 Comparison with test results

To further demonstrate the correctness of the numerical calculation results, the calculation results were compared with the previous model test, the test site was shown in Figure 12. The numerical calculation conditions are consistent with the model test materials and dimensions, and the test measurement point arrangement, detailed scheme and test process are described in the reference (Min, 2018). The ultimate bearing capacity derived from the model test and other scholars’ research was compared with the numerical results of this paper as follows.

FIGURE 12

FIGURE 12. Field test.

The change curves of the ultimate bending moment of three types of pipe roof specimens (models) are shown in Figure 13A. The abscissa coordinates are different types of pipe roof, and the ordinate coordinates are the improvement rate of ultimate bending moment of the three compared with grouting pipe roof when the grouting is full. The test results reveal that the ultimate bending moment of pipe roof specimens with reinforcement bundles and casing pipe is increased by 20.5% and 35% compared with that of grouting pipe roof specimens, respectively, and the amount of steel used for reinforcement bundles is 97.3% of that of the casing pipe, while the strengthening effect on the ultimate bearing capacity of pipe roof is only 58.6% of that of the casing pipe. Comparing the test and numerical ultimate bending moment curves, we can see that the two are in good agreement, and the slight deviation may be due to the slight error of the test results caused by the defects of the steel pipe, and the maximum deflection deformation of the test is smaller than that of the numerical simulation in order to prevent damage to the instrument.

FIGURE 13

FIGURE 13. (A) Variation curve of ultimate bending moment of pipe roof specimens (models) (B) Curve of ultimate bearing capacity coefficient—grouting incompleteness of grouting pipe roof specimens (models).

The comparison of MI-X (ultimate bearing capacity coefficient—grouting incompleteness) curve for the grouting pipe roof specimens (models) is shown in Figure 13B. The test results indicate that the ultimate bending moment of the pipe roof grouting as incompleteness of 10%, 20% and 50% is 79.4%, 70.6%, and 58.8% of that at the full grouting, respectively. As can be seen from Figure 13 (right), the numerical results are in good agreement with the experimental results, validating the applicability and rationality of the numerical model in this paper.

4.2 Comparison with other scholars’ research

Figure 14 shows the comparison of M-u_m (bending moment—mid-span deflection) curves between the grouting pipe roof in this paper and the concrete-filled steel tube in the reference (Mao, 2019; Zhang et al., 2020) when the grouting is full. Both the reference (Mao, 2019; Zhang et al., 2020) and the research in this paper use the Q235 steel pipe, and the strength and elastic modulus of the grouting material inside the tube of both are also close to those in this paper. As shown in Figure 14, the difference in the ultimate bending moment value is attributed to the fact that the steel pipe diameter and length used in this paper are at variance that used in the reference (Mao, 2019; Zhang et al., 2020) test (numerical). Moreover, the numerical simulation results in this paper are in good agreement with the law obtained in reference (Zhang et al., 2020), but while there is a gap with the reference (Mao, 2019). This is due to the fact that the steel tubes used in this paper and reference (Zhang et al., 2020) are stainless steel tubes that have significant strain strengthening properties compared with ordinary steel tubes.

FIGURE 14

FIGURE 14. Comparison of bending moment—mid-span deflection curve.

Figure 15 shows the MI-X (ultimate bearing capacity coefficient—grouting incompleteness) curve of the grouting pipe roof in this paper compared with the concrete-filled steel tube in the reference (Mao, 2019). The numerical results of reference (Mao, 2019) suggest that the ultimate bearing capacity of the concrete-filled steel tube at 2.7%, 4.4%, 6%, and 7.5% of grouted incompleteness is 92.5%, 89.9%, 89.4%, and 86.8% of that at full grouting, respectively. As can be seen from Figure 15, the data fitting curve of the reference (Mao, 2019) is more consistent with the MI-X curve in this paper, laterally verifying the high feasibility of the numerical model in this paper.

FIGURE 15

FIGURE 15. Comparison of ultimate bearing capacity coefficient—grouting incompleteness curve.

5 Conclusion

In this study, the numerical simulations of pure bending loads for three types of pipe roof under 16 working conditions of grouting incompleteness were carried out, and the numerical results obtained were analyzed comparing with the model tests and other scholars’ research. The following conclusions can be drawn.

1) The ultimate bearing capacity of the grouting pipe roof, pipe roof with reinforcement bundles, pipe roof with casing pipe all decreases with the rise of grouting incompleteness. When the grouting incompleteness is only 2%, the ultimate bearing capacity decreases less than that of full grouting, decreasing by 4.6%, 5.2%, and 4.8% respectively; When the grouting incompleteness rises to 25%, the ultimate bearing capacity decreases significantly than that of full grouting, decreasing by 35.3%, 40.4%, and 37.1% respectively, and the ultimate bearing capacity of the pipe roof is rather close to that without grouting.

2) When the grouting is full, the ultimate bearing capacity of the pipe roof can be increased by 17.6% and 44.4% by adding reinforcement bundles and casing pipe respectively, and increased by 7.7%–18.3% and 31.4%–51.6% respectively when the grouting is not full.

3) The disengagement rate of all the three categories of pipe roofs with the increase of grouting incompleteness. Under the same grouting incompleteness, adding reinforcement bundles and casing pipe in the pipe roof can effectively reduce its disengagement rate and the latter has better effect, and the disengagement rate is 62.8%–97.9% and 29.1%–91.9% of that of the grouting pipe roof when the grouting incompleteness is 0%–50% respectively.

4) The numerical simulation results are in good agreement with the experimental results and the research results of other scholars, indicating that the numerical simulation in this study is highly feasible and has an excellent reference value for engineering practice.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YS and MH: Conceptualization, resources, supervision, methodology, funding acquisition and writing- original draft. TZ and XC: Software, writing-original draft, visualization and data curation. YZ, SM, and YJ: Project administration, supervision and writing—review and editing.

Funding

This study was supported by funding from the National Natural Science Foundation of China (Grant No. 42177162) and the Natural Science Foundation of Jiangxi Province of China (20212BAB214009).

Conflict of interest

YS was employed by the Jiangxi Architectural Design Institute Co., Ltd. SM was employed by the China Railway Xi’an Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abed, F., AlHamaydeh, M., and Abdalla, S. (2012). Experimental and numerical investigations of the compressive behavior of concrete filled steel tubes (CFSTs). J. Constr. Steel Res. 80, 429–439. doi:10.1016/j.jcsr.2012.10.005

CrossRef Full Text | Google Scholar

Chang, L., and Chen, J. (2007). Experimental research of the principal structure relationship of cement mortar under uniaxial compression. ShuiLi XueBao (02), 217–220. doi:10.3321/j.issn:0559-9350.2007.02.014

CrossRef Full Text | Google Scholar

Geng, D., Min, S., Shi, Y., Guo, J., and Wang, J. (2019). Research on the effect of pipe reinforcement or casing on mechanical properties of pipe shed. Chin. J. Undergr. Space Eng. 15 (2), 625–632. CNKI: SUN: BASE.0.2019-S2-018.

Google Scholar

Geng, D., Shi, Y., Yang, J., and Yang, F. (2016). Research on forepoling force of long and large pipe roof for shallow tunnel large section under existing highway. J. Huazhong Univ. Sci.& Tech. Nat. Sci. Ed. 44 (06), 98–103. doi:10.13245/j.hust.160618

CrossRef Full Text | Google Scholar

Gou, D., Yang, J., and Zhang, G. (2007). Deformation monitoring and mechanical behaviors of pipe-roof in shallow tunnels. Chin. J. Rock Mech. Eng. 26 (6), 1258–1264. doi:10.3321/j.issn:1000-6915.2007.06.023

CrossRef Full Text | Google Scholar

Li, J. (2008). Synthetical treatment technique for extraordinary collapse of highway shallow tunnel. Chin. J. Undergr. Space Eng. 4 (3), 591–594. doi:10.3969/j.issn.1673-0836.2008.03.038

CrossRef Full Text | Google Scholar

Li, R., Wang, S., Wang, J., Zhang, D., Chen, P., Pan, H., et al. (2022). Mechanical behaviors and supporting effect evaluation of pipe roof in tunneling engineering considering micro-arch effect. Chin. J. Geotechnical Eng., 1–11. Available at: https://kns.cnki.net/kcms/detail/32.1124.TU.20220415.1753.011.html.

Google Scholar

Liu, M., Han, B., and Duo, J. (2019). Investigation on the effect of interface imperfection on the flexural behaviors of concrete filled steel tubular bending members. China Civ. Eng. J. 52 (06), 55–66. CNKI: SUN: TMGC.0.2019-06-006.

Google Scholar

Mao, S. (2019). The study on mechanical properties of concrete filled steel tubular member with separation. Shenyang, China: Shenyang University of Technology. Available at: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=1019046647.nh&DbName=CMFD2019.

Google Scholar

Min, S. (2018). The refined numerical simulation study on bearing characteristics of tunnel pipe shed. Nanchang, China: East China Jiaotong University. CNKI: CDMD:2.1018.819001.

Google Scholar

Miwa, M., and Ogasawara, M. (2005). Tunnelling through an embankment using all ground fasten method. Tunn. Undergr. Space Technol. 20 (2), 121–127. doi:10.1016/j.tust.2003.12.001

CrossRef Full Text | Google Scholar

Musso, G. (1979). Jacked pipe provides roof for underground construction in busy urban area. Civ. Eng. doi:10.1016/0360-1323(79)90007-6

CrossRef Full Text | Google Scholar

Rao, W. (2008). Application and analysis of forepoling and large-section box culvert jacking for underpass highway construction. China Civ. Eng. J. 41 (4), 106–111. doi:10.3321/j.issn:1000-131X.2008.04.017

CrossRef Full Text | Google Scholar

Shi, Y., Guo, J., Geng, D., and Min, S. (2019). Experimental research on effect of grouting plumpness on mechanical properties of tunnel pipe roof. J. Railw. Sci. Eng. 16 (07), 1735–1742. doi:10.19713/j.cnki.43-1423/u.2019.07.018

CrossRef Full Text | Google Scholar

Singh, B., Viladkar, M. N., Samadhiya, N. K., and Sandeep, (1995). A semi-empirical method for the design of support systems in underground openings. Tunn. Undergr. Space Technol. 10 (3), 375–383. doi:10.1016/0886-7798(95)00016-R

CrossRef Full Text | Google Scholar

Su, J., and Wang, T. (2021). Finite element analysis of pipe shed pre-supporting reinforcement effect on A shallow-buried tunnel. IOP Conf. Ser. Earth Environ. Sci. 760 (1), 012059. doi:10.1088/1755-1315/760/1/012059

CrossRef Full Text | Google Scholar

Wang, H., Jia, J., and Yu, S. (2010). Mechanical behavior and parameter optimization of pipe roof reinforcement applied in tunnel. China J. Highw. Transp. 23 (4), 78–83. doi:10.19721/j.cnki.1001-7372.2010.04.013

CrossRef Full Text | Google Scholar

Wang, M. (2004). Development of tunnel and underground space in 21th century in China. J. Railw. Sci. Eng. 1 (1), 7–9. doi:10.19713/j.cnki.43-1423/u.2004.01.002

CrossRef Full Text | Google Scholar

Xia, C., Gong, J., Chen, Y., and Jiang, K. (2008). Analysis of ground settlements of overlength pipe and box culvert advancing under airport taxiway. Chin. J. Rock Mech. Eng. 27 (4), 696–703. doi:10.3724/SP.J.1001.2008.01274

CrossRef Full Text | Google Scholar

Ye, Y. (2001). Effect of concrete debonding on the performance of medium and low length columns of steel pipe concrete. Railw. Eng. (10), 2–5. doi:10.3969/j.issn.1003-1995.2001.10.001

CrossRef Full Text | Google Scholar

Ye, Y., Guhua, L., Shaowei, P., Yanke, Y., Dengfu, S., and Zhijian, C. (2003). Study on the performance of steel pipe concrete after secondary grouting. Highway (8), 81–84. CNKI: SUN: GLGL.0.2003-S1-025.

Google Scholar

Ye, Y., Zhihong, W., and Shaowei, P. (2004). Experimental research on separation of concrete-filled steel tube and effect of pouring pulp. J. Southwest Jiaot. Univ. 39 (3), 381–384. doi:10.3969/j.issn.0258-2724.2004.03.026

CrossRef Full Text | Google Scholar

Zhang, W., Liao, F., Hou, C., Ren, Y., Tan, J., and Ren, M. (2020). Effect of fine aggregate type on flexural behavior of concrete-filled stainless steel tubular members under pure bending. Eng. Mech. 38 (10), 200–214. doi:10.6052/j.issn.1000-4750.2020.10.0746

CrossRef Full Text | Google Scholar

Zhuang, Z. (2009). ABAQUS-based finite element analysis and applications. Beijing: Tsinghua University publishing house Co, Ltd.

Google Scholar